Simulation of Natural Convection by Multirelaxation Time Lattice Boltzmann Method in a Triangular Enclosure
Abstract
:1. Introduction
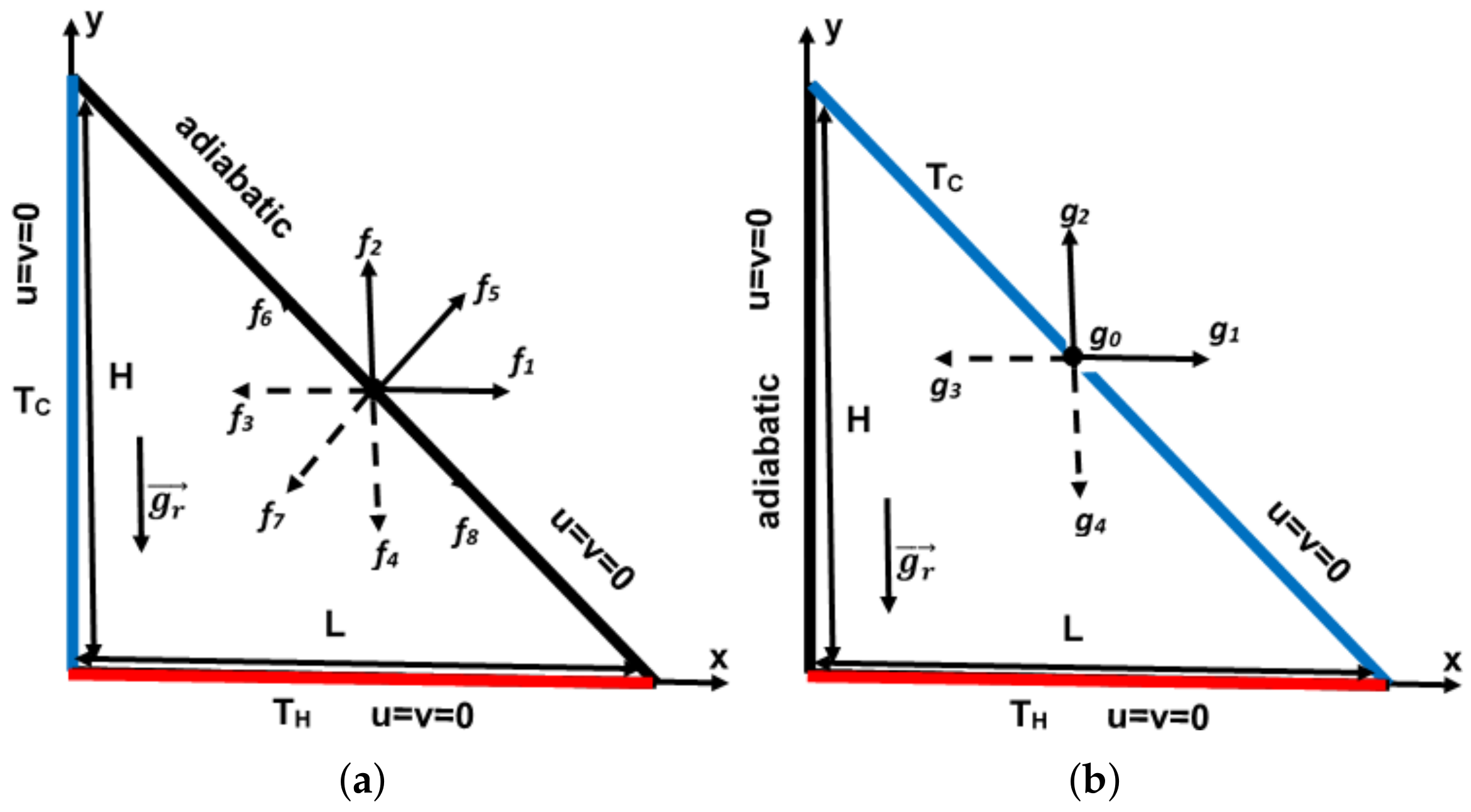
2. Problem Statement
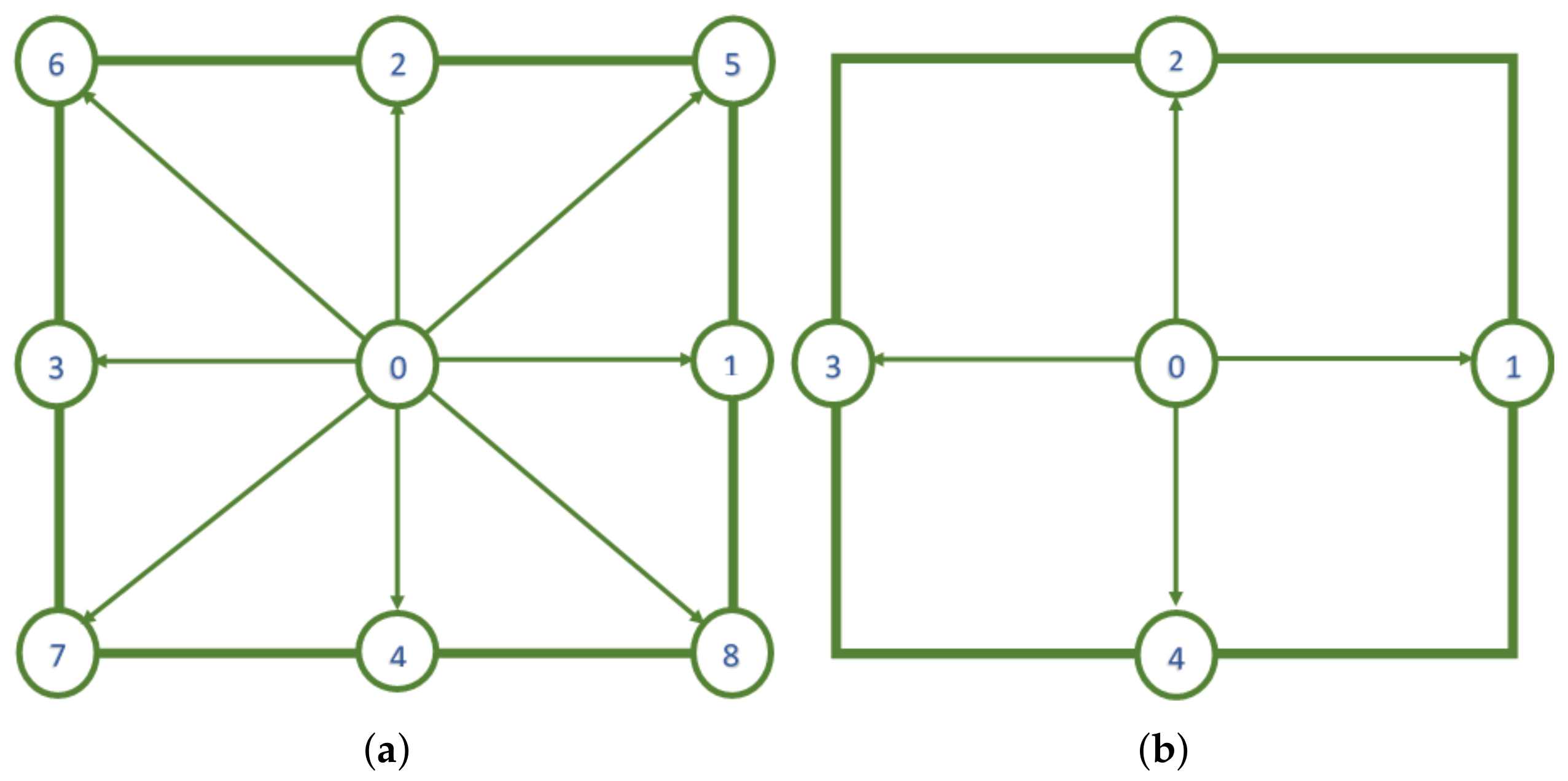
3. Thermal MRT-LBE Model for Fluid Problem
- At the inclined adiabatic wall (case 1), the unknown distribution functions can be determined from the known ones by:
- At the horizontal hot wall (case 1 and 2), the unknown distribution function can be determined from the known ones by:
- At the inclined cold wall (case 2), the unknown distribution functions (see Figure 1b) can be determined from the known ones by:
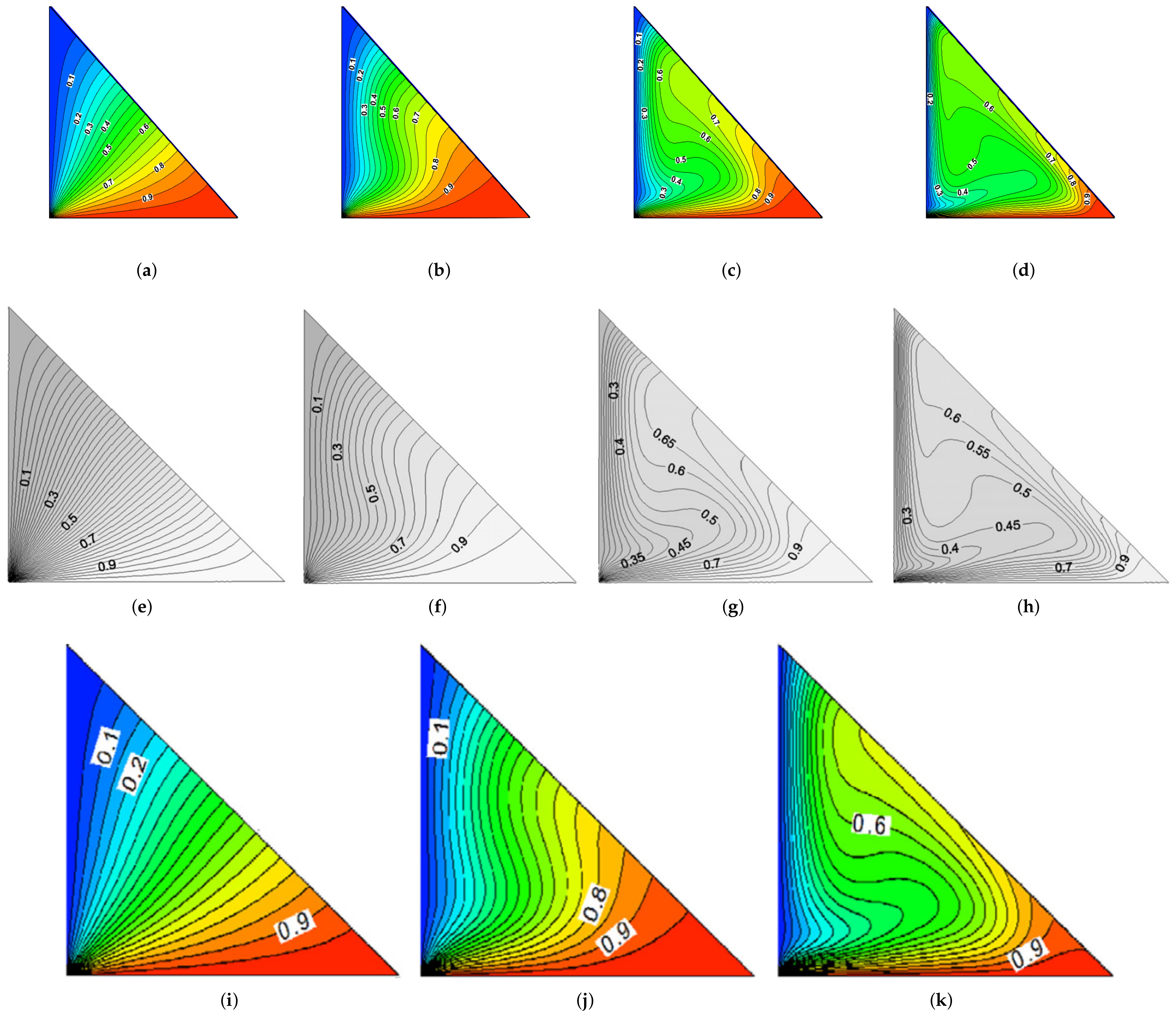
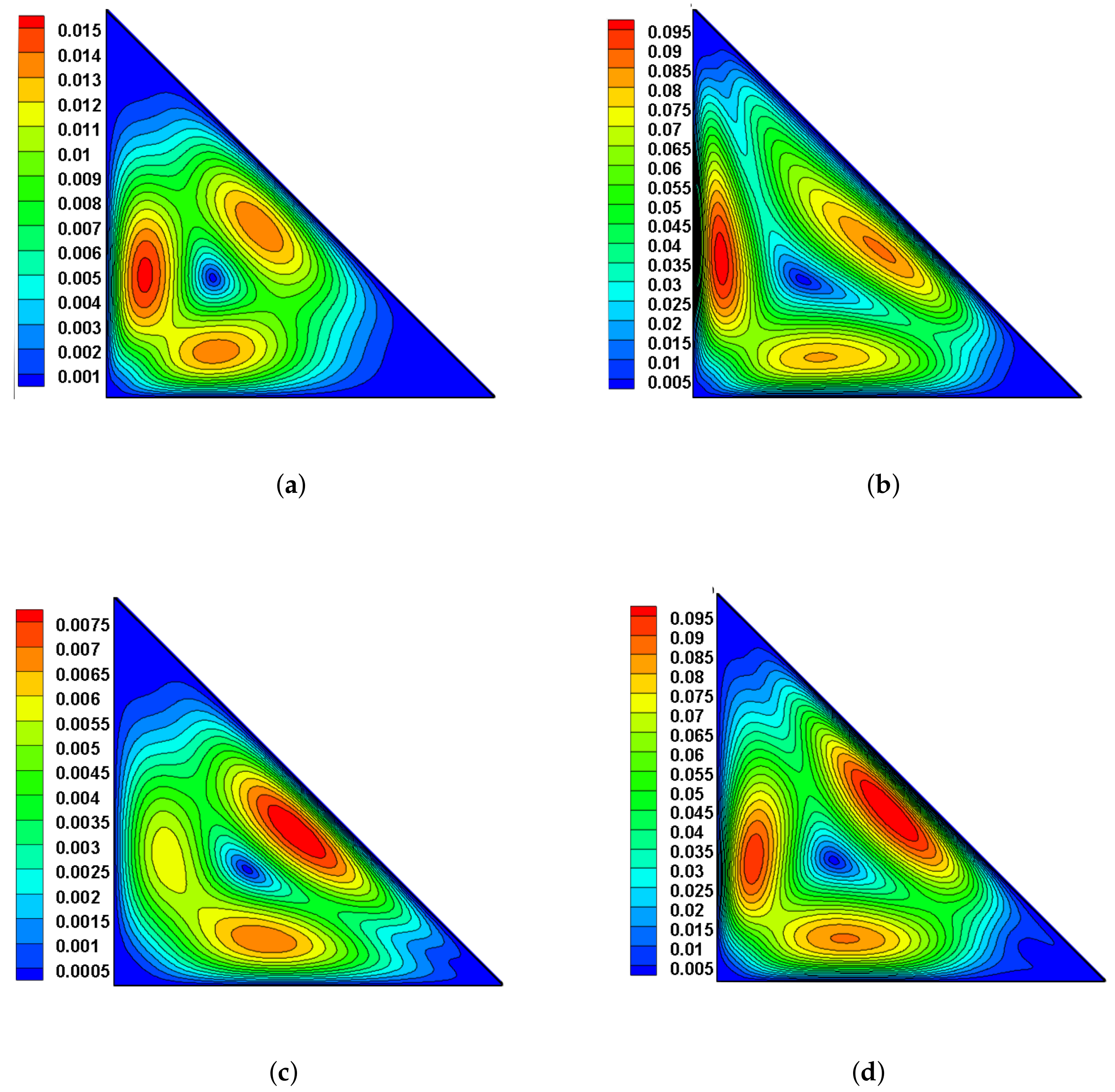
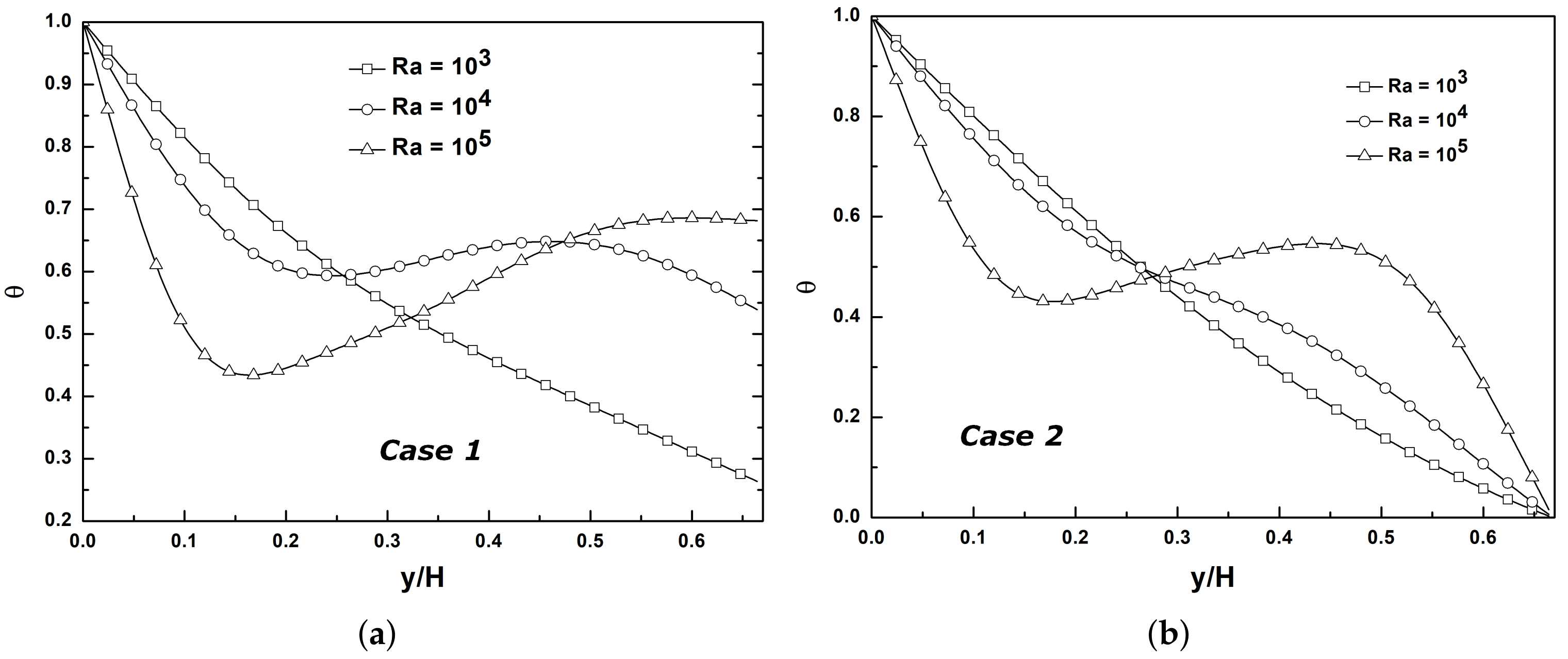
4. Results and Discussion
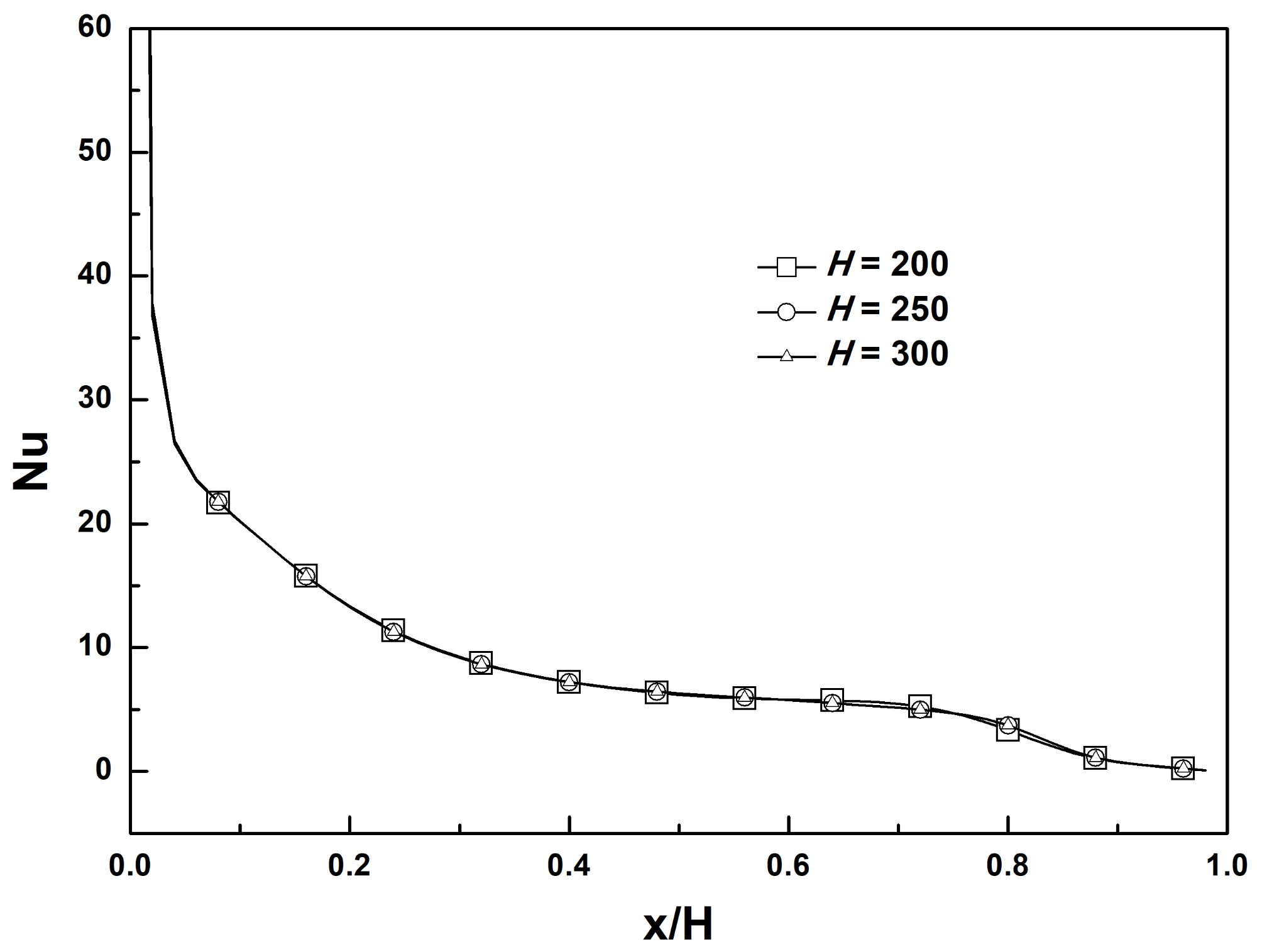
4.1. Mesh Independence Study
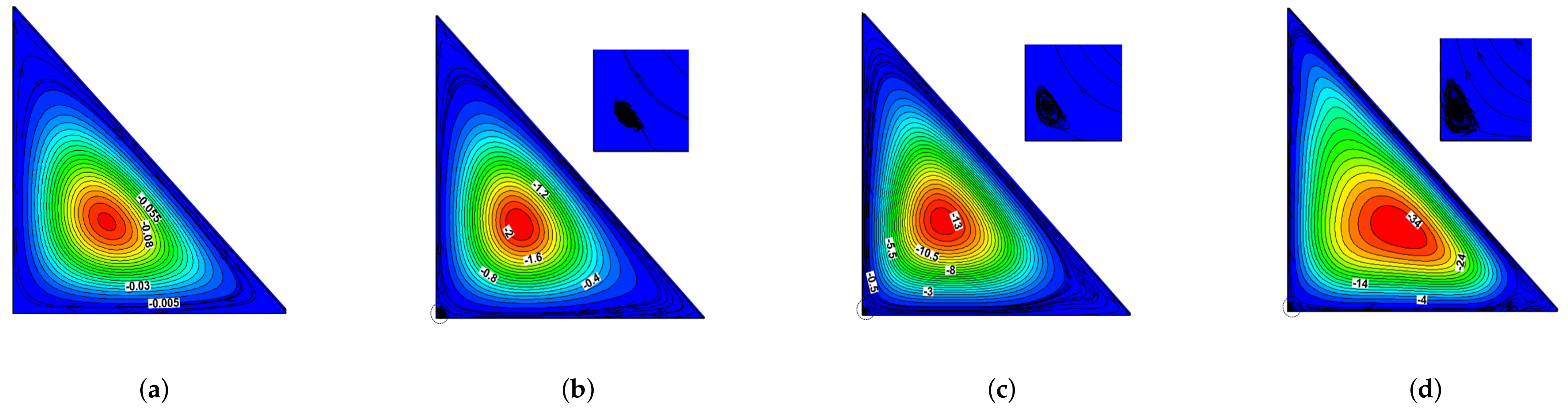
4.2. Validation and Discussion of Flow Properties
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shan, X. Simulation of Rayleigh-Bénard convection using a lattice Boltzmann method. Phys. Rev. E 1997, 55, 2780. [Google Scholar] [CrossRef] [Green Version]
- Sarris, I.E.; Lekakis, I.; Vlachos, N.S. Natural convection in a 2D enclosure with sinusoidal upper wall temperature. Numer. Heat Transf. Part A Appl. 2002, 42, 513–530. [Google Scholar] [CrossRef]
- Tric, E.; Labrosse, G.; Betrouni, M. A first incursion into the 3D structure of natural convection of air in a differentially heated cubic cavity, from accurate numerical solutions. Int. J. Heat Mass Transf. 2000, 43, 4043–4056. [Google Scholar] [CrossRef]
- Peng, Y.; Shu, C.; Chew, Y.T. A 3D incompressible thermal lattice Boltzmann model and its application to simulate natural convection in a cubic cavity. J. Comput. Phys. 2004, 193, 260–274. [Google Scholar] [CrossRef]
- Akinsete, V.A.; Coleman, T.A. Heat transfer by steady laminar free convection in triangular enclosures. Int. J. Heat Mass Transf. 1982, 25, 991–998. [Google Scholar] [CrossRef]
- Asan, H.; Namli, L. Numerical simulation of buoyant flow in a roof of triangular cross-section under winter day boundary conditions. Energy Build. 2001, 33, 753–757. [Google Scholar] [CrossRef]
- Bejan, A. Convection Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Yang, K.T. Natural convection in enclosures. In Handbook of Single-Phase Convective Heat Transfer; Taylor & Francis: Abingdon, UK, 1987. [Google Scholar]
- Hasnaoui, M.; Mansouri, A.E.; Amahmid, A. MRT-LBM simulation of natural convection in a Rayleigh-Benard cavity with linearly varying temperatures on the sides: Application to a micropolar fluid. Front. Heat Mass Transf. 2017, 9. [Google Scholar] [CrossRef] [Green Version]
- Mezrhab, A.; Moussaoui, M.A.; Jami, M. Double MRT thermal lattice Boltzmann method for simulating convective flows. Phys. Lett. A 2010, 374, 3499–3507. [Google Scholar] [CrossRef]
- Hssikou, M.; Elguennouni, Y.; Baliti, J.; Alaoui, M. Heat Transfer of Gas Flow within a Partially Heated or Cooled Square Cavity. Model. Simul. Eng. 2020, 2020, 8886682. [Google Scholar] [CrossRef]
- Hssikou, M.; Elguennouni, Y.; Baliti, J.; Alaoui, M. Lattice Boltzmann method for natural convection in a square cavity with a heated chip. In Proceedings of the International Conference on Intelligent Systems and Advanced Computing Sciences (ISACS), Taza, Morocco, 26–27 December 2019; pp. 1–7. [Google Scholar]
- Basak, T.; Roy, S.; Babu, S.K.; Balakrishnan, A.R. Finite element analysis of natural convection flow in a isosceles triangular enclosure due to uniform and non-uniform heating at the side walls. Int. J. Heat Mass Transf. 2008, 51, 4496–4505. [Google Scholar] [CrossRef]
- Kent, E.F. Numerical analysis of laminar natural convection in isosceles triangular enclosures. Proc. Inst. Mech. Eng. Part D J. Mech. Eng. Sci. 2009, 223, 1157–1169. [Google Scholar] [CrossRef]
- Saleem, K.B.; Alshara, A.K. Natural convection in a triangular cavity filled with air under the effect of external air stream cooling. Heat Transf. Res. 2019, 48, 3186–3213. [Google Scholar] [CrossRef]
- Yesiloz, G.; Orhan, A. Laminar natural convection in right-angled triangular enclosures heated and cooled on adjacent walls. Int. J. Heat Mass Transf. 2013, 60, 365–374. [Google Scholar] [CrossRef]
- Oztop, H.F.; Varol, Y.; Koca, A.; Firat, M. Experimental and numerical analysis of buoyancy-induced flow in inclined triangular enclosures. Int. Commun. Heat Mass Transf. 2012, 39, 1237–1244. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Mejri, I.; Ammar, M.A.; Omri, A. Numerical study of natural convection in an inclined triangular cavity for different thermal boundary conditions: Application of the lattice Boltzmann method. Fluid Dyn. Mater. Process 2013, 9, 353–388. [Google Scholar]
- Mejri, I.; Mahmoudi, A.; Abbassi, M.A.; Omri, A. LBM Simulation of natural convection in an inclined triangular cavity filled with water. Alex. Eng. J. 2016, 55, 1385–1394. [Google Scholar] [CrossRef] [Green Version]
- Ridouane, E.H.; Campo, A.; Hasnaoui, M. Turbulent natural convection in an air-filled isosceles triangular enclosure. Int. J. Heat Fluid Flow 2006, 27, 476–489. [Google Scholar] [CrossRef]
- Koca, A.; Oztop, H.F.; Varol, Y. The effects of Prandtl number on natural convection in triangular enclosures with localized heating from below. Int. Commun. Heat Mass Transf. 2007, 34, 511–519. [Google Scholar] [CrossRef]
- Shahid, H.; Yaqoob, I.; Khan, W.A.; Rafique, A. Mixed convection in an isosceles right triangular lid driven cavity using multi relaxation time lattice Boltzmann method. Int. Commun. Heat Mass Transf. 2021, 128, 105552. [Google Scholar] [CrossRef]
- Rahmati, A.R.; Niazi, S. Application and comparison of different lattice Boltzmann methods on non-uniform meshes for simulation of micro cavity and micro channel flow. Comput. Methods Eng. 2015, 34, 97–118. [Google Scholar] [CrossRef] [Green Version]
- Elguennouni, Y.; Hssikou, M.; Baliti, J.; Alaoui, M. Numerical study of gas microflow within a triangular lid-driven cavity. Adv. Sci. Technol. Eng. Syst. J. 2020, 5, 578–591. [Google Scholar] [CrossRef]
- Mallinson, G.D.; Davis, G.D.V. Three-dimensional natural convection in a box: A numerical study. J. Fluid Mech. 1977, 83, 1–31. [Google Scholar] [CrossRef]
- Mohammed, A.A. Lattice Boltzmann Method: Fundamentals and Engineering Applications with Computer Codes; Springer Nature: London, UK, 2019. [Google Scholar]
- Mezrhab, A.; Jami, M.; Bouzidi, M.; Lallemand, P. Analysis of radiation–natural convection in a divided enclosure using the lattice boltzmann method. Comput. Fluids 2007, 36, 423–434. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]



| H | 150 | 200 | 250 | 300 |
|---|---|---|---|---|
| 32.67627 | 32.79659 | 32.65666 | 32.14074 | |
| 0.64222 | 0.64456 | 0.64215 | 0.64171 |
| -case 1 | Present study | 0.216 | 2.62 | 12.09 | 25.47 |
| Yesiloz et al. [16] | 0.215 | 2.62 | 12.12 | 25.51 | |
| Mejri et al. [19] | 0.23 | 2.57 | 11.70 | ||
| -case 2 | Present study | −0.105 | −2.08 | −13.35 | −27.48 |
| Case 1 | (0.275, 0.31) | (0.278, 0.31) | (0.283, 0.30) | (0.260, 0.31) |
| Case 2 | (0.343, 0.299) | (0.310, 0.309) | (0.302, 0.312) | (0.292, 0.323) |
| Case 1 | 4.60 | 4.88 | 6.83 | 8.03 |
| Case 2 | 7.61 | 7.77 | 9.74 | 11.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baliti, J.; Elguennouni, Y.; Hssikou, M.; Alaoui, M. Simulation of Natural Convection by Multirelaxation Time Lattice Boltzmann Method in a Triangular Enclosure. Fluids 2022, 7, 74. https://doi.org/10.3390/fluids7020074
Baliti J, Elguennouni Y, Hssikou M, Alaoui M. Simulation of Natural Convection by Multirelaxation Time Lattice Boltzmann Method in a Triangular Enclosure. Fluids. 2022; 7(2):74. https://doi.org/10.3390/fluids7020074
Chicago/Turabian StyleBaliti, Jamal, Youssef Elguennouni, Mohamed Hssikou, and Mohammed Alaoui. 2022. "Simulation of Natural Convection by Multirelaxation Time Lattice Boltzmann Method in a Triangular Enclosure" Fluids 7, no. 2: 74. https://doi.org/10.3390/fluids7020074
APA StyleBaliti, J., Elguennouni, Y., Hssikou, M., & Alaoui, M. (2022). Simulation of Natural Convection by Multirelaxation Time Lattice Boltzmann Method in a Triangular Enclosure. Fluids, 7(2), 74. https://doi.org/10.3390/fluids7020074






