1. Introduction
Loop current systems, like the Loop Current in the Gulf of Mexico, which flows between the Yucatan Peninsula and Florida, or the Kuroshio current near the Luzon Strait, between the islands of Luzon and Taiwan, are known to admit at least two fundamental states: gap penetrating and leaping (
Figure 1). Which state the system assumes and when the system will transition between states is a major factor influencing hurricane intensity, offshore energy applications, local fisheries, and regional climate [
1]. Despite decades of scientific inquiry and major field program initiatives, the fundamental question of loop current predictability remains [
1]. Several theories have been proposed to address the underlying physical mechanisms governing transitions between penetrating and leaping states: Farris and Wimbush [
2] related the accumulation of local wind stress exceeding a critical value with transitions from leaping to penetrating states for the Kuroshio. Wind forcing has also been shown to affect the seasonal variation of the Kuroshio Intrusion [
3,
4] including the inertia of the Kuroshio Current upstream of the Luzon Strait [
5,
6,
7]. Metzger and Hurlburt [
8] proposed that mesoscale instabilities cause the Kuroshio penetration to be nondeterministic on long timescales, which is consistent with Yuan et al. [
9] who showed how perturbation from mesoscale eddies influence Kuroshio intrusion variability. Sheremet [
10] considered changes in the inertia of the western boundary current as a major controlling influence on state transitions and was the first to point out the existence of hysteresis in such systems.
This manuscript seeks to extend the original work of Sheremet, who considered an idealized model for a gap-leaping western boundary current. Transitions between penetrating and leaping states were studied as the gap width was varied in a quasi-geostrophic numerical model. When the gap width is sufficiently large, the western boundary current inertia competes with the
-effect in the gap, resulting in leaping and penetrating states with hysteresis. Penetrating-to-leaping transitions occur when the width of the zonal jet flowing into the gap becomes comparable with the gap halfwidth. Leaping-to-penetrating transitions occur when meridional advection balances the
-effect. For sufficiently narrow gaps, there are only direct transitions between leaping and penetrating states (no hysteresis). Sheremet’s results suggest that when analyzing observational data, it is important to take into account the history of parameters in order to interpret loop current state transitions (and not just parameters describing the current state). It should be noted that this is supported qualitatively by the authors of [
2], who related transitions to penetrating states to if local wind stress accumulation exceeded a critical value.
These idealized numerical results have been verified via single-layer model rotating table experiments by Sheremet and Kuehl [
11]. This early confirmation was important as it showed that hysteresis in gap-traversing systems is not a numerical artifact. Kuehl and Sheremet [
12] continued work on the same laboratory model by considering an expanded parameter space. The ranges of flow rates that exhibited hysteresis were studied for different table rotation rates,
, which controls the
-effect in the model. The width of the hysteresis region increased as the rotation rate was increased. The state of the system (penetrating or leaping) was formulated in a two-dimensional phase space as the western boundary current inertia and planetary vorticity varied, which resulted in a mathematical cusp catastrophe surface [
13]. Because of the bifurcation of this surface, it is noted that in such systems transitions from one state to another are a result of the disappearance or turning of a particular solution branch, and not necessarily due to an instability to small-scale perturbations as emphasized by [
14]. Kuehl and Sheremet [
15] further examined hysteresis for a two-layer system to better model more realistic western boundary currents [
16]. The bifurcation set for hysteresis was studied for variable
. Periodic eddy shedding states were studied as well, and it was noted that eddies shed from a periodic state are fundamentally different from eddies shed during a transition event. For strong penetrating flows, Ekman dissipation can no longer balance the vorticity advection and vorticity must be dissipated from the current as westward-traveling eddies, which is consistent with the momentum imbalance paradox of Pichevin and Nof [
17]. Most recently McMahon et al. have extended both the experimental and numerical investigations to include the effects of mean flow through the gap [
18,
19] and applied a Newton iteration solution method to the numerical model which enables identification of unstable loop current states [
20].
Despite the demonstrated resilience of hysteresis to stratification, multiple parameter variations, and mean flow through the gap in the idealized setting, as well as for realistic ocean parameters [
21] including the presence of islands in the gap [
22], eddy forcing [
23,
24,
25], and western boundary current variability [
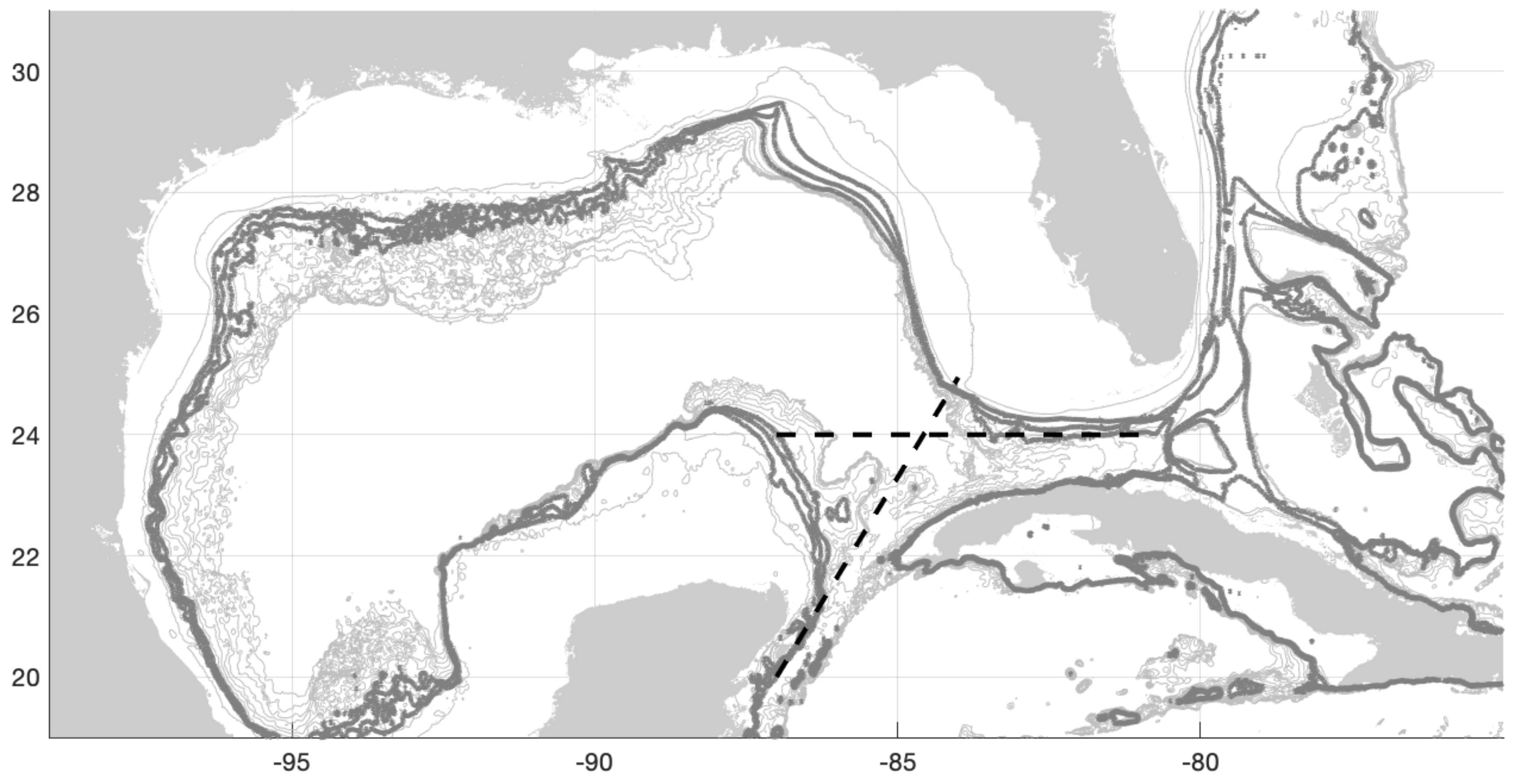
18], the hypothesis has not widely been adopted by the Gulf of Mexico Loop current community. The likely reason for this is the unique geometry of the Gulf of Mexico (
Figure 2). Notice that the Yucatan Peninsula has a zonal “offset” from the southern tip of Florida by about
. Further, the orientation of the boundary current forming along the Yucatan is not parallel to the southern coast of Florida. Instead, the inflowing current makes an approximately
degree angle with the outflowing current (
being straight gap with parallel flow). The goal of this manuscript is to show that hysteresis in such gap-leaping western boundary current systems is robust both to gap angle and gap offset.
2. Numerical Model
The numerical model utilized in this study is a barotropic version of the baroclinic model developed and validated in [
16,
26]. The numerical model was developed to support a series of rotating table laboratory experiments (referenced above). Both the experimental setup and validation of the numerical model have been well-established in the literature, so only a brief summary is provided here. The idealized setup consists of a square tank of width
m with a sloping bottom to induce a topographic
-effect. In
Figure 3, north corresponds to up and east corresponds to right. The flow is driven by a broad Sverdrup interior circulation from the east, which impinges on a north–south oriented vertical ridge, which extends to the surface, where a predominantly inertial western boundary current forms. Note, in the lab and also in the present model study, it is more convenient to consider a southward flowing western boundary current (flowing from top to bottom in the figures), but, due to the north–south invariance of the quasi-geostrophic barotropic equations, this does not present an issue when interpreting our results in the context of northward-flowing oceanic western boundary currents. The ridge is interrupted at its center by a gap with halfwidth
cm, which the western boundary current must negotiate. In the gap region, the western boundary current will either follow geostrophic contours (in this case, constant depth contours) turning into the western basin and forming a loop current or leap directly across the gap. The computations correspond to a mean water depth of
cm, topographic slope of
(where
), and a table rotation rate of
rad/sec (where
).
The nondimensional problem is formulated as the potential vorticity advection–diffusion equation, as in the quasi-geostrophic approximation
where
is the transport function (defined through the Helmholtz decomposition
with
representing Ekman divergence),
is the relative vorticity, and
,
and
is the Ekman depth. The nondimensional parameter
is the relative meridional variation of depth over the basin due to the sloping bottom, and h is the fluid depth. Our laboratory experiments and numerical model allow for small but finite values of
, while the quasi-geostrophic approximation is the limit of infinitely small
. The domain is
,
, with north corresponding to positive y and east corresponding to positive x. The kinematic conditions for solving the elliptic equation are
along all boundaries, except at the eastern boundary
where inflow/outflow is prescribed
, with
varying between 0 and 1. The dynamical conditions are no-slip:
at the western
, eastern
boundaries and along the ridge, and no-stress
at the southern
and northern
boundaries. The “no-slip” is a natural condition of vanishing velocity at a solid boundary. The northern and southern boundaries correspond to the fluid gyre boundaries in the ocean where vorticity and stress are vanishing. In our numerical method, we were restricted by the ridge to be oriented either north–south or diagonally in such a way that the boundary passes through rectangular grid nodes. The values of vorticity at the solid boundaries were calculated assuming the antisymmetry of the tangential velocity component as it was extended outside the fluid domain, which reduces to the formula by Thom [
27] for a straight wall. The vorticity values were different on the different sides of the ridge. The arising parameters
,
with
and
are the nondimensional inertial, Stommel, and Munk boundary layer thicknesses as in the standard theory. Where
is the Sverdrup interior velocity scale,
L is the basin length scale,
is the kinematic viscosity, and
Q is the volume flux. With the viscosity of water
cm
/s, for the cases considered here
,
, and
is varied (typically,
for
cm
/s). The corresponding dimensional values (obtained by multiplication by
L) were
cm,
cm, and
cm, respectively.
The numerical problem is solved using standard finite differences on a rectangular grid dividing the domain into
cells. The parameters
and
represent the dissipative effects, while
characterizes the nonlinearity, the strength of the flow. For small boundary layer Reynolds numbers
, simple explicit iterations with treating the nonlinear terms as perturbations work well, but for the moderate
R the iterations fail to converge [
14]. In this case, Newton’s method has be to employed for finding steady solutions. We consider a state vector
consisting of values at all grid nodes including the boundaries, the size of this vector is
. In a symbolic form, the set of Equation (
1) is represented by
F(
X) = 0. Substituting an initial guess
into Equation (
1) results in the vector of residuals
at each grid node of the same size
M. In order to find the next iteration
that brings residual closer to vanishing
, we need to calculate the Jacobian matrix
(of size
which depends on
) of all first-order partial derivatives of
F with respect to
X and then solve the linear system
The iterations then continue until the residual (standard deviation and pointwise error) vanishes to the machine accuracy,
. It usually took about seven or fewer iteration steps to reach such convergence. The elements of the Jacobian matrix can be calculated analytically by considering the variational problem corresponding to Equation (
1).
where
. The variations of the boundary conditions are trivial. It should be noted that the elements of the Jacobian matrix do not have to be calculated exactly. As long as the iterations converge and the residual
vanishes, we get an exact solution to the original problem (
1). However, in this idealized problem, we do perform exact analytic calculation of the matrix elements. Finite difference approximations result in a sparse banded type of
, and the grids of size up to
can be solved on a computer with 24 GiB of operational memory.
4. Discussion
For the meridional, north–south oriented, ridges without an offset, the mechanism producing the multiple states is intuitively clear: on one hand, the beta-effect (via a potential vorticity gradient across the gap) promotes the boundary current to drift westward and to penetrate through the gap; on the other hand, the meridional advection promotes the current to jump across. Balancing meridional advection and zonal advection against the
-effect lead to two different scaling:
and
(see details in [
10]). Hence, two different sets of critical parameter values at which transitions between penetrating and leaping states occur. This is essentially the root cause of hysteresis in such systems. Furthermore, a cusp bifurcation occurs in the parameter space where the two branches coalesce. The cusp is an invariant feature. If instead of varying the gap width as in [
10], we vary another parameter that promotes the current penetration (in the present case it is the configuration angle or gap offset), we will recover a similar behavior: the range of hysteresis will vary and disappear when the penetration is sufficiently obstructed. In the angled and offset ridges cases, the upstream boundary current may be directed inside the gap thus promoting the intrusion (gap penetration). So the question is, if we increase the inertia (or transport of the boundary current), will it always promote intrusion?
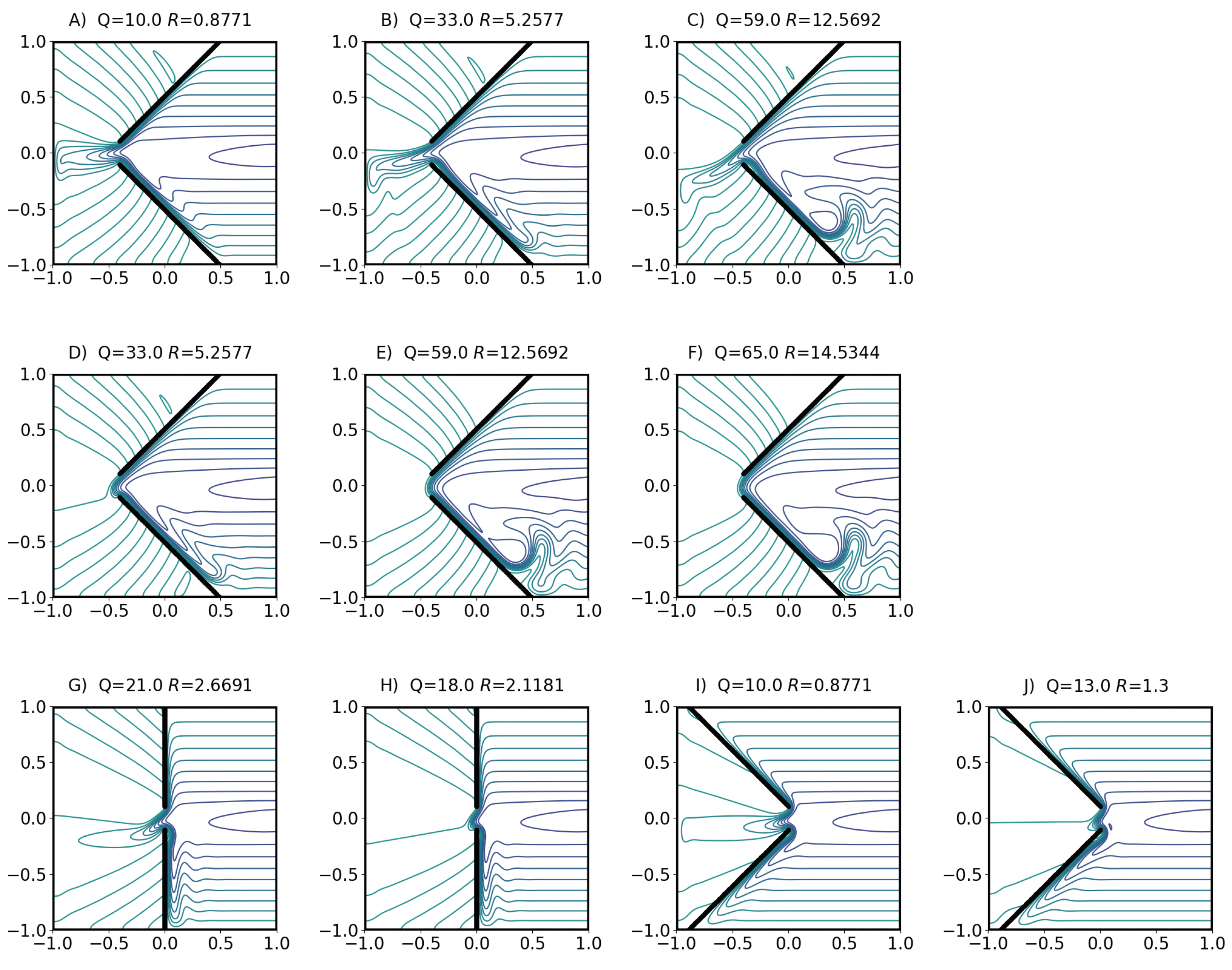
Our previous results (cited above), which are consistent with the findings presented in
Figure 4 and
Figure 5, have shown that as the width scale of the boundary current, which is a combination of
,
, and dominantly
, exceeds the gap halfwidth,
, the current ultimately switches to the gap-leaping regime. This apparent contradiction is most easily explained by considering the offset gap results (
Figure 5). Increasing the gap offset,
, with the jet pointing inside the gap (positive offset) will delay this transition compared to the zero offset case, but not prohibit a leaping state. Once the boundary current length scale exceeds the gap halfwidth, a transition occurs. Essentially, as the inertia of the current increases, the boundary layer length scale grows to a point where the current will not be able to squeeze through the gap, and a leaping state will result.
Note the quadratic trend of the leaping to penetrating transitions (
Figure 6 upward facing triangles, quadratic trend given by solid curve). The transition condition for a straight gap (
) scales as the boundary layer length scale becoming comparable to
. In the case of offset gaps, it is not just the gap halfwidth but also the gap offset must also be accounted. The boundary layers considered are primarily inertial with
. Thus, relative to the straight gap case, we would expect to see a quadratic dependence of critical boundary current transport as a function of
. This is emphasized by the right panel which shows a near-linear dependence of
, where
is the inertial length scale at transition for
. Interestingly, the trend for the penetrating to leaping transition behaves similarly.
This also emphasizes the importance of the parameter
to the penetrating to leaping transition. Or more completely, the ratio of the boundary layer length scale to the gap halfwidth, which is a combination of the Stommel, Munk, and inertial length scale. For typical Gulf of Mexico parameters, the inertial length scale is about 60 km, the Munk length scale is about 30 km, and the Stommel length scale is smaller yet. Thus, typical boundary current length scales would be on the order of 90–100 km. It is also observed that the effective gap halfwidth, between Yucatan and the west Florida shelf, is approximately 150 km. As expected, this puts the Gulf of Mexico Loop Current into a boundary length scale to gap halfwidth ratio parameter regime of around 0.6–0.7, which is consistent with our numerical parameter space. Further, recent results from consideration of realistic Gulf of Mexico topography [
20], suggest the Gulf typically operates in an
R = 5–15 parameter space, also in agreement with our findings.
The results presented in this manuscript are intended to break the stigma that hysteresis in gap-leaping western boundary current systems only occurs for special geometries (straight gaps with zero offset). Indeed, we have explicitly shown that both angled and offset gap geometries exhibit multiple states and hysteresis. The key insight emphasized in this work is that the more the upstream current is directed into the gap due to geometrical configuration (angled or offset gaps), the more distinct the penetrating and leaping flow patterns are, and the bigger the range of hysteresis in the system is. It should also be noted that the methods utilized in this manuscript have recently been applied to the full-scale Gulf of Mexico [
20]. It was found that a barotropic approximation to the upper-layer circulation in the Gulf of Mexico (at full-scale, with a realistic oceanic parameter regime, and for realistic topography similar to
Figure 2) displays hysteresis and multiple steady states. Which, given the above results, should be expected.