Single Contaminated Drops Falling through Stagnant Liquid at Low Reynolds Numbers
Abstract
1. Introduction
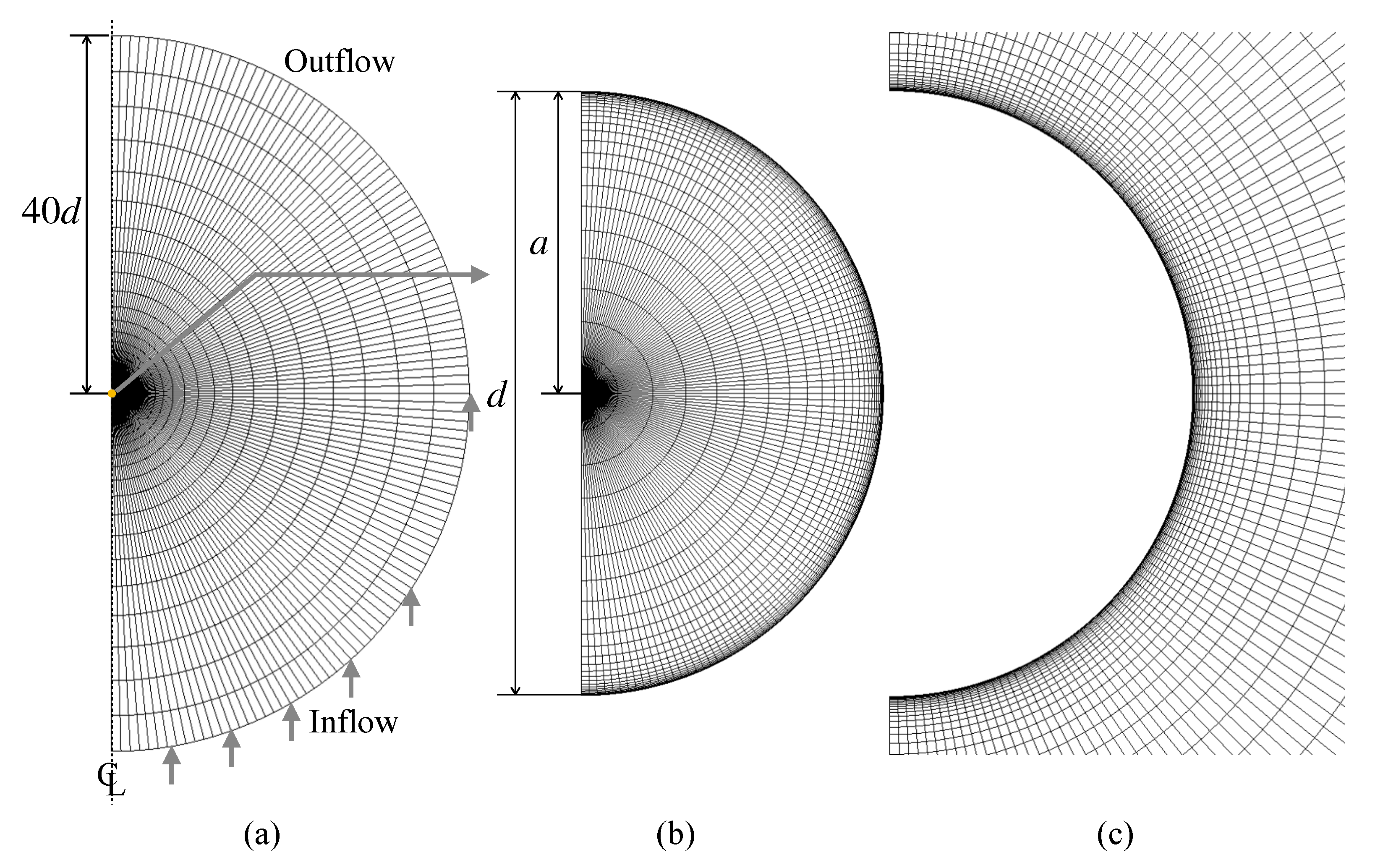
2. Numerical Method
2.1. Governing Equations
2.2. Discretization Schemes
2.2.1. Velocity-Pressure Coupling
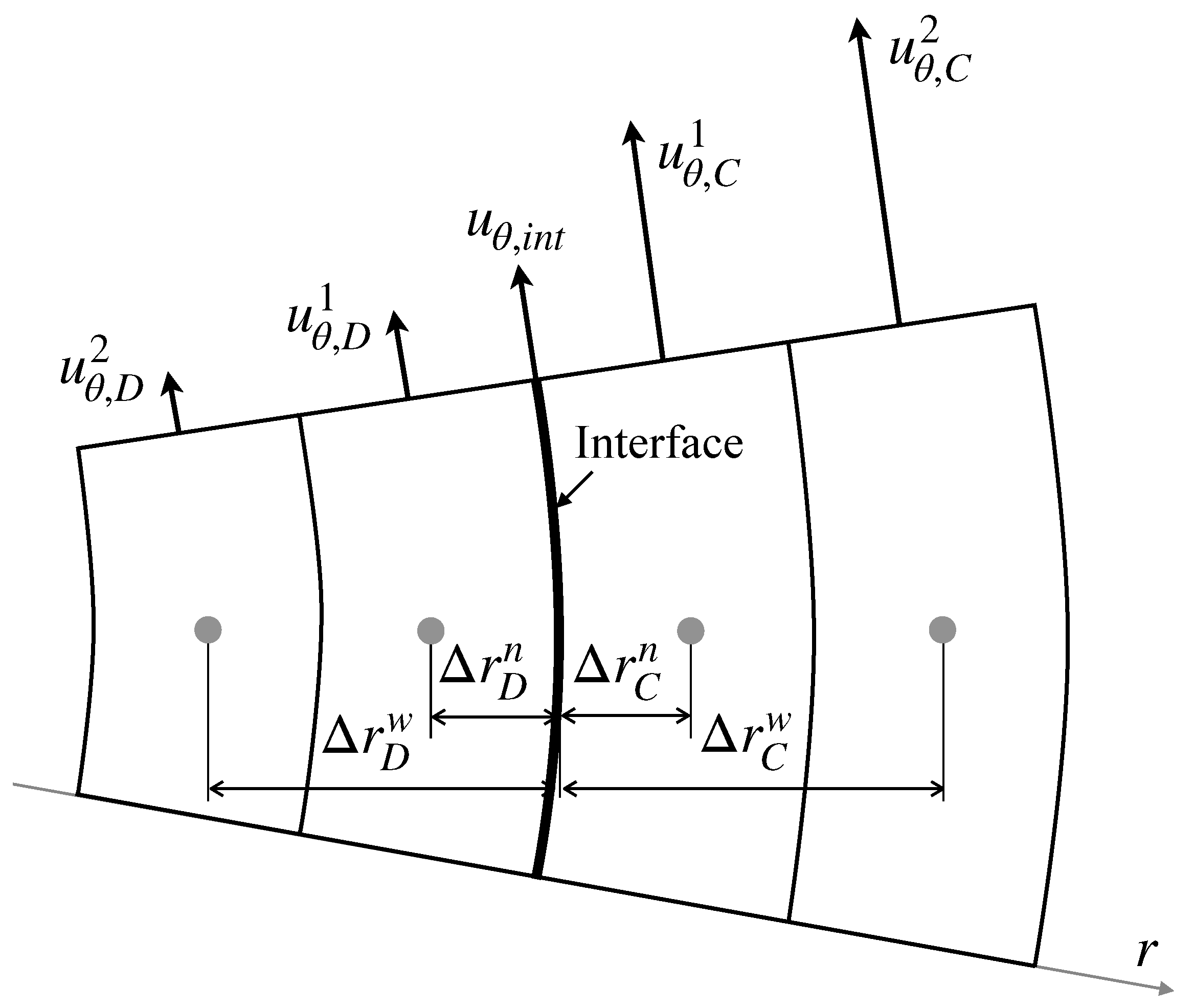
2.2.2. Interface Velocity and Numerical Treatment at Pole
2.2.3. Surfactant Transport Equations
2.2.4. Solution Procedure
- Set the dimensionless groups (, , , , , , , , K and ); generate computational grids inside and outside the drop; and set the initial conditions for each field variable.
- Evaluate the Marangoni stress, , and set the interface velocity, , using the boundary condition (Equation (35)).
- Solve the Poisson equation, Equation (30), to obtain .
- Update the interface velocity, , for .
- Compute the surfactant concentration, , at the interface using Equation (40) with .
- Set the boundary condition of at the interface, Equation (18), with .
- Return to Step 2.
3. Validation of Numerical Method
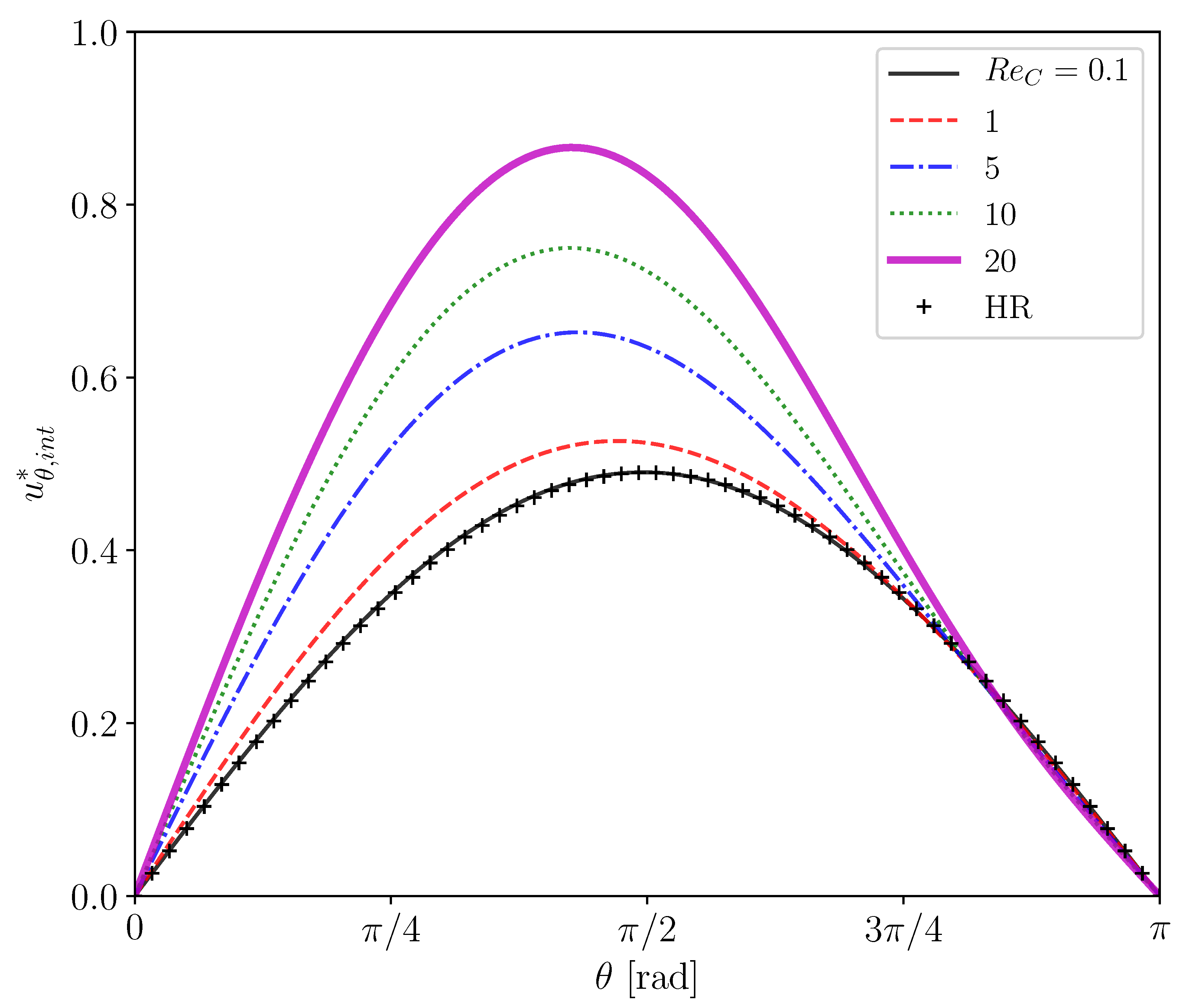
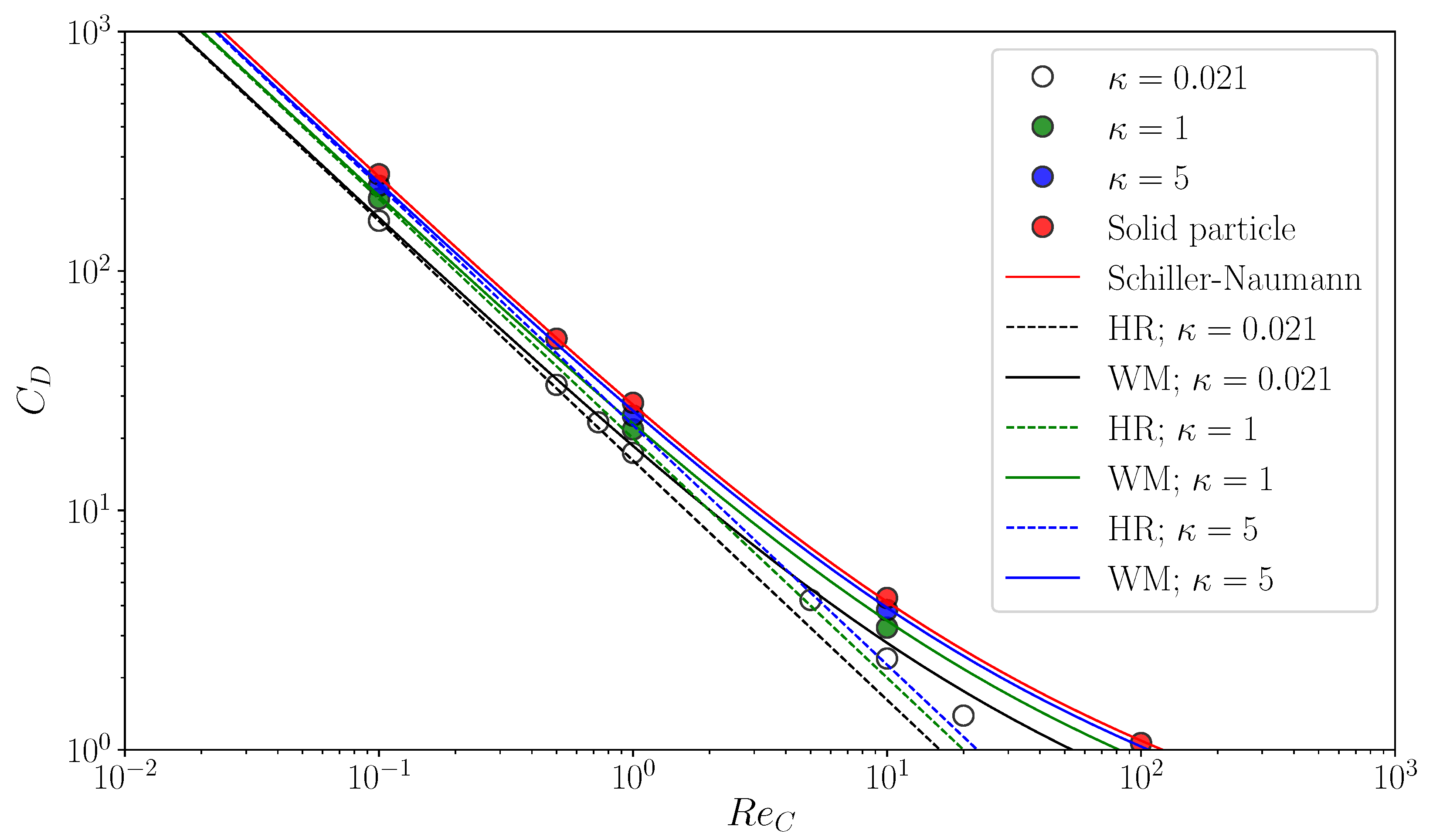
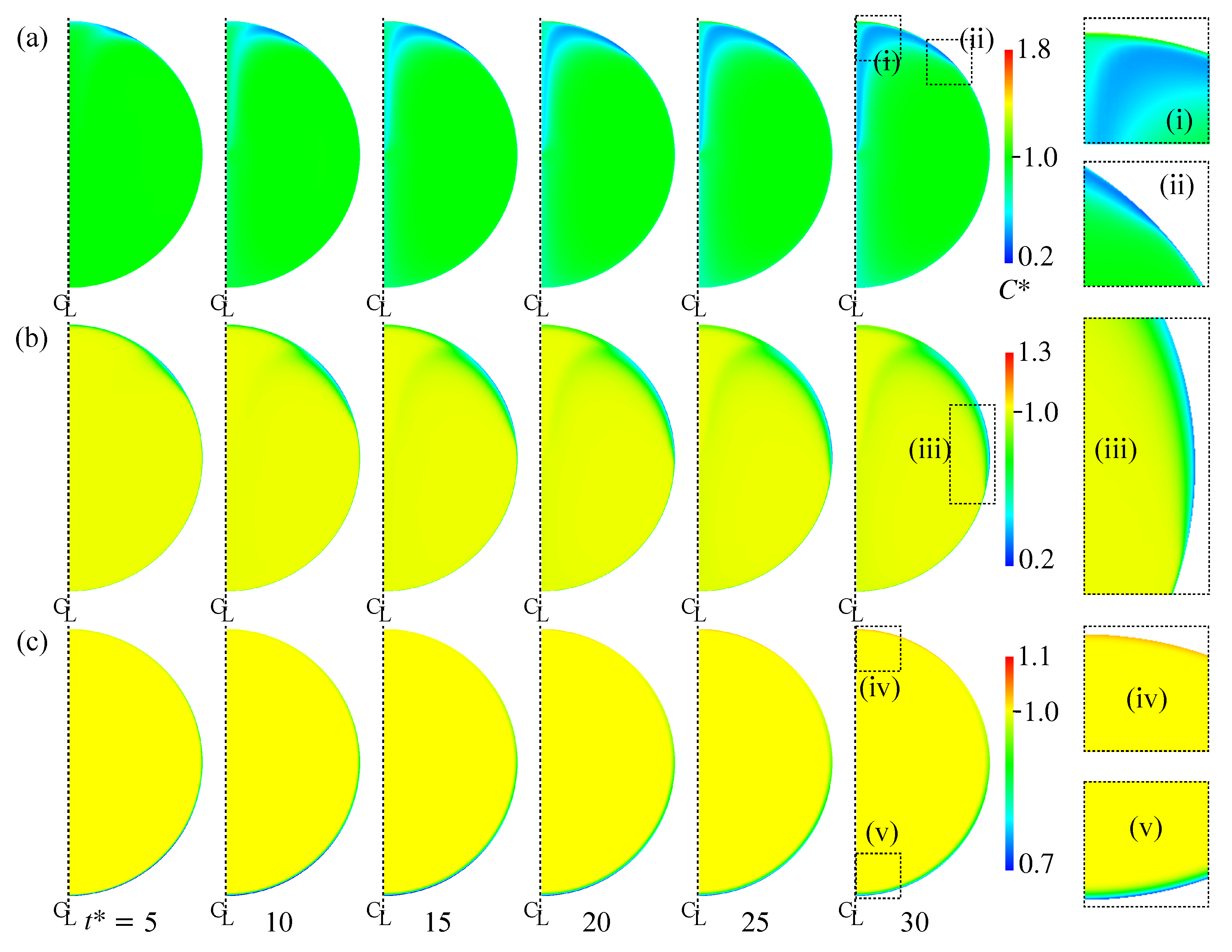
3.1. Clean Drop and Solid Sphere
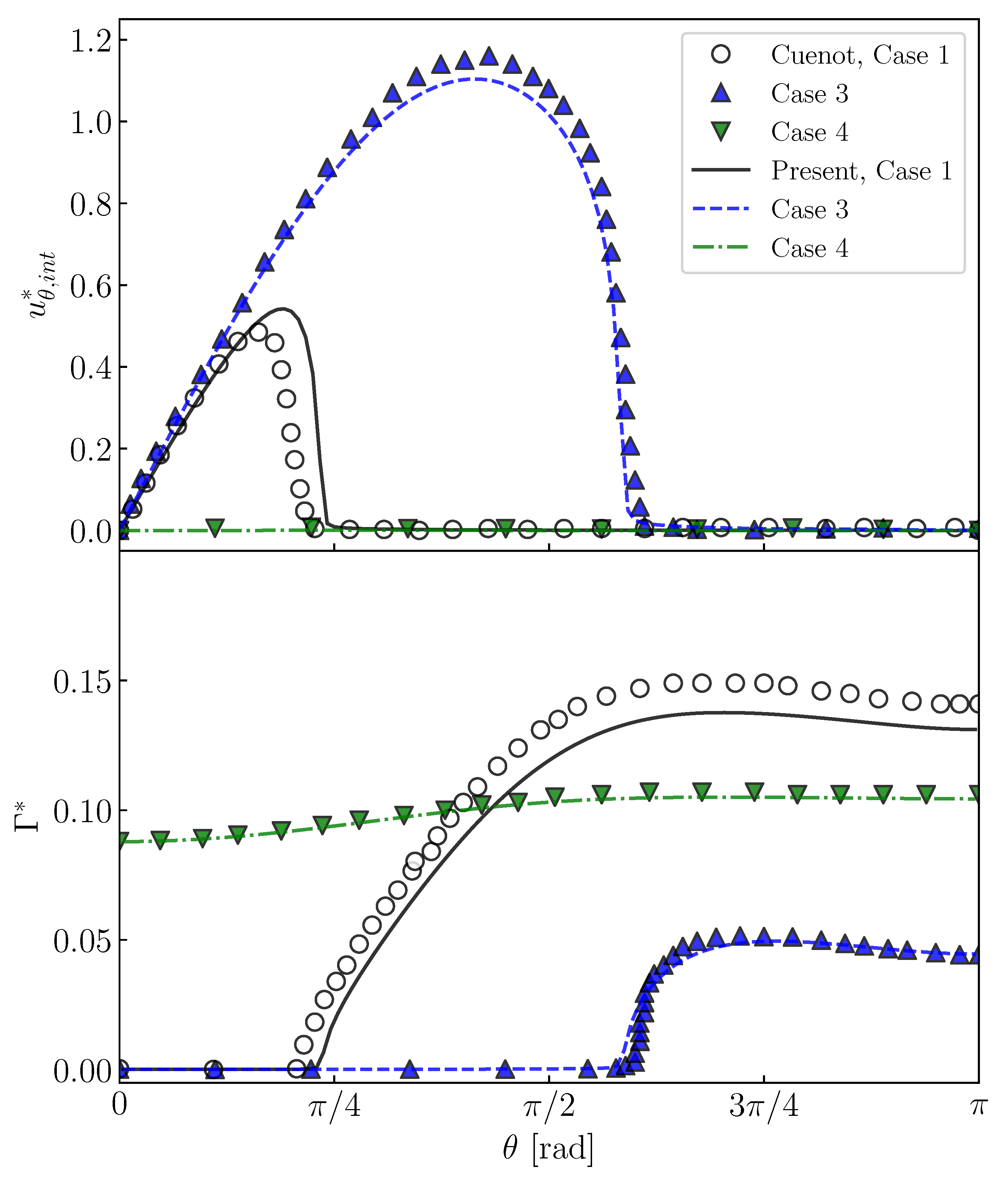
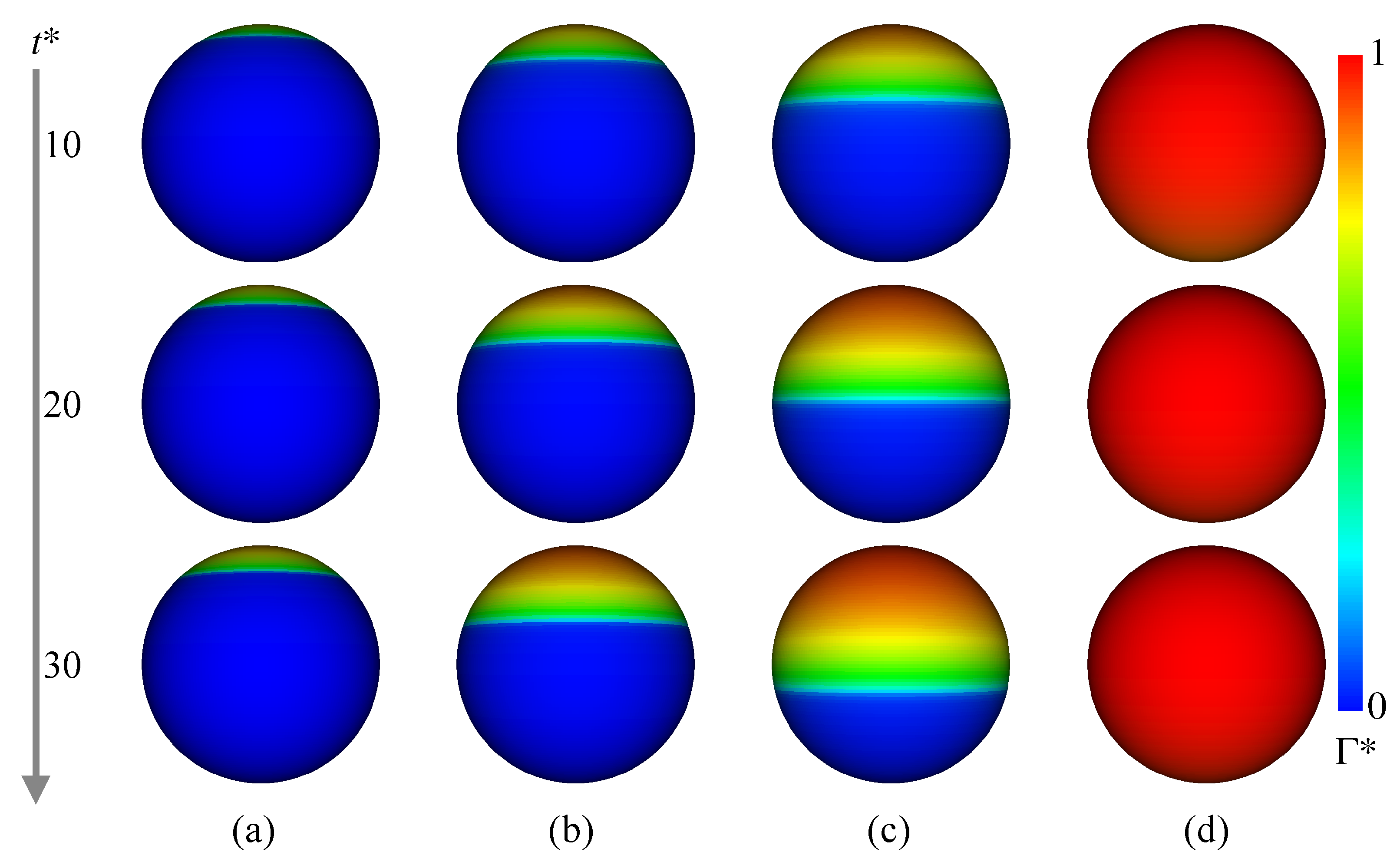
3.2. Contaminated Bubbles
4. Simulations of Contaminated Drops
5. Conclusions
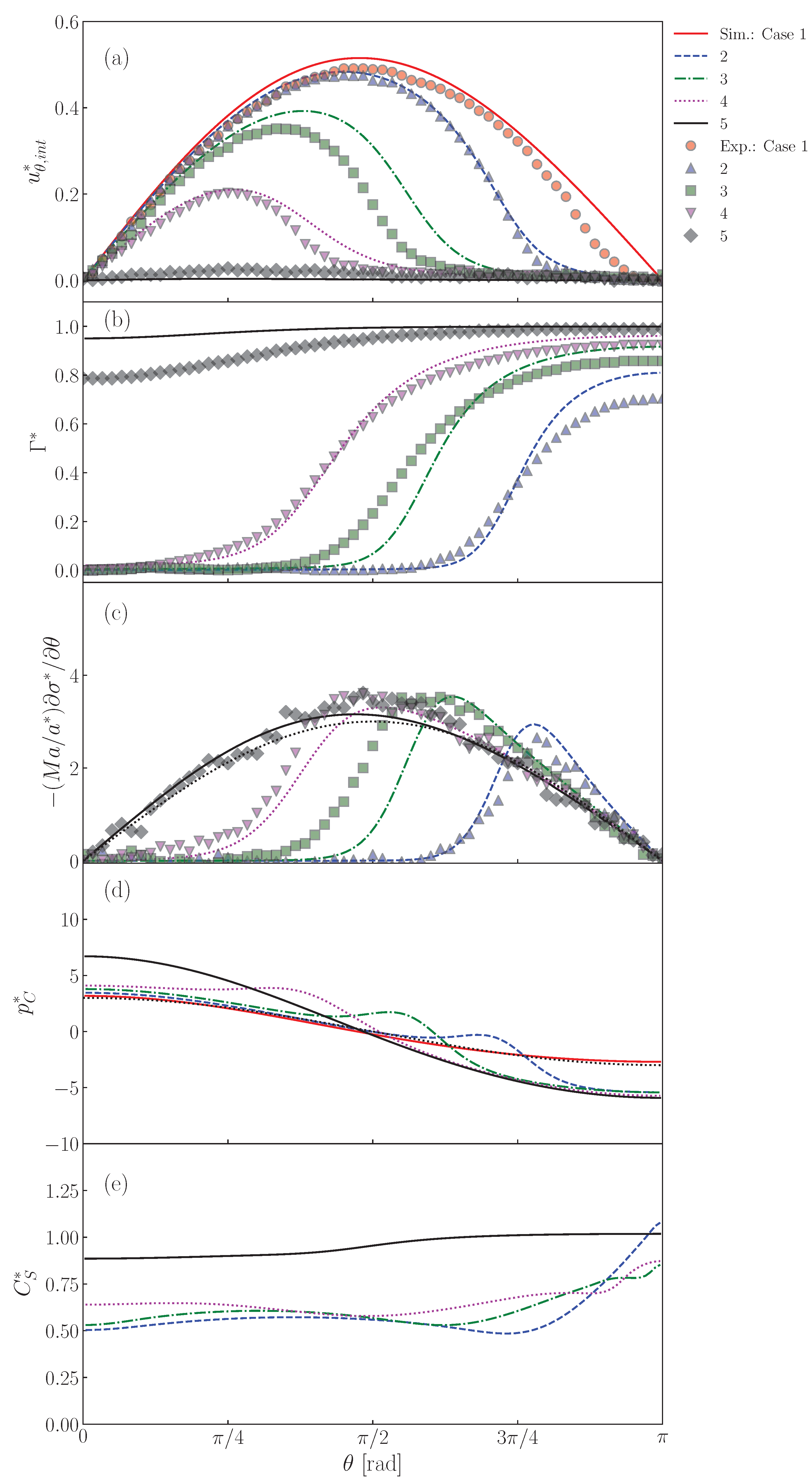
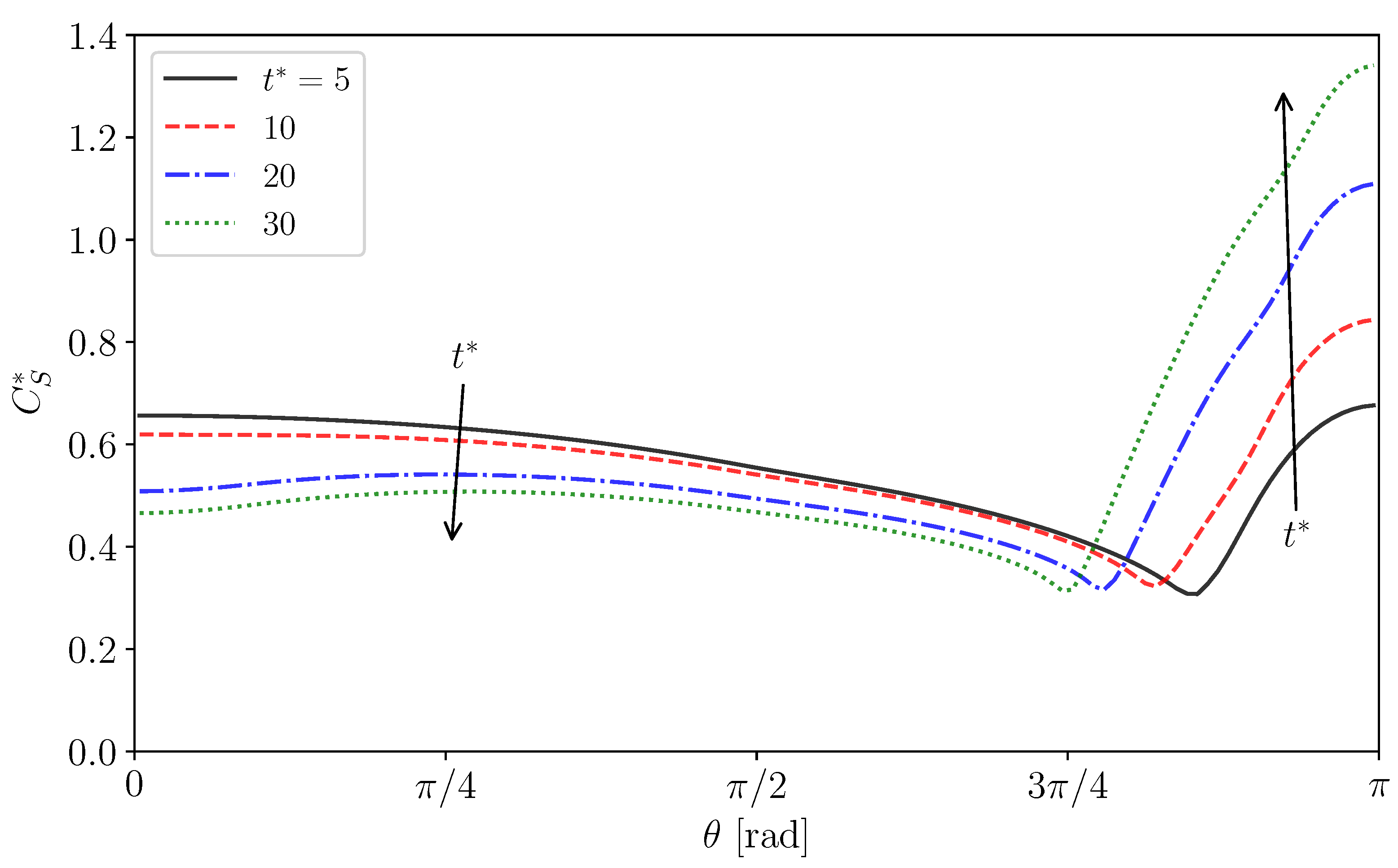
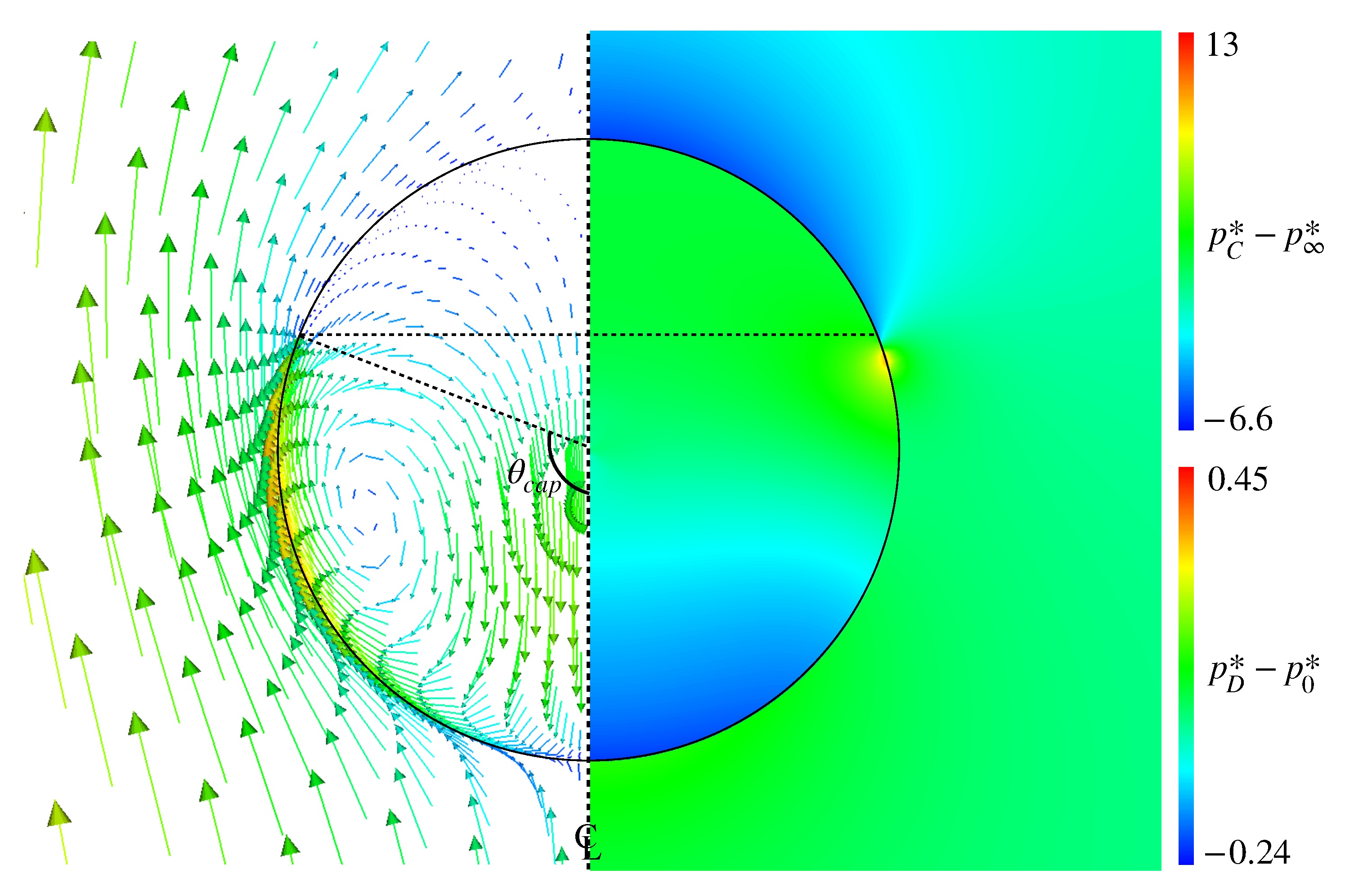
- The predicted interfacial surfactant concentration, , is almost zero for the angle, , smaller than a certain value (), whereas it steeply increases and reaches a large value for . The interface velocity, , decreases as increases and becomes very small for . The increase in increases and decreases . The presence of surfactant attenuates the internal circulation and the increase in makes the circulation region smaller.
- The surfactant flux from the bulk to the interface decreases C in the vicinity of the interface and the weak diffusion cannot compensate for the reduction in C by adsorption. The bulk concentration, , at the interface therefore tends to be smaller than for . The pattern of the low C region is determined by the advection and does not smear out because of a small diffusive flux.
- Peaks appear in the predicted Marangoni stresses in Cases 2–4, while in Case 5 no peaks develop due to a smaller gradient. The peaked distribution of the Marangoni stress also causes similar peaks in the pressure distribution. The locations of the strong Marangoni stress correspond to , whereas the peaks of the pressure appear at slightly smaller . The high-pressure spots prevent the fluid motion along the interface, which results in the formation of the stagnant-cap region in the rear half of the drop and the attenuation of the tangential velocity in the continuous phase.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Differential Operators
Appendix B. Surfactant Property
Appendix C. Contaminated Drops of Lower Peclet Numbers
| Case | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| [mol/m] | 0.0020 | 0.0050 | 0.010 | 0.10 |
| 3.5 | 3.0 | 2.7 | 2.6 | |
| 7.0 | 6.1 | 5.4 | 5.2 |
References
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Takagi, S.; Uda, T.; Watanabe, Y.; Matsumoto, Y. Behavior of a rising bubble in water with surfactant dissolution (1st report, steady behavior). Trans. JSME 2003, 69, 2192–2199. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1987. [Google Scholar]
- Aoki, J.; Hayashi, K.; Hosokawa, S.; Tomiyama, A. Effects of surfactant on mass transfer from single carbon dioxide bubbles in vertical pipes. Chem. Eng. Technol. 2015, 38, 1955–1964. [Google Scholar] [CrossRef]
- Boussinesq, J. Vitesse de la chute lente, devenue uniforme, d’une goutte liquide spherique. dans un fluid visqueux de poids specifique moindre. C. R. Acad. Sci. 1913, 156, 1124–1130. [Google Scholar]
- Scriven, L.E. Dynamics of a fluid interface. Chem. Eng. Sci. 1960, 12, 98–108. [Google Scholar] [CrossRef]
- Hadamard, J.S. Mouvement permanent tent d’une sphere liquide et visquese dans un liquide visqueux. Comptes Rendus I’Acad. Des Sci. 1911, 152, 1735–1738. [Google Scholar]
- Rybczynski, W. On the translatory of a fluid sphere in a viscous medium. Bull. Acad. Sci. Kracow Ser. 1911, 3, 40–46. [Google Scholar]
- Levich, V.G. Physicochemical Hydrodynamics; Prentice Hall: Englewood Cliffs, NJ, USA, 1962. [Google Scholar]
- Cuenot, B.; Magnaudet, J.; Spennato, B. The effects of slightly soluble surfactants on the flow around a spherical bubble. J. Fluid Mech. 1997, 339, 25–53. [Google Scholar] [CrossRef]
- Takagi, S.; Ogasawara, T.; Fukuta, M.; Matsumoto, Y. Surfactant effect on the bubble motions and bubbly flow structures in a vertical channel. Fluid Dyn. Res. 2009, 41, 065003. [Google Scholar] [CrossRef]
- Muradoglu, M.; Tryggvason, G. A front-tracking method for computation of interfacial flows with soluble surfactants. J. Comput. Phys. 2008, 227, 2238–2262. [Google Scholar] [CrossRef]
- Hayashi, K.; Tomiyama, A. Effects of surfactant on terminal velocity of a Taylor bubble in a vertical pipe. Int. J. Multiph. Flow 2012, 39, 78–87. [Google Scholar] [CrossRef]
- Hayashi, K.; Tomiyama, A. Effects of numerical treatment of viscous and surface tension forces. J. Comput. Multiph. Flows 2014, 6, 111–126. [Google Scholar] [CrossRef][Green Version]
- Engberg, R.F.; Wegener, M.; Kenig, E.Y. The influence of Marangoni convection on fluid dynamics of oscillating single rising droplets. Chem. Eng. Sci. 2014, 117, 114–124. [Google Scholar] [CrossRef]
- Atasi, O.; Haut, B.; Pedrono, A.; Scheid, B.; Legendre, D. Influence of soluble surfactants and deformation on the dynamics of centered bubbles in cylindrical microchannels. Langmuir 2018, 34, 10048–10062. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.; Chergui, J.; Juric, D.; Kahouadji, L.; Matar, O.; Craster, R. A hybrid interface tracking-level set technique for multiphase flow with soluble surfactant. J. Comput. Phys. 2018, 359, 409–435. [Google Scholar] [CrossRef]
- Piedfert, A.; Lalanne, B.; Masbernat, O.; Risso, F. Numerical simulations of a rising drop with shape oscillations in the presence of surfactants. Phys. Rev. Fluids 2018, 3, 103605. [Google Scholar] [CrossRef]
- Batchvarov, A.; Kahouadji, L.; Magnini, M.; Constante-Amores, C.; Shin, S.; Chergui, J.; Juric, D.; Craster, R.; Matar, O. Effect of surfactant on elongated bubbles in capillary tubes at high Reynolds number. Phys. Rev. Fluids 2020, 5, 093605. [Google Scholar] [CrossRef]
- Ubal, S.; Brown, N.; Lu, J.; Corvalan, C. Active motion of contaminated microbubbles. Chem. Eng. Sci. 2021, 238, 116574. [Google Scholar] [CrossRef]
- Dukhin, S.S.; Kretzschmar, G.; Miller, R. Dynamics of Adsorption at Liquid Interfaces; Elsevier Science: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Hosokawa, S.; Masukura, Y.; Hayashi, K.; Tomiyama, A. Experimental evaluation of Marangoni stress and surfactant concentration at interface of contaminated single spherical drop using spatiotemporal filter velocimetry. Int. J. Multiph. Flow 2017, 97, 157–167. [Google Scholar] [CrossRef]
- Hosokawa, S.; Tomiyama, A. Spatial Filter Velocimetry based on Time-Series Particle Images. Exp. Fluids 2012, 52, 1361–1372. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Stone, H.A. A simple derivation of the time-dependent convective-diffusion equation for surfactant transport along a deforming interface. Phys. Fluids 1990, 2, 111–112. [Google Scholar] [CrossRef]
- Frumkin, A.; Levich, V.G. On surfactants and interfacial motion. Zhurnal Fiz. Khimii 1947, 21, 1183–1204. (In Russian) [Google Scholar]
- Kim, J.; Moin, P. Application of a Fractional-Step Method to Incompressible Navier-Stokes Equations. J. Comput. Phys. 1985, 323, 308–323. [Google Scholar] [CrossRef]
- Choi, H.; Moin, P. Effects of the computational time step on numerical solutions of turbulent flow. J. Comput. Phys. 1994, 113, 1–4. [Google Scholar] [CrossRef]
- Shu, C.; Osher, S. Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef]
- Mohseni, K.; Colonius, T. Numerical treatment of polar coordinate singularities. J. Comput. Phys. 2000, 157, 787–795. [Google Scholar] [CrossRef]
- Sugioka, K.; Komori, S. Drag and lift forces acting on a spherical water droplet in homogeneous linear shear air flow. J. Fluid Mech. 2007, 570, 155–175. [Google Scholar] [CrossRef]
- Myint, W.; Hosokawa, S.; Tomiyama, A. Terminal velocity of single drops in stagnant liquids. J. Fluid Sci. Technol. 2006, 1, 72–81. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, A. Über die grundlegende Berechnungen bei der Schwerkraft-aufbereitung. Z. Des Vereines Dtsch. Ingenieure 1933, 77, 318–320. [Google Scholar]
- Ward, A.F.H.; Tordai, L. Time-dependence of Boundary Tensions of Solutions: I. the role of diffusion in time-effects. J. Chem. Phys. 1946, 14, 453–461. [Google Scholar] [CrossRef]
- Valkovska, D.S.; Danov, K.D. Determination of Bulk and Surface Diffusion Coefficients from Experimental Data for Thin Liquid Film Drainage. J. Colloid Interface Sci. 2000, 223, 314–316. [Google Scholar] [CrossRef][Green Version]
- Morgan, C.E.; Breward, C.J.W.; Griffiths, I.M.; Howell, P.D.; Penfold, J.; Thomas, R.K.; Tucker, I.; Petkov, J.T.; Webster, J.R.P. Kinetics of Surfactant Desorption at an Air-Solution Interface. J. Colloid Interface Sci. 2012, 28, 17339–17348. [Google Scholar] [CrossRef] [PubMed]
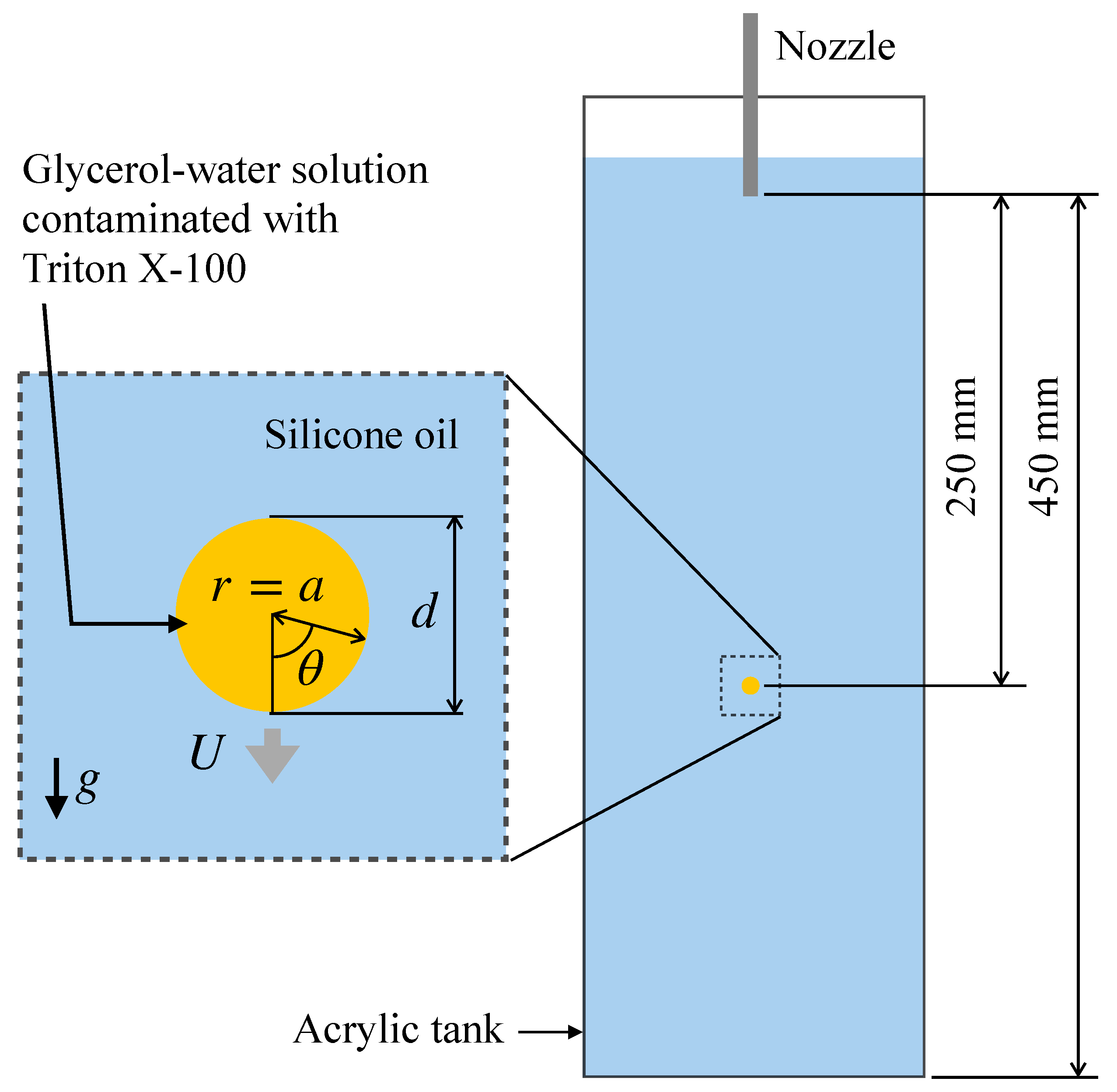
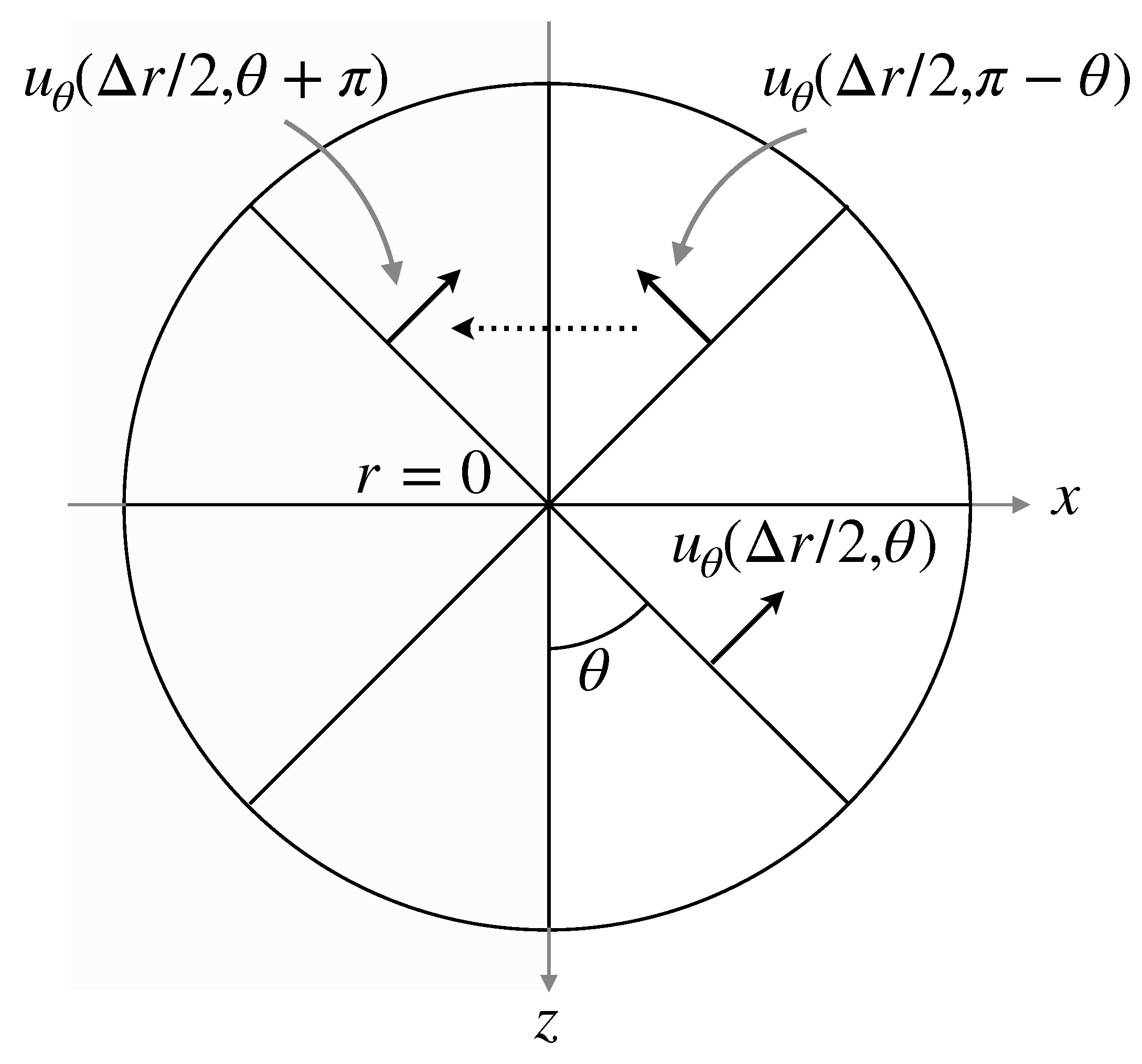

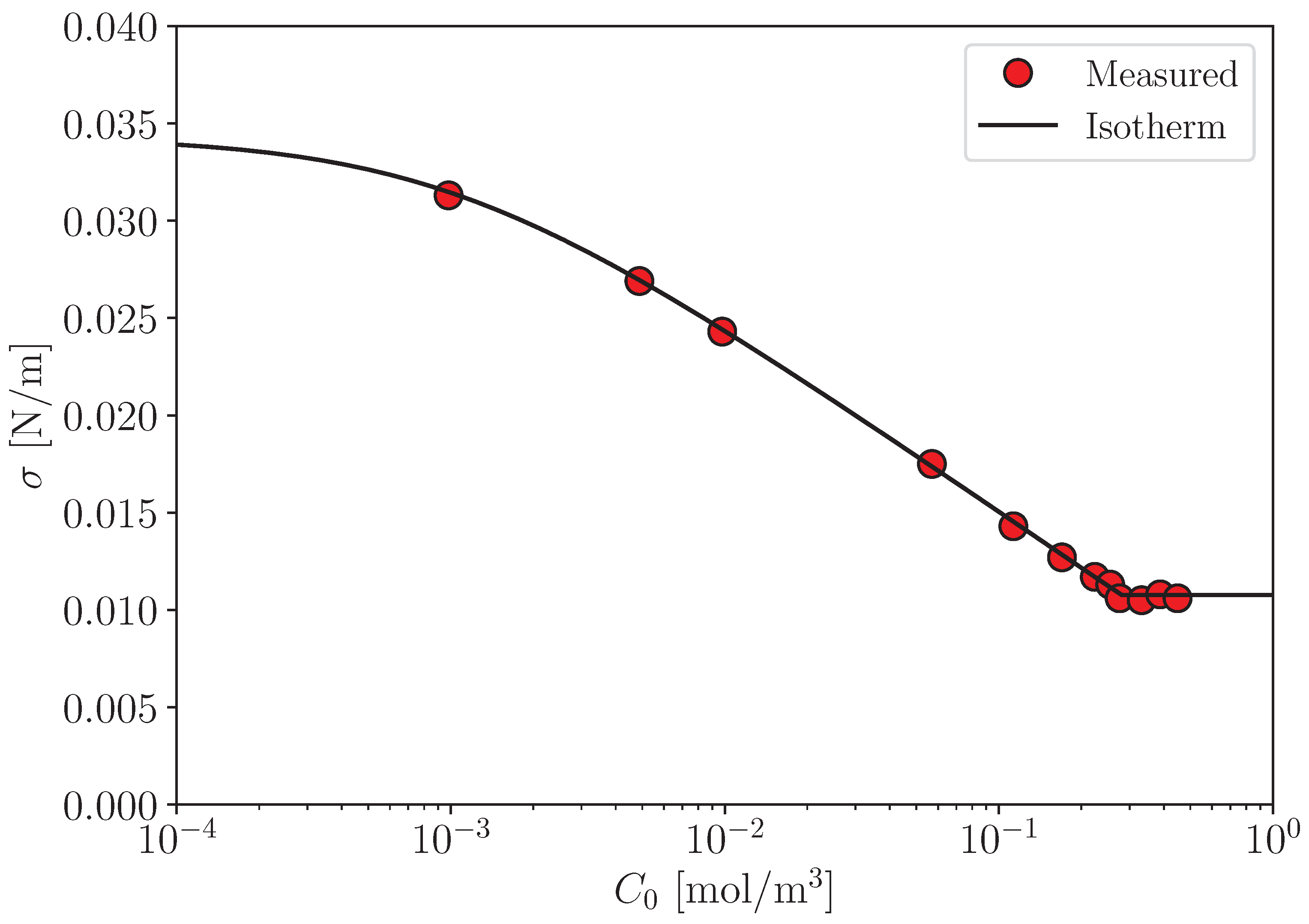
| Phase | Dispersed | Continuous |
|---|---|---|
| [kg/m] | 1132 | 967 |
| [Pa·s] | 0.00613 | 0.299 |
| [N/m] | 0.0343 |
| [m/mol·s] | [1/s] | [mol/m] | [m/s] | [m/s] |
|---|---|---|---|---|
| 9.4 | 0.0096 | 1.69 × 10 | 2 × 10 | 2 × 10 |
| Case | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| [mol/m] | 0 | 0.0020 | 0.0050 | 0.010 | 0.10 |
| 1.17 | 1.17 | 1.17 | 1.17 | 1.17 | |
| 0.021 | 0.021 | 0.021 | 0.021 | 0.021 | |
| 42 | 39 | 34 | 30 | 29 | |
| 0.73 | 0.68 | 0.59 | 0.52 | 0.50 | |
| 0 | 2.0 | 4.9 | 9.8 | 98 | |
| - | 1.1 | 0.91 | 0.80 | 0.77 | |
| - | 1.1 | 0.91 | 0.80 | 0.77 | |
| - | 0.55 | 0.64 | 0.72 | 0.75 | |
| - | 0.0062 | 0.018 | 0.040 | 0.42 | |
| K | - | 0.10 | 0.041 | 0.020 | 0.0020 |
| 8.2 | 8.2 | 8.2 | 8.2 | 8.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayashi, K.; Motoki, Y.; van der Linden, M.J.A.; Deen, N.G.; Hosokawa, S.; Tomiyama, A. Single Contaminated Drops Falling through Stagnant Liquid at Low Reynolds Numbers. Fluids 2022, 7, 55. https://doi.org/10.3390/fluids7020055
Hayashi K, Motoki Y, van der Linden MJA, Deen NG, Hosokawa S, Tomiyama A. Single Contaminated Drops Falling through Stagnant Liquid at Low Reynolds Numbers. Fluids. 2022; 7(2):55. https://doi.org/10.3390/fluids7020055
Chicago/Turabian StyleHayashi, Kosuke, Yuya Motoki, Matheus J. A. van der Linden, Niels G. Deen, Shigeo Hosokawa, and Akio Tomiyama. 2022. "Single Contaminated Drops Falling through Stagnant Liquid at Low Reynolds Numbers" Fluids 7, no. 2: 55. https://doi.org/10.3390/fluids7020055
APA StyleHayashi, K., Motoki, Y., van der Linden, M. J. A., Deen, N. G., Hosokawa, S., & Tomiyama, A. (2022). Single Contaminated Drops Falling through Stagnant Liquid at Low Reynolds Numbers. Fluids, 7(2), 55. https://doi.org/10.3390/fluids7020055