Aerodynamic Shape Optimization of a Symmetric Airfoil from Subsonic to Hypersonic Flight Regimes
Abstract
1. Introduction
2. Background
2.1. Governing Equations of Fluid Dynamics
2.2. Turbulence and Turbulence Model
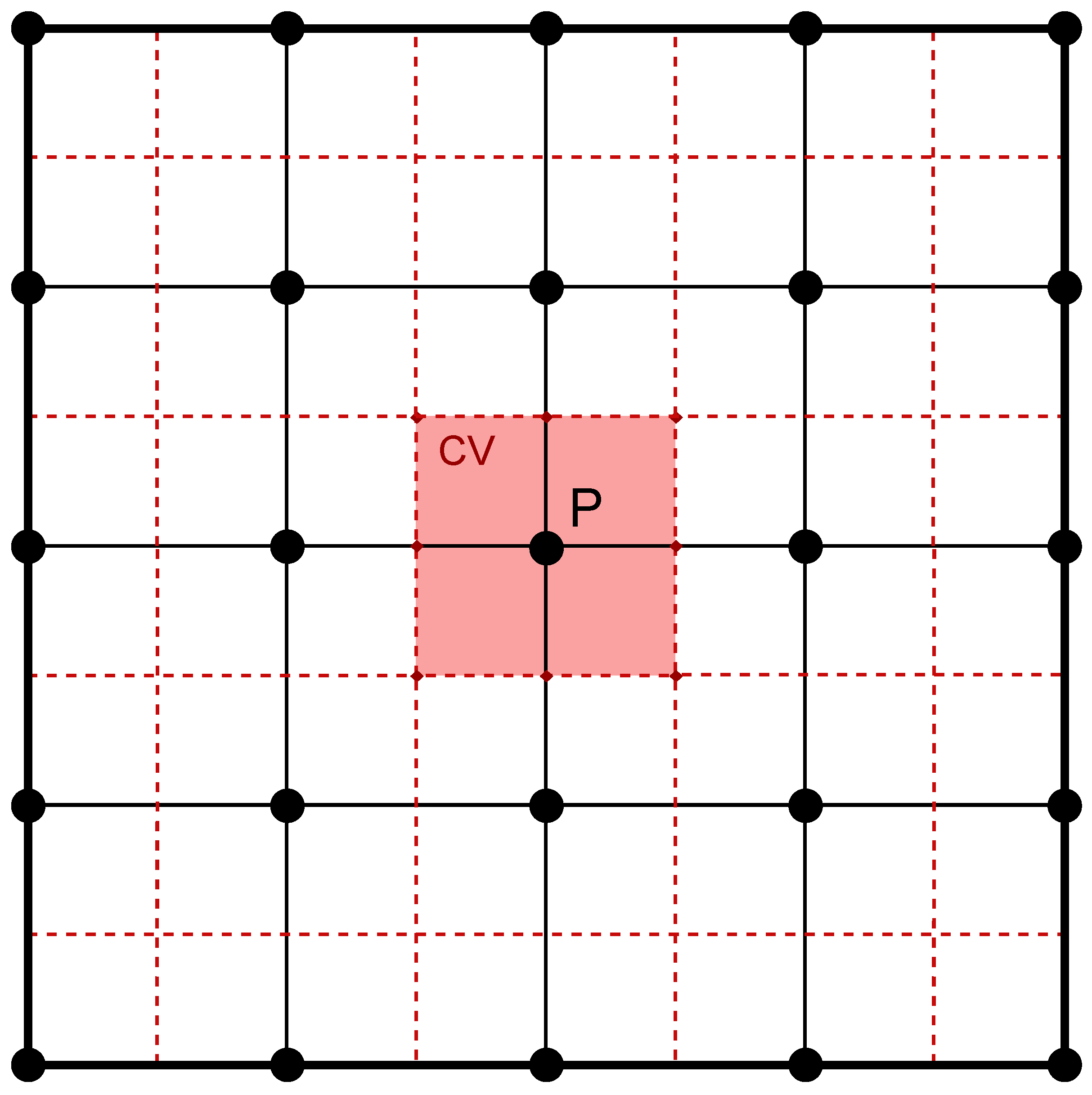
2.3. Finite-Volume Method
3. Methodology
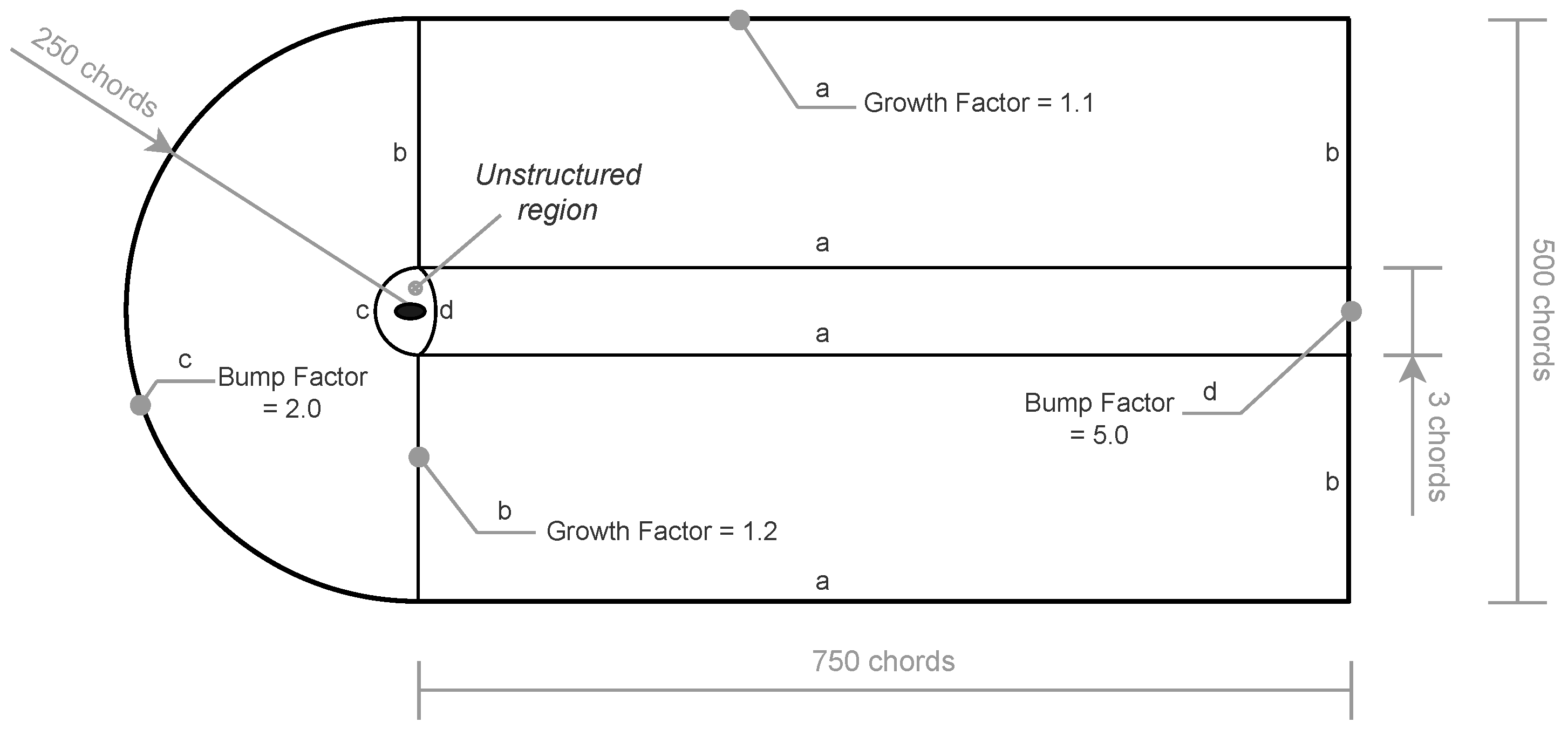
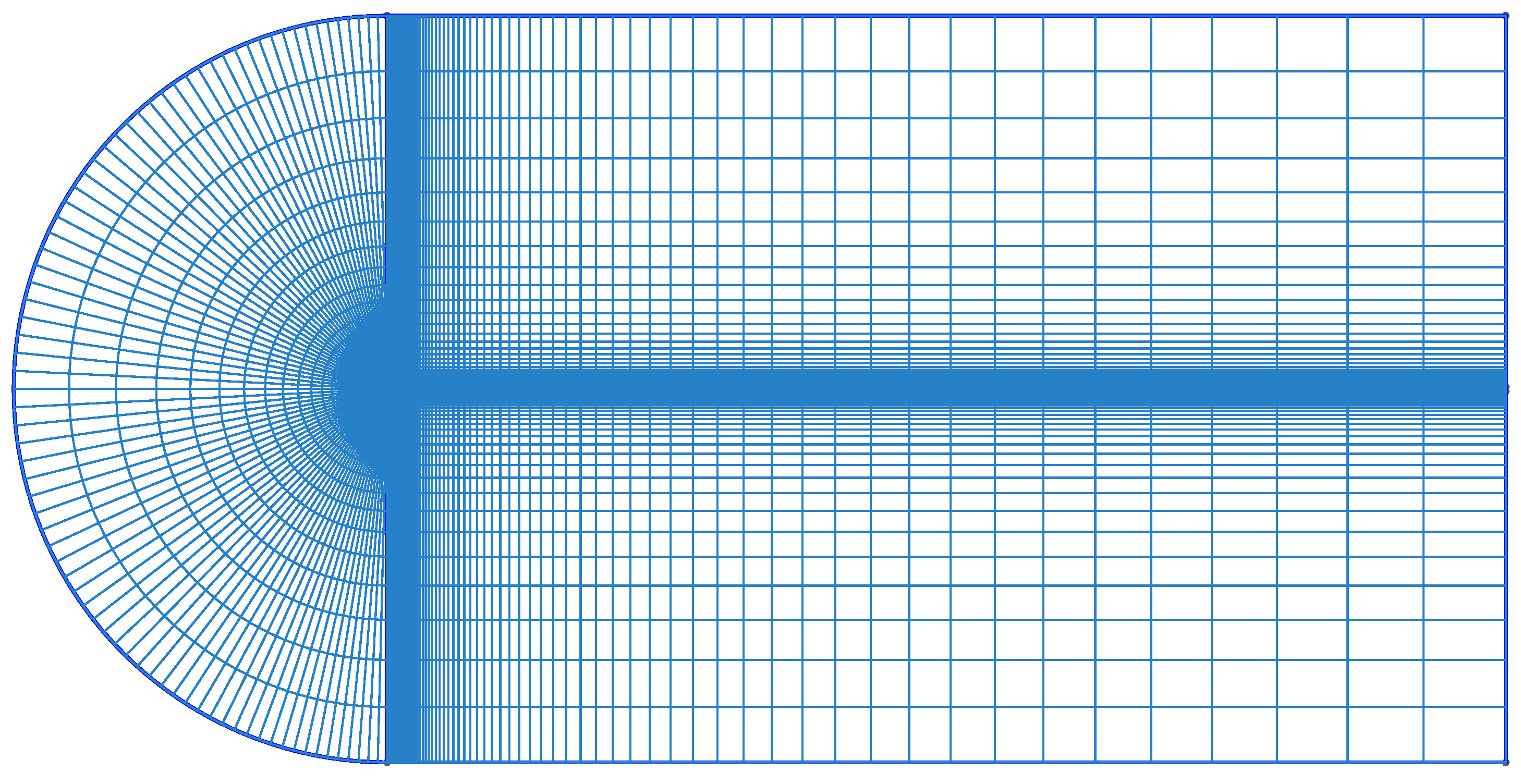
3.1. Airfoil Geometry & Mesh Design
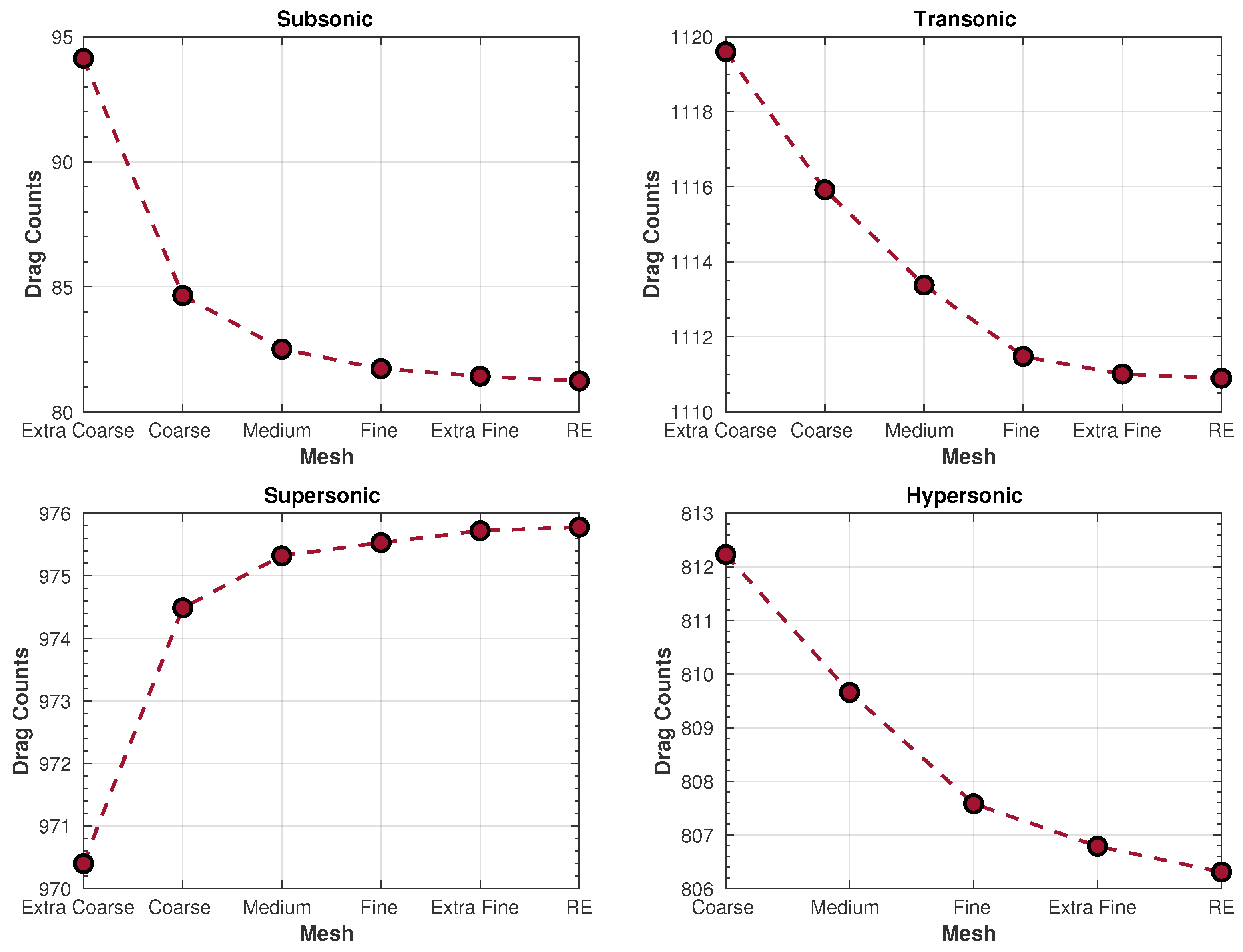
3.2. Grid-Convergence Study (GCS)
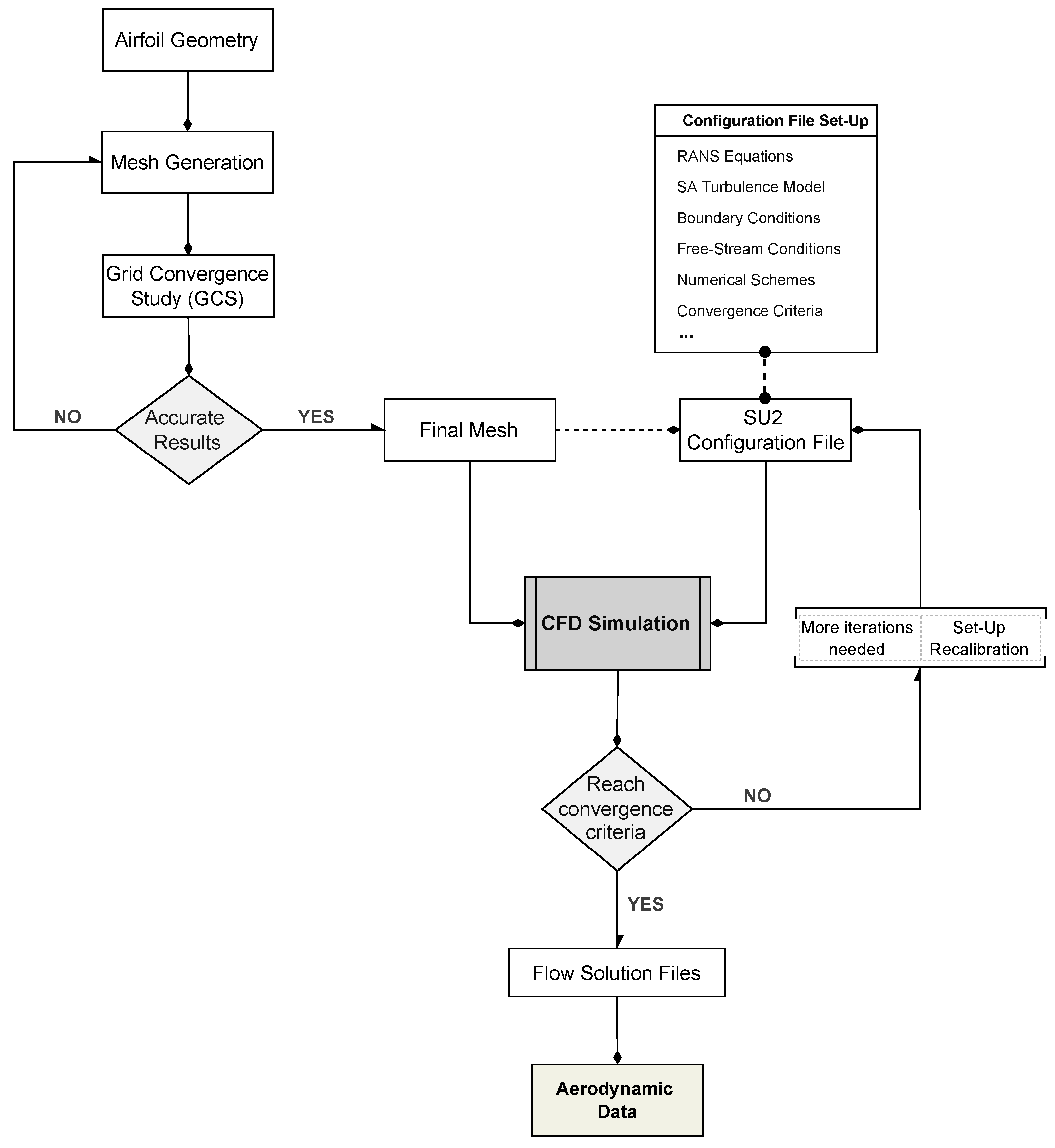
3.3. Baseline Simulations
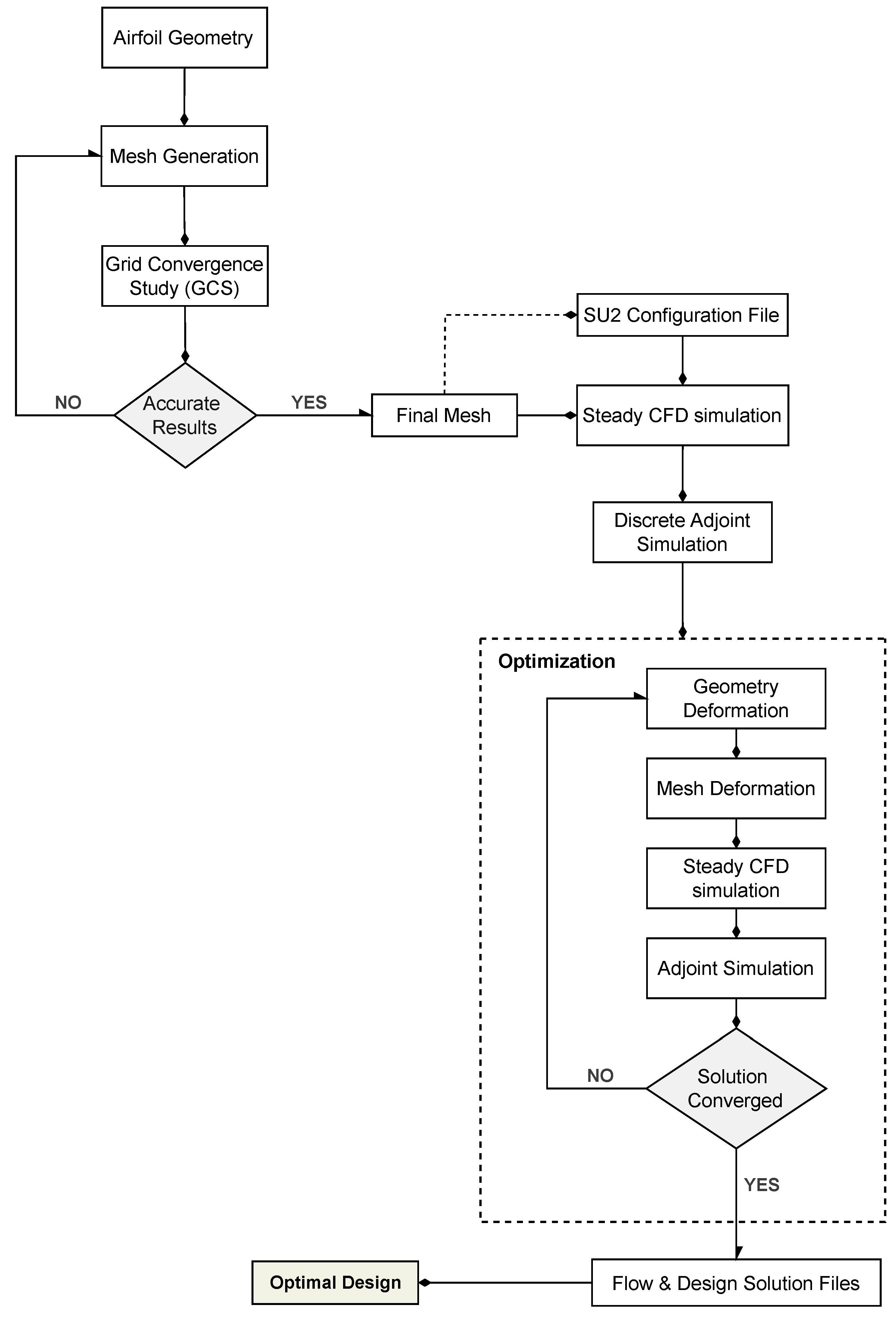
3.4. Optimization Simulations
4. Problem Formulation
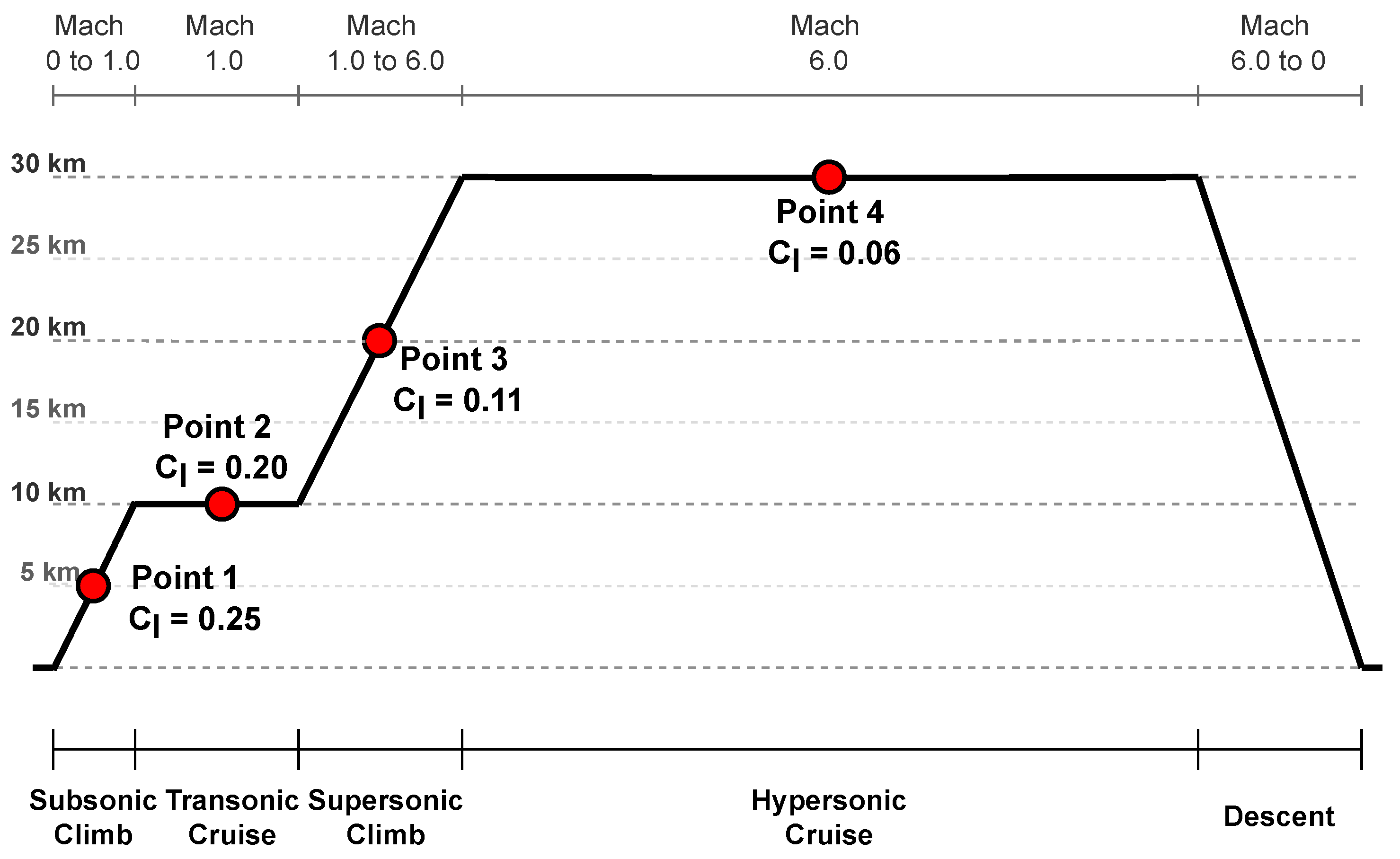
Mission Profile
5. Results and Discussion
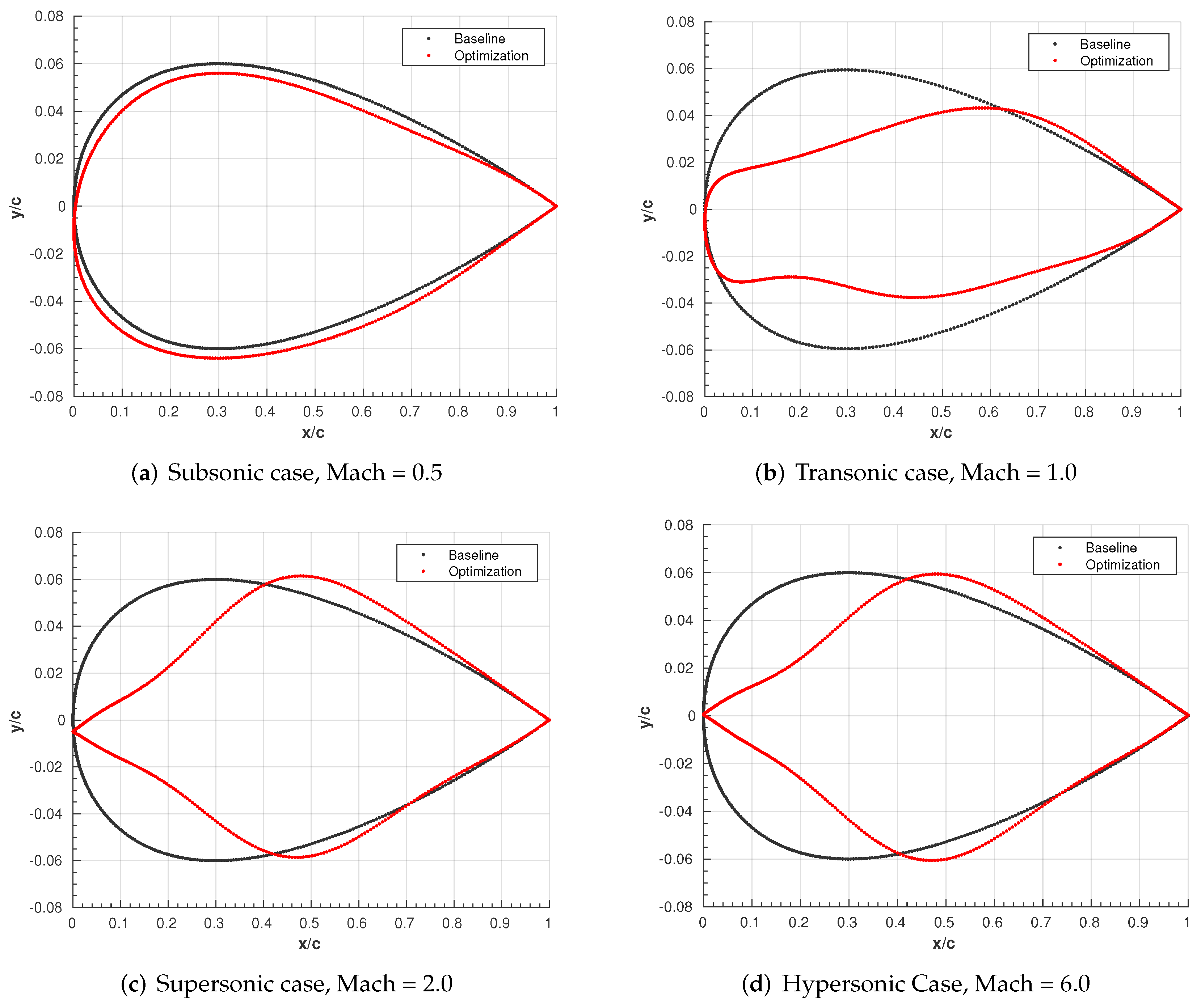
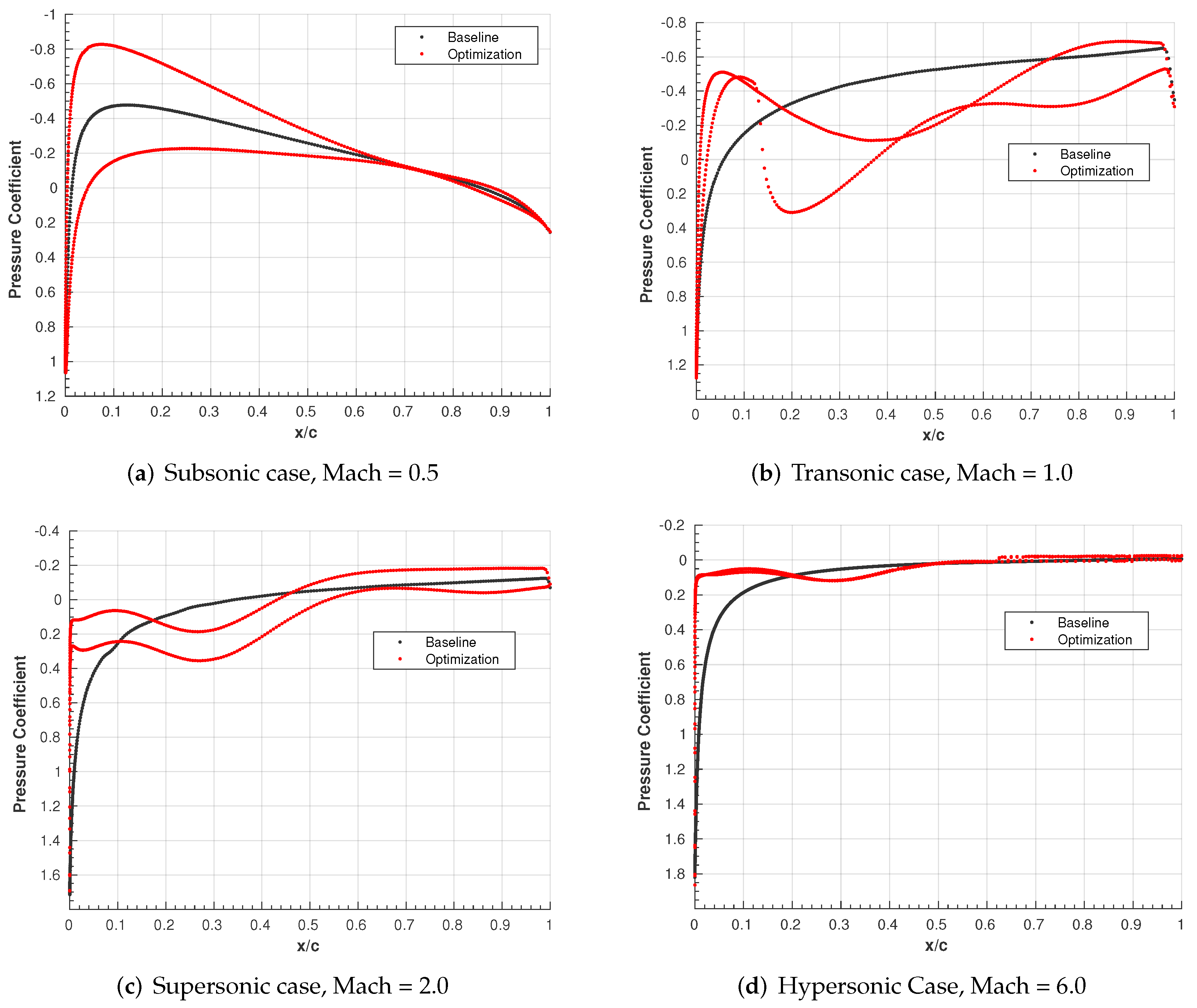
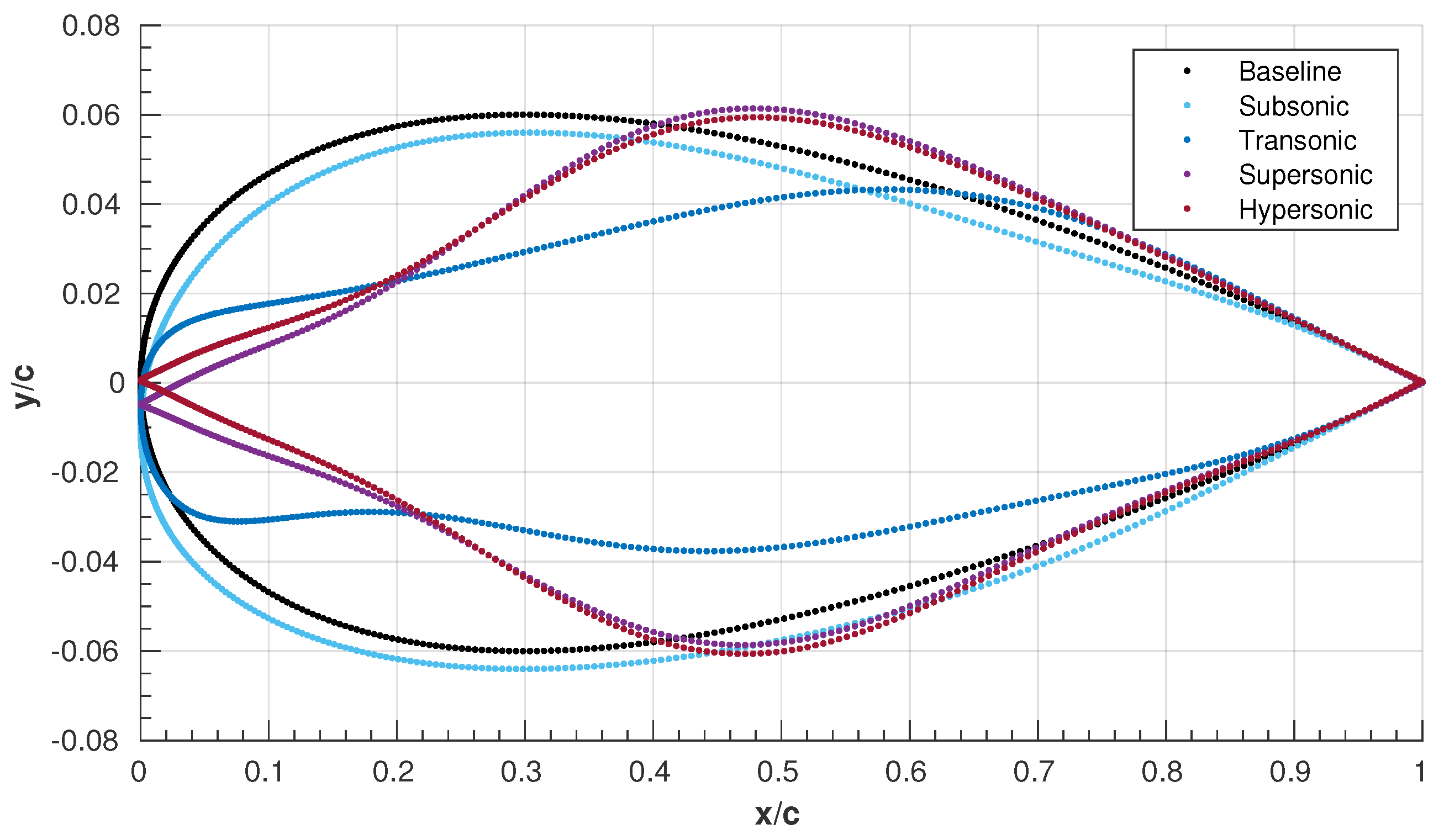
5.1. Gradient-Based Optimizations
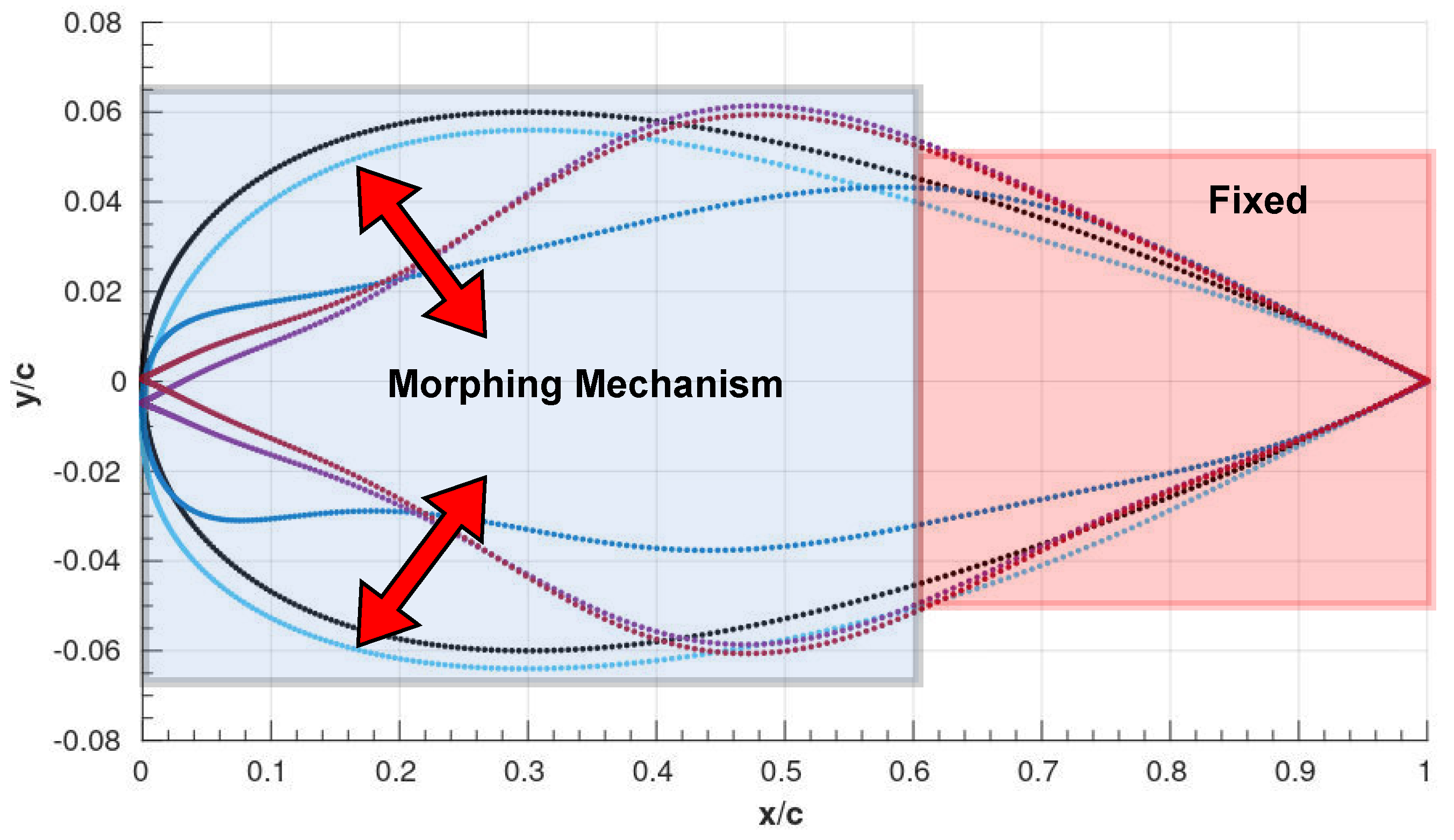
5.2. Morphing Strategy
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations and Acronyms
| ASO | Aerodynamic shape optimization |
| BC | Boundary condition |
| CAD | Computer-aided design |
| CFD | Computational fluid dynamics |
| CV | Control volumes |
| DNS | Direct numerical solution |
| FFD | Free-form deformation |
| FVM | Finite-volume method |
| GBM | Gradient-based method |
| GCS | Grid-convergence study |
| ICAO | International Civil Aviation Organization |
| PDE | Partial differential equations |
| RANS | Reynolds-averaged Navier–Stokes |
| SA | Spalart–Allmaras |
| SU2 | Standford University Unstructured |
| Nomenclature | |
| Convective fluxes | |
| Viscous fluxes | |
| Velocity vector | |
| State variables vector | |
| Design variables | |
| Dynamic viscosity | |
| Density | |
| Shear-stress tensor | |
| Drag coefficient | |
| Lift coefficient | |
| L/D | Lift-to-drag ratio |
| Identity matrix | |
| E | Total energy |
| H | Total enthalpy |
| k | Thermal conductivity |
| p | Pressure |
| Q | Source term |
| r | Grid-refinement ratio |
| Reynolds number | |
| T | Temperature |
| c | Airfoil chord |
| K | Kelvin |
| s.t. | Subject to |
| w.r.t. | With respect to |
| x | x-coordinate |
| y | y-coordinate |
References
- ICAO Annual Report. Available online: https://www.icao.int/annual-report-2019/Documents/ARC_2019_Air%20Transport%20Statistics.pdf (accessed on 24 April 2021).
- Liu, F.; Han, Z.; Zhang, Y.; Song, K.; Song, W.; Gui, F.; Tang, J. Surrogate-based aerodynamic shape optimization of hypersonic flows considering transonic performance. Aerosp. Sci. Technol. 2019, 93, 105345. [Google Scholar] [CrossRef]
- Periodic Reporting for Period 1—STRATOFLY. Available online: https://cordis.europa.eu/project/id/769246/reporting/it (accessed on 18 June 2021).
- Taguchi, H.; Kobayashi, H.; Kojima, T.; Ueno, A.; Imamura, S.; Hongoh, M.; Harada, K. Research on hypersonic aircraft using pre-cooled turbojet engines. Acta Astronaut. 2012, 73, 164–172. [Google Scholar] [CrossRef]
- Viola, N.; Fusaro, R.; Saracoglu, B.; Schram, C.; Grewe, V.; Martinez, J.; Marini, M.; Hernandez, S.; Lammers, K.; Vincent, A.; et al. Main Challenges and Goals of the H2020 STRATOFLY Project. Aerotec. Missili Spaz. 2021, 10, 95–110. [Google Scholar] [CrossRef]
- Bowcutt, K.G. Stratospheric Flying Opportunities for High-Speed Propulsion Concepts: Hypersonic Vehicle Design Challenges. In Proceedings of the von Karman Institute for Fluid Dynamics—Lecture Series, Online, 25–27 May 2021. [Google Scholar]
- Skinner, S.N.; Zare-Behtash, H. State-of-the-art in aerodynamic shape optimisation methods. Appl. Soft Comput. 2018, 62, 933–962. [Google Scholar] [CrossRef]
- Jameson, A. Aerodynamic design via control theory. J. Sci. Comput. 1988, 3, 233–260. [Google Scholar] [CrossRef]
- Liu, B.; Liang, H.; Han, Z.-H.; Yang, G. Surrogate-based aerodynamic shape optimization of a morphing wing considering a wide Mach-number range. Aerosp. Sci. Technol. 2022, 124, 107557. [Google Scholar] [CrossRef]
- Ma, Y.; Yang, T.; Feng, Z.; Zhang, Q. Hypersonic lifting body aerodynamic shape optimization based on the multiobjective evolutionary algorithm based on decomposition. Proc. Inst. Mech. Eng. Part J. Aerosp. Eng. 2015, 229, 1246–1266. [Google Scholar] [CrossRef]
- Peng, W.; Feng, Z.; Yang, T. Rapid Aerodynamic Shape Optimization With Payload Size Constraints for Hypersonic Vehicle. IEEE Access 2019, 7, 84429–84447. [Google Scholar] [CrossRef]
- Martins, J.R.R.A. Aerodynamic design optimization: Challenges and perspectives. Comput. Fluids 2022, 239, 105391. [Google Scholar] [CrossRef]
- Mangano, M.; Martins, J.R.R.A. Multipoint Aerodynamic Shape Optimization for Subsonic and Supersonic Regimes. J. Aircr. 2021, 58, 650–662. [Google Scholar] [CrossRef]
- Reuther, J.; Alonso, J.J.; Rimlinger, M.J.; Jameson, A. Aerodynamic shape optimization of supersonic aircraft configurations via an adjoint formulation on distributed memory parallel computers. Comput. Fluids 1999, 28, 675–700. [Google Scholar] [CrossRef]
- Jim, T.M.S.; Faza, G.A.M.; Palar, P.S.; Shimoyama, K. Bayesian Optimization of a Low-Boom Supersonic Wing Planform. AIAA J. 2021, 59, 4514–4529. [Google Scholar] [CrossRef]
- Deng, F.; Jiao, Z.-h.; Chen, J.; Zhang, D.; Tang, S. Overall Performance Analysis–Oriented Aerodynamic Configuration Optimization Design for Hypersonic Vehicles. J. Spacecr. Rocket. 2017, 54, 1015–1026. [Google Scholar] [CrossRef]
- Seraj, S.; Martins, J.R. Aerodynamic Shape Optimization of a Supersonic Transport Considering Low-Speed Stability. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Weisshaar, T.A. Morphing Aircraft Systems: Historical Perspectives and Future Challenges. J. Aircr. 2013, 50, 337–353. [Google Scholar] [CrossRef]
- Li, D.; Zhao, S.; Da Ronch, A.; Xiang, J.; Drofelnik, J.; Li, Y.; Zhang, L.; Wu, Y.; Kintscher, M.; Monner, H.P.; et al. A review of modelling and analysis of morphing wings. Prog. Aerosp. Sci. 2018, 100, 46–62. [Google Scholar] [CrossRef]
- Anderson, J.D. Fundamentals of Aerodynamics, 5th ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Economon, T.D.; Palacios, F.; Copeland, S.R.; Lukaczyk, T.W.; Alonso, J.J. SU2: An Open-Source Suite for Multiphysics Simulation and Design. AIAA J. 2016, 54, 828–846. [Google Scholar] [CrossRef]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics; Springer: Cham, Swizerland, 2016. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. R. Soc. Math. Phys. Eng. Sci. 1991, 434, 9–13. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar] [CrossRef]
- Nemec, M.; Zingg, D.W.; Pulliam, T.H. Multipoint and Multi-Objective Aerodynamic Shape Optimization. AIAA J. 2004, 42, 1057–1065. [Google Scholar] [CrossRef]
- Waligura, C.J.; Couchman, B.L.; Galbraith, M.C.; Allmaras, S.R.; Harris, W.L. Investigation of Spalart-Allmaras Turbulence Model Modifications for Hypersonic Flows Utilizing Output-Based Grid Adaptation. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Education Limited: Harlow, UK, 2007. [Google Scholar]
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Richardson, L.F. IX. The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam. Proc. R. Soc. Math. Phys. Eng. Sci. 1911, 210, 307–357. [Google Scholar] [CrossRef]
- Nadarajah, S.; Jameson, A. A comparison of the continuous and discrete adjoint approach to automatic aerodynamic optimization. In Proceedings of the 38th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2000. [Google Scholar] [CrossRef]
- Sederberg, T.; Parry, S. Free-form deformation of solid geometric models. In Proceedings of the 13th Annual Conference on Computer Graphics and Interactive Techniques, Dallas, TX, USA, 18–22 August 1986. [Google Scholar] [CrossRef]
- Anderson, J.D. Hypersonic and High-Temperature Gas Dynamics, 2nd ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006. [Google Scholar]



| Mesh | Mesh Elements |
|---|---|
| Extra Coarse | 19,864 |
| Coarse | 40,276 |
| Medium | 89,335 |
| Fine | 217,890 |
| Extra Fine | 604,804 |
| Point | Speed Regime | Mach | Altitude | Temperature | Reynolds Number |
|---|---|---|---|---|---|
| 1 | Subsonic | 0.5 | 5 km | 255.65 K | 7.25 × |
| 2 | Transonic | 1.0 | 10 km | 223.25 K | 8.49 × |
| 3 | Supersonic | 2.0 | 20 km | 216.65 K | 3.69 × |
| 4 | Hypersonic | 6.0 | 30 km | 226.65 K | 2.26 × |
| Point | Speed Regime | Baseline | Optimization | Baseline | Optimization | (%) | |
|---|---|---|---|---|---|---|---|
| 1 | Subsonic | 0.00 | 0.25 | +0.25 | 0.008407 | 0.008559 | +1.81% |
| 2 | Transonic | 0.00 | 0.20 | +0.20 | 0.111338 | 0.067349 | −39.5% |
| 3 | Supersonic | 0.00 | 0.11 | +0.11 | 0.097532 | 0.052138 | −46.5% |
| 4 | Hypersonic | 0.00 | 0.00 | 0.00 | 0.080679 | 0.016742 | −79.2% |
| Point | Speed Regime | Lift-to-Drag (L/D) Baseline | Lift-to-Drag (L/D) Optimization |
|---|---|---|---|
| 1 | Subsonic | 0.00 | 29.20 |
| 2 | Transonic | 0.00 | 2.97 |
| 3 | Supersonic | 0.00 | 2.69 |
| 4 | Hypersonic | 0.00 | 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leite, B.; Afonso, F.; Suleman, A. Aerodynamic Shape Optimization of a Symmetric Airfoil from Subsonic to Hypersonic Flight Regimes. Fluids 2022, 7, 353. https://doi.org/10.3390/fluids7110353
Leite B, Afonso F, Suleman A. Aerodynamic Shape Optimization of a Symmetric Airfoil from Subsonic to Hypersonic Flight Regimes. Fluids. 2022; 7(11):353. https://doi.org/10.3390/fluids7110353
Chicago/Turabian StyleLeite, Bernardo, Frederico Afonso, and Afzal Suleman. 2022. "Aerodynamic Shape Optimization of a Symmetric Airfoil from Subsonic to Hypersonic Flight Regimes" Fluids 7, no. 11: 353. https://doi.org/10.3390/fluids7110353
APA StyleLeite, B., Afonso, F., & Suleman, A. (2022). Aerodynamic Shape Optimization of a Symmetric Airfoil from Subsonic to Hypersonic Flight Regimes. Fluids, 7(11), 353. https://doi.org/10.3390/fluids7110353










