Self-Consistent Hydrodynamic Model of Electron Vortex Fluid in Solids

Abstract

We propose a system of self-consistent equations for electron fluid in solids which describes both longitudinal vortex flows and frozen-in internal electromagnetic fields. It is shown that in the case of an ideal electron fluid, the proposed model describes the electrodynamics of the superconductor, and in the vortex-less case, it leads to modified London equations. In addition, the two-fluid model based on the proposed equations is applied to the description of an ideal electron-hole fluid in a semiconductor. The damping processes in a non-ideal electron fluid are described by modified equations, which take into account collisions with a crystal lattice and internal diffuse friction. The main peculiarities of the proposed equations are illustrated with the analysis of electron sound waves.

1. Introduction

Hydrodynamic models are widely used for the description of an electronic subsystem in solids [1]. Most research is related to the study of vortex-less flows of the electron fluid in normal metals and superconductors [2,3,4], as well as the electron-hole fluid in semiconductors [5,6,7]. However, in recent years, more attention has been paid to the effects associated with the vortex motion of the electron fluid [8,9].

For the description of vortex flows, many authors use the vector fields, including vectors of local speed and vorticity, which satisfy the symmetric Maxwell-type equations [10,11,12,13,14,15,16,17,18]. In particular, this approach is used to describe the plasma motion within the framework of a hydrodynamic two-fluid model [19,20,21,22,23]. However, in these works, an additional equation for the vortex motion is obtained by taking the “curl” operator from the Euler equation, and, therefore, the resulting equation is not independent. Recently, we developed an alternative approach based on the droplet model of fluid introduced by Helmholtz [24], and obtained a closed system of Maxwell-type equations for the vortex flows which takes into account the rotation and twisting of vortex tubes [25]. In particular, we used this approach to derive self-consistent equations for describing the electron-ion plasma [26]. In the present paper, we apply these equations to develop the hydrodynamic description of vortex flows of electron fluid in solids.

2. Hydrodynamic Model of Electron Fluid in Superconductor

2.1. System of Self-Consistent Equations

From the hydrodynamic point of view, a superconductor is an electron-ion system in which the ions are stationary, while the electronic component is a charged ideal liquid without dissipation. The system of hydrodynamic equations describing the electron fluid in a superconductor can be represented [26] in the following form:

$$\begin{array}{l}\frac{1}{s_s}\left(\frac{\partial }{\partial t}+\left({\mathit{v}}_s·\mathsf{\nabla }\right)\right){\mathit{v}}_s+\mathsf{\nabla }{u}_s+\mathsf{\nabla }\times {\mathit{w}}_s={\alpha }_s{\mathit{E}}_s,\\ \frac{1}{s_s}\left(\frac{\partial }{\partial t}+\left({\mathit{v}}_s·\mathsf{\nabla }\right)\right)u_s+\mathsf{\nabla }·{\mathit{v}}_s=0,\\ \frac{1}{s_s}\left(\frac{\partial }{\partial t}+\left({\mathit{v}}_s·\mathsf{\nabla }\right)\right){\mathit{w}}_s+\mathsf{\nabla }{\xi }_s-\mathsf{\nabla }\times {\mathit{v}}_s={\alpha }_s{\mathit{B}}_s,\\ \frac{1}{s_s}\left(\frac{\partial }{\partial t}+\left({\mathit{v}}_s·\mathsf{\nabla }\right)\right){\xi }_s+\mathsf{\nabla }·{\mathit{w}}_s=0.\end{array}$$

(1)

Here, index s means the values that correspond to superconducting electrons. The parameter $s_s$ is the speed of sound in the superconducting electron fluid; ${\mathit{v}}_s$ is the local flow velocity; $u_s$ is a quantity proportional to the enthalpy per unit mass; ${\mathit{w}}_s$ is a quantity characterizing the rotation of the vortex tubes; ${\xi }_s$ is a quantity that characterizes the twisting of the vortex tubes; and ${\mathit{E}}_s$ and ${\mathit{B}}_s$ are the electric and magnetic fields generated by the electron fluid (see below). The parameter ${\alpha }_s$ is defined as

$${\alpha }_s=-\frac{q_s}{m_s{s}_s}$$

(2)

where $q_s$ is the charge of the Cooper pair ($q_s=2\left|e\right|$) and $m_s$ is the mass of the Cooper pair. The variable $u_s$ is

$$\begin{array}{l}{u}_s=\frac{1}{s_s}{h}_s,\\ d{h}_s=\frac{s_s^2}{n_{0s}}d{n}_s,\end{array}$$

(3)

where $h_s$ is the enthalpy per unit mass, and $n_s$ is the Cooper pairs concentration ($n_{0s}$ is equilibrium concentration). The variable ${\mathit{w}}_s$ is

$$\begin{array}{l}{\mathit{w}}_s=2s_s {\Theta }_s,\\ {\omega }_s=\frac{d{\Theta }_s}{dt},\end{array}$$

(4)

where ${\Theta }_s$ is the angular vector of rotation of the vortex tube and ${\omega }_s$ is the angular velocity of the vortex tube rotation. The value ${\xi }_s$ characterizes the twisting of the vortex tube

$$\left|{\xi }_s\right|=s_s{\beta }_s^{},$$

(5)

where ${\beta }_s$ is the twisting angle of the vortex tube.

The internal electric and magnetic fields are generated only due to deviations of electron fluid parameters from equilibrium values [26]. These fields are described by the following system of equations:

$$\begin{array}{l}\mathsf{\nabla }·{\mathit{E}}_s=-4\pi q_s{n}_s,\\ \mathsf{\nabla }·{\mathit{B}}_s=-4\pi q_s{g}_s,\\ \left(\frac{\partial }{\partial t}+\left({\mathit{v}}_s{}_{}·\mathsf{\nabla }\right)\right){\mathit{B}}_s+s_s\mathsf{\nabla }\times {\mathit{E}}_s=4\pi q_s{n}_s{\mathit{w}}_s,\\ \left(\frac{\partial }{\partial t}+\left({\mathit{v}}_s·\mathsf{\nabla }\right)\right){\mathit{E}}_s-s_s\mathsf{\nabla }\times {\mathit{B}}_s=4\pi q_s{n}_s{\mathit{v}}_s.\end{array}$$

(6)

Equations (1) and (6) form the self-consistent system describing the vortex electron fluid.

2.2. System of Linearized Equations

Neglecting the convective derivatives and linearizing the terms

$$\begin{gathered} 4\pi q_s{n}_s{w}_s\approx 4\pi q_s{n}_{0s}{w}_s, \\ 4\pi q_s{n}_s{v}_s\approx 4\pi q_s{n}_{0s}{v}_s, \end{gathered}$$

(7)

in the field equations we obtain the following set of linearized equations:

$$\begin{array}{l}\frac{1}{s_s}\frac{\partial }{\partial t}{\mathit{v}}_s+\mathsf{\nabla }{u}_s+\mathsf{\nabla }\times {\mathit{w}}_s=-\frac{q_s}{m_s{s}_s}{\mathit{E}}_s,\\ \frac{1}{s_s}\frac{\partial }{\partial t}{u}_s+\mathsf{\nabla }·{\mathit{v}}_s=0,\\ \frac{1}{s_s}\frac{\partial }{\partial t}{\mathit{w}}_s+\mathsf{\nabla }{\xi }_s-\mathsf{\nabla }\times {\mathit{v}}_s=-\frac{q_s}{m_s{s}_s}{\mathit{B}}_s,\\ \frac{1}{s_s}\frac{\partial }{\partial t}{\xi }_s+\mathsf{\nabla }·{\mathit{w}}_s=0,\end{array}$$

(8)

and

$$\begin{array}{l}\mathsf{\nabla }·{\mathit{E}}_s=-4\pi q_s{n}_s,\\ \mathsf{\nabla }·{\mathit{B}}_s=-4\pi q_s{g}_s,\\ \frac{\partial {\mathit{B}}_s}{\partial t}+s_s\mathsf{\nabla }\times {\mathit{E}}_s=4\pi q_s{n}_0{}_s{\mathit{w}}_s,\\ \frac{\partial {\mathit{E}}_s}{\partial t}-s_s\mathsf{\nabla }\times {\mathit{B}}_s=4\pi q_s{n}_0{}_s{\mathit{v}}_s.\end{array}$$

(9)

For linearized equations, we obtain the following relations:

$$\frac{1}{2}\frac{\partial }{\partial t}\left({\mathit{v}}_s^2+{\mathit{w}}_s^2+u_s^2+{\xi }_s^2\right)+s_s\mathsf{\nabla }·\left(\left({\mathit{v}}_s\times {\mathit{w}}_s\right)+u_s{\mathit{v}}_s+{\xi }_s{\mathit{w}}_s\right)=-\frac{q_s}{m_s}\left({\mathit{v}}_s·{\mathit{E}}_s+{\mathit{w}}_s·{\mathit{B}}_s\right),$$

(10)

$$\frac{1}{8\pi }\frac{\partial }{\partial t}\left({\mathit{E}}_s^2+{\mathit{B}}_s^2\right)+\frac{s_s}{4\pi }\mathsf{\nabla }·\left({\mathit{E}}_s\times {\mathit{B}}_s\right)=q_s{n}_{0s}\left({\mathit{v}}_s·{\mathit{E}}_s+{\mathit{w}}_s·{\mathit{B}}_s\right).$$

(11)

The value

$$\frac{1}{2}\left({\mathit{v}}_s^2+{\mathit{w}}_s^2+u_s^2+{\xi }_s^2\right)$$

(12)

represents the density of mechanical energy per unit mass. The value

$$s_s\left(\left({\mathit{v}}_s\times {\mathit{w}}_s\right)+u_s{\mathit{v}}_s+{\xi }_s{\mathit{w}}_s\right)$$

(13)

is the mechanical energy flux density. The value

$$\frac{1}{8\pi }\left({\mathit{E}}_s^2+{\mathit{B}}_s^2\right)$$

(14)

is the volume density of the electromagnetic energy of the internal field, and the value

$$\frac{s_s}{4\pi }\left({\mathit{E}}_s\times {\mathit{B}}_s\right)$$

(15)

is the flux density of the electromagnetic energy of the internal field.

2.3. Sound Waves in a Superconducting Condensate

Let us now consider the small fluctuations of superconducting electron fluid parameters near the equilibrium. The fluctuating contributions are denoted by values with tildes

$$\begin{array}{l}{n}_s=n_{0s}+{\tilde{n}}_s,\\ {\mathit{v}}_s={\tilde{\mathit{v}}}_s,\\ g_s={\tilde{g}}_s,\\ {\mathit{w}}_s={\tilde{\mathit{w}}}_s.\end{array}$$

(16)

Then, we find

$$\begin{array}{l}\frac{1}{s_s}\frac{\partial {\tilde{\mathit{v}}}_s}{\partial t}+\frac{s_s}{n_{0s}}\mathsf{\nabla }{\tilde{n}}_s+\mathsf{\nabla }\times {\tilde{\mathit{w}}}_s=-\frac{q_s}{m_s{s}_s}{\tilde{\mathit{E}}}_s,\\ \frac{1}{n_{0s}}\frac{\partial {\tilde{n}}_s}{\partial t}+\mathsf{\nabla }\cdot {\tilde{\mathit{v}}}_s=0,\\ \frac{1}{s_s}\frac{\partial {\tilde{\mathit{w}}}_s}{\partial t}+\frac{s_s}{n_{0s}}\mathsf{\nabla }{\tilde{g}}_s-\mathsf{\nabla }\times {\tilde{\mathit{v}}}_s=-\frac{q_s}{m_{q_s}{s}_s}{\tilde{\mathit{B}}}_s,\\ \frac{1}{n_{0s}}\frac{\partial {\tilde{g}}_s}{\partial t}+\mathsf{\nabla }\cdot {\tilde{\mathit{w}}}_s=0,\end{array}$$

(17)

and

$$\begin{array}{l}\mathsf{\nabla }\cdot {\tilde{\mathit{E}}}_s=-4\pi q_s{\tilde{n}}_s,\\ \mathsf{\nabla }\cdot {\tilde{\mathit{B}}}_s=-4\pi q_s{\tilde{g}}_s,\\ s_s\mathsf{\nabla }\times {\tilde{\mathit{E}}}_s=-\frac{\partial {\tilde{\mathit{B}}}_s}{\partial t}+4\pi q_s{n}_{0s}{\tilde{\mathit{w}}}_s,\\ s_s\mathsf{\nabla }\times {\tilde{\mathit{B}}}_s=\frac{\partial {\tilde{\mathit{E}}}_s}{\partial t}-4\pi q_s{n}_{0s}{\tilde{\mathit{v}}}_s.\end{array}$$

(18)

From Equations (17) and (18), we obtain the following wave equations for the parameters of electron fluid:

$$\begin{array}{l}\left(\frac{{\partial }^2}{\partial t^2}-s_s^2\mathsf{\Delta }+{\omega }_{sp}^2\right){\tilde{n}}_s=0,\\ \left(\frac{{\partial }^2}{\partial t^2}-s_s^2\mathsf{\Delta }+{\omega }_{sp}^2\right){\tilde{\mathit{v}}}_s=0,\\ \left(\frac{{\partial }^2}{\partial t^2}-s_s^2\mathsf{\Delta }+{\omega }_{sp}^2\right){\tilde{g}}_s=0,\\ \left(\frac{{\partial }^2}{\partial t^2}-s_s^2\mathsf{\Delta }+{\omega }_{sp}^2\right){\tilde{\mathit{w}}}_s=0,\end{array}$$

(19)

and for the internal fields

$$\begin{array}{l}\left(\frac{{\partial }^2}{\partial t^2}-s_s^2\mathsf{\Delta }+{\omega }_{sp}^2\right){\tilde{\mathit{E}}}_s=0,\\ \left(\frac{{\partial }^2}{\partial t^2}-s_s^2\mathsf{\Delta }+{\omega }_{sp}^2\right){\tilde{\mathit{B}}}_s=0.\end{array}$$

(20)

Here, the parameter ${\omega }_{sp}^{}$ is the plasma frequency

$${\omega }_{sp}^2=\frac{4\pi n_{0s}{q}_s^2}{m_s}.$$

(21)

Equations (19) and (20) can then be represented as a single generalized wave equation

$$\left(\frac{{\partial }^2}{\partial t^2}-s_s^2\mathsf{\Delta }+{\omega }_{sp}^2\right){\tilde{P}}_s=0,$$

(22)

where the generalized parameter ${\tilde{P}}_s$ takes any value from the set

$${\tilde{P}}_s\in \left\{{\tilde{n}}_s,{\tilde{g}}_s,{\tilde{\mathit{v}}}_s,{\tilde{\mathit{w}}}_s,{\tilde{\mathit{E}}}_s,{\tilde{\mathit{B}}}_s\right\}.$$

(23)

All sound waves described by Equation (22) have the following dispersion relation

$${\omega }^2-s_s^2{k}^2-{\omega }_{sp}^2=0,$$

(24)

where $\omega$ is the frequency and $k$ is the wave number. The schematic plot of the dispersion relation Equation (24) is represented in Figure 1.

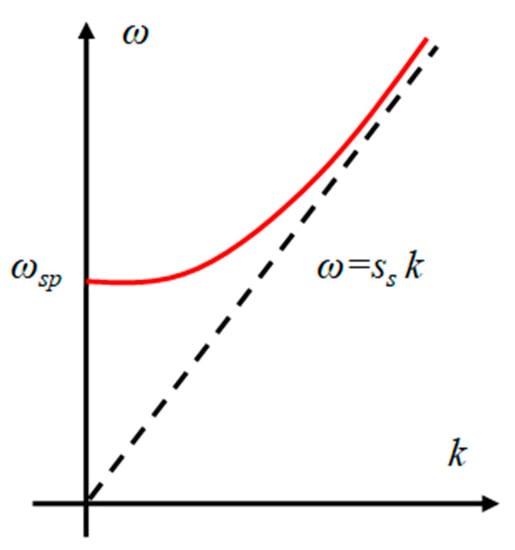
Figure 1. The schematic plot of the dispersion curve for sound waves in the ideal electron fluid of a superconductor.

2.4. Relation to the London Equations

Let us consider the flow of a superconducting condensate without taking into account the vortex motion. Then,

$$\begin{gathered} g_s=0, \\ {\mathit{w}}_s=0, \end{gathered}$$

(25)

and linearized Equation (8) is transformed into

$$\frac{1}{s_s}\frac{\partial {\mathit{v}}_s}{\partial t}+\frac{s_s}{n_{0s}}\mathsf{\nabla }{n}_s=-\frac{q_s}{m_s{s}_s}{\mathit{E}}_s,$$

(26)

$$\mathsf{\nabla }\times {\mathit{v}}_s=\frac{q_s}{m_s{s}_s}{\mathit{B}}_s,$$

(27)

$$\frac{1}{n_{0s}}\frac{\partial n_s}{\partial t}+\mathsf{\nabla }\cdot {\mathit{v}}_s=0.$$

(28)

Rewriting these equations using the usual terms such as the density of charge and current (taking into account the sign of the electron charge), we obtain

$${\mathit{E}}_s=\frac{4\pi }{s_s^2}{\lambda }^2\frac{\partial {\mathit{j}}_s}{\partial t}+4\pi {\lambda }^2\mathsf{\nabla }{\rho }_s,$$

(29)

$${\mathit{B}}_s=-\frac{4\pi }{s_s}{\lambda }^2 \mathsf{\nabla }\times {\mathit{j}}_s,$$

(30)

$$\frac{\partial {\rho }_s}{\partial t}+\mathsf{\nabla }\cdot {\mathit{j}}_s=0,$$

(31)

where

$$\begin{array}{l}{\rho }_s=-q_s{n}_s,\\ {\mathit{j}}_s=-q_s{n}_{0s}{\mathit{v}}_s,\\ {\lambda }^2=\frac{m_s{s}_s^2}{4\pi q_s^2{n}_{0s}}.\end{array}$$

(32)

The corresponding wave equations are

$$\begin{array}{l}\left(\frac{{\partial }^2}{\partial t^2}-s_s^2\mathsf{\Delta }+{\omega }_{sp}^2\right){\rho }_s=0,\\ \left(\frac{{\partial }^2}{\partial t^2}-s_s^2\mathsf{\Delta }+{\omega }_{sp}^2\right){\mathit{j}}_s=0,\end{array}$$

(33)

$$\begin{array}{l}\left(\frac{{\partial }^2}{\partial t^2}-s_s^2\mathsf{\Delta }+{\omega }_{sp}^2\right){\mathit{E}}_s=0,\\ \left(\frac{{\partial }^2}{\partial t^2}-s_s^2\mathsf{\Delta }+{\omega }_{sp}^2\right){\mathit{B}}_s=0.\end{array}$$

(34)

Thus, Equations (29)–(31), (33), and (34) have the form of the London equations [27,28,29]. However, the propagation speed of perturbations in the electron fluid is equal to the speed of electron sound, and not the speed of light, which seems to be more adequate from a physical point of view.

3. Hydrodynamic Model of Ideal Electron-Hole Fluid in Semiconductor

Electron-hole plasma in semiconductors is also often represented as a liquid consisting of charged particles of the opposite sign. To describe sound waves, let us consider the small fluctuations of electron-hole fluid near the equilibrium state

$$\begin{array}{l}{n}_{\alpha }=n_{0\alpha }+{\tilde{n}}_{\alpha },\\ {\mathit{v}}_{\alpha }={\tilde{\mathit{v}}}_{\alpha },\\ g_{\alpha }={\tilde{g}}_{\alpha },\\ {\mathit{w}}_{\alpha }={\tilde{\mathit{w}}}_{\alpha },\\ n_{0e}=n_{0h}=n_0.\end{array}$$

(35)

Here, index $\alpha \in \{e,h\}$ (e is taken for electrons and h is taken for holes). Then, the linearized equations in terms of $n_{\alpha }$ and $g_{\alpha }$ are written as

$$\begin{array}{l}\frac{1}{s_{\alpha }}\frac{\partial {\tilde{\mathit{v}}}_{\alpha }}{\partial t}+\frac{s_{\alpha }}{n_0}\mathsf{\nabla }{\tilde{n}}_{\alpha }+\left[\mathsf{\nabla }\times {\tilde{\mathit{w}}}_{\alpha }\right]=\frac{q_{\alpha }}{m_{\alpha }{s}_{\alpha }}{\tilde{\mathit{E}}}_{\alpha },\\ \frac{1}{n_0}\frac{\partial {\tilde{n}}_{\alpha }}{\partial t}+\left(\mathsf{\nabla }\cdot {\tilde{\mathit{v}}}_{\alpha }\right)=0,\\ \frac{1}{s_{\alpha }}\frac{\partial {\tilde{\mathit{w}}}_{\alpha }}{\partial t}+\frac{s_{\alpha }}{n_0}\mathsf{\nabla }{\tilde{g}}_{\alpha }-\left[\mathsf{\nabla }\times {\tilde{\mathit{v}}}_{\alpha }\right]=\frac{q_{\alpha }}{m_{\alpha }{s}_{\alpha }}{\tilde{\mathit{B}}}_{\alpha },\\ \frac{1}{n_0}\frac{\partial {\tilde{g}}_{\alpha }}{\partial t}+\left(\mathsf{\nabla }\cdot {\tilde{\mathit{w}}}_{\alpha }\right)=0,\end{array}$$

(36)

and

$$\begin{array}{l}\left(\mathsf{\nabla }\cdot {\tilde{\mathit{E}}}_{\alpha }\right)=4\pi e\left({\tilde{n}}_h-{\tilde{n}}_e\right),\\ \left(\mathsf{\nabla }\cdot {\tilde{\mathit{B}}}_{\alpha }\right)=4\pi e\left({\tilde{g}}_h-{\tilde{g}}_e\right),\\ \frac{\partial {\tilde{\mathit{B}}}_{\alpha }}{\partial t}+s_{\alpha }\left[\mathsf{\nabla }\times {\tilde{\mathit{E}}}_{\alpha }\right]=-4\pi e{n}_0\left({\tilde{\mathit{w}}}_h-{\tilde{\mathit{w}}}_e\right),\\ \frac{\partial {\tilde{\mathit{E}}}_{\alpha }}{\partial t}-s_{\alpha }\left[\mathsf{\nabla }\times {\tilde{\mathit{B}}}_{\alpha }\right]=-4\pi e{n}_0\left({\tilde{\mathit{v}}}_h-{\tilde{\mathit{v}}}_e\right).\end{array}$$

(37)

From Equations (36) and (37), we obtain the following wave equations for the fluctuations of electron and hole concentrations:

$$\begin{array}{l}\left(\frac{{\partial }^2}{\partial t^2}-s_h^2\mathsf{\Delta }+{\omega }_{hp}^2\right){\tilde{n}}_h={\omega }_{hp}^2{\tilde{n}}_e,\\ \left(\frac{{\partial }^2}{\partial t^2}-s_e^2\mathsf{\Delta }+{\omega }_{ep}^2\right){\tilde{n}}_e={\omega }_{ep}^2{\tilde{n}}_h.\end{array}$$

(38)

Here, ${\omega }_{hp}$ is the hole plasma frequency and ${\omega }_{ep}$ is the electron plasma frequency:

$${\omega }_{hp}^2=\frac{4\pi n_0{q}_h^2}{m_h},$$

(39)

$${\omega }_{ep}^2=\frac{4\pi n_0{q}_e^2}{m_e}.$$

(40)

Equation (38) can be separated as:

$$\left\{\left(\frac{{\partial }^2}{\partial t^2}-s_e^2\mathsf{\Delta }+{\omega }_{ep}^2\right)\left(\frac{{\partial }^2}{\partial t^2}-s_h^2\mathsf{\Delta }+{\omega }_{hp}^2\right)-{\omega }_{hp}^2{\omega }_{ep}^2\right\}{\tilde{n}}_h=0,$$

(41)

$$\left\{\left(\frac{{\partial }^2}{\partial t^2}-s_e^2\mathsf{\Delta }+{\omega }_{ep}^2\right)\left(\frac{{\partial }^2}{\partial t^2}-s_h^2\mathsf{\Delta }+{\omega }_{hp}^2\right)-{\omega }_{hp}^2{\omega }_{ep}^2\right\}{\tilde{n}}_e=0.$$

(42)

The same equations we obtain for the rest variables describe the electron-hole fluid. The generalized wave equation is written as

$$\left\{\left(\frac{{\partial }^2}{\partial t^2}-s_e^2\mathsf{\Delta }+{\omega }_{ep}^2\right)\left(\frac{{\partial }^2}{\partial t^2}-s_h^2\mathsf{\Delta }+{\omega }_{hp}^2\right)-{\omega }_{hp}^2{\omega }_{ep}^2\right\}{\tilde{P}}_{\alpha }=0,$$

(43)

where the generalized parameter ${\tilde{P}}_{\alpha }$ takes any values from the set

$${\tilde{P}}_{\alpha }\in \left\{{\tilde{n}}_{\alpha },{\tilde{g}}_{\alpha },{\tilde{\mathit{v}}}_{\alpha },{\tilde{\mathit{w}}}_{\alpha },{\tilde{\mathit{E}}}_{\alpha },{\tilde{\mathit{B}}}_{\alpha }\right\}.$$

(44)

All sound waves described by Equation (43) have the following dispersion relation

$$\left({\omega }^2-s_e^2{k}^2-{\omega }_{ep}^2\right)\left({\omega }^2-s_h^2{k}^2-{\omega }_{hp}^2\right)-{\omega }_{hp}^2{\omega }_{ep}^2=0.$$

(45)

The schematic plots illustrating this dispersion relation are represented in Figure 2. If $k=0$, then one has two roots of Equation (45):

$$\begin{array}{l}\omega =0,\\ \omega ={\omega }_{\ast }=\sqrt{{\omega }_{ep}^2+{\omega }_{hp}^2}.\end{array}$$

(46)

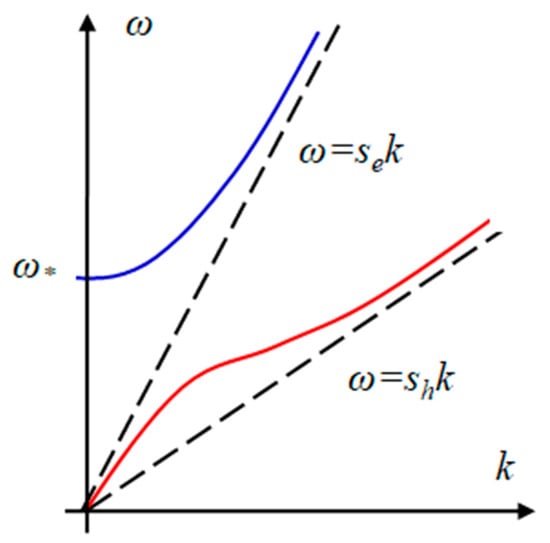
Figure 2. The schematic plots of dispersion curves for sound waves in the electron-hole fluid.

If $k\to \infty$, we have two asymptotes

$$\omega =s_e^{}k,$$

(47)

and

$$\omega =s_h^{}k$$

(48)

We assume that $m_h>m_e$ and $s_h>s_e$.

The upper curve corresponds to the electron sound, while the lower curve corresponds to the hole sound. The group velocity of hole sound in the long wave limit ($k\to 0$) is

$$v_{hg}=\frac{d\omega }{dk}=\sqrt{\frac{s_e^2{\omega }_{hp}^2+s_h^2{\omega }_{ep}^2}{{\omega }_{ep}^2+{\omega }_{hp}^2}},$$

(49)

which is between $s_e>v_{hg}>s_h$.

4. Hydrodynamic Model of Electron Fluid in Normal Metal

In a normal metal, electrons collide with crystal lattice defects and phonons, which are accompanied by energy dissipation processes. Such a damping of electron fluid disturbances can be described by the following replacement of operators in all equations:

$$\frac{\partial }{\partial t}+\left(\mathit{v}\cdot \mathsf{\nabla }\right)\Rightarrow \frac{\partial }{\partial t}+\left(\mathit{v}\cdot \mathsf{\nabla }\right)+\epsilon ,$$

(50)

where $\epsilon$ is the average frequency of collisions. On the other hand, in the case of dense electron fluid, it is also necessary to take into account the diffusion damping of disturbances. Both these damping processes can be described by the following replacement of operators:

$$\frac{\partial }{\partial t}+\left(\mathit{v}\cdot \mathsf{\nabla }\right)\Rightarrow \frac{\partial }{\partial t}+\left(\mathit{v}\cdot \mathsf{\nabla }\right)+\epsilon -\mu \mathsf{\Delta },$$

(51)

where $\mu$ is the coefficient of viscosity. Then, the linearized equations describing the motion of the electron fluid are written as follows:

$$\begin{array}{l}\frac{1}{s_n}\left(\frac{\partial }{\partial t}+\epsilon -\mu \mathsf{\Delta }\right){\mathit{v}}_n+\mathsf{\nabla }{u}_n+\mathsf{\nabla }\times {\mathit{w}}_n=-\frac{q_n}{m_n{s}_n}{\mathit{E}}_n,\\ \frac{1}{s_n}\left(\frac{\partial }{\partial t}+\epsilon -\mu \mathsf{\Delta }\right)u_n+\mathsf{\nabla }\cdot {\mathit{v}}_n=0,\\ \frac{1}{s_n}\left(\frac{\partial }{\partial t}+\epsilon -\mu \mathsf{\Delta }\right){\mathit{w}}_n+\mathsf{\nabla }{\xi }_n-\mathsf{\nabla }\times {\mathit{v}}_n=-\frac{q_n}{m_n{s}_n}{\mathit{B}}_n,\\ \frac{1}{s_n}\left(\frac{\partial }{\partial t}+\epsilon -\mu \mathsf{\Delta }\right){\xi }_n+\mathsf{\nabla }\cdot {\mathit{w}}_n=0,\end{array}$$

(52)

and

$$\begin{array}{l}\mathsf{\nabla }\cdot {\mathit{E}}_n=-4\pi q_n{n}_n,\\ \mathsf{\nabla }\cdot {\mathit{B}}_n=-4\pi q_n{g}_n,\\ \left(\frac{\partial }{\partial t}+\epsilon -\mu \mathsf{\Delta }\right){\mathit{B}}_n+s_n\mathsf{\nabla }\times {\mathit{E}}_n=4\pi q_n{n}_0{}_n{\mathit{w}}_n,\\ \left(\frac{\partial }{\partial t}+\epsilon -\mu \mathsf{\Delta }\right){\mathit{E}}_n-s_n\mathsf{\nabla }\times {\mathit{B}}_n=4\pi q_n{n}_0{}_n{\mathit{v}}_n.\end{array}$$

(53)

From Equations (52) and (53), we obtain the following relations for energy and momentum:

$$\begin{array}{l}\frac{1}{2}\frac{\partial }{\partial t}\left({\mathit{v}}_n^2+{\mathit{w}}_n^2+u_n^2+{\xi }_n^2\right)+\epsilon \left({\mathit{v}}_n^2+{\mathit{w}}_n^2+u_n^2+{\xi }_n^2\right)+s_n\mathsf{\nabla }\cdot \left(\left({\mathit{v}}_n\times {\mathit{w}}_n\right)+u_n{\mathit{v}}_n+{\xi }_n{\mathit{w}}_n\right)\\ -\mu \left(u_n\mathsf{\Delta }{u}_n+{\xi }_n\mathsf{\Delta }{\xi }_n+\left({\mathit{v}}_n\cdot \mathsf{\Delta }{\mathit{v}}_n\right)+\left({\mathit{w}}_n\cdot \mathsf{\Delta }{\mathit{w}}_n\right)\right)=-\frac{q_n}{m_n}\left({\mathit{v}}_n\cdot {\mathit{E}}_n+{\mathit{w}}_n\cdot {\mathit{B}}_n\right),\end{array}$$

(54)

and

$$\begin{array}{l}\frac{1}{8\pi }\frac{\partial }{\partial t}\left({\mathit{E}}_n^2+{\mathit{B}}_n^2\right)+\frac{\epsilon }{4\pi }\left({\mathit{E}}_n^2+{\mathit{B}}_n^2\right)-\mu \left\{\left({\mathit{E}}_n\cdot \mathsf{\Delta }{\mathit{E}}_n\right)+\left({\mathit{B}}_n\cdot \mathsf{\Delta }{\mathit{B}}_n\right)\right\}\\ \frac{s_n}{4\pi }\mathsf{\nabla }\cdot \left({\mathit{E}}_n\times {\mathit{B}}_n\right)=-q_n{n}_0{}_n\left({\mathit{v}}_n\cdot {\mathit{E}}_n+{\mathit{w}}_n\cdot {\mathit{B}}_n\right).\end{array}$$

(55)

To describe sound waves, let us consider the small fluctuations of electron fluid parameters in the normal metal near the equilibrium state

$$\begin{array}{l}{n}_n=n_0{}_n+{\tilde{n}}_n,\\ {\mathit{v}}_n={\tilde{\mathit{v}}}_n,\\ g_n={\tilde{g}}_n,\\ {\mathit{w}}_n={\tilde{\mathit{w}}}_n.\end{array}$$

(56)

Then, the linearized equations for sound waves in electron fluid are

$$\begin{array}{l}\frac{1}{s_n}\left(\frac{\partial }{\partial t}+\epsilon -\mu \mathsf{\Delta }\right){\tilde{\mathit{v}}}_n+\frac{s_n}{n_{0n}}\mathsf{\nabla }{\tilde{n}}_n+\mathsf{\nabla }\times {\tilde{\mathit{w}}}_n=-\frac{q_n}{m_n{s}_n}{\tilde{\mathit{E}}}_n,\\ \frac{1}{n_{0n}}\left(\frac{\partial }{\partial t}+\epsilon -\mu \mathsf{\Delta }\right){\tilde{n}}_n+\mathsf{\nabla }\cdot {\tilde{\mathit{v}}}_n=0,\\ \frac{1}{s_n}\left(\frac{\partial }{\partial t}+\epsilon -\mu \mathsf{\Delta }\right){\tilde{\mathit{w}}}_n+\frac{s_n}{n_{0n}}\mathsf{\nabla }{\tilde{g}}_n-\mathsf{\nabla }\times {\tilde{\mathit{v}}}_n=-\frac{q_n}{m_n{s}_n}{\tilde{\mathit{B}}}_n,\\ \frac{1}{n_{0n}}\left(\frac{\partial }{\partial t}+\epsilon -\mu \mathsf{\Delta }\right){\tilde{g}}_n+\mathsf{\nabla }\cdot {\tilde{\mathit{w}}}_n=0,\end{array}$$

(57)

and the fields satisfy the equations

$$\begin{array}{l}\mathsf{\nabla }\cdot {\tilde{\mathit{E}}}_n=-4\pi q_n{\tilde{n}}_n,\\ \mathsf{\nabla }\cdot {\tilde{\mathit{B}}}_n=-4\pi q_n{\tilde{g}}_n,\\ \left(\frac{\partial }{\partial t}+\epsilon -\mu \mathsf{\Delta }\right){\tilde{\mathit{B}}}_n+s_n\mathsf{\nabla }\times {\tilde{\mathit{E}}}_n=4\pi q_n{n}_0{}_n{\tilde{\mathit{w}}}_n,\\ \left(\frac{\partial }{\partial t}+\epsilon -\mu \mathsf{\Delta }\right){\tilde{\mathit{E}}}_n-s_n\mathsf{\nabla }\times {\tilde{\mathit{B}}}_n=4\pi q_n{n}_0{}_n{\tilde{\mathit{v}}}_n.\end{array}$$

(58)

From Equations (57) and (58), we obtain the following generalized wave equation:

$$\left({\left(\frac{\partial }{\partial t}+\epsilon -\mu \mathsf{\Delta }\right)}^2-s_n^2\mathsf{\Delta }+{\omega }_{np}^2\right){\tilde{P}}_n=0,$$

(59)

where the generalized parameter ${\tilde{P}}_n$ takes any values from the set

$${\tilde{P}}_n\in \left\{{\tilde{n}}_n,{\tilde{g}}_n,{\tilde{\mathit{v}}}_n,{\tilde{\mathit{w}}}_n,{\tilde{\mathit{E}}}_n,{\tilde{\mathit{B}}}_n\right\}.$$

(60)

The dispersion relation for Equation (59) is

$${\omega }^2-2i\omega \left(\epsilon +\mu k^2\right)-{\left(\epsilon +\mu k^2\right)}^2-s_n^2{k}^2-{\omega }_{np}^2=0.$$

(61)

This equation has two roots

$$\omega =i\left(\epsilon +\mu k^2\right)\pm \sqrt{s_n^2{k}^2+{\omega }_{np}^2}.$$

(62)

The real part of Equation (62) is represented in Figure 3a. If $k\to \infty$, it has the asymptote

$$\omega =s_n^{}k.$$

(63)

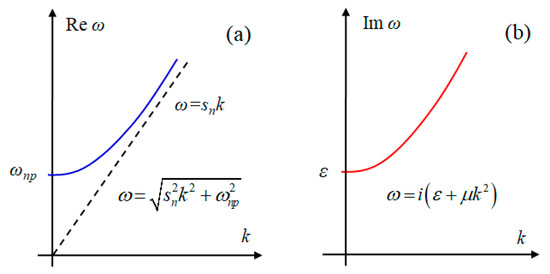
Figure 3. The schematic plots of dispersion curves for electron sound waves in normal metal. (a) The dependence of the frequency on the wave number. (b) The dependence of the decrement on the wave number.

The imaginary part of Equation (62) is represented in Figure 3b. It corresponds to the damped sound waves with decrement $\left(\epsilon +\mu k^2\right)$.

5. Conclusions

We have thus proposed a self-consistent hydrodynamic model for non-radiative electron fluid in solids consisting of the equations for the vortex flow of electron fluid and the equations for the frozen-in electromagnetic field. Frozen fields satisfy modified Maxwell’s equations, which show that they are caused by currents and charge density fluctuations and move along with the electron fluid. To take into account the processes of electromagnetic wave radiation, this model must be supplemented with equations for electromagnetic fields in a vacuum and energy balance equations. Electromagnetic fields from external sources can also be taken into account additively in the system of equations describing the electron fluid [30].

The proposed approach enables the description of superconducting condensate in the superconductor as the ideal electron fluid without dissipation. In the case of vortex-less flow, it leads us to equations very close to the London equations, but the speed of the propagation of small fluctuations is equal to the speed of electron sound, not the speed of light. This seems to be more appropriate from a physical point of view. The damping processes in normal metals can be described by modifying the operator parts of the equations with additional terms that denote the electron collision frequency and internal diffusion friction in electron fluid. Moreover, we have shown that the electron-hole plasma in a semiconductor can be described by similar equations within the two-fluid model.

The advantages of self-consistent equations have been illustrated by the derivation and analysis of the wave equations for electron sound waves in solids.