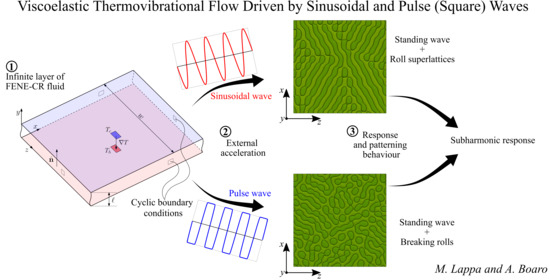
Viscoelastic Thermovibrational Flow Driven by Sinusoidal and Pulse (Square) Waves
Abstract
1. Introduction
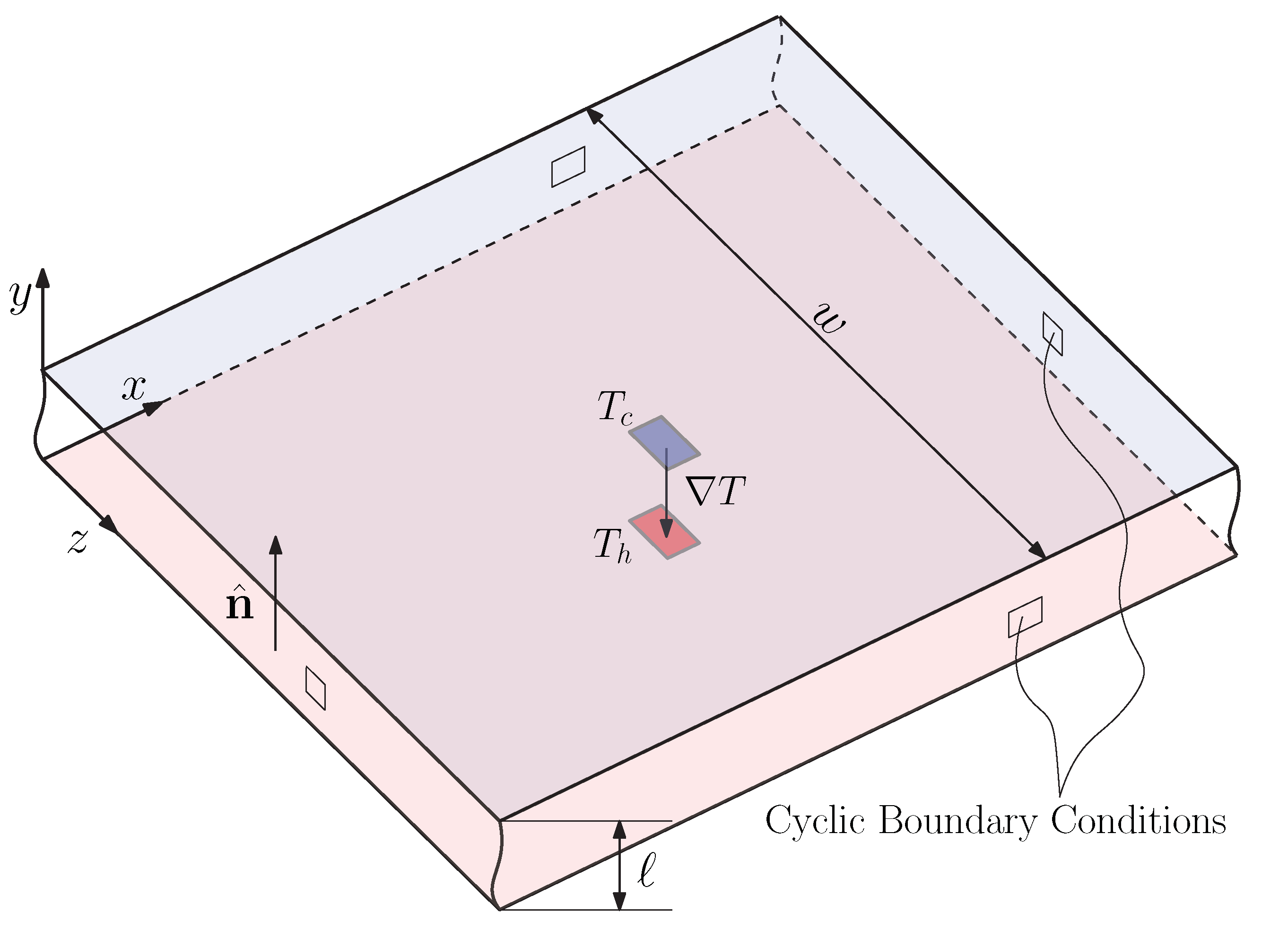
2. Mathematical Model
3. Numerical Method
4. Results
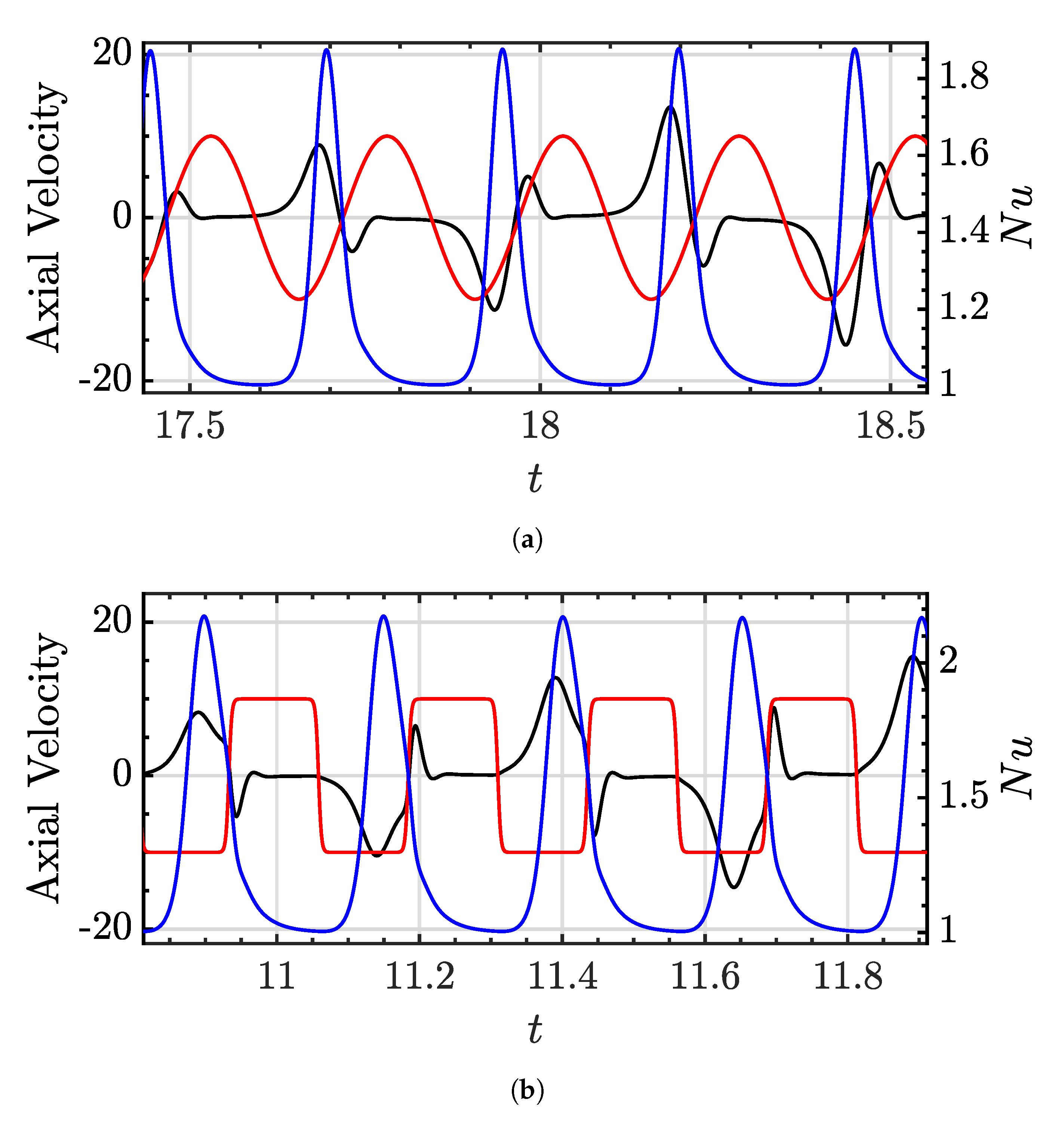
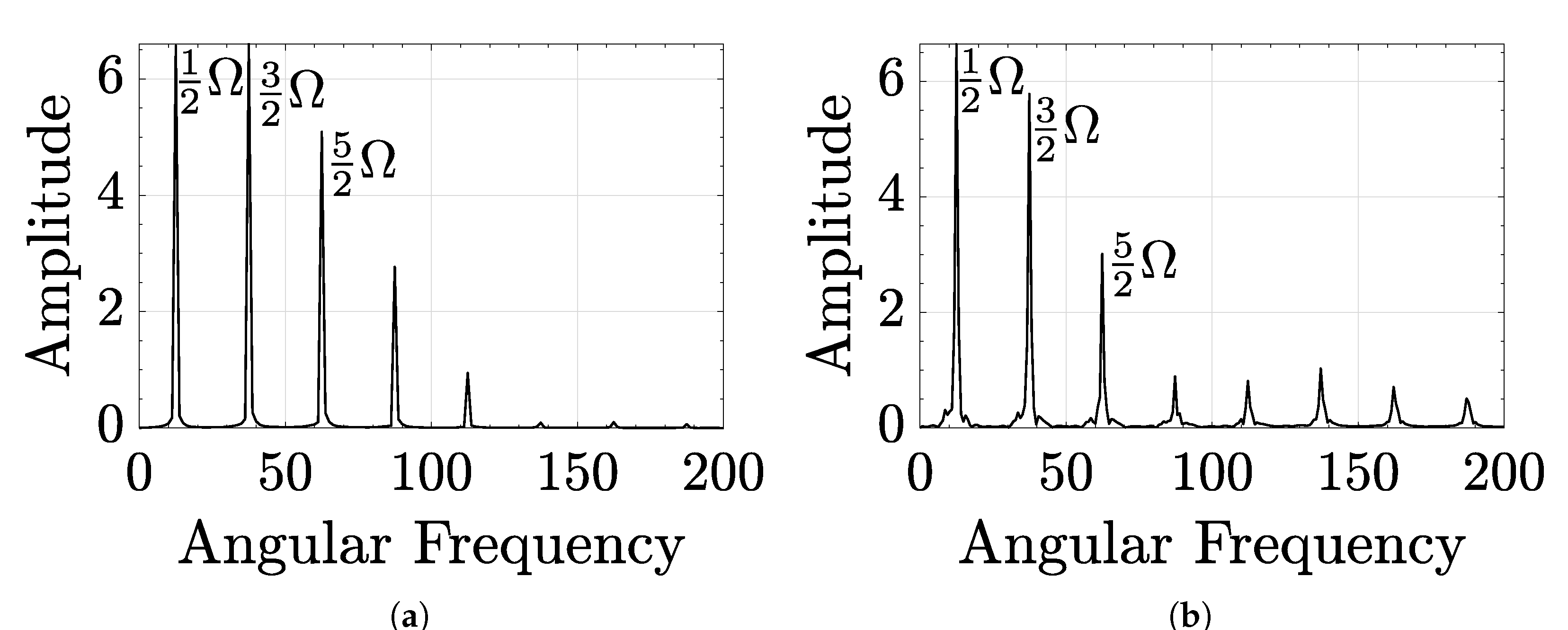
4.1. Forcing and Related System Response
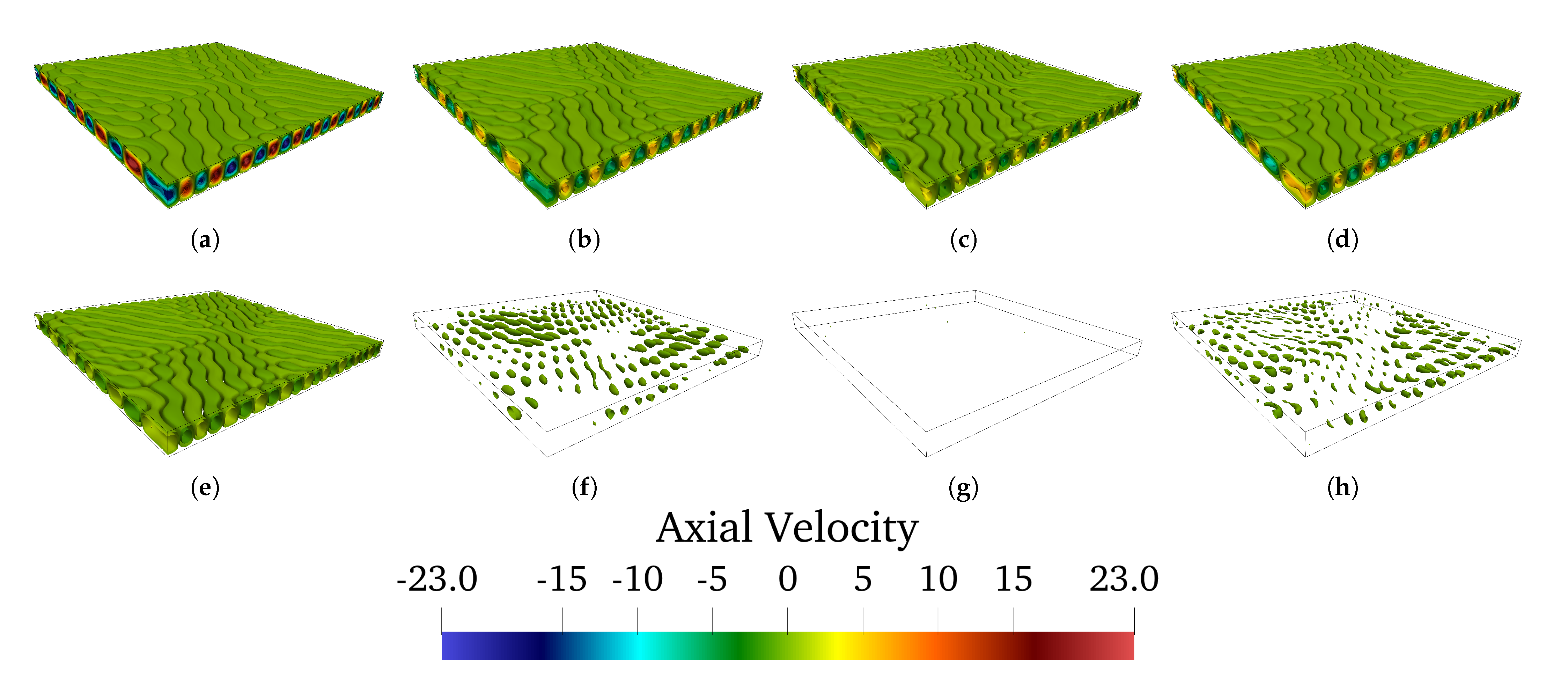
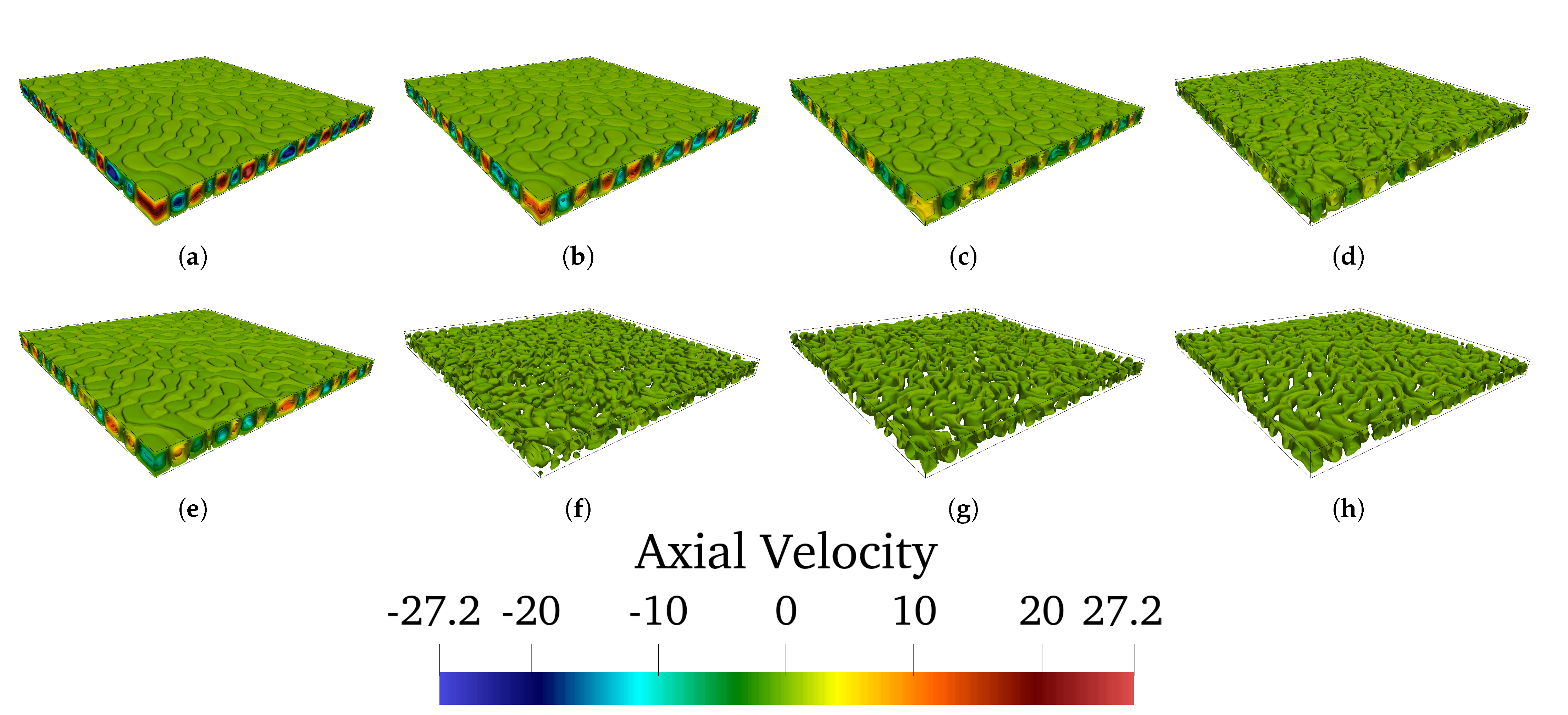
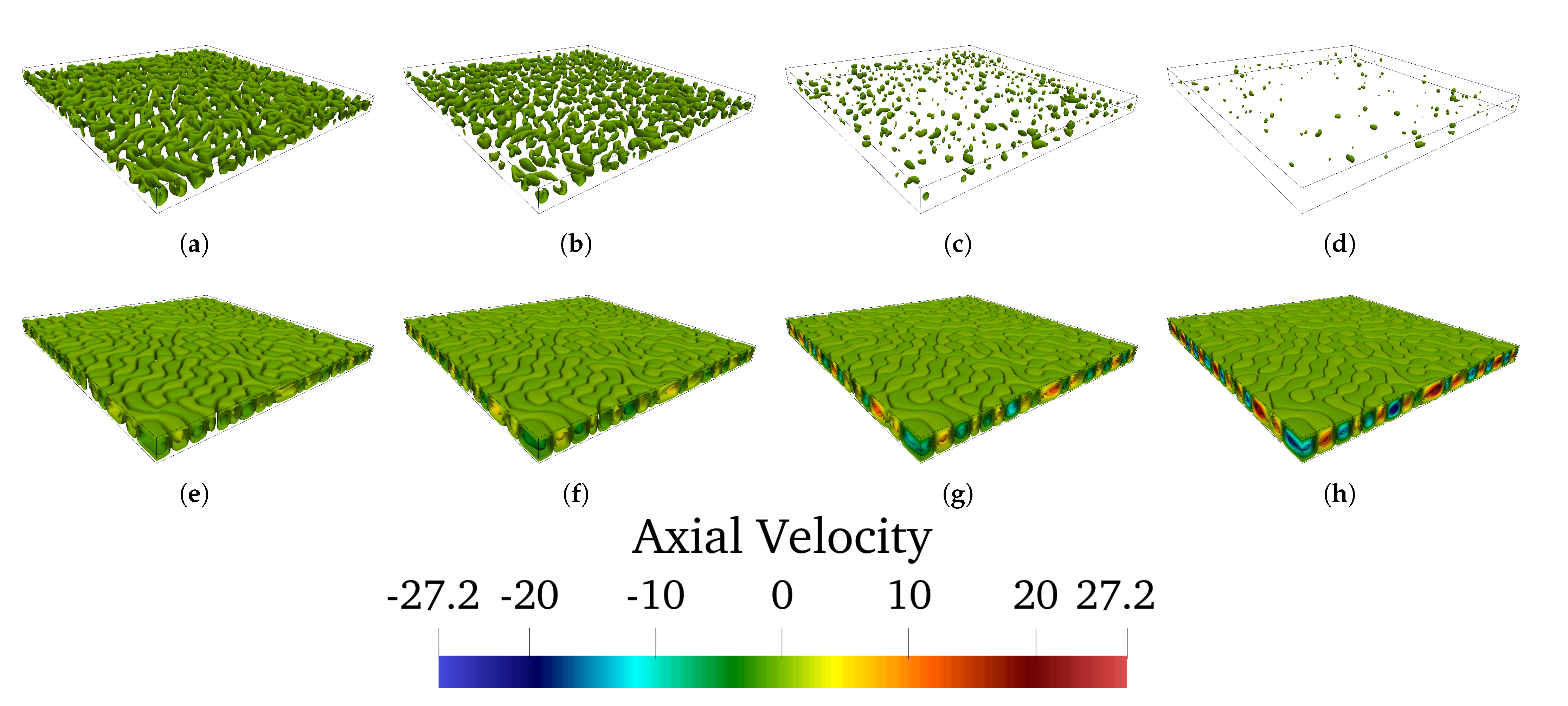
4.2. Patterning Behaviour and 3D Evolution
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lappa, M. Thermal Convection: Patterns, Evolution and Stability; John Wiley & Sons, Ltd.: Chichester, UK, 2009. [Google Scholar] [CrossRef]
- Mialdun, A.; Ryzhkov, I.I.; Melnikov, D.E.; Shevtsova, V. Experimental Evidence of Thermal Vibrational Convection in a Nonuniformly Heated Fluid in a Reduced Gravity Environment. Phys. Rev. Lett. 2008, 101, 084501. [Google Scholar] [CrossRef] [PubMed]
- Savino, R.; Lappa, M. Assessment of Thermovibrational Theory: Application to G -Jitter on the Space Station. J. Spacecr. Rocket. 2003, 40, 201–210. [Google Scholar] [CrossRef]
- Lappa, M. Control of Convection Patterning and Intensity in Shallow Cavities by Harmonic Vibrations. Microgravity Sci. Technol. 2016, 28, 29–39. [Google Scholar] [CrossRef]
- Boaro, A.; Lappa, M. Multicellular states of viscoelastic thermovibrational convection in a square cavity. Phys. Fluids 2021, 33, 033105. [Google Scholar] [CrossRef]
- Busse, F.H.; Whitehead, J.A. Instabilities of convection rolls in a high Prandtl number fluid. J. Fluid Mech. 1971, 47, 305–320. [Google Scholar] [CrossRef]
- Busse, F.H.; Clever, R.M. Instabilities of convection rolls in a fluid of moderate Prandtl number. J. Fluid Mech. 1979, 91, 319–335. [Google Scholar] [CrossRef]
- Clever, R.M.; Busse, F.H. Nonlinear oscillatory convection. J. Fluid Mech. 1987, 176, 403–417. [Google Scholar] [CrossRef]
- Clever, R.M.; Busse, F.H. Convection at very low Prandtl numbers. Phys. Fluids A Fluid Dyn. 1990, 2, 334–339. [Google Scholar] [CrossRef]
- Clever, R.M.; Busse, F.H. Steady and oscillatory bimodal convection. J. Fluid Mech. 1994, 271, 103–118. [Google Scholar] [CrossRef]
- Clever, R.M.; Busse, F.H. Standing and travelling oscillatory blob convection. J. Fluid Mech. 1995, 297, 255–273. [Google Scholar] [CrossRef]
- Green, T. Oscillating Convection in an Elasticoviscous Liquid. Phys. Fluids 1968, 11, 1410–1412. [Google Scholar] [CrossRef]
- Vest, C.M.; Arpaci, V.S. Overstability of a viscoelastic fluid layer heated from below. J. Fluid Mech. 1969, 36, 613–623. [Google Scholar] [CrossRef]
- Sokolov, M.; Tanner, R.I. Convective Stability of a General Viscoelastic Fluid Heated from Below. Phys. Fluids 1972, 15, 534–539. [Google Scholar] [CrossRef]
- Larson, R.G. Instabilities in viscoelastic flows. Rheol. Acta 1992, 31, 213–263. [Google Scholar] [CrossRef]
- Krapivina, E.N.; Lyubimova, T.P. Nonlinear regimes of convection of an elasticoviscous fluid in a closed cavity heated from below. Fluid Dyn. 2000, 35, 473–478. [Google Scholar] [CrossRef]
- Park, H.M.; Shin, K.S.; Sohn, H.S. Numerical simulation of thermal convection of viscoelastic fluids using the grid-by-grid inversion method. Int. J. Heat Mass Transf. 2009, 52, 4851–4861. [Google Scholar] [CrossRef]
- Park, H.M.; Lim, J.Y. A new numerical algorithm for viscoelastic fluid flows: The grid-by-grid inversion method. J. Non-Newton. Fluid Mech. 2010, 165, 238–246. [Google Scholar] [CrossRef]
- Kovalevskaya, K.V.; Lyubimova, T.P. Onset and nonlinear regimes of convection of an elastoviscous fluid in a closed cavity heated from below. Fluid Dyn. 2011, 46, 854–863. [Google Scholar] [CrossRef]
- Park, H.M. Peculiarity in the Rayleigh-Bénard convection of viscoelastic fluids. Int. J. Therm. Sci. 2018, 132, 34–41. [Google Scholar] [CrossRef]
- Simonenko, I.B.; Zen’kovskaya, S. On the effect of high frequency vibrations on the origin of convection. Izv. Akad. Nauk SSSR Ser. Mech. Zhidk. Gaza 1966, 5, 51–55. [Google Scholar]
- Simonenko, I.B. A justification of the averaging method for a problem of convection in a field of rapidly oscillating forces and for other parabolic equations. Math. USSR-Sb. 1972, 16, 245–263. [Google Scholar] [CrossRef]
- Gershuni, G.Z.; Zhukhovitskii, E.M. Free thermal convection in a vibrational field under conditions of weightlessness. Sov. Phys. Dokl. 1979, 24, 894–896. [Google Scholar]
- Gershuni, G.Z.; Zhukhovitskii, E.M.; Yurkov, Y.S. Vibrational thermal convection in a rectangular cavity. Fluid Dyn. 1982, 17, 565–569. [Google Scholar] [CrossRef]
- Gershuni, G.Z.; Zhukhovitskii, E.M. Vibrational thermal convection in zero gravity. Fluid. Mech. Sov. Res. 1986, 15, 63–84. [Google Scholar]
- Lappa, M. Fluids, Materials and Microgravity: Numerical Techniques and Insights into the Physics, 1st ed.; Elsevier Science: Oxford, UK, 2004. [Google Scholar] [CrossRef]
- Bouarab, S.; Mokhtari, F.; Kaddeche, S.; Henry, D.; Botton, V.; Medelfef, A. Theoretical and numerical study on high frequency vibrational convection: Influence of the vibration direction on the flow structure. Phys. Fluids 2019, 31, 043605. [Google Scholar] [CrossRef]
- Hirata, K.; Sasaki, T.; Tanigawa, H. Vibrational effects on convection in a square cavity at zero gravity. J. Fluid Mech. 2001, 445, 327–344. [Google Scholar] [CrossRef]
- Crewdson, G.; Lappa, M. The Zoo of Modes of Convection in Liquids Vibrated along the Direction of the Temperature Gradient. Fluids 2021, 6, 30. [Google Scholar] [CrossRef]
- Boaro, A.; Lappa, M. Competition of overstability and stabilizing effects in viscoelastic thermovibrational flow. Phys. Rev. E 2021, 104, 025102. [Google Scholar] [CrossRef]
- Lappa, M.; Boaro, A. Rayleigh–Bénard convection in viscoelastic liquid bridges. J. Fluid Mech. 2020, 904, A2. [Google Scholar] [CrossRef]
- Lappa, M. Thermally-Driven Flows in Polymeric Liquids. In Reference Module in Materials Science and Materials Engineering; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Lyubimova, T.; Kovalevskaya, K. Gravity modulation effect on the onset of thermal buoyancy convection in a horizontal layer of the Oldroyd fluid. Fluid Dyn. Res. 2016, 48, 061419. [Google Scholar] [CrossRef]
- Bird, R.B.; Dotson, P.J.; Johnson, N. Polymer solution rheology based on a finitely extensible bead—Spring chain model. J. Non-Newton. Fluid Mech. 1980, 7, 213–235. [Google Scholar] [CrossRef]
- Chilcott, M.D.; Rallison, J.M. Creeping flow of dilute polymer solutions past cylinders and spheres. J. Non-Newton. Fluid Mech. 1988, 29, 381–432. [Google Scholar] [CrossRef]
- Rhie, C.M.; Chow, W.L. Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Favero, J.L.; Secchi, A.R.; Cardozo, N.S.M.; Jasak, H. Viscoelastic flow analysis using the software OpenFOAM and differential constitutive equations. J. Non-Newton. Fluid Mech. 2010, 165, 1625–1636. [Google Scholar] [CrossRef]
- Crewdson, G.; Lappa, L. Thermally-driven flows and turbulence in vibrated liquids. Int. J. Thermofluids 2021, 11, 100102. [Google Scholar] [CrossRef]
- Li, Z.; Khayat, R.E. Finite-amplitude Rayleigh–Bénard convection and pattern selection for viscoelastic fluids. J. Fluid Mech. 2005, 529, 221–251. [Google Scholar] [CrossRef]
- Morozov, A.; Spagnolie, S.E. Introduction to Complex Fluids. In Complex Fluids in Biological Systems: Experiment, Theory, and Computation; Spagnolie, S.E., Ed.; Springer: New York, NY, USA, 2015; pp. 3–52. [Google Scholar] [CrossRef]
- Rogers, J.L.; Schatz, M.F.; Brausch, O.; Pesch, W. Superlattice Patterns in Vertically Oscillated Rayleigh-Bénard Convection. Phys. Rev. Lett. 2000, 85, 4281–4284. [Google Scholar] [CrossRef] [PubMed]
- Rogers, J.L.; Schatz, M.F.; Bougie, J.L.; Swift, J.B. Rayleigh-Bénard Convection in a Vertically Oscillated Fluid Layer. Phys. Rev. Lett. 2000, 84, 87–90. [Google Scholar] [CrossRef]
- Rogers, J.L.; Pesch, W.; Schatz, M.F. Pattern formation in vertically oscillated convection. Nonlinearity 2002, 16, C1–C10. [Google Scholar] [CrossRef][Green Version]
- Rogers, J.L.; Pesch, W.; Brausch, O.; Schatz, M.F. Complex-ordered patterns in shaken convection. Phys. Rev. E 2005, 71, 066214. [Google Scholar] [CrossRef]
- Hohenberg, P.C.; Swift, J.B. Hexagons and rolls in periodically modulated Rayleigh-Bénard convection. Phys. Rev. A 1987, 35, 3855–3873. [Google Scholar] [CrossRef] [PubMed]
- Meyer, C.W.; Cannell, D.S.; Ahlers, G.; Swift, J.B.; Hohenberg, P.C. Pattern Competition in Temporally Modulated Rayleigh-Bénard Convection. Phys. Rev. Lett. 1988, 61, 947–950. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lappa, M.; Boaro, A. Viscoelastic Thermovibrational Flow Driven by Sinusoidal and Pulse (Square) Waves. Fluids 2021, 6, 311. https://doi.org/10.3390/fluids6090311
Lappa M, Boaro A. Viscoelastic Thermovibrational Flow Driven by Sinusoidal and Pulse (Square) Waves. Fluids. 2021; 6(9):311. https://doi.org/10.3390/fluids6090311
Chicago/Turabian StyleLappa, Marcello, and Alessio Boaro. 2021. "Viscoelastic Thermovibrational Flow Driven by Sinusoidal and Pulse (Square) Waves" Fluids 6, no. 9: 311. https://doi.org/10.3390/fluids6090311
APA StyleLappa, M., & Boaro, A. (2021). Viscoelastic Thermovibrational Flow Driven by Sinusoidal and Pulse (Square) Waves. Fluids, 6(9), 311. https://doi.org/10.3390/fluids6090311