Abstract
Seiches and resonances are two closely related phenomena that can cause damage to coastal areas. Seiches that occur in a basin at a distinct period named the resonant period may generate resonance when a wave induced by external forces enters the basin and has the same period as the seiches. Studying this period has become essential if we want to understand the resonance better. Thus, in this paper, we derive the resonant period in various shapes of semi-closed basin using the shallow water equations. The equations are then solved analytically using the separation of variables method and numerically using the finite volume method on staggered grid to discover the resonant period for each basin. To validate the numerical scheme, we compare its results against the analytical resonant periods, resulting in a very small error for each basin, suggesting that the numerical model is quite reliable in the estimation of the analytical resonant period. Further, resonant wave profiles are also observed. It is revealed that, in the coupled rectangular basin, the maximum wave elevation is disproportionate to the ratio of the length of the basin, while, in the trapezoidal basin, the ratio of the depth of the basin has no significant impact on the maximum wave elevation.
1. Introduction
Seiches are standing waves that arise in a closed basin (e.g., lake, pool, and reservoir) or semi-closed basin (e.g., bay, port, and harbor) with a unique period. Many theories surrounding seiches originate from Forel’s remarkable publications, which began in 1892 [1]. Seiches may be initiated by a number of exciting forces, such as seismic and atmospheric pressure disturbances, wind, or internal and surface gravity waves [2,3]. These oscillations occur at a particular period commonly called the natural (resonant) period, which strongly depends on the length and depth of the basin in which the seiches occur. The major issue is considered when an external wave enters the basin and has a period that matches the natural period, and therefore resonance happens. Such an occurrence is potentially destructive, as it can destroy moored ships and infrastructures in a port, disrupt coastal activities, and harm the structure located near lakes, reservoirs, or coastlines. The worst consequence that we might encounter is a tsunami wave accompanied by a resonance that ultimately leads to a hazard in the coastal region. Several researchers have documented tsunami cases that are associated with resonance, such as Munger and Cheung [4], Roeber et al. [5], and Yamazaki and Cheung [6], who confirmed the 2006 Kuril, 2009 Samoa, and 2010 Chilean tsunamis over the insular shelves and slopes of Hawaii, American Samoa, and Chile that triggered long oscillations in coastal waters.
In consideration of the negative impacts of tsunami waves on coastlines, we need to find an appropriate way to avoid resonance phenomena. One of the strategies to prevent resonance is to understand the characteristics of seiches over a certain type of basin, particularly its resonant period. Numerous studies have analytically examined the resonant period in the simpler geometric form of basin, which is a rectangular type [7,8,9,10,11]. In addition, many other researchers have discovered the resonant period of the triangular (isosceles) and parabolic shaped basin [9,11]. Magdalena, et. al [12] have extended these studies by involving bottom friction in the derivation of wave resonant period. More complicated bottom topographies, such as semi-closed quartic, triangular (right-angled), trapezoidal, and coupled rectangular type, are rarely studied analytically due to the complexities of the basin depth formula. One of the rare studies that have investigated the quartic basin using an analytical approach was published by Chrystal [1] and Magdalena et al. [13]. However, they only provided the resonant period for closed quartic basin. Meanwhile, for triangular (right-angled), trapezoidal, and coupled rectangular form, e.g., Wilson [14], Rabinovich [15], and Dean and Dalrymple [16] derived analytical solutions from potential theory to approximate the resonant period of seiches in closed basins of those types, while the subject analysis for semi-closed basins has not yet been published, experimentally, analytically, or computationally. Thus, the analytical and numerical solution presented in this paper are new approaches in calculating the resonant period for semi-closed quartic, triangular (right-angled), trapezoidal, and coupled rectangular basin. Moreover, these shapes are more realistic in approximating the structure of a waterbody (e.g., continental shelf, inlet, and gulf) than the simpler geometries mentioned above.
Therefore, in this paper, we propose a mathematical model to simulate seiches, along with corresponding resonance phenomena, in various types of basin, in particular semi-closed quartic, triangular (right-angled), trapezoidal, and coupled rectangular type, in which configurations are modification from Wilson [14]. To focus the study, we only examine the phenomena in semi-closed basins with constant width and no friction force is involved. The main objectives of this paper are to determine the fundamental resonant period of the seiches in each type of basin and analyze the wave profile as a result of the resonance phenomenon. Linear shallow water equations (LSWE) are used, which are to be solved analytically and numerically in order to obtain the resonant period. Separation of the variables method is applied to derive the periods analytically, while the finite volume method on the staggered grid is implemented to formulate a scheme to simulate the model and to acquire the periods numerically. The LSWE model have already been validated previously against the available experimental resonant periods for rectangular, triangular (isosceles), and parabolic cases [9,11]. However, in this work, because we use different basin configurations from the mentioned studies, the analytical approaches in those works are not applicable for our cases. Hence, we need to develop a new analytical procedure in finding the resonant period.
The numerical scheme used in this paper has been tested and validated [17,18,19,20] to emulate various fluid phenomena. In this paper, we apply the same numerical method to simulate the wave resonance phenomenon and obtain the natural period. We also confirm our numerical model, particularly on approximating the resonant period of quartic, triangular (right-angled), trapezoidal, and coupled rectangular semi-closed basin, by comparing the simulations results against the analytical solutions. The accuracy of the numerical method is tested along with the rate of convergence, which has not been provided yet by other works. Further, the profile of the resonant wave is also evaluated to understand the behavior of the wave produced by the resonance phenomenon, depending on the type of basin. From this paper, we expect that the developed model and computational scheme can be conveniently used to extend the topic of the resonant period in the future, so that we can examine seiches, resonance, and their periods in other types of basin that have not been discovered before without the need for a costly experimental model.
The paper is organized into six main sections. Section 1 provides a concise explanation of seiches, resonances, and why those events are dangerous and need to be investigated. Then, the LSWE model used to solve the problem stated in the previous section is introduced in Section 2. The model is then solved analytically in Section 3 and numerically in Section 4. Further, Section 5 presents the simulation results and discussion on the accuracy of our model. Finally, the conclusions of the findings of this study are addressed in Section 6.
2. Mathematical Model
In this section, we introduce the governing equations that are used to model the propagation of seiches in a semi-closed basin with arbitrary bottom topography. It is presumed that the seiches oscillating within the basin follow the shallow water condition where the wavelength is much greater than the maximum depth of the basin (depth ). Another assumption considered in this model is that the surface elevation, denoted by (see Figure 1), is relatively small compared to the total water depth , where is the depth of the basin measured at . Therefore, we can claim that . Thus, it is appropriate to apply the well-known linear shallow water equations (LSWE) as the governing equations of this model. The LSWE are illustrated in Figure 1 and consist of the two equations below.
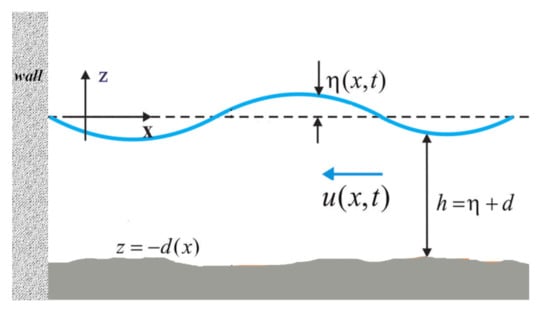
Figure 1.
Description of the shallow water equations model in a semi-closed basin with arbitrary bottom topography.
As pictured in Figure 1, we assume that the seiches in the semi-closed basin are initiated by waves entering the open boundary at the right end of the basin. The waves travel to the left side of the basin at a horizontal velocity of , while the vertical velocity is ignored in this situation. Moreover, the g = 9.81 m/s specified in Equation (2) represents the acceleration due to the force of gravity. In the next section, the model described in this part is used to investigate the period of seiches (resonant period) as well as resonance phenomena in several types of semi-closed basin, including quartic, triangular (right-angled), trapezoidal, and coupled rectangular basin.
3. Analytical Solution
Here, the LSWE model is implemented to determine the resonant period for quartic, triangular (right-angled), trapezoidal, and coupled rectangular semi-closed basin. Firstly, the model is solved using the separation of variables method to obtain the solution of and . We define the function and as monochromatic waves with constant angular frequency , written as
in which and are functions to be determined. Substituting Equations (3) and (4) into Equations (1) and (2) yields
Clearly, the function is the solution of the differential Equation (5), while can be obtained from Equation (6). Then, we can derive the fundamental resonant period of the given basin from the obtained solutions and as well as the boundary conditions of each basin. The fundamental resonant period itself is the seiche period in fundamental mode, which produces the biggest resonant period of the basin.
3.1. Quartic Semi-Closed Basin
The first fundamental resonant period to be discovered is the one that belongs to the quartic semi-closed basin whose depth follows the formula in the domain . Notation is the maximum depth and L is the length of the basin. The illustration of this type of basin is shown in Figure 2. Now, to obtain the differential equation containing for this specific topography, we substitute the depth into Equation (5), and then we have
with hard-wall boundary condition at which can be written mathematically as . According to Equation (6), this condition can be rewritten as
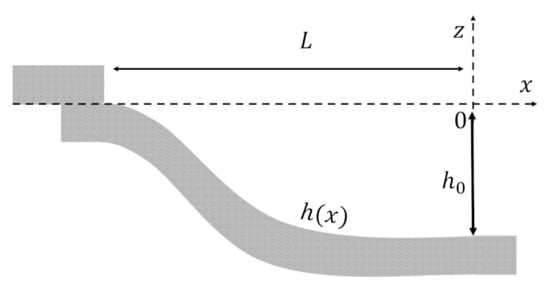
Figure 2.
Illustration of the quartic semi-closed basin.
In addition, there is another boundary condition that is adapted from the theory of the nodal lines in semi-closed basin for fundamental mode [15], which implies that, at the open end of the basin, the wave has minimum amplitude, or, in other words, , which can also be written as
Now, solving Equation (7) gives us the solution read as
in which , while and are certain constants. The derivative of F with respect to x is
where . Substituting Equation (11) into Equation (8) results in . Applying this result to Equation (10), and then substituting the new equation into Equation (9), yields:
where . Hence, we obtain the fundamental resonant period of quartic semi-closed basin, which is
3.2. Triangular (Right-Angled) Semi-Closed Basin
The second type of basin discussed is the triangular (right-angled) semi-closed basin with depth of for domain in which is the maximum depth. By substituting into Equation (5), we have a second-order ordinary differential equation written as
with boundary condition defined according to the illustration in Figure 3, where we have hard-wall boundary condition at . Similar to the previous case, here, we also consider the condition that is following the nodal lines theory, where the wave amplitude is minimum at the open end of the basin or at . Therefore, we have the following conditions:
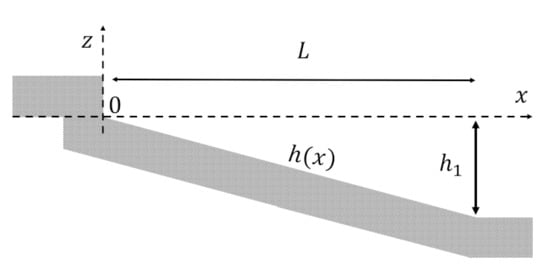
Figure 3.
Triangular (right-angled) semi-closed basin.
Now, solving the differential Equation (14), we obtain
where and denote certain constants, while and are Bessel functions of the first and second kind of order n, respectively. These functions are two linearly independent solutions of the Bessel differential equation. Moreover, the derivative of F with respect to x is written as
Next, to determine the fundamental resonant period, we apply Equation (15) to Equation (18) and obtain
Considering the behavior of Bessel functions of order one near , where and , then must be satisfied so that Equation (19) is also satisfied. Now, using the second condition, we have
For the nontrivial solution to be achieved, must not equals to zero. Thus, to satisfy Equation (20), we need to find the root of the first-kind Bessel function of order zero. In addition, since we aim to obtain the fundamental resonant period, we are looking for the first root of the function, which, from the Wolfram Language website, is found to be . Therefore, must be satisfied. Hence, the sought period is
3.3. Trapezoidal Semi-Closed Basin
In the third case, we determine the fundamental resonant period for trapezoidal semi-closed basin with depth in domain , as depicted in Figure 4. Here, the maximum depth is denoted by notation while is the minimum depth. Three configurations of and are used in this paper to evaluate the effect of the difference in the ratio between the minimum and maximum depth on the value of the resonant period and wave profile: , , and . The detailed derivation is only provided for the first configuration, i.e., .
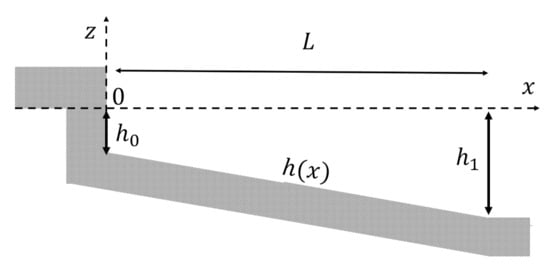
Figure 4.
Trapezoidal semi-closed basin.
By substituting the boundary conditions (23) and (24) into Equations (26) and (25), respectively, we obtain two equations read as
Eliminating from the equations and ignoring the trivial solution, we have
The above result is also obtained if we eliminate instead of . Now, Equation (29) is only satisfied if
Because , the fundamental resonant period for trapezoidal semi-closed basin with is
Furthermore, using the exact same steps and method, we determine the fundamental resonant period for trapezoidal basin with the other two ratios, and , which are
and
respectively.
3.4. Coupled Rectangular Semi-Closed Basin
The last type of basin is the coupled rectangular semi-closed basin, the topography of which is shown in Figure 5 and defined in a piece-wise function
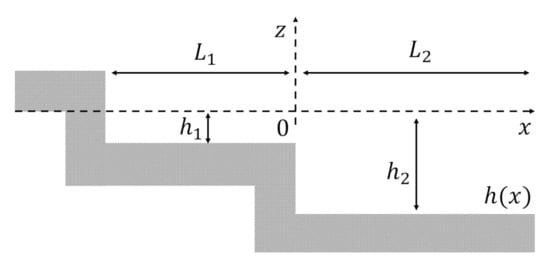
Figure 5.
Coupled rectangular semi-closed basin.
is the water depth in the shallower area with length of , while denotes the water depth in the deeper region with length of . Unlike the previous case, here, the depth ratio between and is fixed to [14]. However, the ratio between the length of the shallower and deeper domain, and , respectively, is varied to observe its effect on the resonant period and wave profile. There are four configurations of the lengths: , , , and . Only the case with length ratio of is explained in detail below.
To start the derivation, we assume that the function from Equation (3) can be rewritten as
Then, we substitute with the mentioned depth ratio and length criteria to Equation (5) with following the piece-wise function (35), which gives us
The solution of Equation (36) is obtained using the characteristic method, read as
where A, B, C, and D are certain constants.
Next, we need to make sure that the solution is continue at the discontinue point, which is , by applying the matching conditions. According to Dean and Dalrymple [16], there are two matching conditions based on the continuity of surface elevation and mass flow rate at , written as
respectively. From the first condition (Equation (38)), we find that , while Equation (39) gives us . Hence, we have a new solution for both and read as
By taking the derivative of and , we obtain
Similar to the previous cases, for this type of basin, we have two boundary conditions:
By eliminating constant A and ignoring the trivial solution, we have
which is also obtained if we eliminate the other constant. Solving Equation (48) yields
which is the fundamental resonant period we are looking for. Moreover, a similar procedure is applied to determine the fundamental resonant period for the coupled rectangular basin with length ratio of , , and . Those resonant periods, respectively, are written as
and
All the results found in this section are listed in Table 1, along with the fundamental resonant periods obtained using numerical approach that are explained in the next section.

Table 1.
The fundamental resonant period obtained for each type of semi-closed basin using analytical and numerical approach.
4. Numerical Scheme
In this section, we aim to observe the propagation of waves in a semi-closed basin when a resonance phenomenon arises using a numerical approach. Hence, we construct a numerical scheme to simulate the occurrence accurately. In addition, this computational scheme is also used to investigate the numerical fundamental resonant period for each type of basin, which is tested and verified against analytical solutions from the previous section.
Firstly, we revisit our mathematical model, i.e., the LSWE model, represented by Equations (1) and (2). Consider as the spatial domain of a semi-closed basin where the waves propagate. Then, the domain is partitioned in a staggered way into . The numerical scheme is formulated based on the staggered grid using the finite volume method, as illustrated in Figure 6. Using this method, the cells centered at full grid points (, ) are used to approximate the mass conservation Equation (1), while their adjacent cells are used to approximate the momentum balance Equation (2). In addition, the value of the horizontal velocity u is stored only in half grid points (, ), whereas and h are calculated only at the full grid points.
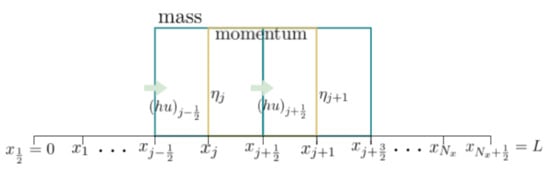
Figure 6.
Illustration of the finite volume method on a staggered grid.
Using the von Neumann stability analysis, it is found that the Courant–Friedrichs–Lewy stability condition of our numerical scheme is . For the following section, we simulate the wave propagation and resonance phenomenon in each type of basin using the scheme (Equations (53) and (54)) in order to obtain the numerical fundamental resonant period. Concerning these simulations, the computational scheme is validated by comparing the numerical results with the analytical solutions obtained previously.
5. Results and Discussion
Now, the numerical scheme established in the previous section is applied to simulate the resonance phenomenon in each type of semi-closed basin discussed. The results are presented to determine the fundamental resonant period numerically as well as to observe the resonant wave profile. The numerical resonant period for each basin is then compared to its analytical counterpart in order to evaluate the reliability of our numerical scheme on simulating resonance phenomena.
For the computation, we set the total length of the basin to be m and the maximum depth to be m in order to fulfill the shallow water requirements. The spatial domain is then divided into cells with length of m. Moreover, the observation time is set to be within the range of s, so that we can capture the occurrence of resonance clearer. As for the initial condition, we assume that the water is calm and undisturbed, which means that and . Then, we presume that an incoming wave with an amplitude of m enters the basin and disturbs the calm water, generating seiches inside the basin. In addition, we use the same boundary conditions explained and illustrated in Section 3.
To calculate the numerical resonant period, we use the trial and error procedure, where we input a certain value of wave period into the model and simulate the wave propagation, then observe whether or not the wave undergoes resonance. These steps are carried out numerous times until the resonance-generating period is found. The resonance itself is indicated by a gradual rise of wave amplitude throughout the observation. Thus, we obtain a numerical fundamental resonant period for each basin with the specific parameters specified above. In addition, we compare the results against the analytical solutions, as listed in Table 1.
In Table 1, the numerical fundamental resonant period for each basin is compared to the corresponding analytical solution to examine the accuracy of our numerical scheme. The error presented in the table is calculated using the formula . Notice that relative errors in nearly all cases are less than , with the exception of a quartic basin case which resulted in an error of around . The larger error shown in quartic basin is most likely caused by the dry area at the end of the domain. In simulations, this dry area is illustrated by the small part at the end of the domain that is significantly close to and is considered as by the numerical system. The existence of this dry area eventually leads to the emergence of wave non-linearity effect that is not captured well by our linear numerical scheme. Therefore, the error in this particular basin is larger than the others.
On the other hand, our analytical model seems to estimate the real fundamental resonant period quite well. This is supported by the observation done by Darbyshire [21] in Slangkop Point, South Africa. In this observation, the fundamental resonant period was measured for a quartic-like coastal area with length of km and depth of m. It was found that the observed resonant period is s. Using our analytical model and numerical scheme, we obtain that the respective are 74.77 and 76.32 s. From those findings, we can calculate the relative errors between analytical and observed as well as between numerical and observed , which are and , respectively. Both errors are considerably small for model comparison against real measurement, since there are many natural factors that are ignored in the linear model, such as friction, non-linearity, and wind. Therefore, it is safe to say that both models successfully estimate the real measured. However, the numerical error is still almost twice as big as the analytical error, which confirms that, in this specific type of basin, our numerical scheme needs to be improved by involving the wave non-linearity effect on the dry area.
Additionally, the accuracy of our computational scheme is determined by calculating the rate of convergence (). Since our model involves two independent variables, x (spatial) and t (time), we evaluate its accuracy from both perspectives. We perform numerous simulations in trapezoidal basin () with the same parameters but different and values in each simulation. In terms of time, we use a fixed m, while varies between and s. The error between analytical and numerical is then calculated for each time step using the formula . Each step’s rate of convergence is computed using . The results are listed in Table 2.

Table 2.
Rates of convergence of our numerical scheme in terms of time (t).
In Table 2, we can see that all values of are within the range of ; thus, the order of accuracy of our numerical scheme in term of time is 1. Then, using the same calculations, we simulate the numerical scheme with fixed s and various of range m. Table 3 presents the calculation results for each spatial step. In this case, the values of are in the range of 0 to 2, indicating that the order of accuracy in term of spatial is 2. As a result, the order of accuracy of our numerical scheme is .

Table 3.
Rates of convergence of our numerical scheme in terms of spatial (x).
Moreover, the same scheme is used to observe the wave profile when resonance phenomenon occurs and how different the behavior of the resonant wave depends on the type of the basin where it happens. Using the same parameters, we simulate wave resonance in each basin with the incoming wave period follows the obtained fundamental resonant period. The results of the simulations for quartic, triangular (right-angled), trapezoidal, and coupled rectangular semi-closed basin are shown in Figure 7, Figure 8 and Figure 9, respectively.
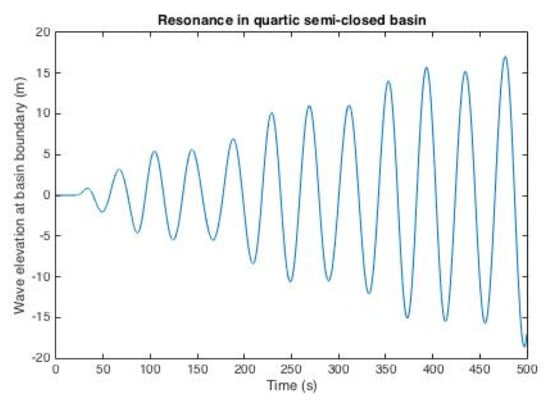
Figure 7.
Simulation result for quartic semi-closed basin.
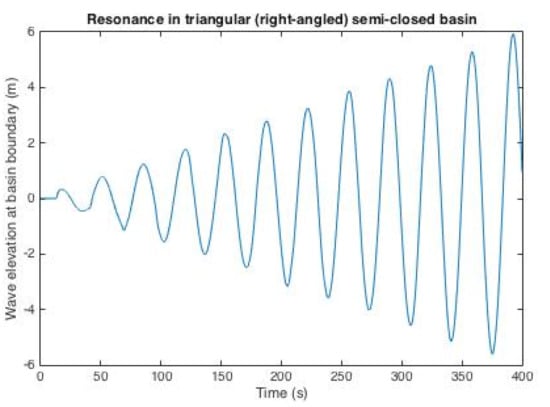
Figure 8.
Simulation result for triangular (right-angled) semi-closed basin.
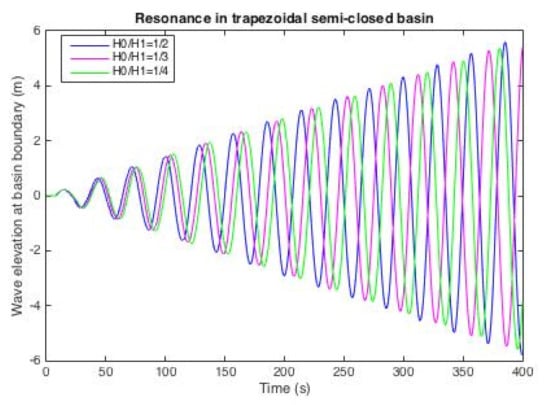
Figure 9.
Simulation results for trapezoidal semi-closed basin.
As shown in Figure 7, Figure 8 and Figure 9, the wave elevation within each basin increases over time, which implies that a resonance occurs when an external wave with a period of enters the basin. Note that resonance occurrences in all cases produce waves with amplitudes that continue to increase and eventually exceed 30 times the initial amplitude (3 m) in the first 200 s. In real life, this could mean that, in just a few minutes after the wave entered the basin, the amplitude would rise dramatically and, as a result, there would be a risk of major destruction of the facility or environment in the coastal region. The worse case would happen if the initial wave has bigger amplitude. In addition, from the results in all types of basin, we are able to conclude that the worse resonance happens in the quartic basin, as the wave amplitude in this basin rises the most, almost seven times the initial amplitude, compared to the other three at only 3–4 times. This outcome might happen because of the same factor explained above, which is the existence of the dry area that eventually leads to the arise of wave non-linearity effect. Because our linear scheme cannot handle the non-linearity very well, the wave amplitude rises more quickly than in other basins. This means, for coastal areas or semi-closed basins in general with quartic type of bottom topography, we need to be more attentive on dealing with resonances and might be need major modification in the numerical scheme itself.
Furthermore, we observe the differences of the resonant wave profile in trapezoidal and coupled rectangular semi-closed basin with different configurations. Figure 10 shows that, considering the variations in configuration of the minimum and maximum depth of the topography in the trapezoidal basin, there are no significant differences in the amplitude increases. This means that the change in the depth ratio will not significantly affect the resonance phenomenon in the trapezoidal basin. On the other hand, the different configurations of the length ratio of the coupled rectangular basin have a significant impact on the resonant wave amplitude. The lowest wave amplitude is produced by the greatest ratio, that is , or when the length of the deeper region is twice as long as the shallower domain. With the same manner, the smallest ratio , which is when the basin has much longer deep domain than the shallow one, gives the highest amplitude. In real life, this discovery might be helpful in deciding the optimum design of a human-made coupled rectangular harbor’s topography, that is keeping the length ratio to be as large as possible. This finding may also be used as a basic information on the construction of a protection structure in this specific type of harbor or other coastal areas.
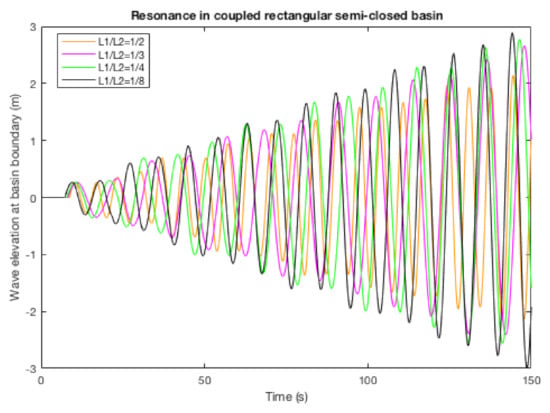
Figure 10.
Simulation results for coupled rectangular semi-closed basin.
6. Conclusions
The seiches and resonance phenomena over quartic, triangular (right-angled), trapezoidal, and coupled rectangular semi-closed basin were successfully simulated using the linear shallow water equations, which are solved analytically and numerically to obtain the fundamental resonant period of each basin. The separation of variables method is used to derive the resonant period from the equations analytically, whereas the numerical resonant periods are determined by applying the finite volume method on a staggered grid to the equations. Comparisons were conducted between the analytical and numerical fundamental resonant period in each basin to verify the formulated numerical scheme, resulting in errors of less than , which means that our scheme is highly accurate on estimating the resonant period. Moreover, the numerical simulations successfully simulated the resonance phenomena in each basin as a result of an external wave, whose period is the same as the derived fundamental resonant period, enters the basin mouth. In the simulation results, this phenomenon is indicated by the gradual increase of the amplitude of the wave. Further, from the numerical simulations, we can draw several noticeable outcomes. In general, since the amplitude of the resonant wave in quartic basin increased the most in a certain period of time, we need to be more attentive on handling the resonance phenomenon in this particular basin. Another perceptible finding is the negative correlation between the ratio of the basin’s length and the wave elevation for coupled rectangular basin. The smaller is the ratio of the basin’s length, the higher is the wave amplitude it produces, and vice versa. On the other hand, we found no significant effect of the various depth ratios of the trapezoidal basin on the increasing of wave amplitude. Furthermore, since this paper only focuses on basins with constant width and no friction force is involved, for further research, we suggest to do some modifications on the basin width and consider including the friction term into the model. The effect of the varying width and friction force to resonant wave amplitude might be an interesting case to study.
Author Contributions
Conceptualization, I.M.; model and methodology, I.M.; analytical solution, N.K.; numerical scheme, I.M.; simulation program, I.M.; numerical simulation, N.K.; investigation, I.M., H.Q.R.; writing—original draft preparation, N.K.; writing—review and editing, I.M. and H.Q.R.; supervision, I.M.; project administration, I.M.; and funding acquisition, I.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the ITB and The Indonesian Ministry of Research, Technology and Higher Education Research Grant.
Acknowledgments
This work was supported by the ITB and The Indonesian Ministry of Research, Technology and Higher Education Research Grant.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| LSWE | Linear Shallow Water Equations |
References
- Chrystal. Hydrodynamical theory of seiches. Trans. R. Soc. Edinb. 1906, 41, 620–630. [Google Scholar]
- Chapman, D.; Giese, G. Seiches. In Encyclopedia of Ocean Sciences, 2nd ed.; Elsevier: New York, NY, USA, 2001; Volume 5, pp. 344–350. [Google Scholar]
- Rozas, C.; de la Fuente, A.; Ulloa, H.; Davies, P.; Nino, Y. Quantifying the effect of wind on internal wave resonance in Lake Villarrica, Chile. Environ. Fluid Mech. 2014, 14, 849–871. [Google Scholar] [CrossRef]
- Munger, S.; Cheung, K.F. Resonance in Hawaii waters from the 2006 Kuril Islands Tsunami. Geophys. Res. Lett. 2008, 35, L07605. [Google Scholar] [CrossRef]
- Roeber, V.; Yamazaki, Y.; Cheung, K.F. Resonance and impact of the 2009 Samoa tsunami around Tutulia, American Samoa. Geophys. Res. Lett. 2010, 37, L21604. [Google Scholar]
- Yamazaki, Y.; Cheung, K.F. Shelf resonance and impact of near-field tsunami generated by the 2010 Chile earthquake. Geophys. Res. Lett. 2011, 38, L12605. [Google Scholar] [CrossRef]
- Hwang, L.S.; Tuck, E.O. On the oscillations of harbours of arbitrary shape. J. Fluid Mech. 1970, 42, 447–464. [Google Scholar] [CrossRef]
- Kabiri-Samani, A.; Ataie-Ashtiani, B. Free Water Surface Oscillations in a Closed Rectangular Basin with Internal Barriers. Sci. Iran. 2008, 15, 315–322. [Google Scholar]
- Magdalena, I.; Rif’atin, H.Q.; Reeve, D.E. Seiches and Harbour Oscillations in A Porous Semi-Closed Basin. Appl. Math. Comput. 2020, 369, 124835. [Google Scholar] [CrossRef]
- Martinez, F.M.; Naverac, V.S. An experimental study of harbor resonance phenomena. In Proceedings of the Twenty-First International Conference on Coastal Engineering, Costa del Sol-Malaga, Spain, 20–25 June 1988; pp. 1280–1292. [Google Scholar]
- Rif’atin, H.Q.; Magdalena, I. Seiches in A Closed Basin of Various Geometric Shapes. J. Phys. Conf. Ser. 2019, 1245, 012061. [Google Scholar] [CrossRef]
- Magdalena, I.; Rif’atin, H.Q.; Matin, A.M.A. Analytical and numerical studies for Seiches in a closed basin with bottom friction. Theor. Appl. Mech. Lett. 2020, 10, 429–437. [Google Scholar] [CrossRef]
- Magdalena, I.; Karima, N.; Rif’atin, H.Q. A Mathematical Model for Investigating The Resonance Phenomenon in Lakes. Wave Motion 2021, 100, 102669. [Google Scholar] [CrossRef]
- Wilson, B. Chapter: Seiches in Advances in Hydroscience; Academic Press: Cambridge, MA, USA, 1972; Volume 8, pp. 1–93. [Google Scholar]
- Rabinovich, A. Chapter 9: Seiches and Harbor Oscillations in Handbook of Coastal and Ocean Engineering; Kim, Y.C., Ed.; World Scientific Publ.: Singapore, 2009; pp. 193–236. [Google Scholar]
- Dean, R.; Dalrymple, R. Water Wave Mechanics for Engineers and Scientist; World Scientific: Singapore, 1991. [Google Scholar]
- Magdalena, I.; Adityawan, M.; Jonathan, C. Numerical model for dam break over a movable bed using finite volume method. Int. J. Geomate 2020, 19, 98–105. [Google Scholar] [CrossRef]
- Magdalena, I.; Erwina, N.; Pudjaprasetya, S. Staggered Momentum Conservative Scheme for Radial Dam break Simulation. J. Sci. Comput. 2015, 65, 867–874. [Google Scholar] [CrossRef]
- Mungkasi, S.; Magdalena, I.; Pudjaprasetya, S.R.; Wiryanto, L.H.; Roberts, S.G. A Staggered Method for The Shallow Water Equations Involving Varying Channel Width and Topography. Int. J. Multiscale Comput. Eng. 2018, 16, 231–244. [Google Scholar] [CrossRef]
- Pudjaprasetya, S.; Magdalena, I. Momentum conservative schemes for shallow water flows. E. Asian J. Appl. Math. 2014, 4, 152–165. [Google Scholar] [CrossRef]
- Darbyshire, M. Long Waves on the Coast of the Cape Peninsula. Dtsch. Hydrogr. Z. 1963, 16, 167–185. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).