Wind-Forced Submesoscale Symmetric Instability around Deep Convection in the Northwestern Mediterranean Sea

Abstract

During the winter from 2009 to 2013, the mixed layer reached the seafloor at about 2500 m in the northwestern Mediterranean Sea. Intense fronts around the deep convection area were repeatedly sampled by autonomous gliders. Subduction down to 200–300 m, sometimes deeper, below the mixed layer was regularly observed testifying of important frontal vertical movements. Potential Vorticity dynamics was diagnosed using glider observations and a high resolution realistic model at 1-km resolution. During down-front wind events in winter, remarkable layers of negative PV were observed in the upper 100 m on the dense side of fronts surrounding the deep convection area and successfully reproduced by the numerical model. Under such conditions, symmetric instability can grow and overturn water along isopycnals within typically 1–5 km cross-frontal slanted cells. Two important hotpspots for the destruction of PV along the topographically-steered Northern Current undergoing frequent down-front winds have been identified in the western part of Gulf of Lion and Ligurian Sea. Fronts were there symmetrically unstable for up to 30 days per winter in the model, whereas localized instability events were found in the open sea, mostly influenced by mesoscale variability. The associated vertical circulations also had an important signature on oxygen and fluorescence, highlighting their under important role for the ventilation of intermediate layers, phytoplankton growth and carbon export.

1. Introduction

The Gulf of Lion in the northwestern Mediterranean Sea (NW Mediterranean) is one of the few oceanic regions where intense atmospheric forcing and oceanic preconditionning allow vertical mixing to reach large depths (>500 m to the seafloor at 2500 m [1]). This phenomenon, known as “open-ocean deep convection” (see Marshall and Schott [2] for a review), is a key process of the ocean thermohaline circulation. Deep convection is characterized by localized and intense diapycnal mixing events [3] important for the ocean ventilation [4,5,6], subsequent intense phytoplankton spring blooms [7,8,9] and carbon sequestration [10]. In accordance with idealized results [11], the net downwelling induced by deep convection however occurs along the boundary circulation where a large amount of heat is released to the atmosphere [12]. In the western Mediterranean Sea, the coupled process of deep convection has been variable over the last decades [13] and affected by abrupt changes in ocean heat and salt contents [14,15,16]. Numerical models predicted a decrease in convection activity due to climate change [17,18] with important consequences on the marine ecosystems [19,20].

Open-ocean deep convection has traditionally been described by three phases [21,22], however overlapping in space and time: A preconditioning phase characterized by a basin-scale cyclonic and more localized (sub)mesoscale circulations associated with a doming of isopycnals toward the surface; a vigorous mixing phase triggered by intense heat losses and evaporation to the atmosphere, typically 100–1000 W m${}^{-2}$ [23] and caused by intense cold/dry wind events; a spreading phase of the newly-formed water mass along neutral density layers initiated when ocean restratification overcomes the destabilizing atmospheric forcing.

During the mixing phase, a mixed patch forms in the area of deep mixing separated from stratified waters by density fronts. Diapycnal mixing increases the available potential energy of the mixed patch feeding eddy kinetic energy by baroclinic instability of the rim current [24,25,26,27]. In particular, Submesoscale Coherent Vortices [28] are generated. They are non-linear eddies in cyclogeostrophic balance with O(1) Rossby number, peak velocities at great depth and a weakly stratified core spreading the newly-formed water mass over long distances due to their extended lifetime (>1 year) [29,30,31,32,33,34,35,36,37].

The horizontal circulation in northwestern Mediterranean Sea follows a basin scale cyclonic gyre [38,39]. In particular, the “Northern Current” (NC) establishes in the northwest of Corsica from the merging of the “West Corsica Current” (WCC) with the Corsica Channel throughflow. The NC then flows along the continental slope from the Ligurian Sea to the Catalan Sea (Figure 1). The cyclonic circulation observed as a permanent feature is mostly in geostrophic balance creating a dome of high density waters in the central basin. The central area of the gyre circulation is thus preconditionned to deep convection [2,21]. The frontal zone of the NC separates low salinity surface waters of Atlantic origin (Atlantic Water, AW) from higher salinity waters in the central basin modified through the action of vertical mixing and evaporation. The front has a thickness of more than 200 m throughout the seasons and a 25-km wide geostrophic jet with peak velocities of 0.3–0.5 m s${}^{-1}$ roughly aligned with the 2000-m isobath (see Prieur et al. [39] for a recent review). Under the effects of surface fluxes (heat, evaporation, wind) and topography [40], the NC undergoes baroclinic instability and meanders with a timescale of O (5–10) days [24,41,42]. This instability tends to restore equilibrium by slanting isopycnal and generating mesoscale meanders and eddies.

In addition to baroclinic instability acting at mesoscale, frontal regions are also prone to an important dynamics at submesoscale generating intense vertical velocities, as suggested by observations and models [43]. The submesoscale regime classically refers to unbalanced flows characterized by O(1) Rossby number and scales smaller than the first baroclinic deformation radius [44]. Significant vertical water displacements of O (10–100) m day${}^{-1}$ occur in such regions [45,46,47,48,49]. High levels of turbulent diapycnal mixing in active fronts [50,51] foster heat transfers from the surface of the ocean to the interior [52,53]. Due to their action at timescales relevant for biology, the vertical injection of nutrients at submesoscale has strong major impacts on phytoplankton growth and marine ecosystems [54,55,56,57]. Fronts are also crucial to the formation of low Potential Vorticity (PV) “mode waters” [58,59] important for the ocean ventilation [60], deep convection [61,62] and carbon sequestration [63].

Potential vorticity is a key variable for the dynamics of frontal regions. By definition, PV is conserved along adiabatic streamlines [64], i.e., in absence of forcing and dissipation. Hence, major sources and sinks of PV are found where isopycnals outcrop at the air–sea interface, or in the bottom boundary layer [65]. Frontal destruction of PV at the surface can be caused by thermodynamic heat losses [66], or mechanical friction due to winds [67]. In particular, Ekman transport by down-front winds (i.e., along the geostrophic flow) advects water from the dense to the light side of a front [68]. This mechanism can cause important buoyancy loss equivalent to O (1000) W m${}^{-2}$ and localized at the front. These fluxes can be significantly larger than air/sea net heat fluxes [69,70,71]. The destruction of PV by winds was also shown to play a role in deep water formation in the northwestern Mediterranean Sea [61].

Alterations of PV may expose frontal regions to instabilities. In particular where potential vorticity has opposite sign of f the Coriolis parameter (i.e., negative in the northern hemisphere), symmetric instability (SI) arises [72]. In the ocean, this instability drives O (0.1–1 km) overturning cells aligned with isopycnals, symmetric in the along-front direction and growing in short O (1–10 h) timescale [73,74]. Large-Eddy Simulations have shown an increase in dissipation rate of turbulent kinetic energy due to SI [75], as well as primary production stimulation at high latitude fronts [54]. SI also generates important mixing in the bottom boundary layer of intense currents [76,77]. It is thus an important submesoscale process, yet still poorly observed and characterized.

Favorable conditions for SI were observed along the frontal region of western boundary currents like the Gulf Stream [73,78] and the Kuroshio [79]. However, these observations are difficult to collect since such unstable fronts are caused by intense atmospheric forcing causing rough sea conditions in which research vessels can hardly operate. This challenge has been met by ocean gliders [80] which allow high horizontal resolution autonomous measurements, from 1 km to 2 km between consecutive 1000 m profiles. Gliders have been widely used to characterize frontal dynamics [69,70,78,81,82,83,84,85] and can overcome winter harsh sea conditions, although their displacement through the water of 20–40 km day${}^{-1}$, fast for the mesoscale of the NC [42], can lead to aliasing of rapidly evolving submesoscale structures.

While observational evidence of SI remains scarce, despite growing interest in characterizing and quantifying submesoscale regime from in situ observations, the increase and repeat use of autonomous platforms such as gliders during the last decade has revealed new insights in submesoscale flows. In this study, we use an extensive observational data set of the fronts surrounding the deep convection area in the northwestern Mediterranean Sea, mainly associated with the NC front, see Figure 1, to evaluate and characterize frontal submesoscale dynamics in interaction with strong winds and heat losses. The PV is further diagnosed in both observations and a very high resolution numerical model. We then assessed the role of down-front winds in generated favorable conditions to SI in terms of PV destruction and Ekman buoyancy fluxes. Key regions regularly prone to SI are linked to topographically-steered circulation and dominant winds. Finally, we discussed the role of SI on vertical circulations at fronts and biogeochemical implications.

2. Materials and Methods

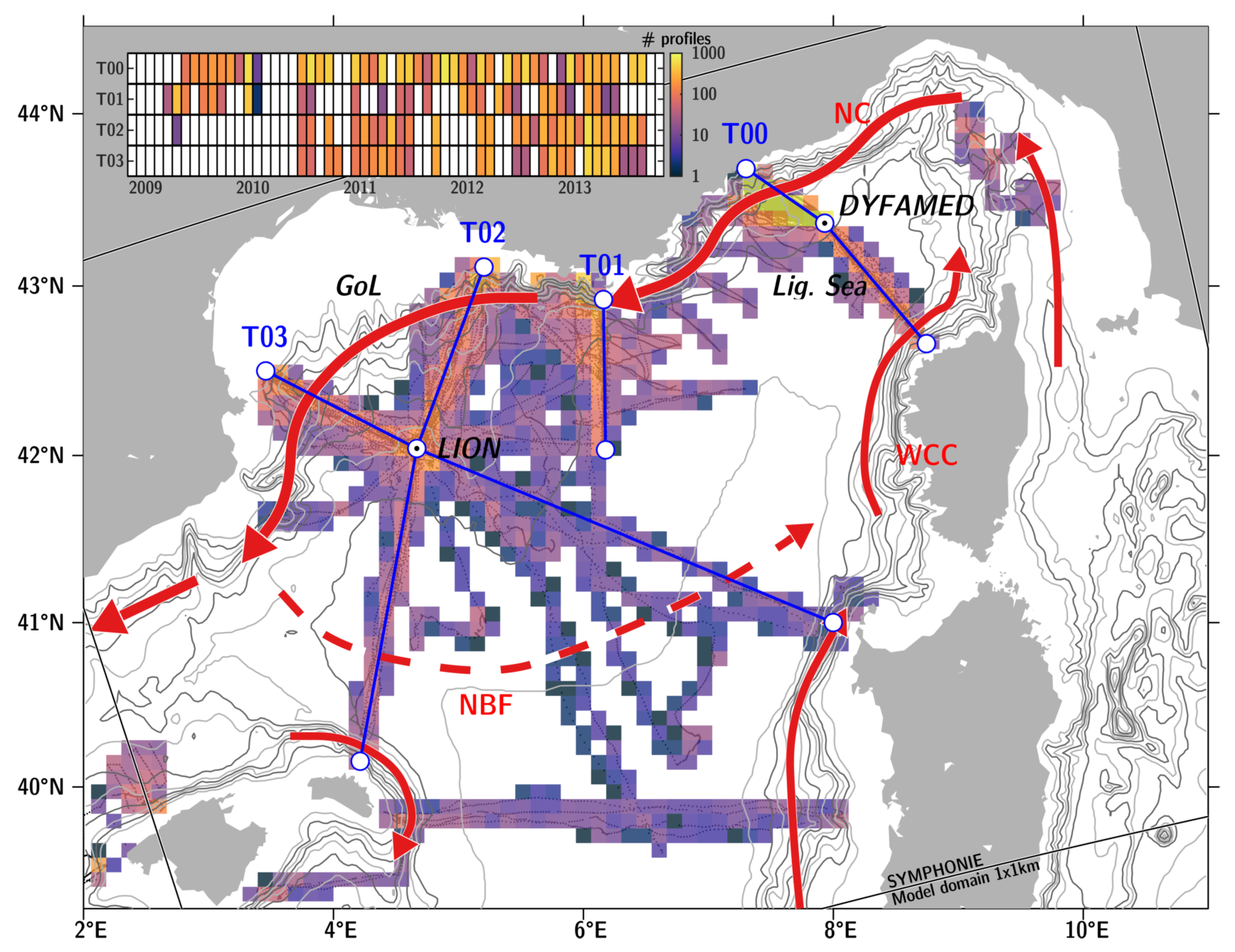
2.1. Glider Measurements

Autonomous ocean gliders are an essential component of Global Ocean Observing System [80]. They sample the ocean along saw-tooth trajectories between the surface and a maximal depth of 1000 m traveling at horizontal speed of 20–40 km per day. Deep profiles are typically separated by 1–3 km and 1–4 h. Gliders can thus sample fronts and eddies characterized by typical horizontal scale of 10–50 km in about 1–3 days. In this study, we used data collected by gliders from November 2008 to October 2013 in the northwestern Mediterranean Sea. This represents a total of about 35,000 profiles from 72 glider missions. Most of the glider data have been collected in the framework of the MOOSE (Mediterranean Ocean Observing System, https://www.moose-network.fr/ (accessed on 16 March 2021), the long-term observatory of the northwestern Mediterranean Sea [86]. Those were collected along repeated transects (see Figure 1: T00, 13061 profiles—33 missions; T01, 3702 profiles—33 missions; T02, 5970 profiles—23 missions; T03, 4685 profiles—21 missions). During the study period, an exceptionally intense deep convection activity was observed in the Gulf of Lion with bottom-reaching mixed layer observed at the LION moored time series during five consecutive winters [1] (Figure 2). The MOOSE endurance glider transects—with experimental transects starting in 2006 and regular missions since 2008—were designed to monitor the convection area, characterize the basin circulation and visit the LION and DYFAMED mooring lines in operation since 2008 [87]) and 2009 [88], respectively, (Figure 1).

Gliders were equipped with Conductivity-Temperature-Depth (CTD) sensor sampling at 2–8 s frequency allowing a vertical resolution of 0.5–2 m. Offset of temperature and salinity were determined for all missions following the approach used in Bosse et al. [34]. In addition, thermal lag effects affecting salinity measurements by unpumped CTD probe in strong thermoclines have been corrected following Garau et al. [89].

Dead reckoning navigation compared to GPS fixes at surface enables gliders to estimate a mean oceanic current averaged during each dive, hereafter referred as depth-average current (DAC). Compass calibration has been carried out before each deployment allowing DAC to be used as reference for geostrophic velocities with typical precision of 1 cm s${}^{-1}$ [90].

Gliders additionally performed oxygen and/or optical fluorescence/turbidity measurements. The fluorescence data shown here were corrected for non-photochemical quenching [91] and adjusted against satellite measurements [92]. This method has been validated against high-performance liquid chromatography measurements [9].

2.2. Numerical Model

SYMPHONIE is an Ocean General Circulation Model (OGCM) based on the Navier–Stokes primitive equations solved on an Arakawa curvilinear C-grid under the hydrostatic and Boussinesq approximations [93]. The regional configuration encompassed a significantly larger region than the deep convection zone from the Balearic Sea to the Tyrrhenian Sea (Figure 1). The vertical grid had 40 generalized $\sigma$-levels with varying thickness from 2.5 m near the surface to 150 m to the bottom (and about 15 m at 100 m along the Northern Current). The horizontal grid size was 1 km (effective resolution of about 5 km [94]) in order to resolve mesoscale eddies and fronts as well as the upper bound of the submesoscale (the first baroclinic deformation radius being about 5–10 km in this region [31]). This regional configuration has been validated against numerous in situ observations (Figure 2) and reproduced long-lived 5 km radius SCVs formed by deep convection [36]. It was also coupled to a biogeochemical model in order to study vertical transfers of nutrients and carbon export by deep convection [95,96].

Mixing processes associated with deep convection involves small-scale downwelling plumes in non-hydrostatic balance characterized by <1 km diameter and intense vertical velocities up to 10–15 cm s${}^{-1}$ [97]. These are not resolved by hydrostatic OGCM with kilometric resolution. Here, a non-penetrative adjustment algorithm redistributes surface buoyancy losses throughout the mixed layer [98] while the vertical diffusion coefficient computed by the Gaspar et al. [99] turbulence closure scheme increases up to O (1 m${}^2$ s${}^{-2}$) generating instantaneous and adiabatic parametrized mixing. Radiative, momentum, heat and salt fluxes at the air–sea interface were provided by the dynamical downscaling at 50-km of ERA-Intrerim reanalysis over Europe performed by the CNRM–ARPEGE atmospheric model [100].

The numerical setup is similar to the one described in Damien et al. [36]. Mercator PSY2V4R3 at 1/12${}^{\circ }$ (7 km) resolution [101] were used to prescribed initial and open boundary conditions. The simulation period extended from 1st of October 2010 to 31st of December 2011. Daily average outputs were saved for the whole simulation period. A complete seasonal cycle of winter convection was simulated and a focus was put on the last 12 months (January to December 2011).

2.3. Thermodynamic and Wind Effects of Surface Forcing

Surface forcing (air/sea heat fluxes and wind) was also retrieved during the study period from CNRM–ALADIN reanalysis (a downscaling of ERA-Interim atmospheric model at 12-km resolution with 6h outputs) and used to interpolate atmospheric forcing in space and time along glider sampling.

A complex principal component analysis was performed from daily average wind stress from CNRM-ALADIN during the period 2009–2013 in order to evaluate the dominant wind forcing patterns.

During the winter, large amounts of latent and sensible heat are transferred from the ocean to the atmosphere at the basin scale. As mentioned earlier, winds can also have a dominant effect on the upper ocean buoyancy budget through the action of Ekman transport across fronts. The Ekman buoyancy flux can be quantified as an equivalent heat flux according to [102]:

$$Q_{Ek}=\frac{\rho C_P}{\alpha g}\overrightarrow{M_e}·\overrightarrow{\nabla }b{{|}_{z=0}=\frac{C_P}{\alpha gf}\left(\overrightarrow{\tau }\times \widehat{z}\right)·\overrightarrow{\nabla b}|}_{z=0}$$

(1)

with $\overrightarrow{M_e}$ the Ekman transport, $\rho$ the surface density, $b=-g\rho /{\rho }_0$ the buoyancy of the fluids, $\overrightarrow{\tau }$ the wind stress and f the Coriolis parameter. Non-linear Ekman transport could be considered [103] enhancing (resp. descreasing) fluxes in anticyclonic (resp. cyclonic) areas by 30–50% depending on the local Rossby number. However, as the pattern of fluxes induced by winds friction in frontal regions were not affected, the linear expression was kept for the sake of simplicity.

The equivalent Ekman heat flux ($Q_{Ek}$) was estimated in both model and glider data. Due to the fact that gliders sample along their trajectory and are not able to capture the front orientation, this can lead to a wrong sign or amplitude of this parameter as discussed in Thompson et al. [82] for open-ocean fronts. However in the case of topographically-steered geostrophic fronts and glider sampling perpendicular to isobaths (like the MOOSE endurance lines crossing the NC here), the front orientation can be more confidently defined using glider DAC, as also done by du Plessis et al. [69].

2.4. Potential Vorticity

For continuously stratified flows, q (in m${}^{-1}$ s${}^{-1}$) is defined as [104]:

$$q=(f\widehat{z}+\overrightarrow{\nabla }\times \overrightarrow{u})·\overrightarrow{\nabla }b/g=({\zeta }^a{N}^2+{\partial }_{z}u{\partial }_{y}b-{\partial }_{z}vs.{\partial }_{x}b)/g$$

(2)

where $\overrightarrow{u}=(u,v,w)$ is the velocity field, g the gravitational acceleration, ${\zeta }^a=f+{\partial }_{x}vs.-{\partial }_{y}u$ the absolute vorticity and $N^2\equiv {\partial }_{z}b$ the squared Brunt-Väisälä frequency.

Assuming the flow being mainly in geostrophic balance ($\overrightarrow{u}=\overrightarrow{u_g}$), the thermal wind balance implies ${\partial }_z{u}_g=-f^{-1}{\partial }_{y}b$ and ${\partial }_z{v}_g=f^{-1}{\partial }_{x}b$. The geostrophic PV then simplifies as:

$$q=(f{\zeta }_g^a{N}^2-|\overrightarrow{{\nabla }_h}b{|}^2)/fg=q_N+q_{bc}$$

(3)

with ${\zeta }_g^a$ the absolute vorticity of the geostrophic flow and ${\overrightarrow{\nabla }}_h=({\partial }_x,{\partial }_y)$ the horizontal gradient operator. PV is here separated in two terms: $q_N$ the stratification term linked to stratification and absolute vorticty of the fluid, and $q_{bc}$ the baroclinic term due to the horizontal buoyancy gradient (i.e., front sharpness).

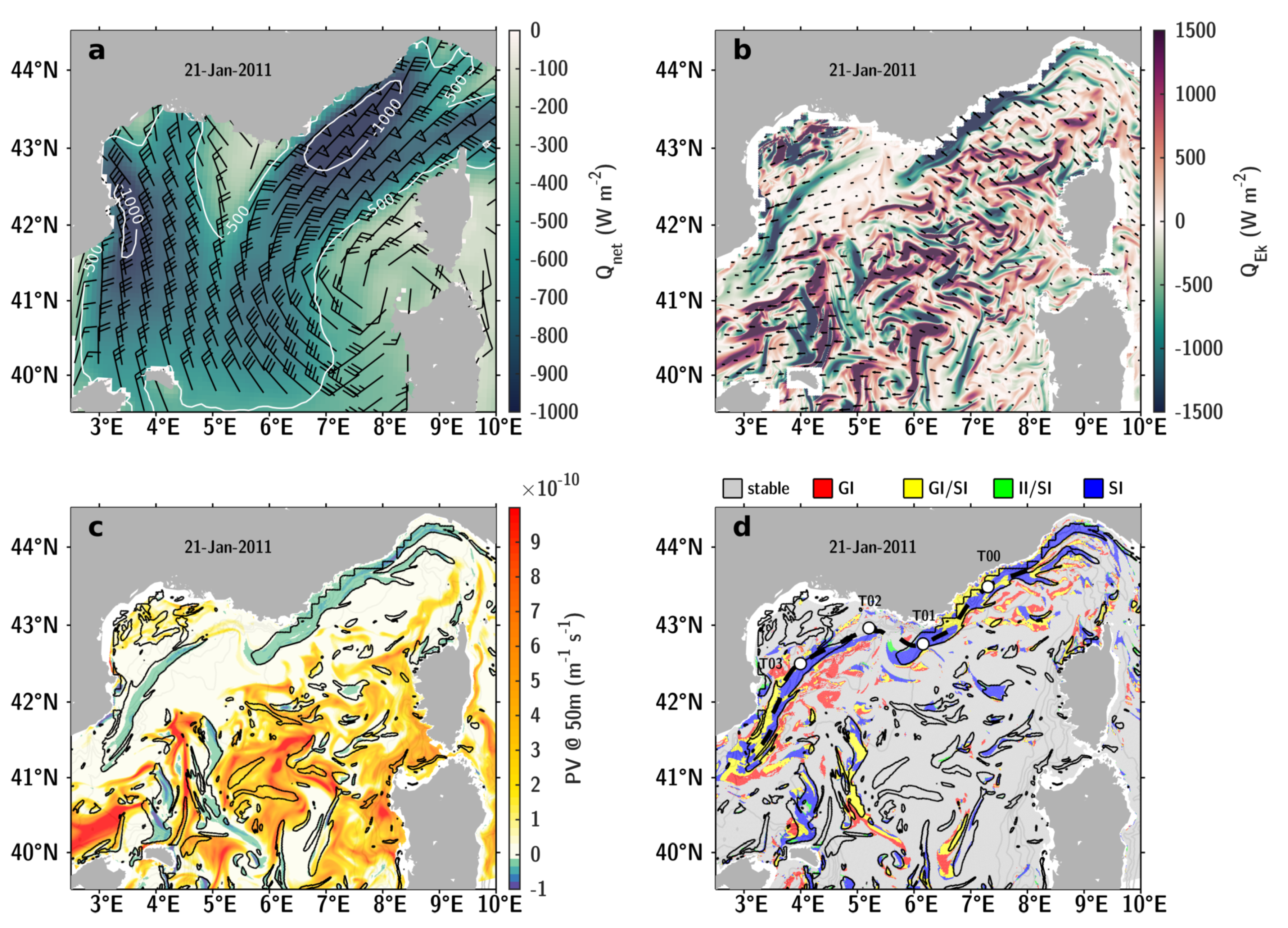
2.5. Flow Instabilities

Potential vorticity can be used to characterize the different types of frontal instability. For instance, symmetric instability arises when q has opposite sign of f (i.e., negative in the northern hemisphere) [72]. This is the case of intense fronts where the vertical stratification term in PV is dominated by horizontal buoyancy gradients: $f(f+{\zeta }_g)N^2<{\left|\overrightarrow{{\nabla }_h}b\right|}^2$. This instability generates cross-front perturbations aligned with sloping isopycnals resulting in important vertical exchanges and turbulence [54,73].

The PV expression (3) can then be rewritten in a more compact way using the balanced Richardson ($R{i}_B=f^2{N}^2/{\left|\overrightarrow{{\nabla }_h}b\right|}^2$) and Rossby ($Ro={\zeta }_g/f$) numbers:

$$q=f{N}^2(1+Ro-R{i}_B^{-1})/g$$

(4)

Different regimes of instability can be categorized: slantwise convection or symmetric instability (SI) for $q<0$ and $N^2>0$, vertical convection or gravitational instability (GI) for N${}^2$ < 0, inertial instability (II) for $Ro<-1$ and mixed regimes (II/SI and GI/SI). These regimes can more easily be classified introducing the Richardson angle [73]: ${\mathsf{\Phi }}_B={tan}^{-1}(-R{i}_B^{-1})$. This angle associates a infinite range of Richardson numbers with finite angles useful to describe the different kind of instability that can result. In particular, the criterion for SI then becomes: $-\pi /2<{\mathsf{\Phi }}_B<min({\mathsf{\Phi }}_C,-\pi /4)$ where ${\mathsf{\Phi }}_c={tan}^{-1}(-1-Ro)$ (see Figure 1 in Thomas et al. [73] for a sketch summarizing all the different cases). We here described flow instabilities in observations and model following this framework.

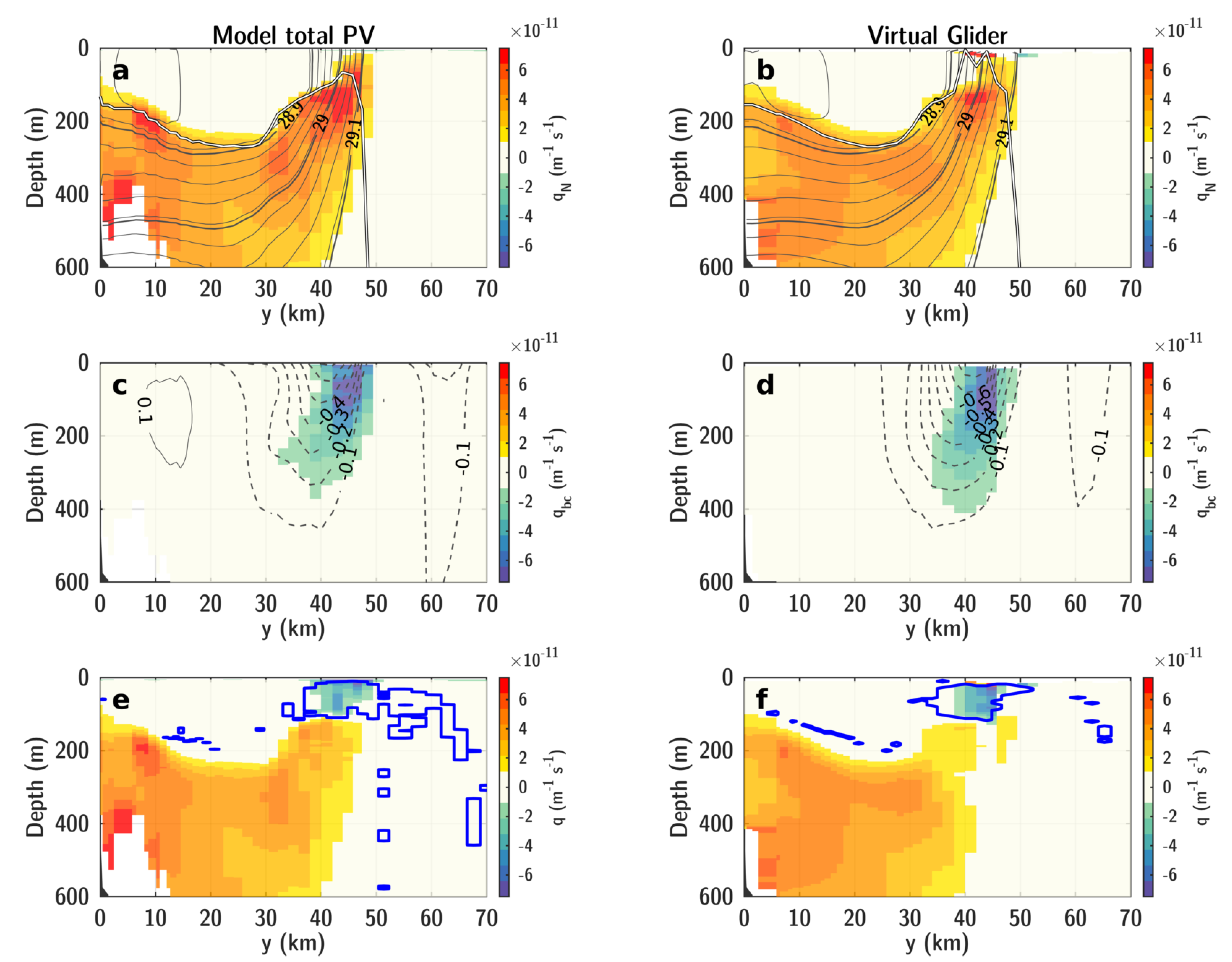
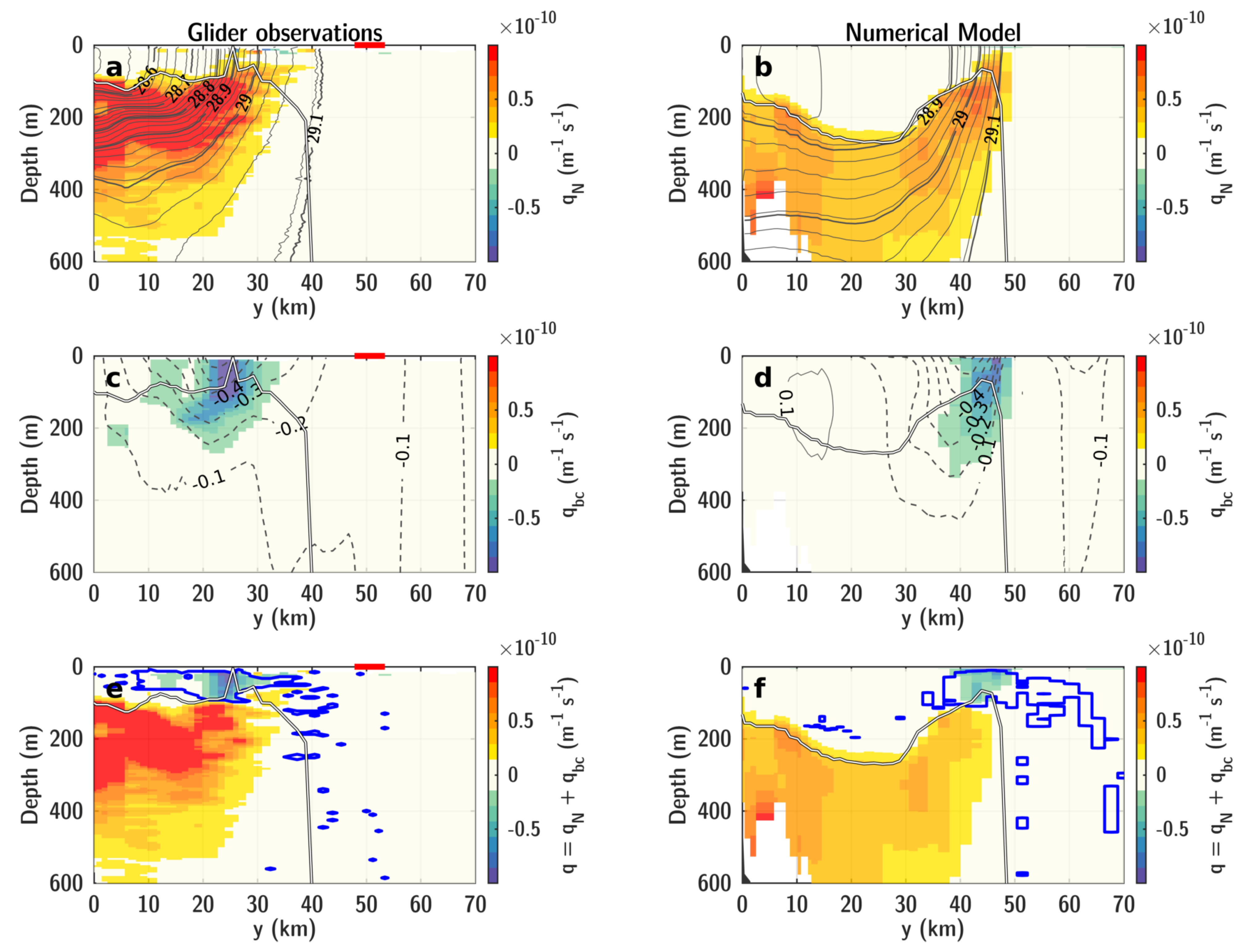
2.6. Estimating PV with Gliders

In the following, the along-front direction was arbitrary defined as the x axis with y pointing in the glider trajectory (right-handed coordinate system). Computing PV requires the estimation of both vertical and horizontal buoyancy gradients. A first approach neglecting cross-track geostrophic velocities ($v=0$) and gradients (${\partial }_x(.)=0$) yields: $q_g=(f-{\partial }_{y}u)N^2/g-{\left|{\partial }_{y}b\right|}^2/fg$, as done in a number of studies [81,82,83,105].

Small-scale isopycnal oscillations due to unbalanced flows and waves need to be filtered out in glider data before the geostrophic shear could be estimated [106]. Here, this was done using a Gaussian moving average ($\sigma =2.5$ km) on the buoyancy field as in Bosse et al. [107]. Absolute geostrophic velocities u were then computed by vertically integrating the thermal wind balance along the glider trajectory and using the DAC component perpendicular to the glider track as absolute reference.

As the glider trajectory will likely not cross fronts at exact right angle, geostrophic shear and vorticity will thus be underestimated by a factor $|sin\theta |$ where $\theta$ is the angle between the glider DAC and the glider track assuming that DAC are representative of the front orientation. This factor is even squared in both PV terms. To avoid large bias, we here adopted the local streamwise coordinate system orientated by glider DACs (details of the method can be found in Todd et al. [78] and in supplementary information of Bosse and Fer [85]). The correcting factor in PV is lower than 2 when the angle $\theta$ is smaller than 45${}^{\circ }$. We therefore excluded PV values according to this threshold in order to reduce the uncertainties of glider-based PV estimates.

2.7. Validation of Glider-Based PV

In order to validate glider-based PV estimates, we have simulated the glider sampling in outputs of the numerical model. The 1-km horizontal resolution of the model is comparable to the glider sampling and able to reproduce a realistic glider sampling. Temperature, salinity and DAC were interpolated in space and time along an actual glider trajectory with a focus on the NC frontal dynamics during an intense wind event (Figure 3). To do so, we used the glider mission MOOSE T02–02, which lasted for 87 days (from 12 November 2010 to 7 February 2011) and sampled four times the northern part of T02 and T03 sections from the Gulf of Lion’s shelf to the LION mooring line (Figure 1).

The geostrophic assumption was first tested by computing total and geostrophic PV calculated using, respectively, the total horizontal velocities Equation (2), and geostrophic ones Equation (3). Model geostrophic velocities were computed by integrating the thermal-wind balance referenced by surface currents given by gradients of sea surface height. The total and geostrophic PV in the model exhibit differences mainly in the upper layer where ageotrophic motions mostly prevail. In the upper 25 m, their deviated from each other by $0.75\pm 2.7\times {10}^{-11}$ m${}^{-1}$ s${}^{-1}$ and by an order of magnitude lower below between 25 and 1000 m: $0.13\pm 2.4\times {10}^{-12}$ m${}^{-1}$ s${}^{-1}$. This difference is about an order of magnitude lower than the PV magnitude observed in frontal regions of about 10${}^{-11}$ m${}^{-1}$ s${}^{-1}$. Thus, the geostrophic PV can capture the main frontal PV structure and the associated instability regimes (77% of the SI occurences diagnosed with total PV were also found using geostrophic PV).

The same calculation as the one used with observations was then performed with the virtual glider data and compared with total model geostrophic PV in order to assess the effect of the glider sampling and PV calculation (Figure 3). The stratification term $q_N$ is accurately reproduced without large biases (mean deviation of 1–10%, see

Table 1. Glider-based to total geostrophic PV ratio in the SYMPHONIE model with and without cross-stream correction considered for the front section shown in Figure 3. Numbers are given for the two most representative regions: stable and symmetrically unstable. Accurate detection of stability regimes (in percentage) are also given with reference ot the ones obtained using the total PV.

Regime	${\mathit{q}}_{\mathit{N}}^{\mathit{g}}/{\mathit{q}}_{\mathit{N}}^{\mathit{tot}}$	${\mathit{q}}_{\mathit{N}}^{\mathit{g},\mathit{cor}}/{\mathit{q}}_{\mathit{N}}^{\mathit{tot}}$	${\mathit{q}}_{\mathit{bc}}^{\mathit{g}}/{\mathit{q}}_{\mathit{bc}}^{\mathit{tot}}$	${\mathit{q}}_{\mathit{bc}}^{\mathit{g},\mathit{cor}}\mathbf{/}{\mathit{q}}_{\mathit{bc}}^{\mathit{tot}}$	${\mathit{q}}^{\mathit{g}}\mathbf{/}{\mathit{q}}^{\mathit{tot}}$	${\mathit{q}}^{\mathit{g}\mathbf{,}\mathit{cor}}\mathbf{/}{\mathit{q}}^{\mathit{tot}}$	detec %	detec %, cor
stable	0.99 ± 0.22	0.98 ± 0.21	0.42 ± 1.3	0.47 ± 2	1 ± 0.25	0.99 ± 0.32	92	92
SI	1.1 ± 2.2	1.1 ± 1.7	0.72 ± 0.37	1.2 ± 0.53	0.61 ± 0.41	0.97 ± 0.53	79	83

) and the cross-stream correction has no effect. The main bias in the PV calculation is however introduced by the baroclinic term $q_{bc}$, whose intensity is underestimated by 30 to 60% in absence of correction (see Table 1). The front width looks slightly wider as the result of the horizontal averaging. The cross-stream geometric correction seems particularly important to correct it, especially in regions subjected to SI where it results in overestimation by 20% of the baroclinic term on average. In the end, the geometrically-corrected total PV is in much better agreement (1–5% difference compared to 40% without correction). Stable and symmetrically unstable regions are well captured in 90% to 80% of the occurrences.

To conclude, glider-based PV seems to accurately characterize PV at fronts and detect SI events. Calculation in cross-stream axis provides a better estimate compared to cross-track ones, especially in intense frontal regions. The main difficulty of observing SI events remains the timing of the front crossing, as these features evolve rapidly.

3. Results

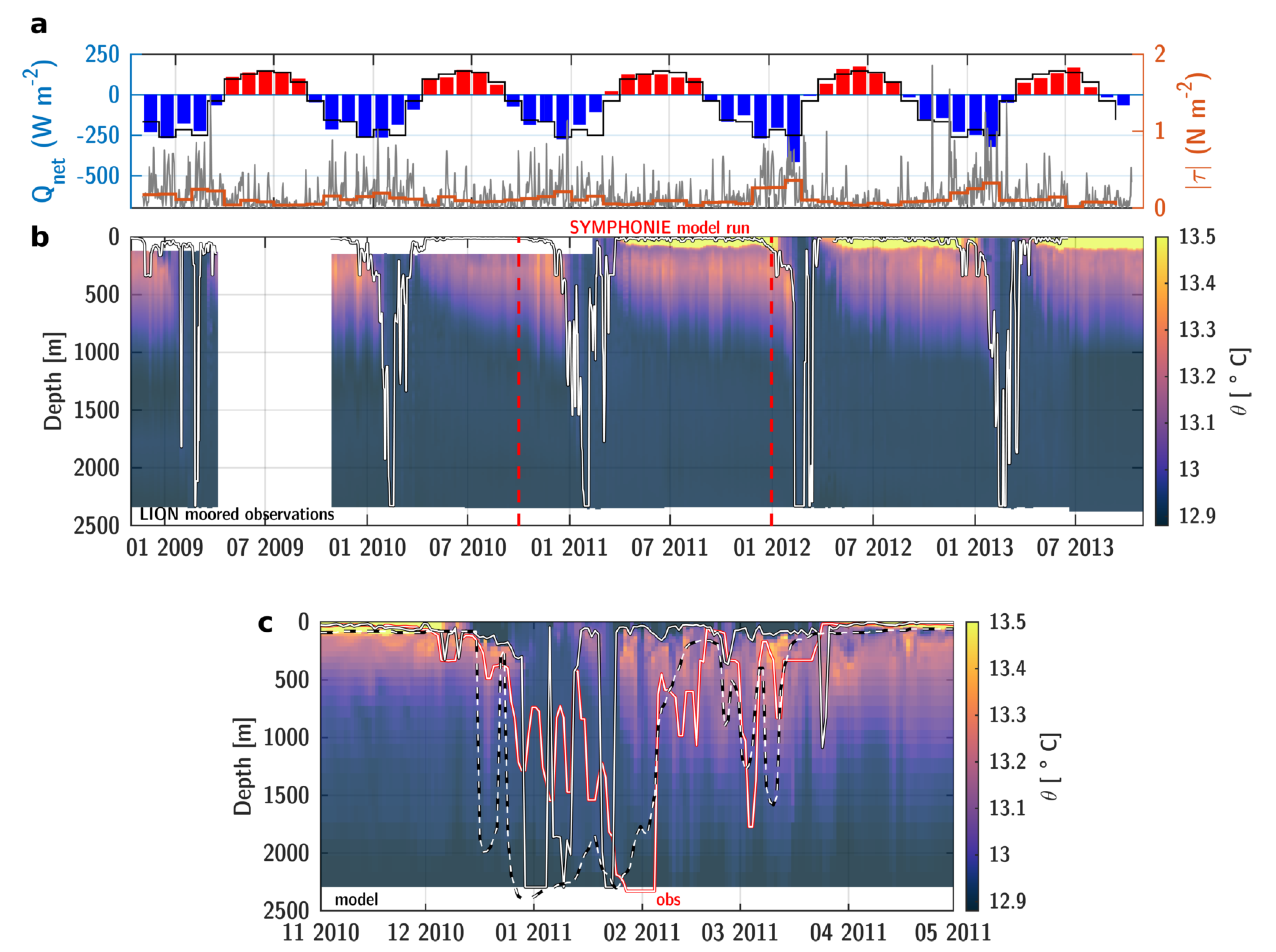
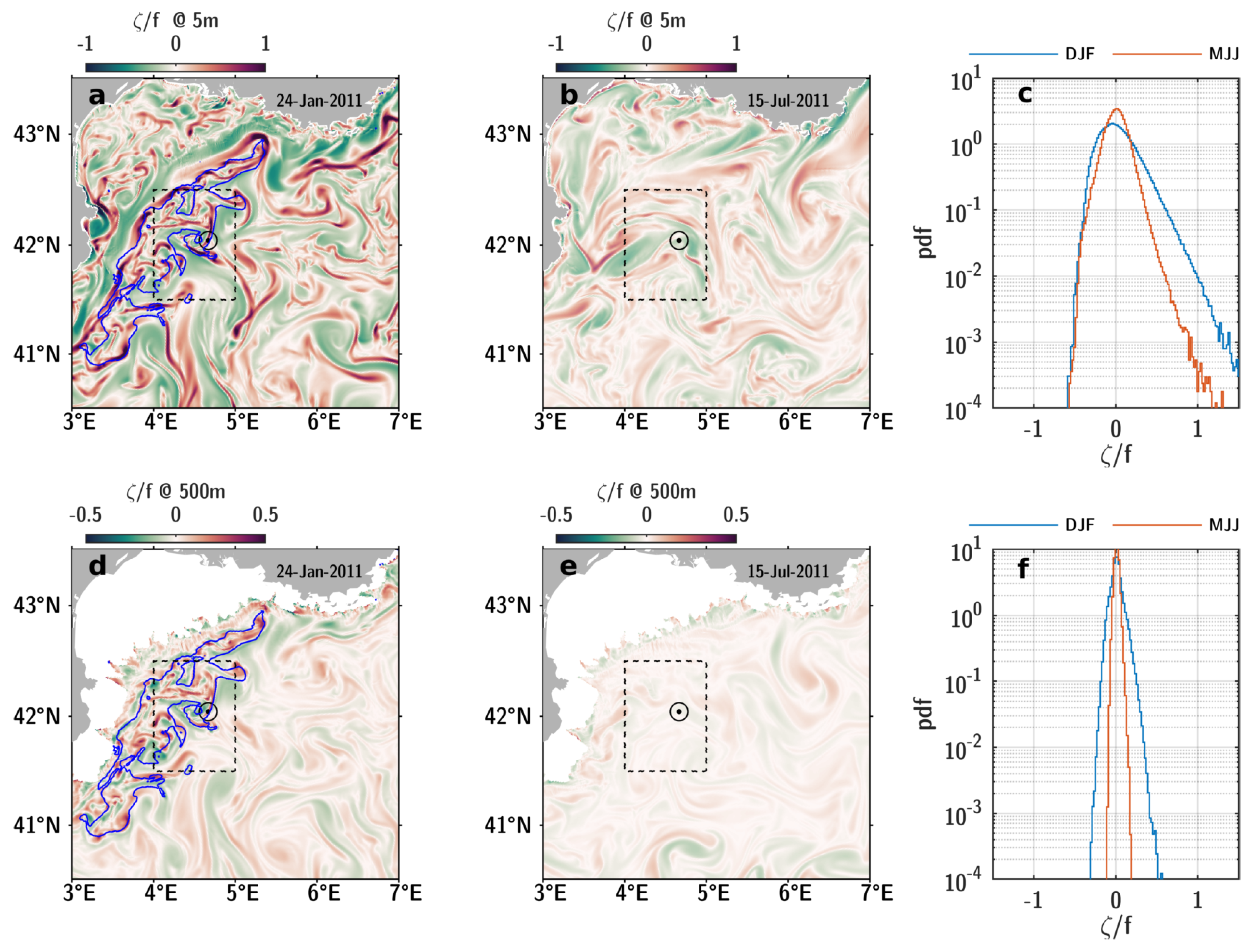
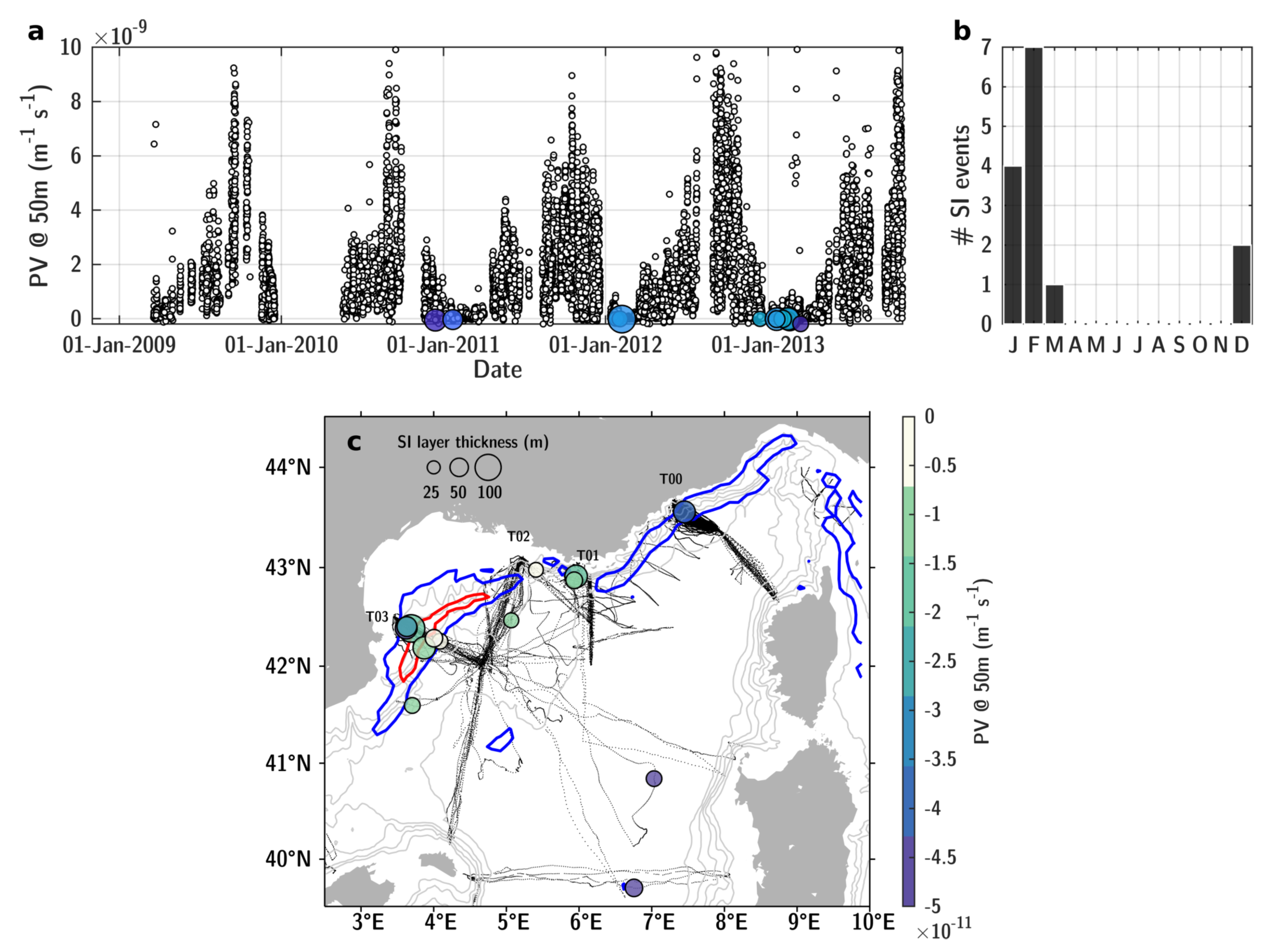
3.1. Deep Convection and Seasonality of Submesoscale

Dry and cold northerly winds (“Mistral” and “Tramontane”) prevail in the northwestern Mediterranean Sea in winter resulting in intense heat losses to the atmosphere (monthly average of about 250 W m${}^{-2}$, Figure 2a). The Gulf of Lion region has been subjected to very intense mixing events from 2009 to 2013. The MLD reached the seafloor ever winter at about 2500 m typically around February, as observed by the LION moored time series (Figure 2b). The SYMPHONIE model realistically reproduced the deep convection of winter 2011. The modeled MLD time series at the nearest grid point from the LION mooring site compared reasonably well with a root mean square error (rmse) of 530 m (white line in Figure 2c). A better representation in timing and amplitude of convection events was however found by considering a larger area around the LION mooring site lowering down the rmse to about 340 m (dashed white line in Figure 2c). This could be due to the shape and position of the mixed patch in the model, which is mostly localized along the NC (blue contours in Figure 4a) and does not extend as much offshore, as ocean color seen by satellite revealed. This highlights the local and basin-scale preconditionning of vertical mixing by (sub)mesoscale eddies [34,40]. During the study period, satellite images showed a maximum deep convection area of 15,800–24,100 km${}^2$ in winter 2011 [1] compared in the model to a maximum area where the MLD exceeded 500 m of 9100 km${}^2$ reached on 24 January. This is satisfactory for our study of frontal processes in the presence of deep mixed layer, but illustrates the difficulty to represent deep convection in regional and global numerical models and the importance of convection parameterization (see for instance [108]).

The horizontal pattern of vorticity exhibited (sub)mesoscale features such as meanders, fronts and eddies with notably smaller scales in the northern domain where the vertical mixing was the deepest. The dynamics in the convection area had a marked seasonal cycle in the model (Figure 4). Surface relative vorticity was strongly skewed toward positive values. Vorticity significantly larger than f were observed during the winter, while such high values were almost absent during the summer months. Anticylonic vorticity stayed bounded at around $-0.6f$ in both seasons. At 500 m, the dynamics was less energetic with vorticty distribution tapering during summer (Figure 4f). The skew toward cyclonic vorticity was still present at subsurface but less marked. The distribution showed a clear seasonal increase toward higher vorticity in winter with values up to $\left|Ro\right|\sim 0.5$.

Deep convection sharply modifies the ocean dynamics as vertical mixing diminishes the deformation radius in the mixed layer ($R_d=NH/f$ where N is the buoyancy frequency, H the mixed layer and f the Coriolis frequency) and energize small scale dynamics compared to summer stratified conditions [109]. Winter mixing also feeds the available potential energy that is transferred into eddy kinetic energy during the restratification phase [22].

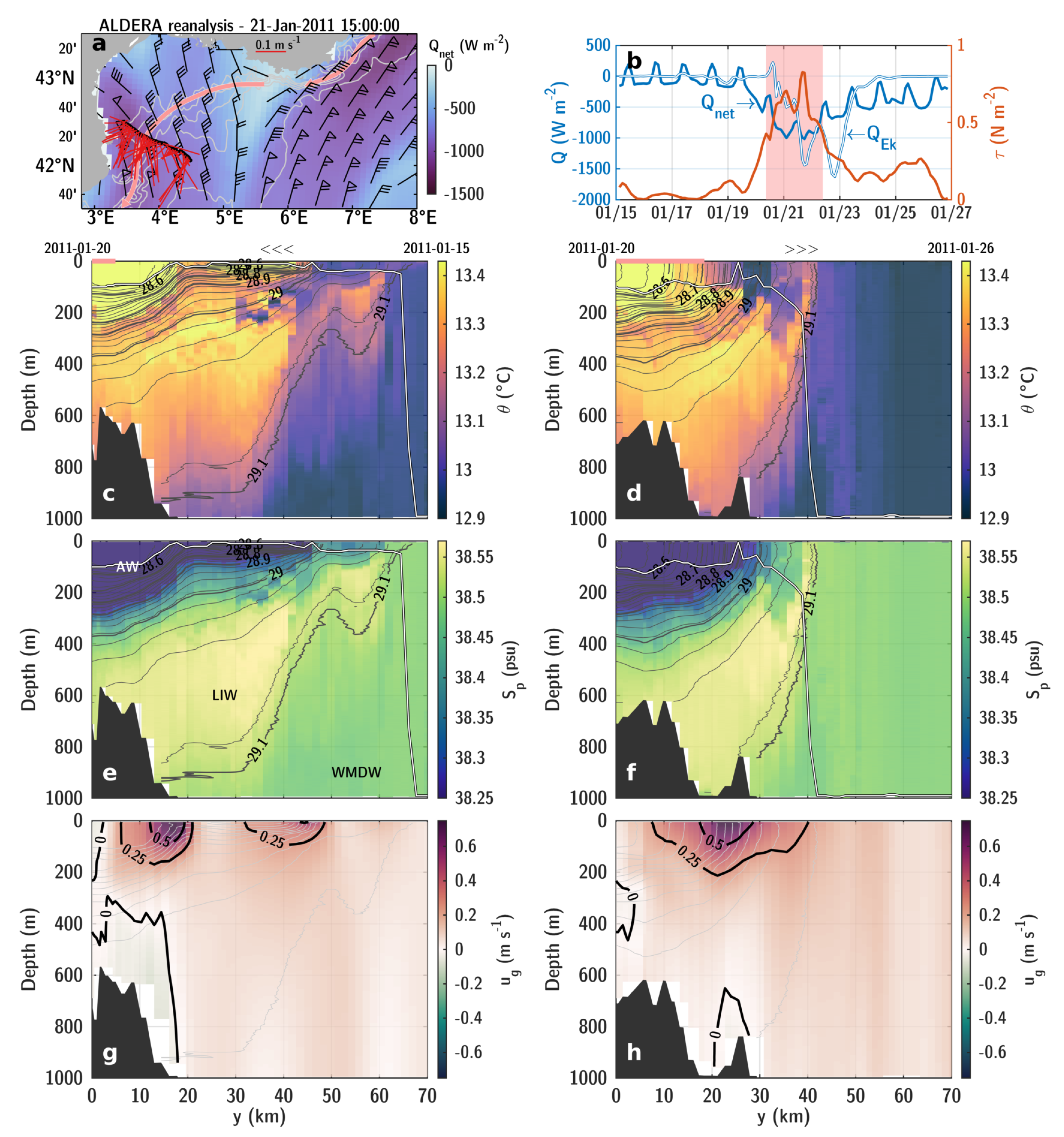
3.2. Northern Current Frontal Dynamics during a Down-Front Wind Event

Between 15 to 27 January 2011, a glider sampled the NC front back and forth along T03 section (Figure 5a). The two sections showed very different frontal situations following an intense wind event occurring on the 21st of January. For two days, wind stress exceeded 0.4 N m${}^{-2}$ and heat losses 500 W m${}^{-2}$. The wind orientation was mostly from the north where the glider sampled the NC, thus being roughly aligned with the NC pathway.

In the first section during calm conditions, the NC front was sampled over a wide area of about 50 km (Figure 5c). This width was larger than the generally observed NC width [39] and could result from the meandering of the NC jet. Isopycnals near the surface were relatively flat except above the continental slope where the NC front separates coastal warm/fresh AW (also influenced by river runoffs [110]) from higher salinity modified AW found offshore. The associated frontal jet was about 10 km wide with geostrophic velocities larger than 0.5 m s${}^{-1}$. An secondary frontal jet was also sampled about 30 km offshore from the slope with a weaker velocity signal. The detachment of a 10-km diameter anticyclonic eddy from the NC can also be observed at about $y=55$ km.

In the second section during and following the wind event (Figure 5d), isopycnals were much steeper. Geostrophic transport increased (wider frontal jet) with no sign of eddies offshore where the MLD directly dropped below 1000 m. This sharp contrast resulted from the intense surface forcing activating vertical mixing in the convection area. Following the wind event, temperature and salinity interleaving structures were observed in the NC frontal area (y between 20 and 40 km). Below the steepest isopycnals, where Levantine Intermediate Water (LIW) outcrop (${\sigma }_{\theta }=$ 29.05–29.1 kg m${}^{-3}$), along isopycnals up- and downward interleavings of warm/salty and cold/fresh waters can be observed.

The wind event was aligned in the down-front direction with the NC (Figure 5a). As a result, the isopycnals of the front steepened significantly and the stratification generally decreased in the upper 100 m (Figure 6a). In the same area, horizontal buoyancy gradients intensified through the mechanical action of winds (Figure 6b) and the negative baroclinic term in PV became dominant in the vicinity of the NC front. A layer of negative PV (unstable to symmetric instability, SI) was then observed by the glider from the surface down to about 100 m (Figure 6e). This zone of instability coincides with elevated Ekman equivalent heat loss generated by the down-front winds reaching about 1500 W m${}^{-2}$ (estimated from ALADIN reanalysis winds and in situ glider-based buoyancy gradients, see Figure 5b). This flux locally overtook the net surface heat loss, highlighting the important role of wind in the NC front dynamics. The SI layer also corresponded to the area where temperature and salinity interleaving were present (Figure 4d).

The numerical model showed a similar behavior in terms of PV dynamics with the appearance of a SI layer in the upper 100 m. In the model, the thermocline intensity was however slightly less stratified (Figure 6b). This was due to important vertical mixing on the light side of the NC front in the model (slope/shelf region) with MLD reaching almost 300 m compared to about 100 m in observations. Saltier surface waters in the model with practical salinity of 38.3 were observed compared to 38.1 in observations highlighting the importance of coastal processes (e.g, river runoffs). Note also that the front being narrower and shifted offshore by about 20 km, it delayed the front crossing by about a day after the maximum winds. A negative PV layer was still found in the model despite lower Ekman equivalent heat flux at the front of about 500 W m${}^{-2}$ against 1500 W m${}^{-2}$ in observations.

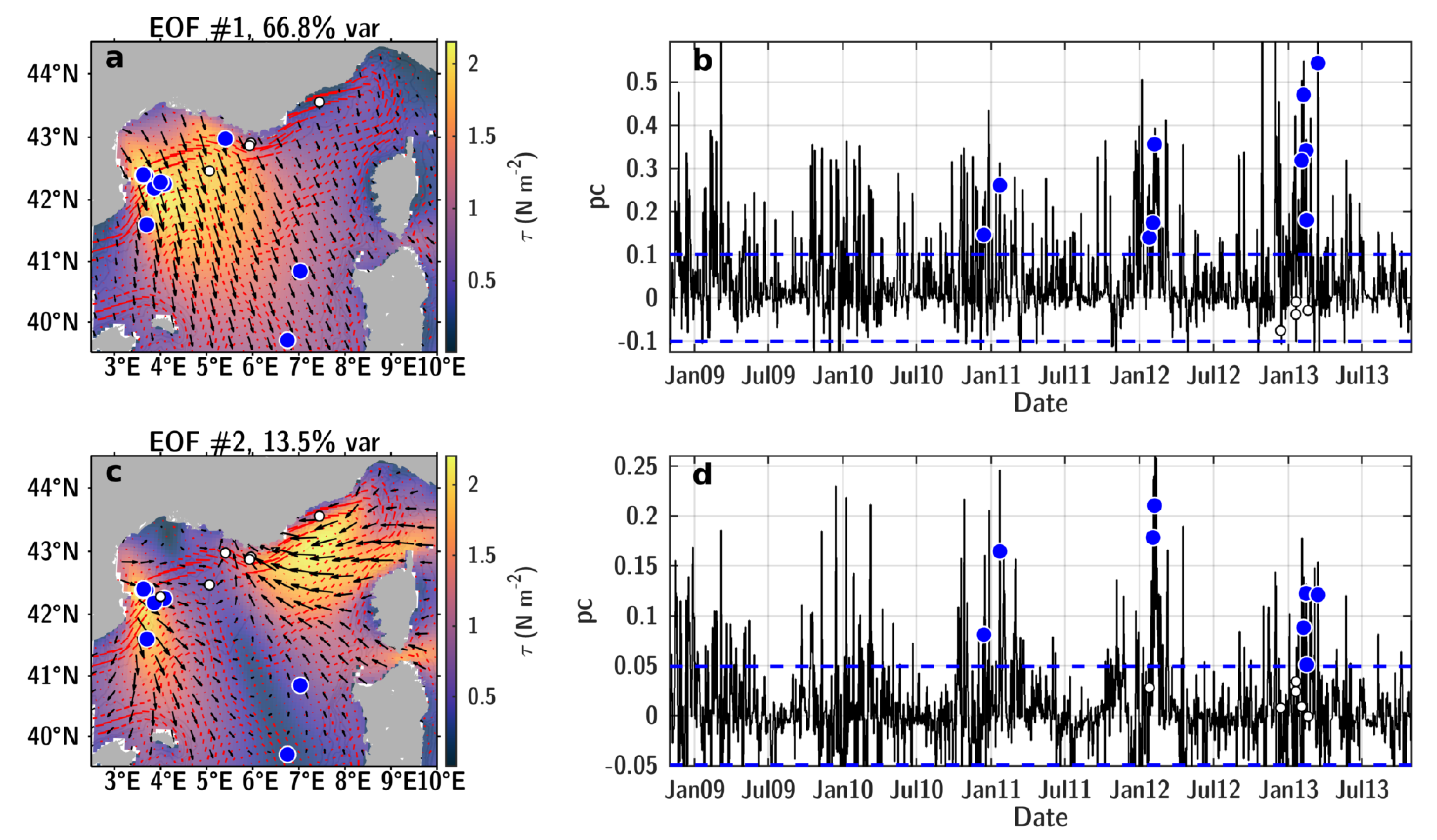
3.3. The Basin-Scale PV Response to Typical Winter Mistral Wind Event

As the numerical model well reproduced the main features of the PV field, further insights in the processes at play and their horizontal distribution can be assessed. The surface forcing at the basin scale at the apex of the wind event on 21 January is shown in Figure 7a,b. The Ekman equivalent heat flux was of similar amplitude as the net surface heat flux, or even locally dominating in frontal areas. The Ekman flux was particularly intense over a large area along the NC front from the Ligurian Sea to the western part of the Gulf of Lion. The wind pattern was indeed a combination of typical northerly Mistral and intense easterly winds corresponding to down-front winds for the NC in the western Gulf of Lion and Ligurian Sea. In the open sea, the fronts orientation mainly influenced by the mesoscale had thus a more variable structure. Consequently, the associated Ekman fluxes were locally intense in negative and positive values over smaller and less organized areas compared to the signal observed along the topographically-steered NC.

Below the Ekman layer (typically $h_{Ek}=\sqrt{2K_m/\left|f\right|}\sim 50$ m with $K_m\sim 0.1$ m${}^2$ s${}^{-1}$ the turbulent diffusivity), ageostrophic Ekman currents are generally small compared to the geostrophic component. The geostrophic and total PV at 15 m had opposite signs in areas of positive Ekman buoyancy fluxes due to restratifying agesotrophic circulations stabilizing surface fronts. On the other hand, geostrophic PV showed very little difference with the total one deeper at 50 m and is thus be a good proxy to detect symmetrically unstable mesoscale fronts (Figure 7c,d). During the wind event, all areas of negative PV subjected to SI matched strong Ekman heat losses larger than 500 W m${}^{-2}$. SI layers can extend further down to 100 m depth or more (see for instance Figure 6e). At 50 m, they were mostly found in 150–200 km bands along the NC in both the western Gulf of Lion and the Ligurian Sea, but also in the open sea in 10–50 km associated with mesoscale fronts (Figure 7d). Those offshore patches showed a more random distribution and evolved on timescale of a few days typical of the mesoscale (see Video S1 in Supplementary Materials). Strong Ekman heat losses were not always sufficient to trigger SI at 50 m offshore. The destruction of PV at fronts indeed needs to be intense and sustained in time in order to force SI at a mesoscale front. This is then less likely to occur in the open sea compared to the NC aligned with topography.

3.4. Seasonal PV Destruction Along the Northern Current Front

The numerical model characterized the frontal dynamics of the NC over a complete seasonal cycle. The net surface heat flux followed the seasonal cycle from positive to negative values (−250 to 100 W m${}^{-2}$ on average) with short periods (1–10 days) of intense heat losses reaching $-1000$ W m${}^{-2}$ (Figure 8a). During the simulated year, there were about 10 to 20 days of values below $-500$ W m${}^{-2}$ along the NC with more frequent days of strong heat losses in the western Gulf of Lion (Figure 8e). On the contrary, the Ekman equivalent heat flux only depends on the wind intensity and its orientation relative to the NC front. It thus reached intense positive and negative values during all seasons (from −1000 to +1000 W m${}^{-2}$) with a slightly calmer period from April to June. During the winter, there were almost 20 days with $Q_{Ek}<-500$ W m${}^{-2}$ in the western Gulf of Lion and about 10 in the Ligurian Sea. These numbers represent about half of the about 30–40 days found over the year showing the importance of the winter period regarding the wind forcing.

Potential vorticity at 50 m responded to the combined effect of both surface thermodynamic and mechanical forcing. The seasonal restratification promoted positive values by increasing stratification, while PV decreased to low values during the winter at around ${10}^{-11}$ m s${}^{-1}$. The strong down-front wind events regularly destroyed PV down to at lest 50 m causing negative values and generate favorable conditions to SI in ∼200-km bands along the NC (Figure 8d). The western part of the Gulf of Lion (around T03) was the main hotspot for SI with almost 40 days of instability per year (Figure 8h) and almost all of them occurring during the winter months (Figure 8g). Farther east in the Ligurian Sea, the NC was also frequently symmetrically unstable during about 20 days (again mostly during the winter). These two regions of the NC were identifed as hotspots for SI in the numerical model, in close relationship to the dominant down-front winds prevailing in the area and intense Ekman buoyancy losses.

3.5. Symmetric Instability in the Northern Current Observed by Gliders

In glider observations, SI events were defined from PV estimates and the balanced Richardson angle (see Section 2.5). Specific SI events were identified where SI was present at 50 m over at least 25 m in the vertical and two successive glider profiles. The characteristics of the corresponding SI fronts in terms of negative PV value, thickness and cross-front width are summarized in

Table 2. Characteristics of frontal SI events detected by glider: q, L, H correspond to the mean PV, width and thickness; ${\lambda }_{SI}$ refers to the theoretical SI wavelength; $Q_{Ek}$ is the minimum Ekman equivalent heat flux observed along the glider-track within a 48 h window around each event.

	Date	Location	q (m${}^{-1}$ s${}^{-1}$) $\times {10}^{-11}$	L (km)	H (m)	${\mathit{\lambda }}_{\mathit{SI}}$ (km)	Q${}_{\mathit{Ek}}$ (W m${}^{-2}$) min in 48 h
1	13 December 2010	NC, GoL west	−4.7	8.9	71	6.2	−1810
2	22 January 2011	NC, GoL west	−2.8	22.0	58	4.0	−1620
3	25 January 2012	NC, GoL east	−0.37	6.2	32	0.8	−30
4	2 February 2012	NC, GoL west	−0.46	5.8	36	1.0	−560
5	6 February 2012	NC, GoL west	−1.8	12.5	106	5.7	−2930
6	13 December 2012	Open-sea	−0.79	4.7	33	1.2	−120
7	19 January 2013	NC, GoL east	−1.6	12.1	75	3.8	−110
8	19 January 2013	NC, GoL east	−1.3	5.5	42	1.9	−380
9	2 February 2013	NC, GoL west	−0.66	4.8	45	1.5	−1870
10	7 February 2013	NC, GoL west	−0.92	5.0	37	1.5	−3160
11	13 February 2013	Open-sea	−5.7	5.0	45	4.7	−640
12	14 February 2013	NC, GoL west	−0.8	10.3	73	2.7	−260
13	18 February 2013	NC, Ligurian	−3.7	7.3	70	5.3	−200
14	15 March 2013	Open-sea	−19	5.5	36	6.6	−3970
mean			−1.7 ± 1.1	8.3 ± 4.8	54 ± 22	3.3 ± 2.1	−1260 ± 1310

. Bear in mind that profiles with an angle between the DAC and glider track exceeded 45${}^{\circ }$ were excluded (see Section 2.6). On average, the detected SI events had a PV signal of about $-1.6\times {10}^{-11}$ m s${}^{-1}$ over 8.3 km cross-front distance (from 4.7 to 22 km) and 54 m thickness (from 32 to 106 m). The width of SI layers was smaller than the mesoscale of the NC front, even though this submesoscale instability develops within steep fronts whose scale is determined typically by the mesoscale. In line with model detection of SI, it is interesting to note that more events were also detected in the western Gulf of Lion (7/14) than in the Ligurian Sea (1/14), eastern Gulf of Lion (3/14) or the open sea (3/14).

The glider-based estimation of PV reproduced the seasonal cycle (Figure 9a). SI layers at 50 m were only detected during the winters 2011, 2012 and 2013, mostly because of a lack of data during the winters 2009 and 2010. SI events at 50 m were only detected from October to March with a highest occurrence in February (7 events out of 14, Figure 9b). This generally corresponds to the month of deepest MLD and lowest stratification. SI layers at depths shallower than 50 m might still be present during other months, but their detection and characterization by gliders would be less robust due to the sampling so we decided to discard them from the statistics.

Regarding the characteristics of symmetric instability in unstable fronts, Thomas and Lee [102] inferred a wavelength in relationship with the negative PV signal q and thickness H of the SI layers: ${\lambda }_{SI}=4H\sqrt{-fq}/f^2$. On average, ${\lambda }_{SI}$ was about 3.3 km. Note that length is smaller than the cross-front scale of SI layers of 8.3 km on average. Even if this number might be underestimated given the short scales in space and time of negative PV signals, it corresponds on average to about 2 wavelengths. This is more or less what can be observed in Figure 5 corresponding to event 3 in Table 2 showing SI extending over about 20 km and 60 m deep with two unstable wavelengths revealed by temperature and salinity interleavings.

3.6. Wind Forcing of Symmetric Instability

Northerly dry Mistral events seems to dominate the wind forcing of the northwestern Mediterranean Sea, as exemplified by the first empirical orthogonal function (EOF) explaining about 66.8% of the wind stress variability (Figure 10). The second EOF corresponding to 13.5% of the variance represents easterly winds in the Ligurian Sea combined with westerly and northerly winds in the western GoL. The first two EOFs are both situations of down-front winds along the NC in the two hotspots of SI identified in the model (western Gulf of Lion and Ligurian Sea).

In terms of SI events, the majority of them occurred during strong Mistral or easterly winds: 10/14 (reps. 8/14) of the detected SI events have a principal component for the first (resp. second) EOF larger than one standard deviation (std). In a general manner, SI events were closely linked to the dominant wind patterns in the area and presence of topographically-steered front of the Northern Current. Over the study period, 25% of the year the wind were favorable to PV destruction in the two hotspots for SI along the NC (western Gulf of Lion and Ligurian Sea) with one of the first two EOFs exceeding one std. This was also confirmed by the strongly negative Ekman equivalent heat flux reported by gliders during the sampling SI events. The minimum Ekman buoyancy flux found within a 48 h window was on average $-1260$ W m${}^{-2}$ and 8/14 events had values dropping below −500 W m${}^{-2}$. At least half of the SI events were thus associated with intense down-front wind events. Observing strong negative Ekman equivalent heat flux requires the front sampling to be synchronous with the down-front winds, which might not be the case for every SI events.

3.7. Vertical Circulations and Biogeochemical Implications

Symmetric instability forced by down-front winds can generate important vertical velocities. This is also suggested by glider temperature and salinity sections (see Figure 5 and Figure 11 showing another SI layer triggered by a strong Mistral event in February 2013). A glider crossed the NC front along the T03 section at the time of maximum wind. The wind stress reached 1.5 N m${}^{-2}$, while net surface heat losses peaked at about 1200 W m${}^{-2}$ and Ekman equivalent buoyancy fluxes reached almost −2000 W m${}^{-2}$ (Figure 11b). A SI layer of about 50 m in thickness and 5 km in cross-front direction was captured at the NC front by the glider. The temperature and salinity sections exhibit a clear pattern of alternated vertical displacements below the mixed layer depth (Figure 11g,h).

Cold/fresh water was subducted down to 200 to 400 m below the NC front in two cells transporting high oxygen and chlorophyll waters (Figure 11e,f). In the mixed layer, especially when the winds were strong and the mixing active, phytoplankton was diluted on the vertical by convective convective plumes whose amplitude can reach 0 (1000 m days${}^{-1}$) in the deep convection area [97]. Following Niewiadomska et al. [111] who described the optical properties of subduction along the one of the first glider deployment along the MOOSE T00 endurance line, the sign of frontal ageostrophic secondary circulation can easily be identified. At short timescale, vertical circulations modulate the chlorophyll distribution as a passive tracer with patches transferred at depth and low-chlorophyll water lifted toward the surface. Upward movements could also inject nutrients into the sunlit layer and fuel phytoplankton growth. Higher chlorophyll concentrations could well be observed at the surface near the unstable front. However, it is hard to disentangle the dynamical processes that can affect chlorophyll concentration (dilution, restratification, lateral advection, …) from local production.

Phytoplankton concentration should decay below the sunlit layer in the absence of fluxes that can sustain the phytoplankton population. For a surface chlorophyll concentration of 0.5–1.5 mg m${}^{-3}$ observed at the front, the euphotic layer, where only 1% of the surface photosynthetic available radiation remains, can be estimated to 30–45 m following Morel and Berthon [112]. In the deepest patch of chlorophyll observed at around 200–400 m, phytoplankton cells were thus well below the euphotic layer. This signal could not be caused by local production but should result from important vertical displacements. Considering a survival timescale of phytoplankton in absence of light of about 1–10 days, this would indicate intense vertical circulations of O (10–100 m day${}^{-1}$) along the NC front below the unstratified mixed layer.

Numerical model suggested that frontal regions unstable to SI are organized in O (100 km) bands along the NC front. Considering vertical displacements $w^{\prime }$ of O (10–100 m day${}^{-1}$) roughly estimated from the subduction of phytoplankton below the mixed layer in O (1 km) cross-front patches, this would represent a subduction/obduction rate of 0.01–0.1 Sv along the whole unstable frontal area. This would apply only when SI is active (i.e., 20–40 days in the two hotspots of the western Gulf of Lion and Ligurian Sea). Along isopycnal temperature and salinity anomalies $T^{\prime }$/$S^{\prime }$ associated with interleaving could also be observed with the order of magnitude of 0.2 ${}^{\circ }$C/0.05 (see for instance Figure 5 or Figure 11). The sign of the anomalies was correlated to the vertical velocities, so all contribute to an upward heat flux of typically $F_Q=\rho C{p}_0<w^{\prime }{T}^{\prime }>\sim$100–1000 W m${}^{-2}$. This rough scaling shows that vertical heat fluxes generated by SI in the NC could be comparable to fluxes due to surface heat flux or mechanical effect of winds. This process thus needs a particular attention in order to close the heat/salt budgets of the NC. Similarly, the oxygen budget of intermediate layers might also be importantly affected by SI, as well as vertical fluxes of nutrients and carbon. Bear in mind that other (sub)mesoscale processes, for instance slower but more persistent baroclinic mixed layer instabilities [113], might also played an important role in the front heat, salt and momentum balance.

4. Discussion

The topographically-steered path of the NC in the northwestern Mediterranean Sea enables sustained destruction of PV over large areas regularly subjected to down-front winds. This current system also interact with deep convection where vertical mixing reaching depths from 500 to 2500 m intensifies intensity and depth of horizontal density gradients between the NC, an area subjected to lateral advection, and the preconditioned convection area offshore. This interaction contributes to important PV destruction by weakening the water column stratification. The main winds (Mistral and Tramontane in the Gulf of Lion, and easterlies in the Ligurian Sea) foster down-front winds in 100–200 km bands along the NC and symmetric instability especially in two hotspots: the western Gulf of Lion and the Ligurian Sea. Whether this instability remains important in the open sea, and especially along the North Balearic Front, needs to be further investigated. Previous studies reported important effect of down-front winds in the Atlantic and the Southern Ocean [69,70,82]. However, these regions are characterized by larger deformation radius (50–100 km). In the northwestern Mediterranean Sea, the mesoscale is generally smaller (10–30 km) and evolves quickly (1–5 days). This might be a limiting factor to sustain destruction of PV outside of the topographically-steered circulation. A Lagrangian water parcel caught in a front meandering at the mesoscale would indeed stay aligned in the down-front direction during period of time possibly shorter than the timescale of the wind event. The quantification of the relative importance of other sources of vertical circulations (e.g., frontogenesis [43,46]) and their seasonal dependence and forcing deserves to be studied specifically.

The horizontal and vertical resolution and viscosity are key ingredients for a numerical model to be able to resolve SI, as shown by Bachman and Taylor [114] in an idealized front. In a realistic model, the parameterized vertical mixing scheme makes it however harder to disentangle the relative contribution of restratification by SI from the increasing vertical diffusivity. Following on the example of the NC front after the intense down-front event on 21 January 2011 showing deep and extended negative PV layers, a closer inspection at hourly outputs showed how unbalanced motions rapidly ceased after restoring the front in geostrophic balance within about a day after the peak winds (not shown). Within the SI layer, important positive and negative vertical velocities also emerged in the model (up to ∼100 m per day) suggesting that the SYMPHONIE numerical model at 1 km resolution could at least marginally resolve some submesoscale features of the front. However, a horizontal resolution of 0 (100 m) seems required to better resolve SI because of the isopycnal slope in the Northern Current can reach value close to 0.1. The intensity and thickness of the negative PV layers can indeed lead to larger wavelengths of the instability [102], easier to be resolved numerically.

Gliders were able to characterize symmetrically unstable fronts in the northwestern Mediterranean Sea, adding to regions such as the Equatorial Pacific [81], the Southern Ocean [69,70,83], the Atlantic Ocean [82,84] and the Gulf Stream [78]. The key to capture negative PV was to sample the front during or shortly after a down-front wind event. Glider track orthogonal to the frontal jet is also important, although cross-stream coordinate system can correct the geometrical bias in horizontal gradients observed by gliders [78,85]. The constrained path of topographically-steered currents (like the Northern Current) helped gliders sample perpendicular to the flow. A sustain effort in deployment during several year (as part of the MOOSE observatory [86]) was also important in order to cover the seasonality of the instabilities and to draw statistics from a significant number of events.

Observations further showed the impacts of the vertical exchanges generated by SI on physical (temperature, salinity) and biogeochemical (oxygen, chlorophyll-a fluorescence) properties. The impact was important below the mixed layer at intermediate depths (200–600 m) where one finds the warm, salty and relatively poor in oxygen Levantine Intermediate Water. The subduction of cold, fresh and oxygenated patches below unstable fronts could thus have an important impact on the heat, salt and oxygen budgets of the Northern Current. In addition SI being a recurrent feature in the NC during the winter, it could importantly impact the vertical fluxes of nutrients, boost phytoplankton growth and drive the export of carbon. The present work could be extended pending a specific and important work on the harmonization of oxygen and optical measurements (fluorescence and backscatter) from the MOOSE gliders. Finally, among the processes impacting vertical fluxes, the enhanced turbulence during SI events numerically predicted by Taylor and Ferrari [75] could also be resolved using gliders equipped with high frequency shear probes [115].

High resolution observations and simulations were shown to be complementary. While glider observed episodic signatures of SI at fronts, the model reproducing those signals could be used to map the processes spatially and extend the analysis over a full seasonal cycle. Based on these results, a similar synergy could be applied with a coupled physics-biogeochemitry numerical model to tackle the open questions about the impact of SI along the NC for the ventilation of intermediate layers and carbon sequestration.

More generally, the regular instances of symmetric instability during the winter around the deep convection region of the northwestern Mediterranean Sea raises the question of whether it is also the case in other deep convection sites (e.g., the Labrador, Irminger, Greenland and Weddel Seas). The role of submesoscale dynamics on deep convection has been shown to be important in the Labrador Sea highlighting the need to account for their effects in a large-scale earth system model [62]. All those sites are regions of intense dry and cold winds occurring in bursts. The interaction of those winds with the topographically-steered circulation could reveal hotspots of SI. The large buoyancy fluxes generated at the front by mechanical effect near deep convection regions further promote restratification or instabilities (SI, gravitational or mixed). Furthermore, given the scale of the associated heat fluxes, wind-driven submesoscale likely influences the intensity and position of deep convection at a larger scale. Numerical experiment including parametrization of SI (e.g., Bachman et al. [74]) with regional ocean model could also be used in order to evaluate the future evolution of deep convection in a more realistic approach.