The Effect of Patterned Micro-Structure on the Apparent Contact Angle and Three-Dimensional Contact Line
Abstract
1. Introduction
2. Surface Reproduction
2.1. Structured Surface Pattern
2.2. Direct LASER Writing (DLW) Lithography
2.3. Nickel Electroforming
2.4. Hot Embossing
2.5. Reproduction Quality
3. Experimental Setup
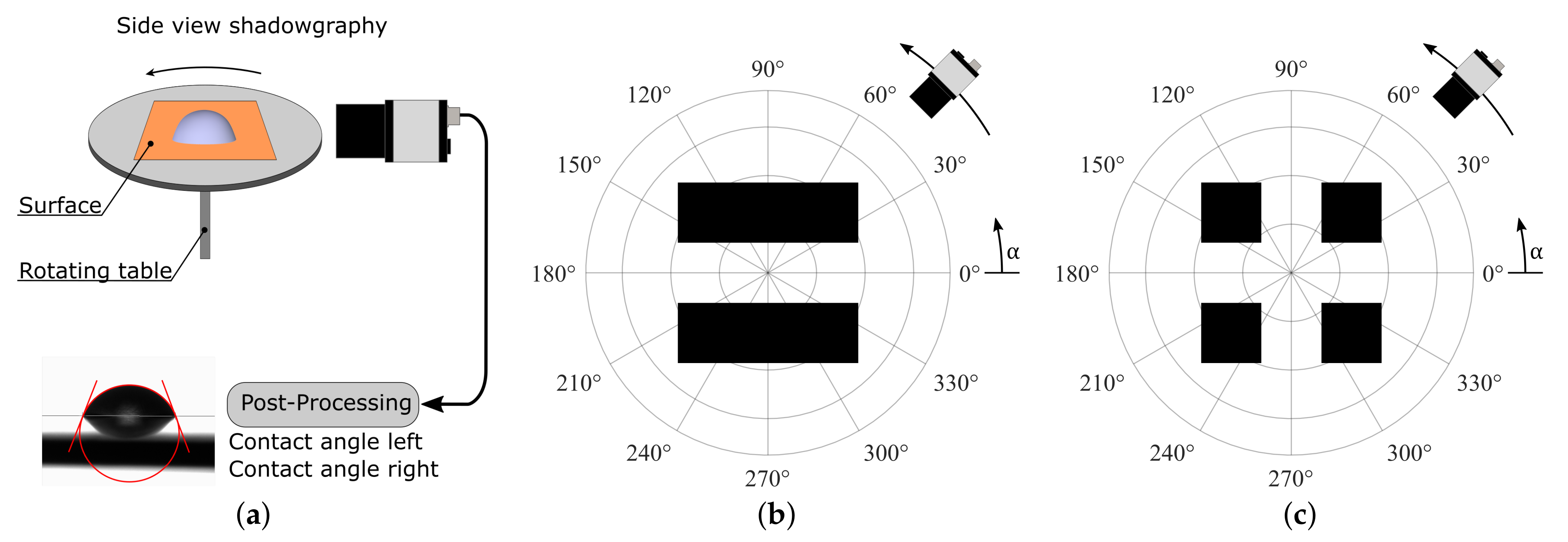
3.1. Measurement Principle
3.2. Contact Angle Measurement Device
3.3. Measurement Procedure
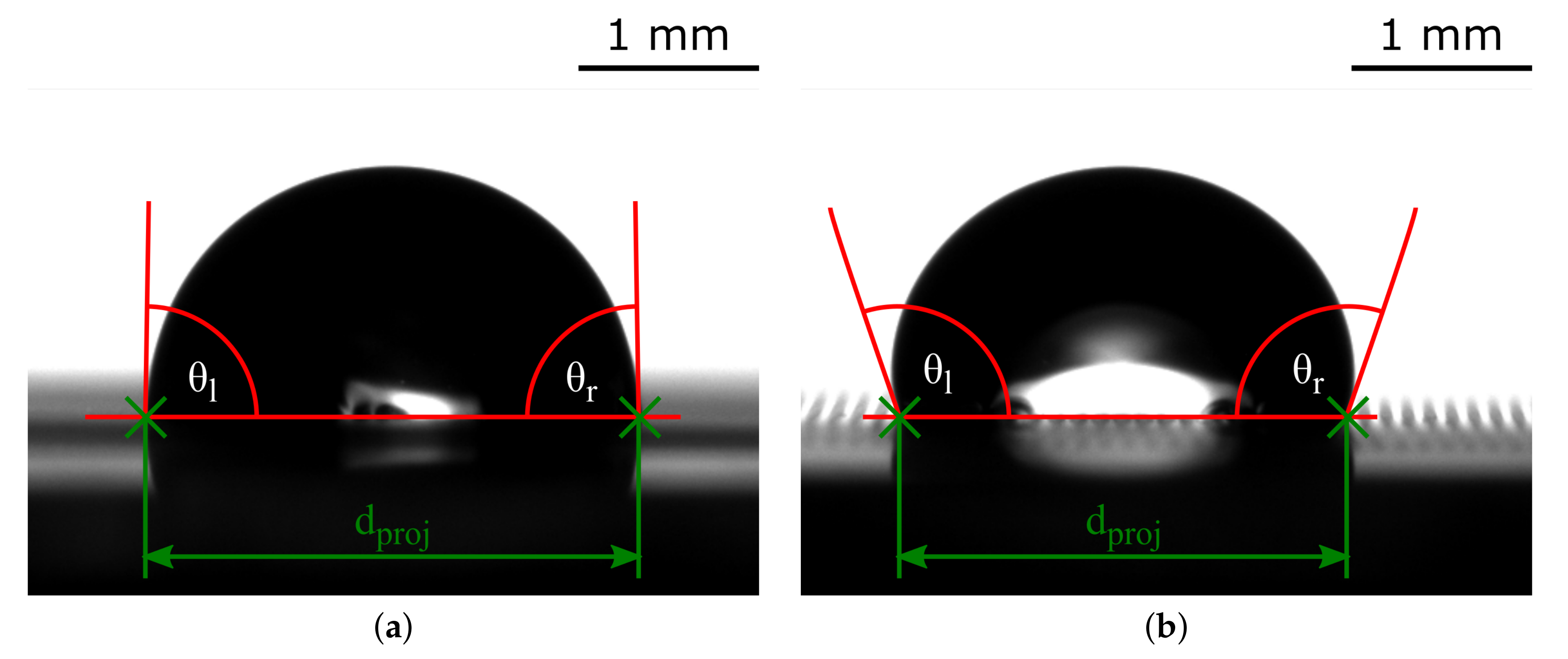
3.4. Evaluation Routine for Optical Contour Analysis of Droplet Shadowgraphs
4. Results and Discussion
4.1. Prediction of Apparent Contact Angles on Smooth Surfaces
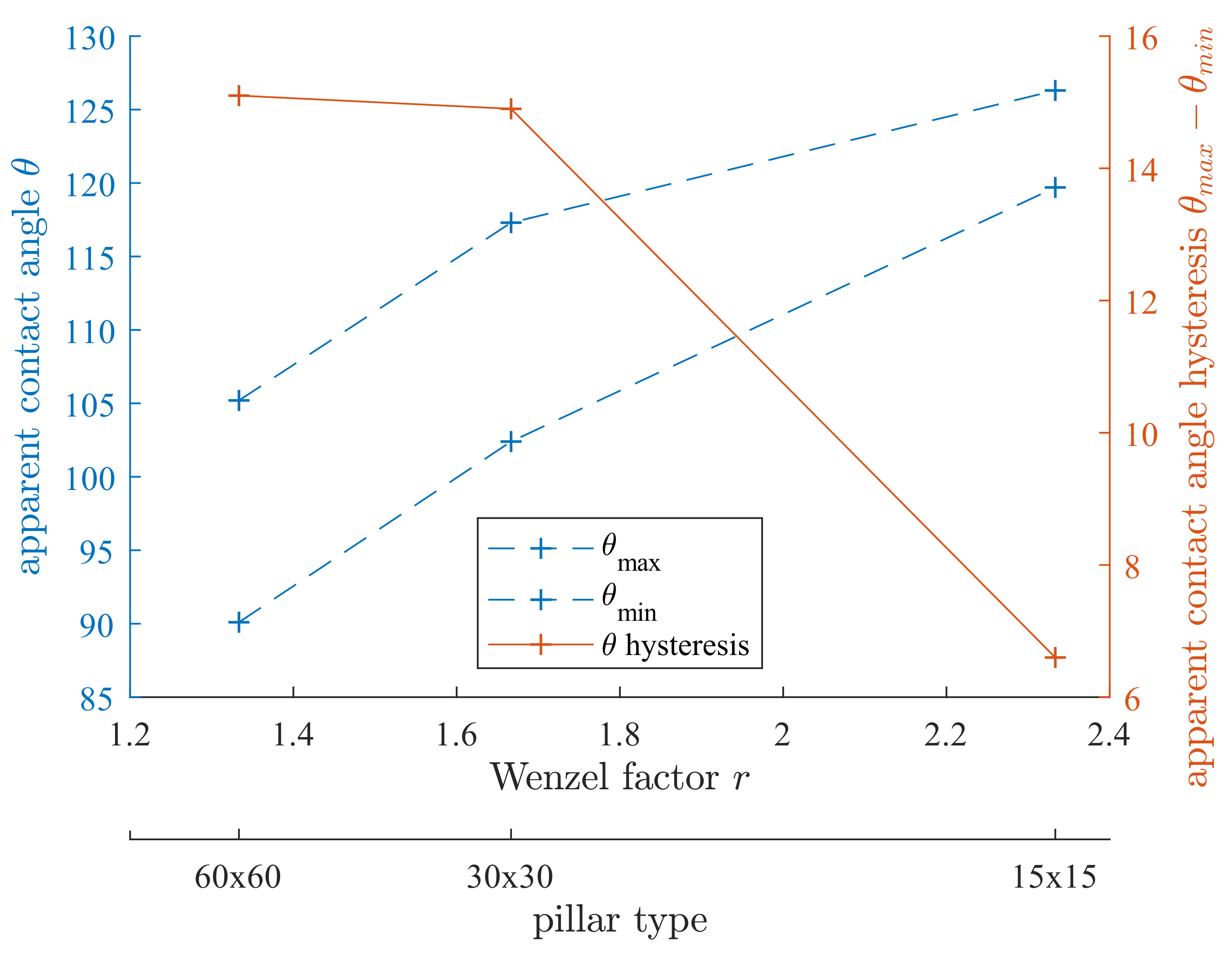
4.2. Results of Apparent Contact Angle Measurements on Structured Surfaces
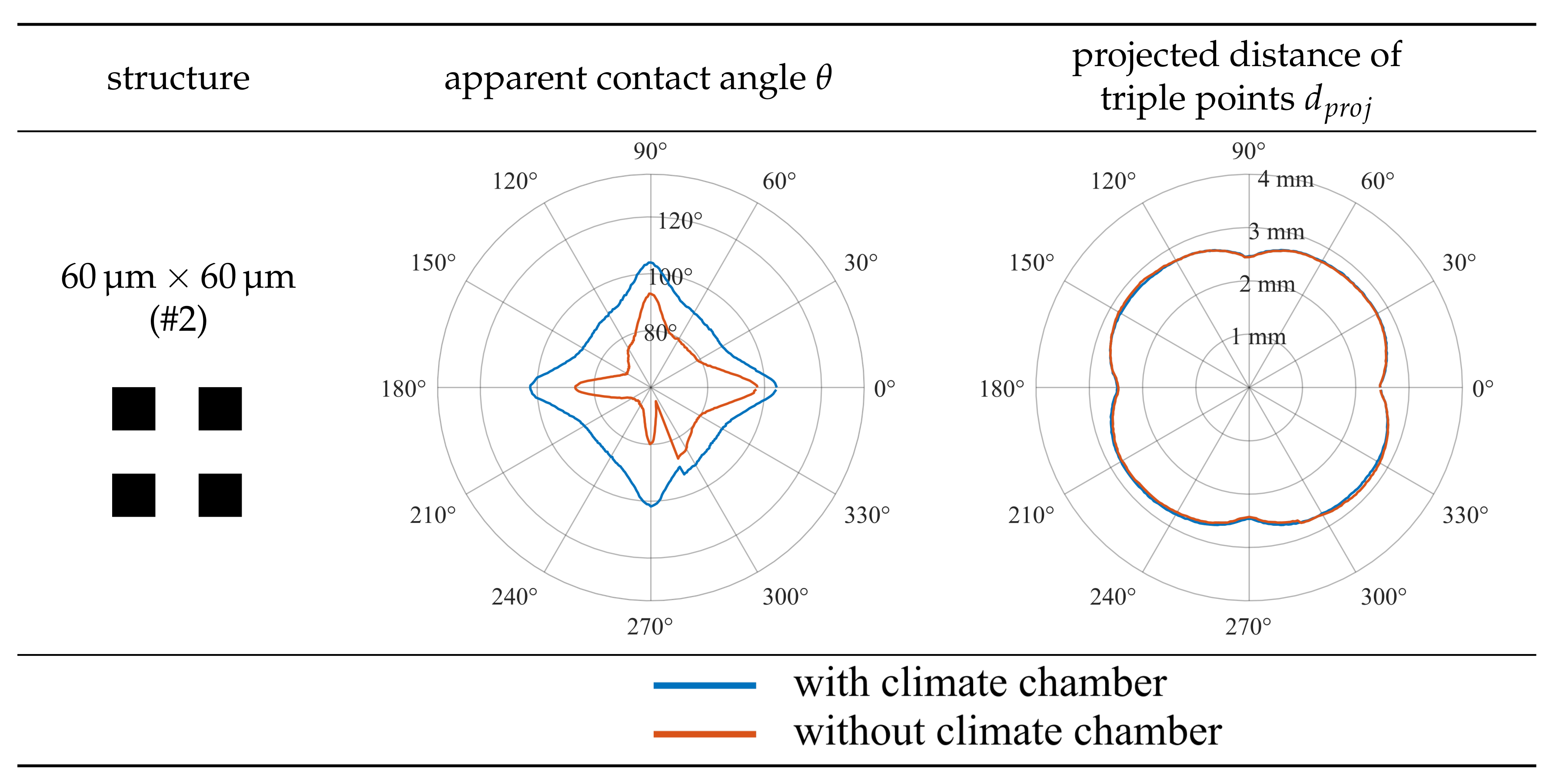
4.3. Effectiveness of the Climate Chamber and Error in Apparent Contact Angle Measurements
5. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Hensel, R.; Helbig, R.; Aland, S.; Braun, H.G.; Voigt, A.; Neinhuis, C.; Werner, C. Wetting Resistance at Its Topographical Limit: The Benefit of Mushroom and Serif T Structures. Langmuir 2013, 29, 1100–1112. [Google Scholar] [CrossRef]
- Parker, A.R.; Lawrence, C.R. Water capture by a desert beetle. Nature 2001, 414, 33–34. [Google Scholar] [CrossRef]
- Bico, J.; Tordeux, C.; Quéré, D. Rough wetting. Europhys. Lett. (EPL) 2001, 55, 214–220. [Google Scholar] [CrossRef]
- Courbin, L.; Bird, J.C.; Reyssat, M.; Stone, H.A. Dynamics of wetting: From inertial spreading to viscous imbibition. J. Phys. Condens. Matter 2009, 21, 464127. [Google Scholar] [CrossRef]
- Huang, X.; Gates, I. Apparent Contact Angle around the Periphery of a Liquid Drop on Roughened Surfaces. Sci. Rep. 2020, 10, 8220. [Google Scholar] [CrossRef]
- Foltyn, P.; Restle, F.; Weigand, B. 360∘ Evaluation of Projected Contact Angles of Static Droplets on Structured Surfaces; Droplet Impact Phenomena & Spray Investigations (DIPSI): Bergamo, Italy, 2019; pp. 14–17. [Google Scholar] [CrossRef]
- Kalinin, Y.V.; Berejnov, V.; Thorne, R.E. Contact Line Pinning by Microfabricated Patterns: Effects of Microscale Topography. Langmuir 2009, 25, 5391–5397. [Google Scholar] [CrossRef]
- Morita, M.; Koga, T.; Otsuka, H.; Takahara, A. Macroscopic-Wetting Anisotropy on the Line-Patterned Surface of Fluoroalkylsilane Monolayers. Langmuir 2005, 21, 911–918. [Google Scholar] [CrossRef]
- Rioboo, R.; Marengo, M.; Tropea, C. Time evolution of liquid drop impact onto solid, dry surfaces. Exp. Fluids 2002, 33, 112–124. [Google Scholar] [CrossRef]
- Josserand, C.; Lemoyne, L.; Troeger, R.; Zaleski, S. Droplet impact on a dry surface: Triggering the splash with a small obstacle. J. Fluid Mech. 2005, 524, 47–56. [Google Scholar] [CrossRef]
- Antonini, C.; Amirfazli, A.; Marengo, M. Drop impact and wettability: From hydrophilic to superhydrophobic surfaces. Phys. Fluids 2012, 24, 102104. [Google Scholar] [CrossRef]
- Sivakumar, D.; Katagiri, K.; Sato, T.; Nishiyama, H. Spreading behavior of an impacting drop on a structured rough surface. Phys. Fluids 2005, 17, 100608. [Google Scholar] [CrossRef]
- Vaikuntanathan, V.; Sivakumar, D. Maximum Spreading of Liquid Drops Impacting on Groove-Textured Surfaces: Effect of Surface Texture. Langmuir 2016, 32, 2399–2409. [Google Scholar] [CrossRef]
- Malouin, B.A.; Koratkar, N.A.; Hirsa, A.H.; Wang, Z. Directed rebounding of droplets by microscale surface roughness gradients. Appl. Phys. Lett. 2010, 96, 234103. [Google Scholar] [CrossRef]
- De Gennes, P.G. Wetting: Statics and dynamics. Rev. Mod. Phys. 1985, 57, 827–863. [Google Scholar] [CrossRef]
- Wenzel, R.N. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Cassie, A.B.D.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546–551. [Google Scholar] [CrossRef]
- McHale, G.; Shirtcliffe, N.J.; Aqil, S.; Perry, C.C.; Newton, M.I. Topography Driven Spreading. Phys. Rev. Lett. 2004, 93, 036102. [Google Scholar] [CrossRef] [PubMed]
- Extrand, C.W.; Moon, S.I. Contact Angles on Spherical Surfaces. Langmuir 2008, 24, 9470–9473. [Google Scholar] [CrossRef]
- Gibbs, J.W.V. The Collected Works of J. Willard Gibbs: 1 Thermodynamics, Reprint ed.; Yale Univ. Press: New Haven, CT, USA, 1957; Volume 1, p. XXVIII. [Google Scholar]
- Öner, D.; McCarthy, T.J. Ultrahydrophobic Surfaces. Effects of Topography Length Scales on Wettability. Langmuir 2000, 16, 7777–7782. [Google Scholar] [CrossRef]
- Langbein, D. (Ed.) Capillary Surfaces. In Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 2002; Volume 178. [Google Scholar] [CrossRef]
- Kim, D.; Pugno, N.M.; Ryu, S. Wetting theory for small droplets on textured solid surfaces. Sci. Rep. 2016, 6, 37813. [Google Scholar] [CrossRef]
- Raj, R.; Adera, S.; Enright, R.; Wang, E.N. High-resolution liquid patterns via three-dimensional droplet shape control. Nat. Commun. 2014, 5, 4975. [Google Scholar] [CrossRef] [PubMed]
- Santini, M.; Guilizzoni, M.; Fest-Santini, S. X-ray computed microtomography for drop shape analysis and contact angle measurement. J. Colloid Interface Sci. 2013, 409, 204–210. [Google Scholar] [CrossRef]
- Marmur, A.; Della Volpe, C.; Siboni, S.; Amirfazli, A.; Drelich, J.W. Contact angles and wettability: Towards common and accurate terminology. Surf. Innov. 2017, 5, 3–8. [Google Scholar] [CrossRef]
- Drelich, J.; Wilbur, J.L.; Miller, J.D.; Whitesides, G.M. Contact Angles for Liquid Drops at a Model Heterogeneous Surface Consisting of Alternating and Parallel Hydrophobic/Hydrophilic Strips. Langmuir 1996, 12, 1913–1922. [Google Scholar] [CrossRef]
- Foltyn, P.; Guttmann, M.; Schneider, M.; Fest-Santini, S.; Wildenschild, D.; Weigand, B. Fabrication and evaluation methods of micro-structured surfaces for droplet impact experiments. In Droplet Interactions and Spray Processes; Lamanna, G., Tonini, S., Cossali, E., Weigand, B., Eds.; Fluid Mechanics and Its Applications; Springer: Berlin/Heidelberg, Germany, 2020; pp. IX, 294. [Google Scholar]
- Silverio, V.; de Freitas, S.C. Microfabrication Techniques for Microfluidic Devices. In Complex Fluid-Flows in Microfluidics; Galindo-Rosales, F.J., Ed.; Springer International Publishing: Cham, Switzerland, 2018; Chapter 2; pp. 25–51. [Google Scholar] [CrossRef]
- Wissmann, M.; Barié, N.; Guttmann, M.; Schneider, M.; Kolew, A.; Besser, H.; Pfleging, W.; Hofmann, A.; Erps, J.V.; Beri, S.; et al. Mould insert fabrication of a single-mode fibre connector alignment structure optimized by justified partial metallization. J. Micromech. Microeng. 2015, 25, 035008. [Google Scholar] [CrossRef]
- Heckele, M.; Schomburg, W.K. Review on micro molding of thermoplastic polymers. J. Micromech. Microeng. 2003, 14, R1–R14. [Google Scholar] [CrossRef]
- Worgull, M. Hot Embossing: Theory and Technology of Microreplication (Micro and Nano Technologies); Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- MATLAB™. MATLAB™ Version 9.6 (R2019a); The MathWorks Inc.: Natick, MA, USA, 2019. [Google Scholar]
- MATLAB™. Image Processing Toolbox™ User’s Guide; The MathWorks Inc.: Natick, MA, USA, 2019; Volume R2019a. [Google Scholar]
- Andersen, N.K.; Gal, O.; Trujillo-Pino, A. Drop Shape Analysis. Fit Contact Angle by Double Ellipses or Polynomials; The MathWorks Inc.: Natick, MA, USA, 2016. [Google Scholar]
- Hunyadi, L. Fitting Quadratic Curves and Surfaces; The MathWorks Inc.: Natick, MA, USA, 2014. [Google Scholar]
- Hunyadi, L.; Vajk, I. Constrained quadratic errors-in-variables fitting. Vis. Comput. 2014, 30, 1347–1358. [Google Scholar] [CrossRef]
- Greiveldinger, M.; Shanahan, M.E. A Critique of the Mathematical Coherence of Acid/Base Interfacial Free Energy Theory. J. Colloid Interface Sci. 1999, 215, 170–178. [Google Scholar] [CrossRef]
- Owens, D.K.; Wendt, R.C. Estimation of the surface free energy of polymers. J. Appl. Polym. Sci. 1969, 13, 1741–1747. [Google Scholar] [CrossRef]
- Rabel, W. Einige Aspekte der Benetzungstheorie und ihre Anwendung auf die Untersuchung und Veränderung der Oberflächeneigenschaften von Polymeren. Farbe Lacke 1971, 77, 997–1005. [Google Scholar]
- Kaelble, D.H. Dispersion-Polar Surface Tension Properties of Organic Solids. J. Adhes. 1970, 2, 66–81. [Google Scholar] [CrossRef]
- Fowkes, F.M. Attractive Forces At Interfaces. Ind. Eng. Chem. 1964, 56, 40–52. [Google Scholar] [CrossRef]
- Ström, G.; Fredriksson, M.; Stenius, P. Contact angles, work of adhesion, and interfacial tensions at a dissolving Hydrocarbon surface. J. Colloid Interface Sci. 1987, 119, 352–361. [Google Scholar] [CrossRef]
- DataPhysics Instruments GmbH. Surface Tensions/Energies. 2018. Available online: https://www.dataphysics-instruments.com/Downloads/Surface-Tensions-Energies.pdf (accessed on 9 April 2019).
- Quéré, D. Non-sticking drops. Rep. Prog. Phys. 2005, 68, 2495–2532. [Google Scholar] [CrossRef]
- Courbin, L.; Denieul, E.; Dressaire, E.; Roper, M.; Ajdari, A.; Stone, H.A. Imbibition by polygonal spreading on microdecorated surfaces. Nat. Mater. 2007, 6, 661–664. [Google Scholar] [CrossRef] [PubMed]
- Ruzicka, M. On dimensionless numbers. Chem. Eng. Res. Des. 2008, 86, 835–868. [Google Scholar] [CrossRef]
- Gnielinski, V. G9 Fluid-Particle Heat Transfer in Flow Through Packed Beds of Solids. In VDI Heat Atlas; Springer: Berlin/Heidelberg, Germany, 2010; pp. 743–744. [Google Scholar] [CrossRef]
- Ruberto, S.; Reutzsch, J.; Roth, N.; Weigand, B. A systematic experimental study on the evaporation rate of supercooled water droplets at subzero temperatures and varying relative humidity. Exp. Fluids 2017, 58, 55. [Google Scholar] [CrossRef]
- Seck, A.; Geist, S.; Harbeck, J.; Weigand, B.; Joos, F. Evaporation Modeling of Water Droplets in a Transonic Compressor Cascade under Fogging Conditions. Int. J. Turbomach. Propuls. Power 2019, 5, 5. [Google Scholar] [CrossRef]
- Andersen, N.K.; Taboryski, R. Drop shape analysis for determination of dynamic contact angles by double sided elliptical fitting method. Meas. Sci. Technol. 2017, 28, 047003. [Google Scholar] [CrossRef]
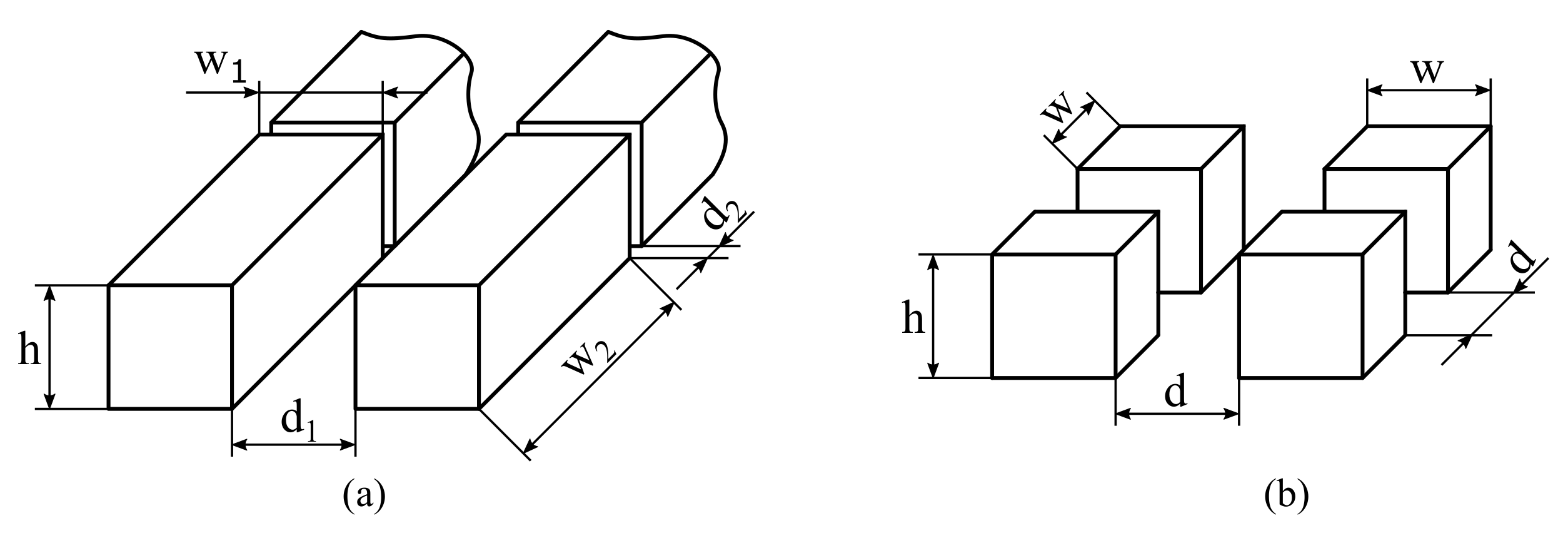





| No. | Edge Length | Distance | Height | |
|---|---|---|---|---|
| #1 | ||||
| #2 | ||||
| #3 | ||||
| #4 |
| Structure Contact | Angle | proj. Distance of Triple Points | Rel. Standard Deviation of |
|---|---|---|---|
| Grooves | |||
| (#1) | |||
| (#2) | |||
| (#3) | |||
| (#4) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foltyn, P.; Restle, F.; Wissmann, M.; Hengsbach, S.; Weigand, B. The Effect of Patterned Micro-Structure on the Apparent Contact Angle and Three-Dimensional Contact Line. Fluids 2021, 6, 92. https://doi.org/10.3390/fluids6020092
Foltyn P, Restle F, Wissmann M, Hengsbach S, Weigand B. The Effect of Patterned Micro-Structure on the Apparent Contact Angle and Three-Dimensional Contact Line. Fluids. 2021; 6(2):92. https://doi.org/10.3390/fluids6020092
Chicago/Turabian StyleFoltyn, Patrick, Ferdinand Restle, Markus Wissmann, Stefan Hengsbach, and Bernhard Weigand. 2021. "The Effect of Patterned Micro-Structure on the Apparent Contact Angle and Three-Dimensional Contact Line" Fluids 6, no. 2: 92. https://doi.org/10.3390/fluids6020092
APA StyleFoltyn, P., Restle, F., Wissmann, M., Hengsbach, S., & Weigand, B. (2021). The Effect of Patterned Micro-Structure on the Apparent Contact Angle and Three-Dimensional Contact Line. Fluids, 6(2), 92. https://doi.org/10.3390/fluids6020092







