Experimental Characterization of the Heat Transfer in Multi-Microchannel Heat Sinks for Two-Phase Cooling of Power Electronics
Abstract
1. Introduction
1.1. Synthesized Literature Review
1.2. Outline of the Study
2. Experimental Methods
2.1. The Flow Conditioning Loop
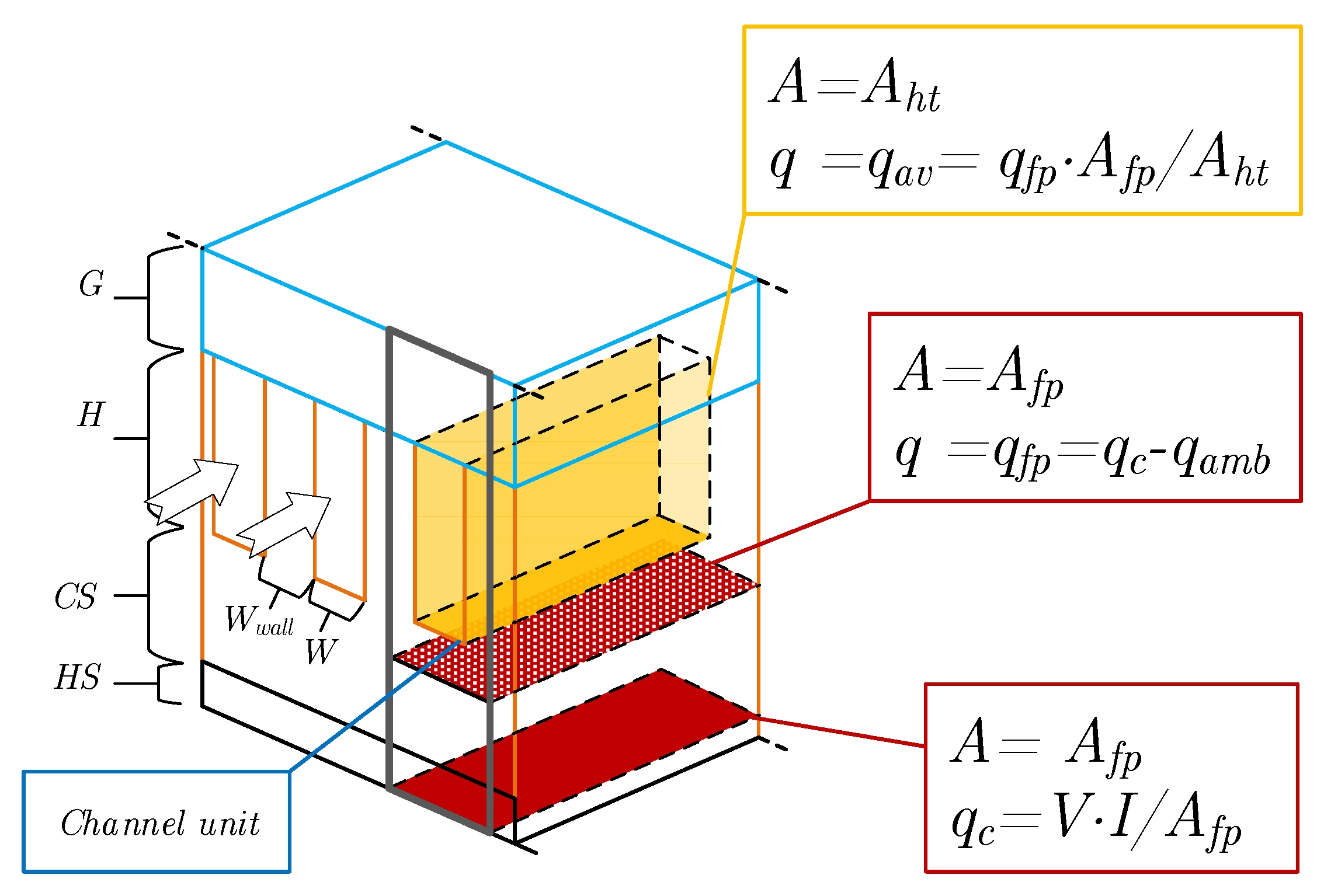
2.2. The Test Section
Channel Geometry
2.3. Experimental Procedure and Test Conditions
Heat Loss Characterization
2.4. Data Reduction
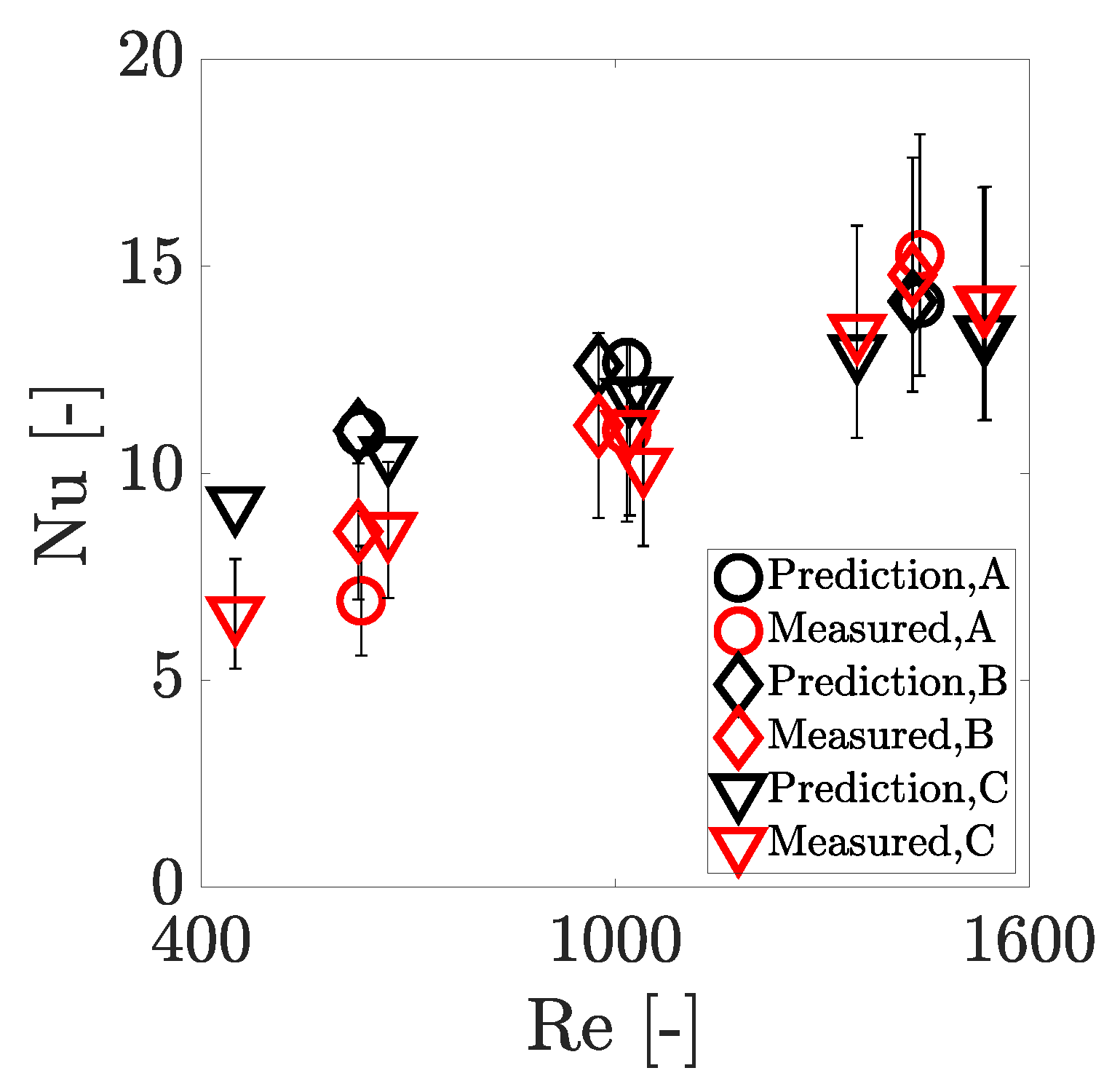
Methodology Validation
3. Results
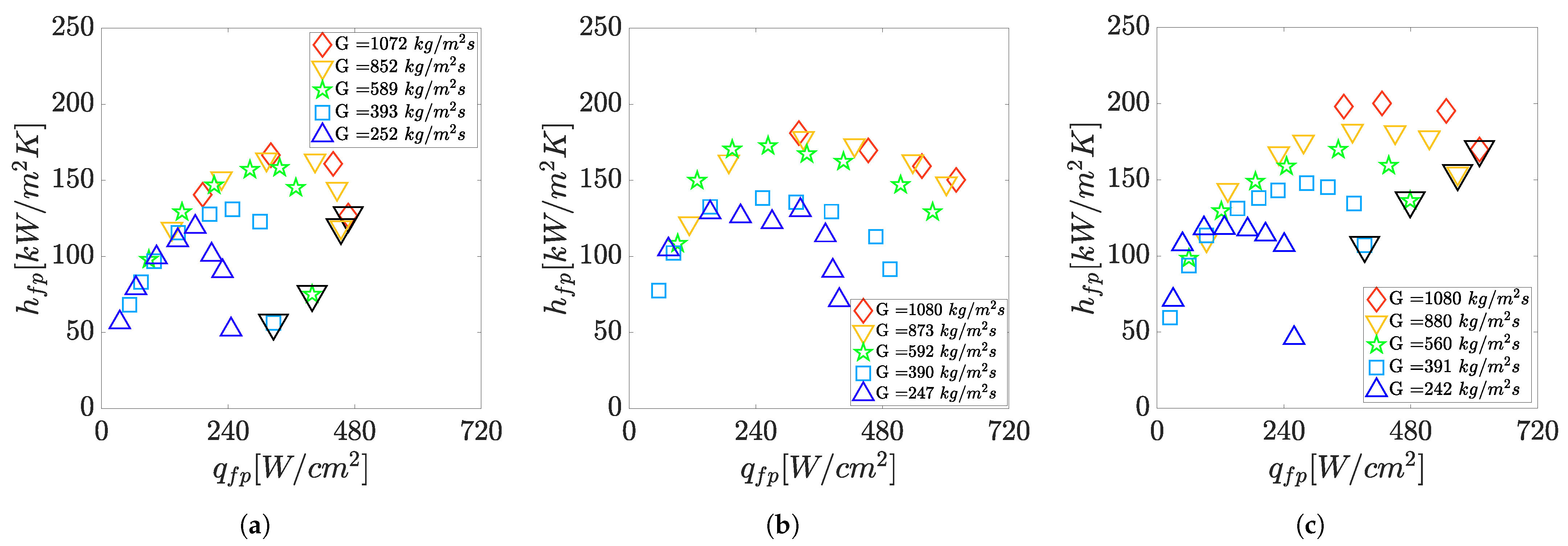
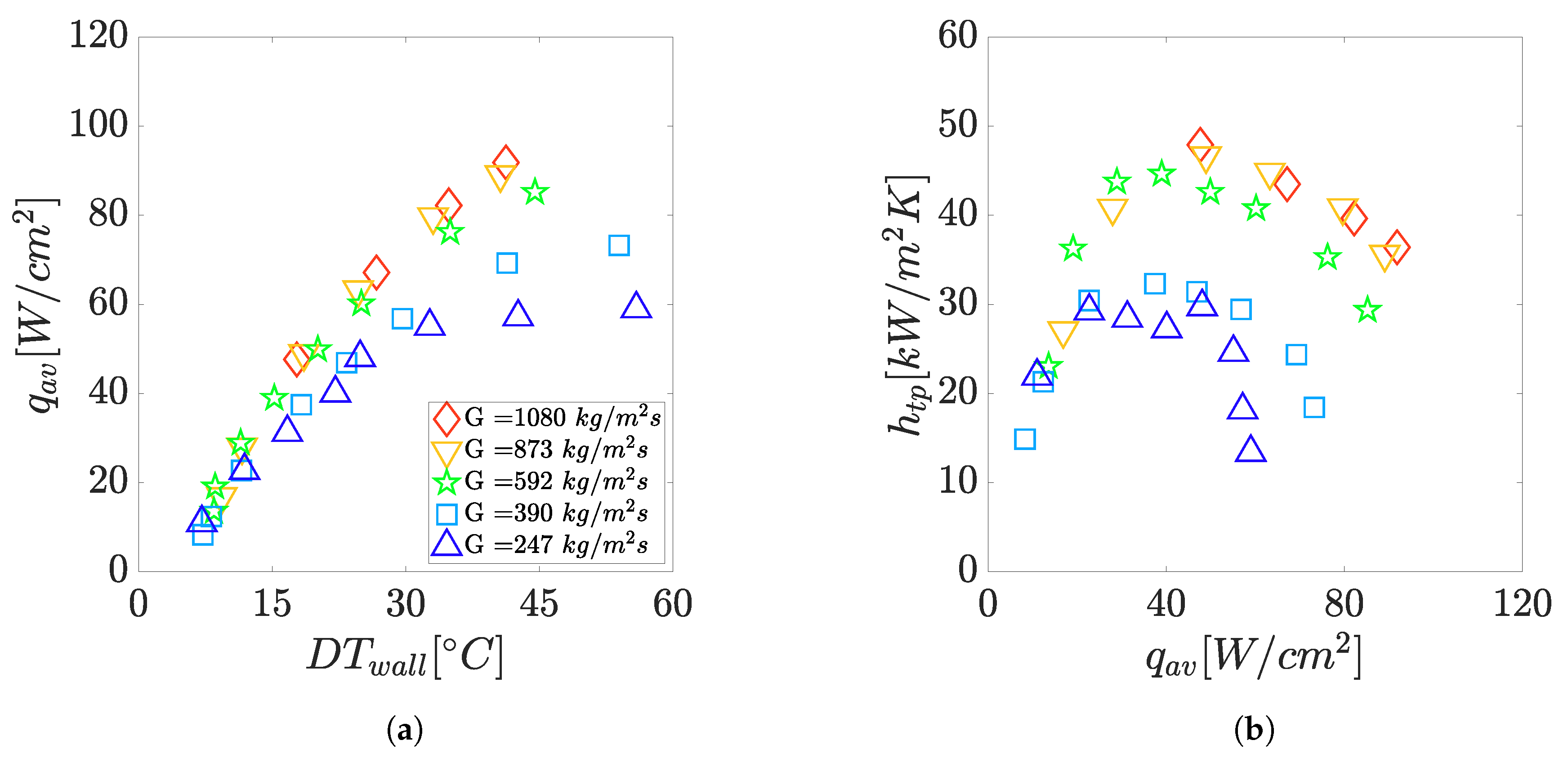
3.1. Footprint Heat Transfer Coefficients
3.2. Visualization and Flow Maps
- Bubbly flow: It mainly covered measurements in which isolated, coalescing bubbles or Taylor bubbles (at the bottom of the channels) with isolated or coalescing bubbles (at the top of the channels) appeared.
- Slug/churn flow: It covered tests in which vapor slugs intermittently appeared with a churn flow at the channel outlet. Bubble nucleation could be observed in the upper part of the channels and in the liquid film surrounding the vapor core during the slug flow.
- Semi-annular flow: It covered tests in which a wispy-annular flow intermittently appeared with a churn flow at the channel outlet. The liquid-vapor interface was irregular and continuously disturbed by bubble nucleation.
- Annular flow with incomplete wetting: It covered tests in which a stable wispy-annular flow was present and incomplete wetting intermittently appeared. Boiling activities could be observed in the liquid.
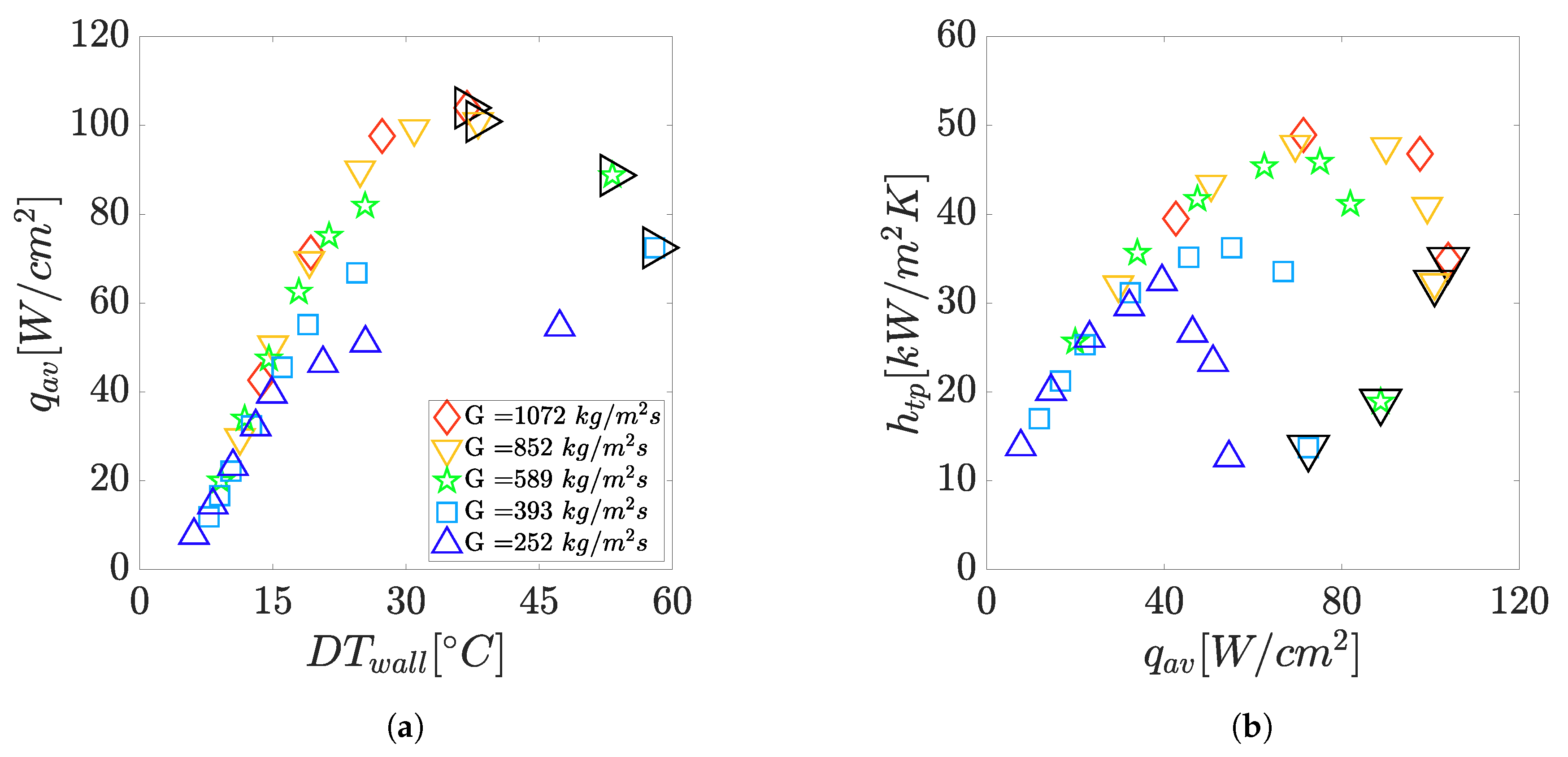
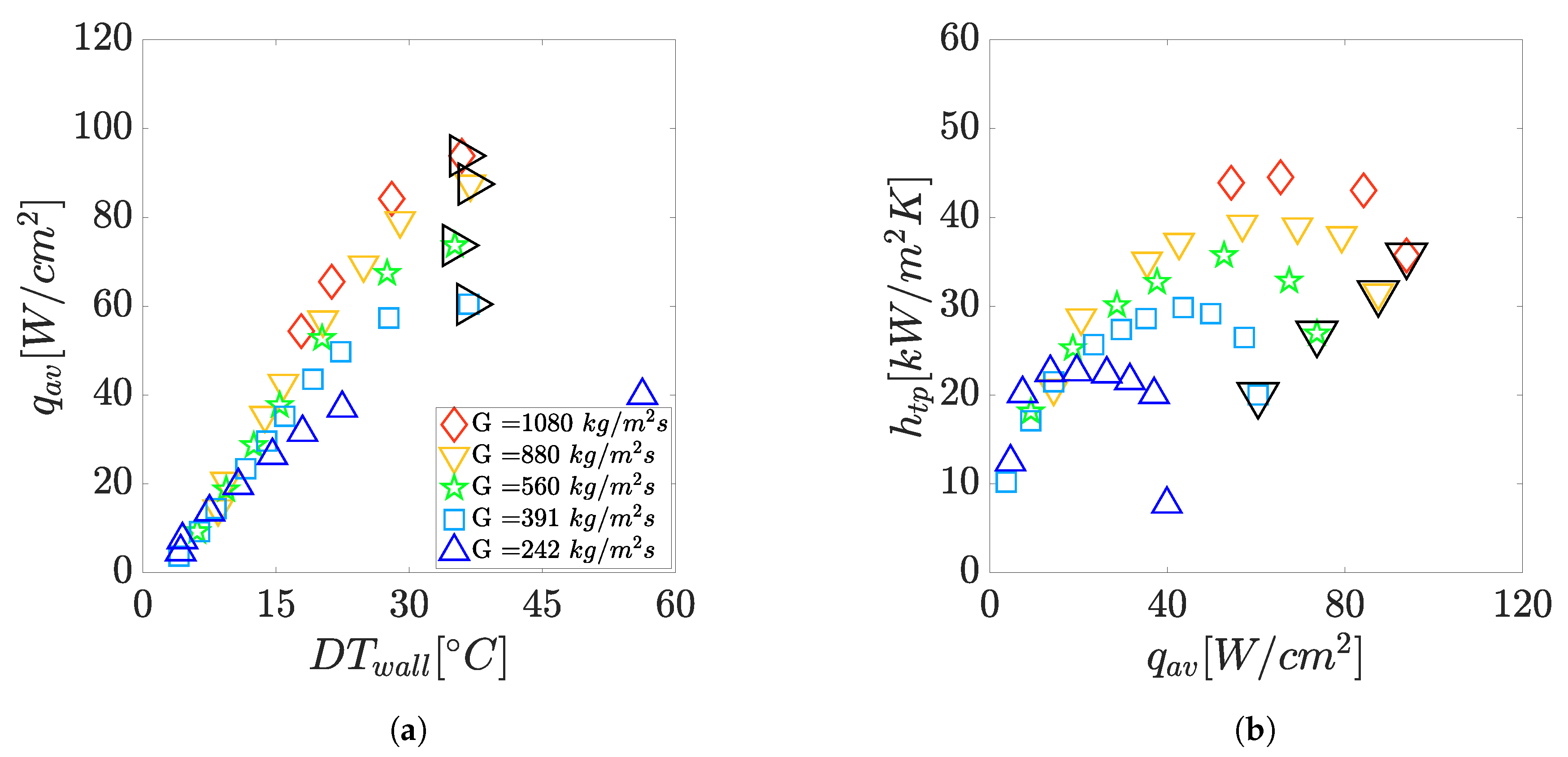
3.3. Flow Boiling Characteristics in the Channels
3.4. Comparison of the Geometries
3.4.1. Effect of the Wall Thickness
3.4.2. Effect of the Channel Hydraulic Diameter
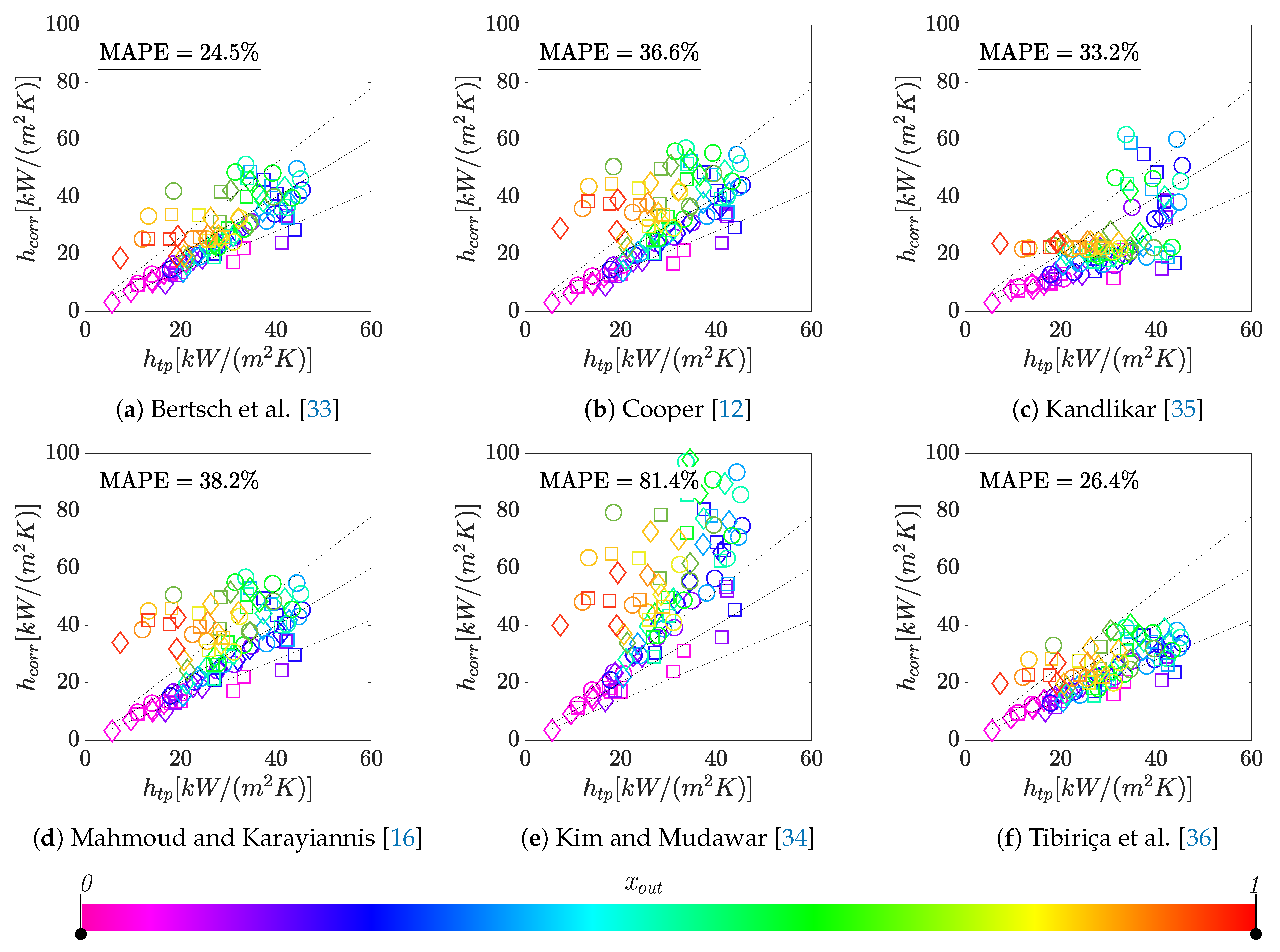
3.5. Comparison with Correlations
4. Discussion
4.1. Comparison of the Heat Sinks at Footprint Level
4.2. Flow Maps
4.3. Flow Boiling Characteristics in the Channels
4.3.1. Effect of Wall Thickness
4.3.2. Effect of the Hydraulic Diameter
4.4. Comparison with Correlations
5. Conclusions
- The flow boiling heat transfer in the multi-microchannels showed a dependence on the channel heat and mass flux. A firstly increasing and then decreasing trend with respect to the channel heat flux was observed for all the multi-microchannels geometries. The mass flux influenced mainly the decreasing regions, where incomplete wetting or boiling suppression could occur. The visualization suggested that incomplete channel wetting could take place during a wispy-annular flow regime. Boiling was found to be continuously present in the microchannels for almost all the conditions investigated.
- The flow patterns observed at the end of the channels were bubbly flow, intermittent slug/churn flow, semi-annular flow, and wispy-annular flow with incomplete wetting. A comparison at the same outlet vapor quality showed that a dominance of the intermittent slug/churn flow was present for the multi-microchannels with the thinnest walls, while thicker walls seemed to facilitate the establishment of semi-annular flow. The wall thickness, and thus the heat flux distribution in the walls, could influence the transition boundaries from one regime to another for multi-microchannels which are asymmetrically heated. Further investigation is suggested to asses the effect of wall thickness on the flow patterns in a microchannel heat sink.
- The channel average heat transfer coefficient was influenced by the wall thickness at a fixed channel dimension. Thin walls in very short channels may be beneficial for area enhancement but may alter the uniformity of the heat flux distribution in the channel walls, thus complicating the exact control over the experimental conditions and affecting the average heat transfer performance. Further investigation is needed to enlighten more a potential effect of the wall thickness in microchannel heat sinks.
- The decrease of the hydraulic diameter at a fixed channel-width/wall-thickness ratio had a negative influence on the channel-level heat transfer coefficient for medium-to-high average channel heat flux. For the conditions tested, the improved heat transfer by increased area enhancement obtained with a reduced channel hydraulic diameter was found to be compromised by lower critical heat fluxes at the channels.
- For the same footprint area, the heat sink B and C, which featured higher area enhancements, showed a better heat dissipation during the flow boiling of R-134a. Up to 620 could be dissipated, keeping the heater temperature below 150 . For the conditions tested, the study suggests that enhancing the area by a reduction in the wall thickness could provide better performances than a reduction in the hydraulic diameter, when high-aspect ratio channels are employed to dissipate footprint heat fluxes in hundreds of .
- Footprint heat transfer coefficients were influenced by the footprint heat flux and channel average mass flux. Depending on the operating mass and heat flux, a footprint heat transfer coefficient in the range of 100 to 200 could be achieved over a footprint area of 1 with a maximum operational temperature of the heat sink of 150 . The order of magnitude of the heat transfer coefficients for the investigated solutions agree with the high heat transfer coefficient obtained in other studies with copper microchannels and high aspect ratio [13,14], as well as represents a novel cooling method for power electronics with the possibility to dissipate several hundreds of . A comprehensive assessment of the performances, however, would request to consider also the influence of the operating constraints specific to the applications, such as maximum pressure drop and environment conditions.
- The average channel heat transfer coefficients were best predicted by the Bertsch et al. correlation [33], with a mean absolute percent error of 24.5% over the experimental data obtained in this study. The correlation was thus satisfactory in predicting the average heat transfer coefficients in the high aspect ratio channels used for the presented investigation. Notably, among all the three geometries, the heat sink with the thinnest walls was the one predicted with the lowest accuracy for most of the correlations investigated.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- EPE European Power Electronics and Drives Association. Position Paper on Energy Efficiency—The Role of Power Electronics; EPE European Power Electronics and Drives Association: Brussels, Belgium, 2007; pp. 1–18. [Google Scholar]
- Tuckerman, D.B.; Pease, R.F.W. High-performance heat sinking for VLSI. IEEE Electron Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Palm, B. Heat transfer in microchannels. Microscale Thermophys. Eng. 2001, 5, 155–175. [Google Scholar] [CrossRef]
- Lazarek, G.M.; Black, S.H. Evaporative heat transfer, pressure drop and critical heat flux in a small vertical tube with R-113. Int. J. Heat Mass Transf. 1982, 25, 945–960. [Google Scholar] [CrossRef]
- Moriyama, K. The thermohydraulic characteristics of two-phase flow in extremely narrow channels (the frictional pressure drop and heat transfer of boiling two-phase flow, analytical model). Heat Transf. Jpn. Res. 1992, 21, 838–856. [Google Scholar]
- Agostini, B.; Fabbri, M.; Park, J.E.; Wojtan, L.; Thome, J.R.; Michel, B. State of the art of high heat flux cooling technologies. Heat Transf. Eng. 2007, 28, 258–281. [Google Scholar] [CrossRef]
- Kheirabadi, A.C.; Groulx, D. Cooling of server electronics: A design review of existing technology. Appl. Therm. Eng. 2016, 105, 622–638. [Google Scholar] [CrossRef]
- Karayiannis, T.G.; Mahmoud, M.M. Flow boiling in microchannels: Fundamentals and applications. Appl. Therm. Eng. 2017, 115, 1372–1397. [Google Scholar] [CrossRef]
- Karayiannis, T.G.; Mahmoud, M.M.; Kenning, D.B. A study of discrepancies in flow boiling results in small to microdiameter metallic tubes. Exp. Therm. Fluid Sci. 2012, 36, 126–142. [Google Scholar] [CrossRef]
- Bertsch, S.S.; Groll, E.A.; Garimella, S.V. Refrigerant flow boiling heat transfer in parallel microchannels as a function of local vapor quality. Int. J. Heat Mass Transf. 2008, 51, 4775–4787. [Google Scholar] [CrossRef]
- Bertsch, S.S.; Groll, E.A.; Garimella, S.V. Effects of heat flux, mass flux, vapor quality, and saturation temperature on flow boiling heat transfer in microchannels. Int. J. Multiph. Flow 2009, 35, 142–154. [Google Scholar] [CrossRef]
- Cooper, M.G. Heat Flow Rates in Saturated Nucleate Pool Boiling-A Wide-Ranging Examination Using Reduced Properties. Adv. Heat Transf. 1984, 16, 157–239. [Google Scholar] [CrossRef]
- Madhour, Y.; Olivier, J.; Costa-Patry, E.; Paredes, S.; Michel, B.; Thome, J.R. Flow boiling of R134a in a multi-microchannel heat sink with hotspot heaters for energy-efficient microelectronic CPU cooling applications. IEEE Trans. Compon. Packag. Manuf. Technol. 2011, 1, 873–883. [Google Scholar] [CrossRef]
- do Nascimento, F.J.; Leão, H.L.S.L.; Ribatski, G. An experimental study on flow boiling heat transfer of R134a in a microchannel-based heat sink. Exp. Therm. Fluid Sci. 2013, 45, 117–127. [Google Scholar] [CrossRef]
- Fayyadh, E.M.; Mahmoud, M.M.; Sefiane, K.; Karayiannis, T.G. Flow boiling heat transfer of R134a in multi microchannels. Int. J. Heat Mass Transf. 2017, 110, 422–436. [Google Scholar] [CrossRef]
- Mahmoud, M.M.; Karayiannis, T.G. Heat transfer correlation for flow boiling in small to micro tubes. Int. J. Heat Mass Transf. 2013, 66, 553–574. [Google Scholar] [CrossRef]
- Lee, J.; Mudawar, I. Two-phase flow in high-heat-flux micro-channel heat sink for refrigeration cooling applications: Part II—Heat transfer characteristics. Int. J. Heat Mass Transf. 2005, 48, 941–955. [Google Scholar] [CrossRef]
- Thiangtham, P.; Keepaiboon, C.; Kiatpachai, P.; Asirvatham, L.G.; Mahian, O.; Dalkilic, A.S.; Wongwises, S. An experimental study on two-phase flow patterns and heat transfer characteristics during boiling of R134a flowing through a multi-microchannel heat sink. Int. J. Heat Mass Transf. 2016, 98, 390–400. [Google Scholar] [CrossRef]
- Dalkılıç, A.S.; Özman, C.; Sakamatapan, K.; Wongwises, S. Experimental investigation on the flow boiling of R134a in a multi-microchannel heat sink. Int. Commun. Heat Mass Transf. 2018, 91, 125–137. [Google Scholar] [CrossRef]
- Joint Comitee for Guides in Metrology. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; Technical Report. Clin. Chem. 2008, 50, 977–978. [Google Scholar] [CrossRef]
- Young, P.L.; Brackbill, T.P.; Kandlikar, S.G. Estimating roughness parameters resulting from various machining techniques for fluid flow applications. In Proceedings of the 5th International Conference on Nanochannels, Microchannels and Minichannels, Puebla, Mexico, 18–20 June 2007; pp. 827–836. [Google Scholar] [CrossRef]
- Jones, B.J.; McHale, J.P.; Garimella, S.V. The Influence of Surface Roughness on Nucleate Pool Boiling Heat Transfer. J. Heat Transf. 2009, 131, 121009. [Google Scholar] [CrossRef]
- Jafari, R.; Okutucu-Özyurt, T.; Ünver, H.Ö.; Bayer, Ö. Experimental investigation of surface roughness effects on the flow boiling of R134a in microchannels. Exp. Therm. Fluid Sci. 2016, 79, 222–230. [Google Scholar] [CrossRef]
- Incropera, F.P. Fundamentals of Heat and Mass Transfer; John Wiley: New York, NY, USA, 2007; p. 997. [Google Scholar]
- Shanks, H.R.; Maycock, P.D.; Sidles, P.H.; Danielson, G.C. Thermal conductivity of silicon from 300 to 1400°K. Phys. Rev. 1963, 130, 1743–1748. [Google Scholar] [CrossRef]
- Idelchik, I.E. Handbook of Hydraulic Resistance, 2nd Edition. J. Press. Vessel. Technol. 1987, 109, 260–261. [Google Scholar] [CrossRef]
- Chalfi, T.Y.; Ghiaasiaan, S.M. Pressure drop caused by flow area changes in capillaries under low flow conditions. Int. J. Multiph. Flow 2008, 34, 2–12. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]
- Shah, R.; London, A. Rectangular Ducts. Laminar Flow Forced Convect. Ducts 1978, 196–222. [Google Scholar] [CrossRef]
- Montgomery, S.R.; Wibulswas, P. Laminar flow heat transfer for simultaneously developing velocity and temperature profiles in ducts of rectangular cross section. Appl. Sci. Res. 1968, 18, 247–259. [Google Scholar] [CrossRef]
- Huo, X.; Chen, L.; Tian, Y.S.; Karayiannis, T.G. Flow boiling and flow regimes in small diameter tubes. Appl. Therm. Eng. 2004, 24, 1225–1239. [Google Scholar] [CrossRef]
- Revellin, R.; Thome, J.R. A new type of diabatic flow pattern map for boiling heat transfer in microchannels. J. Micromech. Microeng. 2007, 17, 788–796. [Google Scholar] [CrossRef]
- Bertsch, S.S.; Groll, E.A.; Garimella, S.V. A composite heat transfer correlation for saturated flow boiling in small channels. Int. J. Heat Mass Transf. 2009, 52, 2110–2118. [Google Scholar] [CrossRef]
- Kim, S.M.; Mudawar, I. Universal approach to predicting saturated flow boiling heat transfer in mini/micro-channels—Part II. Two-phase heat transfer coefficient. Int. J. Heat Mass Transf. 2013, 64, 1239–1256. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Balasubramanian, P. An Extension of the Flow Boiling Correlation to Transition, Laminar, and Deep Laminar Flows and Microchannels. Heat Transf. Eng. 2004, 25, 86–93. [Google Scholar] [CrossRef]
- Tibiriçá, C.B.; Rocha, D.M.; Sueth, I.L.S., Jr.; Bochio, G.; Shimizu, G.K.K.; Barbosa, M.C.; dos Santos Ferreira, S. A complete set of simple and optimized correlations for microchannel flow boiling and two-phase flow applications. Appl. Therm. Eng. 2017, 126, 774–795. [Google Scholar] [CrossRef]




 B = Bubbly flow,
B = Bubbly flow,  S/C = slug/churn flow (intermittent),
S/C = slug/churn flow (intermittent),  SA = Semi-annular flow,
SA = Semi-annular flow,  A + D = Annular flow with incomplete wetting.
A + D = Annular flow with incomplete wetting.
 B = Bubbly flow,
B = Bubbly flow,  S/C = slug/churn flow (intermittent),
S/C = slug/churn flow (intermittent),  SA = Semi-annular flow,
SA = Semi-annular flow,  A + D = Annular flow with incomplete wetting.
A + D = Annular flow with incomplete wetting.
 ), Geometry B (
), Geometry B ( ), and Geometry C (
), and Geometry C ( ) at a nominal saturation temperature of 30 °C at the outlet of the channels and different mass fluxes G: (a) G = 400 kg/m2s, (b) G = 580 kg/m2s, (c) G = 870 kg/m2s.
) at a nominal saturation temperature of 30 °C at the outlet of the channels and different mass fluxes G: (a) G = 400 kg/m2s, (b) G = 580 kg/m2s, (c) G = 870 kg/m2s.
 ), Geometry B (
), Geometry B ( ), and Geometry C (
), and Geometry C ( ) at a nominal saturation temperature of 30 °C at the outlet of the channels and different mass fluxes G: (a) G = 400 kg/m2s, (b) G = 580 kg/m2s, (c) G = 870 kg/m2s.
) at a nominal saturation temperature of 30 °C at the outlet of the channels and different mass fluxes G: (a) G = 400 kg/m2s, (b) G = 580 kg/m2s, (c) G = 870 kg/m2s.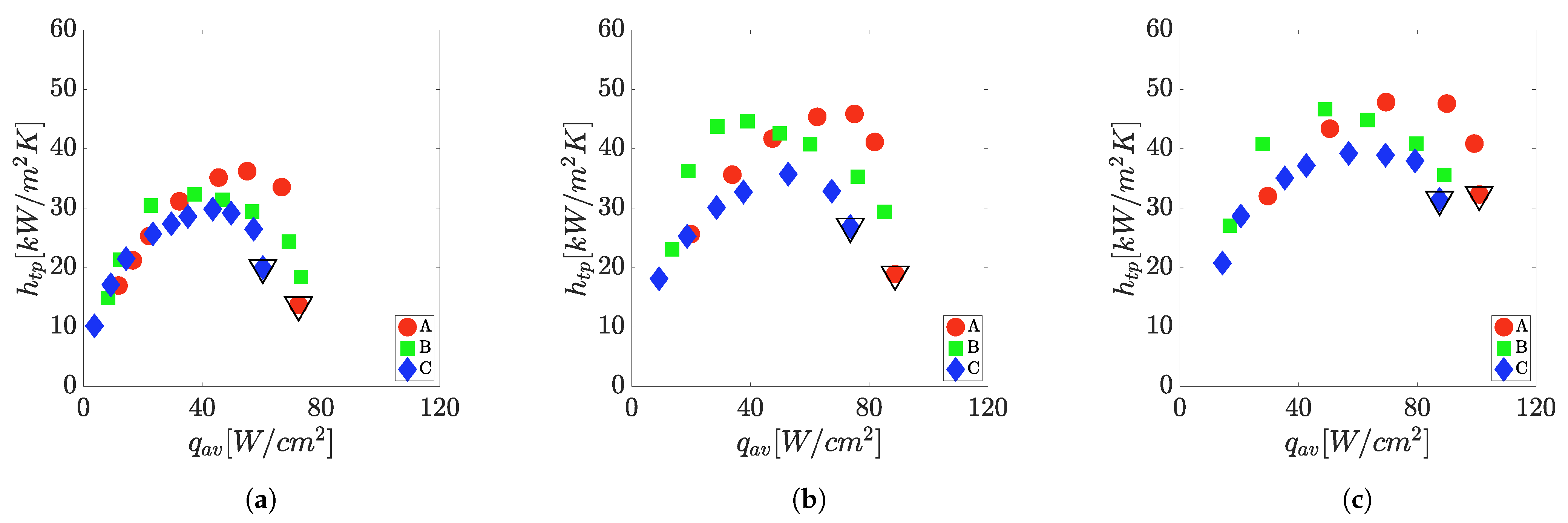
| Author | N | H | W | L | G | Co | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| [-] | [µm] | [µm] | [µm] | [mm] | [µm] | [] | [-] | [-] | [-] | [-] | |
| Lee and Mudawar [17] | 53 | 713 | 231 | 349 | 25.3 | 231 | 127–654 | 0.10 | 2.61 | 8.22 | 187.7 |
| Bertsch et al. [10] | 17 | 1905 | 762 | 1089 | 9.5 | 762 | 20–80 | 0.14 | 0.79 | 8.24 | 106–423 |
| Bertsch et al. [11] | 33 | 953 | 381 | 544 | 9.5 | 381 | 42–334 | 0.14 | 1.60 | 3.90 | 108–643 |
| 17 | 1905 | 762 | 1089 | 9.5 | 762 | 334 | 0.14 | 0.79 | 3.20 | 1766 | |
| Madhour et al. [13] | 100 | 680 | 100 | 174 | 15.0 | 72 | 205–1000 | 0.44 | 3.57 | 6.30 | 294–1433 |
| DoNascimento et al. [14] | 50 | 500 | 100 | 166 | 15 | 200 | 400–1500 | 0.14 | 5.06 | 1.10 | 331–1240 |
| Thiangtham et al. [18] | 27 | 470 | 382 | 421 | 40.0 | 416 | 150–600 | 0.12 | 2.10 | 1.51 | 289–1156 |
| Fayydah et al. [15] | 25 | 700 | 300 | 420 | 20.0 | 200 | 50–300 | 0.16 | 2.00 | 5.93 | 107–642 |
| Dalkiliç et al. [19] | 27 | 470 | 382 | 421 | 40.0 | 416 | 800–1200 | 0.11–0.15 | 2.0–2.2 | 3.48 | 1463–2528 |
| Present study | 17 | 1200 | 300 | 480 | 10.0 | 300 | 250–1100 | 0.16 | 1.66 | 12.16 | 619–2724 |
| 25 | 1200 | 300 | 480 | 10.0 | 100 | 250–1100 | 0.16 | 1.66 | 12.61 | 619–2724 | |
| 25 | 1200 | 200 | 343 | 10.0 | 200 | 250–1100 | 0.16 | 2.32 | 8.79 | 442–1945 |
| Instrument | u | Units | Range |
|---|---|---|---|
| Thermocouples, T-type | C | 18–50 | |
| Thermocouples, K-type | C | 18–50 | |
| RTDs | C | 25–160 | |
| Pressure sensor, low range | bar | 0–10 | |
| Pressure sensor, high range | bar | 0–21 | |
| Mass flow meter | kg/h | 5–55 | |
| Power supply | W | 0–1500 |
| Label | H | W | ||||
|---|---|---|---|---|---|---|
| (µm) | (µm) | (µm) | (µm) | (µm) | ||
| Geometry A | 1176 | 293 | 306 | 470 | 21 | 17 |
| Geometry B | 1193 | 283 | 115 | 457 | 7 | 25 |
| Geometry C | 1167 | 198 | 200 | 338 | 25 | 25 |
| Geometry A | Geometry B | Geometry C | Overall | ||
|---|---|---|---|---|---|
| MAPE | MAPE | MAPE | MAPE | ||
| Bertsch et al. [33] | 25% | 28% | 21% | 25% | 76% |
| Cooper [12] | 36% | 41% | 34% | 37% | 63% |
| Kandlikar [35] | 33% | 37% | 31% | 33% | 47% |
| Karayiannis and Mahmoud [8] | 36% | 42% | 38% | 38% | 63% |
| Kim and Mudawar [34] | 84% | 71% | 83% | 81% | 31% |
| Tibiriça et al. [36] | 29% | 29% | 23% | 26% | 70% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Criscuolo, G.; Brix Markussen, W.; Meyer, K.E.; Palm, B.; Ryhl Kærn, M. Experimental Characterization of the Heat Transfer in Multi-Microchannel Heat Sinks for Two-Phase Cooling of Power Electronics. Fluids 2021, 6, 55. https://doi.org/10.3390/fluids6020055
Criscuolo G, Brix Markussen W, Meyer KE, Palm B, Ryhl Kærn M. Experimental Characterization of the Heat Transfer in Multi-Microchannel Heat Sinks for Two-Phase Cooling of Power Electronics. Fluids. 2021; 6(2):55. https://doi.org/10.3390/fluids6020055
Chicago/Turabian StyleCriscuolo, Gennaro, Wiebke Brix Markussen, Knud Erik Meyer, Björn Palm, and Martin Ryhl Kærn. 2021. "Experimental Characterization of the Heat Transfer in Multi-Microchannel Heat Sinks for Two-Phase Cooling of Power Electronics" Fluids 6, no. 2: 55. https://doi.org/10.3390/fluids6020055
APA StyleCriscuolo, G., Brix Markussen, W., Meyer, K. E., Palm, B., & Ryhl Kærn, M. (2021). Experimental Characterization of the Heat Transfer in Multi-Microchannel Heat Sinks for Two-Phase Cooling of Power Electronics. Fluids, 6(2), 55. https://doi.org/10.3390/fluids6020055






