Mantle Electrical Conductivity and the Magnetic Field at the Core–Mantle Boundary
Abstract
1. Introduction
2. Mathematical Model
2.1. Mantle Conductivity
2.2. Exterior Geomagnetic Field
2.3. Intermediate Magnetic Field
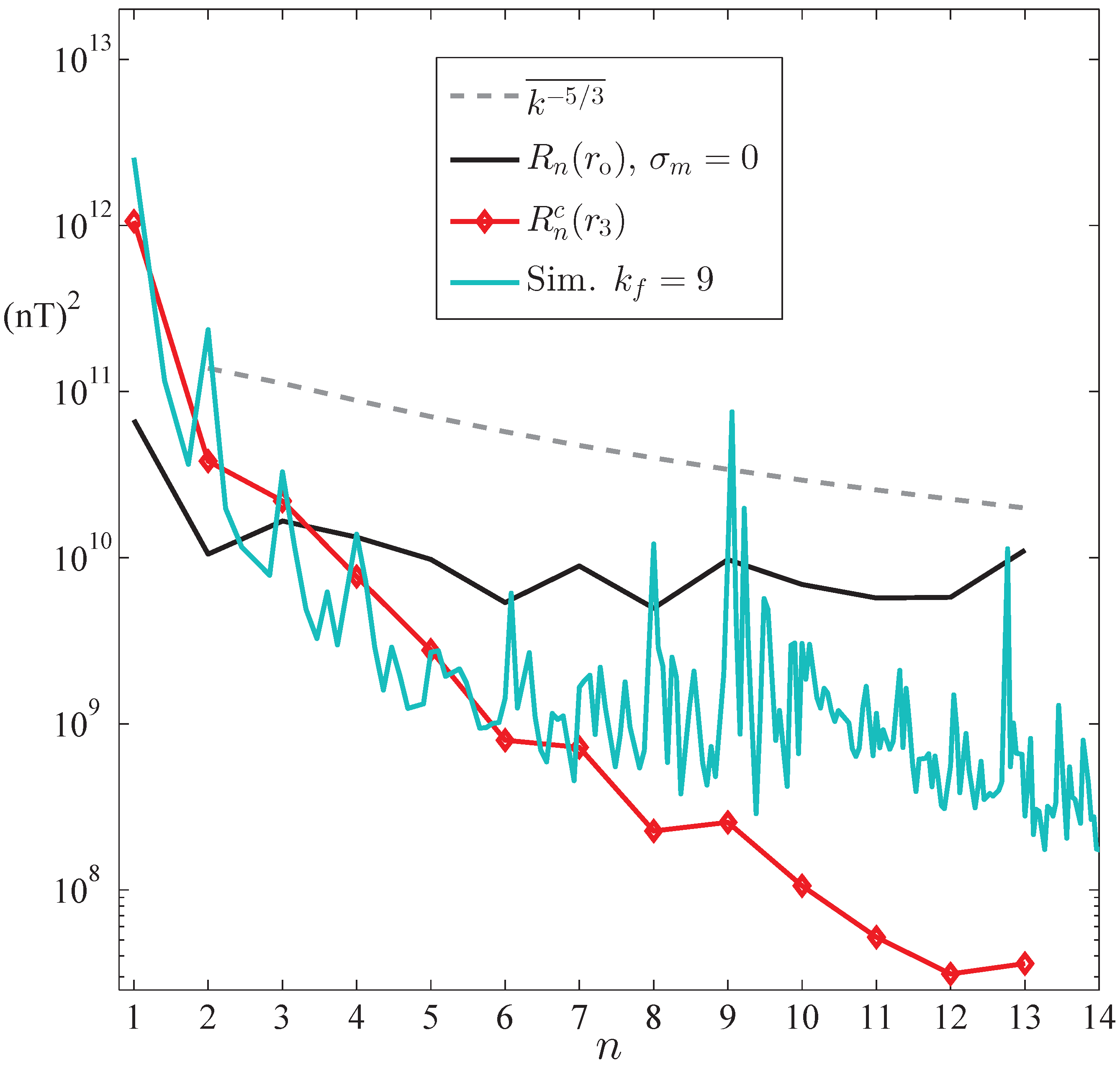
2.4. Power Spectrum of the Geomagnetic Field
2.5. Heat Produced by the Surface Current at
3. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Civet, F.; Thébault, E.; Verhoeven, O.; Langlais, B.; Saturnino, D. Electrical conductivity of the Earth’s mantle from the first Swarm magnetic field measurements. Geophys. Res. Lett. 2015, 42, 3338–3346. [Google Scholar] [CrossRef]
- Grayver, A.V.; Munch, F.D.; Kuvshinov, A.V.; Khan, A.; Sabaka, T.J.; Tøffner-Clausen, L. Joint inversion of satellite-detected tidal and magnetospheric signals constrains electrical conductivity and water content of the upper mantle and transition zone. Geophys. Res. Lett. 2017, 44, 6074–6081. [Google Scholar] [CrossRef]
- Velímský, J.; Knopp, O. Lateral variations of electrical conductivity in the lower mantle constrained by Swarm and CryoSat?2 missions. Earth Planets Space 2021, 73, 4. [Google Scholar] [CrossRef]
- Kuvshinov, A.; Semenov, A. Global 3-D imaging of mantle electrical conductivity based on inversion of observatory C–responses–I. An approach and its verification. Geophys. J. Int. 2012, 189, 1335–1352. [Google Scholar] [CrossRef]
- Thébault, E.; Finlay, C.C.; Beggan, C.D.; Alken, P.; Aubert, J.; Barrois, O.M.; Bertr, F.; Bondar, T.; Boness, A.; Brocco, L.; et al. International Geomagnetic Reference Field: The 13th generation. Earth Planets Space 2021, 73, 49. [Google Scholar] [CrossRef]
- Roberts, P.H.; Glatzmaier, G.A. A test of the frozen-flux approximation using a new geodynamo model. Phil. Trans. R. Soc. Lond. A 2000, 358, 1109–1121. [Google Scholar] [CrossRef]
- Dahlburg, R.B.; Picone, J.M.; Karpen, J.T. Compressible Dynamic Alignment. In Solar System Plasma Physics; Waite, J.H., Jr., Burch, J.L., Moore, R.L., Eds.; Amer. Geophys. Union: Washington, DC, USA, 1989; Volume 54, pp. 95–98. [Google Scholar]
- Mason, J.; Cattaneo, F.; Boldyrev, S. Dynamic Alignment in Driven Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 2006, 97, 255002. [Google Scholar] [CrossRef] [PubMed]
- Boldyrev, S. Spectrum of Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 2006, 96, 115002. [Google Scholar] [CrossRef] [PubMed]
- Telloni, D.; Perri, S.; Carbone, V.; Bruno, R. Selective Decay and Dynamic Alignment in the MHD Turbulence: The Role of the Rugged Invariants. AIP Conf. Proc. 2016, 1720, 040015. [Google Scholar]
- Chandrasekhar, S.; Kendall, C.P. On Force–Free Magnetic Fields. Astrophys. J. 1957, 12, 457–460. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Woltjer, L. On Force—Free Magnetic fields. Proc. Nat. Acad. Sci. USA 1958, 44, 285–289. [Google Scholar] [CrossRef]
- Taylor, J.B. Relaxation of toroidal plasma and generation of reverse magnetic fields. Phys. Rev. Lett. 1974, 33, 1139–1141. [Google Scholar] [CrossRef]
- Kageyama, A.; Tetsuya, S. Computer simulation of a magnetohydrodynamic dynamo. II. Phys. Plasmas 1995, 2, 1421–1431. [Google Scholar] [CrossRef]
- Huguet, L.; Amit, H. Magnetic energy transfer at the top of the Earth’s core. Geophys. J. Int. 2012, 190, 856–870. [Google Scholar] [CrossRef]
- Lowes, F. Spatial power spectrum of the main geomagnetic field. Geophys. J. R. Astr. Soc. 1974, 36, 717–730. [Google Scholar] [CrossRef]
- Frick, P.G.; Reshetnyak, M.Y.; Sokoloff, D.D. Cascade Models of Turbulence for the Earth’s Liquid Core. Doklady Earth Sci. 2002, 387, 988–991. [Google Scholar]
- Ballani, L.; Greiner–Mai, H.; Stromeyer, D. Determining the magnetic field in the core–mantle boundary zone by non–harmonic downward continuation. Geophys. J. Int. 2002, 149, 374–389. [Google Scholar] [CrossRef]
- Glatzmaier, G.A.; Roberts, P.H. A three-dimensional self-consistent computer simulation of a geomagnetic field reversal. Nature 1995, 377, 203–209. [Google Scholar] [CrossRef]
- Glatzmaier, G.A.; Roberts, P.H. A three-dimensional convective dynamo solution with rotating and finitely conducting inner core and mantle. Phys. Earth Planet. Int. 1995, 91, 63–75. [Google Scholar] [CrossRef]
- Yoshino, T.; Kamada, S.; Zhao, C.; Ohtani, E.; Hirao, N. Electrical conductivity model of Al-bearing bridgmanite with implications for the electrical structure of the Earth’s lower mantle. Earth Planet. Sci. Lett. 2016, 434, 208–219. [Google Scholar] [CrossRef]
- Bhattacharyya, A. Secular variation of the poloidal magnetic field at the core–mantle boundary. Geophys. J. Int. 1998, 132, 181–190. [Google Scholar] [CrossRef][Green Version]
- Winch, D.E.; Ivers, D.J.; Turner, J.P.R.; Stening, R.J. Geomagnetism and Schmidt quasi-normalization. Geophys. J. Int. 2005, 160, 487–504. [Google Scholar] [CrossRef]
- Shebalin, J.V. Broken ergodicity, magnetic helicity, and the MHD dynamo. Geophys. Astrophys. Fluid Dyn. 2013, 107, 353–375. [Google Scholar] [CrossRef]
- Langle, R.A.; Estes, R.H. A Geomagnetic Field Spectrum. Geophys. Res. Lett. 1982, 9, 250–253. [Google Scholar] [CrossRef]
- Shebalin, J.V. Magnetohydrodynamic turbulence and the geodynamo. Phys. Earth Planet. Inter. 2018, 285, 59–75. [Google Scholar] [CrossRef]
- Shebalin, J.V. Magnetic Helicity and the Geodynamo. Fluids 2021, 6, 99. [Google Scholar] [CrossRef]
- Nimmo, F. Energetics of the Core. In Treatise on Geophysics 8: Core Dynamics; Olson, P., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 31–65. [Google Scholar]

| Case, | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| (S/m) | 4 | 40 | 200 | ||
| (kS) | 7.56 | 29.5 | 94.7 | 341 | 2414 |
| (km) | 4425 | 4091 | 3925 | 3815 | 3721 |
| (mT) | 0.424 | 0.717 | 1.03 | 1.41 | 2.01 |
| (GW) | 53.4 | 33.7 | 20.1 | 9.93 | 2.72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shebalin, J.V. Mantle Electrical Conductivity and the Magnetic Field at the Core–Mantle Boundary. Fluids 2021, 6, 403. https://doi.org/10.3390/fluids6110403
Shebalin JV. Mantle Electrical Conductivity and the Magnetic Field at the Core–Mantle Boundary. Fluids. 2021; 6(11):403. https://doi.org/10.3390/fluids6110403
Chicago/Turabian StyleShebalin, John V. 2021. "Mantle Electrical Conductivity and the Magnetic Field at the Core–Mantle Boundary" Fluids 6, no. 11: 403. https://doi.org/10.3390/fluids6110403
APA StyleShebalin, J. V. (2021). Mantle Electrical Conductivity and the Magnetic Field at the Core–Mantle Boundary. Fluids, 6(11), 403. https://doi.org/10.3390/fluids6110403






