Interaction Features of Internal Wave Breathers in a Stratified Ocean
Abstract
1. Introduction
2. The mKdV Equation and Its Breather Solution
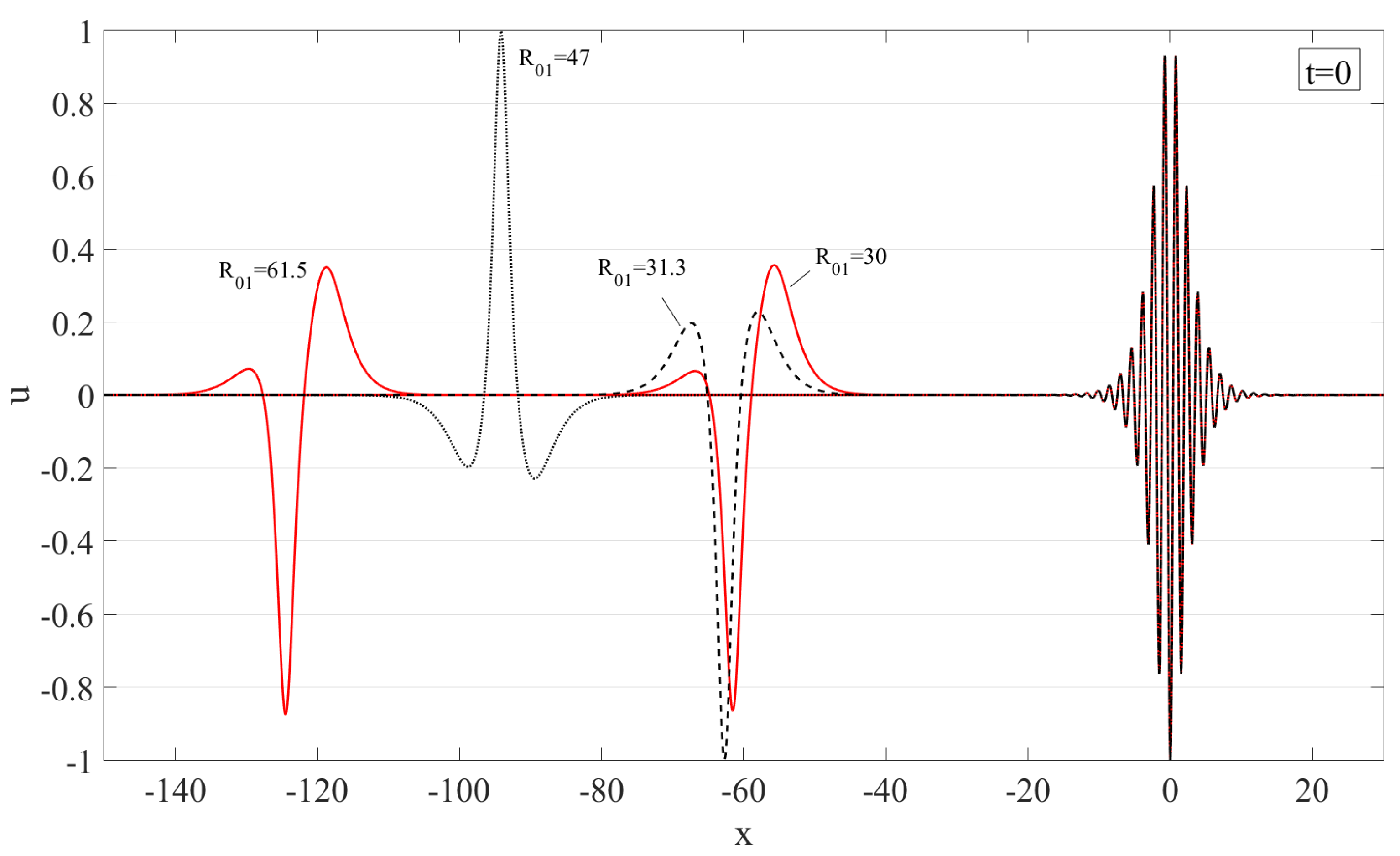
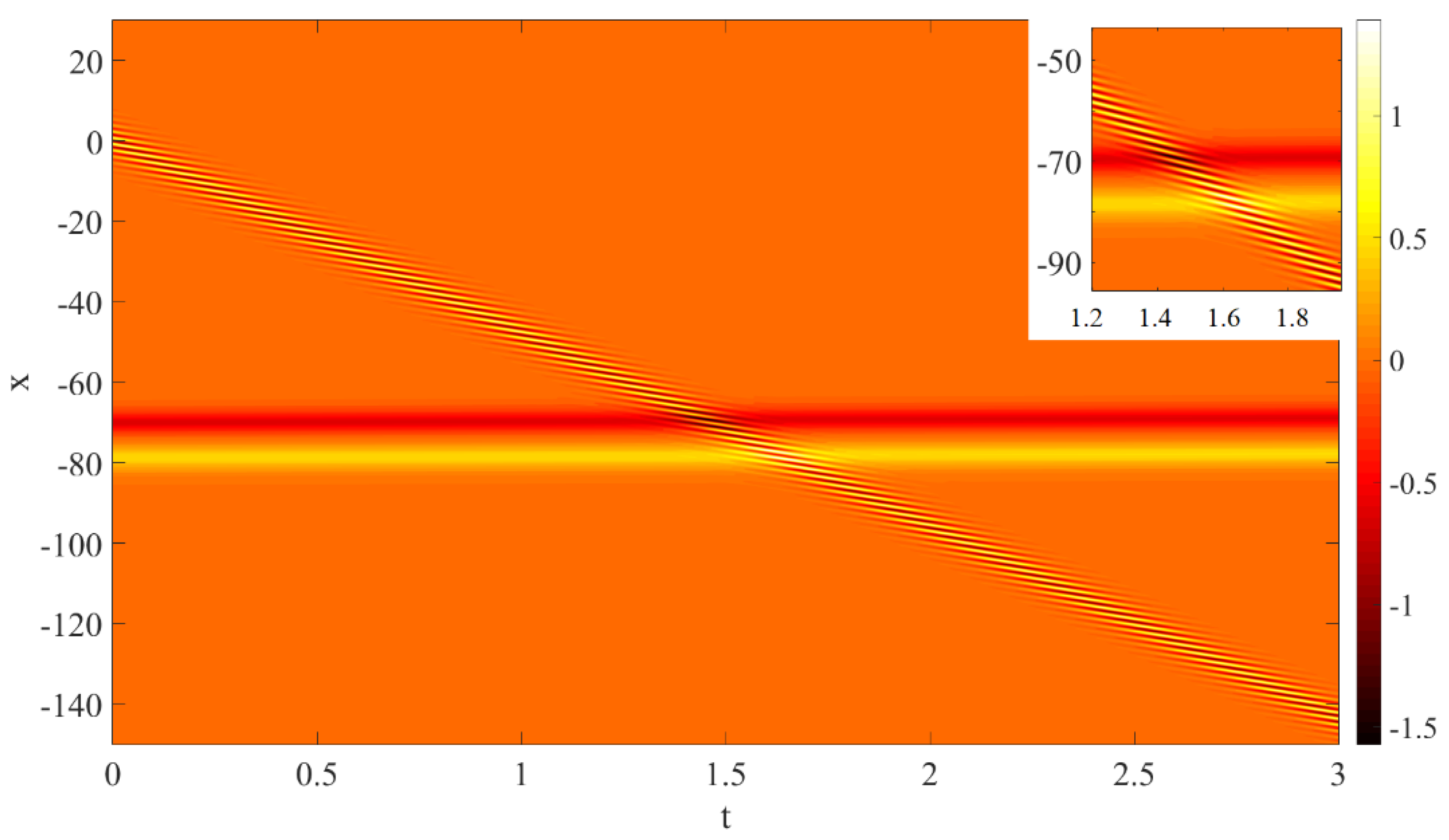
3. Pairwise Breather Interaction
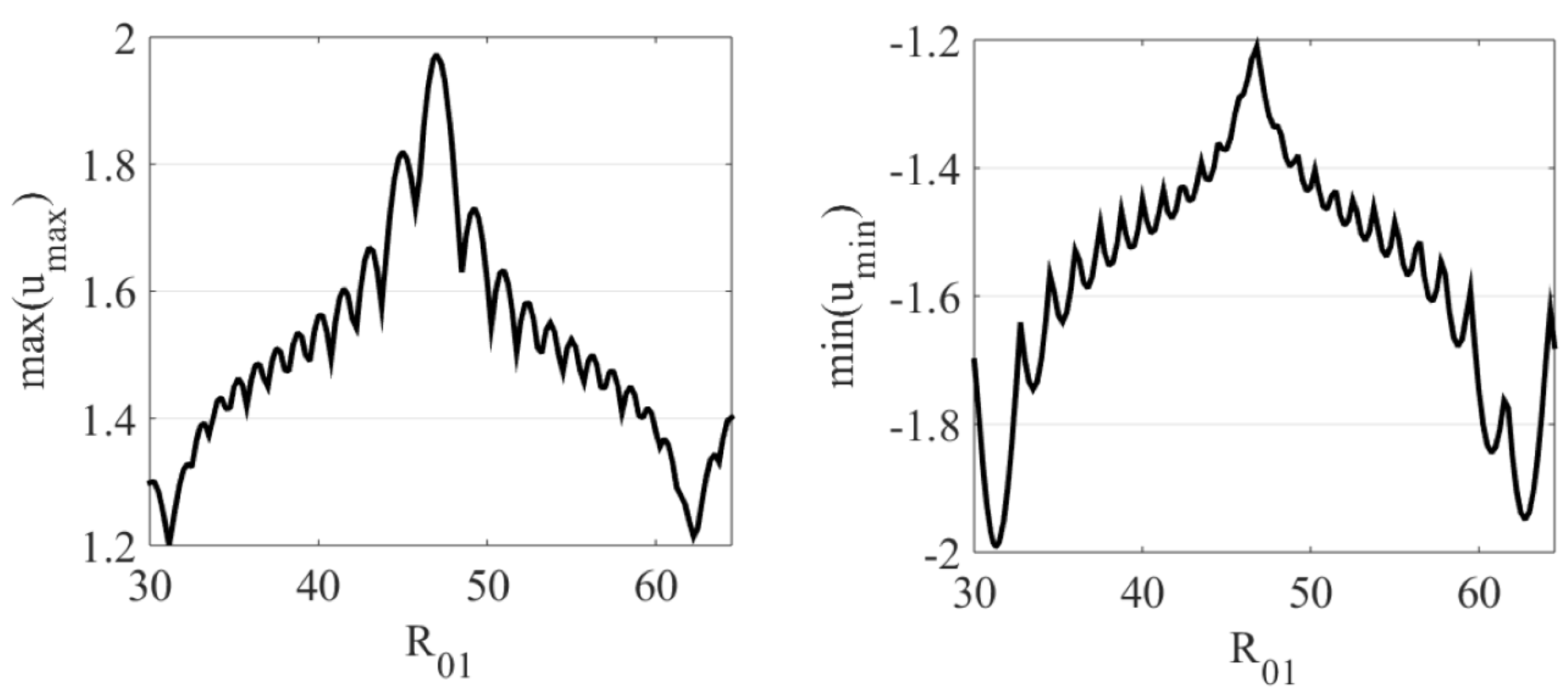
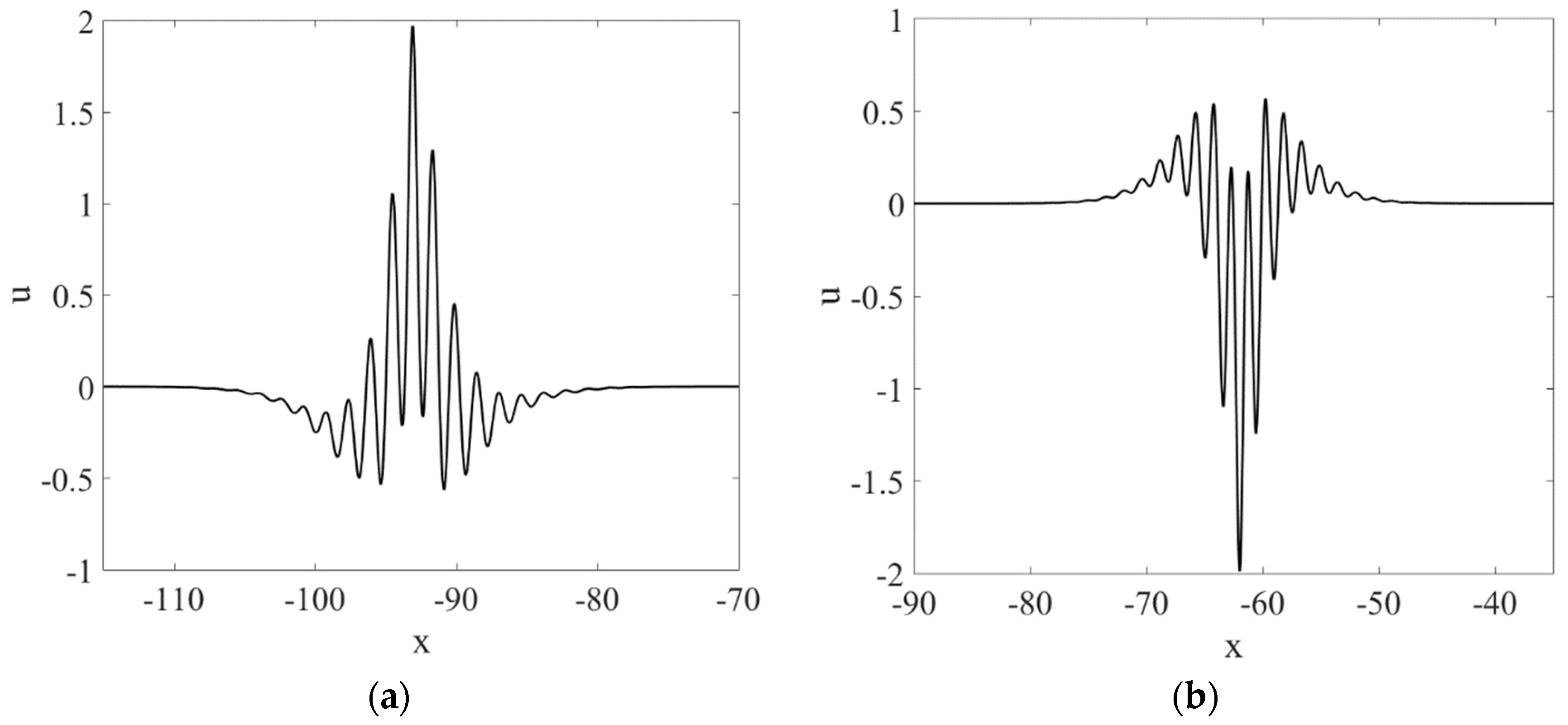
4. Wave Field Extrema
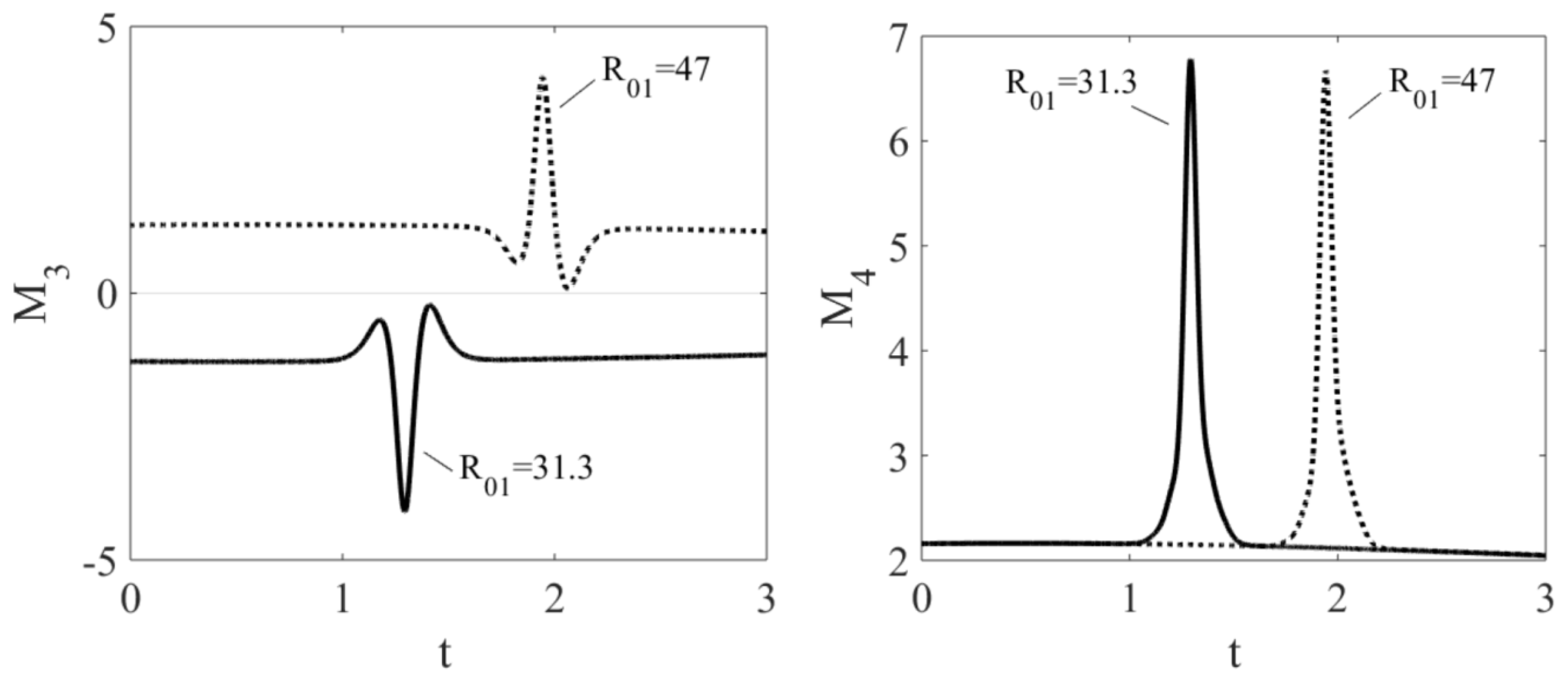
5. Moments and Spectra of the Wave Fields
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zakharov, V.E.; Manakov, S.V.; Novikov, S.P.; Pitaevskii, L.P. Theory of Solitons. In The Method of the Inverse Problem; Nauka: Moscow, Russia, 1980; p. 339. [Google Scholar]
- Slyunyaev, A.V. Dynamics of localized waves with large amplitude in a weakly dispersive medium with a quadratic and positive cubic nonlinearity. JETP 2001, 92, 529–534. [Google Scholar] [CrossRef]
- Slyunyaev, A.V.; Pelinovskii, E.N. Dynamics of large-amplitude solitons. JETP 1999, 89, 173–181. [Google Scholar] [CrossRef]
- Anco, S.C.; Ngatat, N.T.; Willoughby, M. Interaction properties of complex modified kortewegde Vries (mKdV) solitons. Physica D 2011, 240, 1378–1394. [Google Scholar] [CrossRef]
- Ali, R.; Chatterjee, P. Three-Soliton Interaction and Soliton Turbulence in Superthermal Dusty Plasmas. Zeitschrift für Naturforschung A 2019, 74, 757–766. [Google Scholar] [CrossRef]
- Kachulin, D.; Gelash, A. On the phase dependence of the soliton collisions in the Dyachenko–Zakharov envelope equation. Nonlin. Processes Geophys. 2018, 25, 553–563. [Google Scholar] [CrossRef]
- Kurkina, O.E.; Kurkin, A.A.; Ruvinskaya, E.A.; Pelinovsky, E.N.; Soomere, T. Dynamics of solitons in a nonintegrable version of the modified Korteweg-de Vries equation. JETP Lett. 2012, 95, 91–95. [Google Scholar] [CrossRef]
- Agafontsev, D.S.; Zakharov, V.E. Integrable turbulence generated from modulational instability of cnoidal waves. Nonlinearity 2016, 29, 3551–3578. [Google Scholar] [CrossRef]
- Kachulin, D.; Dyachenko, A.; Dremov, S. Multiple Soliton Interactions on the Surface of Deep Water. Fluids 2020, 5, 65. [Google Scholar] [CrossRef]
- Kachulin, D.; Dyachenko, A.; Zakharov, V. Soliton Turbulence in Approximate and Exact Models for Deep Water Waves. Fluids 2020, 5, 67. [Google Scholar] [CrossRef]
- Pelinovsky, E.; Shurgalina, E. KDV soliton gas: Interactions and turbulence. In Challenges in Complexity: Dynamics, Patterns, Cognition; Aronson, I., Pikovsky, A., Rulkov, N., Tsimring, L., Eds.; Series: Nonlinear Systems and Complexity; Springer: Berlin, Germany, 2017; Volume 20, pp. 295–306. [Google Scholar]
- Didenkulova, E.G.; Pelinovsky, E.N. The Role of a Thick Soliton in the Dynamics of the Soliton Gas within the Framework of the Gardner Equation. Radiophys. Quantum Electron. 2019, 61, 623–632. [Google Scholar] [CrossRef]
- Dutykh, D.; Pelinovsky, E. Numerical simulation of a solitonic gas in KdV and KdV–BBM equations. Phys. Lett. A 2014, 378, 3102–3110. [Google Scholar] [CrossRef]
- Shurgalina, E.G.; Pelinovsky, E.N. Nonlinear dynamics of a soliton gas: Modified Korteweg-de Vries equation framework. Phys. Lett. A 2016, 380, 2049–2053. [Google Scholar] [CrossRef]
- Gelash, A.A.; Agafontsev, D.S. Strongly interacting soliton gas and formation of rogue waves. Phys. Rev. E. 2018, 98, 1–11. [Google Scholar] [CrossRef]
- Pelinovsky, E.N.; Shurgalina, E.G. Formation of freak waves in a soliton gas described by the modified Korteweg–de Vries equation. Dokl. Phys. 2016, 61, 423–426. [Google Scholar] [CrossRef]
- Didenkulova (Shurgalina), E.G. Numerical modeling of soliton turbulence within the focusing Gardner equation: Rogue wave emergence. Physica D 2019, 399, 35–41. [Google Scholar] [CrossRef]
- Soto-Crespo, J.M.; Devine, N.; Akhmediev, N. Integrable Turbulence and Rogue Waves: Breathers or Solitons? Phys. Rev. Lett. 2016, 116, 103901. [Google Scholar] [CrossRef] [PubMed]
- Pelinovsky, E.N.; Shurgalina, E.G.; Sergeeva, A.V.; Talipova, T.G.; El, G.A.; Grimshaw, R.H.J. Two-soliton interaction as an elementary act of soliton turbulence in integrable systems. Phys. Lett. A 2013, 377, 272–275. [Google Scholar] [CrossRef]
- Pelinovsky, E.N.; Shurgalina, E.G. Two-soliton interaction in the frameworks of modified Korteweg – de Vries equation. Radiophys. Quantum Electron. 2015, 57, 737–744. [Google Scholar] [CrossRef]
- Shurgalina, E.G. The features of the paired soliton interactions within the framework of the Gardner equation. Radiophys. Quantum Electron. 2018, 60, 703–708. [Google Scholar] [CrossRef]
- Shurgalina, E.G. The mechanism of the formation of freak waves in the result of interaction of internal waves in stratified basin. Fluid Dyn. 2018, 53, 59–64. [Google Scholar] [CrossRef]
- Slunyaev, A.V.; Pelinovsky, E.N. Role of multiple soliton interactions in the generation of rogue waves: The modified korteweg-de vries framework. Phys. Rev. Lett. 2016, 117, 214501. [Google Scholar] [CrossRef]
- Slunyaev, A. On the optimal focusing of solitons and breathers in long-wave models. Stud. Appl. Math. 2019, 142, 385–413. [Google Scholar] [CrossRef]
- Fedele, F. On the persistence of breathers at deep water. JETP Lett. 2014, 98, 523–527. [Google Scholar] [CrossRef]
- Kachulin, D.; Dyachenko, A.; Gelash, A. Interactions of coherent structures on the surface of deep water. Fluids 2019, 4, 83. [Google Scholar] [CrossRef]
- Wang, J.; Ma, Q.W.; Yan, S.; Chabchoub, A. Breather Rogue Waves in Random Seas. Phys. Rev. Appl. 2018, 9, 014016. [Google Scholar] [CrossRef]
- Lamb, K.G.; Polukhina, O.; Talipova, T.; Pelinovsky, E.; Xiao, W.; Kurkin, A. Breather generation in fully nonlinear models of a stratified fluid. Phys. Rev. E 2007, 75, 046306. [Google Scholar] [CrossRef] [PubMed]
- Talipova, T.; Kurkina, O.; Kurkin, A.; Didenkulova, E.; Pelinovsky, E. Internal Wave Breathers in the Slightly Stratified Fluid. Microgravity Sci. Technol. 2020, 32, 69–77. [Google Scholar] [CrossRef]
- Rouvinskaya, E.; Talipova, T.; Kurkina, O.; Soomere, T.; Tyugin, D. Transformation of internal breathers in the idealised shelf sea conditions. Cont. Shelf Res. 2015, 110, 60–71. [Google Scholar] [CrossRef]
- Nakayama, K.; Lamb, K. Breathers in a three-layer fluid. J. Fluid Mech. 2020, 903, A40. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E.; Talipova, T. The modified Korteweg–de Vries equation in the theory of large-amplitude internal waves. Nonlinear Process. Geophys. 1997, 4, 237–250. [Google Scholar] [CrossRef]
- Clarke, S.; Grimshaw, R.; Miller, P.; Pelinovsky, E.; Talipova, T. On the generation of solitons and breathers in the modified Korteweg—de Vries equation. Chaos 2000, 10, 383–392. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Lee, J.H.; Lozovatsky, I.; Jang, S.-T.; Jang, C.J.; Hong, C.S.; Fernando, H.J.S. Episodes of nonlinear internal waves in the northern East China Sea. Geophys. Res. Lett. 2006, 33, L18601. [Google Scholar] [CrossRef]
- Shroyer, E.L.; Moum, J.N.; Nash, J.D. Mode 2 waves on the continental shelf: Ephemeral components of the nonlinear internal wavefield. JGR 2010, 115, C07001. [Google Scholar] [CrossRef]
- Chow, K.W.; Grimshaw, R.H.J.; Ding, E. Interactions of breathers and solitons in the extended Korteweg–de Vries equation. Wave Motion 2005, 43, 158–166. [Google Scholar] [CrossRef]
- Didenkulova, E.; Pelinovsky, E. Soliton–Breather Interaction: The Modified Korteweg–de Vries Equation Framework. Symmetry 2020, 12, 1445. [Google Scholar] [CrossRef]
- Kevrekidis, P.G.; Saxena, A.; Bishop, A.R. Interaction between sine-Gordon breathers. Phys. Rev. E 2001, 64, 026613. [Google Scholar] [CrossRef] [PubMed]
- Kevrekidis, P.G.; Khare, A.; Saxena, A. Solitary wave interactions in dispersive equations using Manton’s approach. Phys. Rev. E 2004, 70, 057603. [Google Scholar] [CrossRef]
- Nishida, M.; Nishida, M.; Furukawa, Y.; Fujii, T.; Hatakenaka, N. Breather-breather interactions in sine-Gordon systems using collective coordinate approach. Phys. Rev. E 2009, 80, 036603. [Google Scholar] [CrossRef]
- Rouvinskaya, E.A.; Kurkina, O.E.; Kurkin, A.A.; Korol, A.A. Dynamics of breathers in the framework of the Gardner equation. In Proceedings of the International Scientific and Technical Conference “Information Systems and Technologies”, Nizhny Novgorod, Russia, 21 April 2017. [Google Scholar]
- Talipova, T.; Pelinovsky, E.; Lamb, K.; Grimshaw, R.; Holloway, P. Cubic nonlinearity effects in the propagation of intense internal waves. Doklady Earth Sci. 1999, 365, 241–244. [Google Scholar]
- Didenkulova, E.; Pelinovsky, E. Breather’s Properties within the Framework of the Modified Korteweg–de Vries Equation. Symmetry 2020, 12, 638. [Google Scholar] [CrossRef]
- Fronberg, B. A Practical Guide to Pseudospectral Methods; Cambridge University Press: Cambridge, UK, 1998; p. 231. [Google Scholar]
- Monin, A.S.; Yaglom, A.M. Statistical Fluid Mechanics; MIT Press: Cambridge, MA, USA, 1971; p. 769. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Didenkulova, E.; Pelinovsky, E. Interaction Features of Internal Wave Breathers in a Stratified Ocean. Fluids 2020, 5, 205. https://doi.org/10.3390/fluids5040205
Didenkulova E, Pelinovsky E. Interaction Features of Internal Wave Breathers in a Stratified Ocean. Fluids. 2020; 5(4):205. https://doi.org/10.3390/fluids5040205
Chicago/Turabian StyleDidenkulova, Ekaterina, and Efim Pelinovsky. 2020. "Interaction Features of Internal Wave Breathers in a Stratified Ocean" Fluids 5, no. 4: 205. https://doi.org/10.3390/fluids5040205
APA StyleDidenkulova, E., & Pelinovsky, E. (2020). Interaction Features of Internal Wave Breathers in a Stratified Ocean. Fluids, 5(4), 205. https://doi.org/10.3390/fluids5040205





