An Elementary Model for a Self-Accelerating Outward Propagating Flame Subject to the Rayleigh–Taylor Instability: Transition to Detonation

Abstract

Within the Boussinesq approximation, an elementary model for the deflagration-to-detonation transition triggered by self-acceleration of an expanding flame is formulated and explored. The self-acceleration is sustained by the intrinsic Rayleigh–Taylor instability until the Deshaies–Joulin deflagrability threshold is reached, followed by an abrupt transition to detonation. Emergence of the threshold is caused by positive feedback between the accelerating flame and the flame-driven pressure shock that results in the thermal runaway when the flame speed reaches a critical level. The model offers a simple mechanism that may be responsible for the transition to detonation in thermonuclear supernovae.

1. Introduction

Understanding supernovae explosions is a fundamental astrophysical issue that has frustrated theorists since the effect was first clearly identified by Zwicky in 1933, and it is still commonly regarded as an unsolved problem (Röpke [1]). There is a general consensus that the Type Ia supernova explosion of a degenerate carbon white dwarf star is a manifestation of the deflagration-to-detonation transition (DDT) triggered by an outward-propagating thermonuclear flame subjected to Darrieus–Landau (DL) and Rayleigh–Taylor (RT) corrugations causing the flame to accelerate prior to the transition [2].

The present study offers an elementary model of the DDT event by synthesizing a weakly nonlinear equation of the RT-instability with the Deshaies–Joulin (DJ) theory of thermal runaway [3].

Unlike terrestrial chemical flames, in thermonuclear flames the thermal expansion of reaction products is relatively small [1,4,5,6], which justifies utilization of the Boussinesq distinguished limit [7]. The Boussinesq quasi-constant-density approximation, in turn, suppresses development of the DL-instability, whose impact is generally deemed inferior to that of the RT.

In the DJ analysis [3], the upper bound for the flame speed is caused by positive feedback between the advancing flame and the flame-driven pressure shock that results in the thermal runaway when the flame speed reaches a critical level. The crucial point of the DJ approach is that at the DDT threshold the corrugated flame may stay perfectly subsonic (see also [8,9,10]). This premise allows one to deal with the small (yet nonzero) Mach number approximation with all the technical advantages it provides. Moreover, the ability of a subsonic flame to trigger the transition challenges the common view that to ensure DDT the flame should cross the threshold of the DJ-deflagration.

2. Modelling

For the Boussinesq limit the appropriately scaled dispersion relation for an upward propagating planar flame reads (see Zeldovich et al. [11], Equation (3.57) at $\alpha \to 1$, while keeping $(\alpha -1)g$ finite), (Figure 1):

$$\omega =\frac{1}{2}\left(\sqrt{k^2{(k-1)}^2+Gk}-k-k^2\right)$$

(1)

Here k is the perturbation wave-number in units of $1/l_M,l_M=$ Markstein length, $\omega$ = perturbation growth rate in units of $U_b/l_M$, $U_b$ = planar flame speed relative to the burned gas under isobaric conditions, $G=2(\alpha -1)g{l}_M/U_b^2$ = buoyancy parameter, $\alpha$ = ratio of unburned to burned gas densities, and g = acceleration due to gravity.

For thermonuclear flames the Lewis number may be regarded as infinitely large [4]. Hence, $l_M=\frac{1}{2}\beta l_{th}$ [11,12], where $\beta$ = Zeldovich number and $l_{th}$ = flame width.

Similar to the weakly nonlinear equation for the DL-instability [12,13], the analogous equation for an upward-propagating planar flame subjected to the RT-instability may be written as

$$\frac{\partial {\mathsf{\Phi }}^{\left(0\right)}}{\partial t}=1+\frac{1}{2}{\left(\frac{\partial {\mathsf{\Phi }}^{\left(0\right)}}{\partial x}\right)}^2+I\left[{\mathsf{\Phi }}^{\left(0\right)}\right]$$

(2)

where

$$I\left[{\mathsf{\Phi }}^{\left(0\right)}\right]=\sum _{n=1}^{\infty }\omega \left(\frac{2\pi n}{\mathsf{\Lambda }}\right)\left\{\frac{2}{\mathsf{\Lambda }}{\int }_{-\frac{1}{2}\mathsf{\Lambda }}^{\frac{1}{2}\mathsf{\Lambda }}{\mathsf{\Phi }}^{\left(0\right)}(x^{\prime },t)cos\left[\left(\frac{2\pi n}{\mathsf{\Lambda }}\right)(x-x^{\prime })\right]\right\}d{x}^{\prime }$$

(3)

Equations (2) and (3) are considered over a finite interval, $-\mathsf{\Lambda }/2<x<\mathsf{\Lambda }/2,$ with periodic boundary conditions:

$${\mathsf{\Phi }}^{\left(0\right)}\left(-\frac{1}{2}\mathsf{\Lambda },t\right)={\mathsf{\Phi }}^{\left(0\right)}\left(\frac{1}{2}\mathsf{\Lambda },t\right),$$

(4)

$${\mathsf{\Phi }}_x^{\left(0\right)}\left(-\frac{1}{2}\mathsf{\Lambda },t\right)={\mathsf{\Phi }}_x^{\left(0\right)}\left(\frac{1}{2}\mathsf{\Lambda },t\right)$$

Here ($x,t$) are scaled spatio-temporal coordinates in units of $l_M$ and $l_M/U_b$, ${\mathsf{\Phi }}^{\left(0\right)}$ = flame profile in units of $l_M$. The superscript in ${\mathsf{\Phi }}^{\left(0\right)}$ corresponds to the zero-Mach-number (isobaric) limit.

To accommodate the precompression-induced runaway we adopt the relation suggested by the DJ small-Mach-number approximation [3], (Figure 2).

$$\frac{lnm}{m}=\kappa \mathsf{\Sigma }$$

(5)

where

$$m={\mathsf{\Phi }}_t^{\left(M\right)}/{\mathsf{\Phi }}_t^{\left(0\right)}$$

(6)

and

$$\mathsf{\Sigma }=\overline{1+\frac{1}{2}{\left({\mathsf{\Phi }}_x^{\left(0\right)}\right)}^2}=\overline{{\mathsf{\Phi }}_t^{\left(0\right)}}$$

(7)

is the folding factor. The overbar means the average over the channel cross-section.

$$\kappa =\frac{1}{2}\beta (\gamma -1)\mathrm{Ma}$$

(8)

is the compressibility parameter, $\mathrm{Ma}=U_u/a_u$ is the Mach number, $\gamma =c_p/c_v$ is the adiabatic index, and $a_u$, $U_u=U_b/\alpha$ are sonic and flame velocities relative to the unburned gas. The superscript in ${\mathsf{\Phi }}^{\left(M\right)}$ corresponds to the small-Mach-number approximation.

Equation (5) readily implies that at the deflagrability (DDT) threshold, (Figure 2)

$$\kappa {\mathsf{\Sigma }}_{DDT}=e^{-1}$$

(9)

Equation (8) pertains to the one-step Arrhenius kinetics and the ideal gas equation of state. For the thermonuclear flame the structure of the compressibility parameter ($\kappa$) is more involved (Section 4) but this should not affect the overall dynamical picture.

Following [14], for an outward propagating flame $r=R^{\left(0\right)}(\phi ,t)$ Equations (2) and (3) are modified to

$$\frac{\partial R^{\left(0\right)}}{\partial t}=1+\frac{1}{2{\overline{R^{\left(0\right)}}}^2}{\left(\frac{\partial R^{\left(0\right)}}{\partial \phi }\right)}^2+I\left[R^{\left(0\right)}\right]$$

(10)

where

$$I\left[R^{\left(0\right)}\right]=\frac{1}{\pi }\sum _{n=1}^{\infty }\omega \left(\frac{n}{\overline{R^{\left(0\right)}}}\right){\int }_0^{2\pi }cos\left[n(\phi -{\phi }^{\prime })\right]R^{\left(0\right)}({\phi }^{\prime },t)d{\phi }^{\prime }$$

(11)

and

$$\overline{R^{\left(0\right)}}=\frac{1}{2\pi }{\int }_0^{2\pi }{R}^{\left(0\right)}(\phi ,t)d\phi$$

(12)

Solutions of the model (10)–(12) are valid as long as $R^{\left(0\right)}(\phi ,t)$ remains positive.

Similarly, Equations (6) and (7) are modified to

$$m=R_t^{\left(M\right)}/R_t^{\left(0\right)}$$

(13)

$$\mathsf{\Sigma }=\overline{1+\frac{1}{2{\overline{R^0}}^2}{\left(\frac{\partial R^{\left(0\right)}}{\partial \phi }\right)}^2}=\overline{\frac{\partial R^{\left(0\right)}}{\partial t}}$$

(14)

In Equation (1) for $\omega (n/\overline{R^{\left(0\right)}})$ of Equation (11) the buoyancy factor G is treated as a prescribed $\overline{R^{\left(0\right)}}$-independent parameter. This premise, while not holding in stars, is presumably adequate enough for mimicking the impact of buoyancy-induced instability.

For an outward propagating flame Equation (5) may be recast as

$$\overline{\frac{\partial R^{\left(M\right)}}{\partial t}}=\left[\overline{1+\frac{1}{2{\overline{R^{\left(0\right)}}}^2}{\left(\frac{\partial R^{\left(0\right)}}{\partial \phi }\right)}^2}\right]exp\left[\kappa \left(\frac{\overline{\partial R^{\left(M\right)}}}{\partial t}\right)\right]$$

(15)

This equation may be synthesized with Equation (10) yielding a unified model covering both the RT-instability as well as the deflagrability limit:

$$\frac{\partial R}{\partial t}=\left[1+\frac{1}{2{\overline{R}}^2}{\left(\frac{\partial R}{\partial \phi }\right)}^2\right]exp\left[\kappa \left(\frac{\partial R}{\partial t}\right)\right]+I\left[R\right]$$

(16)

Note that averaging of Equation (16) over $0<\phi <2\pi$ results in the relation similar to Equation (15), but without the distinction between $R^{\left(0\right)}$ and $R^{\left(M\right)}$.

3. Numerical Experiments

This section is concerned with numerical simulations of two models based on Equations (10) and (16). Here ${\sum }_{n=1}^{\infty }$ is naturally replaced by ${\sum }_{n=1}^N$ with large enough N. The numerical method employed is outlined in our recent study of a related problem [15].

The initial condition is specified as a weighted sum of cosines:

$$R(\phi ,0)=R_0+A\sum _{n=1}^{N/2}{n}^{2}exp(-n/10)cos(n\phi +{\phi }_n)$$

(17)

where A is the normalizing factor and ${\phi }_n$ are produced by the pseudo-random generator (Figure 3).

Parameters G and $\kappa$ are specified as $G=0.002$ and $\kappa =0.1$, corresponding e.g., to $\alpha =2,\beta =40,g=2·{10}^9$ cm/s ${}^2$, $l_{th}=0.1$ cm, $l_M=2$ cm, $U_u={10}^6$ cm/s, $U_b=\alpha U_u=2·{10}^6$ cm/s, $\mathrm{Ma}=0.01$, $a_u={10}^8$ cm/s, and $\gamma =(4/3+5/3)/2=1.5$, which are quite realistic [2,4,5,6].

Figure 4 and Figure 5 show the results of simulations of Equation (10). In the course of its evolution, the flame front assumes a quasi-periodic configuration comprising forward-propagating bubble-like structures trailed by cusps. Small bubbles gradually merge forming larger and faster advancing bubbles, thus exhibiting a strong inverse cascade. The effect was first observed by Vladimirova and Rosner [7] for upward-propagating flames in channels described by a set of Navier–Stokes and advection-diffusion-reaction equations. The inverse cascade effect is also known to occur for flames subjected to the DL-instability but, interestingly enough, not for the diffusively unstable cellular flames [14].

Simulation was terminated when rearward moving cusps reached the center ($r=0$).

At $\kappa =0.1$ Equation (9) readily yields ${\mathsf{\Sigma }}_{DDT}=D={\overline{R}}_t^{\left(0\right)}=3.7$, which in dimensional units corresponds to $7.4·{10}^6$ m/s. Here at the DDT point $t_{DDT}=6·{10}^4$ ($0.06$ s) and ${\overline{R}}_{DDT}^{\left(0\right)}=9.8·{10}^4$ ($1.96·{10}^5$ cm).

Figure 6 and Figure 7 correspond to Equation (16), where the deflagrative mode terminates at $D={\overline{R}}_t=1.9$ ($3.8·{10}^6$ cm/s), $t_{DDT}=3.5·{10}^4$ ($0.035$ s), and ${\overline{R}}_{DDT}^{\left(0\right)}=4.3·{10}^4$ ($8.6·{10}^4$ cm). In Figure 7 the last profile corresponds to the deflagrability threshold.

Occurrence of the inverse cascade is most graphically manifested in the channel geometry.

Figure 8 and Figure 9 depict the developing solution of Equations (2)–(4) for $\mathsf{\Lambda }=\mathrm{80,000}$. The incipient multi-bubble structure of the accelerating flame gradually disappears, yielding a single dome-like configuration propagating at a constant velocity.

4. Concluding Remarks

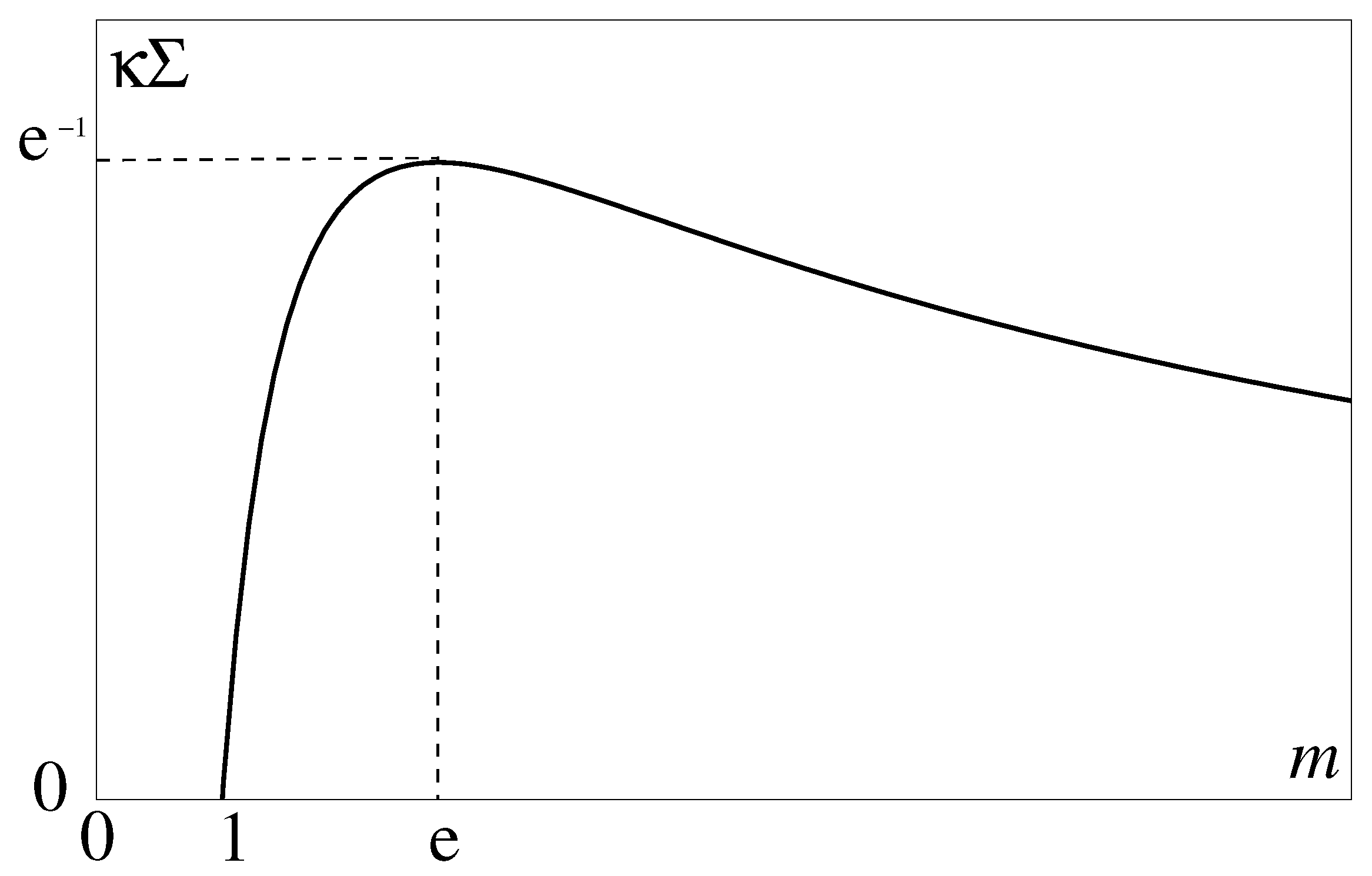
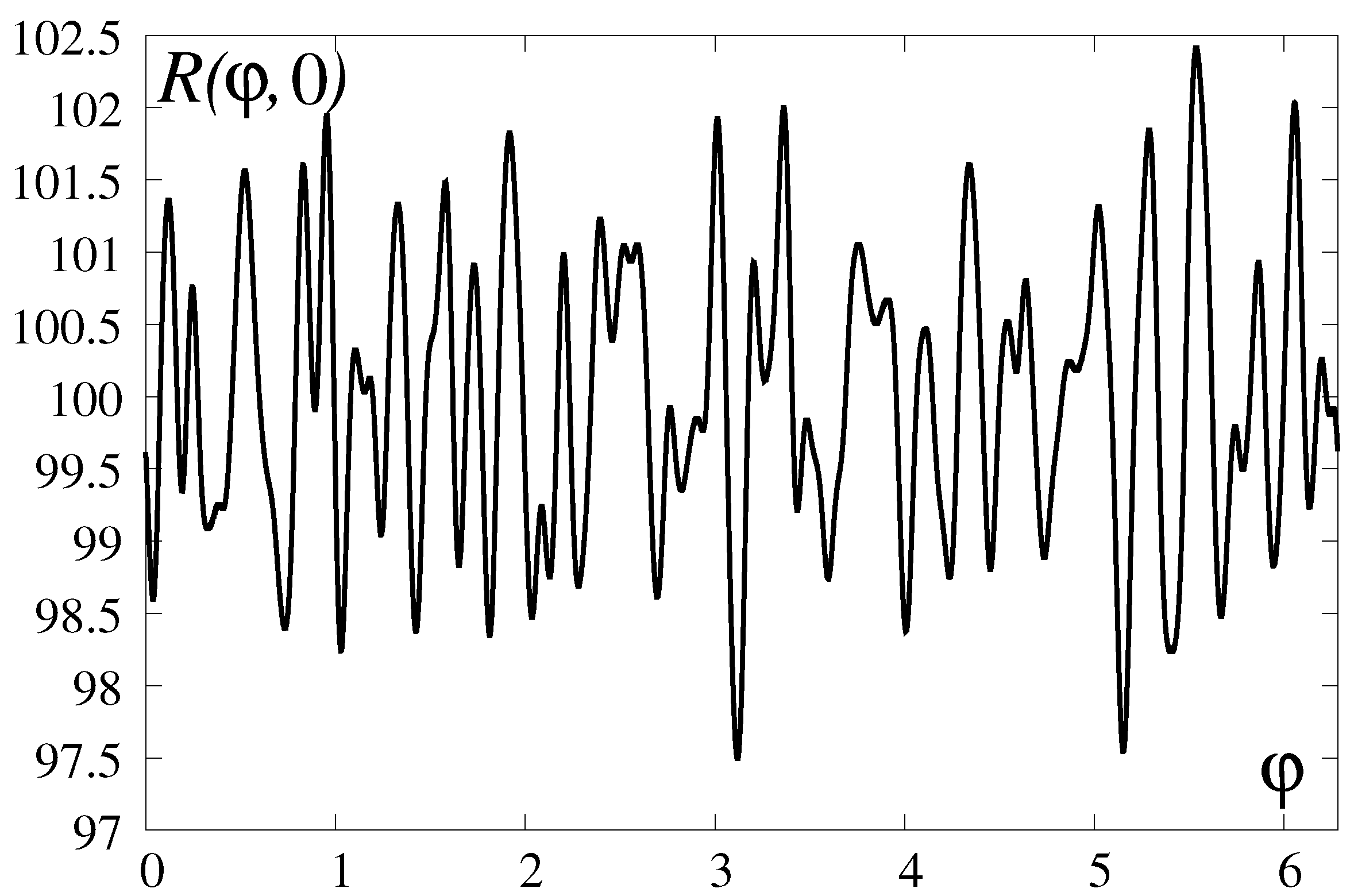
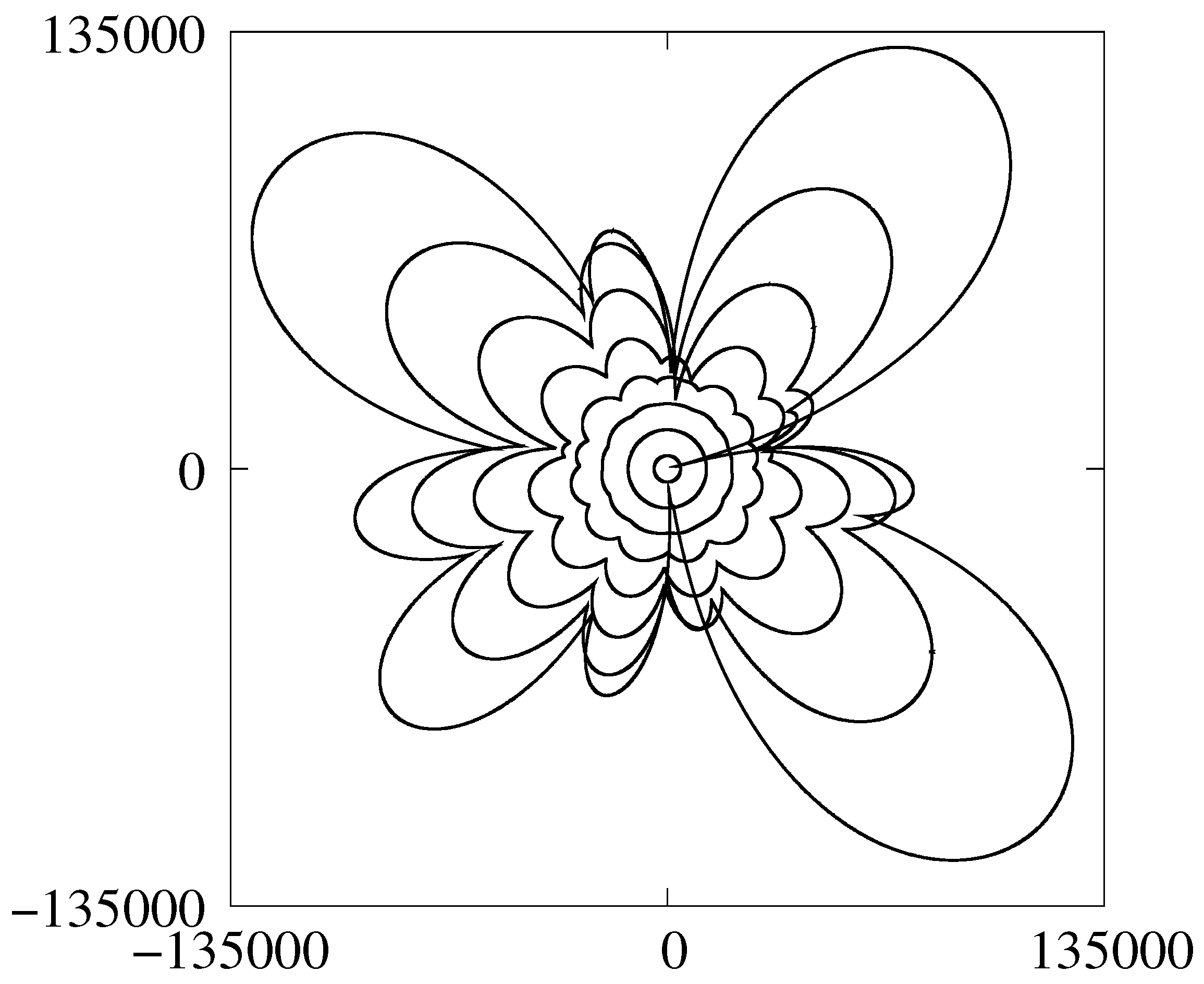
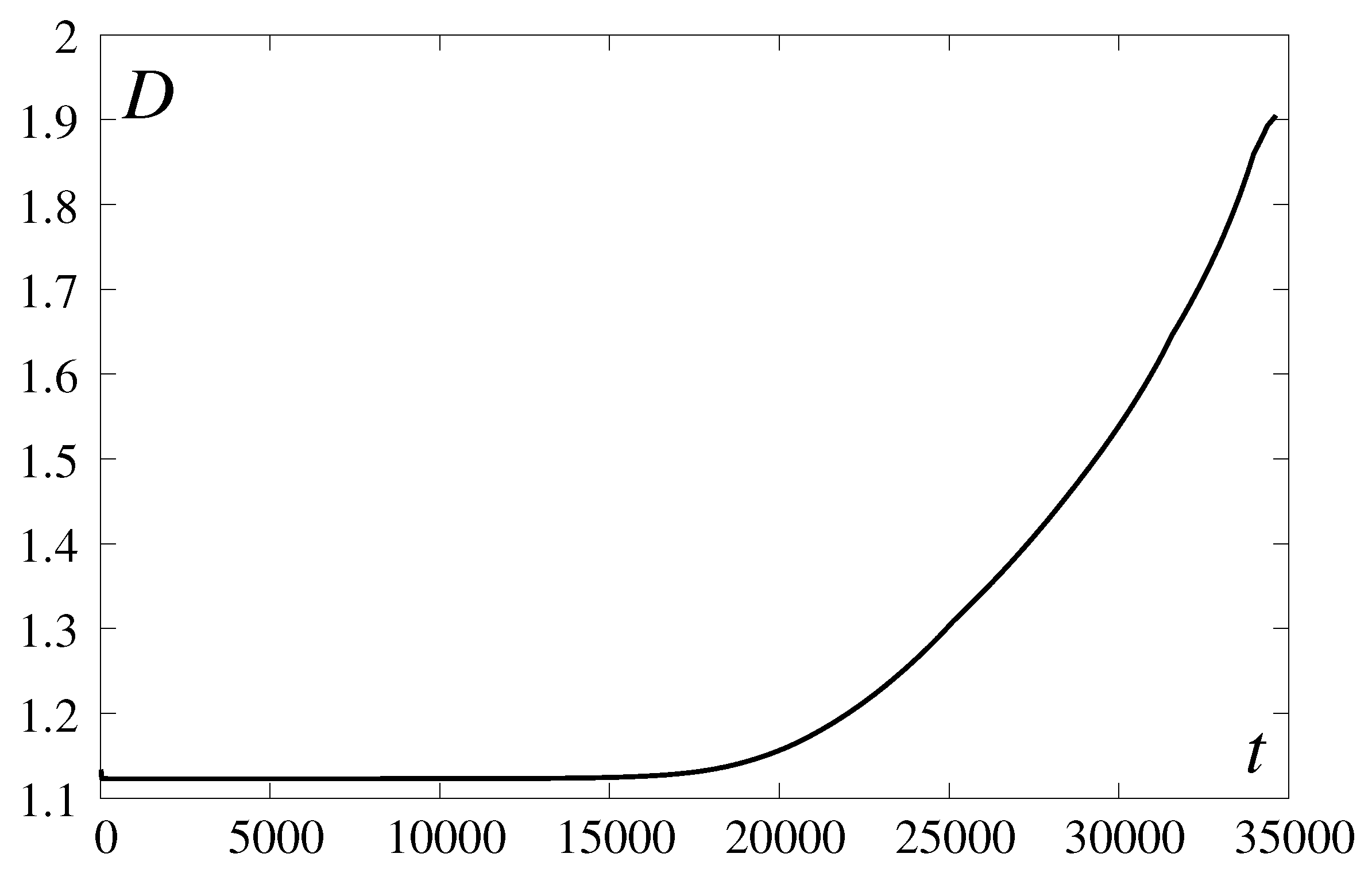
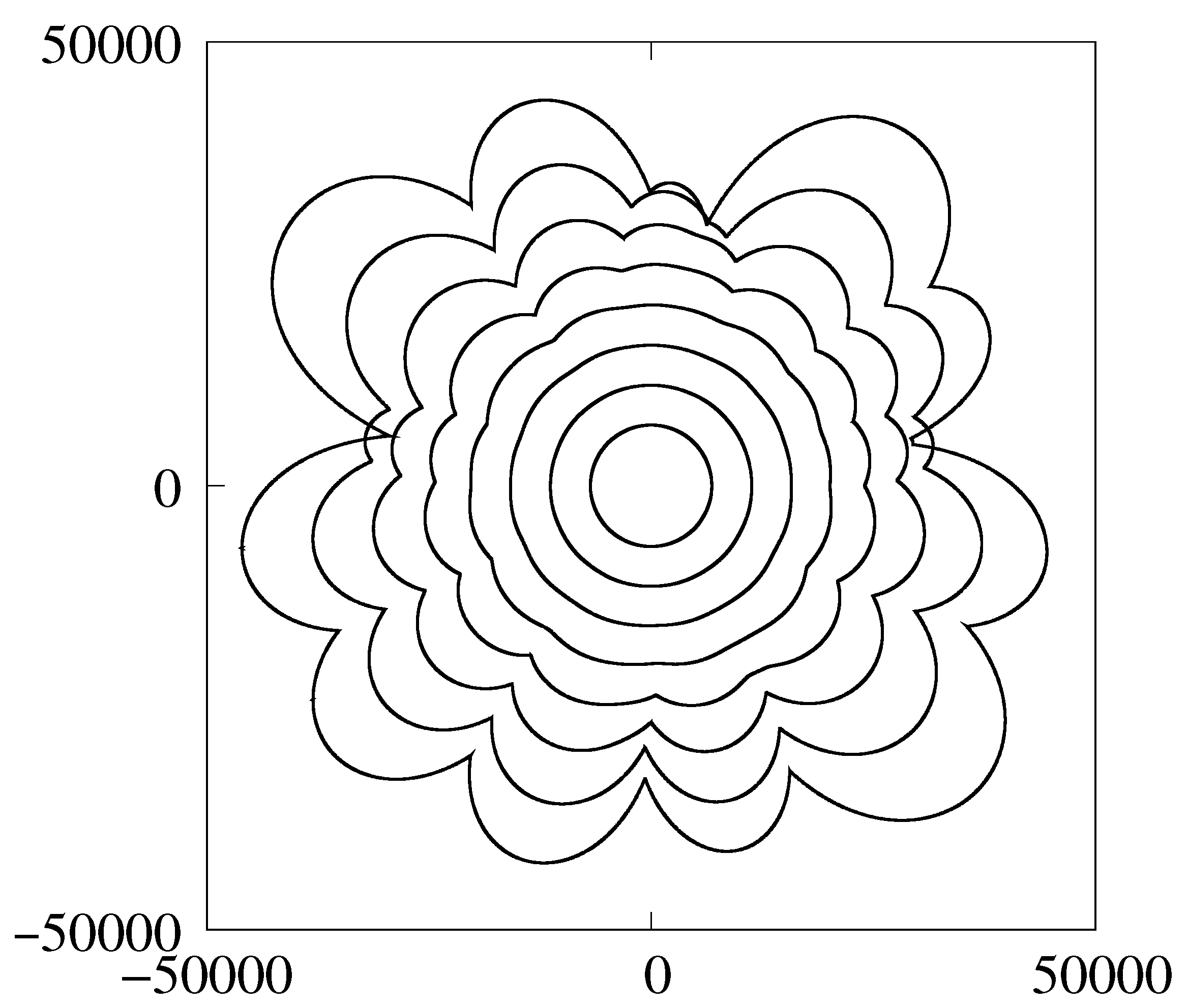
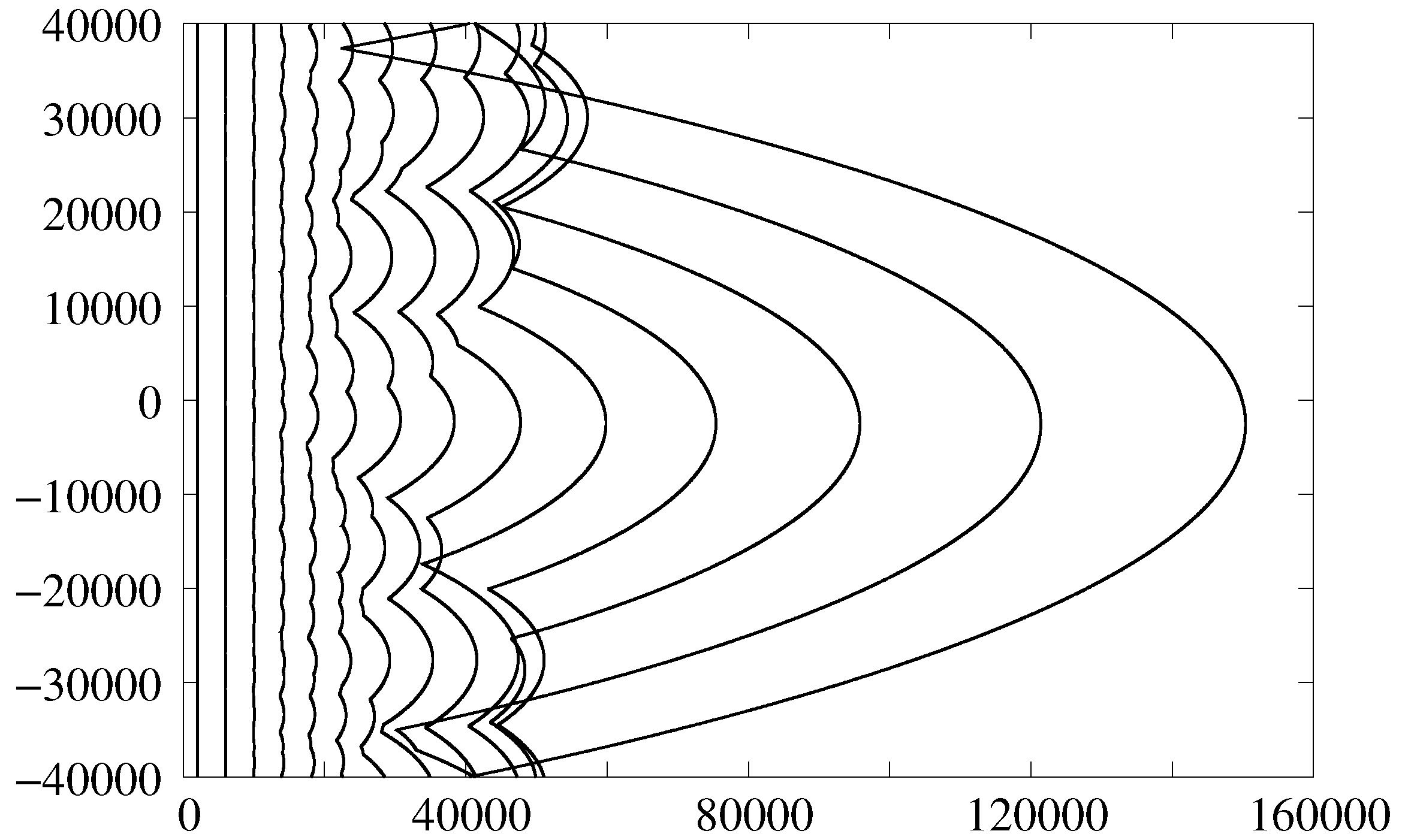
• The proposed weakly nonlinear models are certainly unable to capture the full morphology of the RT-mushrooming [7]. Yet, the models proved adequate enough to imitate the buoyancy-induced corrugations, the inverse cascade, self-acceleration of the front, and occurrence of the deflagrability threshold—the precursor of DDT.
• Due to the constancy of the buoyancy factor kept at $G=0.002$, the spatio-temporal scales ${\overline{R}}_{DDT}$ and $t_{DDT}$ are likely to be grossly underestimated. Accounting for G vanishing at $R\to 0$ is expected to yield much larger numbers.
• The gap between deflagrability limits based on Equations (9), (10) and (16) is quite significant but is likely to decrease with a diminishing $\kappa$.
• Our preliminary exploration of the problem for one-step nuclear reaction kinetics and the equation of state for the degenerate electron gas shows that in this case the structure of the compressibility parameter $\kappa$ is much more involved. This, however, does not affect the form of Equation (16) and the associated dynamical picture.