SISO Piezo Based Circuit Development for Active Structural Vibration Control

Abstract

This paper deals with the issue of developing a smart vibration control platform following an innovative model-based approach. As a matter of fact, obtaining accurate information on system response in pre-design and design phases may reduce both computational and experimental efforts. From this perspective, a multi-degree-of-freedom (MDOF) electro-mechanical coupled system has been numerically schematized implementing a finite element formulation: a robust simulation tool integrating finite element model (FEM) features with Simulink^® capabilities has been developed. Piezo strain actuation has been modelled with a 2D finite element description: the effects exerted on the structure (converse effect) have been applied as lumped loads at the piezo nodes interface. The sensing (direct effect) has instead been modelled with a 2D piezoelectric constitutive equation and experimentally validated as well. The theoretical study led to the practical development of an integrated circuit which allowed for assessing the vibration control performance. The analysis of critical parameters, description of integrated numerical models, and a discussion of experimental results are addressed step by step to get a global overview of the engineering process. The single mode control has been experimentally validated for a simple benchmark like an aluminum cantilevered beam. The piezo sensor-actuator collocated couple has been placed according to an optimization process based on the maximum stored electrical energy. Finally, a good level of correlation has been observed between the forecasting model and the experimental application: the frequency analysis allowed for characterizing the piezo couple behavior even far from the resonance peak.

1. Outlook

An innovative vibro-acoustic active control system for engineering transportation application has been numerically conceptualized and then validated by experimental evidence. This paper addresses the vibration control of elastic structures using piezoelectric transducers as a collocated sensor-actuator pair. The encouraging results achieved in basic test cases can be extended to more complex structures when excited by external sources, i.e., flow turbulence, tonal loads, engines, etc.

2. Introduction

2.1. Literature Background

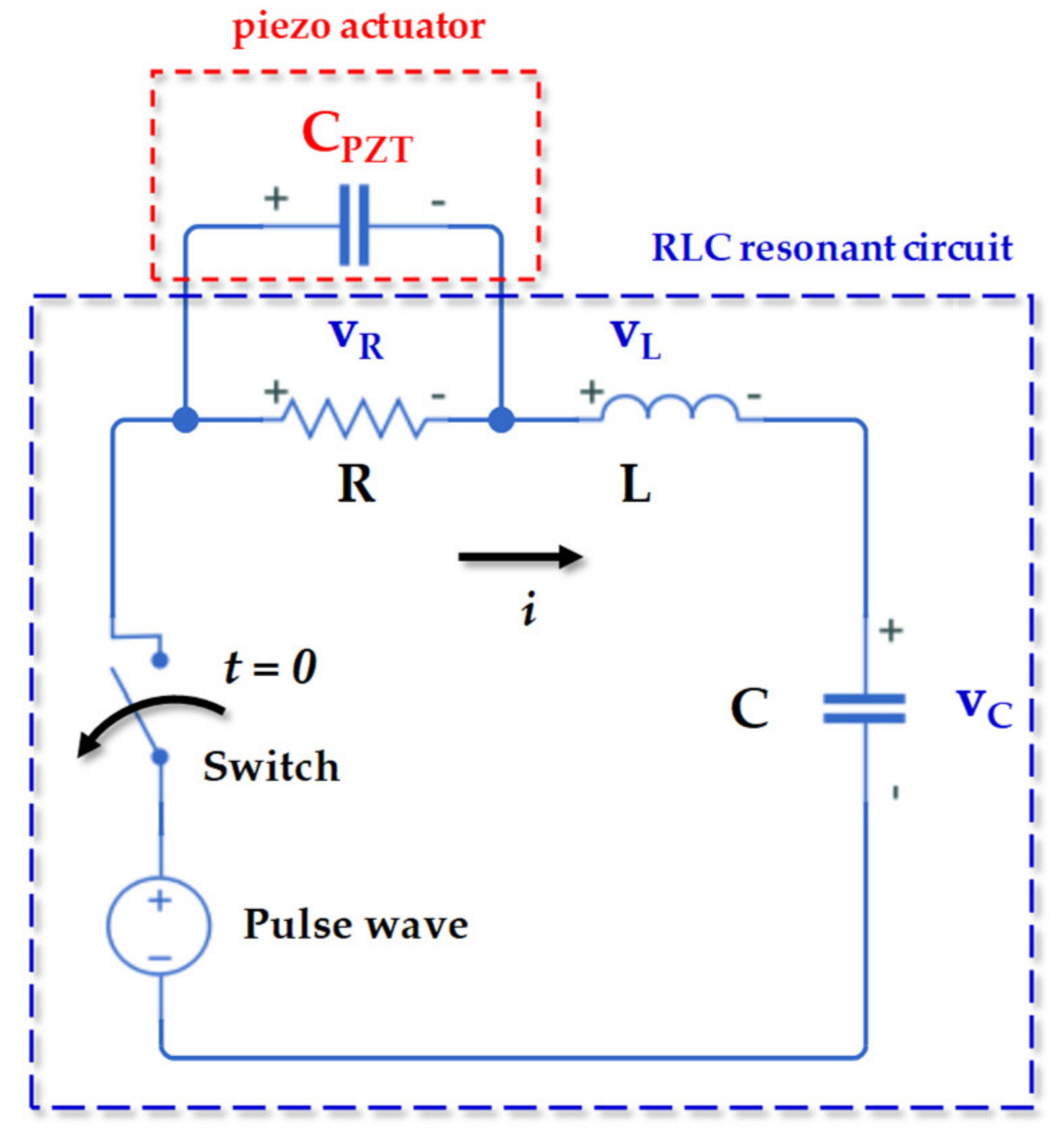
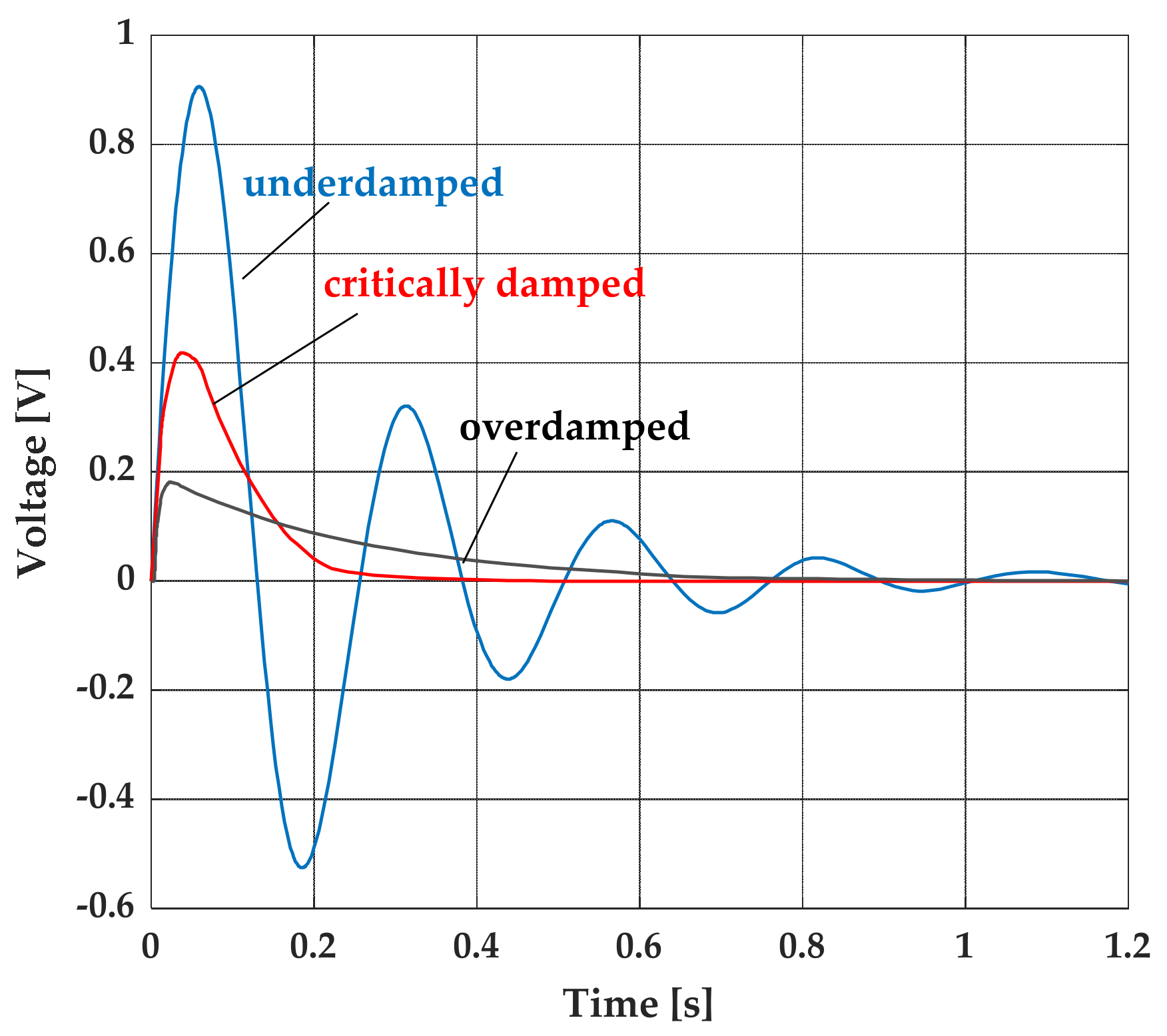
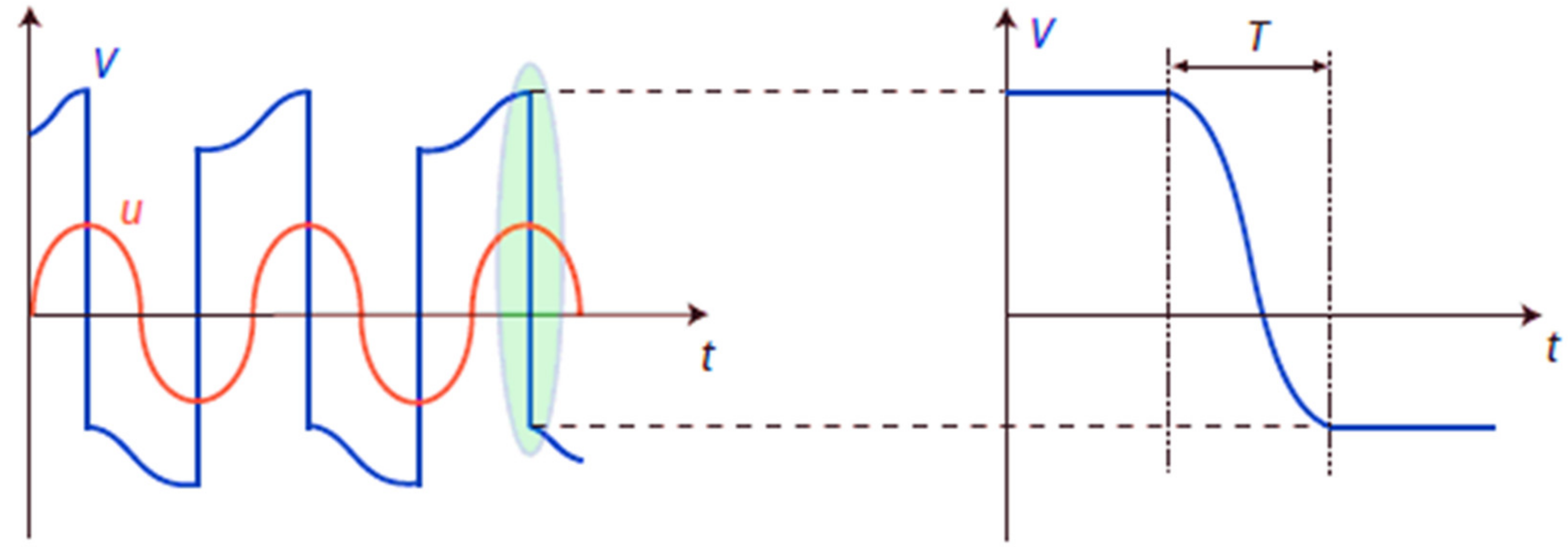
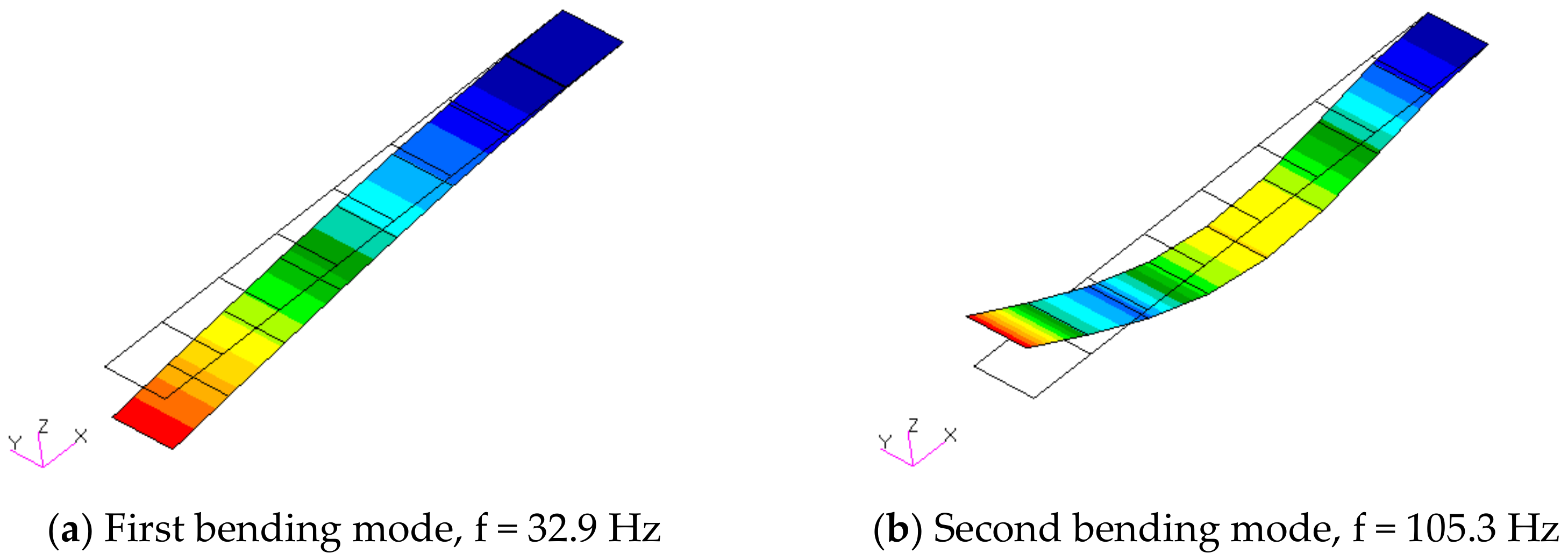
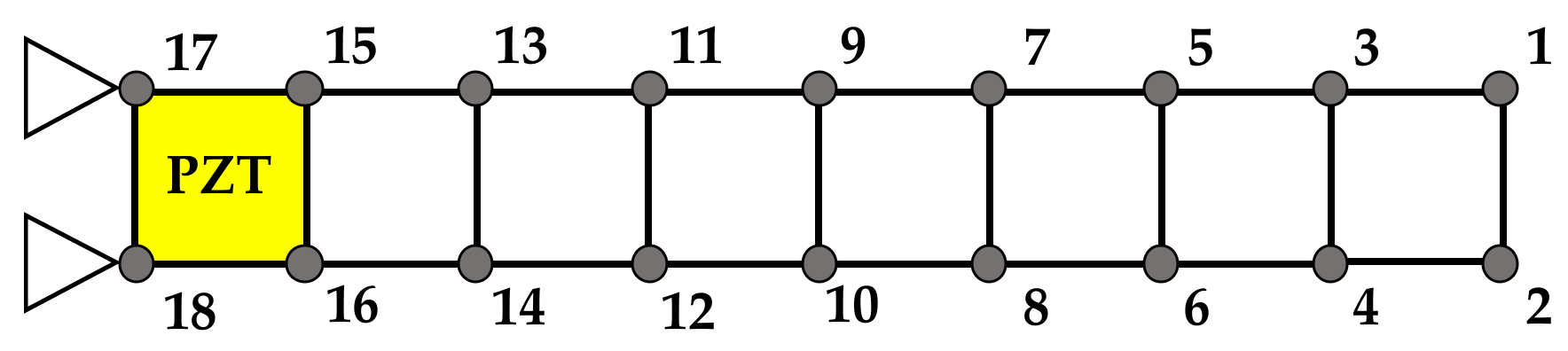
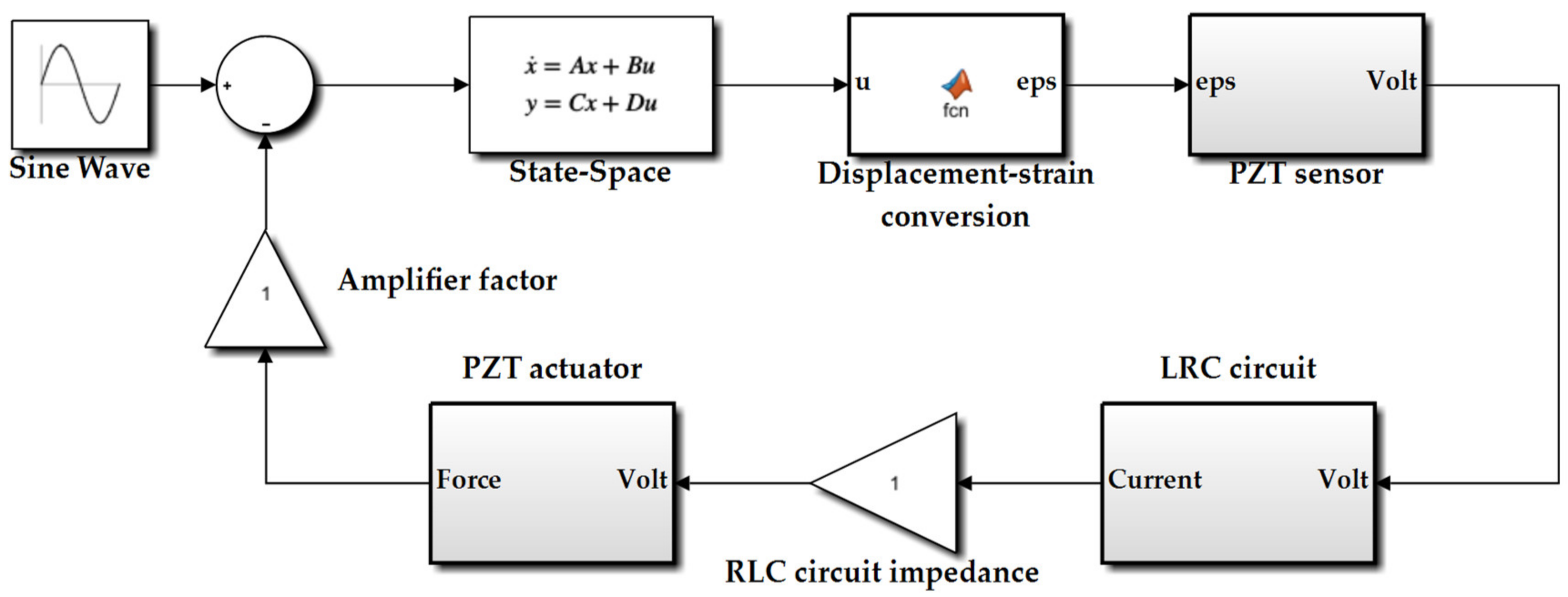
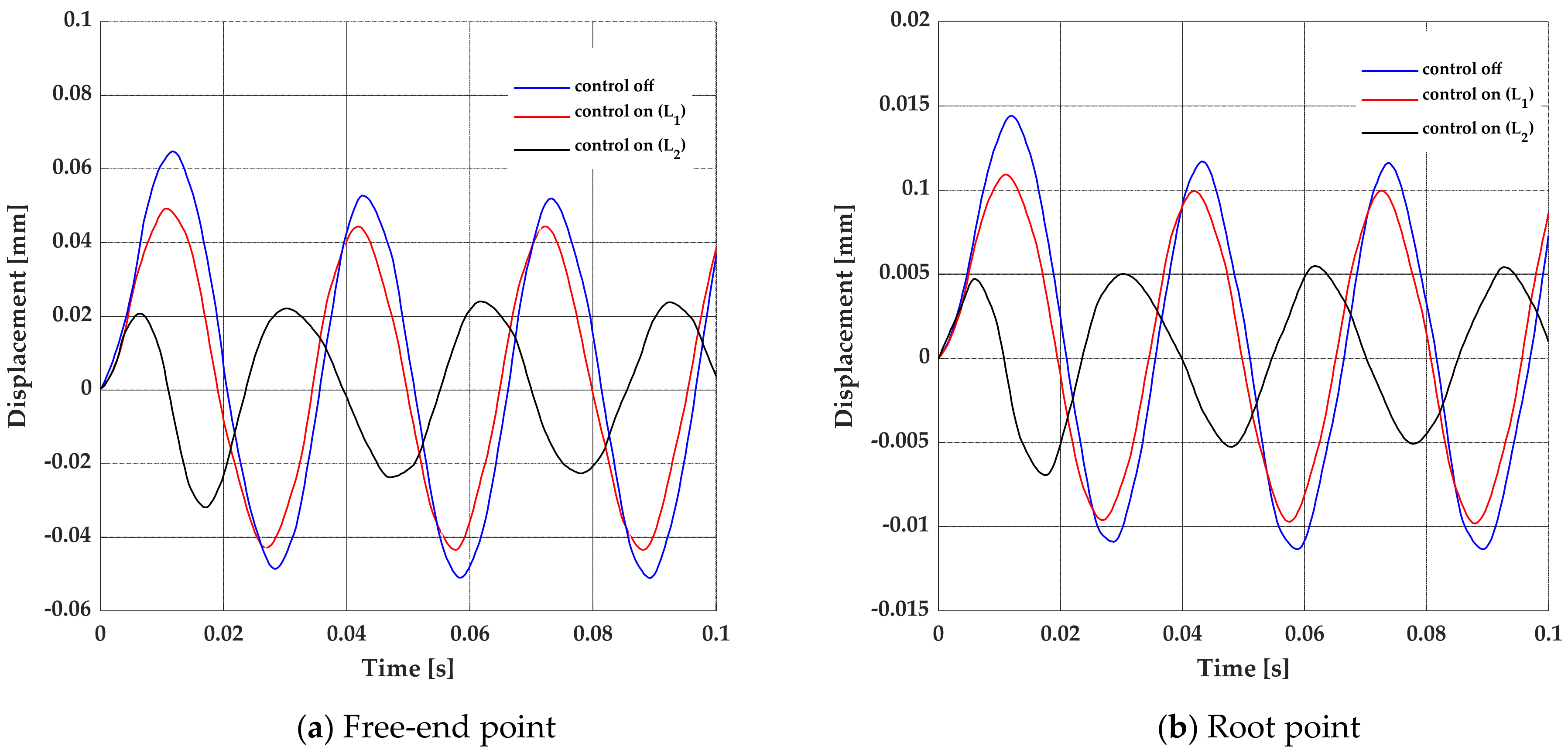
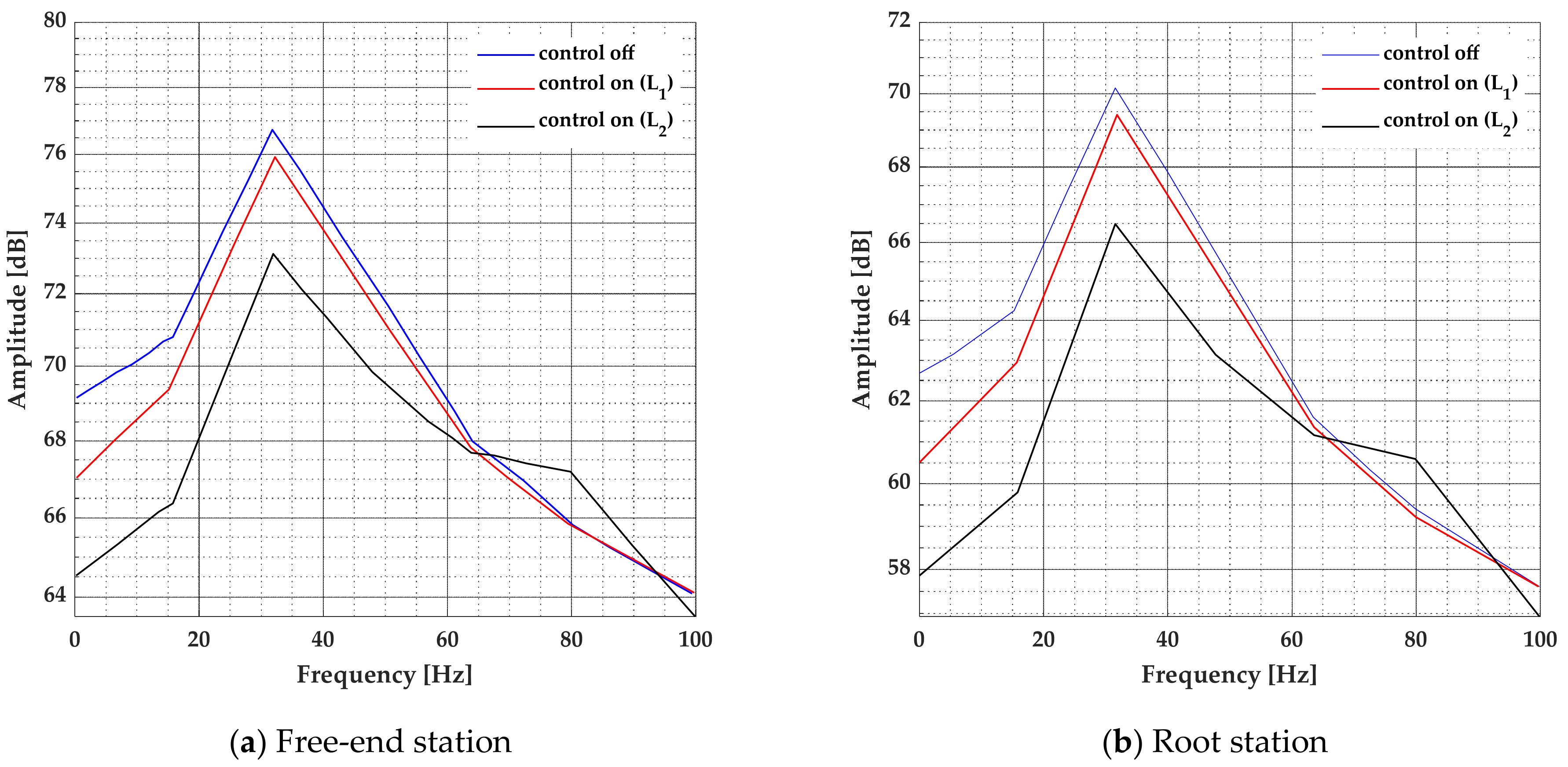
The optimization of structural vibrations still represents a real engineering challenge in various fields of application. Modern techniques are based on scientific concepts developed 30 years ago which are accompanied by technological spreads in order to develop increasingly performing devices. Conducting materials, metamaterials, integrated electronic circuits, and so on represent the current means that allow for the achievement of these research goals. The passive control technique widely used in the applications of means of transport and industrial machines is certainly among the most commonly adopted: they do not require external power systems and their operation is simply based on mechanical coupling with the host structure. As a result of advances in the electronics and materials field, a growing interest has arisen in the implementation of active or semi-active control systems: many studies have shown their real feasibility even with complex applications. The low cost of the actuators, often made of PZT (lead zirconate titanate) material, and the simple implementation in control circuits are certainly among the motivating factors in their use. Studies on the performance of piezoelectric materials as known are not so recent: their applications have been shown to be a viable concept for vibration reduction in many fields. Crawley and de Luis [1] proposed an analytical approach for a static case including several actuator geometries to be bonded on flexible substrates. A dynamic modeling technique for the vibration suppression of plate structures by using piezo patches is detailed in [2]. The first real applications in aerospace structures were made by [3,4]. Both numerical and test results showed the potentiality of such technology for controlling noise radiated by panels [5,6]. The performance evaluation, in terms of vibration and noise attenuation, of a framed panel comprising a single-input-single-output (SISO) control technique was discussed. In particular, a simple analogic control system that implements a positive position feedback control law with self-adaptive gain has been proposed and widely tested. From this perspective, a “collocated” SISO control system, where the sensor and the actuator are placed at the same location, can be a very advantageous solution: it does not require any particular signal elaboration (displacement or velocity feedback, easily achieved by hardware). Due to the piezoelectric effect, a percentage of the vibrational mechanical energy can be converted into electric energy and dissipated suitably by means of a shunt circuit that compounds a mechanism of passive damping. The shunt represents a special application of SISO-based control. Shunt circuits are mainly used to condition voltage signals, which, thanks to the piezoelectric properties, are representative of the dynamic deformation energy of the structure. Lesieutre discusses the four commonly used types of shunt circuits: resistive, resonant, capacitive, and switched [7]. Richard et al. [8] investigated the technique based on a synchronized switch for broadband vibration damping. An inductive element was used for inverting the voltage signal on a piezo transducer so as to counteract the external disturbance action. Guyomar et al. [9] addressed the study of a new technique, namely synchronized switch harvesting (SSH), for electrical energy generation by the structural vibration provided by piezoelectric actuators patches. CIRA (Italian Research Aerospace Centre) engaged a considerable interest in the development of control methodologies based on the aid of shunt circuits [10,11,12,13]. An energetic approach comprising both theoretical and simulation studies addressed the design of a first switching shunt control (SSC) architecture for the vibration control of a beam structure, [10]. An integrated design scheme for a SSC circuit, suitably combining properties from multi-degree-of-freedom (MDOF) structural FE models has been analysed in [11]. An in-house simulation code is described in [12] which, by implementing the Newmark–Beta integration method, solved in the time domain the coupled equations of dynamics (with and without control effect) with particular reference to beam systems. The study was also extended to 2D composite plates using a multi-channel system capable of controlling several pairs of piezoelectric actuator/sensor working independently as SISO systems, [13]. Attention was also paid to the conception of the individual electronic components in order to improve the performance of the control boards. Numerical and experimental studies have led to the design of a synthetic inductor also useful for multi-modal applications, [14], as well as the possibility of optimizing the number of components used in order to streamline the circuit assembly complexity, [15]. The effect of changing positions of piezo patches along the analyzed structure are discussed in [16]. The piezoelectric transducer shunted with a RL couple [17], or the electromagnetic transducer shunted with a RC couple [18] are the two-order circuit that can generate an electrical resonance. The work [19] provides the description of a first experimental circuit for the vibration control of a flat aluminium plate by a resonant piezoelectric shunt in a water environment. The main electrical components of the resonant shunt, i.e., inductance and resistor, have been designed relying on the resonance frequencies in open loop and closed loop conditions. Parametric FEM computations and periodical structure theory for geometric and electric parameter optimizations of a piezo control circuit have been carried out in [20]. This work provides an efficient but also general formulation for the prediction of dynamic behaviour of all kinds of elastic slender structures with shunted piezo patches. A novel concept of a nonlinear piezoelectric tuned vibration absorber (NPTVA) is introduced by the authors of [21]. They propose the design of a fully passive nonlinear inductor using the principle of magnetic saturation. The control performance with single or multiple inductors has been verified considering a beam with piezoelectric patches. The literary bibliography dealing with active and passive control methodologies is huge: some recent reviews have amply discussed the developments, especially regarding the applications of shunt piezoelectric systems. Yan et al. [22] summarize the control principles, including descriptive equations and circuit diagrams, while also pressing on the current challenges and prospects of this technology in vibration and noise control. Marakakis et al. [23] point out the optimization criteria of such systems by operating both on the design and positioning of the piezoelectric devices and on the enhancement of the system characteristics.

2.2. Research Objective

The authors of present paper already carried out experimental activities on the semi-active vibration control with reference to simple isotropic structures by using “collocated” piezo devices, [24]. The current study deals with the development of an integrated circuit for the vibration control implementation. A full in-house finite element procedure, according to a local equation describing the fully coupled system, has been implemented in a Simulink^® environment to assess the operating principle of a SISO shunted control law. Piezo strain actuation and sensing have been modelled with a well-established analytic approach using the “direct” and “inverse” effect. The authors propose a resolution method based on the state-space transformation which can lead to a considerable reduction of the computational cost with respect to other integration techniques. The authors would like to propose a design methodology that can be easily extended to structures even more complex than the one analysed: the first order model developed now in Simulink^® can work in real-time by extracting the characteristic matrices from any finite element solver solving the dynamic problem in spectral domain. The equations of structural mechanics are solved separately without considering the piezoelectric contribution. The electro-mechanical action of the piezoelectric is implemented only downstream and only at the nodes of interest. Relying upon the basic theoretical considerations, the authors therefore addressed some key insights for the development of an innovative hardware control platform. The study addressed the design of a novel circuit, based on a pulse train generator and solid-state devices: this has been realised to implement the synchronized SISO control. In this paper, an electronic board implementing complementary metal-oxide semiconductor (CMOS) pulse shaper has been proposed for the shunt switching purpose. CMOS operational amplifier is suitable for technology applications requiring low broadband noise and low supply current as well. Literature reference for this kind of integrated component, [25]. The overall system incorporates a MOS transistors bridge, an integrator, one small capacitor, and one resistor. At this point, the semi-active control is based on the impulsive excitation of a supplementary resonant RLC-series circuit suitable to control the synchronized charge of the piezoelectric actuator. In perspective of optimizing the dynamic performance of the circuit, an innovative feedback technique has been investigated by modulating the signal of resistor of the RLC control circuit unlike many applications where it is taken across the capacitance. The actual effectiveness was experienced using a real prototype. The control board operation was checked before without applying the signal amplifier: the performance of the piezo actuator alone has come to a reduction of up to 3 dB. By increasing the gain to 95% of amplifier power, the reduction reaches 12 dB, in line with numerical expectations. The board followed the design criteria for meeting the demands of low-power, small-size, and high-performance requirements. The development of a cheap and low weight electronic platform is the added value of the work. From such a perspective, there are not many bibliographical references on the application of such novel components for micro electro-mechanical systems (MEMS) application.

3. Physical Principle Overview

3.1. State-Space Representation of Structural Model

Modelling of a structure with attached piezoelectric actuators using FE approach can be performed like any conventional numerical formulation. Actually, the structural characteristics in the form of known matrices; mass and stiffness, have been extracted as DMIG (direct matrix input at a grid) from MSC Nastran^® (MSC Software, Newport Beach, CA, USA) analysis. In dynamic analysis, the main properties (i.e., mass, damping, and stiffness) may be provided, in part or entirely, as properties of FEM grid points through the use of these direct input matrices. Mathematical representation through structured matrices is the basis of reduction Guyan technique. This method allows for reducing huge number of degrees of freedom of dynamic models minimizing the loss of accuracy in the representation of inertial and elasticity distributions. The DMIG card accommodates entries by components of geometric grid points, scalar points, or extra points introduced for dynamic analysis. The proportional damping assumption (Basile model) has been implemented to transcribe the matrix of modal damping coefficients. In such a way, the matrices have been used to express the dynamic equilibrium of the excited system in the state-space domain. A first procedure for modelling structures containing piezoelectric actuators using MSC Nastran^® and Matlab^® was already developed by the NASA Research Center [26]. The paper describes the utility and functionality of one set of validated modelling tools. The innovative aspect of this approach is to separate the state space equation for structure’s behaviour description, from the piezo numerical model, despite solving the coupled problem. The simplicity of this approach ensures smaller and flexible codes, that can be adapted to different mock-up experiments reducing the computational complexity. It is possible solving a system of 6N-C differential equations, where N is the nodes’ number in which the structure has been discretized and C is the number of kinematic constraint in accordance with finite element (FE) model analysed. Considering that each node has 6 DOFs, 3 translational and 3 rotational, it is possible to reduce the number of equations just considering the most relevant displacement directions. This system can be written in compact form using the FE matrixes as follows Equation (1):

$$\left[M\right]\left\{\ddot{z}\left(t\right)\right\}+\left[D\right]\left\{\dot{z}\left(t\right)\right\}+\left[K\right]\left\{z\left(t\right)\right\}=\left\{F\left(t\right)\right\}$$

(1)

The relation Equation (1) represents the dynamic equilibrium for a linear non-conservative (with damping) system in the presence of time applied load F(t). It is univocally described by a finite set of physical coordinates. Globally, the system comprises n linear differential equations of the second order with constant coefficients. [M], [D], and [K] represent, respectively, the mass, damping, and stiffness matrix. The second degree ODE (ordinary differential equation) system could be reduced in the state-space domain: this arrangement allowed for solving just a first order system. The following feedback formulation was developed in [27] for a passive absorber problem and in [28] for piezoceramic actuators. Considering a new variable basis η_i, the physical coordinates representing the nodal displacement and velocity can be reported as Equations (2) and (3):

$$\left\{{\eta }_1\left(t\right)\right\}=\left\{z\left(t\right)\right\}$$

(2)

$$\left\{{\eta }_2\left(t\right)\right\}=\left\{\dot{z}\left(t\right)\right\}$$

(3)

The formulation of dynamic equilibrium in state-space domain is therefore given by Equations (4)–(6). The matrix M is by definition square and with a non-zero determinant so it can be inverted as indicated in Equation (4).

$$\left\{\begin{array}{l}\left\{\dot{{\eta }_1}\left(t\right)\right\}= \left\{{\eta }_2\left(t\right)\right\}\\ \left\{\dot{{\eta }_2}\left(t\right)\right\}= -{\left[M\right]}^{-1}\left[K\right]\left\{{\eta }_1\left(t\right)\right\} -{\left[M\right]}^{-1}\left[D\right]\left\{{\eta }_2\left(t\right)\right\}+ {\left[M\right]}^{-1}\left\{F\left(t\right)\right\}\end{array}\right.$$

(4)

$$\left[\begin{array}{c}\left\{\dot{{\eta }_1}\left(t\right)\right\}\\ \left\{\dot{{\eta }_2}\left(t\right)\right\}\end{array}\right]= \left[ \begin{array}{cc}O& I\\ -{\left[M\right]}^{-1}\left[K\right]& -{\left[M\right]}^{-1}\left[D\right]\end{array} \right]\left[\begin{array}{c}\left\{{\eta }_1\left(t\right)\right\}\\ \left\{{\eta }_2\left(t\right)\right\}\end{array}\right]+ \left[\begin{array}{c}O\\ {\left[M\right]}^{-1}\end{array}\right]\left\{F\left(t\right)\right\}$$

(5)

$$\left.\left\{\dot{\eta }\left(t\right)\right\}=\left[A\right] \left\{\eta \left(t\right)\right\}+\left[B\right] F(t\right)$$

(6)

where [A] is the state matrix Equation (7), [B] the input array Equation (8), and 󠄅{F} the external disturbance.

$$\left[A\right]= \left[ \begin{array}{cc}O& I\\ -{\left[M\right]}^{-1}\left[K\right]& -{\left[M\right]}^{-1}\left[D\right]\end{array} \right]$$

(7)

$$\left[B\right]= \left[\begin{array}{c}O\\ {\left[M\right]}^{-1}\end{array}\right]$$

(8)

In order to characterize the time-domain response of the state-space system, it is necessary to introduce the output equations as function of time, Equations (9) and (10):

$$\left[\begin{array}{c}{y}_1\left(t\right)\\ y_2\left(t\right)\end{array}\right]= \left[\begin{array}{cc}I& 0\\ 0& I\end{array}\right] \left[\begin{array}{c}{\eta }_1\left(t\right)\\ {\eta }_2\left(t\right)\end{array}\right]$$

(9)

$$\left\{y\left(t\right)\right\}=\left[C\right]\left\{\eta \left(t\right)\right\}$$

(10)

3.2. Piezo Actuator and Sensor Constitutive Models

The control with piezoelectric element is activated by system deformation that generate to an electric potential by the piezo direct effect of the sensor. Such voltage is expressible in relation to the displacement by the strain actuation theory. The main hypothesis of this theory in 1D structures are:

• perfect bonding of the actuators to the structural surfaces;
• linear strain along the thickness of the beam element;
• constant strain along the thickness of the piezo elements.

In 2D structures, another hypothesis is necessary:

• the Poisson’s moduli of the two materials (piezo and beam materials) are equal to 1/3.

Maybe add a very short explanation about what are the Poisson’s ratio. The first hypothesis is usually verified, since the thickness of the bonding layer is less than 0.1 mm. The second and third hypothesis are also verified when the ratio of the structure to piezoelectric thickness is large. The 2D hypothesis is usually verified in practical applications. In the hypothesis of 1D behaviour, the formula that regulates the output voltage V_out from a piezo sensor is Equation (11):

$$V_{out}=g_{31}{E}_{PZT}{t}_{PZT}{\epsilon }_{PZT}$$

(11)

where g₃₁ is the piezoelectric coefficient while E_PZT, t_PZT and ε_PZT are the elastic modulus, thickness and strain state of piezo. Further, if the strain field is bi-dimensional:

$$V_{out}= \frac{g_{31}{E}_{PZT}{t}_{PZT}{\epsilon }_g}{1-{\nu }_{PZT}}$$

(12)

where ε_g is the sum of the strains, developed along the two in-plane directions and ν_PZT the piezoelectric Poisson’s ratio. With reference to a plate having thickness t_b, it is possible to compute the strains in a simple way, starting from the transverse z-displacement, w(x,y) by the following relationship Equation (13), as per [5]:

$${\epsilon }_g=-\frac{t_b}{2}\left(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial y^2}\right)$$

(13)

that, expressed in finite differences, becomes:

$${\epsilon }_g=-\frac{t_b}{2}\left(\frac{w_{j+1}-2w_j+w_{j-1}}{\Delta x^2}+\frac{w-2w_j+w_{j-1}}{\Delta y^2}\right)$$

(14)

which is valid for a uniform discretization in x and y directions. The voltage previously calculated in (11) is proportional to the force transmission F_t from the actuator to the structure and can be expressed as:

$$F_t=\frac{\psi }{\psi +{\alpha }_{PZT}}{E}_{PZT}{b}_{PZT}{d}_{31}{V}_{out}$$

(15)

where α_PZT is a coefficient whose value is about 6 for bending excitation (2 in case of extensional excitation but not used in this application), ψ is the ratio between the beam and piezoelectric Young modulus and b_PZT indicated the piezo width (in-plane dimension), [1,29,30]. This equation is valid for a 1D case, and instead, in a 2D case, Equation (15) becomes:

$$F_t=\frac{3}{2}\frac{\left.\psi (\psi +4\right)}{\left(\psi +2)(\psi +6\right)}{E}_{PZT}{b}_{PZT}{d}_{31}{V}_{out}$$

(16)

More details of the modelling aspects of piezoelectric actuators and sensors may be found in references [1,5,31].

3.3. RLC Control Circuit

The semi-active control here discussed is based on the impulsive excitation of an auxiliary resonant RLC-series circuit: the conceptual architecture comprises additionally a switch component able to control the synchronized closing of this circuit and then the timed charge of the active piezoelectric actuator. Since the internal inductance and resistance of the piezo-actuator material could be considered negligible in comparison to the shunt circuit, the active properties can also be modelled by just a capacitance C_PZT (relative to PZT patch), as shown in Figure 1. Assuming that the supplementary RLC circuit in the Figure 1 is powered by an external voltage source (representative of the external disturbance), the main purpose is to optimize the time response when the circuit switch is closed so as to supply the maximum energy to the piezo actuator. In the assumption of a “collocated” arrangement of piezo pair actuator/sensor, this signal is nothing other than the feedback action for balancing the disturbance signal introduced by the vibration (i.e., acquired by the piezo sensor). Generally, the feedback control signal was taken across the capacitance C of the shunt circuit. The authors investigated that the same signal (for piezo-actuator) could be maximized if detected across the shunt resistor R. Actually, adjusting this shunt resistance R up to an optimal value, a pulse of minimum duration and without further oscillations could be achieved, representing basically the critical damping condition of RLC resonant circuit. Thus, it is interesting to analyze the RLC scheme in Figure 1 in order to determine its transient characteristics once the switch is closed.

The equation that describes the response of the system is obtained by applying Kirchhoff Voltage Law (KVL) around the mesh as per (17):

$$v_R+v_L+v_C=v_s$$

(17)

The current flowing in the circuit is given by (18):

$$i=C\frac{d{v}_C}{dt}$$

(18)

While the voltages in the resistance and inductance are:

$$v_R=Ri=RC\frac{d{v}_C}{dt}$$

(19)

$$v_L=L\frac{di}{dt}=LC\frac{d^2{v}_C}{d{t}^2}$$

(20)

Substituting Equations (19) and (20) into Equation (17), the dynamic equilibrium is obtained:

$$\frac{d^2{v}_C}{d{t}^2}+\frac{R}{L}\frac{d{v}_C}{dt}+\frac{1}{LC}{v}_C=\frac{1}{LC}{v}_s$$

(21)

Assuming a solution having a form Ae^st and by substituting into Equation (21) in its homogenous form, the characteristic Equation (21) in Laplace domain can be solved:

$$s^2+\frac{R}{L}s+\frac{1}{LC}=0$$

(22)

or also expressible as:

$$s^2+2{\alpha }_{shunt}s+{\omega }_{shunt}^2=0$$

(23)

by defining two performance parameters:

$${\alpha }_{shunt}=\frac{R}{2L}$$

(24)

$${\omega }_{shunt}=\frac{1}{T_{shunt}}=\frac{1}{\sqrt{LC}}$$

(25)

The roots of the characteristic Equation (21) are:

$$s_1=-{\alpha }_{shunt}+\sqrt{{\alpha }_{shunt}{}^2-{\omega }_{shunt}{}^2}$$

(26)

$$s_2=-{\alpha }_{shunt}-\sqrt{{\alpha }_{shunt}{}^2-{\omega }_{shunt}{}^2}$$

(27)

The value of the term: $\sqrt{{\alpha }_{shunt}{}^2-{\omega }_{shunt}{}^2}$ determines the behavior of the response. Three types of responses are possible:

• α_shunt = ω_shunt then s₁ and s₂ are equal and real numbers: no oscillatory behavior (i.e., critically damped system);
• α_shunt > ω_shunt. Here s₁ and s₂ are real numbers but are unequal: no oscillatory behavior (over damped system);
• α_shunt < ω_shunt. In this case, the roots s₁ and s₂ are complex:

$$s_1=-{\alpha }_{shunt}+j\sqrt{{\omega }_{shunt}{}^2-{\alpha }_{shunt}{}^2}$$

(28)

$$s_2=-{\alpha }_{shunt}-j\sqrt{{\omega }_{shunt}{}^2-{\alpha }_{shunt}{}^2}$$

(29)

And the system exhibits oscillatory behavior (i.e., under damped system).

In particular, as the resistance R increases the value of α_shunt, namely damping factor, increases and the system is driven towards an over damped response, as per Figure 2. In resonance condition, i.e., when the natural frequency of the circuit is very close to the voltage source one, the circuit could absorb the maximum amount of energy from the external voltage source itself. The resistance R plays a key role on the resonance amplitude of the circuit: a too small a value would lead to an unstable response of the system while an excessively large value would reduce the reactivity of the circuit. In the current application, the voltage drop of the resistor should be as much as possible of a purely impulsive nature with low oscillations and therefore used for powering the piezo actuator in order to have an instantaneous response against the external vibration. The switch is kept closed until the voltage on the piezoelectric element has been inversed: it happens approximately to a time T_shunt equal to a half pseudoperiod of the electric shunt circuit. The pseudopulsation of the electrical switching ω_shunt is simply related to capacity C and inductance L through the Equation (25). The relationship between piezo voltage and mechanical vibration waveforms is strictly proportional, as indicated by Equation (11), when the switch is open and no electrical load is connected to it as well. Nominally, the switch is always in open status, except once a dynamic disturbance occurs where a voltage inversion is observable, as in Figure 3.

The main objective of the control system will be to define a transient law in order to excite the RLC oscillator by maximizing the electrical energy input to the piezo-actuator. The only force that can satisfy these energy requirements is of an impulsive nature. In this regard, an additional circuit architecture is considered where the power source, originally sinusoidal, is such as to provide an impulse signal. Let’s examine the response of the circuit shown in Figure 1 where the form of the source voltage vs. is impulsive. The time response in (21) can be written in terms of complex transfer function:

$$H\left(s\right)=\frac{v_C}{v_s}=\frac{1}{LC{s}^2+RCs+1}$$

(30)

$$H\left(s\right)=\frac{{\omega }_{shunt}^2}{s^2+2{\alpha }_{shunt}s+{\omega }_{shunt}^2}$$

(31)

To obtain the impulse response, the transfer function is further extended to:

$$H\left(s\right)=\frac{{\omega }_{shunt}^2}{\left(s+{\alpha }_{shunt}+j{\omega }_d\right)\left(s+{\alpha }_{shunt}-j{\omega }_d\right)}=\left({\omega }_d+\frac{{\alpha }^2}{{\omega }_d}\right)\left(\frac{{\omega }_d}{{(s+{\alpha }_{shunt})}^2+{\omega }_d^2}\right)$$

(32)

where:

$${\omega }_d=\sqrt{{\omega }_{shunt}^2-{\alpha }_{shunt}{}^2}$$

(33)

represents the damped frequency. Taking the inverse Laplace transform, the time impulse response is:

$$h\left(t\right)=\left({\omega }_d+\frac{{\alpha }^2}{{\omega }_d}\right)e^{-\alpha t}sin\left({\omega }_{d}t\right)$$

(34)

If an input consists of a pulse that is sufficiently short in duration, the continuous-time system will respond the same as it would to an impulse with the same area. Since the response is the same, the objective will be to replace an approximate signal consisting of an impulses train, if h is adequately small. Based on these considerations, the damping mechanism can be explained by electro-mechanical analogy: the RLC circuit response could be compared de facto to the typical behaviour of a mechanical tuned absorber. As vibrations occur and the strain deformation reaches its maximum value, the switch turns on (closed state) for a fraction of the excitation period. The piezo actuator receives as input a voltage signal from the sensor; the voltage is generated from the structural vibration which will deform the piezo that will convert mechanical energy of the structure into electrical energy (“direct” piezoelectric effect). Instantly, the circuit filters and amplifies this input signal, sending it to the piezo actuator which reacts to the vibrations (“converse” effect). By tuning the resonance frequency f_shunt of this circuit to the open-circuit resonance frequency of the structure equipped with a piezo transducer, a vibration reduction next to the resonant peak of interest could be achieved. The dissipation is based on the conversion of part of the mechanical energy to electrical energy by means of the resistive component R of the circuit. Anyway, an optimal range should be defined to optimize synchronized switching performance: a lower and upper limit with respect the structural resonance frequency (f_str) should be guaranteed. A thumb-rule is reported in relationship (35):

$$10f_{str}\le f_{shunt}\le 50f_{str}$$

(35)

where:

$$f_{shunt}=\frac{{\omega }_{shunt}}{2\pi }$$

(36)

Such best practise is used to set the values of these spectral limits: for the lower limit, a target of maximum 10 times the highest structural resonance frequency is choosen for the RLC frequency. More arbitrary is used to be the setting of upper threshold, generally imposed equal to about 50 times the structural frequency so to avoid any spillover effect could inhibit the performance of the circuit itself. In the present case, starting from a given piezo capacitance, the values of R and L have been extrapolated to maximize the circuit impedance enclosed in a certain spectral range. These rules allow in principle to choose starting values for the application of the control. Theoretically, the inductance values in line with the resonance frequencies can also reach impractical values (100 H). This occurs above all at low vibration frequencies: large wavelengths require high masses (i.e., inductances) to be cut down.

4. Case Study: Cantilever Beam

4.1. FE Model Order Reduction

The benchmark chosen as test article for this study is an aluminum beam with thickness of 2 mm, and total dimensions of 250 × 30 mm. The beam is clamped on one edge and free on the other one. A simple FE model representing these characteristics (geometric data, mechanical properties, boundary conditions) has been built up: the main FEM properties are listed in the

Table 1. FEM mean Features.

Element Type	CQUAD
Number of nodes	18
Number of elements	8
Constrained nodes	2 (dof: 1,2,3,4,5,6)
Total dofs	108

while the first two natural frequencies descending from modal analysis in

Table 2. Beam natural frequencies (FEA results).

ID Mode	Natural Frequency, f [Hz]
I	32.90
II	105.28

. Figure 4 represents the first two normal modes of the structure analysed: in this context a simple model has been used just to investigate the applicability of the control strategy. Using MSC Nastran^®, it is possible to derive a reduced model in terms of constitutive matrixes: mass and stiffness. The mass and stiffness matrixes are calculated as DMIGs [32], while the damping matrix is obtained by linear combination of M (mass matrix) and K (stiffness matrix) multiplied by the structural damping factor (Basile assumption). Such model synthesis allowed for implementing the structural characteristics in another programming environment.

4.2. Basic Principle Assessment

For the realization of the SISO-control numerical model is necessary to import in the Matlab^® environment the matrices of mass and stiffness, previously calculated, which are characterized by the following dimensions: [M] = [108 × 108] and [K] = [108 × 108]. The damping matrix can be formulated as a linear combination of M and K as per (37):

$$\left[D\right]=\left[M\right]+\mathsf{\zeta }\left[K\right]$$

(37)

where ζ (assumed equal to 0.01) is the structural damping coefficient. At the end, three matrixes having the same size [108 × 108] in agreement with the 6 DOFs of each node have been imported within Matlab^®. These matrixes have been initially calculated for a free-free structure beam but in this simulation it is required to modify them for a cantilever condition: the DOFs of the nodes 17 and 18 (supposed overlap with the clamp, see Figure 5) have therefore been deleted, leading to the “constrained” form of constitutive matrices. Obviously, the matrixes dimensions are changed, and in fact 12 rows and 12 columns have been eliminated, obtaining: [M] = [96 × 96], [K] = [96 × 96] and [D] = [96 × 96]. With a Matlab^® function that solves the eigenvalues problem, the natural frequencies of the reduced DMIG-based system have been calculated: such results should be for a matter of fact coherent with the MSC Nastran^® normal modes analysis (reported above in Table 2). The results representative of the synthetized model are outlined in

Table 3. Beam natural frequencies (reduced model results).

ID Mode	Natural Frequency, f [Hz]
I	32.92
II	105.30
III	220.09

.

According to Equations (5) and (6), the state space based model has been therefore built up: in Simulink^®, it has been possible to simulate the piezo-actuator action, comparing the vertical displacements of the system in control OFF and control ON condition. On the beam two rectangular-shaped piezoelectric components are supposed to be installed by “collocated” configuration: one on the upper side of the beam used as sensor, the other one sited on the opposite side in the same position of the piezo sensor. This piezo element will be used as actuator. The two piezoelectric patches are positioned at the root of the clamped beam because, here, the maximum strain for the flexural modes of interest is expected (as represented in Figure 5). The action of piezo couple has been discretized on four nodes of the whole grid. The numeration used for the analysis is with the nodes 17 and 18 overlap with the clamp (Figure 5). The following tables (

Table 4. Beam mechanical properties (Al 7075 T6).

In-Plane Dimensions (mm)	250 × 30
Total thickness (mm)	2
Young modulus E (GPa)	72
Poisson’s ratio	0.33
Density (kg/m3)	2700
Structural damping, ς	0.01

,

Table 5. PZT mechanical properties.

PZT Model	PPK-11
N° of PZT	1
In-plane dimension (aPZT x bPZT) (mm)	30 × 25
Thickness (mm)	0.5
Young modulus (GPa)	62
Poisson ratio	0.33
Density (kg/m3)	8000

and

Table 6. PZT electro-mechanical properties.

Property	Value
PZT Coefficient g31 (V/m)	−8.0 × 10−3
PZT coefficient d31 (m/V)	−350 × 10−12
PZT coefficient d33 (m/V)	680 × 10−12
Relative dielectric constant	5000

) summarize the main mechanical and electrical properties of the beam and piezo elements.

The cyclic flow is described in few key-steps. A swept-sine signal source that causes beam’s vibrations has been considered to excite the interest spectral bandwidth [0, 100 Hz] (Figure 6). The state-space logical block gives as output 16 displacements and 16 velocities. The output is controlled by the matrix [C] in Equation (33). The output of the derivative block is the strain where the piezo-sensor is located. Such a value is passed to the piezo-sensor logical block, to calculate the equivalent voltage by Equation (12) (“direct” effect). The output signal is then sent to the RLC control circuit, implemented with a transfer function and a gain that simulate circuit’s impedance; the signal becomes the voltage field input of piezo-actuator block where the force transmitted by piezo -actuator to structure is calculated with Equation (16) (“inverse” effect). The force is then sent in feed-back to the external noise and summed with it: the output force level should normally be multiplied by the gain factor of the piezo amplifier. Initially, this gain is considered unitary. In this way, the effective force is decreased and used as new input to the state-space block.

The run simulations have been performed just for two values of inductance L, as detailed in

Table 7. SISO simulative gains: open loop (OL) and closed loop (CL).

Grid Point	Inductance L (H)	Output (dB)—OL	Output (dB)—CL
piezo node	10−3	70.1	69.1
	4.8	70.1	66.8
tip node	10−3	76.5	75.2
	4.8	76.5	72.8

. The performance results have been compared in Figure 7 and Figure 8, in particular calculating both the root and tip modal displacement. The outcomes are reported in time domain and as FFT as well for the evaluation of the methodology.

The simulations although preliminary allowed for well characterize the dynamic behaviour of the whole control system. In the spectral region below the resonance frequency, the response is influenced by the structural stiffness: the induced expansion/contraction of piezo-actuator makes the beam more rigid and so with less deflection. The damping effect is dominant close to the resonance region: the maximum power transfer occurs when the load resistance is matched to the impedance of the piezoelectric device (impedance mismatch condition). At higher frequencies, the response trend depends mainly on the inertial distribution. As expected, the vibration reduction increases as the inductance grows (electro-mechanical similitude): the decreased vibration energy flows towards higher frequencies but at the same time the secondary resonance frequencies tend to shift to lower values. For this reason, a remarkable change of transfer function trend of L₂-configuration after 60 Hz is observable in Figure 8. The second mode shape originally at about 105 Hz becomes next to 80 Hz. Therefore, the optimal choice of the inductance value is crucial for the dynamic stability of the structure: if on the one hand a good reduction of the vibration is appreciated, on the other side secondary modal shapes may appear close in bandwidth. Finally, a dynamic gain up to 3 dB has been estimated at this stage, assuming a unitary value of the amplifying factor. These results which represent the minimum performance of the closed circuit condition are summarized in Table 7. After this investigation, a sensitivity analysis was performed by changing the amplification parameter: as expected, the dynamic gain of the control increases as the piezo-actuator provides more energy. However, a maximum optimal threshold is reached beyond which the control action becomes disadvantageous when the value of force generated exceeds that of the external excitation (see Figure 9).

5. Hardware Development

The numerical simulations allowed for characterizing the behaviour of a “collocated” architecture of a piezoelectrics pair. The research has evolved into an experimental direction aimed at validating the goodness but also the limits of the design criteria. In this paragraph, the following aspects will be described in detail:

• architecture of SISO Switch circuit and “dry test” of the circuit;
• dynamic test on a benchmark to verify the vibration reduction performance.

5.1. Control System Implementation

The control system uses basically the signals from a piezo sensor and the gain variation amplifier, driving thus a collocated piezo actuator to counteract the vibration disturbance. The circuit operating principle is based on a logical sequence of electronic functions whose final purpose is to trigger a switch suitably synchronized with the maximum disturbance value. With reference to the Figure 10, which represents the circuit schematic, the main functioning steps are detailed below.

• The vibration produces the deformation of the piezo pair (sensor and actuator) bonded on the structure. The piezo sensor strain is so converted into a voltage signal through the direct piezo constant g₁₃.
• Such an initial voltage signal (pilot signal) from the piezo sensor is offset by 90-degrees by means of an electronic integrator.
• The shift signal activates a tachometer which generates a pulse train signal. A zero-crossing solid component controls the pulse period: a pulse is produced once the phase shift wave goes to zero (zero-crossing function) and therefore at maximum of pilot signal as well.
• The generated logic pulse train activates an operational amplifier (MOSFET, CMOS) switch whose output is OFF/ON state. In such a way, the switch state is approximately synchronized on the maximum vibration value. In order to amplify the input pulse peak, the CMOS device is additionally powered from a single supply voltage unit.
• The switch allows for supplying an auxiliary RLC circuit consistently with the pulse frequency. The RLC circuit should work in critical damping condition: the electrical parameters have to optimized in order to maximize the voltage on resistor without uncontrolled oscillations. The resistance value is regulated up to get a very sharp impulse with minimum surrounding fluctuations. Consequently, the drop voltage on the resistor will be the input signal for the piezo actuator which, converted in a mechanical action (converse effect, d₃₁), will react to the external vibration source.

A preliminary prototype (Figure 11) of the control circuit was made at vibro-acoustic and smart structures laboratory of the University of Naples “Federico II”. Several functional tests have been carried out to investigate the performance of the whole device. That is unless the surrounding noise of the signals, especially in the action of the zero-crossing circuit, could be improved with a future improvement of the device, per Figure 12. The data were collected and processed using an ONO-SOKKY spectrum analyser.

5.2. Experimental Results

Test on Cantilever Beam

Once the logical functions were verified, a simple dynamic test was carried out on an instrumented metallic bar. Both time histories and spectra have been analysed in order to characterize the effect of the control on the disturbance. The structure was excited by a piezoelectric ceramic patch bonded on its upper surface, driven by a 200 mV (peak-to-peak) sweep signal. A preliminary dry run is carried out to find the optimal voltage level of excitation: low voltage levels are preferable as an excessively amplified signal could introduce background noise components such as to affect the measurement. An electro-mechanical excitation, i.e., a shaker, has therefore been applied in order to insert a greater energy level into the system. Due to the cantilever arrangement, the maximum deformation is expected near the constraint. Such a primary source of disturbance is driven by an appropriate impedance matching circuit and voltage transformers. The ONO-SOKKY spectrum analyzer that can provide swept-sine, chirp, and random excitation was used as source control. Vertical point response (acceleration, velocity, and displacement) has been detected through a laser vibrometer with respect to the free-tip of the beam. The transfer function has been therefore assessed with respect the load cell signal. A schematic for the test-set up in the following testing activities is presented in Figure 13. A non-contact measurement technique allowed for not affecting mass distribution and therefore the modal characteristics of bar. According to the numerical model evaluation, the experimental investigation was carried out by choosing two inductance value (0.001 H and 5 H) and assuming an unitary amplification factor. In order to assess the capabilities of the control system, the frequency response function representative of the free-end vibration has been recorded in both on and off control conditions. Measurements without considering any additional amplification effect have shown a vibration reduction of the order of 3 dB, emitted by the bar when excited by a swept-sine excitation, Figure 14a. The experimental evidence has demonstrated the same trend already assessed by means of theoretical models: the closed-loop activation influences the dynamic behaviour of the system even outside the controlled frequency. The inductance like an inertial element generate a shift of the secondary natural frequencies and for this reason an inversion of the amplitude curves can be observed after about 60 Hz. However, the controlled frequency remains almost the same: in resonance conditions, the more noticeable effect is introduced just by the modal damping. At the lower frequencies, the system exhibits a large stiffness thanks to the action of a piezo-actuator which leads to counteracting the vibration. The main purpose is just to verify the functioning of the control platform: performance improvement, indirect spillover analysis, component optimization will be the subject of future analysis. The control board operation has been checked before without applying the signal amplifier: by increasing the gain to 95% of amplifier power (Figure 14b), the reduction reaches 12 dB, in line with numerical expectations.

6. Conclusions

The present work presented an innovative technique for active vibration control using a SISO “collocated” strategy. Using the capabilities of a standard FEM code, the possibility of numerically simulating the dynamic behavior of the structure together with a control law has been demonstrated, assuming that a proper model of the piezo-sensor and piezo-actuator was defined. A multi-dofs fully coupled system has been designed applying a finite element formulation. A full numerical procedure, according to characteristics equations describing the fully coupled system has been then realized in a Simulink^® environment. The structural matrices, i.e., DMIG, have been extracted from Nastran^® and separately reassembled considering also the electro-mechanical coupling terms to be added: in particular, 2D piezo strain actuation theory has been modelled with reference to a simple system. The effects exerted by piezo on the structure have been applied as actuation forces at the piezo nodes interface (converse piezoelectric effect). Similarly, the sensing has been modelled with a 2D piezoelectric constitutive equation based on voltage rates (direct piezoelectric effect). As core of the research, a cheap circuit, based on a tachometer and CMOS devices has been realised to implement the synchronized shunt control. The tachometer device can produce a pulse train signal triggering the CMOS flawlessly synchronized with the zero-crossing of the input. This model could be used as design and optimization tool to determine, for example, the number and the positions of the piezoelectrics in order to attenuate the vibration levels at specific frequency ranges. Average vibration reductions of about 3 dB have been assessed without the additional effect of an amplification factor: a sensitivity analysis allowed to forecast a dynamic gain of up to 10 dB. A conceptual hardware board has been realized, experimentally demonstrating the methodology for an aluminium beam. In more detail, the piezo-actuator has been controlled by an external RLC-based circuit. Sensible vibration reduction up to 3 dB without significant evidence of any loss of stability has been assessed with respect to the first mode shape. The control board operation was checked before without applying the signal amplifier: the performance of the piezo-actuator alone has come to a reduction of up to 3 dB. By increasing the gain to 95% of amplifier power, the reduction reaches 12 dB, in line with numerical expectations. The control system presented here was tested as a preliminary prototype for future research activities. The main objective was just to validate the feasibility system: the vibrations damping gained here is actually the result of a single piezo device, without power amplification for its actuation. This strongly encourages testing systems with multiple active elements. These capabilities may be applied to explore the opportunity to design and optimize the number and position of the piezo in order to attenuate the vibro-acoustic levels at particular mode shapes. Moreover, current activities are addressed to assess the sound proofing capabilities of the switching shunt device.