On the Effect of Block Roughness in Ogee Spillways with Flip Buckets
Abstract
1. Introduction
2. Methods
2.1. Energy-Dissipation Analysis
2.2. Multiphase (Water/Air) Hydraulic Model
3. Experimental and Numerical Test Cases
3.1. Experiment Facilities
3.2. Numerical Domain
- inlet boundary condition was set as discharge flow rate (Q);
- outflow (O) boundary condition was used downstream (at a sufficiently far location to prevent boundary effects on the results);
- the bottom and side boundaries were treated as a rigid wall (W), and no-slip conditions were applied at the wall boundaries;
- an atmospheric boundary condition was set to the upper boundary of the channel, which allowed for the flow to enter and leave the domain; and
- symmetry boundary condition (S) was also used at the inner boundaries.
4. Results
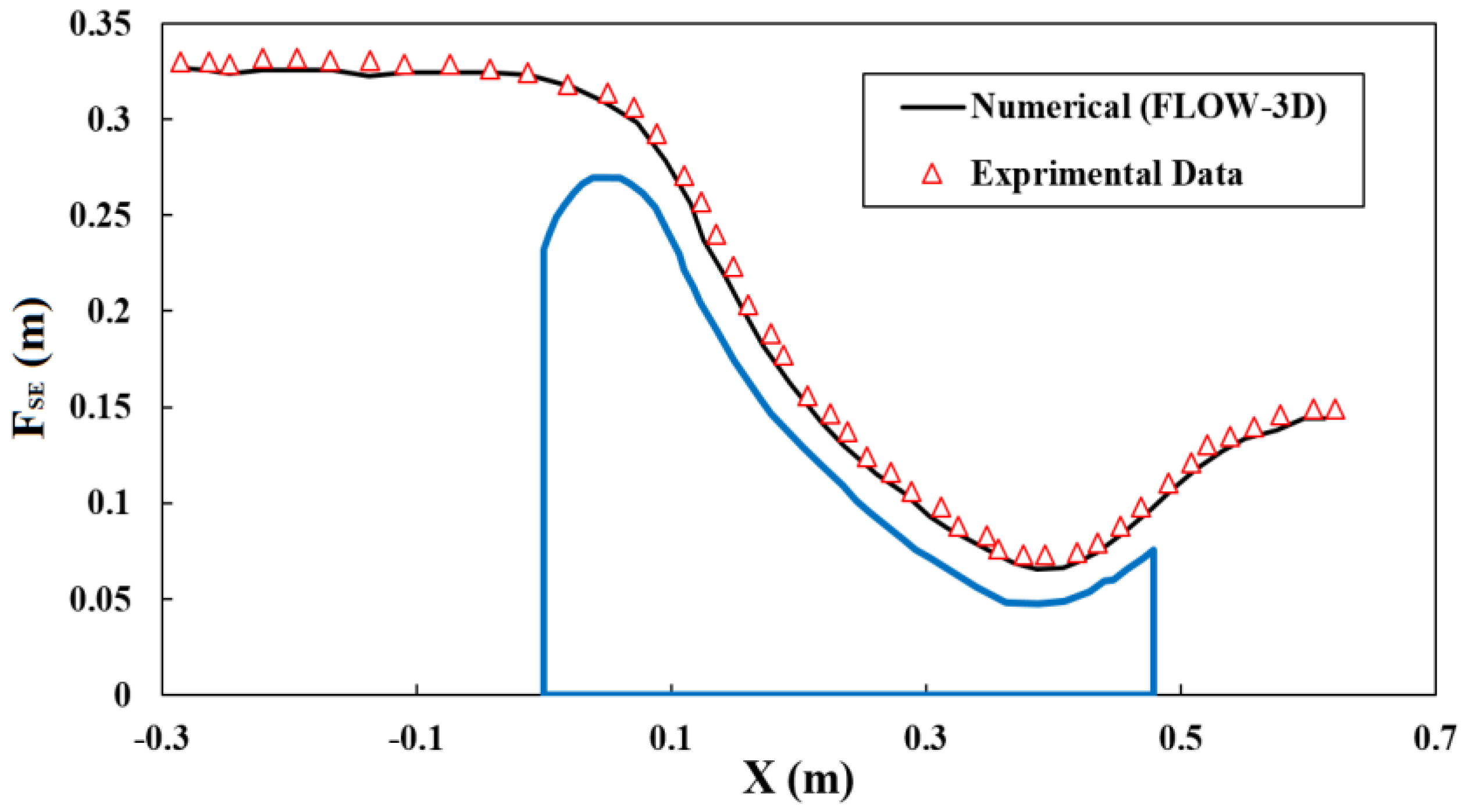
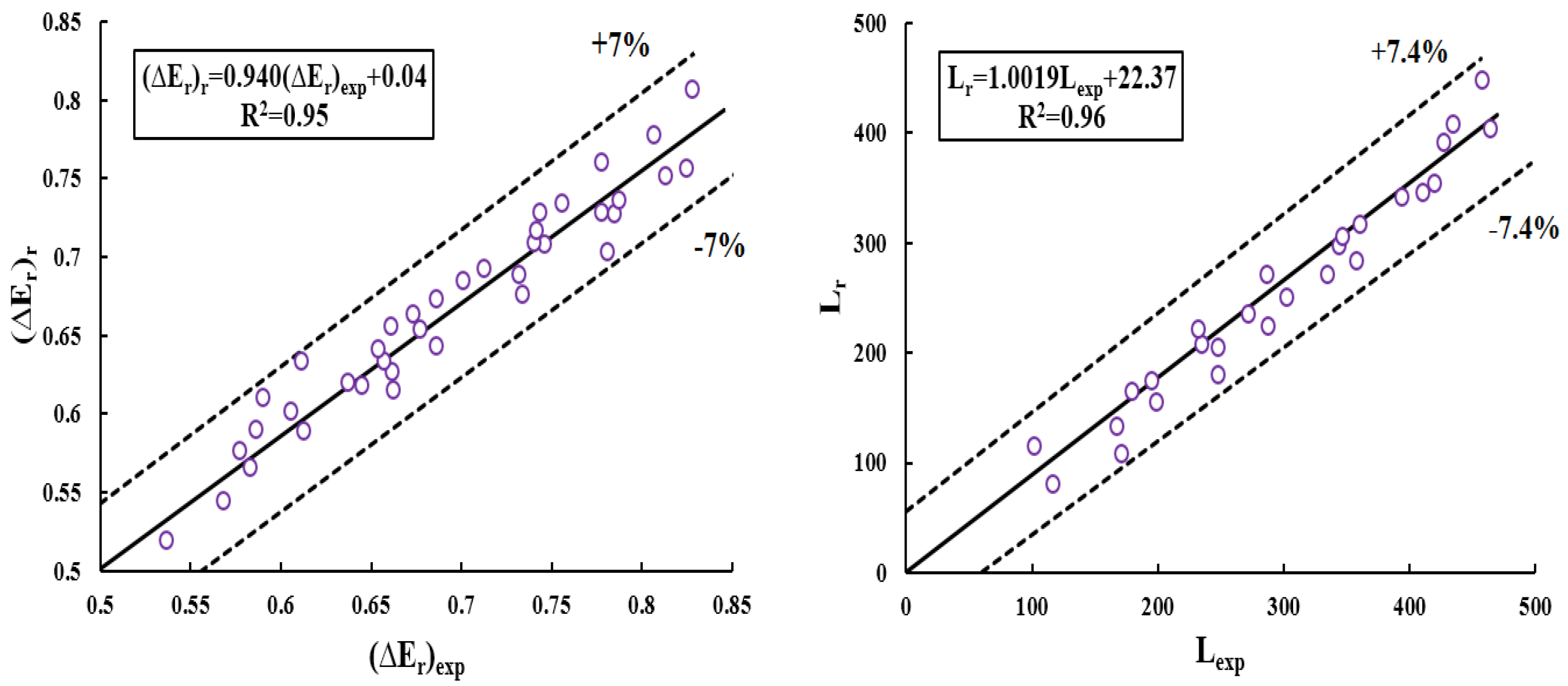
4.1. Verification of Numerical Model and Laboratory Results
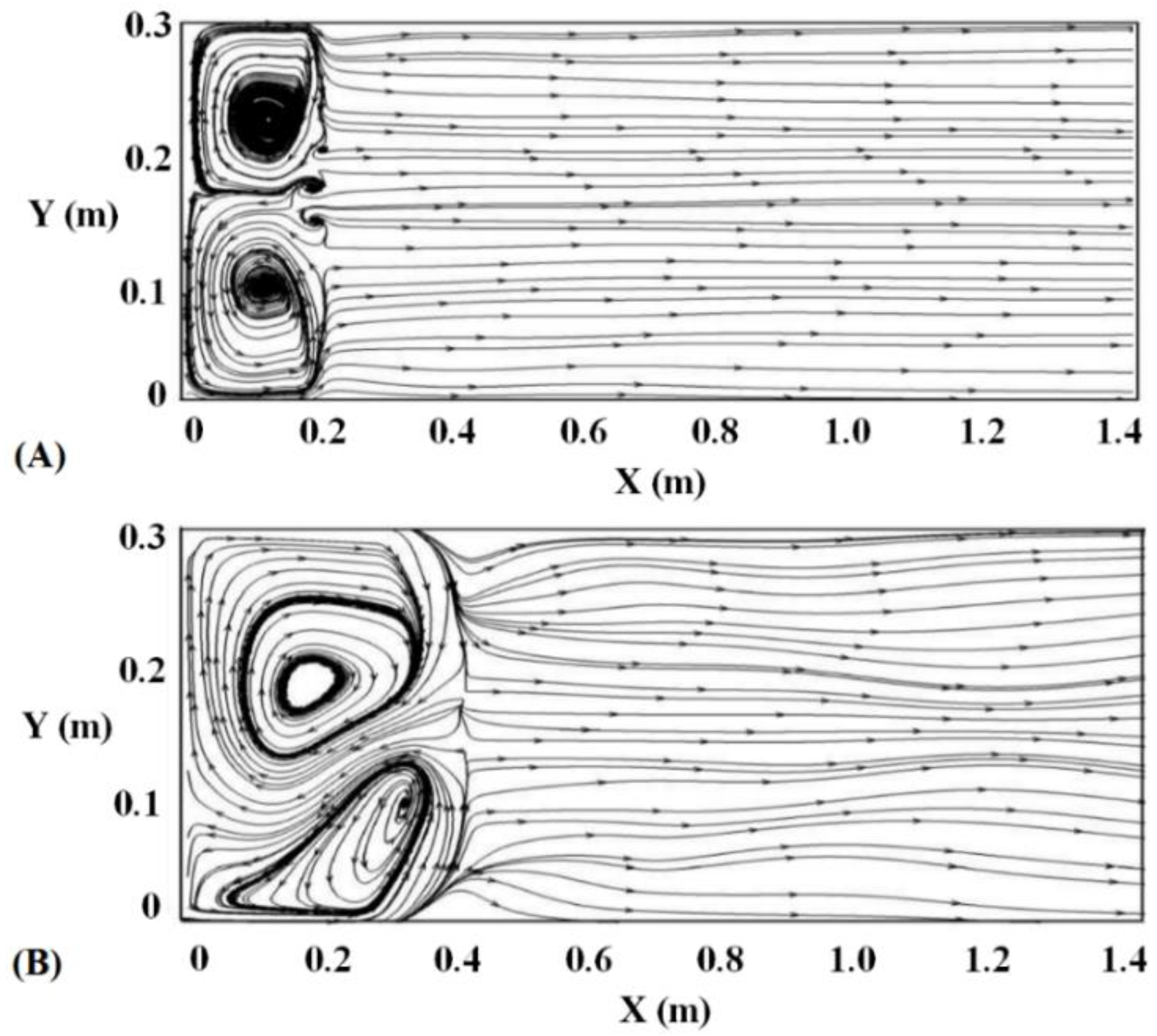
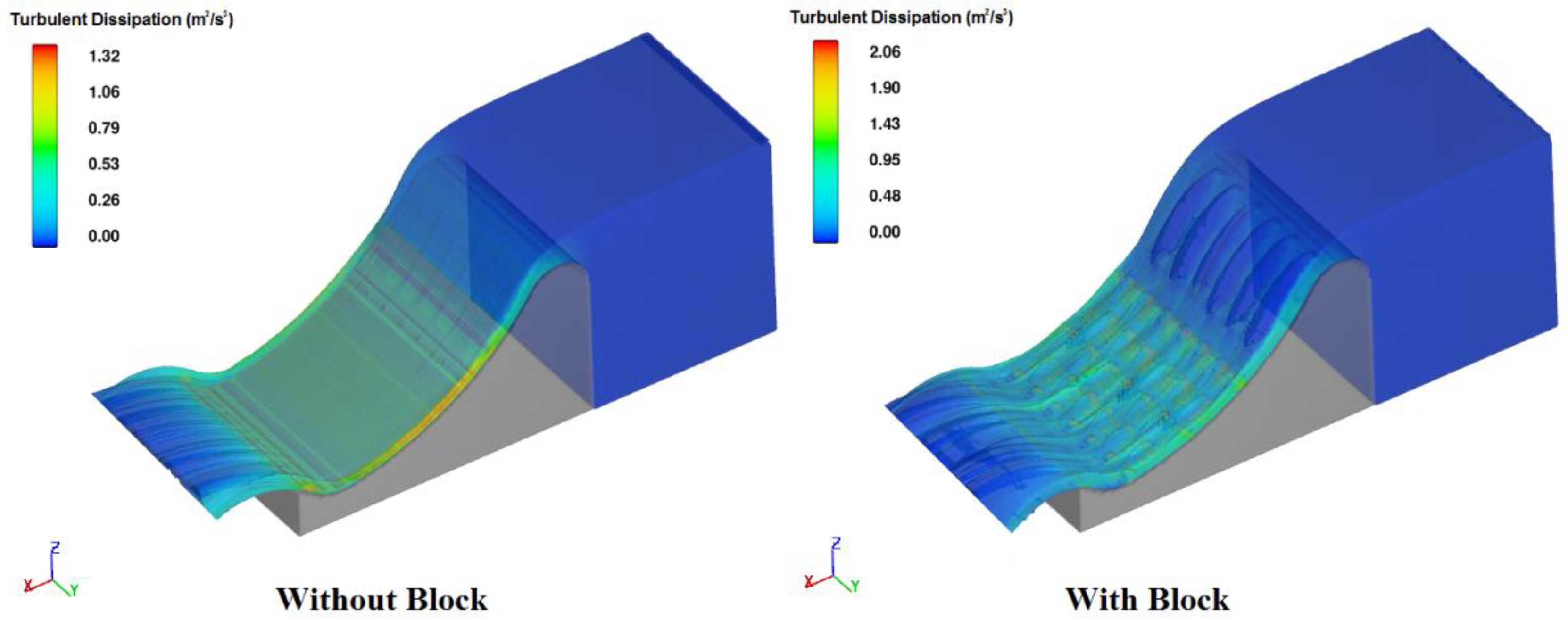
4.2. Flow Pattern Downstream of Ogee Spillway with Block Bed and Different Buckets
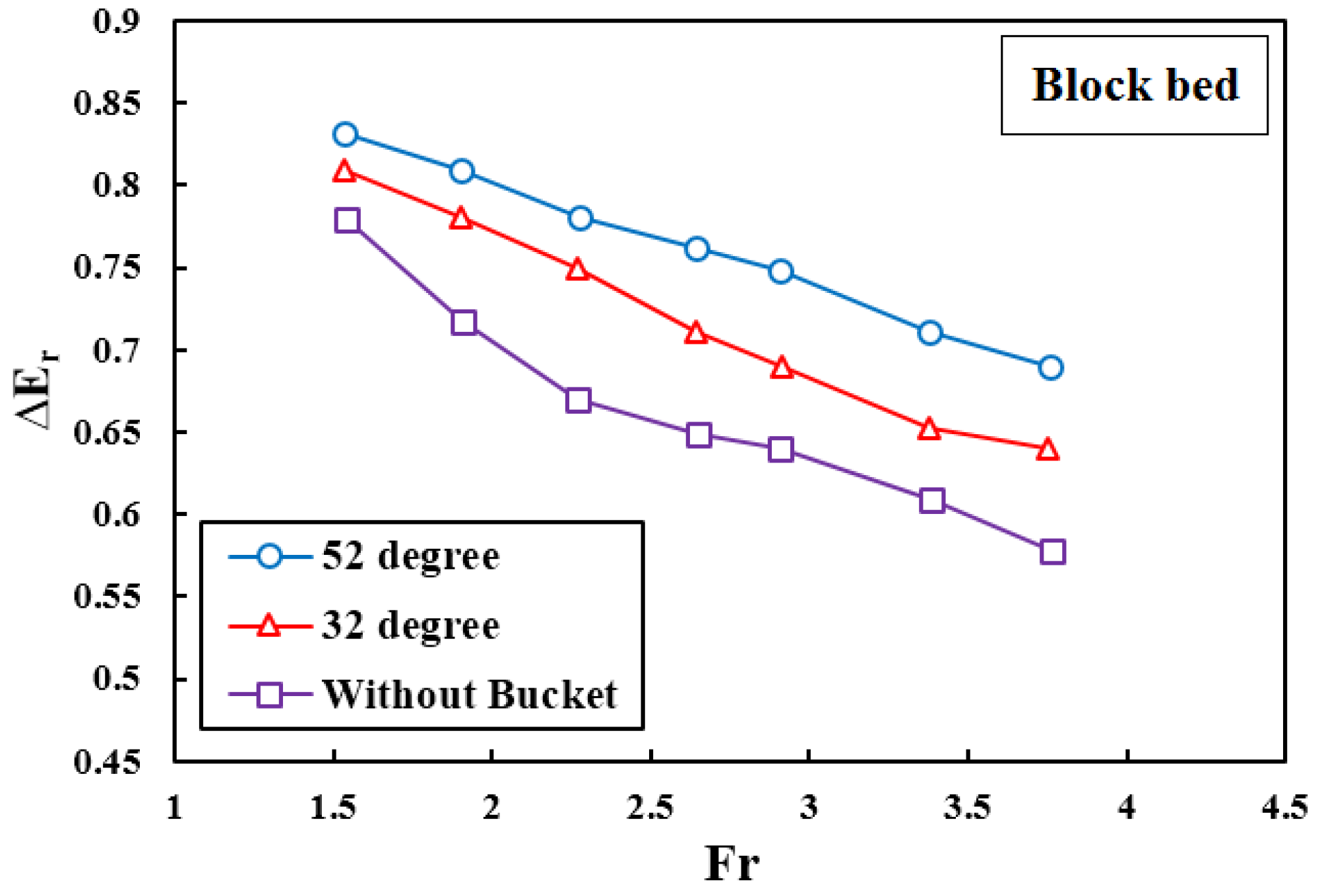
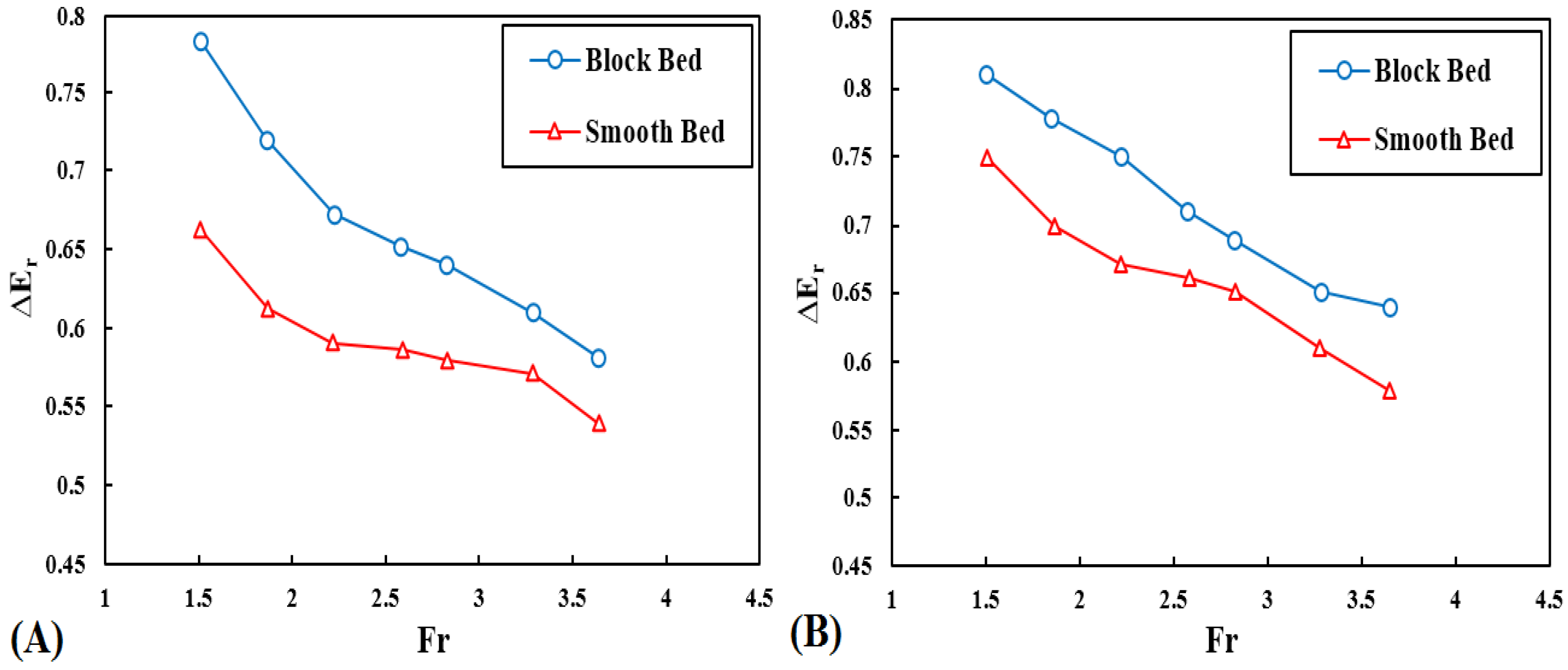
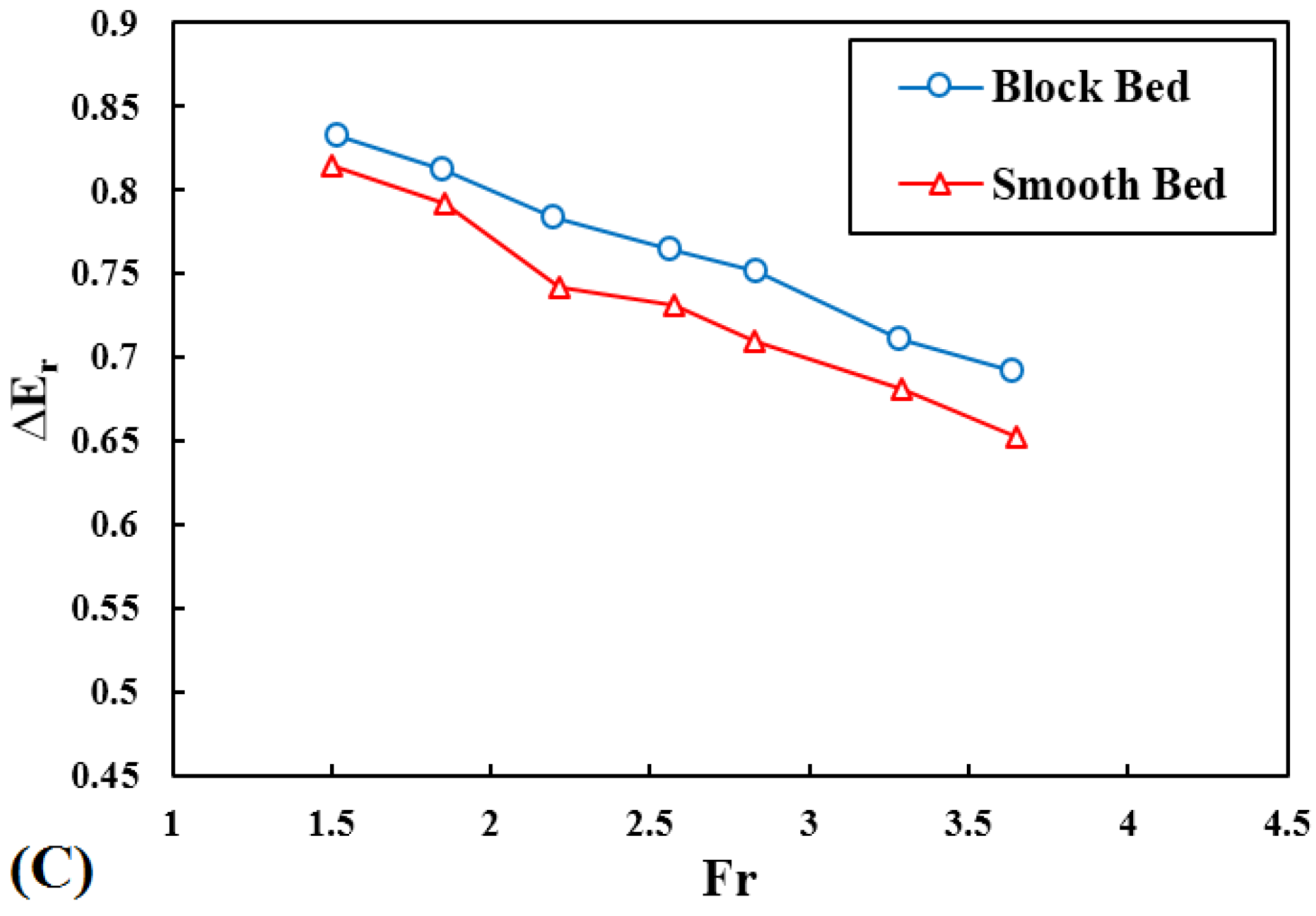
4.3. Energy Dissipation in Ogee Spillway with Block Bed and Different Buckets
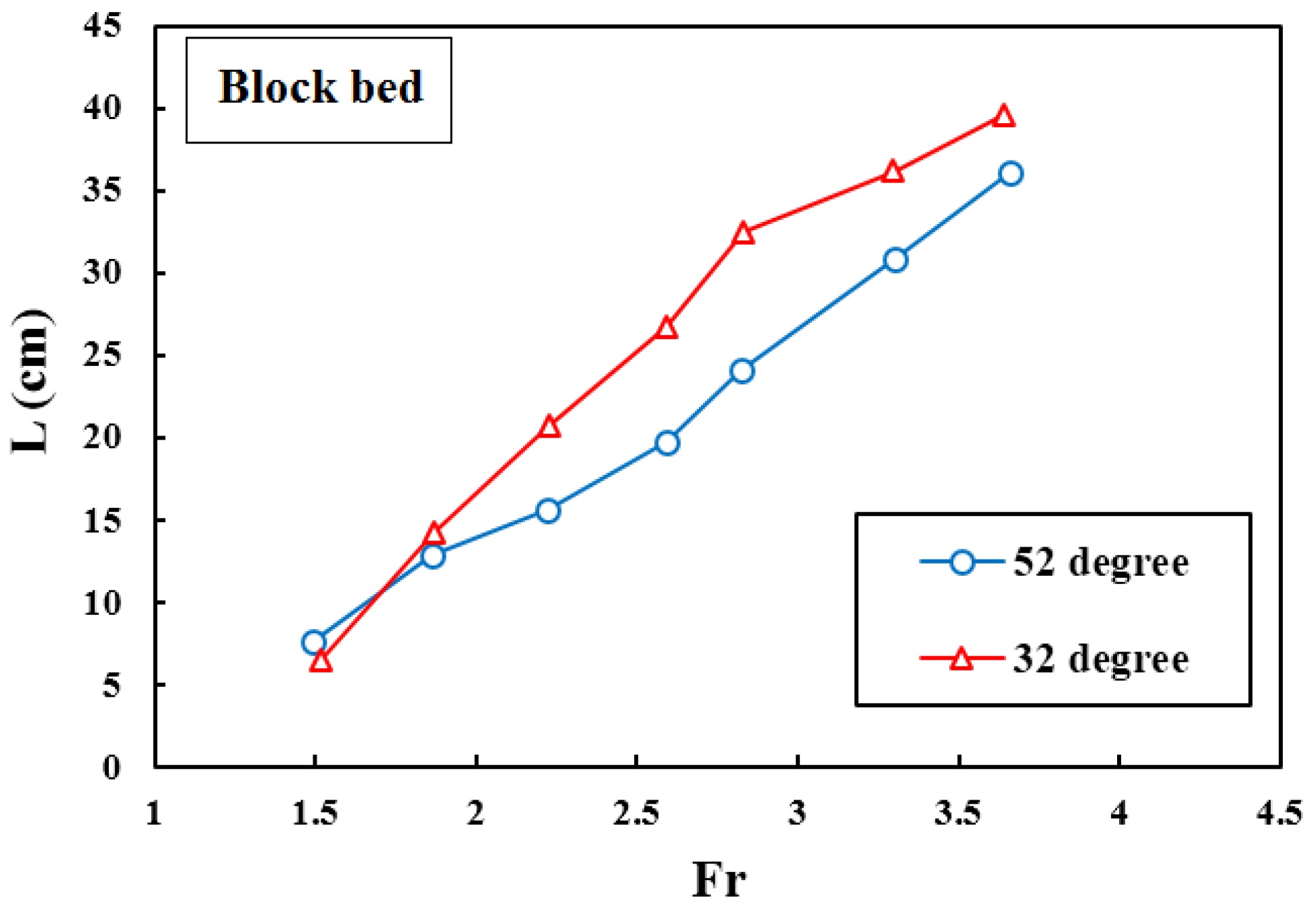
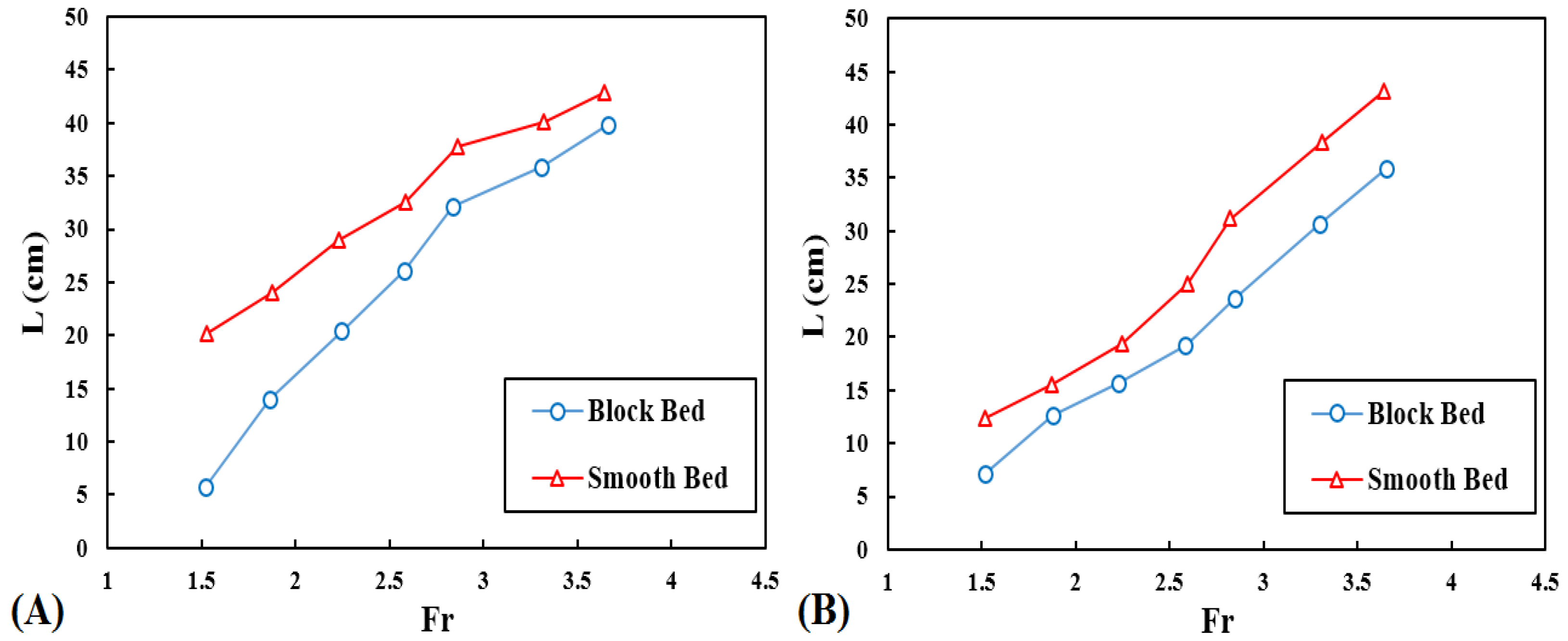
4.4. Jet Length in Ogee Spillway with Block Bed and Different Buckets
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vischer, D.L.; Hager, W.H. Dam Hydraulics; Wiley: Hoboken, NJ, USA; Chichester, UK, 1998. [Google Scholar]
- Yamini, O.A.; Kavianpour, M.R.; Movahedi, A. Pressure distribution on the bed of the compound flip buckets. J. Comput. Multiph. Flows 2015, 7, 181–194. [Google Scholar] [CrossRef][Green Version]
- Maitre, R.; Obolensky, S. Etude de Quelques Caractéristiques de l’Ecoulement dans la Partie Aval des Evacuateurs de Surface. Houille Blanche 1954, 4, 481–511. [Google Scholar] [CrossRef]
- Rhone, T.J.; Peterka, A.J. Improved tunnel spillway flip buckets. J. Hydraul. Eng. 1959, 126, 1270–1291. [Google Scholar]
- Juon, R.; Hager, W.H. Flip bucket without and with deflectors. J. Hydraul. Eng. 2000, 126, 837–845. [Google Scholar] [CrossRef]
- Dargahi, B. Experimental study and 3D numerical simulations for a free-overflow spillway. J. Hydraul. Eng. 2006, 132, 899–907. [Google Scholar] [CrossRef]
- Steiner, R.; Heller, V.; Hager, W.H.; Minor, H.E. Deflector Ski Jump Hydraulics. J. Hydraul. Eng. 2008, 134, 562–571. [Google Scholar] [CrossRef]
- Kermannejad, J.; Fathi Moghadam, M. Dynamic pressure of flip bucket jets. World Appl. Sci. J. 2011, 9, 1448–1454. [Google Scholar]
- Zhenwei, M.U.; Zhiyan, Z. Numerical simulation of 3-D flow field of spillway based on VOF method. Procedia Eng. 2012, 28, 808–812. [Google Scholar] [CrossRef]
- Parsaie, A.; Dehdar-Behbahani, S.; Haghiabi, A.H. Numerical modeling of cavitation on spillway’s flip bucket. Front. Struct. Civ. Eng. 2016, 10, 438–444. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Ghaderi, A. Numerical Investigation of Inverse Curvature Ogee Spillway. Civ. Eng. J. 2017, 3, 1146–1156. [Google Scholar] [CrossRef]
- Yamini, O.A.; Kavianpour, M.R.; Mousavi, S.H.; Movahedi, A.; Bavandpour, M. Experimental investigation of pressure fluctuation on the bed of compound flip buckets. ISH J. Hydraul. Eng. 2017, 1, 1–8. [Google Scholar]
- Peterka, A.J. Hydraulic design of stilling basins and energy dissipators. In A Water Resources Technical Publication, Engineering Monograph, No. 25; United States Department of the Interior Bureau of Reclamation: Denver, CO, USA, 1984. [Google Scholar]
- Kaya, N.; Emiroglu, M.E. Study of oxygen transfer efficiency at baffled chutes. Presented Meet. Proc. Inst. Civ. Eng. Water Manag. 2010, 163, 447–456. [Google Scholar] [CrossRef]
- Elnikhely, E. Investigation and analysis of scour downstream of a spillway. Ain Shams Eng. J. 2017, 9, 2275–2282. [Google Scholar] [CrossRef]
- Pfister, M.; Chanson, H. Two-phase air-water flows: Scale effects in physical modelling. J. Hydrodyn. 2014, 26, 291–298. [Google Scholar] [CrossRef]
- Flow Science Inc. FLOW-3D V 11.2 User’s Manual; Flow Science Inc.: Santa Fe, NM, USA, 2016. [Google Scholar]
- Ghaderi, A.; Abbasi, S. CFD simulation of local scouring around airfoil-shaped bridge piers with and without collar. Sādhanā 2019, 44, 216. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization Group Analysis of Turbulence: Basic Theory. J. Sci. Comput. 1986, 1, 1–51. [Google Scholar] [CrossRef]
- Cable, M. An Evaluation of Turbulence Models for the Numerical Study of Forced and Natural Convective Flow in Atria. Master’s Thesis, Queens University, Kingston, ON, Canada, 2009. [Google Scholar]
- Savage, B.; Johnson, M. Flow over ogee spillway: Physical and numerical model case study. J. Hydraul. Eng. 2001, 127, 640–649. [Google Scholar] [CrossRef]
- Aydin, M.C.; Ozturk, M. Verification and validation of a computational fluid dynamics (CFD) model for air entrainment at spillway aerators. Can. J. Civ. Eng. 2009, 36, 826–836. [Google Scholar] [CrossRef]
- Sangsefidi, Y.; MacVicar, B.; Ghodsian, M.; Mehraein, M.; Torabi, M.; Savage, B.M. Evaluation of flow characteristics in labyrinth weirs using response surface methodology. Flow Meas. Instrum. 2019, 69, 101617. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Joudi, A.R.; Ghahramanzadeh, A.; Ghaderi, A. Investigation of flow pressure distribution over a stepped spillway. Adv. Appl. Fluid Mech. 2016, 19, 811. [Google Scholar] [CrossRef]
- Zahabi, H.; Torabi, M.; Alamatian, E.; Bahiraei, M.; Goodarzi, M. Effects of geometry and hydraulic characteristics of shallow reservoirs on sediment entrapment. Water 2018, 10, 1725. [Google Scholar] [CrossRef]
- Ghaderi, A.; Abbasi, S.; Abraham, J.; Azamathulla, H.M. Efficiency of Trapezoidal Labyrinth Shaped Stepped Spillways. Flow Meas. Instrum. 2020, 72, 101711. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Ghahramanzadeh, A.; Ghaderi, A.; Joudi, A.R.; Abraham, J. Investigation of the Effect of Edge Shape on Characteristics of Flow under Vertical Gates. J. Am. Water Work. Assoc. 2016, 108, 425–432. [Google Scholar] [CrossRef]
- Yakhot, V.; Orsarg, S.A.; Thangam, S.; Gatski, T.B.; Speziale, C.G. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids 1992, 4, 1510–1520. [Google Scholar] [CrossRef]
- Biscarini, C.; Di Francesco, S.; Manciola, P. CFD modelling approach for dam break flow studies. Hydrol. Earth Syst. Sci. 2010, 14, 705–718. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Minaei, O.; Abraham, J.; Dadashi, S.; Ghaderi, A. 3-D Numerical simulation of water flow over a broad-crested weir with openings. ISH J. Hydraul. Eng. 2019, 1–9. [Google Scholar] [CrossRef]
- Ghaderi, A.; Dasineh, M.; Abbasi, S.; Abraham, J. Investigation of trapezoidal sharp-crested side weir discharge coefficients under subcritical flow regimes using CFD. Appl. Water Sci. 2020, 10, 31. [Google Scholar] [CrossRef]
- Johnson, M. Discharge Coefficient Scale Effects Analysis for Weirs. Ph.D. Thesis, Utah State University, Logan, UT, USA, 1996. [Google Scholar]
- Moradinejad, A.; Saneie, M.; Ghaderi, A.; Shahri, S.M.Z. Experimental study of flow pattern and sediment behavior near the intake structures using the spur dike and skimming wall. Appl. Water Sci. 2019, 9, 195. [Google Scholar] [CrossRef]
- Ghaderi, A.; Daneshfaraz, R.; Dasineh, M.; Di Francesco, S. Energy Dissipation and Hydraulics of Flow over Trapezoidal–Triangular Labyrinth Weirs. Water 2020, 12, 1992. [Google Scholar] [CrossRef]
- Ghaderi, A.; Daneshfaraz, R.; Torabi, M.; Abraham, J.; Azamathulla, H.M. Experimental investigation oneffective scouring parameters downstream from stepped spillways. Water Supply 2020. [Google Scholar] [CrossRef]
- United States Bureau of Reclamation. Design of Small Dams; United States Department of Interior—Bureau of Reclamation: Washington, DC, USA, 1987.
- Choufu, L.; Abbasi, S.; Pourshahbaz, H.; Taghvaei, P.; Tfwala, S. Investigation of flow, erosion, and sedimentation pattern around varied groynes under different hydraulic and geometric conditions: A numerical study. Water 2019, 11, 235. [Google Scholar] [CrossRef]
- Di Francesco, S.; Zarghami, A.; Biscarini, C.; Manciola, P. Wall roughness effect in the lattice Boltzmann method. AIP Conf. Proc. 2013, 1558, 1677–1680. [Google Scholar]
- Biscarini, C.; Di Francesco, S.; Ridolfi, E.; Manciola, P. On the Simulation of Floods in a Narrow Bending Valley: The Malpasset Dam Break Case Study. Water 2016, 8, 545. [Google Scholar] [CrossRef]
- Venturi, S.; Di Francesco, S.; Geier, M.; Manciola, P. Forcing for a Cascaded Lattice Boltzmann Shallow Water Model. Water 2020, 12, 439. [Google Scholar] [CrossRef]
- Venturi, S.; Di Francesco, S.; Geier, M.; Manciola, P. A new collision operator for lattice Boltzmann shallow water model: A convergence and stability study. Adv. Water Resour. 2020, 135, 103474. [Google Scholar] [CrossRef]
- Ghaderi, A.; Daneshfaraz, R.; Abbasi, S.; Abraham, J. Numerical analysis of the hydraulic characteristics of modified labyrinth weirs. Int. J. Energy Water Resour. 2020, 1–12. [Google Scholar] [CrossRef]
- Pourshahbaz, H.; Abbasi, S.; Pandey, M.; Pu, J.H.; Taghvaei, P.; Tofangdar, N. Morphology and hydrodynamics numerical simulation around groynes. ISH J. Hydraul. Eng. 2020, 1–9. [Google Scholar] [CrossRef]
- Longo, S.; Ciriello, V.; Chiapponi, L.; Di Federico, V. Combined effect of rheology and confining boundaries on spreading of gravity currents in porous media. Adv. Water Resour. 2015, 79, 140–152. [Google Scholar] [CrossRef]
- Ciriello, V.; Longo, S.; Chiapponi, L.; Di Federico, V. Porous gravity currents: A survey to determine the joint influence of fluid rheology and variations of medium properties. Adv. Water Resour. 2016, 92, 105–115. [Google Scholar] [CrossRef]
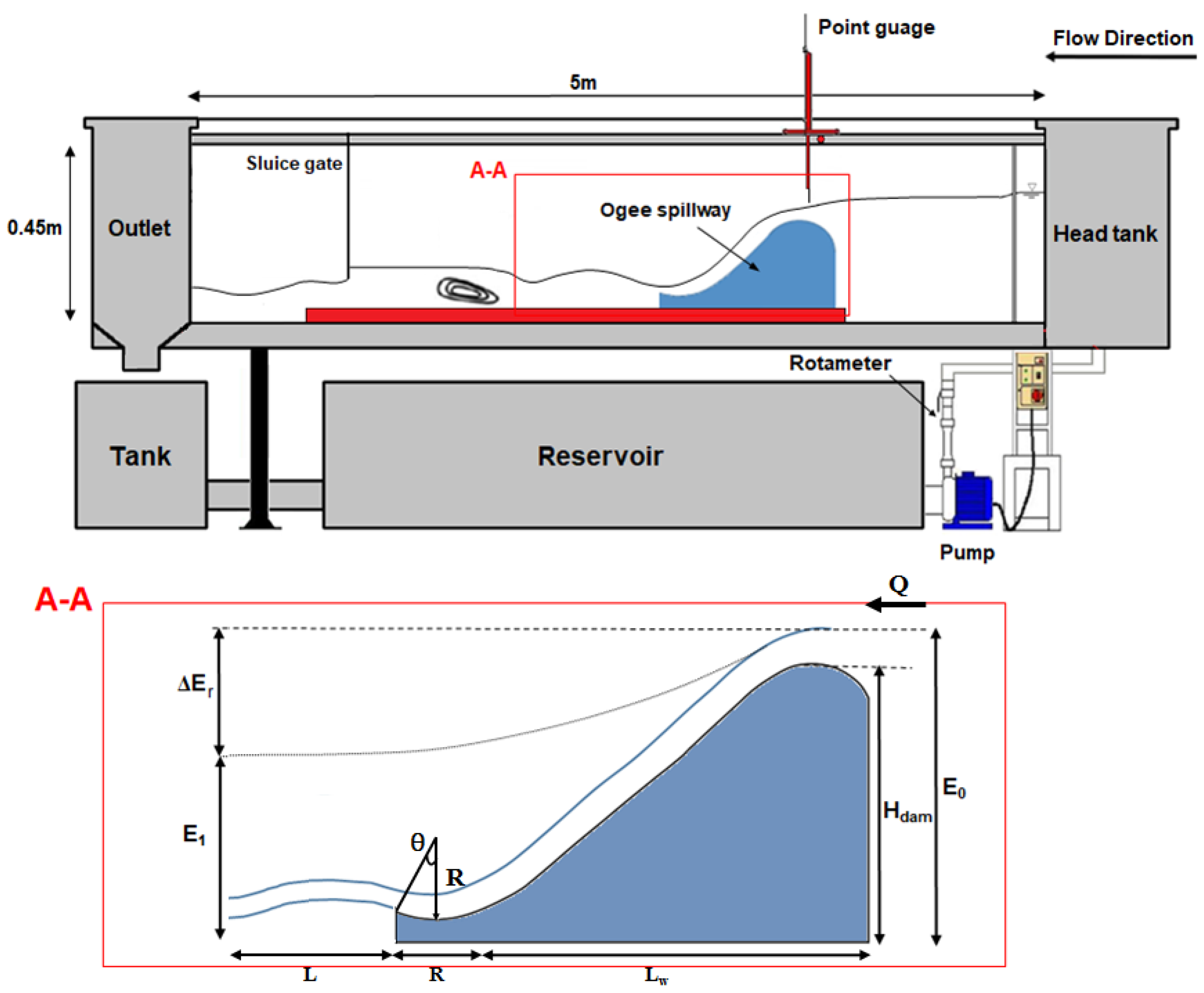

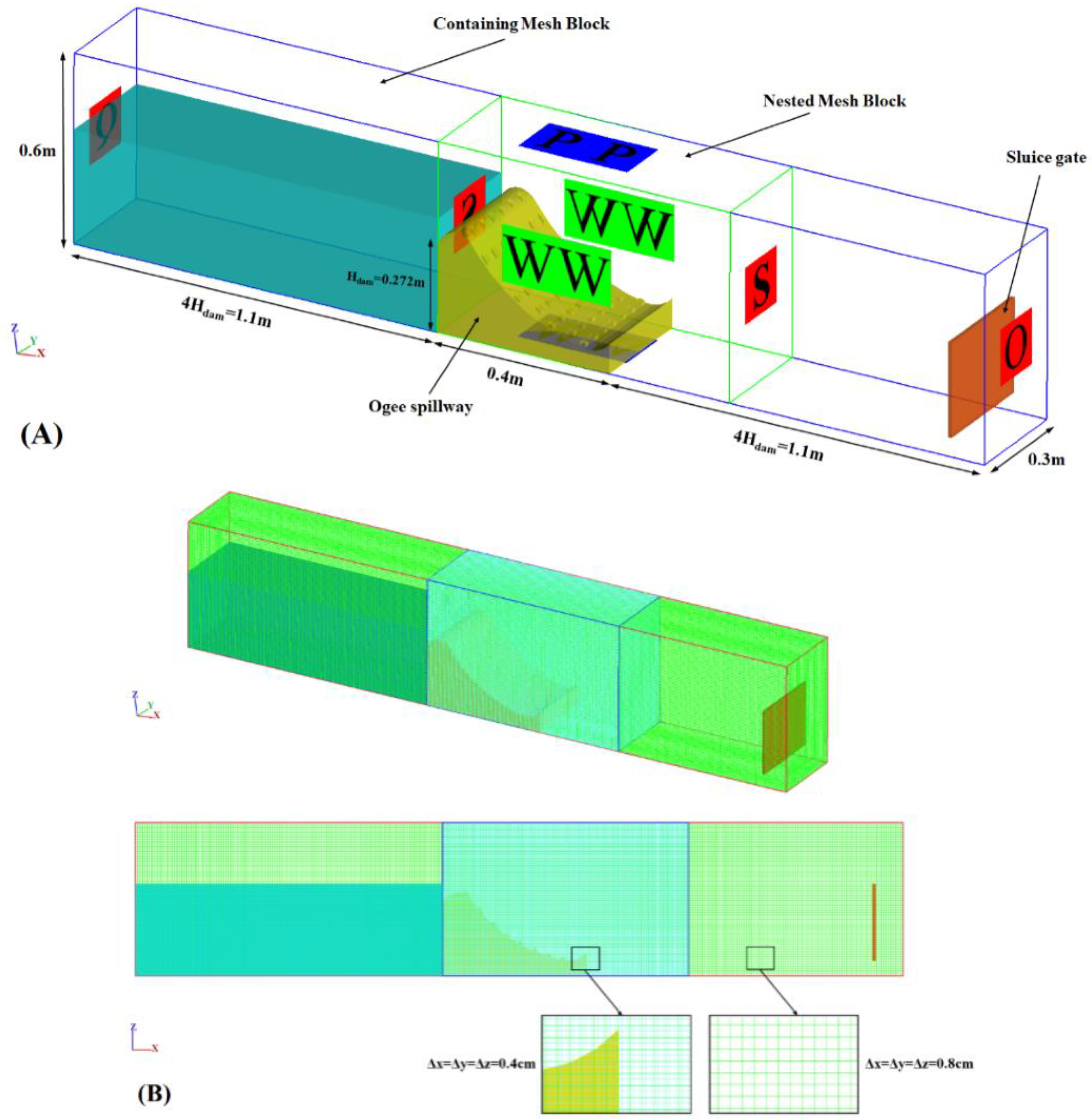


| Range | Q (m3/s) | y (cm) | R (cm) | Fr | Re | |
|---|---|---|---|---|---|---|
| Min | 0.005 | 5.3 | 12 | 32 | 1.29 | 20,700 |
| Max | 0.014 | 11.7 | 19 | 52 | 3.62 | 38,950 |
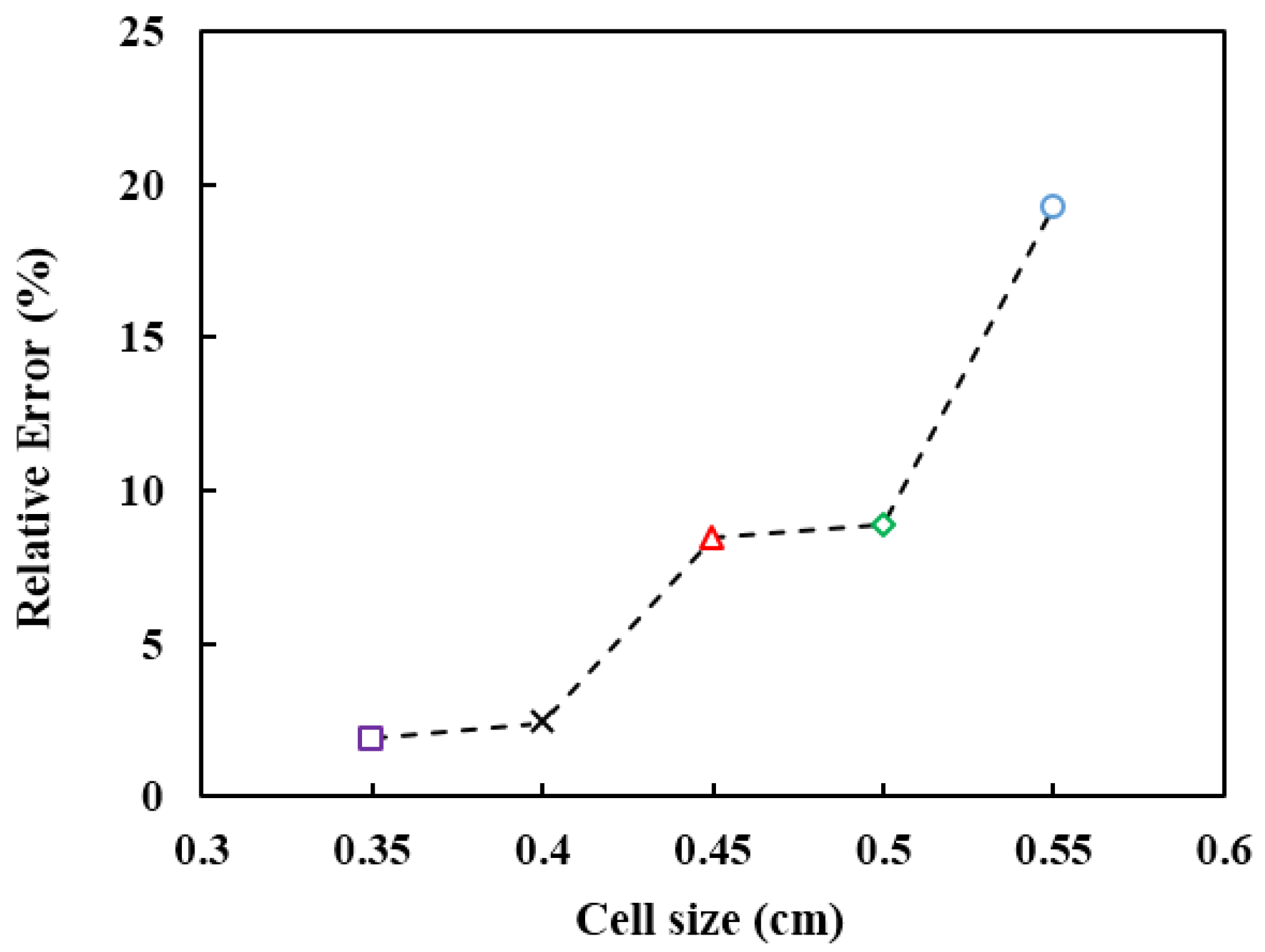
| Test No. | Coarser Cell Size (cm) | Finer Cell Size (cm) | Total Mesh Number | MAPE (%) * | ** RMSE (cm) |
|---|---|---|---|---|---|
| T1 | 1.2 | 0.55 | 944,125 | 19.24 | 4.6 |
| T2 | 1.1 | 0.50 | 1,335,000 | 8.89 | 1.94 |
| T3 | 0.95 | 0.45 | 1,769,834 | 8.45 | 1.75 |
| T4 | 0.80 | 0.40 | 2,541,311 | 2.42 | 0.39 |
| T5 | 0.70 | 0.35 | 3,906,163 | 1.90 | 0.33 |
| X(m) | FsE (m)Exp | FsE (m)Num | Relative Errors (%) | RMSE (cm) |
|---|---|---|---|---|
| −0.28 | 0.326 | 0.330 | 1.22 | 0.04 |
| −0.20 | 0.327 | 0.331 | 1.22 | 0.04 |
| −0.15 | 0.325 | 0.330 | 1.53 | 0.05 |
| −0.10 | 0.324 | 0.328 | 1.22 | 0.04 |
| −0.05 | 0.324 | 0.325 | 0.38 | 0.01 |
| 0.00 | 0.322 | 0.323 | 0.38 | 0.01 |
| 0.05 | 0.309 | 0.313 | 1.22 | 0.04 |
| 0.15 | 0.217 | 0.223 | 2.76 | 0.06 |
| 0.25 | 0.116 | 0.124 | 6.89 | 0.08 |
| 0.35 | 0.074 | 0.076 | 2.07 | 0.02 |
| 0.45 | 0.083 | 0.088 | 1.53 | 0.05 |
| 0.55 | 0.133 | 0.139 | 2.76 | 0.06 |
| 0.60 | 0.144 | 0.148 | 1.22 | 0.04 |
| 0.65 | 0.146 | 0.149 | 2.03 | 0.03 |
| Mean | 1.88 | 0.04 | ||
| Q(m3/s) | Mean Relative Errors (%) | Mean RMSE(cm) |
|---|---|---|
| 0.005 | 1.42 | 0.02 |
| 0.007 | 1.21 | 0.04 |
| 0.0085 | 1.88 | 0.04 |
| 0.010 | 1.56 | 0.03 |
| 0.011 | 1.42 | 0.04 |
| 0.013 | 1.26 | 0.03 |
| 0.014 | 1.47 | 0.04 |
| Take-Off Angles (θ) | Bed | Q (m3/s) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.005 | 0.007 | 0.0085 | 0.010 | 0.011 | 0.013 | 0.014 | |||
| ∆Er | Without flip bucket | Smooth | 0.66 | 0.61 | 0.59 | 0.59 | 0.58 | 0.57 | 0.54 |
| Blocked | 0.78 | 0.72 | 0.67 | 0.65 | 0.64 | 0.61 | 0.58 | ||
| 32° | Smooth | 0.75 | 0.70 | 0.67 | 0.66 | 0.66 | 0.61 | 0.58 | |
| Blocked | 0.81 | 0.78 | 0.75 | 0.71 | 0.69 | 0.65 | 0.64 | ||
| 52° | Smooth | 0.83 | 0.79 | 0.74 | 0.73 | 0.71 | 0.68 | 0.65 | |
| Blocked | 0.83 | 0.81 | 0.78 | 0.76 | 0.75 | 0.71 | 0.69 | ||
| Take-Off Angles (θ) | Bed | Q (m3/s) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.005 | 0.0070 | 0.0085 | 0.010 | 0.011 | 0.013 | 0.014 | |||
| L | 32° | Smooth | 20.5 | 24.5 | 29.5 | 32.7 | 37.7 | 40.3 | 42.8 |
| Blocked | 8.6 | 14.0 | 20.5 | 32.0 | 32.0 | 35.9 | 39.5 | ||
| 52° | Smooth | 12.4 | 15.5 | 19.2 | 31.0 | 31.0 | 38.5 | 43.0 | |
| Blocked | 7.4 | 12.5 | 15.5 | 23.5 | 23.5 | 30.7 | 36.0 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daneshfaraz, R.; Ghaderi, A.; Akhtari, A.; Di Francesco, S. On the Effect of Block Roughness in Ogee Spillways with Flip Buckets. Fluids 2020, 5, 182. https://doi.org/10.3390/fluids5040182
Daneshfaraz R, Ghaderi A, Akhtari A, Di Francesco S. On the Effect of Block Roughness in Ogee Spillways with Flip Buckets. Fluids. 2020; 5(4):182. https://doi.org/10.3390/fluids5040182
Chicago/Turabian StyleDaneshfaraz, Rasoul, Amir Ghaderi, Aliakbar Akhtari, and Silvia Di Francesco. 2020. "On the Effect of Block Roughness in Ogee Spillways with Flip Buckets" Fluids 5, no. 4: 182. https://doi.org/10.3390/fluids5040182
APA StyleDaneshfaraz, R., Ghaderi, A., Akhtari, A., & Di Francesco, S. (2020). On the Effect of Block Roughness in Ogee Spillways with Flip Buckets. Fluids, 5(4), 182. https://doi.org/10.3390/fluids5040182







