The Effect of the Vadasz Number on the Onset of Thermal Convection in Rotating Bidispersive Porous Media
Abstract
1. Introduction
2. Preliminaries
3. Linear Instability
3.1. Steady Convection
3.2. Oscillatory Convection
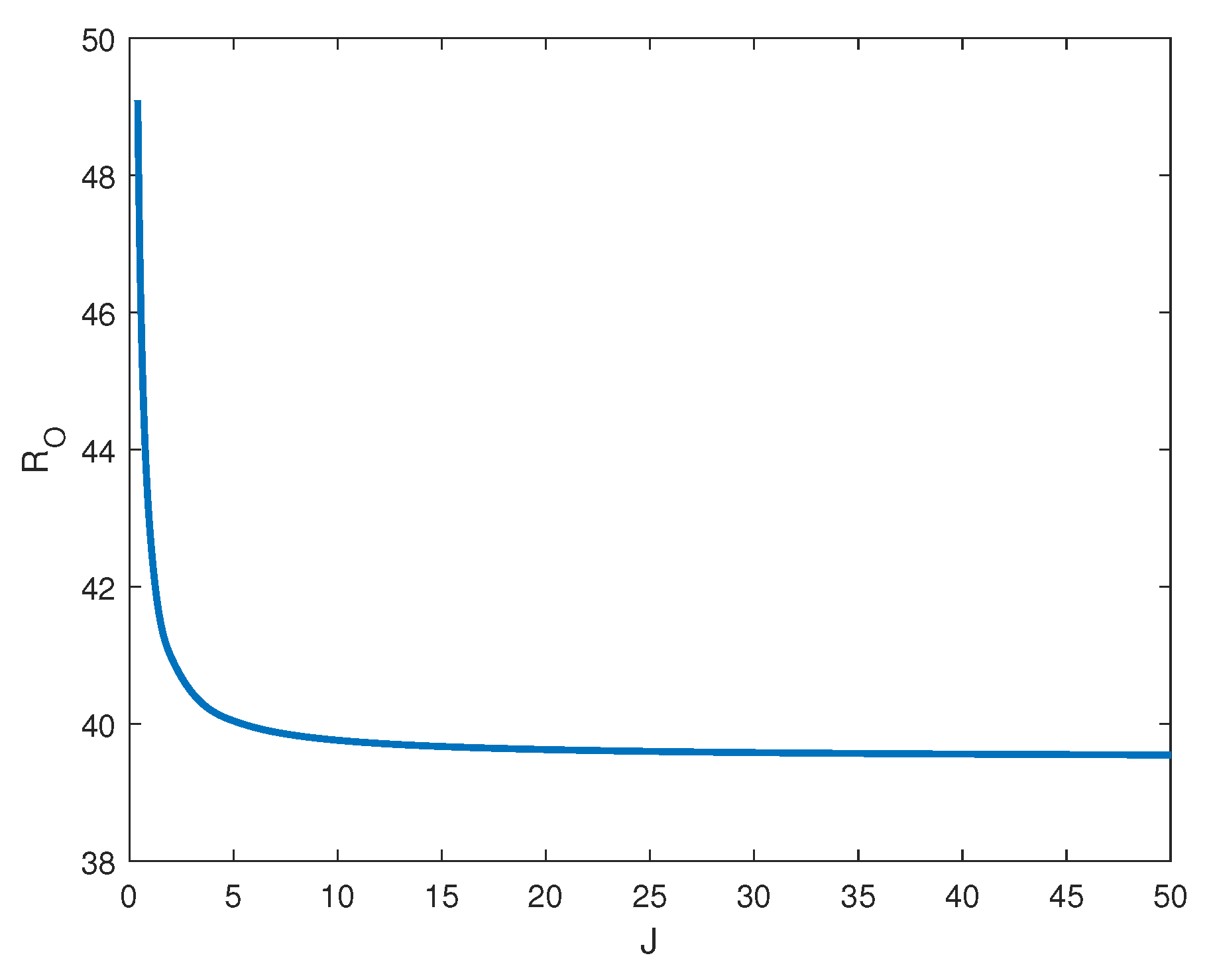
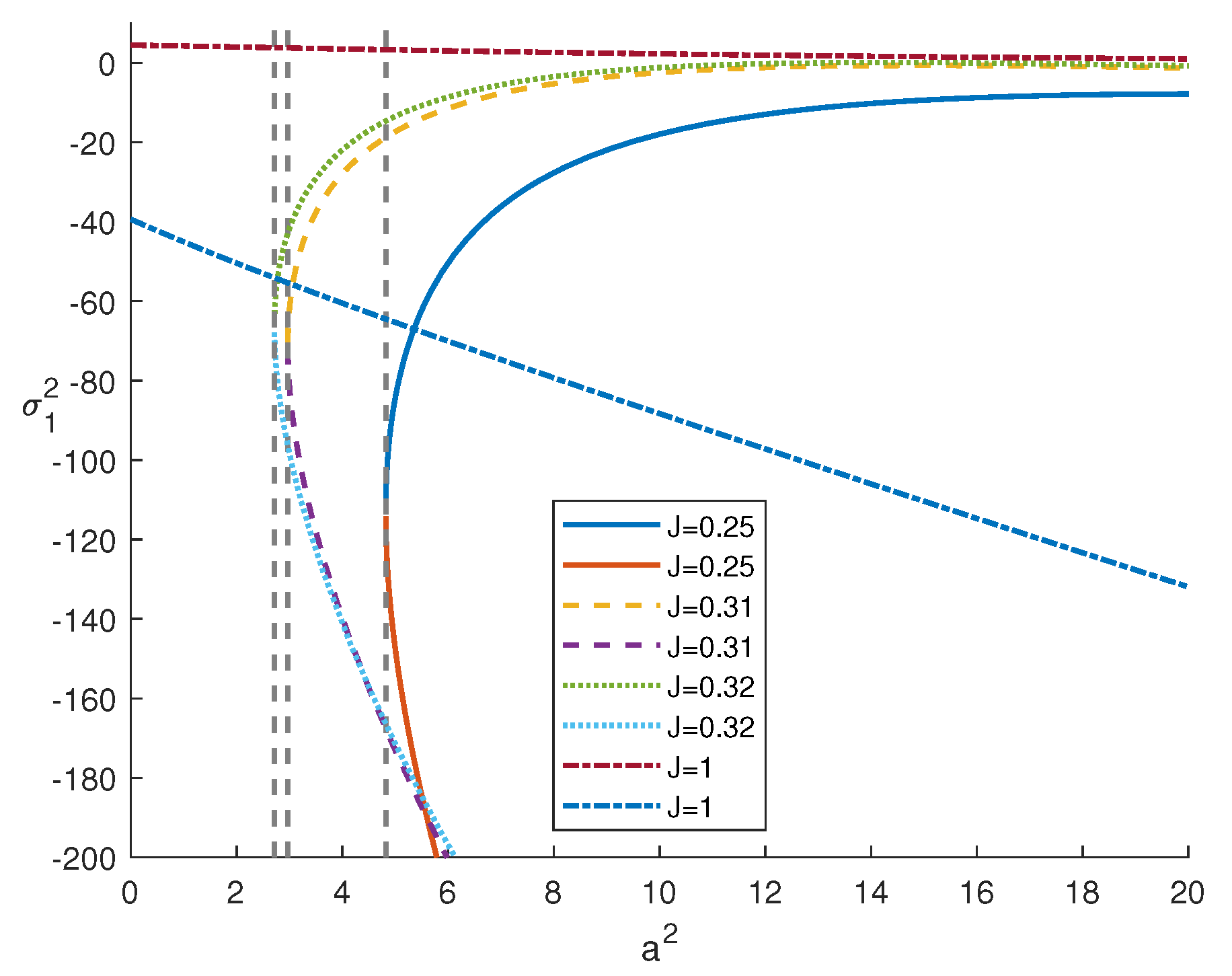
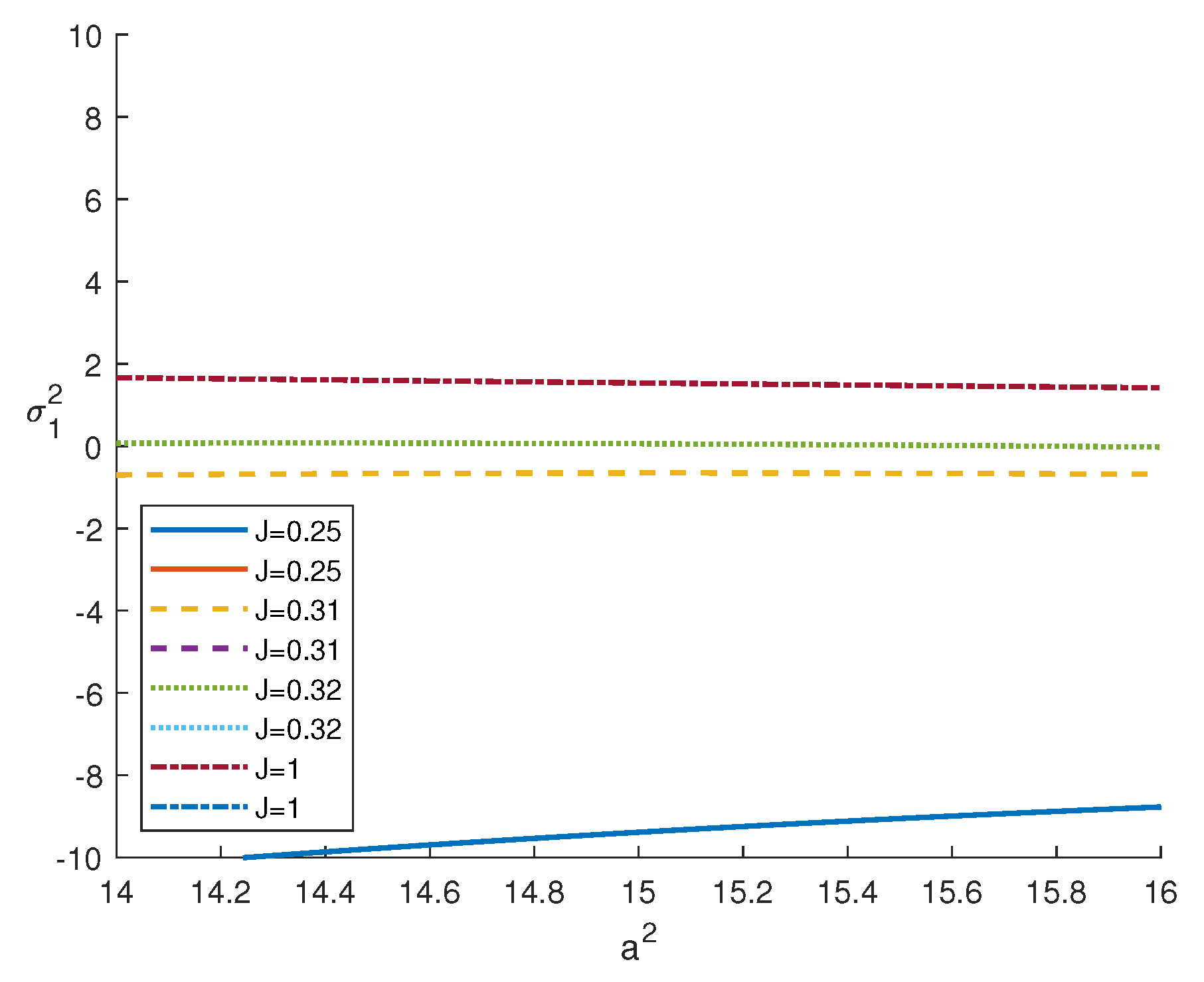
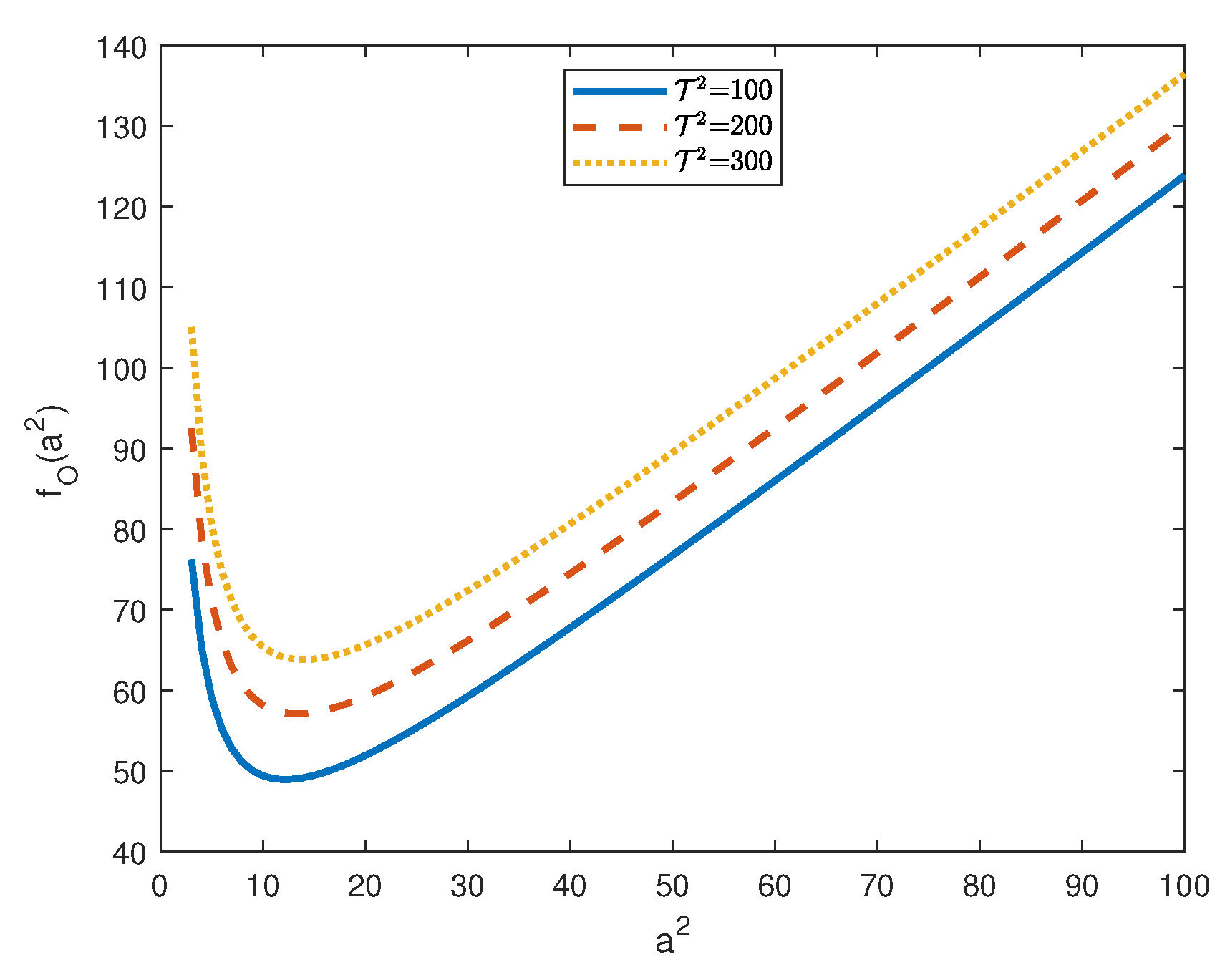
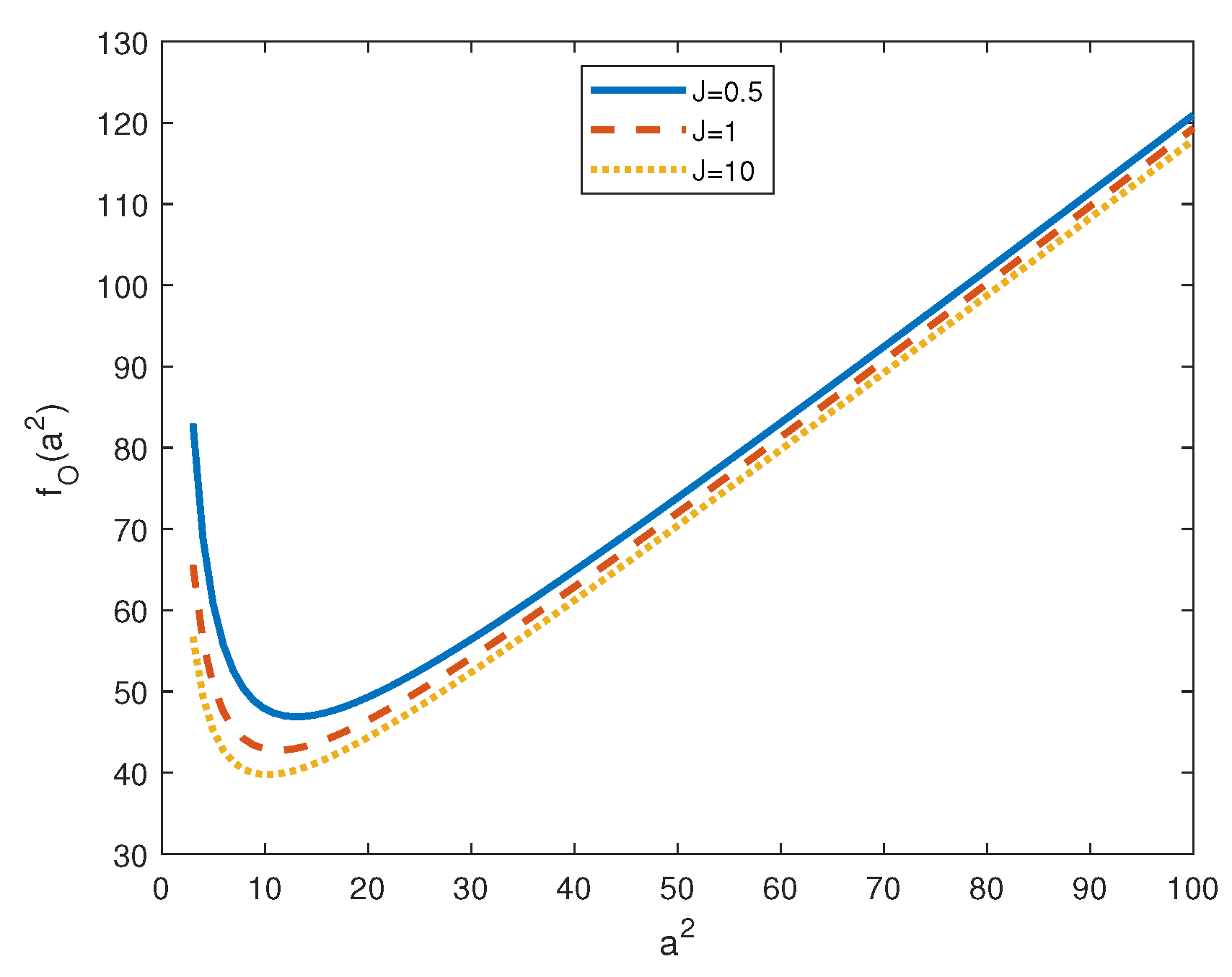
4. Numerical Results
- (1)
- analyze the asymptotic behaviour of with respect to and J; and,
- (2)
- compare and to establish whether the convection arises through a steady state (stationary convection) or via an oscillatory state (oscillatory convection).
- (i)
- if or if , then convection can only arise via a steady state;
- (ii)
- if , convection can only arise via an oscillatory state.
5. Conclusions
- does not depend on the acceleration coefficient, i.e., inertial effects do not affect ;
- increases with the Taylor number, i.e., has—as one is expected—a stabilizing effect on the onset of steady convection; and,
- is a decreasing function of J and there exists a threshold for the inertia coefficient, such that exists and convection arises via an oscillatory state; and,
- is an increasing functions of and there exists a threshold for the Taylor number, such that, for , the convection arises via an oscillatory state.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Capone, F.; Gentile, M.; Hill, A.A. Convection problems in anisotropic porous media with nonhomogeneous porosity and thermal diffusivity. Acta Appl. Math. 2012, 122, 85–91. [Google Scholar] [CrossRef]
- Capone, F.; Rionero, S. Porous MHD convection: Stabilizing effect of magnetic field and bifurcation analysis. Ricerche Mat. 2016, 65, 163–186. [Google Scholar] [CrossRef]
- Straughan, B. Stability and Wave Motion in Porous Media. Applied Mathematical Sciences; Springer: Berlin, Germany, 2008; Volume 165. [Google Scholar]
- Chen, Z.Q.; Cheng, P.; Hsu, C.T. A theoretical and experimental study on stagnant thermal conductivity of bi-dispersed porous media. Int. Commun. Heat Mass Tranf. 2000, 27, 601–610. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Cheng, P.; Zhao, T.S. An experimental study of two phase flow and boiling heat transfer in bi-disperse porous channels. Int. Commun. Heat Mass Transf. 2000, 27, 293–302. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The onset of convection in a bidisperse porous medium. Int. J. Heat Mass Transf. 2006, 49, 3068–3074. [Google Scholar] [CrossRef]
- Lin, F.C.; Liu, B.H.; Huang, C.T.; Chen, Y.M. Evaporative heat transfer model of a loop heat pipe with bidisperse wick structure. Int. J. Heat Mass Transf. 2011, 54, 4621–4629. [Google Scholar] [CrossRef]
- Borja, R.L.; Liu, X.; White, J.A. Multiphysics hillslope processes triggering landslides. Acta Geotech. 2012, 7, 261–269. [Google Scholar] [CrossRef]
- Straughan, B. Convection with Local Thermal Non-Equilibrium and Microfluidic Effects. In Advances in Mechanics and Mathematics; Springer: Cham, Switzerland, 2015; Volume 32. [Google Scholar]
- Straughan, B. Effect of inertia on double diffusive bidispersive convection. Int. J. Heat Mass Trasnf. 2019, 129, 389–396. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 5th ed.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Rees, D.A.S. The effect of inertia on free convection from a horizontal surface embedded in a porous medium. Int. J. Heat Mass Trasnf. 1996, 39, 3425–3430. [Google Scholar] [CrossRef]
- Rees, D.A.S. The effect of inertia on the onset of mixed convection in a porous layer heated from below. Int. Comm. Heat Mass Transf. 1997, 24, 277–283. [Google Scholar] [CrossRef]
- Rabbani, S.; Abderrahmane, H.; Sassi, M. Inertial Effects on Dynamics of Immiscible Viscous Fingering in Homogenous Porous Media. Fluids 2019, 4, 79. [Google Scholar] [CrossRef]
- Capone, F.; De Luca, R. Porous MHD convection: Effect of Vadasz inertia term. Transp. Porous Med. 2017, 118, 519–536. [Google Scholar] [CrossRef]
- Capone, F.; De Luca, R.; Vitiello, M. Double-diffusive Soret convection phenomenon in porous media: Effect of Vadasz inertia term. Ricerche Mat. 2019, 68, 581–595. [Google Scholar] [CrossRef]
- Capone, F.; Rionero, S. Inertia effect on the onset of convection in rotating porous layers via the “auxiliary system method”. Int. J. Non-Linear Mech. 2013, 57, 193–200. [Google Scholar] [CrossRef]
- Vadasz, P. Coriolis effect on gravity-driven convection in a rotating porous layer heated from below. J. Fluid Mech. 1998, 376, 351–375. [Google Scholar] [CrossRef]
- Dogdson, E.; Rees, D.A.S. The onset of Prandtl-Darcy-Prats convection in a horizontal porous layer. Transp. Porous Med. 2013, 99, 175–189. [Google Scholar]
- Capone, F.; Gentile, M. Sharp stability results in LTNE rotating anisotropic porous layer. Int. J. Therm. Sci. 2019, 134, 661–664. [Google Scholar] [CrossRef]
- De Luca, R.; Rionero, S. Steady and oscillatory convection in rotating fluid layers heated and salted from below. Int. J. Non-Linear Mech. 2016, 78, 121–130. [Google Scholar] [CrossRef]
- Capone, F.; De Luca, R. On the stability-instability of vertical throughflows in double diffusive mixtures saturating rotating porous layers with large pores. Ric. Mat. 2014, 63, 119–148. [Google Scholar] [CrossRef]
- De Luca, R.; Rionero, S. Dynamic of rotating fluid layers: L2-absorbing sets and onset of convection. Acta Mech. 2017, 228, 4025–4037. [Google Scholar] [CrossRef]
- Vadasz, P. Fluid Flow and Heat Transfer in Rotating Porous Media; Springer Briefs in Thermal Engineering and Applied Science (eBook); Springer International Publishing: New York, NY, USA, 2016. [Google Scholar]
- Vadasz, P. Instability and convection in rotating porous media: A review. Fluids 2019, 4, 147. [Google Scholar] [CrossRef]
- Falsaperla, P.; Mulone, G.; Straughan, B. Inertia effects on rotating porous convection. Int. J. Heat Mass Transf. 2011, 54, 1352–1359. [Google Scholar] [CrossRef]
- Capone, R.F.; De Luca, M. Gentile, Coriolis effect on thermal convection in a rotating bidispersive porous layer. Proc. R. Soc. Lond. A 2020. [Google Scholar] [CrossRef]
- Falsaperla, P.; Mulone, G.; Straughan, B. Bidispersive inclined convection. Proc. R. Soc. A 2016, 472, 20160480. [Google Scholar] [CrossRef] [PubMed]



| J | ||
|---|---|---|
| 0 | ∄ | ∄ |
| 0.25 | ∄ | ∄ |
| 0.31 | ∄ | ∄ |
| 0.32 | 15.3410 | 51.9150 |
| 0.35 | 14.7812 | 59.7010 |
| 0.4 | 14.0459 | 49.0951 |
| 0.7 | 11.9923 | 44.4657 |
| 1 | 11.2881 | 42.7649 |
| 5 | 10.3196 | 40.0417 |
| 10 | 10.2433 | 39.7591 |
| 7 | 15.3031 | ∄ | 45.5293 | ∄ |
| 7.07 | 15.3234 | 12.5623 | 45.6906 | 46.0730 |
| 7.1 | 15.3320 | 12.5674 | 45.7596 | 46.0815 |
| 7.2 | 15.3603 | 12.5844 | 45.9885 | 46.1098 |
| 7.26 | 15.3769 | 12.5946 | 46.1253 | 46.1268 |
| 7.27 | 15.2796 | 12.5963 | 46.1480 | 46.1296 |
| 7.3 | 15.3878 | 12.6014 | 46.2162 | 46.1381 |
| 7.5 | 15.4410 | 12.6353 | 46.6677 | 46.1945 |
| 10 | 15.919 | 13.0503 | 51.9256 | 46.8876 |
| 20 | 16.1538 | 14.5717 | 67.9956 | 49.4695 |
| 50 | 15.2776 | 18.2109 | 95.5668 | 55.9909 |
| J | CONVECTION | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 10 | 7 | 2 | 30 | 1.3 | 22.74 | 15.78 | 198.64 | 202.89 | STEADY |
| 10 | 7 | 2 | 100 | 1.3 | 37.07 | 21.08 | 437.66 | 289.54 | OSCILLATORY |
| 0.8 | 1.5 | 0.2 | 300 | 10 | 19.25 | 13.92 | 193.25 | 63.84 | OSCILLATORY |
| 0.8 | 0.5 | 0.2 | 100 | 1 | 21.27 | ∄ | 120.07 | ∄ | STEADY |
| 0.8 | 0.5 | 0.2 | 100 | 1.5 | 21.27 | 17.10 | 120.07 | 44.72 | OSCILLATORY |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capone, F.; De Luca, R. The Effect of the Vadasz Number on the Onset of Thermal Convection in Rotating Bidispersive Porous Media. Fluids 2020, 5, 173. https://doi.org/10.3390/fluids5040173
Capone F, De Luca R. The Effect of the Vadasz Number on the Onset of Thermal Convection in Rotating Bidispersive Porous Media. Fluids. 2020; 5(4):173. https://doi.org/10.3390/fluids5040173
Chicago/Turabian StyleCapone, Florinda, and Roberta De Luca. 2020. "The Effect of the Vadasz Number on the Onset of Thermal Convection in Rotating Bidispersive Porous Media" Fluids 5, no. 4: 173. https://doi.org/10.3390/fluids5040173
APA StyleCapone, F., & De Luca, R. (2020). The Effect of the Vadasz Number on the Onset of Thermal Convection in Rotating Bidispersive Porous Media. Fluids, 5(4), 173. https://doi.org/10.3390/fluids5040173






