Jellyfish and Fish Solve the Challenges of Turning Dynamics Similarly to Achieve High Maneuverability

Abstract

Turning maneuvers by aquatic animals are essential for fundamental life functions such as finding food or mates while avoiding predation. However, turning requires resolution of a fundamental dilemma based in rotational mechanics: the force powering a turn (torque) is favored by an expanded body configuration that maximizes lever arm length, yet minimizing the resistance to a turn (the moment of inertia) is favored by a contracted body configuration. How do animals balance these opposing demands? Here, we directly measure instantaneous forces along the bodies of two animal models—the radially symmetric Aurelia aurita jellyfish, and the bilaterally symmetric Danio rerio zebrafish—to evaluate their turning dynamics. Both began turns with a small, rapid shift in body kinematics that preceded major axial rotation. Although small in absolute magnitude, the high fluid accelerations achieved by these initial motions generated powerful pressure gradients that maximized torque at the start of a turn. This pattern allows these animals to initially maximize torque production before major body curvature changes. Both animals then subsequently minimized the moment of inertia, and hence resistance to axial rotation, by body bending. This sequential solution provides insight into the advantages of re-arranging mass by bending during routine swimming turns.

1. Introduction

The study of aquatic locomotion has primarily focused on the dynamics and energetics of linear, unidirectional swimming. This approach has yielded important insights but largely reflects longstanding constraints in the empirical measurement, numerical simulation, and theoretical modeling of animal swimming. Experiments conducted in a water channel constrain animal swimming to the single direction of the oncoming flow. With the exception of notable efforts to quantify C-start and S-start behaviors of some fishes [1,2,3], experimental [4,5] and theoretical [6] biomechanical models of animal swimming focus primarily on linear translation. The implicit assumption that swimming is primarily unidirectional has influenced prevailing notions regarding the kinematic parameters that are most important for efficient swimming and body design. Specifically, the observation that swimming animals maintain nearly constant values of Strouhal number St = fA/U (where f is the stroke frequency, A is the stroke amplitude, and U is the unidirectional, steady state swimming speed) has encouraged many efforts to explain the efficiency of animal swimming on the basis of the unidirectional swimming parameters that define the Strouhal number [7,8,9]. Likewise, other measures employed to compare swimming efficiency between animals, such as cost of transport [10,11] and Froude efficiency [12,13,14] inherently place animal swimming within the context of linear pathways between points in a fluid.

This emphasis on unidirectional swimming belies the fact that actual animal swimming in nature is rarely linear, but instead, is more typically characterized by frequent changes in direction that are mediated by turning maneuvers. The importance of turning has long been documented in studies of aquatic animal ecology. Efforts to model the circuitous trajectories of animals have often focused on Brownian motion or Levy walks [15,16,17]. Regardless of behavioral assumptions about swimmers, many studies of empirically measured pathways have demonstrated that across a variety of spatial scales, swimming animals exhibit predominantly non-linear pathways with frequent turns that change their trajectories. Recognition that swimmers in nature turn frequently is important from a biomechanical perspective because turning maneuvers require rotational motions of the swimmer’s major body axis. 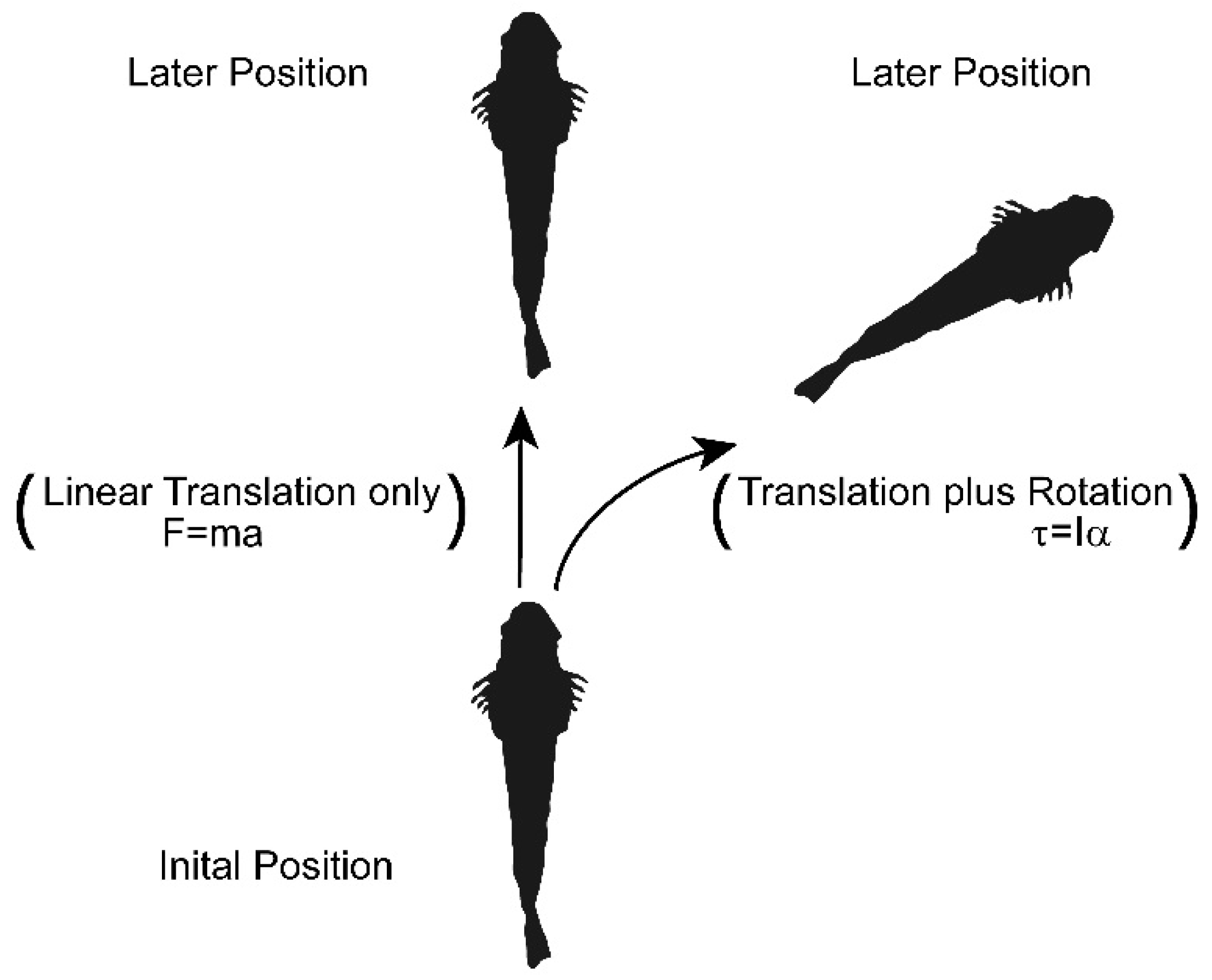The mechanics of rotational motion parallel, but differ from, the more studied mechanics of linear translation by swimmers (Figure 1). In contrast to the large body of knowledge concerning thrust production and force generation during linear swimming, there is not a similar body of mechanical information evaluating torque generation and moment of inertia minimization by flexible bodies such as animal swimmers. Consequently, greater understanding of maneuverability by animal swimmers requires deeper examination of their rotational mechanics to complement existing knowledge of their translational mechanics.

Evaluation of rotational mechanics involves a previously unaddressed issue that is essential for turning by animal swimmers. The same body configurations that maximize the forces powering a turn (torque) also maximize that body’s the resistance to turning (moment of inertia). Torque (τ) generation relies upon a force (F) applied at a distance (r) from the axis of rotation (r is also termed the lever arm) according to the relationship τ = Fr. The longer the lever arm, r, the greater is the torque applied by a limited force to power a turn. Consequently, the most force-efficient body configuration for turning is an elongate or expanded body that maximizes r and requires the least amount of force to affect axial rotation. However, there is an inherent problem with expanded body forms for turning because expanded bodies also maximize the moment of inertia (I), that resists angular rotation of a body according to the relationship τ = Iα where α is angular acceleration. For a limited torque, the greatest angular acceleration will be achieved when the body’s moment of inertia (I) is minimized. I depends upon the arrangement of a body’s mass around the axis of rotation according to the relationship I_P = $\sum _{i=1}^{N}m$_ir_i² where I_P represents the sum moments of inertia for the constituent parts (i … N) of a swimmers body with m_i denoting that body part’s mass (e.g., the head or tail of the body) and r_i its distance from the whole-body center of rotation. There are straightforward means to minimize I_P, e.g., the mass of the body can be re-arranged to place body components closer to the axis of whole-body rotation. This is commonly achieved by bending body parts closer to the axis during a turn. Flexible bodies that allow bending by animal swimmers permit dramatically greater angular velocities during turns than are possible for rigid animal bodies or rigid human-engineered structures [18]. However, it remains unclear how these flexible swimmers resolve the fundamentally conflicting demands of high torque production (expanded body configuration) with those of low moment of inertia (contracted body configuration) to achieve high turning performance. The results are important for understanding maneuverability by swimming animals, and potentially, human engineered vehicles.

We hypothesized that the high frequency and energetic demands of turning by natural swimmers could produce a selective force on swimming performance that might lead to similar solutions for widely divergent animal models. Such patterns would be missed by the conventional biomechanical focus on unidirectional translational swimming, yet are essential for efficient aquatic locomotion by these swimmers in their natural environments.

To evaluate this question broadly, we used two model species with extremely divergent body types, neural organization, and phylogenetic relatedness. The jellyfish Aurelia aurita is a member of the oldest animal group to use muscle-driven swimming and one of the most energetically efficient metazoan swimmers [11]. Medusae such as A. aurita are characterized by a radially symmetric body plan with a comparatively simple level of neuromuscular organization [19]. By contrast, the zebrafish Danio rerio represents the evolution of a bilaterally symmetric body plan with comparatively complex neuromuscular organization representative of modern fish species [20]. In both cases, we quantified their natural swimming motions using a combination of high-speed videography and laser-based flow measurements.

2. Materials and Methods

2.1. Animals and Imaging

The zebrafish (Danio rerio) used in this study were adults acquired from the Zebrafish Facility at the Marine Biological Laboratory (MBL). All procedures were in accordance with standards set by the National Institutes of Health and approved by the Institutional Animal Care and Use Committee at the MBL. Zebrafish were maintained at room temperature (23–25 °C) in 37 L aquaria until imaged while swimming. Swimming and turning behaviors were recorded as individual fish swam along the center of an acrylic raceway tank (1.5 × 0.5 m). Aurelia aurita medusae were obtained from the New England Aquarium and maintained at 25 °C in 20 l aquaria. Medusae were recorded while freely swimming in a 0.3 × 0.1 × 0.25 m glass vessel, using methods reported previously [11]. Many individuals of both species were recorded, but only those that swam within the laser light plane could be used for analysis. The number of separate individuals satisfying this criterion was greatest for the start of the turn (n = 10 for both species). A number of individuals subsequently moved out of the laser sheet while completing a turn. Time course analysis for full turns was limited to separate individuals that completed full turns within the laser light sheet (n = 4 for zebrafish and n = 6 for medusae).

2.2. Particle Image Velocimetry (PIV)

We used high-speed digital particle image velocimetry (PIV) to obtain resulting flow fields around the fish and medusae. Recordings were acquired by a high-speed digital video camera (Fastcam 1024 PCI; Photron, San Diego, CA, USA) at 1000 frames per second and at a spatial resolution of 1024 × 1024 pixels with a scale factor of 0.178 mm per pixel. Seeding particles (10 µm hollow glass beads; Potters Industries, Malvern, PA, USA) were laser-sheet illuminated for PIV measurements. Medusae were illuminated with a laser sheet (680 nm, 2W continuous wave; LaVision, Ypsilanti, MI, USA) oriented perpendicular to the camera’s optical axis to provide a distinctive body outline for image analysis and to ensure the animal remained in-plane, which ensures accuracy of 2D estimates of position and velocity. The semitransparent bodies of medusae allowed a single laser light sheet passing through the central axis of the body to illuminate fluid surrounding the entire body. Fish were not transparent and so were illuminated by two laser sheets (532 nm, 600 mW continuous wave, Laserglow Technologies, North York, ON, Canada) mounted in the same plane on opposite sides of the tank to eliminate shadows on either side of the body as each animal swam within the field of view [21].

Fluid velocity vectors for both fish and medusae were determined from sequential images using a cross-correlation algorithm (LaVision software). Image pairs were analyzed with shifting overlapping interrogation windows of a decreasing size of 32 × 32 pixels to 16 × 16 pixels. Masking of the body of the fish before image interrogation confirmed the absence of surface artifacts in the PIV measurements. While the medusae were not masked for velocity analyses, our previous work with medusae [11], indicated that adverse effects from surface artifacts are minimal.

2.3. Pressure and Torque Measurement

Direct measurements of instantaneous forces acting along animal bodies were made throughout complete turning sequences. These measurements were produced at high spatial and temporal resolution, providing instantaneous values at highly localized points on the body [22,23,24], contrasting with, for example, net force calculation based on vortex circulation. Our approach involved converting velocity fields collected via PIV through a custom program in MATLAB that computed the corresponding pressure fields. The algorithm integrates the Navier–Stokes equations along eight paths emanating from each point in the field of view and terminating at the boundaries of the field of view. The pressure at each point is determined by computing the median pressure from the eight integration results. Bodies of the fish and medusae were masked prior to computation to prevent surface artefacts in the pressure and torque results. Masks were generated using a custom MATLAB (Mathworks, Inc., Natick, MA, USA) program that automatically identified the boundary of the animal body based on image contrast at the interface between the animal body and the surrounding fluid, and body outlines were smoothed prior to later analyses. The zebrafish’s anatomy allowed for these outlines to enclose the body while allowing flow calculations directly alongside all surfaces, but for medusae, the semitransparent bell and opaque gonads outside the laser light sheet interfere with the view of the subumbrellar surface within the bell cavity. As such, the outlines around the medusae traced the exumbrellar surface and, on the oral side of the body, the bell margin to prevent erroneous pressure calculations within the bell cavity from affecting pressure calculations in the areas adjacent to the medusan oral sides. These methods have been previously validated against experimental and computational data, including numerical simulations of anguilliform swimming [22] and direct force and torque measurements of a flapping foil [24]. The MATLAB code is available for free download at http://dabirilab.com/software.

The fluid force normal to the body surface due to the local fluid pressure was determined by integrating the calculated pressure along the corresponding surfaces of the body [24]. Validations against measurements made on physical models show that these calculation techniques based on 2D PIV images are robust to a small degree of out-of-plane flow such as that induced by a fish’s slight rolling motions during turns, so long as the fish remains centered in the imaging plane [24]. The body outline of each animal was divided into segments of equal length (zebrafish: 84 segments, medusa: 70–85 segments) for spatial integration. Again, for medusae, bell components outside the laser sheet can interfere with images of the subumbrellar surface within the bell cavity, so surface segments on the oral side of the body traced the bell margin even as it protruded out of the PIV imaging plane. Although these bell margin surface segments were required to mask the animal body during pressure calculation as indicated above, the central segments—defined as the central two-thirds of the bell’s radius—did not represent surfaces visible within the PIV laser light sheet, and so forces and torques calculated on these central bell segments were not included in later analyses. The areas where calculations were conducted are visible in the force vector plots in Figure 2i–l.

Because the surface geometry was specified in a single plane, the force calculations were evaluated per unit depth (i.e., giving units of Newtons per meter of depth perpendicular to the measurement plane). The corresponding torque was calculated as the vector product of the moment arm from each location on the body surface to the center of mass, and the local force due to pressure at the same location on the body surface. The resulting torque calculations have units of Newton-meters per meter, corresponding to the aforementioned planar measurements. MATLAB codes for force and torque calculations similar to those conducted presently as well as the segment-making methods have been validated in earlier work [24] and are available on Github (https://github.com/kelseynlucas).

2.4. Turning Equations of Motion

The mass moment of inertia of a body is a measure of how its mass is distributed relative to a reference axis, often taken as the geometric centroid. It is given by

$$I={\int }_V{r}^{2}dm$$

(1)

where V is the region occupied by the body mass, and r is the distance of each infinitesimal portion of body mass from the reference axis. In the present case, this mass moment of inertia was approximated using the area moment of inertia, which is a measure of how the body area in a cross section is distributed relative to the reference axis:

$$I_A={\iint }_A{r}^{2}dA$$

(2)

where A is the region occupied by a two-dimensional cross-section of the body. The cross-section in the present measurements was the body symmetry plane illuminated by the laser sheet during PIV measurements. The area moment of inertia (henceforth called the moment of inertia for brevity) was calculated using a custom program in MATLAB as described in the following section.

The torque exerted on a body is related to changes to both its angular motion and its moment of inertia by the following relation:

$$\tau =\frac{d\left(I\omega \right)}{dt}=I\frac{d\omega }{dt}+\omega \frac{dI}{dt}$$

(3)

where ω is the angular velocity of the body. The first term of the summation incorporates the rate of change of angular velocity, i.e., the angular acceleration. The second term depends on the change in the moment of inertia, i.e., changes in body shape or mass.

2.5. Moment of Inertia and Angular Velocity Measurements

Calculations of the moment of inertia for turning sequences used the same smoothed animal body outlines automatically detected for pressure and torque calculation. A separate custom MATLAB algorithm subsequently calculated the moment of area for each image. Animal bodies were partitioned as for the force and torque measurements above, with each of segment of area a_i having a centroid located at distance r_i from the whole body centroid. The area moment of inertia for each frame p was then calculated as:

$$I_{\mathrm{P}}\approx {\sum }_{i=1}^N{a}_i{r_i}^2$$

(4)

where the summation was taken over the N body segments. Angular velocities of zebrafish during turns used local body surface position changes to calculate the angle of the line segment connecting the anterior head region with that of the body centroid. The rate of change of that angle in a lab-fixed frame determined the fish angular velocity. The hemi-ellipsoidal shape of medusae and shifts within the bell during contraction required a different approach for angular measurements. Medusan angular changes were measured by changes of relatively fixed structures within the bell, the gonads, during medusan turning. The angle of the selected gonads were measured relative to the lab-fixed frame in successive images using Image J v1.48 software (National Institutes of Health, Bethesda, MD, USA).

3. Results

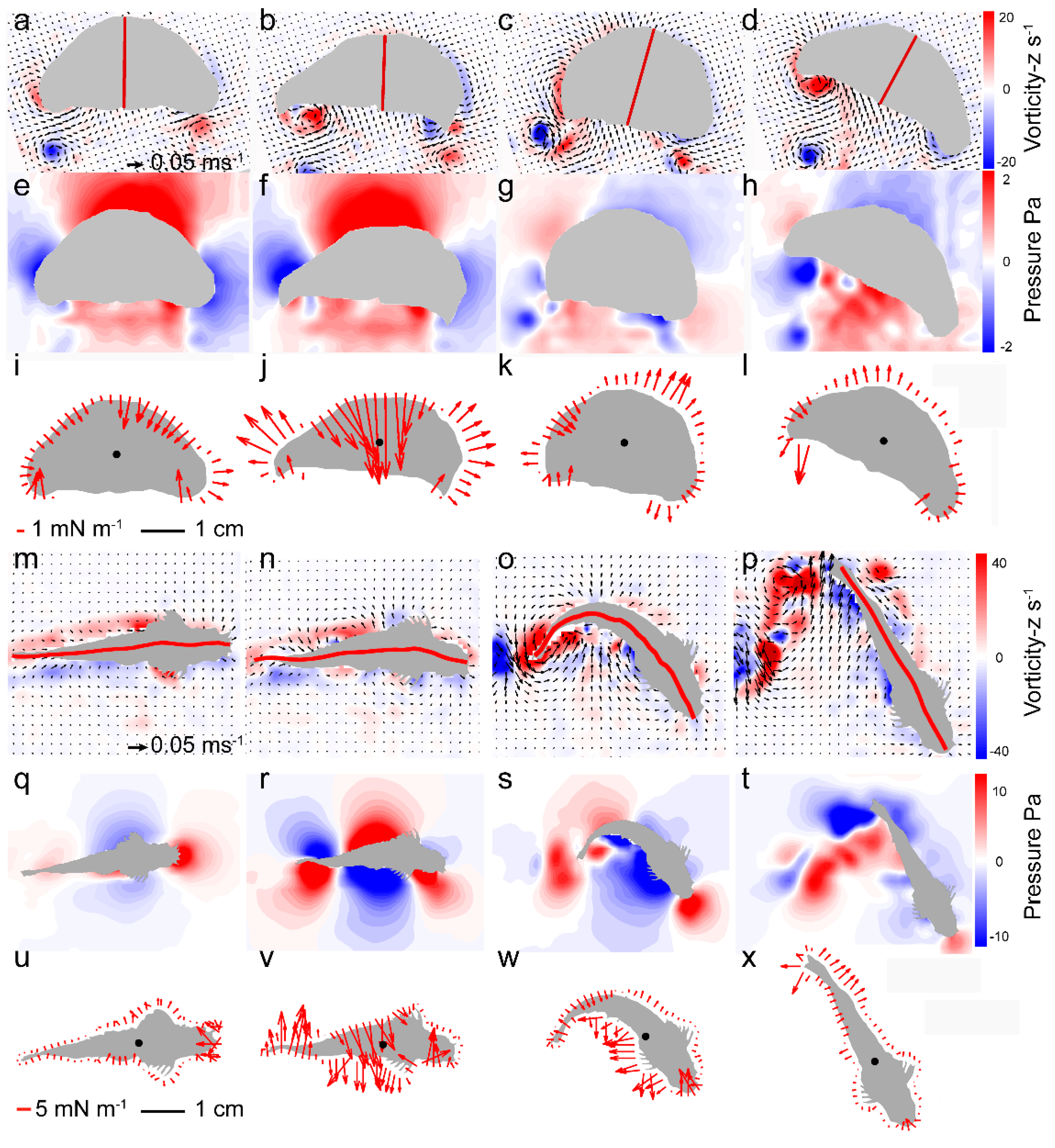
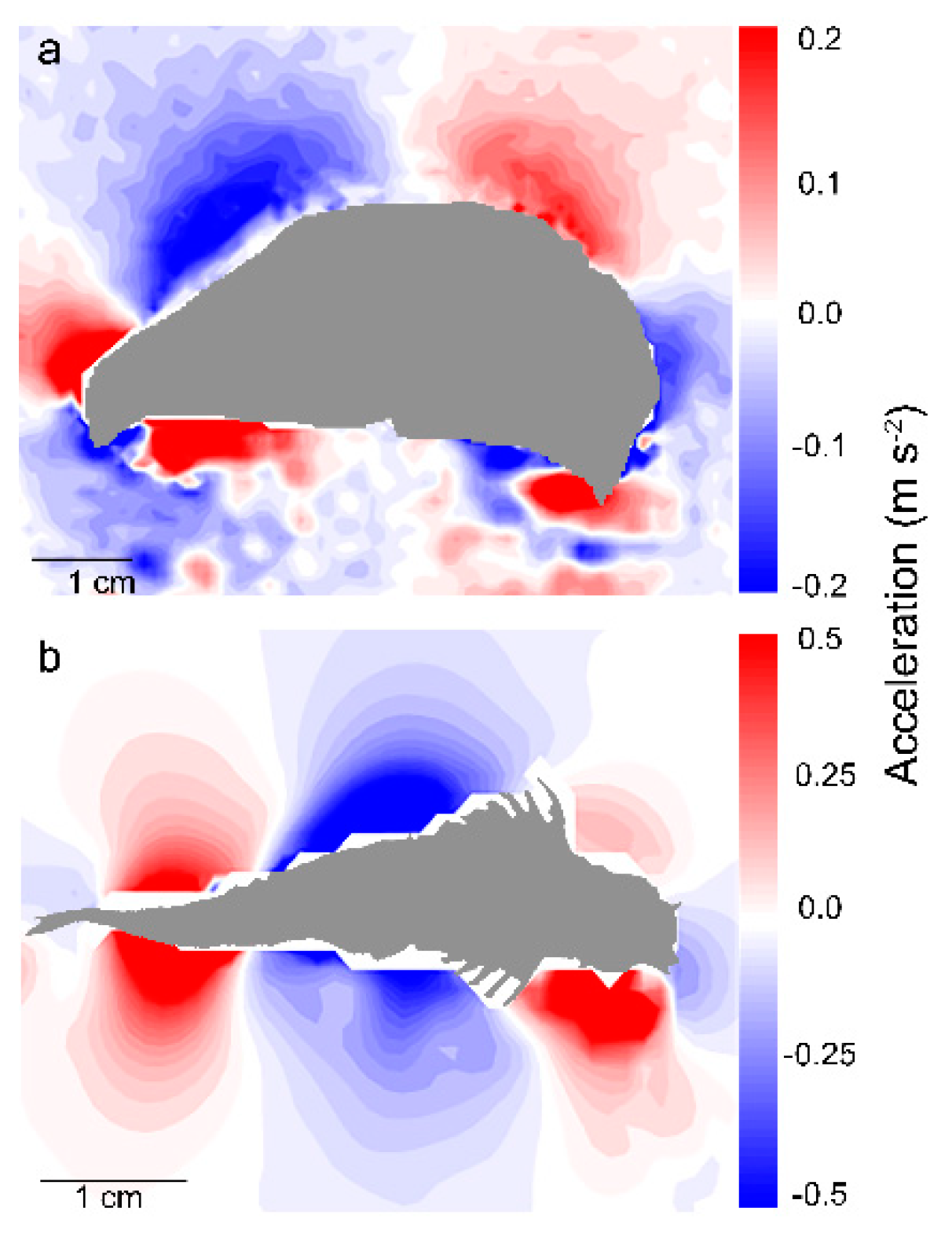
Jellyfish (Figure 2a–l)-and zebrafish (Figure 2m–x) both exhibited frequent bouts of turning, during which flow measurements revealed pronounced changes in fluid velocities and pressure fields in the water adjacent to the animal (Figure 2f,r, for jellyfish and fish, respectively). These substantial pressure fields preceded the more pronounced body motions that occurred during the subsequent turn that changed the animal swimming direction (Figure 2c,o, respectively).

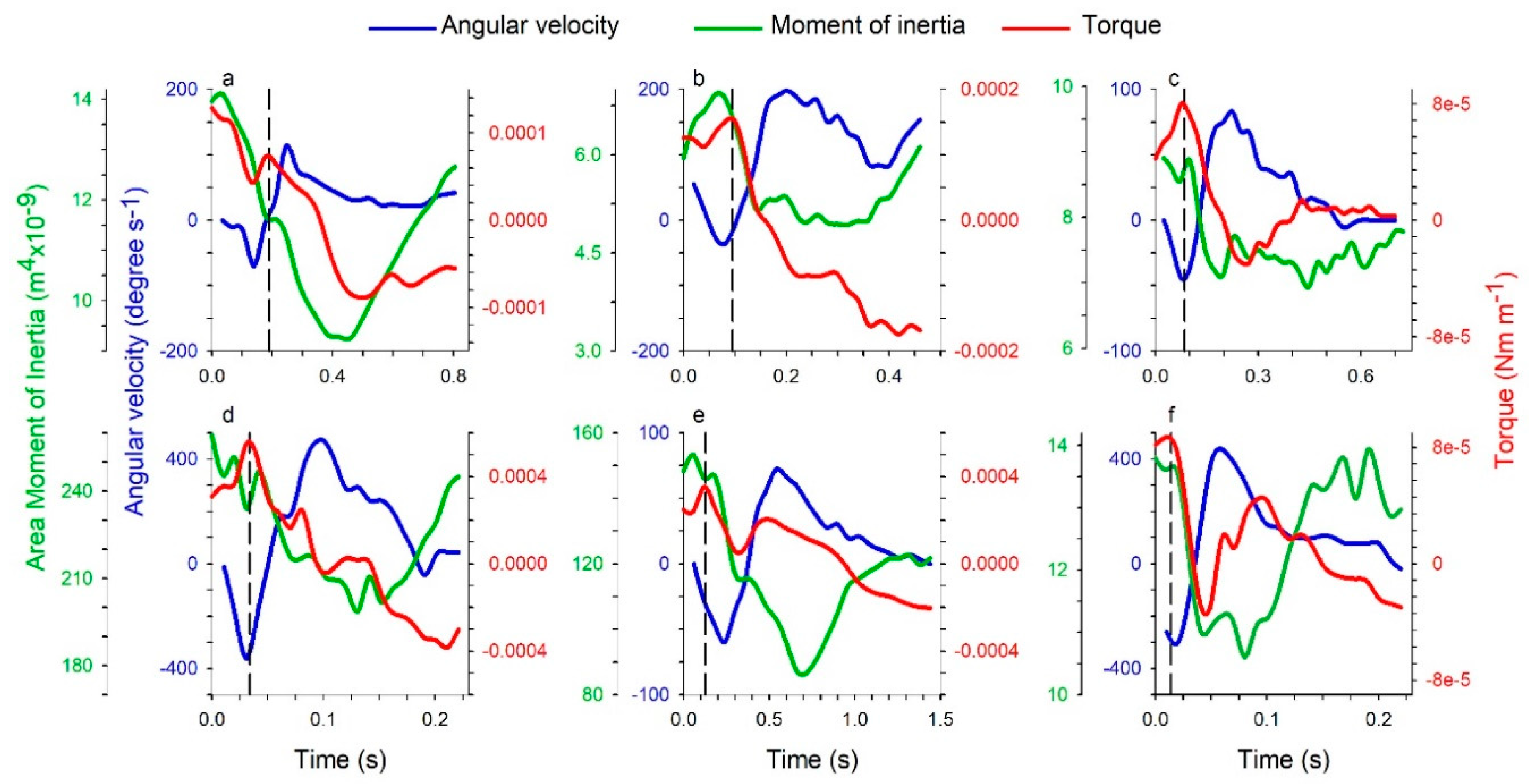
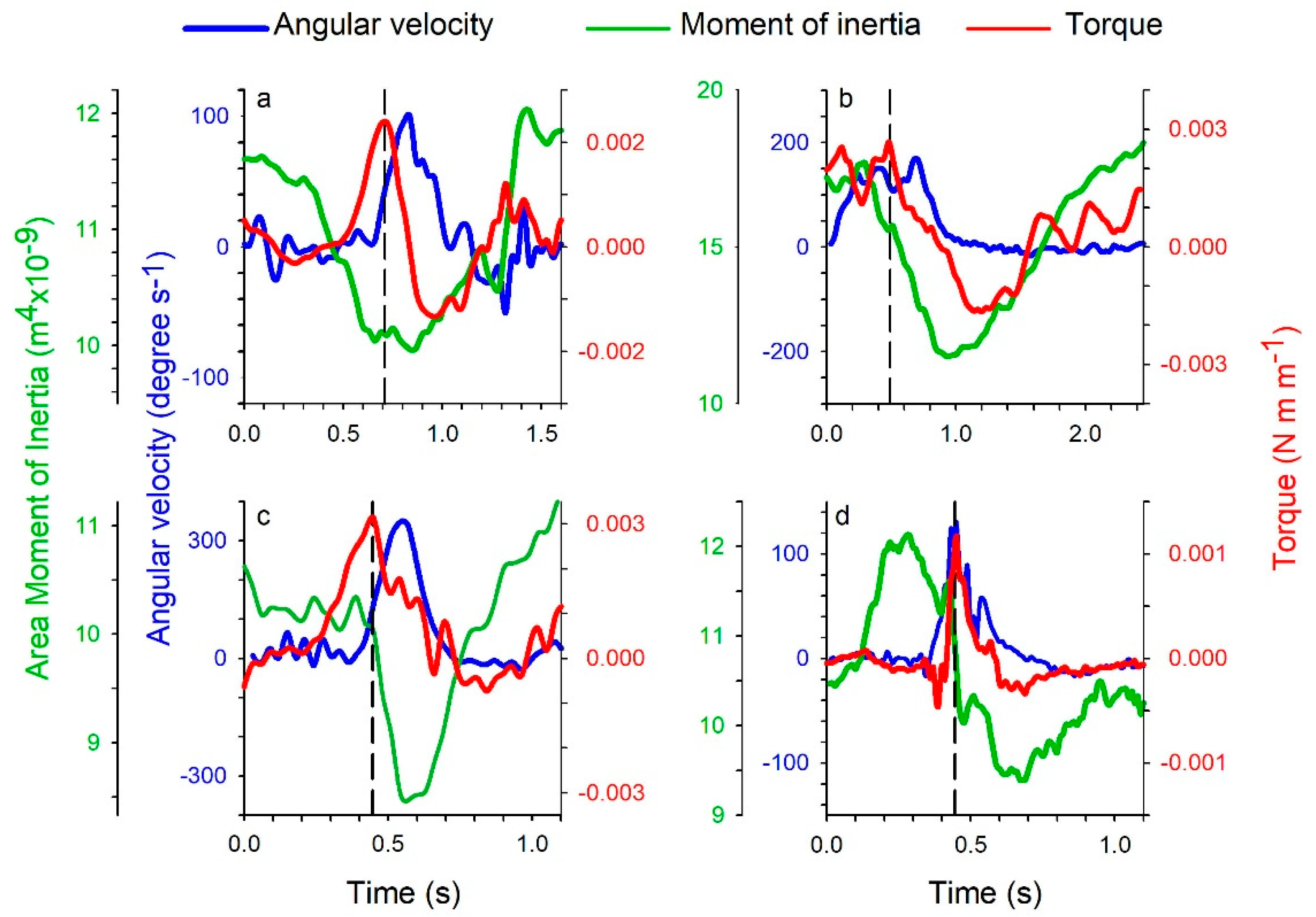
Examination of the body shape during the period of transient pressure buildup led to the discovery of a small, rapid asymmetric shift in the curvature of the animal body immediately preceding the turn for both the jellyfish (1.5 ± 1.0 percent change in curvature, n = 10 individuals) and the zebrafish (0.8 ± 0.2 percent, n = 10 individuals). Although the amplitude of this initial body bend was small, it occurred over a sufficiently short period of time—few milliseconds—that the corresponding acceleration of the body was large relative to accelerations during unidirectional swimming. These fluid accelerations occurred along much of the body surface as the extreme outset of the turn (Figure 3). The measured peak accelerations preceding the turn were over 1 m s⁻². This motion was transmitted to the adjacent water via a process known as the acceleration reaction or added-mass effect [25].

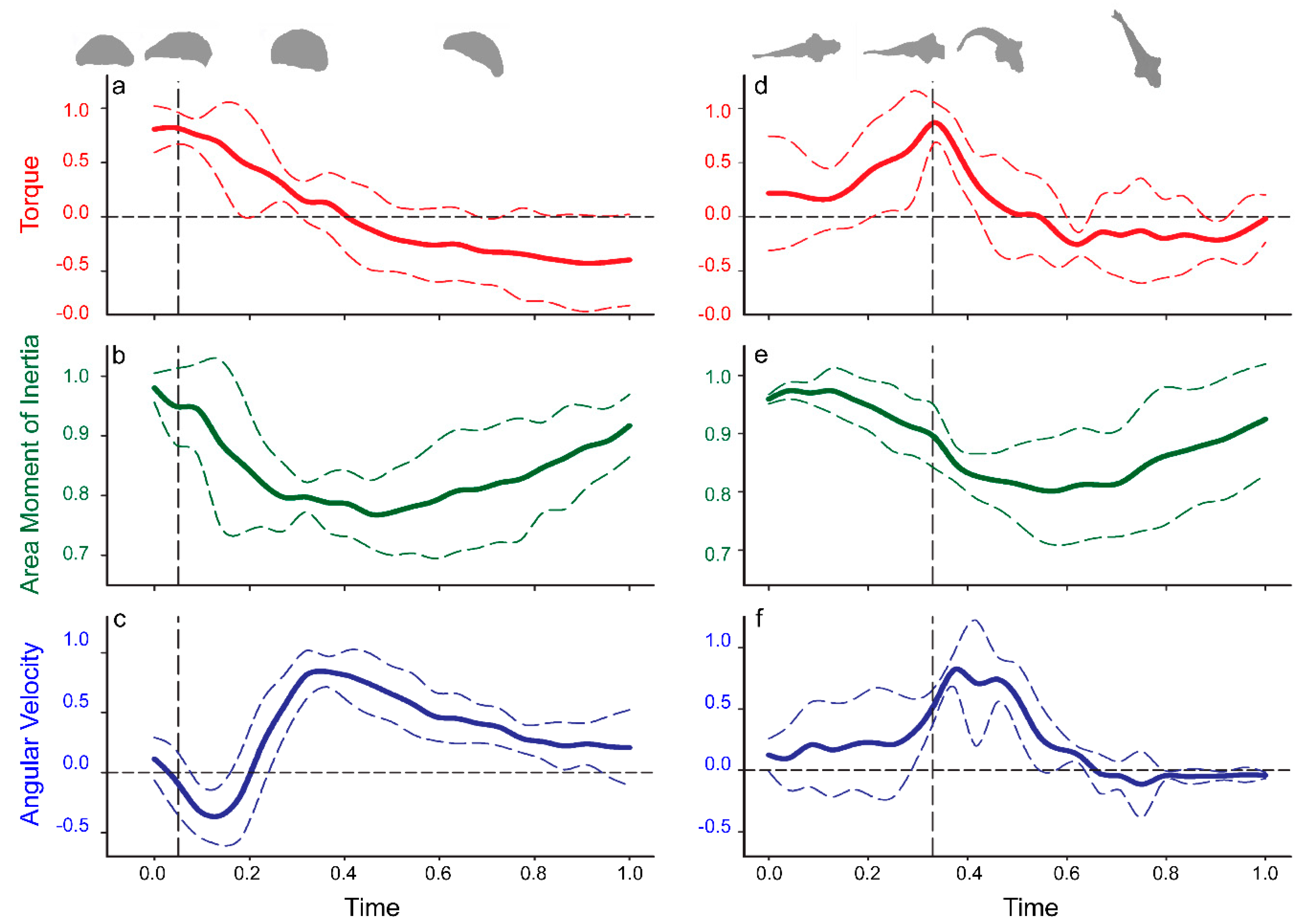
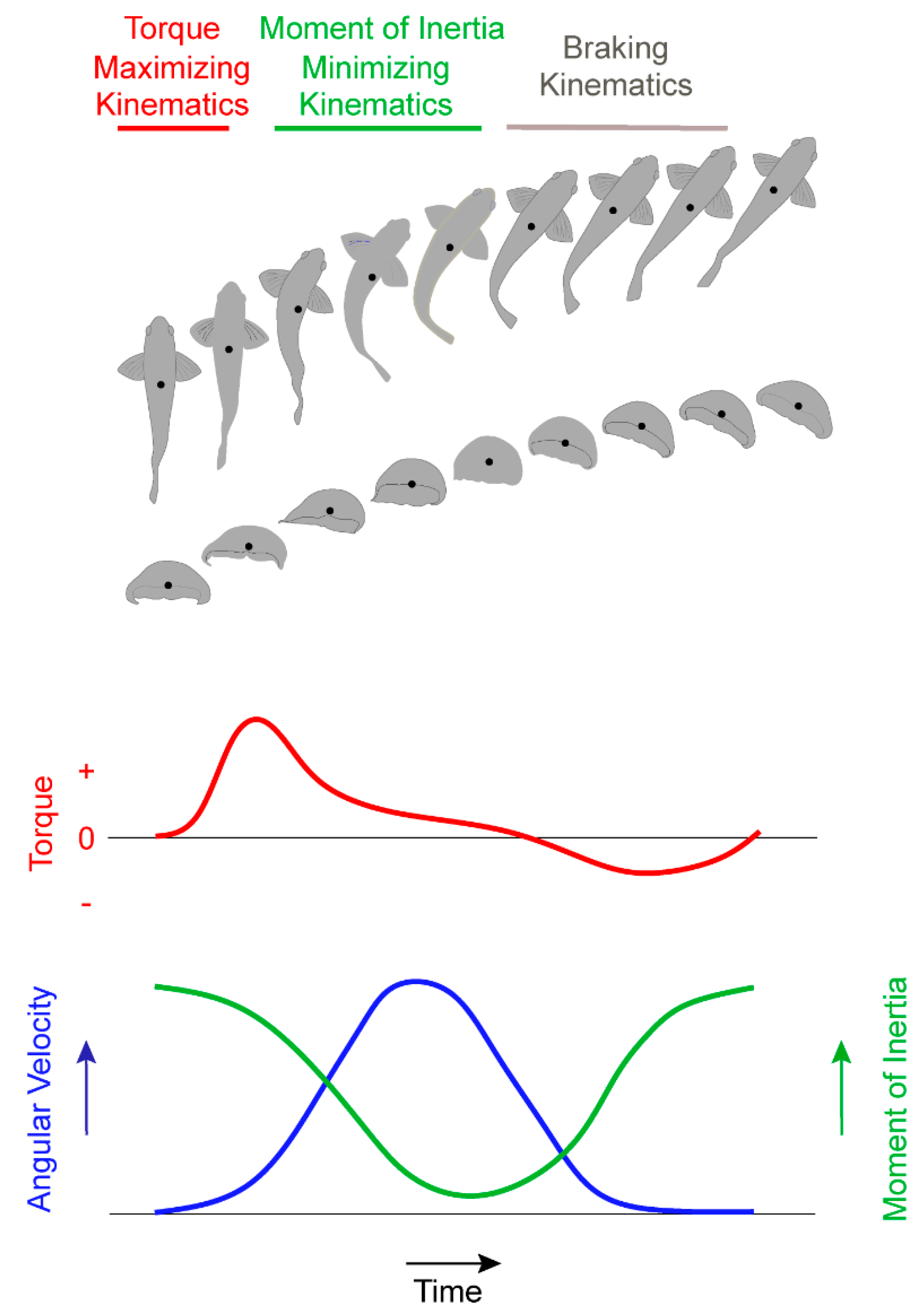
Because the water is effectively incompressible, the fluid in contact with the body responded to the high local body acceleration by an increase in the local fluid pressure where the body was advancing (pushing the water), and a decrease in the local pressure where the body surface retreated from the local water (pulling the water with it). When integrated over the full animal body, the pressure field created by the small, asymmetric body bending leads to a large net torque capable of turning the organism toward a new heading. The more pronounced body motions that occur after the generation of this pressure field do not contribute greatly to torque generation, but they do reduce the moment of inertia of the body (Figure 4; see also Figure A1 and Figure A2). Therefore, the body kinematics that follow peak pressure generation enhance the effect of the generated torque by amplifying the resulting angular acceleration so that the body rotates rapidly through a turn. This sequence of asymmetric body kinematics that initially maximizes torque forces and subsequently minimizes the moment of inertia resolves the fundamental competition between these two components of rotational motion during turns. Although the maximum torque generation and minimum moment of inertia do not occur simultaneously (Figure 5), the inertia of the fluid and of the animal body allows the initial pressure transient to affect subsequent turning dynamics even as fluid viscosity resists body acceleration during a turn.

4. Discussion

We observed strikingly similar turning dynamics for both the jellyfish and the zebrafish, despite their substantially different body organization and swimming kinematics (Figure 2, Figure 3 and Figure 4). The dynamical importance of the observed pressure fields for both the jellyfish and zebrafish was confirmed by computing the net torque (per meter depth) and area moment of inertia of the body. For turns of varying net change in heading, the initial pressure pattern created by the animals was nearly constant. The ultimate magnitude of each turning maneuver was instead modulated by asymmetrical changes in body shape that tuned the moment of inertia and thereby controlled the angular acceleration of the body. In all cases, the relationships between pressure measurements and turning kinematics followed a similar sequential pattern (Figure 4).

An essential feature of animal turning by the mechanisms described here is the flexibility of the body, which enables the animal to dynamically redistribute its mass to manipulate the lever arm of the propulsive surfaces used to initiate the turn (e.g., the bell margin of the jellyfish and the caudal fin of the zebrafish) and the body moment of inertia (Figure 5). For animal swimmers with flexibility and size scales favoring this process, the performance advantages of this turning strategy may select for very similar turning kinematics despite the vastly different animal forms studied here.

While the present results motivate further study of turning in other swimming animals whose locomotion lies between jellyfish and zebrafish, we anticipate that extension of these findings will depend upon scaling factors that influence the size range over which this approach is effective. In the regime of swimming at low Reynolds numbers (Re = ULν⁻¹, where U and L are the nominal animal swimming speed and size, respectively, and ν is the kinematic viscosity of the water), angular momentum generated during periods of maximum torque would experience rapid viscous dissipation, leaving little remaining angular momentum to complete the turn during the subsequent period of major body bending. For large animals with body lengths on the order of tens of meters, power requirements for rapid body bending may exceed the available muscle capacity. In geometrically similar animals, angular acceleration scales to the −2/3 power of body mass [26], making it more difficult for large animals to generate the initial pressure transient or to alter their moment of inertia through body rearrangement to increase their angular velocity. Hence, very large swimmers such as whales may not bend as readily as smaller animal swimmers such as zebrafish [27]. However, the majority of animal swimmers exist within the millimeter to meter size range [28,29], in which a time-varying lever arm enabled by body bending would provide favorable performance advantages relative to rigid body turning mechanics.

Although the patterns that we describe here—torque maximization followed by concomitant alterations in moment of inertia and angular velocity—may appear unexpected for animal swimmers, a well-developed body of research in the field of human gymnastic diving provides a more intuitive guide to the mechanics of animal turning. Human divers generate all of their angular momentum before they leave the springboard and subsequent alterations in turning velocity come about solely by modulation of the diver’s moment of inertia [30]. The diver’s ability to rapidly rotate through somersaults and aerial maneuvers depends on the ability to redistribute body mass and alter the diver’s moment of inertia [31]. Although the animal models documented here capitalized on self-generated pressure fields rather than a springboard, they utilized analogous patterns to human divers for increasing angular velocity by decreasing moment of inertia during through turning maneuvers. The essential physical relationships between time-varying lever arm deployment, moment of inertia and angular velocity provide a very basic mechanical process enabling rapid turning. For animal swimmers within the size scales favoring this process, the performance advantages of this sequence may select for very similar turning kinematics and provide insight into the convergence of very different animal forms, such as medusae and fish, on similar turning mechanics.

These observations of a large dynamical impact from small kinematic shifts can motivate further study of the neuromuscular control of aquatic locomotion and engineered systems that aim to be inspired by animal swimming. In particular, while nature has not converged upon unidirectional locomotion that leverages similar kinematic subtleties as in turning (i.e., steady, straight swimming does not exhibit the small body motions observed here), it might be feasible to achieve net propulsion using such an approach in a robotic system. The pronounced pressure fields observed presently in the jellyfish and zebrafish are incompatible with unidirectional translation, as they achieve high net torque but low net force due to the balance of high and low pressure on either side of the animal. However, it is conceivable that modified kinematics could result in net propulsive force.

More broadly, an appreciation of the important role of turning maneuvers in the success of aquatic locomotion can influence efforts to understand the role of physical forces in the evolution and ecology of other animal swimmers. The methods employed here to study freely swimming organisms and to quantify their dynamics in terms of pressure field manipulations provide a powerful tool to enable new insights into aquatic locomotion. The solution arrived at by our study organisms allows them to initially maximize torque production before major body curvature changes that subsequently minimize the moment of inertia by bending. Further testing with other animal swimmers will be important for evaluating whether this pattern has influenced the widespread capability of swimmers to re-arrange their mass by flexible bending. Application of similar non-invasive approaches can provide new pathways to understanding the complex physical exchanges that take place between animals and their surrounding fluids.