Assessment of CFD Solvers and Turbulent Models for Water Free Jets in Spillways
Abstract
1. Introduction
2. Numerical Modelling
2.1. Comparison of the Used Solvers
- subscript defines the phase;
- —phase fraction;
- —velocity;
- —pressure;
- —combined turbulent (Reynolds) and viscous stress;
- —inter-phase momentum transfer term.
2.2. Turbulence Models
- —turbulent kinetic energy;
- —effective diffusivity for ;
- —turbulent kinetic energy production rate;
- —turbulent kinetic energy dissipation rate;
- —effective diffusivity for ;
- , and —model coefficients, , , ;
- —turbulent kinetic energy production rate;
- —model coefficient, ;
- —internal source term for k
- —turbulent kinetic energy dissipation rate;
- —effective diffusivity for ;
- —viscosity;
- —closure coefficient;
- —lending function;
- ;
- —internal source term for .
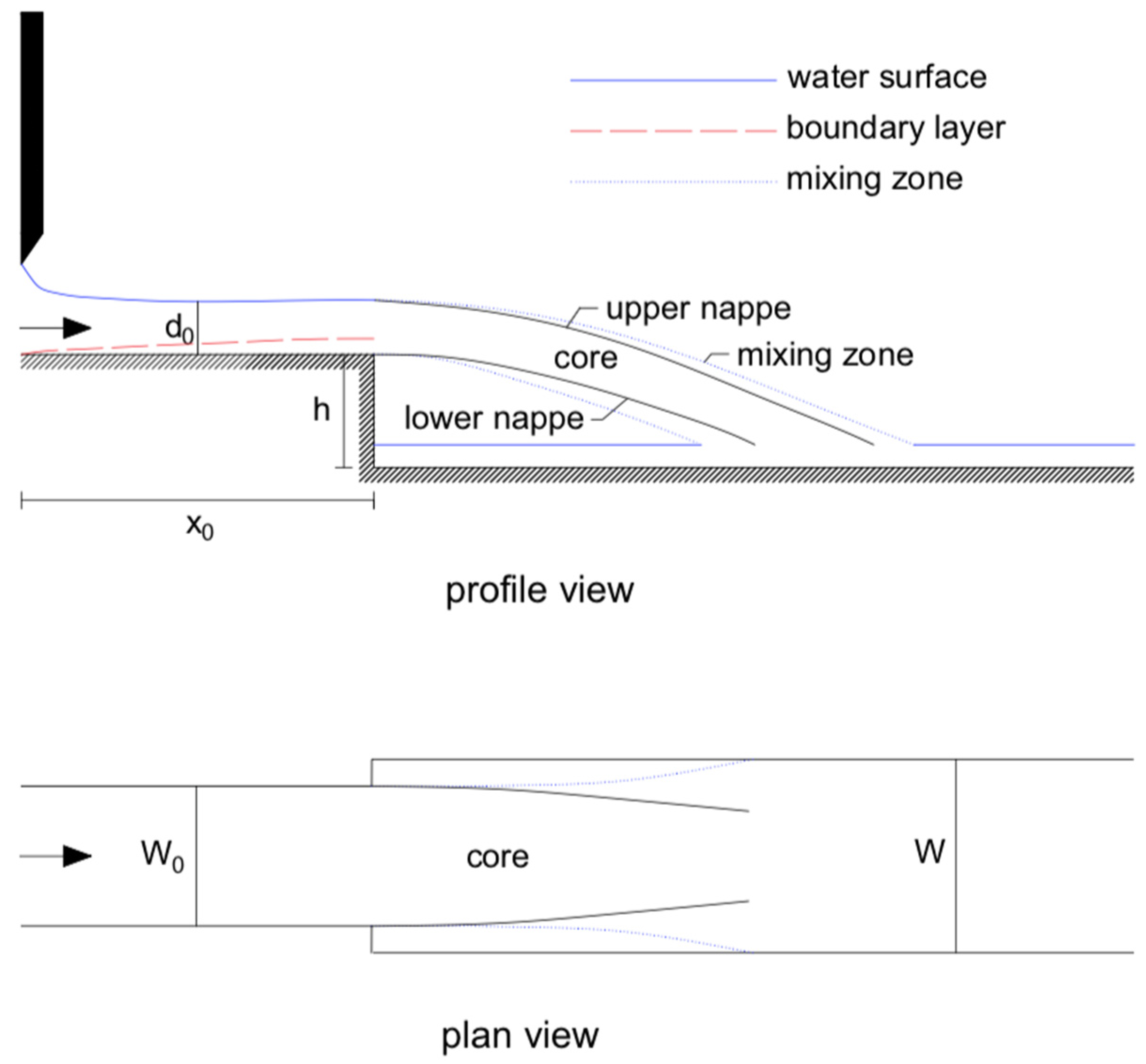
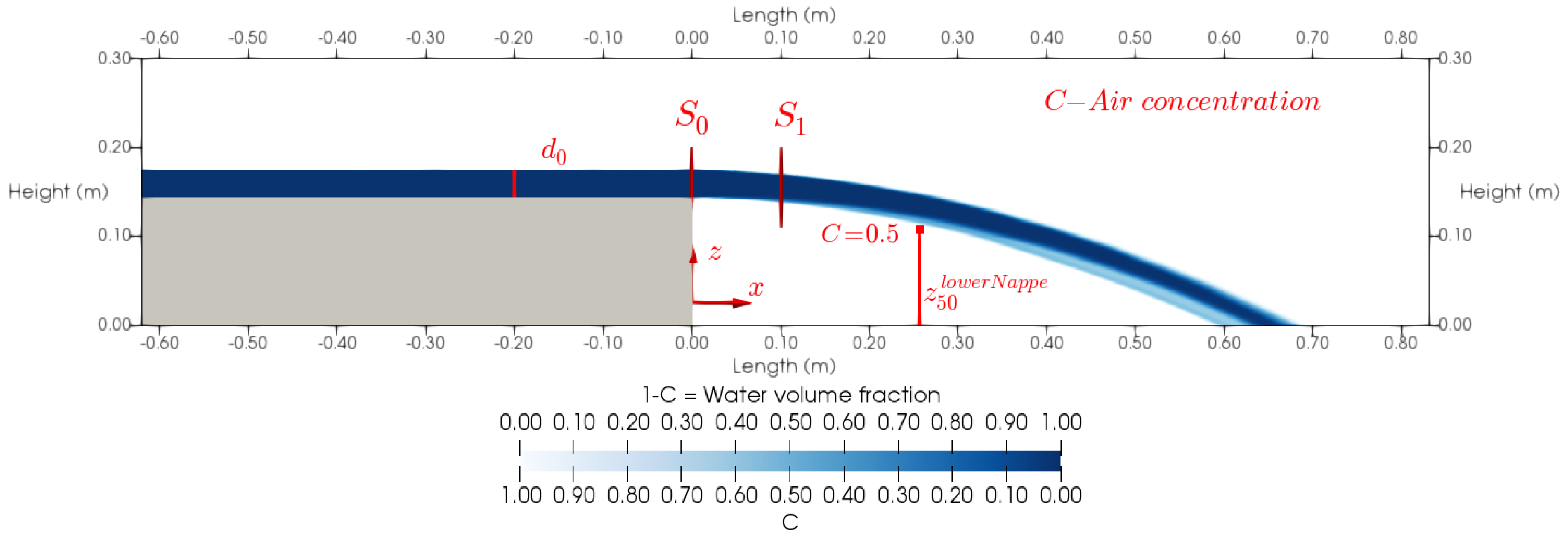
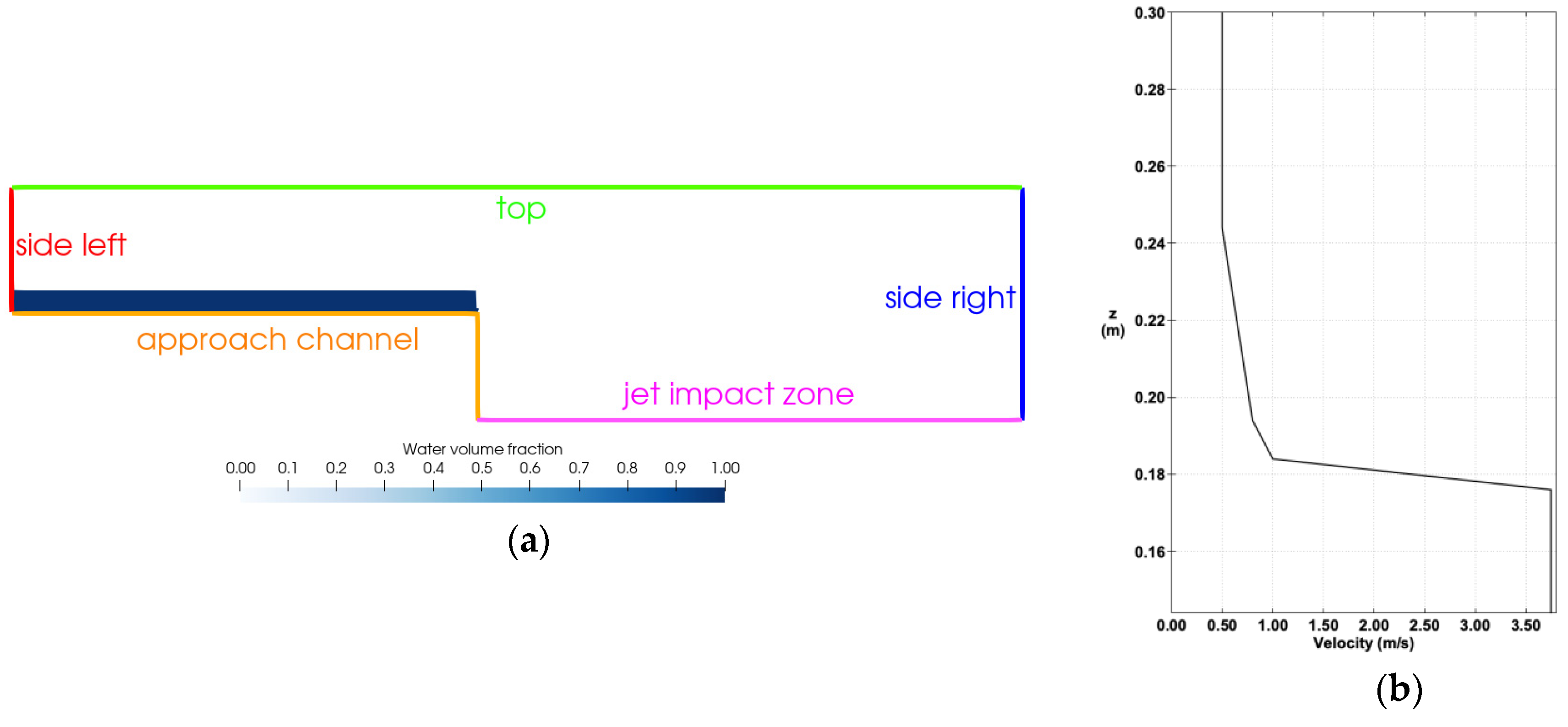
2.3. Mesh
- —vertical distance (m);
- —vertical distance of the point with C = 0.5 in the upper nappe to the floor (m);
- —vertical distance of the point with C = 0.5 in the lower nappe to the floor (m);
- —approach flow depth (m);
- —flow velocity (m/s);
- —potential velocity of the flow at a cross-section (m/s);
- —distance from the step (m).
2.4. Boundary Conditions
2.5. Numerical Schemes
3. Results and Discussion
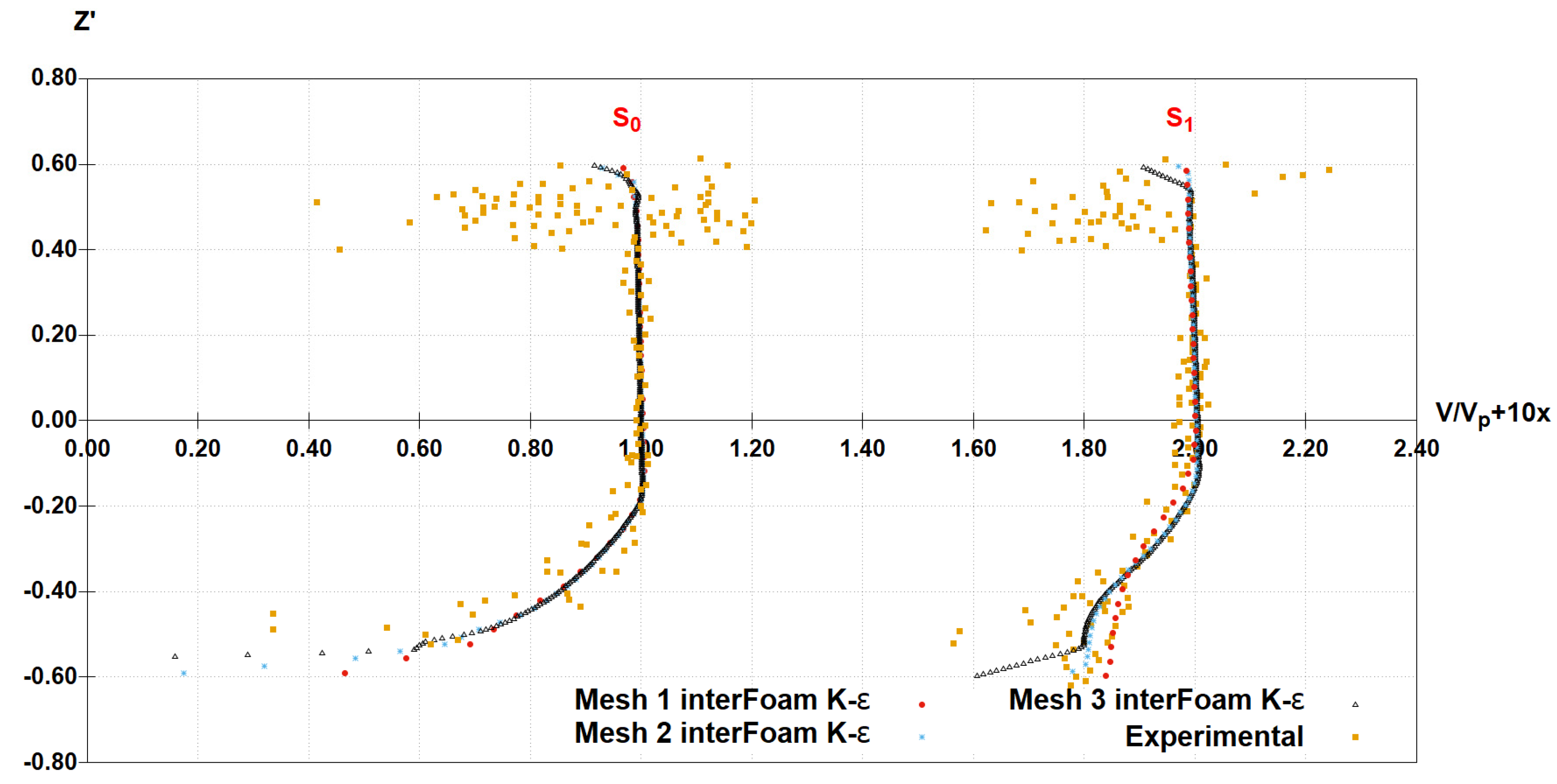
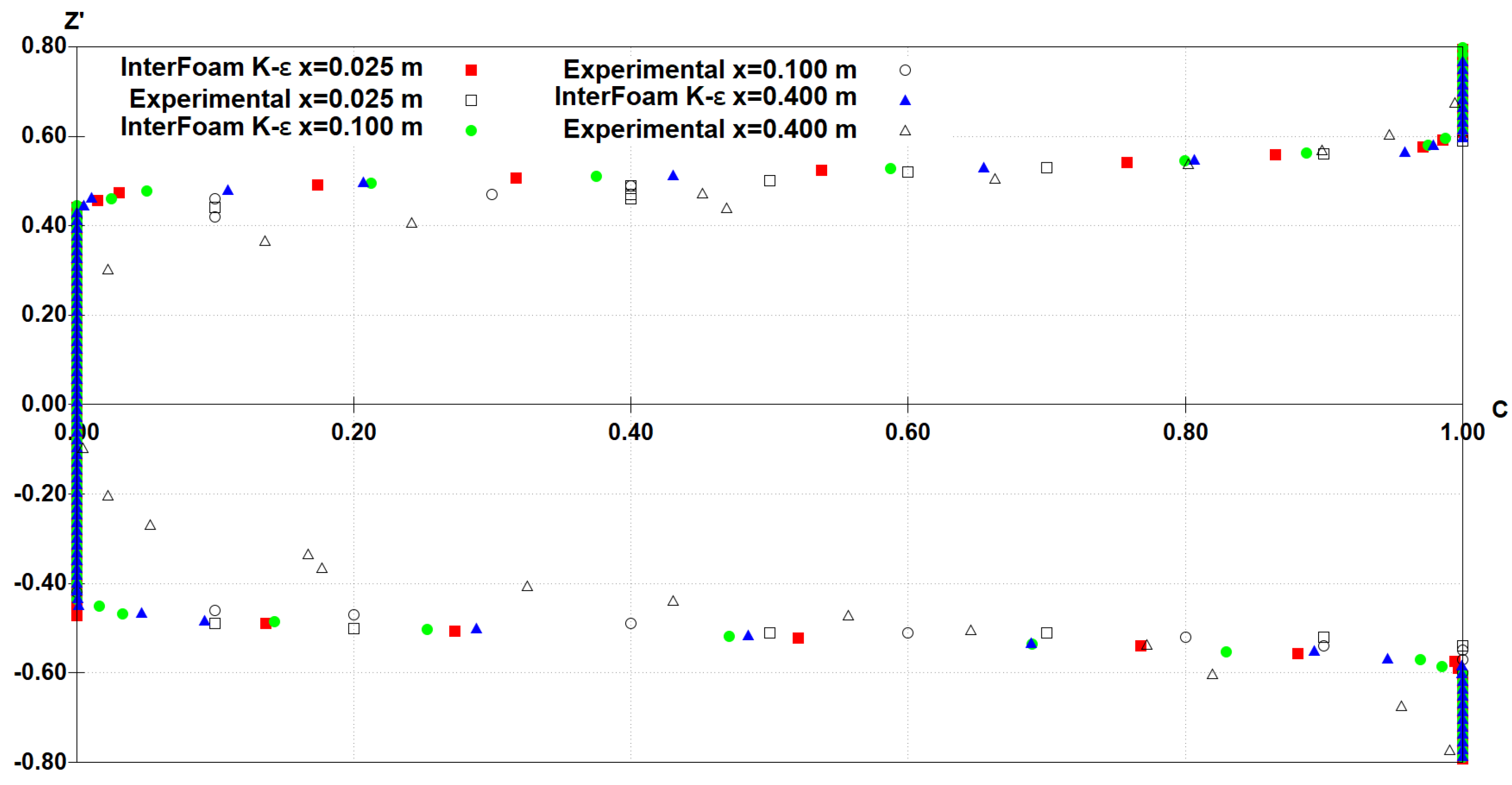
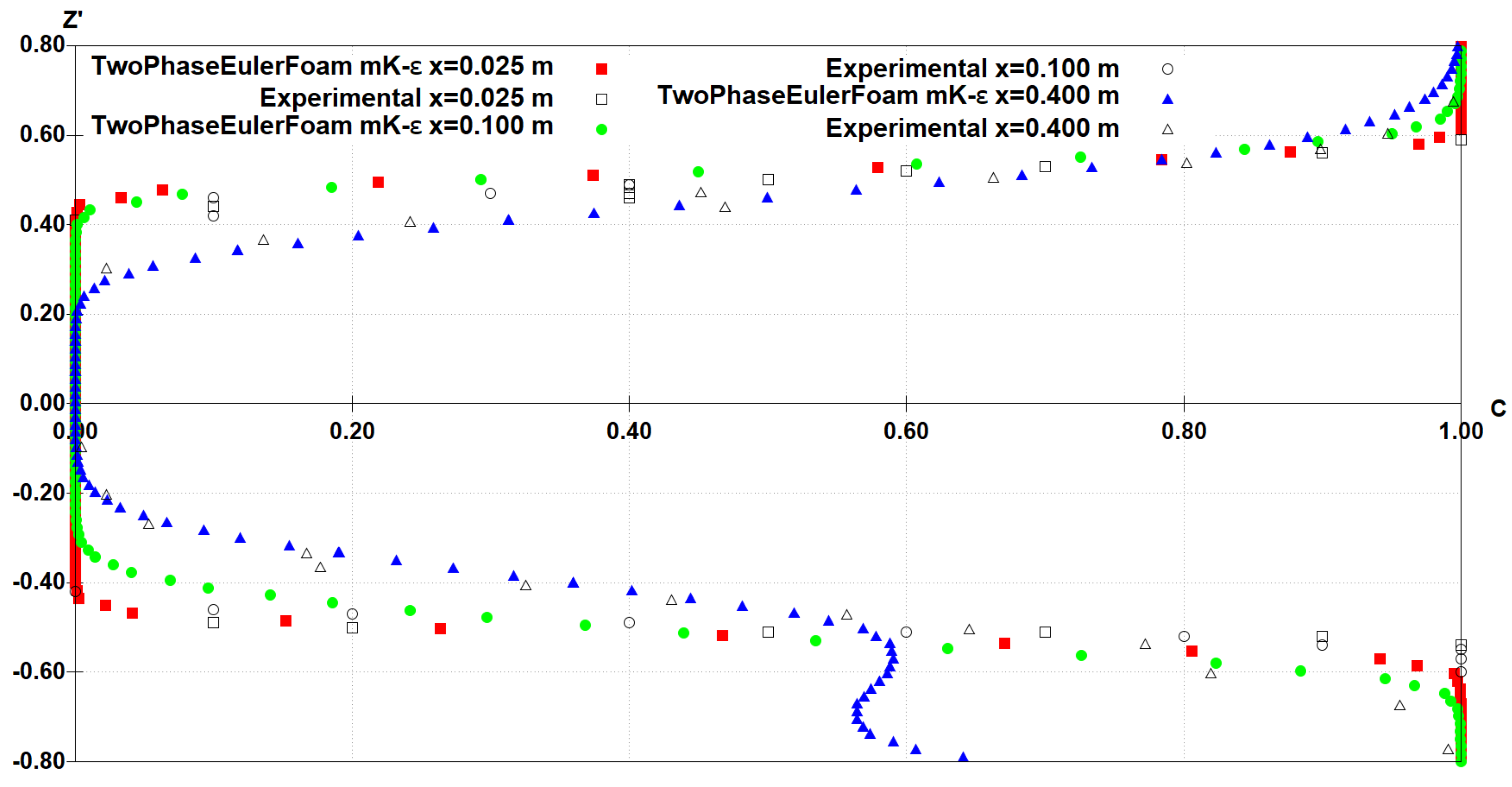
3.1. Velocity
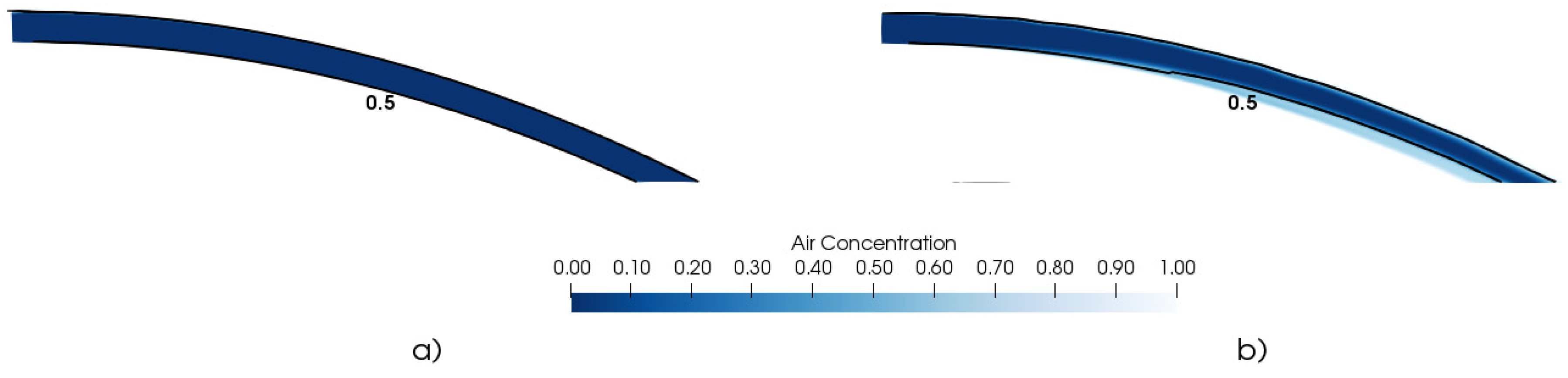
3.2. Air Concentration
3.3. Turbulence Intensity
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Heller, V.; Hager, W.H.; Minor, H. Ski Jump Hydraulics. J. Hydraul. Eng. 2005, 131, 46–51. [Google Scholar] [CrossRef]
- Bollaert, E.F.R.; Schleiss, A.J. Scour of rock due to the impact of plunging high velocity jets Part I: A state-of-the-art review. J. Hydraul. Res. 2003, 41, 451–464. [Google Scholar] [CrossRef]
- Whittaker, J.G.; Schleiss, A.J. Scour Related to Energy Dissipaters for High. In Head Structures ETHZ VAW Report No. 73; Swiss Federal Institute of Technology Zurich: Zürich, Switzerland, 1984. [Google Scholar]
- Duarte, R.; Bollaert, E.F.R.; Schleiss, A.J.; Pinheiro, A. Dynamic pressures around a confined block impacted by plunging aerated high-velocity jets. In Proceedings of the 2nd European IAHR Congress, Munich, Germany, 27–29 June 2012. [Google Scholar]
- Beltaos, S.; Rajaratnam, N. Plane Turbulent Impinging Jets. J. Hydraul. Res. 1973, 11, 29–59. [Google Scholar] [CrossRef]
- Ervine, D.A.; Elsawy, E.M. Effect of turbulence intensity on the rate of air entrainment by plunging water jets. Proc. Inst. Civ. Eng. 1980, 69, 425–445. [Google Scholar] [CrossRef]
- Ervine, D.A.; Falvey, H.T. Behavior of Turbulent Water Jets in the Atmosphere and in Plunge Pools. Proc. Inst. Civ. Eng. 1987, 83, 295–314. [Google Scholar]
- Rajaratnam, N.; Rizvi, S.A.H.; Steffler, P.M.; Smy, P.R. An experimental study of very high velocity circular water jets in air. J. Hydraul. Res. 1994, 32, 461–470. [Google Scholar] [CrossRef]
- Toombes, L.; Chanson, H. Free-surface aeration and momentum exchange at a bottom outlet. J. Hydraul. Res. 2007, 45, 100–110. [Google Scholar] [CrossRef]
- Lin, C.; Hwung, W.Y.; Hsieh, S.C.; Chang, K.A. Experimental study on mean velocity characteristics of flow over vertical drop. J. Hydraul. Res. 2007, 45, 33–42. [Google Scholar] [CrossRef]
- Steiner, R.; Heller, V.; Hager, W.H.; Minor, H.-E. Deflector Ski Jump Hydraulics Remo. J. Hydraul. Eng. 2008, 134, 1094–1100. [Google Scholar] [CrossRef]
- Pfister, M.; Hager, W.H.; Boes, R.M. Trajectories and air flow features of ski jump-generated jets. J. Hydraul. Res. 2014, 52, 336–346. [Google Scholar] [CrossRef]
- Ho, D.K.H.; Riddette, K.M. Application of computational fluid dynamics to evaluate hydraulic performance of spillways in Australia. Aust. J. Civ. Eng. 2010, 6, 81–104. [Google Scholar] [CrossRef]
- Deshpande, S.S.; Trujillo, M.F.; Wu, X.; Chahine, G. Computational and experimental characterization of a liquid jet plunging into a quiescent pool at shallow inclination. J. Heat Fluid Flow 2012, 34, 1–14. [Google Scholar] [CrossRef]
- Castillo, L.G.; Carrillo, J.M.; Sordo-Ward, Á. Simulation of overflow nappe impingement jets. J. Hydroinformatics 2014, 16, 922–940. [Google Scholar] [CrossRef]
- Shonibare, O.Y.; Wardle, K.E. Numerical investigation of vertical plunging jet using a hybrid multifluid-VOF multiphase CFD solver. Int. J. Chem. Eng. 2015. [Google Scholar] [CrossRef]
- Castillo, L.G.; Carrillo, J.M.; Bombardelli, F.A. Distribution of mean flow and turbulence statistics in plunge pools. J. Hydroinformatics 2017, 19, 173–190. [Google Scholar] [CrossRef]
- OpenCFD Limited. OpenFOAM User Guide; OpenCFD Limited: Bracknell, UK, 2018. [Google Scholar]
- Manafpour, M.; Ebrahimnezhadian, H. The Multiphase Capability of Openfoam CFD Toolbox in Solving Flow Field in Hydraulic Structure. In Proceedings of the 4th International Conference on Long-Term Behavior and Eco-Friendly Dams, Tehran, Iran, 17–19 October 2017; pp. 323–330. [Google Scholar] [CrossRef]
- Schulze, L.; Thorenz, C. The Multiphase Capabilities of the CFD Toolbox OpenFOAM for Hydraulic Engineering Applications. In Proceedings of the ICHE 2014, Hamburg, Germany, 28 September–2 October 2014; pp. 1007–1014. [Google Scholar]
- Bombardelli, F. Computational multi-phase fluid dynamics to address flows past hydraulic structures. In Proceedings of the 4th IAHR International Symposium on Hydraulic Structures, Porto, Portugal, 9–11 February 2012. [Google Scholar]
- Wang, Y.; Politano, M.; Weber, L. Spillway jet regime and total dissolved gas prediction with a multiphase flow model. J. Hydraul. Res. 2019, 57, 26–38. [Google Scholar] [CrossRef]
- Deshpande, S.S.; Anumolu, L.; Trujillo, M.F. Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Discov. 2012, 5, 014016. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretized fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Behzadi, A.; Issa, R.I.; Rusche, H. Modelling of dispersed bubble and droplet flow at high phase fractions. Chem. Eng. Sci. 2004, 59, 759–770. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. Turbul. Heat Mass Transfer. 2003, 4, 625–632. [Google Scholar]
- Rusche, H. Compaction of a Clay Loam Soil in Pannonian Region of Croatia under Different Tillage Systems. Ph.D. Thesis, Imperial College of Science, Technology & Medicine, London, UK, 2002. [Google Scholar]
- Falvey, H.T. Air-Water Hydraulic Flow in Structures; Engineering Monograph No. 41; United States Department of the Interior, Water and Power Resources Service: Denver, CO, USA, 1980.
- Chanson, H. Velocity measurements within high velocity air-water jets. J. Hydraul. Res. 1993, 31, 365–382. [Google Scholar] [CrossRef]





| Features | interFoam | twoPhaseEulerFoam |
|---|---|---|
| Formulation | Euler-Euler (VOF) | Euler-Euler (Dispersed) |
| Phases | Two continuous | One continuous One dispersed |
| Mass and momentum equations | One set of equations | Two sets of equations |
| Interphase mass and momentum transfer | No | Yes |
| Mesh | Sub-Domains | Cell Dimensions (mm) | Number of Cells in a Cross-Section of the Jet | Total Number of Cells of the Mesh | y+ |
|---|---|---|---|---|---|
| 1 | All domain | 2.00 | ≈15 | 86.430 | 150 |
| 2 | Far from the jet Jet and vicinity | 2.00 1.00 | ≈30 | 227.545 | 75 |
| 3 | Far from the jet Jet and vicinity | 2.00 0.25 | ≈120 | 2.074.297 | 75 |
| Term | interFoam | twoPhaseEulerFoam |
|---|---|---|
| convection | Gauss Van Leer | Gauss Van Leer |
| artificial compression | Gauss linear | Gauss Van Leer |
| momentum transport | Gauss linear Upwind grad(U) | Gauss upwind |
| turbulence | Gauss upwind | Gauss upwind |
| Inlet Turbulence Intensity (%) | interFoam (%) | twoPhaseEulerFoam (%) |
|---|---|---|
| 10.00 | 1.86 | 2.67 |
| 1.00 | 1.83 | 2.65 |
| 0.10 | 1.93 | 2.66 |
| 0.01 | 1.87 | 2.75 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muralha, A.; Melo, J.F.; Ramos, H.M. Assessment of CFD Solvers and Turbulent Models for Water Free Jets in Spillways. Fluids 2020, 5, 104. https://doi.org/10.3390/fluids5030104
Muralha A, Melo JF, Ramos HM. Assessment of CFD Solvers and Turbulent Models for Water Free Jets in Spillways. Fluids. 2020; 5(3):104. https://doi.org/10.3390/fluids5030104
Chicago/Turabian StyleMuralha, António, José F. Melo, and Helena M. Ramos. 2020. "Assessment of CFD Solvers and Turbulent Models for Water Free Jets in Spillways" Fluids 5, no. 3: 104. https://doi.org/10.3390/fluids5030104
APA StyleMuralha, A., Melo, J. F., & Ramos, H. M. (2020). Assessment of CFD Solvers and Turbulent Models for Water Free Jets in Spillways. Fluids, 5(3), 104. https://doi.org/10.3390/fluids5030104







