Soliton Turbulence in Approximate and Exact Models for Deep Water Waves

Abstract

We investigate and compare soliton turbulence appearing as a result of modulational instability of the homogeneous wave train in three nonlinear models for surface gravity waves: the nonlinear Schrödinger equation, the super compact Zakharov equation, and the fully nonlinear equations written in conformal variables. We show that even at a low level of energy and average wave steepness, the wave dynamics in the nonlinear Schrödinger equation fundamentally differ from the dynamics in more accurate models. We study energy losses of wind waves due to their breaking for large values of total energy in the super compact Zakharov equation and in the exact equations and show that in both models, the wave system loses 50% of energy very slowly, during few days.

1. Introduction

Turbulence in nonlinear continuous media often accompanied by the appearance of localized nonlinear structures. In those cases, when the equations describing the medium have stable soliton solutions, the solitons are natural candidates for the role of such structures, and turbulence can be called soliton turbulence.

The study of soliton turbulence in various nonlinear models is of considerable interest that can be confirmed by numerous works. The problem of a statistical description of a large number of solitons in the framework of the Korteweg-de Vries equation was first considered in [1]. The kinetic equation was obtained that describes the distribution function of soliton parameters for the case of a low density of solitons. The turbulence of rarified soliton gas plays the key role in the formation of wave field statistics (see the works [2,3]). With the use of direct numerical simulations methods, the collective behaviour of soliton ensembles was also studied in [4]. The general case of dense soliton gas was considered in [5,6].

The Nonlinear Schrödinger Equation (NLS) is a special case of such models and a universal model for wave turbulence studying. However, it is an integrable equation, and turbulence in the framework of the NLS equation has essential peculiarities. The interaction of solitons in this model in some sense can be called simple. Collisions of the NLS solitons are completely “elastic”, that is, there are no energy exchanges between them and their basic parameters, amplitudes and velocities, do not change. One of the main parameters that play an important role in the dynamics of solitons pairwise interactions is the relative phase of solitons at the moment of their collision. For example, the maximum amplitude amplification of the solitons in a collision is determined by the synchronization of their phases. Phase synchronization also plays an important role in the formation of extreme amplitude waves or rogue waves. In recent works [7,8] phase synchronization in multisoliton ensembles was studied analytically. Using the inverse scattering transform formalism, the authors of work [9] show that the dense soliton gas is the model of the asymptotic stage of the noise-induced modulation instability in the NLS equation. Rarefied soliton gas was also reproduced experimentally in an optical fiber ring resonator with the initial wavefield taken as arithmetic superposition of individual solitons [10] and in water wave tank [11].

It was really mentioned that the NLS equation is completely integrable. It makes it possible to construct the infinite amount of its periodic solution expressed in terms of Jacobi theta-functions. Some of these solutions described the nonlinear stage of modulation instability of the Stokes waves. The theory of these solutions is far elaborated in [12,13,14]. Some of these solutions are beautiful. We plan to study all of them numerically in the closed future.

The soliton turbulence can appear as a result of the modulational instability of the homogeneous wave train. In the pioneer work [15] the evolution of a nonlinear wave train in deep water was studied experimentally and numerically. In particular, it was shown that at later stages of evolution, the wave train exhibits the Fermi-Pasta-Ulam recurrence phenomenon, which is consistent with the results of numerical simulation in the framework of the nonlinear Schrödinger equation. In a later work [16], it was shown that an arbitrary-shaped pulse ultimately decays into a set of solitons, the number of which is determined by the initial conditions. An experimental study of the spatial evolution of unidirectional waves on the water with the formation of nonlinear coherent structures coexisting with smaller stochastic waves was carried out in [17]. The properties of extreme water waves developing as a result of modulation instability of initially uniform slightly modulated wave train in the framework of NLS equation and full Euler equations were examined in work [18]. The authors identified a maximum possible amplitudes of non-breaking waves in the wide range of initial wave train parameters.

In this work, we investigate and compare soliton turbulence appearing as a result of modulational instability of the homogeneous wave train on the surface of deep water in the framework approximate and exact nonlinear hydrodynamic models.

The set of equations describing a two-dimensional potential flow of an ideal incompressible fluid of infinite depth with a one-dimensional free surface in a gravity field are well known and can be written as:

$$\begin{array}{c}{\varphi }_{xx}+{\varphi }_{yy}=0({\varphi }_y\to 0,y\to -\infty ),\hfill \\ {\eta }_t+{\eta }_x{\varphi }_x={\varphi }_y{\mid }_{y=\eta },\hfill \\ {\varphi }_t+\frac{1}{2}({\varphi }_x^2+{\varphi }_y^2)+g\eta =0{\mid }_{y=\eta }.\hfill \end{array}$$

(1)

Here x and y are the horizontal and vertical coordinates, t is time, g is the free-fall acceleration, $\eta (x,t)$ is the shape of the surface, $\varphi (x,y,t)$ is the hydrodynamic potential inside the fluid. The first equation in (1) is the Laplace equation for the hydrodynamic potential, while the second and third equations are kinematic and dynamic conditions at the fluid surface.

As well known, a one-dimensional potential flow of an ideal fluid of infinite depth in the presence of gravity is a Hamiltonian system. As was shown by Zakharov [19], the surface elevation $\eta (x,t)$ and the velocity potential at the surface ${\psi (x,t)=\varphi (x,y,t)|}_{y=\eta }$ of the fluid are canonically conjugated variables and satisfy the following equations:

$$\frac{\partial \psi }{\partial t}=-\frac{\delta H}{\delta \eta },\frac{\partial \eta }{\partial t}=\frac{\delta H}{\delta \psi }.$$

(2)

Here H is the Hamiltonian, i.e., total energy of the fluid:

$$\begin{array}{ccc}H\hfill & =& \frac{1}{2}\int dx{\int }_{-\infty }^{\eta }{|\nabla \varphi |}^{2}dy+\frac{g}{2}\int {\eta }^{2}dx.\hfill \end{array}$$

(3)

In the assumption of small wave steepness the Hamiltonian can be represented as the infinite series of powers of $\eta$ and $\psi$ (see [19]). We consider this series up to the fourth order term:

$$\begin{array}{ccc}H\hfill & =& \frac{1}{2}\int (g{\eta }^2+\psi \widehat{k}\psi )dx-\frac{1}{2}\int \{{(\widehat{k}\psi )}^2-{({\psi }_x)}^2\}\eta dx+\frac{1}{2}\int \{{\psi }_{xx}{\eta }^2\widehat{k}\psi +\psi \widehat{k}(\eta \widehat{k}(\eta \widehat{k}\psi ))\}dx.\hfill \end{array}$$

(4)

Here the operator $\widehat{k}$ means multiplication by $\left|k\right|$ in k-space.

In 2011 (see papers [20,21]), Dyachenko and Zakharov assuming that all waves propagate in a single direction applied a canonical transformation to remove all cubic nonlinear terms and to drastically simplify fourth-order terms in the truncated Hamiltonian (4). This transformation is possible due to the unexpected cancellation of non-trivial four-wave interactions in the one-dimensional case [22]. In 2017 analyzing the form of the coefficient of four-wave interactions, we found another the most optimal canonical transformation to new normal variables, which allows us to simplify the fourth-order term in the Hamiltonian further (see [23]). The water wave equation in terms of these variables has a remarkably simple form that we named “the super compact equation”. The super compact equation includes only two nonlinear terms—wave term and an advection term, that can describe the initial stage of wave-breaking. Due to the specific type of cubic nonlinearity in that equation, it allows introducing an exact envelope for waves without the assumption of narrowness bandwidth (see [24]). This compact Dyachenko-Zakharov envelope equation reduces to the well-known Dysthe equation and further to the NLS equation in the limit of small steepness and assumption of the narrowband spectrum.

In this work, we observe soliton turbulence appearing as a result of modulational instability of the homogeneous wave train in the framework nonlinear hydrodynamic models for free surface waves:

• the nonlinear Schrödinger equation (NLS),
• the super compact Zakharov equation [23] (SCZ),
• the fully nonlinear equations written in conformal variables [25] (RV).

The measure of the nonlinearity of wave at the surface of deep water is their average steepness $\mu =<\nabla \eta >$. We perform the series of numerical simulations in the framework of these models for a very long time (about hundred of thousands of characteristic wave period) varying initial measures of nonlinearity $\mu \simeq 0.04-0.08$. We set the same initial conditions for all models, which allows us to compare the results and identify the applicability of approximate weakly nonlinear equations.

We also take into account energy dissipation due to wave breaking in the super compact Zakharov equation and the fully nonlinear equations using the simple model of dissipation of such waves that we proposed earlier in [24]. The results obtained in the framework of super compact Zakharov equation and the RV equations show that for moderate values of the average slope of the wave for a hundred thousand characteristic periods of the wave, the sea loses about 40–50% of its energy.

2. Nonlinear Models for Deep Water Gravity Waves

In this section, we very briefly derive three nonlinear hydrodynamic models for free surface waves: the super compact Zakharov equation based on the truncated Hamiltonian (4), the nonlinear Schrödinger equation and the fully nonlinear equations written in conformal variables. All the details of the derivation can be found in [23,26].

2.1. Super Compact Zakharov Equation and the Nonlinear Schrödinger Equation

We use canonical transformation from the pair of classical physical Hamiltonian variables $\eta (x,t)$ and $\psi (x,t)$ to normal complex variable $c(x,t)$. This canonical transformation can be written as power series of $c_k$ up to the third order:

$$\begin{array}{ccc}{\eta }_k\hfill & =& {\eta }_k^{\left(1\right)}+{\eta }_k^{\left(2\right)}+{\eta }_k^{\left(3\right)}\hfill \\ {\psi }_k\hfill & =& {\psi }_k^{\left(1\right)}+{\psi }_k^{\left(2\right)}+{\psi }_k^{\left(3\right)}.\hfill \end{array}$$

(5)

and described in detail in [23]. As a result of the transformation the Hamiltonian takes the following form in x-space:

$$\begin{array}{ccc}H\hfill & =& \int c^{*}{\widehat{V}}_{k}cdx+\frac{1}{2}\int \left[\frac{i}{4}(c^2\frac{\partial }{\partial x}{c^{*}}^2-{c^{*}}^2\frac{\partial }{\partial x}{c}^2)-{\left|c\right|}^2\widehat{k}{\left(\right|c|}^2)\right]dx\hfill \end{array}$$

(6)

Here the operator ${\widehat{V}}_k$ is multiplication by $\frac{{\omega }_k}{k}$ in Fourier space. And the equation of motion or the super compact Zakharov (SCZ) equation then is the following:

$$\begin{array}{c}\frac{\partial c}{\partial t}+i{\widehat{\omega }}_{k}c-i{\partial }_x^{+}\left({\left|c\right|}^2\frac{\partial c}{\partial x}\right)={\partial }_x^{+}\left(\mathcal{U}c\right).\hfill \end{array}$$

(7)

Here the operator ${\widehat{\omega }}_k$ is Fourier multiplier by the $\sqrt{gk}$. The operator ${\partial }_x^{+}$ in the Fourier space is $ik\theta \left(k\right)$, where $\theta \left(k\right)$ is the Heaviside step function. And we also introduce the advection velocity $\mathcal{U}$:

$$\begin{array}{c}\mathcal{U}=\widehat{k}\left({\left|c\right|}^2\right)\hfill \end{array}$$

(8)

The physical variables $\eta$ and $\psi$ can be recovered by the canonical transformation (5). An important property of this canonical transformation is that the linear and second order terms can be written in x–space, in a compact way:

$$\begin{array}{ccc}{\eta }^{(1)}(x)\hfill & =& \frac{1}{\sqrt{2}{g}^{\frac{1}{4}}}({\widehat{k}}^{-\frac{1}{4}}c(x)+{\widehat{k}}^{-\frac{1}{4}}c{(x)}^{*}),\hfill \\ {\psi }^{(1)}(x)\hfill & =& -i\frac{g^{\frac{1}{4}}}{\sqrt{2}}({\widehat{k}}^{-\frac{3}{4}}c(x)-{\widehat{k}}^{-\frac{3}{4}}c{(x)}^{*}),\hfill \\ {\eta }^{(2)}(x)\hfill & =& \frac{\widehat{k}}{4\sqrt{g}}{[{\widehat{k}}^{-\frac{1}{4}}c(x)-{\widehat{k}}^{-\frac{1}{4}}{c}^{*}(x)]}^2,\hfill \\ {\psi }^{(2)}(x)\hfill & =& \frac{i}{2}[{\widehat{k}}^{-\frac{1}{4}}{c}^{*}(x){\widehat{k}}^{\frac{1}{4}}{c}^{*}(x)-{\widehat{k}}^{-\frac{1}{4}}c(x){\widehat{k}}^{\frac{1}{4}}c(x)]+\frac{1}{2}\widehat{H}[{\widehat{k}}^{-\frac{1}{4}}c(x){\widehat{k}}^{\frac{1}{4}}{c}^{*}(x)+{\widehat{k}}^{-\frac{1}{4}}{c}^{*}(x){\widehat{k}}^{\frac{1}{4}}c(x)].\hfill \end{array}$$

(9)

Here $\widehat{H}$—is the Hilbert transformation with eigenvalue $i\mathbf{sign}\left(k\right)$ and operators ${\widehat{k}}^{\alpha }$ act in Fourier space as multiplication by ${\left|k\right|}^{\alpha }$.

Now if we suppose that Fourier spectrum of waves has a maximum at $k=k_0$ we can introduce envelope function $C(x,t)$:

$$c(x,t)=C(x,t){\mathrm{e}}^{i(k_{0}x-{\omega }_{k_0}t)},$$

(10)

where ${\omega }_{k_0}=\sqrt{g{k}_0}$ is the corresponding linear frequency. Using the Equation (10), which is actually canonical transformation, one can easily derive the exact equation for the envelope C that we named “Dyachenko–Zakharov envelope equation” [24].

The Dyachenko-Zakharov envelope equation written in the reference frame moving with the group velocity $V_0=\frac{{\omega }_{k_0}}{2k_0}$ has the following form:

$$\begin{array}{ccc}\frac{\partial C}{\partial t}\hfill & +& i\left[{\omega }_{k_0+k}-{\omega }_{k_0}-\frac{\partial {\omega }_{k_0}}{\partial k_0}\widehat{k}\right]{\widehat{\theta }}_{k_0+k}C+i{k}_0^2{\widehat{\theta }}_{k_0+k}\left[{\left|C\right|}^{2}C\right]\hfill \\ & +& k_0{\widehat{\theta }}_{k_0+k}\left[C\frac{\partial }{\partial x}{\left|C\right|}^2+{2\left|C\right|}^2\frac{\partial C}{\partial x}-i\widehat{k}{\left(\right|C|}^2)C\right]\hfill \\ & -& {\widehat{\theta }}_{k_0+k}\frac{\partial }{\partial x}\left[\widehat{k}{\left(\right|C|}^2{)C+i|C|}^2\frac{\partial C}{\partial x}\right]=0.\hfill \end{array}$$

(11)

The Dyachenko-Zakharov envelope Equation (11) is Hamiltonian, and the Hamiltonian is

$$\mathcal{H}=\int C^{*}\widehat{\widetilde{V_k}}Cdx+\frac{1}{2}\int {\left|C\right|}^2\left[k_0{\left|C\right|}^2+\frac{i}{2}(C{C}^{\prime *}-C^{*}{C}^{\prime })-\widehat{k}{\left|C\right|}^2\right]dx,$$

(12)

where the operator $\widehat{\widetilde{V_k}}$ has the following form in k–space:

$${\tilde{V}}_k=\frac{\left[{\omega }_{k_0+k}-{\omega }_{k_0}-\frac{\partial {\omega }_{k_0}}{\partial k_0}k\right]}{k_0+k}.$$

(13)

The Dyachenko-Zakharov envelope equation was derived without any assumptions about the spectral width of the wave packet. Moreover, the Equation (11) is the exact envelope form of the Equation (7) and has the same range of applicability.

One can extract the nonlinear Schrödinger (NLS) equation in the assumption of narrowband spectrum:

$$\frac{\partial C}{\partial t}+\frac{i{\omega }_{k_0}}{8k_0^2}\frac{{\partial }^{2}C}{\partial x^2}+i{k}_0^2\left[{\left|C\right|}^{2}C\right]=0.$$

(14)

The Hamiltonian has the following form:

$$H=-\frac{{\omega }_{k_0}}{8k_0^3}\int |\frac{\partial C}{\partial x}{|}^{2}dx+\frac{k_0}{2}\int {\left|C\right|}^{4}dx.$$

(15)

2.2. Fully Nonlinear Conformal Equations

Following the work [26] we perform conformal mapping of the free surface liquid domain $z=x+iy$ confined by a free boundary $y=\eta (x,t)$ onto a half-plane of the new complex variable $w=u+iv$ having a fixed boundary $v⩽0$ –– see Figure 1 and Figure 2. This transformation can be written in the following form:

$$y=\widehat{H}(x(u,t)-u),x(u,t)=u-\widehat{H}y(u,t).$$

(16)

Then we use the following variables suggested by Dyachenko [25]:

$$R=\frac{1}{z_w},V=i{\Phi }_z=i\frac{{\Phi }_w}{z_w}.$$

(17)

We define the functions U and B using the Hilbert operator and the projection operator $\widehat{P}=\frac{1}{2}(1+i\widehat{H})$ as:

$$\begin{array}{c}U=\widehat{P}(V{R}^{*}+V^{*}R),B=\widehat{P}\left(V{V}^{*}\right).\hfill \end{array}$$

Here and below the asterisks stands for complex conjugation. In the new variables (17) the fully nonlinear (RV) equations have the following form:

$$\begin{array}{c}{R}_t=i(U{R}_w-R{U}_w),\hfill \\ V_t=i(U{V}_w-R{B}_w)+g(R-1),\hfill \end{array}$$

(18)

with the boundary conditions:

$$\begin{array}{c}R\to 1,V\to 0,\mathrm{at}v\to -\infty .\hfill \end{array}$$

(19)

3. Numerical Simulation of Soliton Turbulence. Initial Conditions

In this section we explain how we generate initial conditions for numerical experiments on soliton turbulence in the following nonlinear models for water waves:

• the NLS Equation (14),
• the SCZ Equation (7),
• the RV Equation (18).

The pseudo-spectral Fourier method was used for the SCZ, and RV equations solving the fourth-order Runga-Kutta method was applied to calculate time evolution. The time integration step was chosen to ensure that the values of the integrals of motion—energy, momentum, and mass—are kept accurate to 10 decimal places. The FFTW3 library [27] was used for the fast Fourier transform procedure. The multiplication of grid functions was carried out in x-space and to calculate derivatives and nonlocal terms, the direct and inverse Fourier transform were used. The source codes for numerical simulation of soliton turbulence in the frame of SCZ and RV equations can be found by the following links: http://kachulin.itp.ac.ru/sceq/ and http://kachulin.itp.ac.ru/rveq/.

We perform simulations in periodic domain of length $L=10$ km with gravity acceleration $g=9.81{\mathrm{m}/\mathrm{s}}^2$. The initial conditions for numerical experiments in all three models are identical. They represent a homogeneous wave train with two harmonic perturbations having a random phase:

$$c(x,t=0)=c_0{e}^{i{k}_{0}x+{\varphi }_0}+\delta c_0{e}^{i(k_0\pm k_p)x+{\varphi }_{\pm p}}.$$

(20)

Here, ${\varphi }_0$ and ${\varphi }_{\pm p}$ are the random, but identical for all models, phases of monochromatic wave and the perturbations correspondingly.

We set the initial conditions in the SCZ equation in the form (20) and in the NLS equation directly using the transformation from $c(x,t=0)$ to the envelope function—see Equation (10).

Then we generate this initial conditions in conformal variables $R(u,t=0)$ and $V(u,t=0)$ for the fully nonlinear conformal Equation (18) with the following procedure.

First, we recover the surface profile $\eta (x,t=0)$ and the velocity potential on it $\psi (x,t=0)$ employing the canonical transformation (9). The conformal mapping described in the Section 2.2 satisfies the following equation:

$$y\left(u\right)=\eta (u-\widehat{H}y\left(u\right)),$$

(21)

which can be solved by the iterative procedure:

$$y^{n+1}\left(u\right)=\eta (u-\widehat{H}{y}^n\left(u\right)).$$

(22)

Here the index n stands for the step of the iteration. After the conformal mapping is found by the use of (22), we compute the function R only using its definition (17). Now in order to find the function V by its definition (17) we need to know the potential $\Phi \left(w\right)$ in conformal variables. The potential $\Psi \left(u\right)$ in conformal variables can be computed using the Fourier transform of the known spectrum of the potential on the free surface ${\psi }_k$ as:

$$\Psi \left(u\right)=\sum _{k=-N/2+1}^{N/2}{\psi }_k{e}^{i\frac{2\pi }{L}kx\left(u\right)},$$

(23)

where N is the number of grid points.

The carrier wave number $k_0$ in all numerical experiments is equal to $\frac{2\pi }{100}$, so that the characteristic wavelength is ${\lambda }_0=100$ m and the time period of the carrier wave is $T_0=\frac{2\pi }{{\omega }_{k_0}}\approx 8$ s. The perturbations amplitude is 20 times less that the amplitude of the carrier wave $\delta c_0=\frac{c_0}{20}$, while $c_0$ is chosen so that in different experiments the average steepness take the values $\mu =0.04,0.06,0.08$. In addition for each average steepness $\mu$ we vary the dimensionless relative wave number of perturbation ${\tilde{k}}_p=\frac{L}{2\pi }{k}_p$ so that:

• ${\tilde{k}}_p=1$. In this case the harmonics adjacent to the carrier are perturbed.
• ${\tilde{k}}_p$∼the wave number of the maximum increment of modulation instability. For the average steepnesses $\mu =0.04,0.06$ and $0.08$ we set ${\tilde{k}}_p=10,15$ and 20 correspondingly.

4. Numerical Simulations of Soliton Turbulence

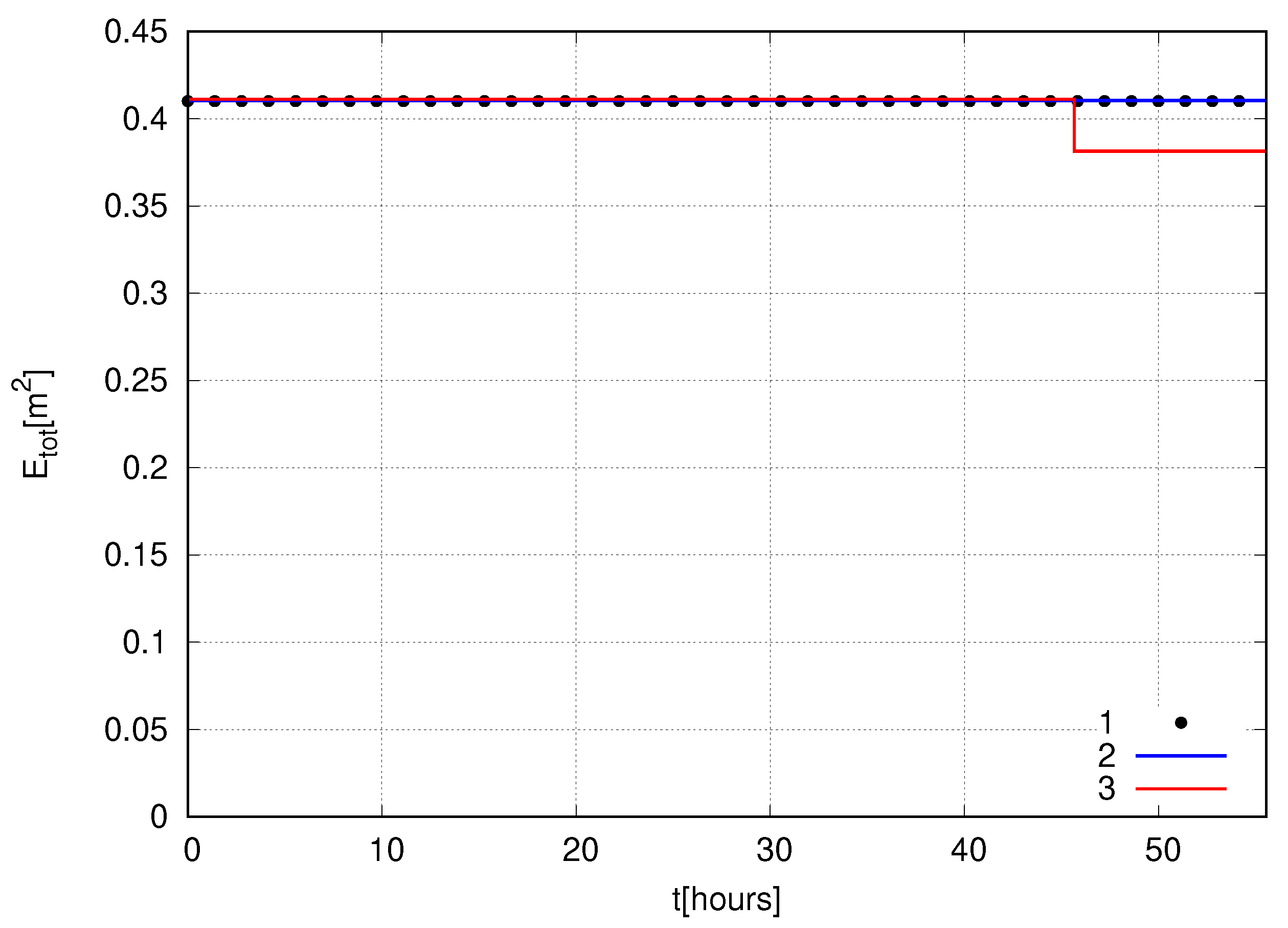
In this section, we focus on the case of low wave energies performing numerical simulations in the three different nonlinear models for water waves. Figure 3 shows the dependence of total energy on time in these models. These dependencies were obtained in simulation with average wave steepness $\mu =0.04$ and the dimensionless perturbation wavenumber ${\tilde{k}}_p=10$ corresponding to the maximum increment of modulation instability. One can see from Figure 3 that in the NLS and the SCZ models, the total energy conserves throughout the entire simulation time. Meanwhile, in the fully nonlinear model, the formation of pre-breaking waves leads to the switching on of the damping at the time moment $t_{damp}\sim 45$ h—see Figure 3. We discuss the details of the damping model in the next section and now compare surface dynamics in different models until the time moment $t_{damp}$.

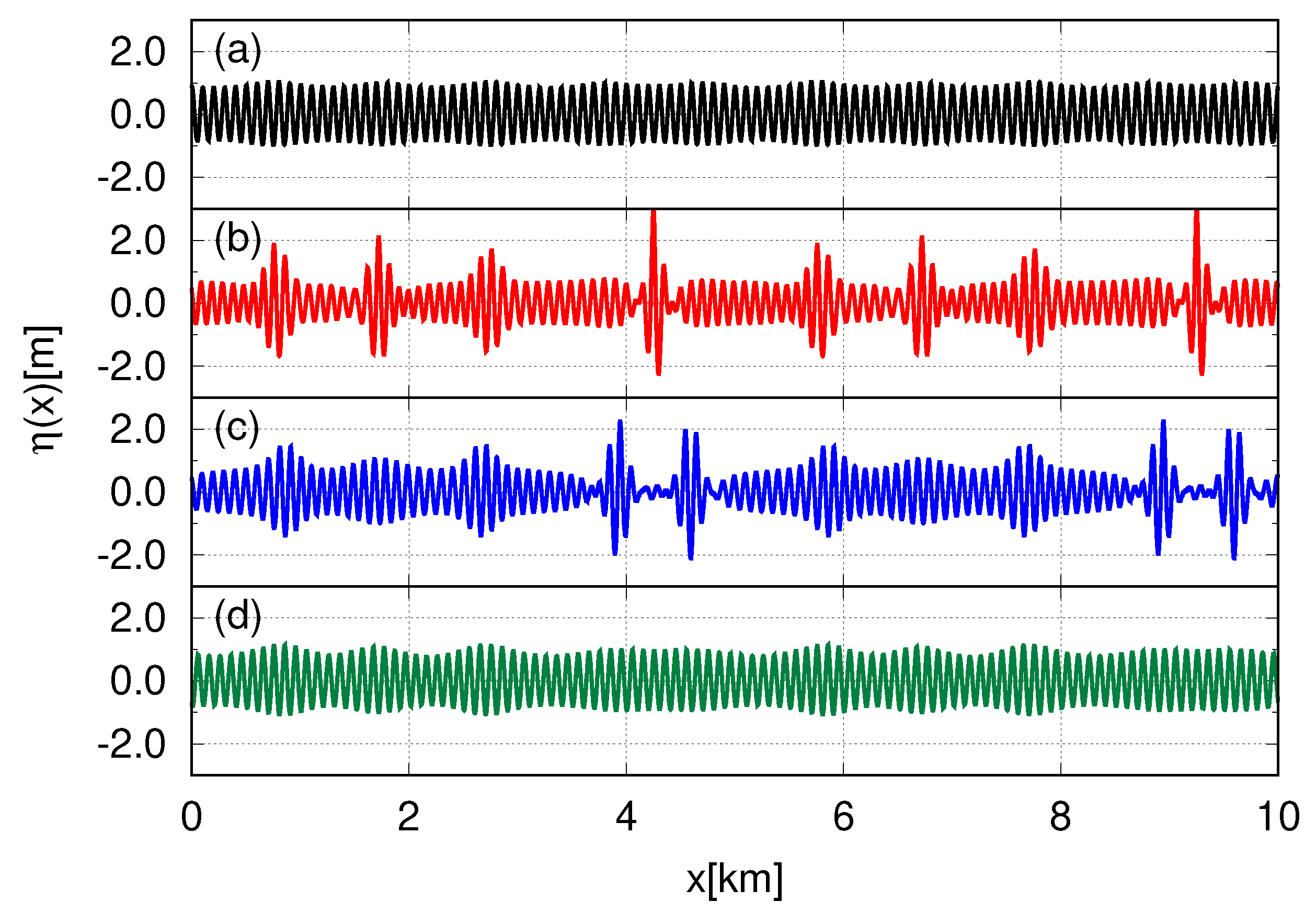
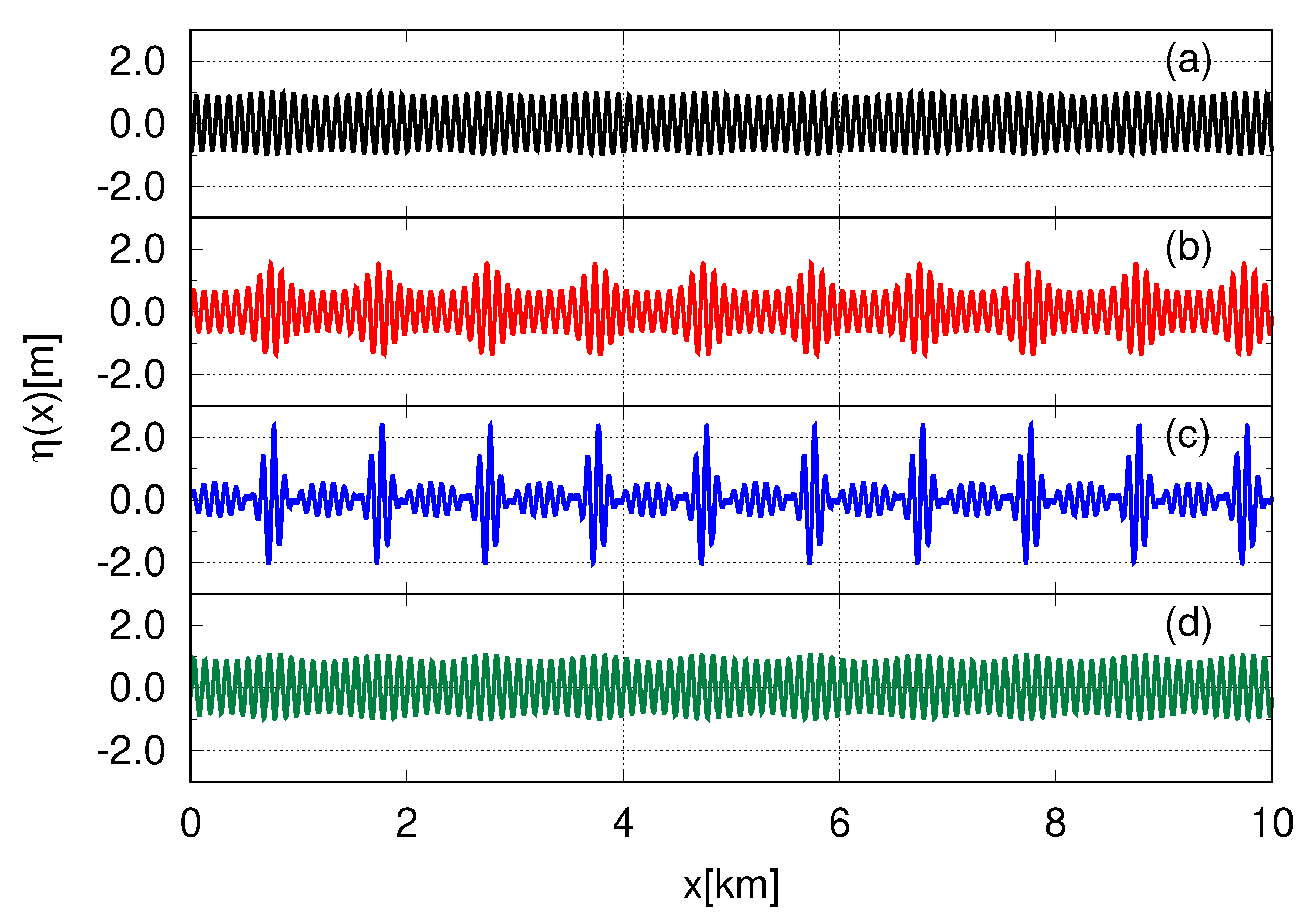
The modulation instability results in the formation of spatially periodic structures on the surface of the water–breathers. Besides, the breathers demonstrate an approximate periodic behavior in time—see the snapshots of the surface evolution during one such time period in Figure 4. We observe about 10 periods of the breather’s evolution in each of three nonlinear models for water waves after what, and the free surface dynamics become more complex. However, for substantial evolution time, we report significant differences in the evolution of the free surface when the NLS equation compared to the more accurate models—see the discussion below.

The entire free surface dynamics computed in different models can be found at the following links:

• http://kachulin.itp.ac.ru/STmovies/NLSeq-surface-mu-0-04-dk-10.avi—in the NLS equation,
• http://kachulin.itp.ac.ru/STmovies/cDZeq-surface-mu-0-04-dk-10.avi—in the SCZ equation,
• http://kachulin.itp.ac.ru/STmovies/RVeq-surface-mu-0-04-dk-10.avi—in the RV equations.

Note that the simulations of the nonlinear Schrödinger equation and the super compact Zakharov equation were carried out in a reference frame moving with group velocity $V_0=\frac{1}{2}\sqrt{\frac{g}{k_0}}$, while simulations of the exact equations in the laboratory frame of reference.

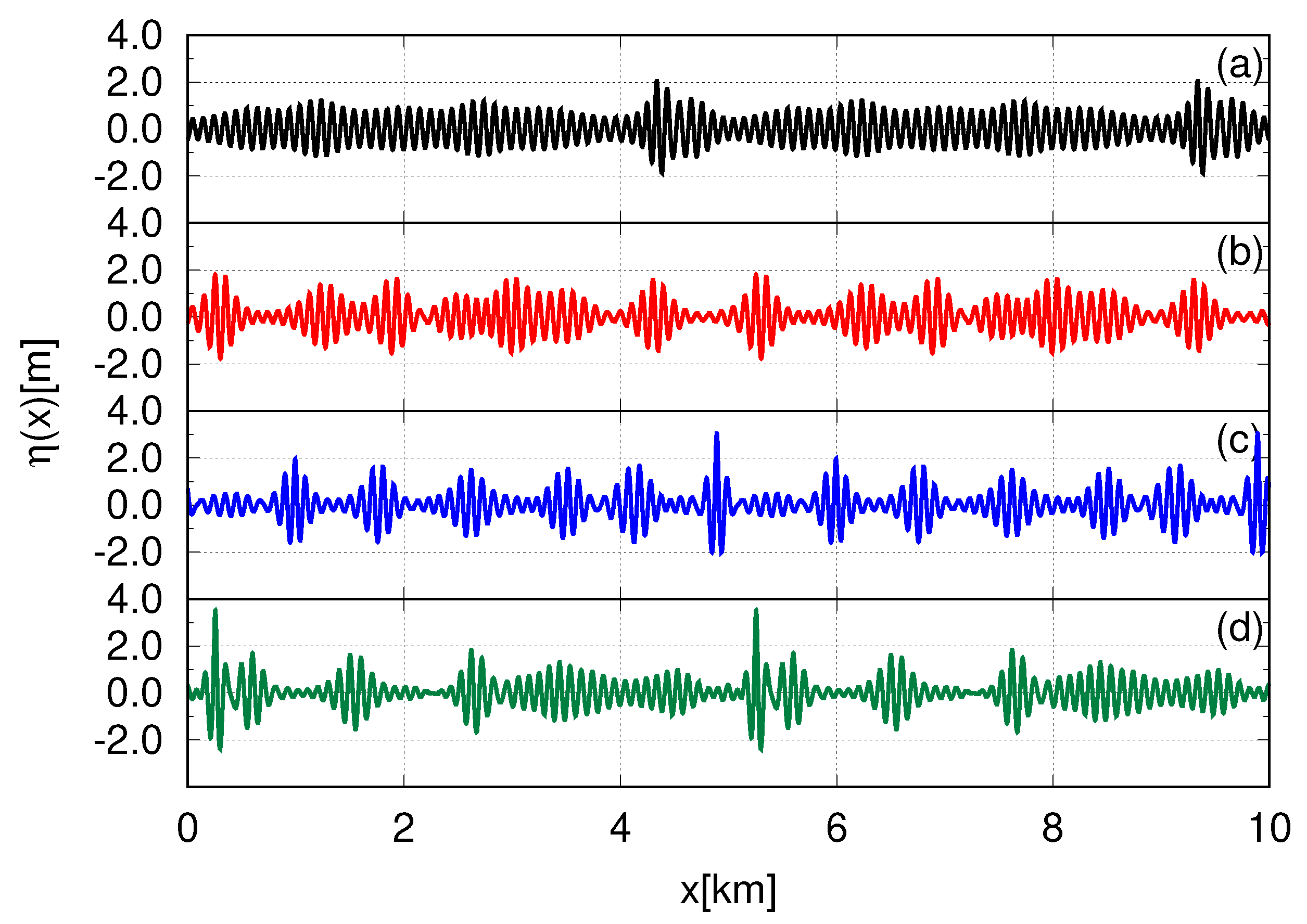
Figure 5 shows how the NLS equation dynamics become more complex at large simulation times, $t\approx 20$ h, exhibiting several different breather structures, though approximate periodic recurrences of the weakly modulated plane wave can be observed. At the large time we observe an almost complete reassemble of the initial condition comprised of 10 breathers structures on the fluid surface—see Figure 6.

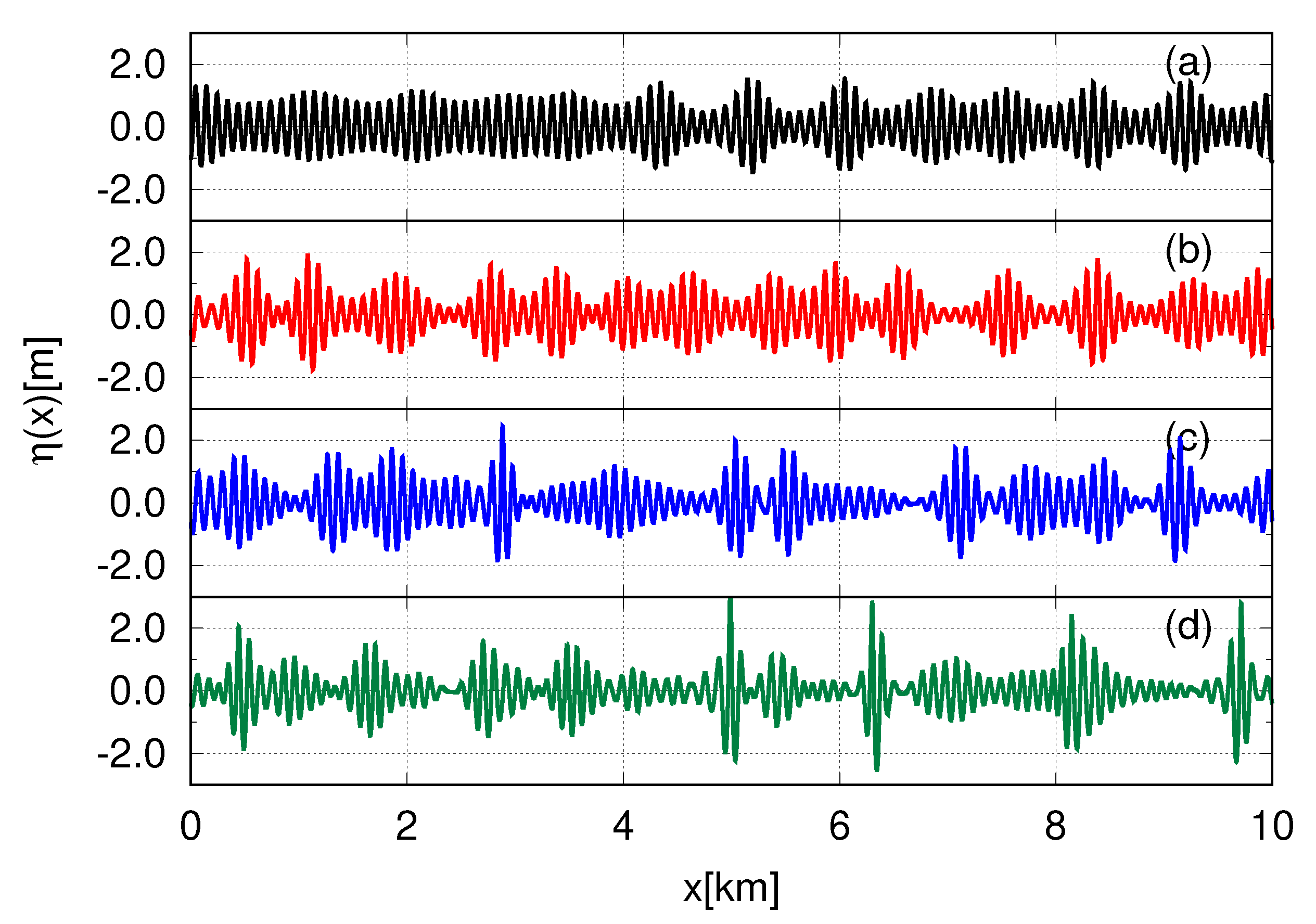
One of the key results of this work is that in both the super compact Zakharov and the fully nonlinear models the surface waves split into a set of interacting soliton structures at about the same time ($t\approx 20$ h), after what no recurrence to the initial weakly modulated plane wave can be observed—see Figure 7 and Figure 8.

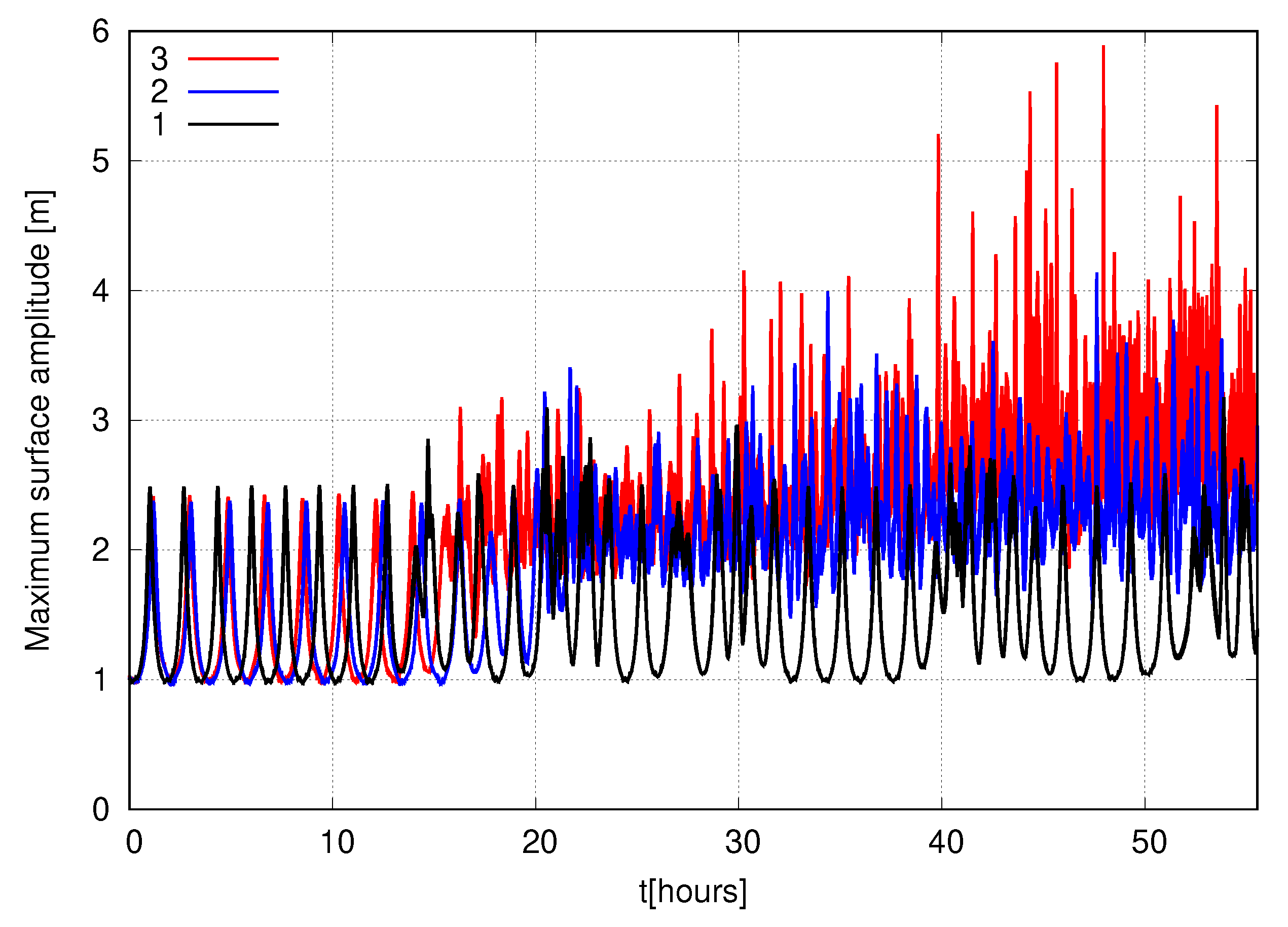
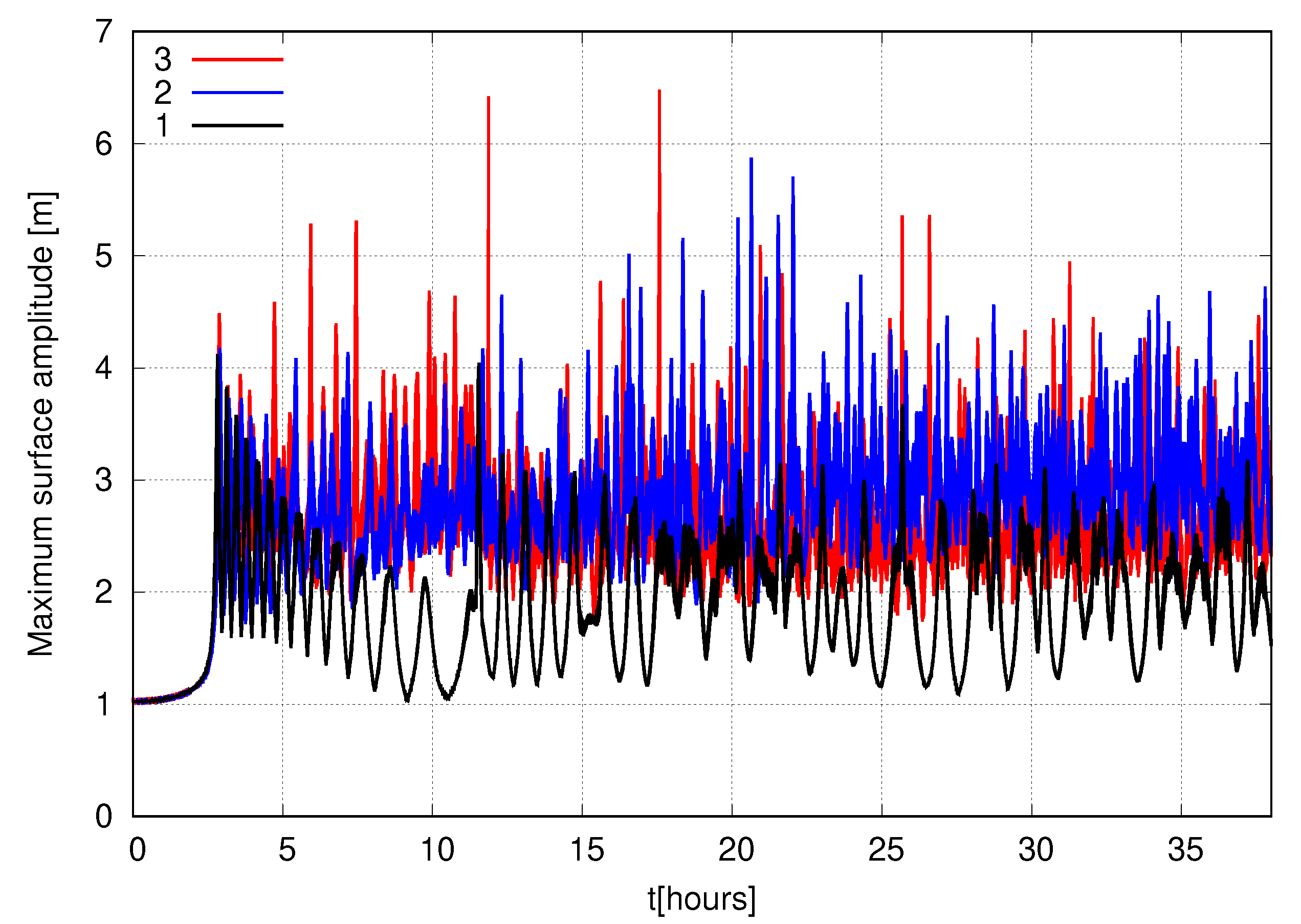
Dependence of maximum value of the surface amplitude on time turned out to be a crucial characteristic allowing to identify a fundamental difference between wavefield evolution in the three considered models—see Figure 9. We find that this function is almost periodic in time and does not exceed 3 m for the NLS equation model, meanwhile in more accurate models, it loses periodicity and starts to reach 4–6 m after $t\approx 20$ h of simulations—see again Figure 9.

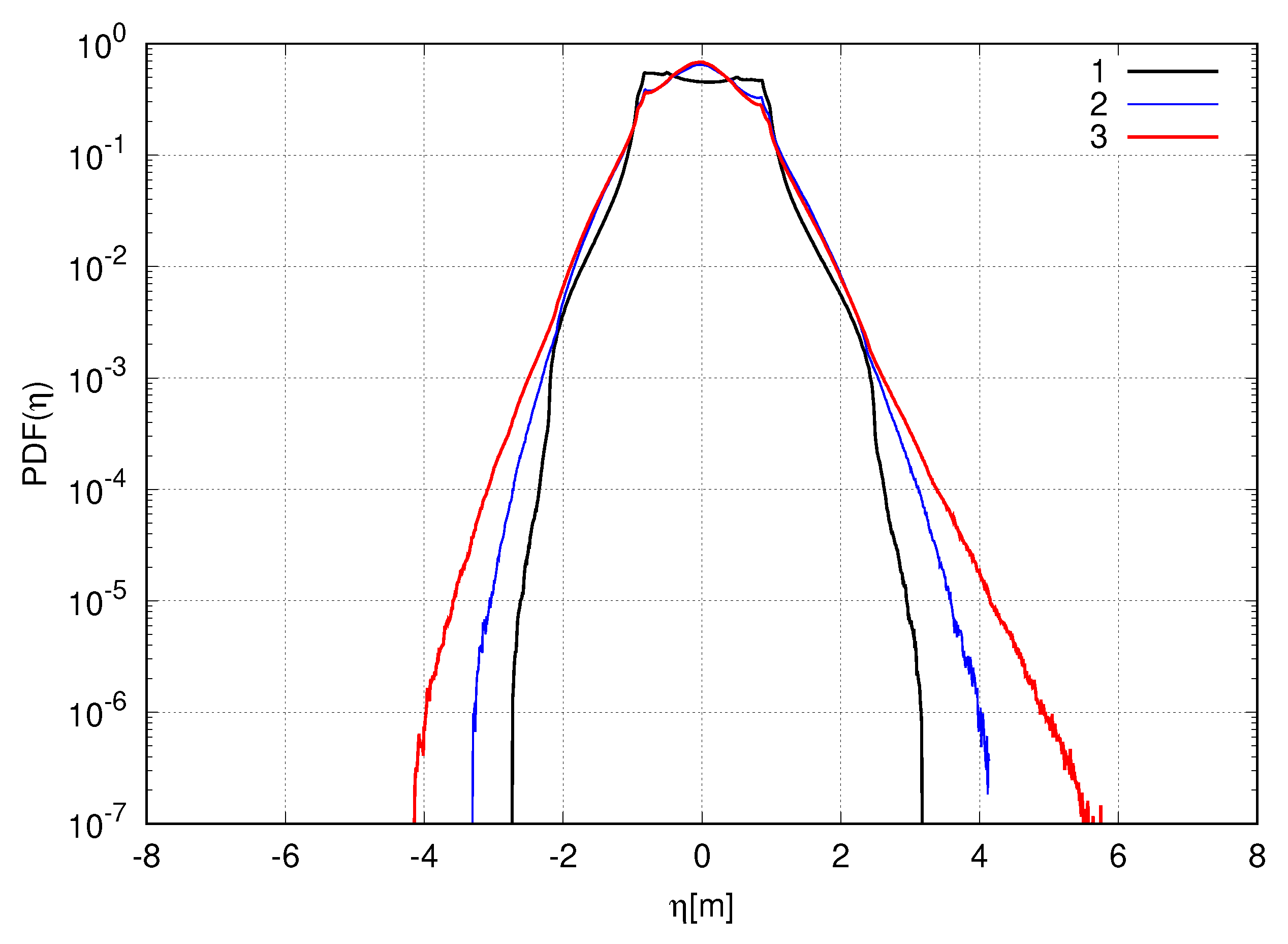
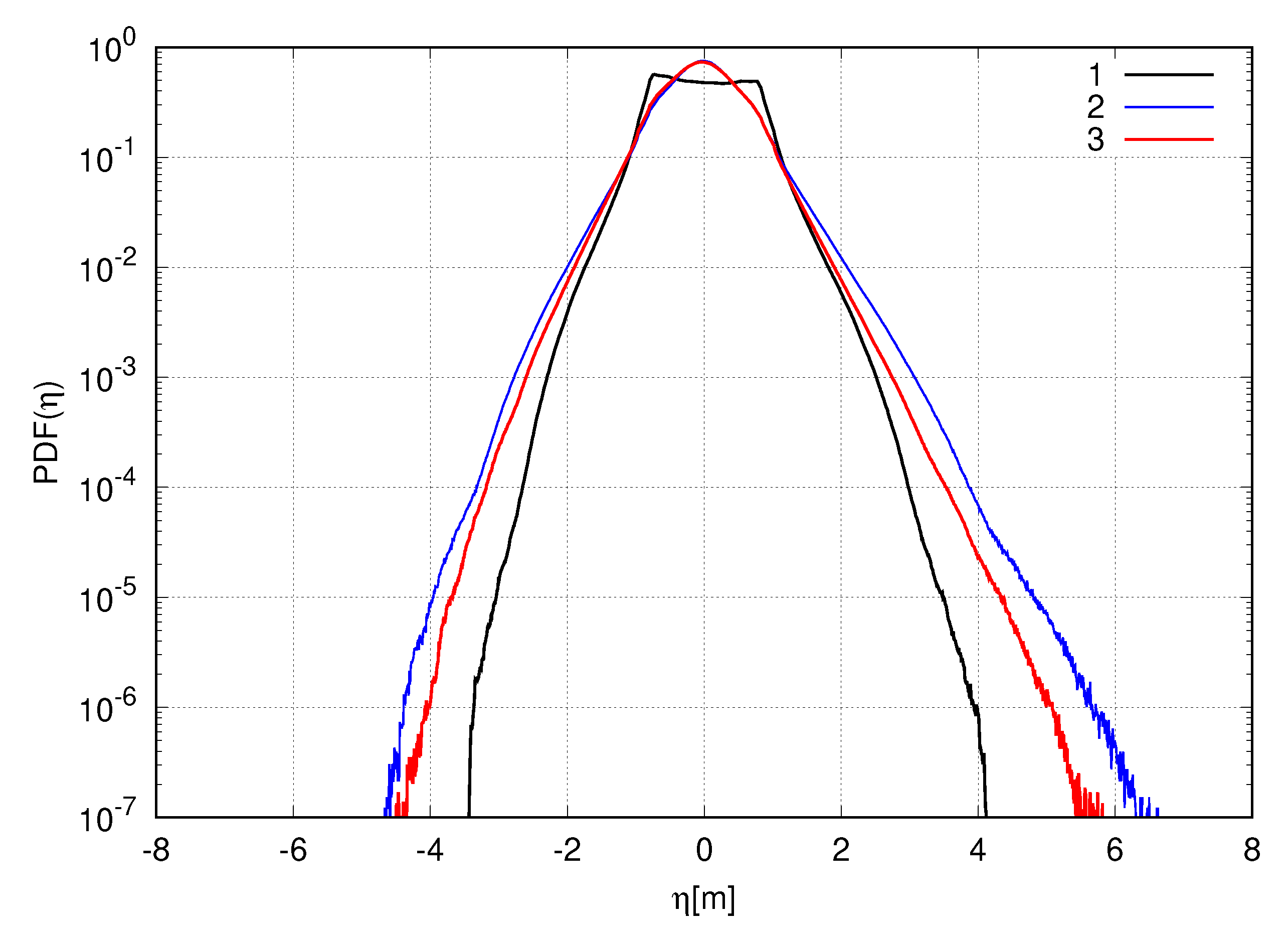
Then we compare the statistical behavior of the studied models by computing the probability density functions of the surface amplitude $PDF\left(\eta \right)$ averaged in time over the whole simulation—see Figure 10. We find that the NLS equation exhibits a low probability of high amplitude wave formation in comparison to the more accurate models. For example, the probability of formation of the 3-m waves in the NLS equation is from 10 to 100 times less than in the last ones. In contrast, there is a non-zero probability of formation of waves, exceed 3 m in the SCZ and the RV equations, while in the NLS equation, such events have not been detected. It is also important to note that the function $PDF\left(\eta \right)$ corresponding to the NLS equation model has kinks at $\eta \sim 1$ m due to the quasiperiodicity of the free surface dynamics discussed above.

Now we study soliton turbulence in the different models at $\mu =0.04$ and ${\tilde{k}}_p=1$, i.e., in the case when the harmonics adjacent to the carrier are perturbed. Figure 11 shows the observed total wave energy dependencies on time. One can see that the total energy conserves throughout the whole simulation for the NLS equation and the SCZ equation. It was necessary to use the damping for the fully nonlinear model twice—at $t\approx 11.5$ h and $t\approx 17$ h.

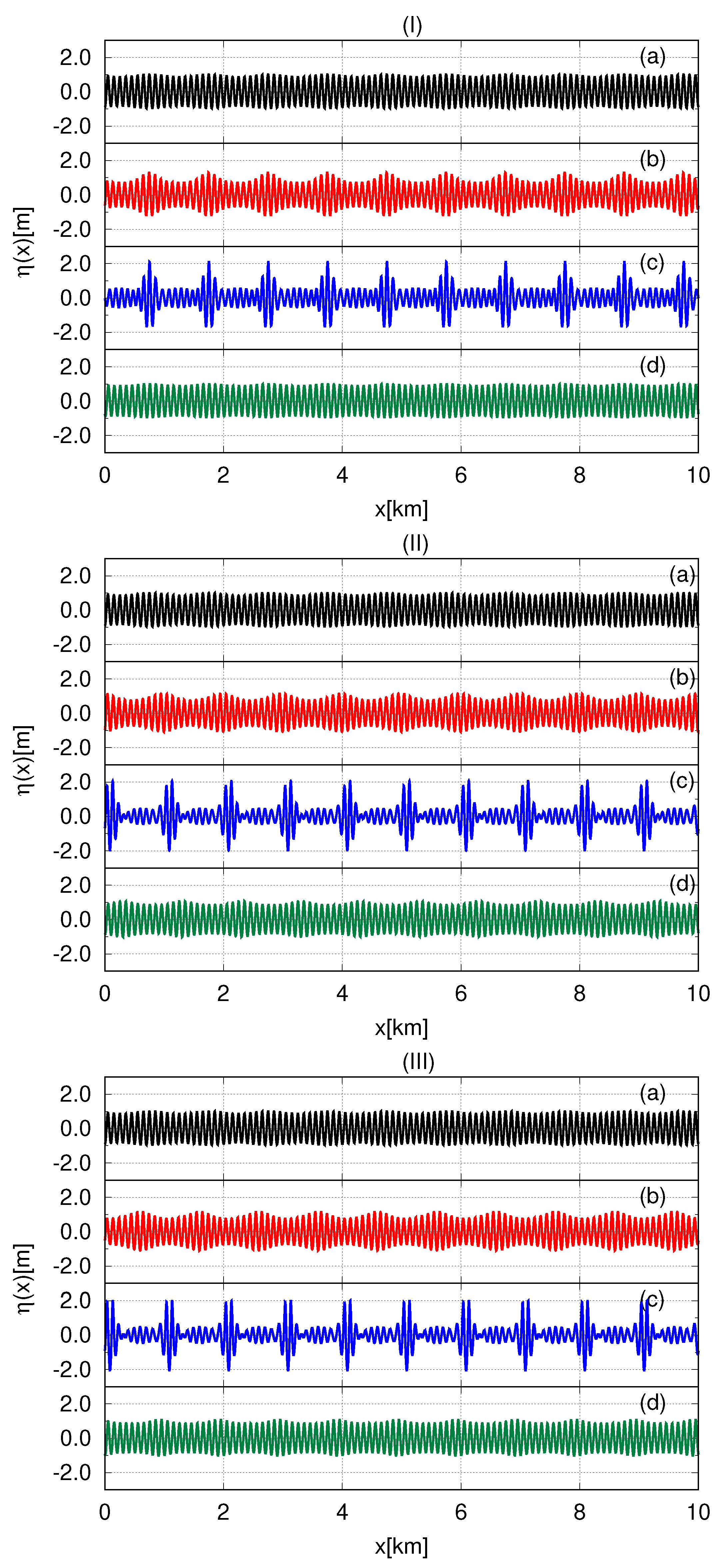
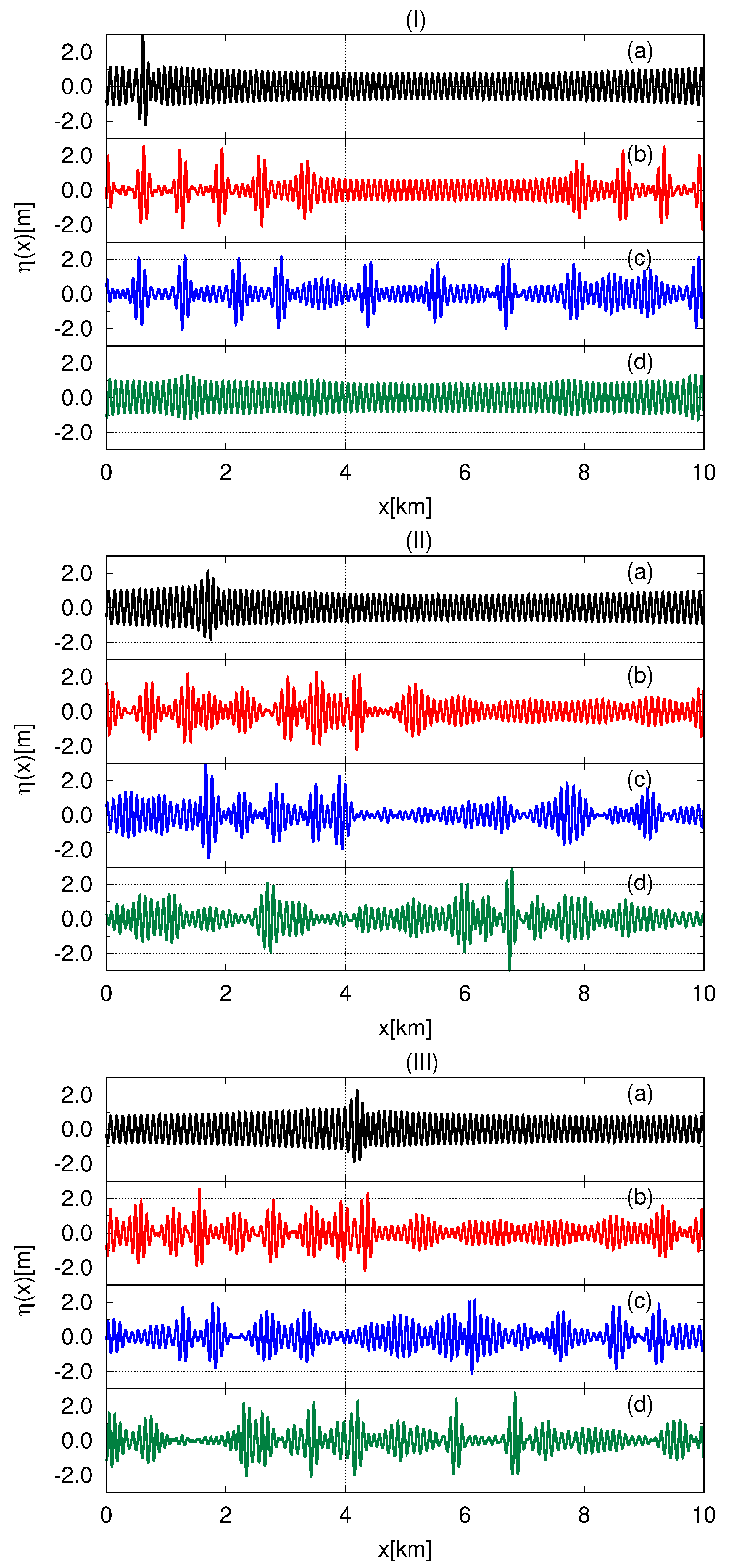
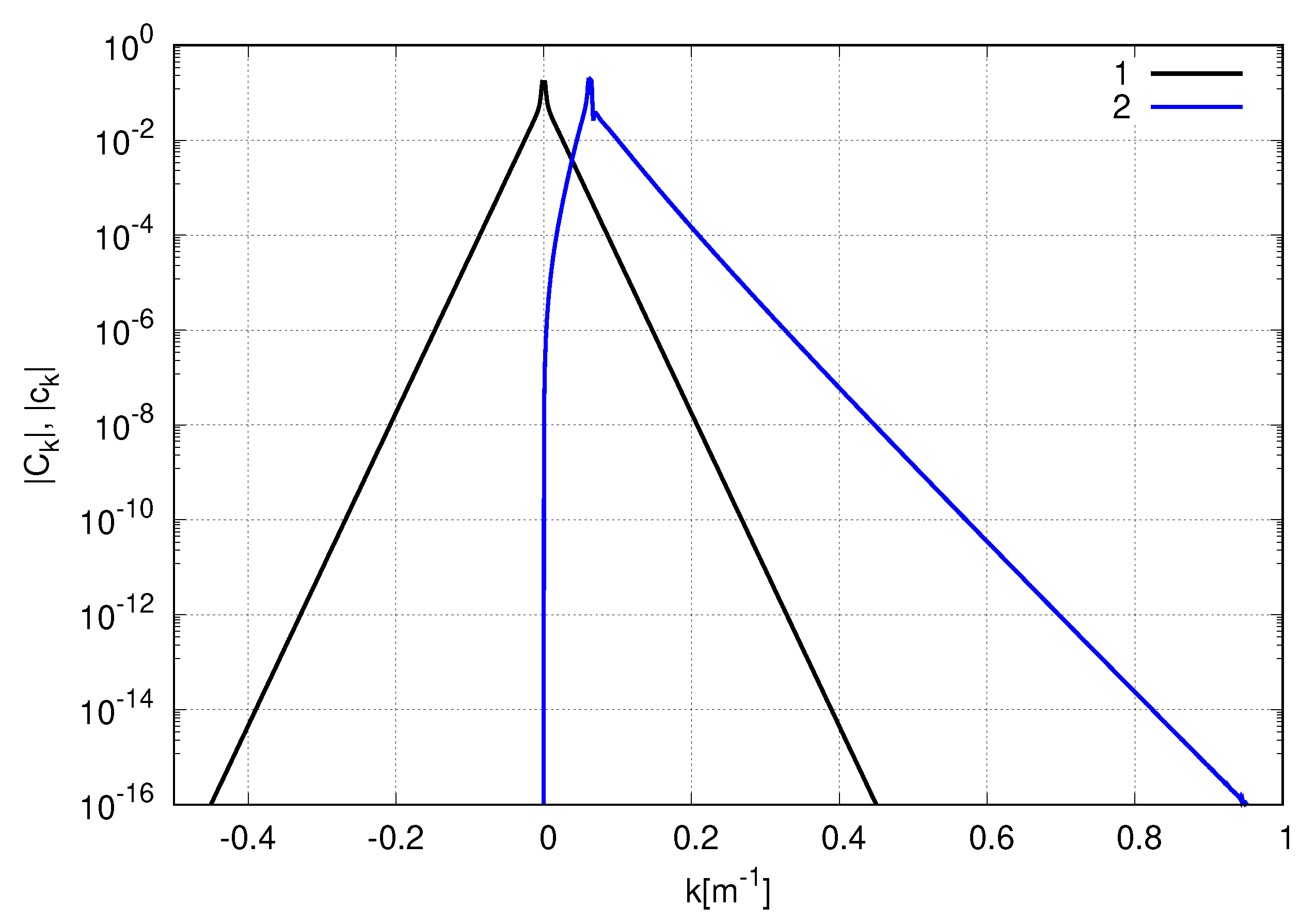
Snapshots of surface dynamics in the three considered models are presented in Figure 12. At the initial stage in each model, the modulation instability leads to the appearance of a single wave of high amplitude on the free surface—see panels (a) in Figure 12. At this time, the spectra broaden significantly—see Figure 13, which shows the dependence of the spectra of the envelope function $C\left(x\right)$ of the NLS equation and function $c\left(x\right)$ of the SCZ equation. Then this wave splits into a set of coherent wave structures—see panels (b) in Figure 12. In the NLS model, these structures resemble breathers having similar velocities, approximately equal to the group velocity $V_0=\frac{1}{2}\sqrt{\frac{g}{k_0}}$ corresponding to the characteristic wavelength $\frac{2\pi }{k_0}$. In the more accurate nonlinear models, the arising objects mostly resemble localized soliton structures having different velocities and interacting with each other. As a result of their collision, large-amplitude waves can appear on the surface. In the RV equations, such waves reach the pre-breaking stage at $t\approx 11.5$ h and $t\approx 17$ h. Furthermore, therefore at these moments, the damping was switched on.

The entire free surface dynamics, computed in different models, can be found by the following links:

• http://kachulin.itp.ac.ru/STmovies/NLSeq-surface-mu-0-04-dk-1.avi—in the NLS equation,
• http://kachulin.itp.ac.ru/STmovies/cDZeq-surface-mu-0-04-dk-1.avi—in the SCZ equation,
• http://kachulin.itp.ac.ru/STmovies/RVeq-surface-mu-0-04-dk-1.avi—in the fully nonlinear model.

Similar to the case studied in the first part of this section, now we again observe that the surface dynamics demonstrate almost recurrence to the initial weakly modulated plane wave for the NLS equation. While the more accurate models exhibit fundamentally different complex dynamics of soliton turbulence—compare panel (d) in Figure 12I with panels (d) in Figure 12II,III.

Found differences between the dynamics of the nonlinear Schrödinger equation and the more accurate models at $\mu =0.04$ and ${\tilde{k}}_p=1$ are also confirmed by the measured dependence of the maximum surface amplitude on time shown in Figure 14 and the $PDF\left(\eta \right)$ shown in Figure 15. Not that the registered probability of large-amplitude wave formation in the fully nonlinear model is less than in the super compact Zakharov equation (see Figure 15) due to the fact that the PDFs are measured by averaging over the entire simulation time. Meanwhile, in the case of the fully nonlinear model, the total energy decreased due to the use of damping, and therefore large-amplitude waves appear less often at the end of the simulation. Also, Figure 14 shows that at large times the maximum amplitude of the surface in the super compact equation is almost always higher than in the full model.

We conclude that even at a low level of energy and average wave steepness, the wave dynamics in the nonlinear Schrödinger equation fundamentally differs from the dynamics in the more accurate models. Meanwhile, the super compact Zakharov equation model demonstrates similar results when compared to the fully nonlinear equations. This is since in the soliton turbulence observed by us, even at low energy levels, high and steep waves appear on the water surface. The appearance of such waves is accompanied by a significant broadening of the spectrum—see again Figure 13. The NLS equation is a weakly nonlinear model, and, unlike the more accurate model, the SCZ equation, it was obtained using the additional assumption of the narrowband spectrum. Such events go beyond the applicability of the nonlinear Schrödinger equation, and therefore the surface dynamic is described incorrectly by this model.

In the next section, we compare numerical simulations of soliton turbulence for large values of total energy and averaged wave steepness only for the super compact Zakharov equation and the exact equations. We will pay special attention to the energy losses of wind waves due to their breaking.

5. Energy Losses Due to Wave Breaking at High Energy Levels

Recall that, modulation instability leads to the formation of high amplitude and/or large steepness waves that can break. Therefore we add damping providing dissipation of energy for pre-breaking waves to the super compact Zakharov equation and the exact equations in conformal variables.

Previously we studied in detail the initial stage of wave breaking and proposed model for damping, which removes only the pre-breaking waves, leaving the other part of the surface unchanged [24]. The idea of our damping model is the following. Fourier spectrum exhibits exponential behavior at large wavenumbers shortly before the wave breaking. The slope of the exponent determines the distance from the real axis to the nearest singularity in the lower half-plane $x+iy$. This singularity moves closer and closer to the real axis at the pre-breaking stage. In order to prevent the wave breaking, we move the singularity closest to the x-axis away from it. More precisely, we multiply the Fourier spectrum by a special attenuation function that decreases exponentially at large wavenumbers k:

$$C_k\Rightarrow C_k{e}^{{\gamma }_k},{\gamma }_k\sim -k\mathrm{at}\mathrm{large}k$$

(24)

We use breaking criterion based on advection velocity (8) in numerical simulation in the framework of the SCZ equation. Bjorkavag and Kalisch in the paper [28] showed that using a similar criterion for Boussinesq models gives good qualitative agreement with the experiments. If the value of the advection velocity exceeds half the group velocity, we stop the calculation and remove the pre-breaking wave. We “fix” the wave spectrum using the following damping function:

$${\gamma }_k=\left\{\begin{array}{c}0,\mathrm{if}0<k\le k_0\hfill \\ -D\sqrt{log\left[cosh{\left(\alpha (k-k_0)\right)}^2\right]},\mathrm{if}k>k_0\hfill \end{array}\right.$$

(25)

and the coefficients were chosen as $D=400$ and $\alpha =0.75$.

Similarly, we took into account damping for the RV equations. Practically, in this case, the needed number of points N of the computational grid is about 2–4 times more than required for the SCZ equation for the same initial conditions due to specific properties of conformal mapping. Therefore we vary N in the numerical experiments with the exact model. Initially, the calculation was carried out on a grid with $N=\mathrm{16,384}$ points, so that the number of negative harmonics in the spectrum of R and V was 8192. When the spectrum of R (and V) became wider, and the average amplitude of 100 highest harmonics $R_{av,N}$ exceeded the threshold value $R_{th}$ equals to 10 times of the roundoff error, the number of computational nodes was doubled to $\tilde{N}=\mathrm{32,768}$.

We define the average amplitude $R_{av,N}$ as

$$R_{av,N}=\frac{1}{100}\sum _{k=-\frac{N}{2}+100}^{-\frac{N}{2}}\left|R_k\right|$$

(26)

If the wave does not break and the width of the spectrum decreases, the number of computational points decreases to its initial value $N=$16,384. If the spectrum continues its expansion and the average amplitude of the 100 higher harmonics in the R spectra $R_{av,\tilde{N}}$ with the number of the grid points $\tilde{N}=$32,798 exceeds the roundoff error by a factor of ${10}^{10}$, then the simulation stops and we remove the pre-breaking wave.

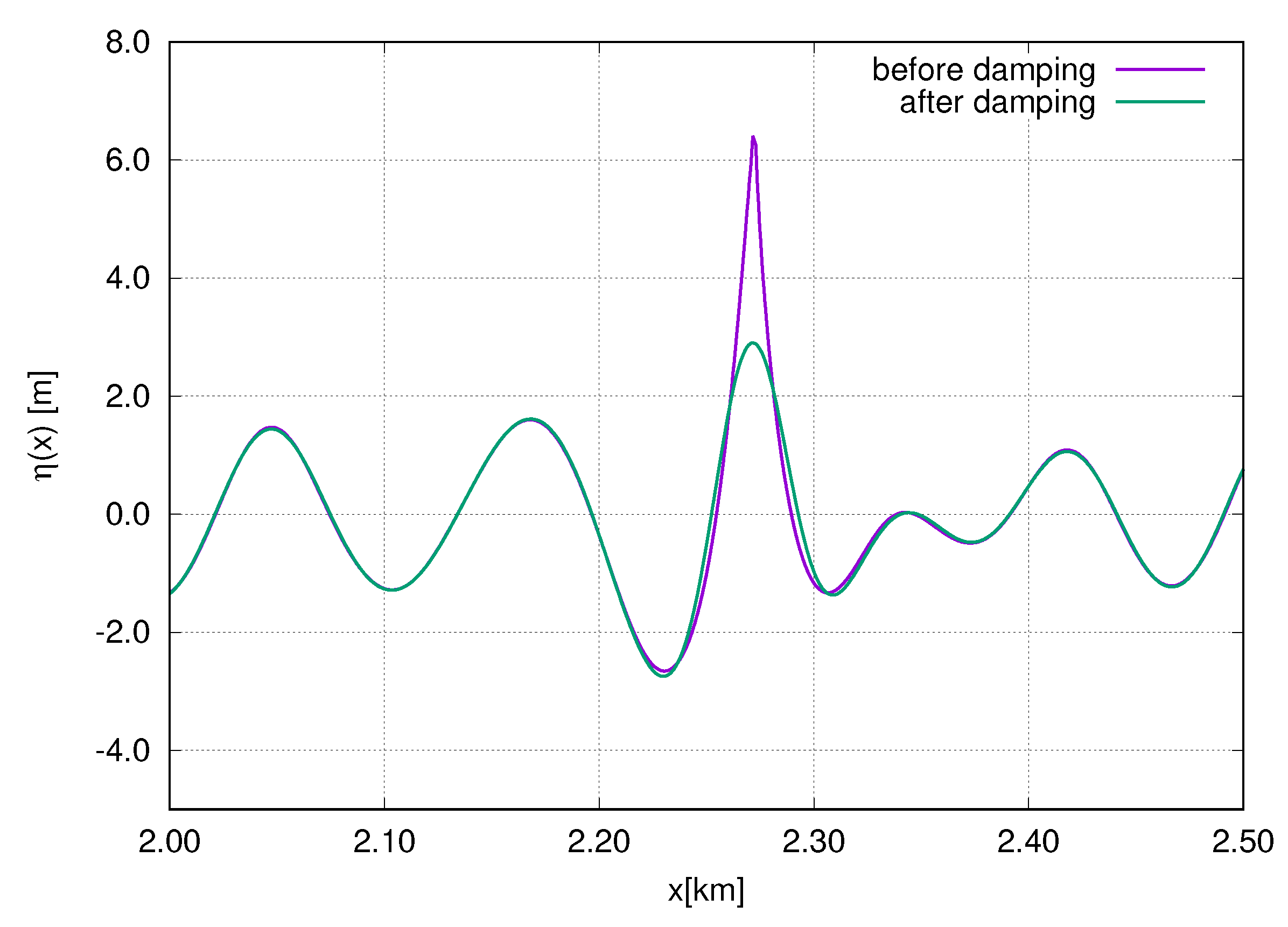
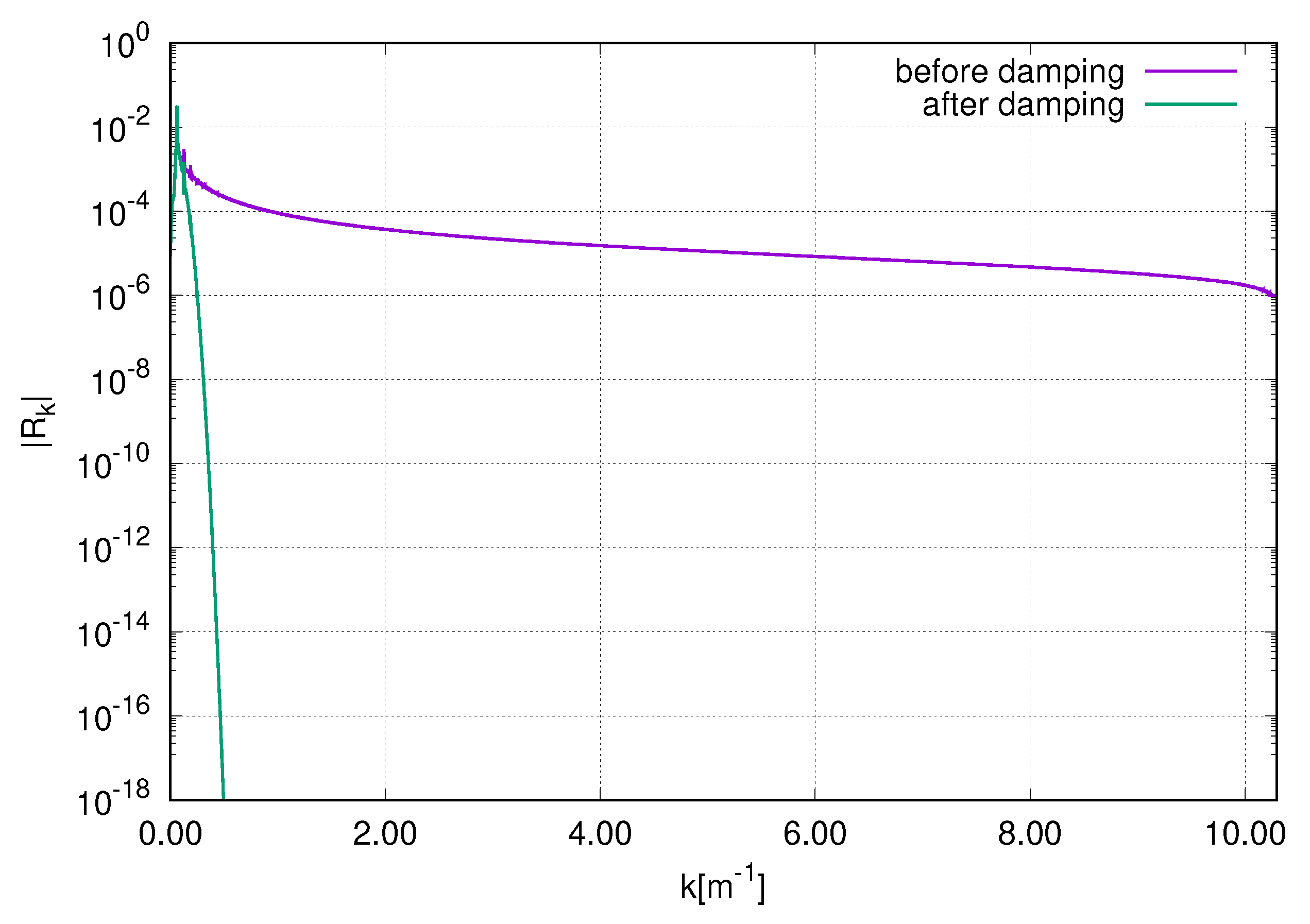
Modulation instability at high “levels of nonlinearity” ($\mu =0.06$ and $\mu =0.08$ ) leads to the formation of an pre-breaking wave on the free surface. Figure 16 and Figure 17 show the free surface profile $\eta \left(x\right)$ and the spectrum of R immediately before and after the damping for numerical simulation in the framework of RV equations.

One can see the spectrum dynamics in more details shortly before the damping right after that by following link: http://kachulin.itp.ac.ru/STmovies/spectrum-wb.avi, while corresponding dynamics of the free surface profile by http://kachulin.itp.ac.ru/STmovies/surface-wb.avi and http://kachulin.itp.ac.ru/STmovies/surface-wb-zoom.avi.

The free surface profiles shown in Figure 16 demonstrate that damping acts only at the wave breaking point and does not affect the rest part of the water surface.

In numerical experiments with initial parameters $\mu =0.06$, ${\tilde{k}}_p=1$ and $\mu =0.08$, ${\tilde{k}}_p=1$ the pre-breaking waves split into a set of interacting solitons in both models. The surface dynamics in these cases is similar to that which was discussed in the previous section. The difference is that at high energy levels, collisions of solitons more likely lead to the formation of large-amplitude waves.

The entire dynamics of the free surface obtained in numerical experiments with parameters $\mu =0.06$, ${\tilde{k}}_p=1$ can be found by the links:

• http://kachulin.itp.ac.ru/STmovies/cDZeq-surface-mu-0-06-dk-10.avi—for the SCZ equation,
• http://kachulin.itp.ac.ru/STmovies/RVeq-surface-mu-0-06-dk-10.avi—for the RV equations.

The entire dynamics of the free surface obtained in numerical experiments with parameters $\mu =0.08$, ${\tilde{k}}_p=1$ can be found by the links:

• http://kachulin.itp.ac.ru/STmovies/cDZeq-surface-mu-0-08-dk-10.avi—for the SCZ equation,
• http://kachulin.itp.ac.ru/STmovies/RVeq-surface-mu-0-08-dk-10.avi—for the RV equations.

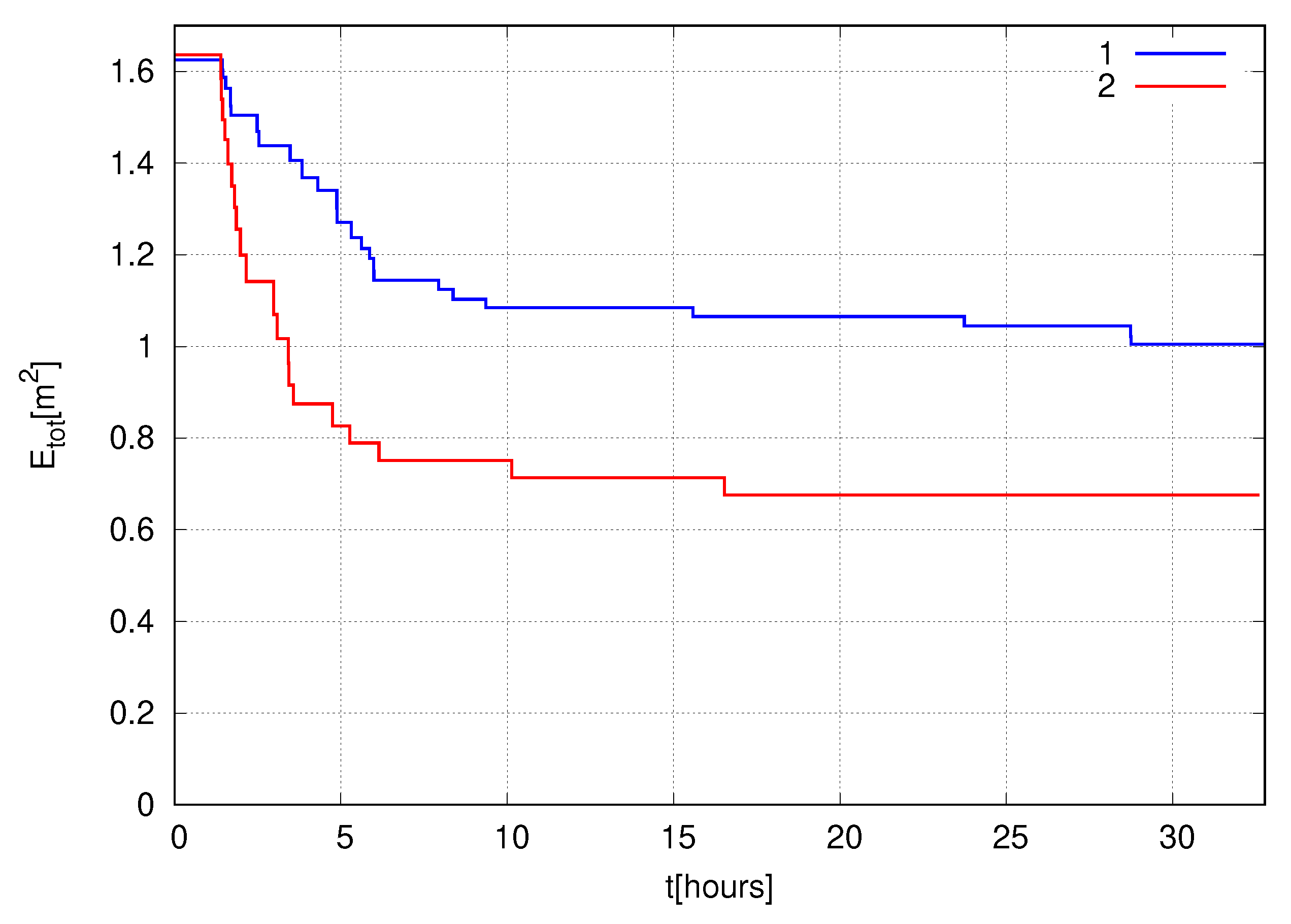
Figure 18 and Figure 19 show the total energy dependence on time in both models for the cases $\mu =0.06$, ${\tilde{k}}_p=1$ and $\mu =0.08$, ${\tilde{k}}_p=1$ correspondingly.

As one can see from Figure 18 and Figure 19, the energy loss due to wave breaking is higher for the exact model in comparison with the approximate Zakharov equation. The differences in energy losses observed in two models considered can be explained by two following reasons. First, the super compact Zakharov equation is the approximate model corresponding to the Hamiltonian expanded in powers of $\eta$ and $\psi$ up to the fourth-order term. The expansion was done under the assumption of low wave steepness. Therefore, the dynamics of pre-breaking waves with large values of steepness will differ from the results obtained by using the exact RV equations. Second, the function $c\left(x\right)$ in the SCZ equation and the function of $R\left(u\right)$ in the exact equations differ in sense. $c\left(x\right)$ is a complex normal Hamiltonian variable and related to the natural Hamiltonian variables $\eta \left(x\right)$ and $\psi \left(x\right)$ by canonical transformation (5), while the function of $R\left(u\right)$ is related to conformal mapping by definition (17). Thus, although the fundamental idea of energy loss accounting is the same in these two models, it seems impossible to achieve complete agreement on damping procedure. However, in both models, the wave systems lose only about 40–50% of their energy for two days.

6. Conclusions

In this work, we investigate and compare soliton turbulence appearing as a result of modulational instability of the homogeneous wave train in three nonlinear models for surface gravity waves: the nonlinear Schrödinger equation, the super compact Zakharov equation, and the fully nonlinear equations written in conformal variables.

We find that even at a low level of energy and average wave steepness, the wave dynamics in the simplest model—the nonlinear Schrödinger equation—fundamentally differs from the dynamics in the exact model, while simulations using the super compact Zakharov equation provide similar to the exact model results.

Then we study energy losses of wind waves due to their breaking for large values of total energy and average wave steepness in the Zakharov model and in the exact equations. We show that the energy loss due to wave breaking in the exact model is higher than in the Zakharov approximate model, and in both models, the wave system loses 50% of energy very slowly during few days.