Abstract
The paper presents the long-time dynamics with multiple collisions of breathers in the super compact Zakharov equation for unidirectional deep water waves. Solutions in the form of breathers were found numerically by the Petviashvili method. In the terms of envelope and the assumption of the narrow spectral width the super compact equation turns into the well known exact integrable model—nonlinear Schrödinger equation, and the breather solution in this case turns into envelope soliton. The results of numerical simulations show that two main scenarios of long-time dynamics occur during numerous collisions of breathers. In the first case, one of the breathers regularly takes a number of particles from the other one at each collision and in the second one a structure resembling the bi-soliton solution of nonlinear Schrödinger equation arises during the collision. Despite these scenarios, it is shown that after numerous collisions the only one breather having initially a larger number of particles remains.
1. Introduction
Turbulence in nonlinear continuous media often accompanied by the appearance of localized nonlinear structures. In those cases, when the equations describing the medium have stable soliton solutions, the solitons are natural candidates for the role of such structures, and turbulence can be called soliton turbulence.
The study of soliton turbulence in various nonlinear models is of considerable interest that can be confirmed by numerous works. The problem of a statistical description of a large number of solitons in the framework of the Korteweg-de Vries equation was first considered in [1]. The kinetic equation was obtained that describes the distribution function of soliton parameters for the case of a low density of solitons. The turbulence of rarified soliton gas plays the key role in the formation of wave field statistics (see the works [2,3]). With the use of direct numerical simulations methods, the collective behaviour of soliton ensembles was also studied in [4]. The general case of dense soliton gas was considered in [5,6].
The nonlinear Schrödinger equation (NLSE) is a special case of such models and a universal model for wave turbulence studying. However, it is an integrable equation, and turbulence in the framework of the NLSE has essential peculiarities. Collisions of the NLS solitons are completely “elastic”, that is, there are no energy exchanges between them and their basic parameters, amplitudes and velocities, do not change. One of the main parameters that plays an important role in the dynamics of solitons pairwise interactions is the relative phase of solitons at the moment of the collision. For example, the maximum amplitude amplification of solitons in a collision is determined by the synchronization of their phases. Phase synchronization also plays an important role in the formation of extreme amplitude waves or rogue waves. In recent works [7] and [8] phase synchronization in multisoliton ensembles was studied analytically. Using the inverse scattering transform formalism, the authors of work [9] show that the dense soliton gas is the model of the asymptotic stage of the noise-induced modulation instability in the NLSE. Rarefied soliton gas was also reproduced experimentally in an optical fiber ring resonator with the initial wavefield taken as arithmetic superposition of individual solitons [10] and in water wave tank [11].
A completely different situation is observed in non-integrable systems. The interaction of solitons is nontrivial, their number can change, as well as their energy, amplitude or velocity. In work [12] it was studied the dynamics of soliton turbulence in nonintegrable, but NLSE-like, equations with power-law nonlinearity. The restriction on the type of nonlinearity chosen in that work allowed the authors to use the available analytical soliton solutions to obtain the analytical estimation for changing in the number of particles of solitons during their pairwise interaction. Based on the balance of the number of particles, momentum and energy, this relation shows that after numerous interactions only one soliton remains at the end. A few numerical simulations confirmed this result in various nonintegrable equations with simple power-law nonlinearity.
In our work we consider multiple interactions of breathers on the surface of deep water in the super-compact Zakharov equation (SCZE). It is currently the simplest form for the 1D deep water waves equation (see [13]) derived from the compact Zakharov equation [14,15]. The breathers were obtained in [16] and the envelope of such a breather can be called the soliton. It is shown in [17] that special solutions of the SCZE called breathers can exchange energy during their pairwise interactions. The integrability of the 1D Zakharov equation, as well as the SCZE, is analyzed numerically and analitically in [18]. It is found that the six-wave interaction amplitude is not zero for the equation. Thus, it is not integrable. However, the integrable NLSE model can be derived from the SCZE model as shown in [19] and the breather solution in this case corresponds to the NLSE envelope soliton, as previously noted. In addition, the results of numerical experiments show that the radiation of incoherent waves is small and it is clearly observed that the phases of breathers are synchronized at the moment of collision [17,18]. This allows us, in a sense, to consider the SCZE very similar to the NLSE or NLSE-like and call it “almost integrable”.
On the basis of the above, we believe that the use of the NLSE model for our further evaluations is reasonable, despite its approximation. We can also expect that numerous breathers interactions in the SCZE model will result in the formation of a single breather.
2. The Super Compact Zakharov Equation and the Nonlinear Schrödinger Equation
The super-compact Zakharov equation for unidirectional deep water waves has the following form [13]:
here the operator is Fourier multiplier by the , where g is free fall acceleration. The operator in the Fourier space is where is the Heaviside step function.
Physical variables of surface and potential can be recovered by canonical transformation (see details in [13]):
The operator corresponds to the multiplication by in Fourier space.
The SCZE has a breather solution:
where is the breather group velocity. The breather solution can be found numerically only, for example, by the Petviashvili method (see details in [13]). Introducing the envelope variable such that and assuming the narrow spectral width, one can easily derive the NLSE (see [19])):
Here the Equation (3) is written in the reference frame moving with the velocity . The NLSE is a completely integrable model and an exact one-soliton and multisoliton solutions are well-known (see [20,21]).
3. Numerical Simulations of Multiple Soliton Interactions
In this section, we discuss the long-time dynamics of breather (soliton) interactions in the SCZE. To begin with, consider the numerous pairwise collisions of only two breathers. Their interaction was studied in the periodic domain of length L in a reference frame moving at a velocity of . The breathers had the same amplitudes and the following velocity values: and , . The initial conditions were chosen as in work [17]. The pseudo-spectral Fourier method was used for the SCZE solving the fourth-order Runga-Kutta method was applied to calculate time evolution. The FFTW3 library [22] was used for the fast Fourier transform procedure. The multiplication of grid functions was carried out in x-space and to calculate derivatives and nonlocal terms, the direct and inverse Fourier transform were used. One of the breathers having a higher velocity also had a larger number of particles. In terms of Hamiltonian variable the expression for number of particles has the following form:
Here —particle number density. For the sake of brevity, we label the soliton that initially had a larger number of particles by the indices 1 while the soliton that initially had a smaller number of particles by the indices 2.
In work [17], the dynamics of one pairwise breather collision were studied in details, and the results were compared with well-known dynamics of the NLSE solitons pairwise interaction. Unlike the NLSE, the SCZE breathers interacting for time, exchange their energy (number of particles and momentum). Moreover, this exchange depends on the value of breather’s relative phase at the moment of collision.
To make sure that the long-time interaction of breathers is independent of their initial phase, we perform 32 experiments with different initial phase values of breather one evenly distributed over an interval of 2.
The initial state of breathers is shown in Figure 1a,b by the black dashed line. Cases a and b correspond to different initial phases of soliton 1. The results showed that in all experiments, only one soliton shown by the solid red curve in the same figure ultimately remained. Nevertheless, the dynamics of their interaction were different, and two main scenarios were discovered.
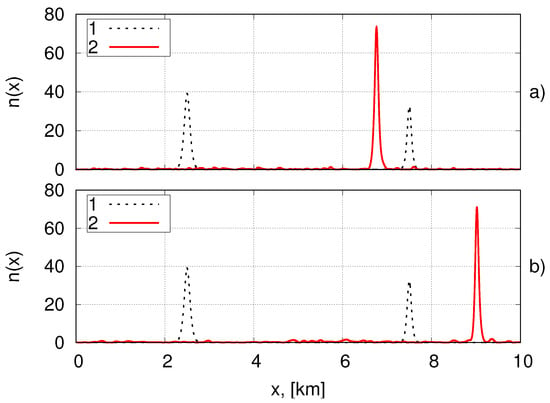
Figure 1.
The number of particles densities for two different numerical experiments. Black dashed curves 1 in panels (a) and (b) correspond to initial states and red solid curves 2 in panels (a) and (b) to final states.
3.1. The First Scenario of Two Breathers Collision Dynamics
The first scenario is that soliton 1 takes the number of particles from soliton 2 in the result of each interaction, and eventually, soliton 2 is absorbed. Such a scenario occurs in 19 of 32 experiments and is well supported by Figure 2 panel (a) showing the time dependence of the number of particles for each soliton and normalized by the total number of particles N. It can be clearly seen that increases while decreases until the absorption of soliton 2 shown by a vertical black line. After that, reaches a constant and vanishes. A similar behaviour can be noticed with momentum and normalized by full momentum P (see panel (b)). Panel (c) shows the values of and having the dimension of wave numbers. The difference between them initially increases, which means an increase in velocities difference. Hence, soliton 1 began to move slower and reaches a constant velocity. As for Soliton 2, it first slowed down, then accelerated and finally was absorbed. The entire dynamics can be found in the following link: http://kachulin.itp.ac.ru/MultSolInt/SolInt-2-scenario-1-n(x).avi. The scenario dynamics fits in well with the results of [12].
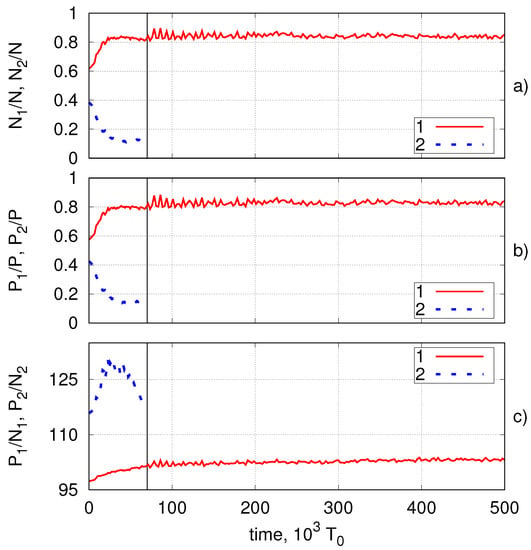
Figure 2.
Time dependence for number of particles (a), momentum (b) and wave number (c) in the first scenario.
Following [12], one can obtain relations for changing the number of particles of each breather after their collision using the conservation laws for the number of particles, momentum, and energy. Unfortunately, in the SCZE the relations for a single breather cannot be expressed explicitly in terms of its parameters, the group velocity, and amplitude since the breather solution itself cannot be written explicitly. On the other hand, a strong resemblance to the NLSE suggests that such a procedure can also be performed in the SCZE.
The NLS Equation (3) is integrable via the inverse scattering transform in 1-D [20] and has the infinite set of integral of motions. The expressions for them having the dimension of the number of particles, the total momentum, and the total energy take the following form:
For a single soliton the full momentum P and the total energy E can be determined by number of particles and soliton velocity U:
In the case of a weakly nonlinear wave with quanta the expressions for momentum and energy can be written as:
Let us consider the pairwise interaction of two solitons initially having different number of particles and velocities (, ) and (, ) with a formation of incoherent waves radiation . Initially two solitons located in x-space far from each other and the full number of particles, momentum and energy is the sum of the corresponding values of each soliton. As a result of the collision the parameters of solitons change slightly and incoherent waves radiation is observed. The parameters of solitons interacted can be denoted now as , when they are again far away from each other, and and are denote the number of particles and the wave number of incoherent waves.
Assuming that the changes in the number of particles and velocities are small, we can obtain the following expressions for the number of particles changes and of soliton 1 and 2 correspondingly:
Here and are the velocities changes of soliton 1 and 2 correspondingly.
Let us consider the case when breathers have very close velocities and . It will be recalled that and it cannot be less than at least of N per collision, otherwise we would not have seen that much radiation in our experiments after numerous breathers collisions. The difference in breathers velocities initially is and we consider their velocities close. Despite their velocities change after each collision, this change is not significant and it can be clearly seen in Figure 2 (panel c). According to the figure the maximum change in the wave number can be observed for soliton 2. In the beggining its wave number is increasing which means that its velocity becomes even less than the initial one, and . In this case according to the Equation (10) . At some point the velocity starts to increase. Let us estimate its maximum change. The evaluation of the maximum velocity change can be done using expression (7) for P. Indeed, the value of changed from to . Therefore, the maximum change in the relative velocity of the second soliton in more than 25 collisions is , and in one collision it can be roughly estimated as . Based on our estimates we believe that the effect of velocity changing in expressions (10) can be significant only when , and this is in the “worst” case. Even in this case the change does not exceed the estimated one, although it is very close. However, these “worst” cases either occur very rarely or do not occur at all. Therefore, it is assumed that the value of will be positive, and the value of will be negative. It means that soliton 1 will constantly increase the number of particles during the collision, and soliton 2, in turn, will constantly lose it. This is exactly what is observed in the experiment.
3.2. The Second Scenario of Two Breathers Collision Dynamics
Another scenario is less common. It can be observed in remaining 13 of 32 experiments and related to the bi-soliton solution in the NLSE. When the breathers velocities become even closer to each other, , they bind for a while into one periodically oscillating structure resembling the NLSE bi-soliton. In contrast to the NLSE, the structure is unstable in the SCZE. The dynamics of this scenario can no longer be described by expressions (10) due to the complex and intense interactions between breathers. Interacting in this way for some time, they significantly exchange their number of particles, that goes against our assumptions about a small change in the number of particles. The end result in scenario 2 remains the same – one of the breathers absorbs the another one that can be seen in panel (a) of Figure 3. The momentum dependence is the same again (panel (b)). Dimensionless wave numbers (panel (c)) tend to certain values throughout the interaction process of solitons, indicating that their velocities become closer up to the moment when one soliton remains. The entire dynamics can be found in http://kachulin.itp.ac.ru/MultSolInt/SolInt-2-scenario-2-n(x).avi. The detailed dynamics of “bi-breather” structure is presented in http://kachulin.itp.ac.ru/MultSolInt/SolInt-2-scenario-2-BS-|c(x)|.mp4.
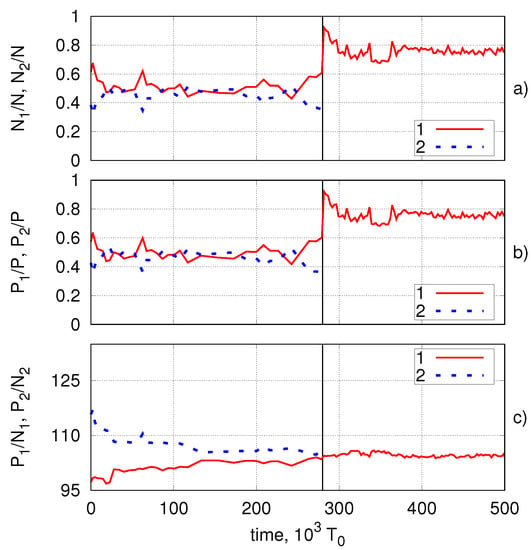
Figure 3.
Time dependence for number of particles (a), momentum (b) and wave number (c) in the second scenario.
The exact bound bi-soliton solution of NLSE (3) can be written as:
This solution is periodic in time with period . An interesting fact is that if the bi-soliton solution (11) is set as the initial condition in the SCZE, then it will exist for a large number of periods. Therefore, it is expected this <<bi-breather>> to be the solution of the SCZE. Figure 4 presents the bi-breather dynamics: the top panel (a) shows the initial state (11) and the bottom panel illustrate the state at time . Here —the characteristic period of the wave. The entire evolution of bi-soliton solution in the SCZE is presented in http://kachulin.itp.ac.ru/MultSolInt/BSNLSE-SCZE-|c(x)|.mp4.
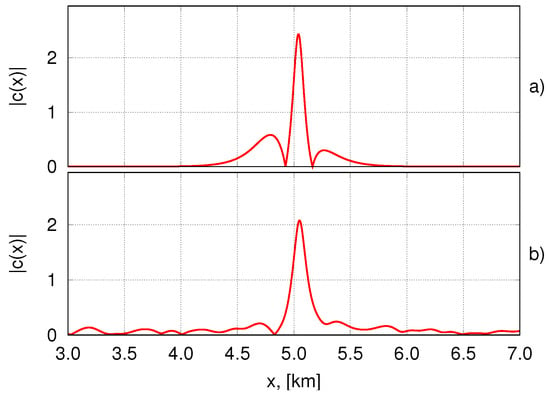
Figure 4.
Bi-breather evolution in the SCZE. Initial state (t = 0) is shown on the top panel (a). State at time is shown on the bottom panel (b).
3.3. The Interaction of a Larger Number of Breathers
An increasing number of solitons in the domain will not lead to any drastic changes. They still interact according to two previously discovered scenarios, and still, the only one remains. The cases of three and five solitons with arbitrarily phases are performed in Figure 5 and Figure 6. Video with three soliton dynamics can be found in http://kachulin.itp.ac.ru/MultSolInt/SolInt-3-|c(x)|.mp4 and with five soliton dynamics in http://kachulin.itp.ac.ru/MultSolInt/SolInt-5-|c(x)|.mp4. To increase the number of solitons causes difficulties in calculations. Since one soliton is always taking the particle number from all the others, this will inevitably lead to the wave breaking and the calculation end. Such a case, for instance, can be seen in Figure 6d, corresponding to the time moment immediately before wave breaks. On the other hand, the initial can be decreased to avoid the wave breaking, but in this case, the steepness of the waves also decreases. It will result in a significant weakening of the energy exchanging effects, and thus much longer calculation time will be required to observe any result.
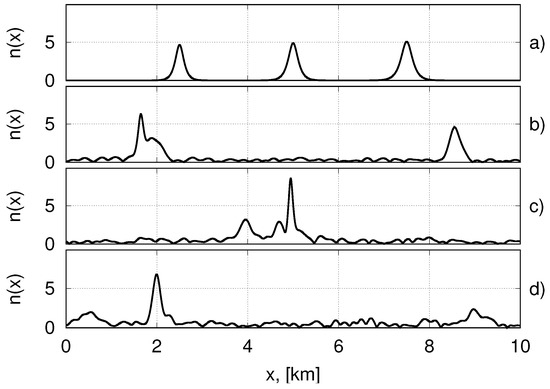
Figure 5.
The evolution of three interacting breathers. The ordinate shows the particles number density . The top panel (a) presents the initial state ( s). Panels (b) and (c) correspond to the states with s. and s. The lower panel (d) presents the state where the only one soliton remained ( s.)
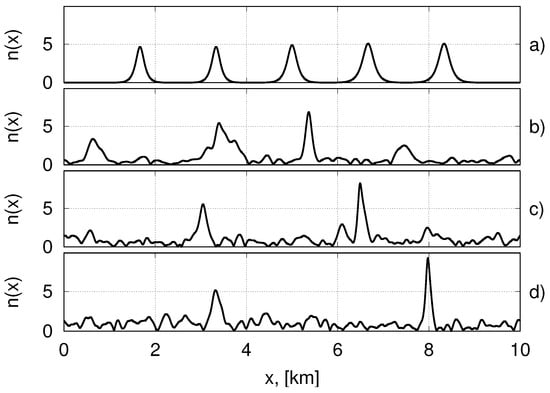
Figure 6.
The evolution of five interacting breathers. The ordinate shows the particles number density . The top panel (a) presents the initial state ( s.). Panels (b) and (c) correspond to the states with s. and s. The lower panel (d) presents the state of pre-breaking wave.
Nevertheless, despite the difficulties considered above, one cannot but to see that in all cases the tendency is the same. Namely, regardless of the number of solitons, there will always be the only one in the end.
4. Conclusions
We studied long-time dynamics in the SCZE for unidirectional deep water waves. We showed that after numerous collisions of breathers, only one soliton having a larger number of particles initially remains. Despite one outcome, two different scenarios of soliton dynamics were observed. In the first scenario, the “strong” soliton, which initially has a larger number of particles, increases after each interaction, while the “weak” soliton decreases. In the second scenario, the breathers velocities become very close after a certain number of pair interactions, due to the energy, momentum, and the number of particles exchanging. It leads to the formation of a bound soliton or “molecule” from a pair of solitons, which is similar to the well-known exact bound bi-soliton solution of the NLSE. After a certain number of time periods, this bound pair of solitons turns into one large soliton. The first scenario can be analytically described by the NLSE estimations, in contrast to the second one, where there is a complex and incomprehensible interaction of breathers. The initial conditions in all experiments differed only in the relative phase which means that phases play an essential role in the formation of the necessary conditions for two scenarios considered and dynamics in general. In addition, it was revealed that the NLSE bi-soliton solution taken as a initial condition for the SCZE for a hundred thousand wave periods. It gives hope that there is a “bi-breather” solution in the non-integrable SCZE similar with the bi-soliton solution of the integrable NLSE and perhaps it can be found analytically or numerically.
Author Contributions
Investigation, writing–review and editing, D.K., A.D., S.D.; software and visualisation, D.K., S.D.; writing–original draft preparation, D.K., A.D., S.D. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the Russian Science Foundation (Grant No. 18-71-00079 to D.K., S.D.).
Acknowledgments
Simulations were performed at the Novosibirsk Supercomputer Center of Novosibirsk State University.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NLSE | nonlinear Schrödinger equation |
| SCZE | super compact Zakharov equation |
References
- Zakharov, V.E. Kinetic equation for solitons. Sov. Phys. JETP 1971, 33, 538. [Google Scholar]
- Pelinovsky, E.N.; Shurgalina, E.; Sergeeva, A.; Talipova, T.G.; El, G.; Grimshaw, R.H. Two-soliton interaction as an elementary act of soliton turbulence in integrable systems. Phys. Lett. A 2013, 377, 272–275. [Google Scholar] [CrossRef]
- Shurgalina, E.; Pelinovsky, E. Nonlinear dynamics of a soliton gas: Modified Korteweg–de Vries equation framework. Phys. Lett. A 2016, 380, 2049–2053. [Google Scholar] [CrossRef]
- Dutykh, D.; Pelinovsky, E. Numerical simulation of a solitonic gas in KdV and KdV–BBM equations. Phys. Lett. A 2014, 378, 3102–3110. [Google Scholar] [CrossRef]
- El, G.A.; Kamchatnov, A.M. Kinetic equation for a dense soliton gas. Phys. Rev. Lett. 2005, 95, 204101. [Google Scholar] [CrossRef]
- El, G.A. Critical density of a soliton gas. Chaos Interdiscip. J. Nonlinear Sci. 2016, 26, 023105. [Google Scholar] [CrossRef]
- Sun, Y.H. Soliton synchronization in the focusing nonlinear Schrödinger equation. Phys. Rev. E 2016, 93, 052222. [Google Scholar] [CrossRef]
- Gelash, A. Formation of rogue waves from a locally perturbed condensate. Phys. Rev. E 2018, 97, 022208. [Google Scholar] [CrossRef]
- Gelash, A.; Agafontsev, D.; Zakharov, V.; El, G.; Randoux, S.; Suret, P. Bound state soliton gas dynamics underlying the spontaneous modulational instability. Phys. Rev. Lett. 2019, 123, 234102. [Google Scholar] [CrossRef]
- Schwache, A.; Mitschke, F. Properties of an optical soliton gas. Phys. Rev. E 1997, 55, 7720. [Google Scholar] [CrossRef]
- Redor, I.; Barthélemy, E.; Michallet, H.; Onorato, M.; Mordant, N. Experimental evidence of a hydrodynamic soliton gas. Phys. Rev. Lett. 2019, 122, 214502. [Google Scholar] [CrossRef] [PubMed]
- Dyachenko, A.; Zakharov, V.; Pushkarev, A.; Shvets, V.; Yan’kov, V. Soliton turbulence in nonintegrable wave systems. Sov. Phys. JETP 1989, 69, 1144. [Google Scholar]
- Dyachenko, A.; Kachulin, D.; Zakharov, V.E. Super compact equation for water waves. J. Fluid Mech. 2017, 828, 661–679. [Google Scholar] [CrossRef]
- Dyachenko, A.I.; Zakharov, V.E. Compact equation for gravity waves on deep water. JETP Lett. 2011, 93, 701. [Google Scholar] [CrossRef]
- Dyachenko, A.; Zakharov, V.E. A dynamic equation for water waves in one horizontal dimension. Eur. J. Mech. B/Fluids 2012, 32, 17–21. [Google Scholar] [CrossRef]
- Dyachenko, A.; Kachulin, D.; Zakharov, V. Collisions of two breathers at the surface of deep water. Nat. Hazards Earth Syst. Sci. 2013, 13, 3205. [Google Scholar] [CrossRef]
- Kachulin, D.; Gelash, A. On the phase dependence of the soliton collisions in the Dyachenko–Zakharov envelope equation. Nonlinear Process. Geophys. 2018, 25, 553–563. [Google Scholar] [CrossRef]
- Dyachenko, A.I.; Kachulin, D.; Zakharov, V.E. On the nonintegrability of the free surface hydrodynamics. JETP Lett. 2013, 98, 43–47. [Google Scholar] [CrossRef]
- Dyachenko, A.; Kachulin, D.; Zakharov, V.E. Envelope equation for water waves. J. Ocean Eng. Mar. Energy 2017, 3, 409–415. [Google Scholar] [CrossRef]
- Zakharov, V.; Shabat, A. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 1972, 34, 62–69. [Google Scholar]
- Peregrine, D.H. Water waves, nonlinear Schrödinger equations and their solutions. ANZIAM J. 1983, 25, 16–43. [Google Scholar] [CrossRef]
- Frigo, M.; Johnson, S. The Design and Implementation of FFTW3. Proc. IEEE 2005, 93, 216–231. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).