Influence of Shear-Thinning Blood Rheology on the Laminar-Turbulent Transition over a Backward Facing Step
Abstract
1. Introduction
2. Methods
2.1. Governing Equations
2.1.1. Menter’s SST Model
2.1.2. Smagorinsky SGS Model
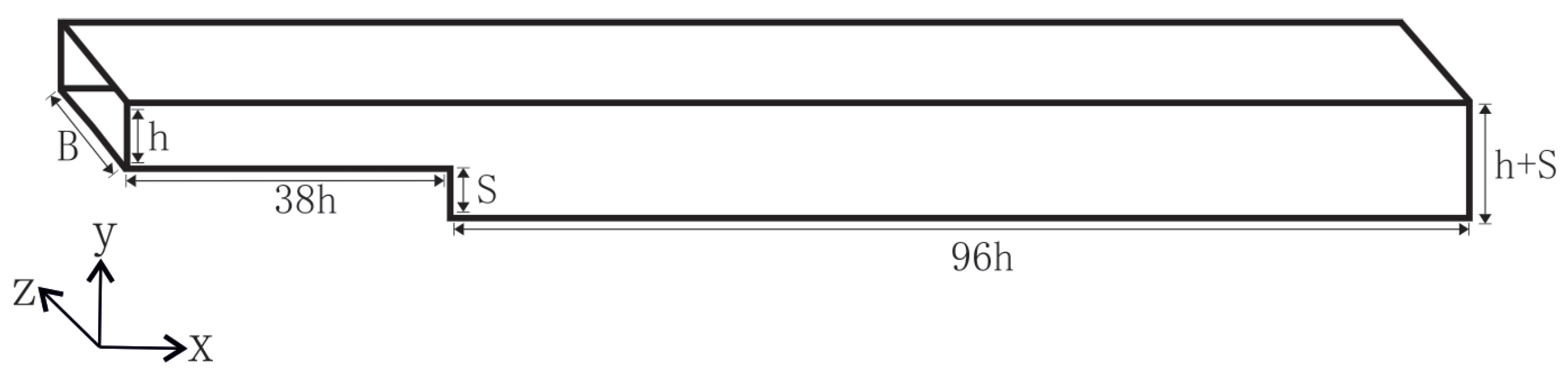
2.2. Computational Domain
2.3. Mesh Generation and Sensitivity Study
2.4. Boundary Conditions
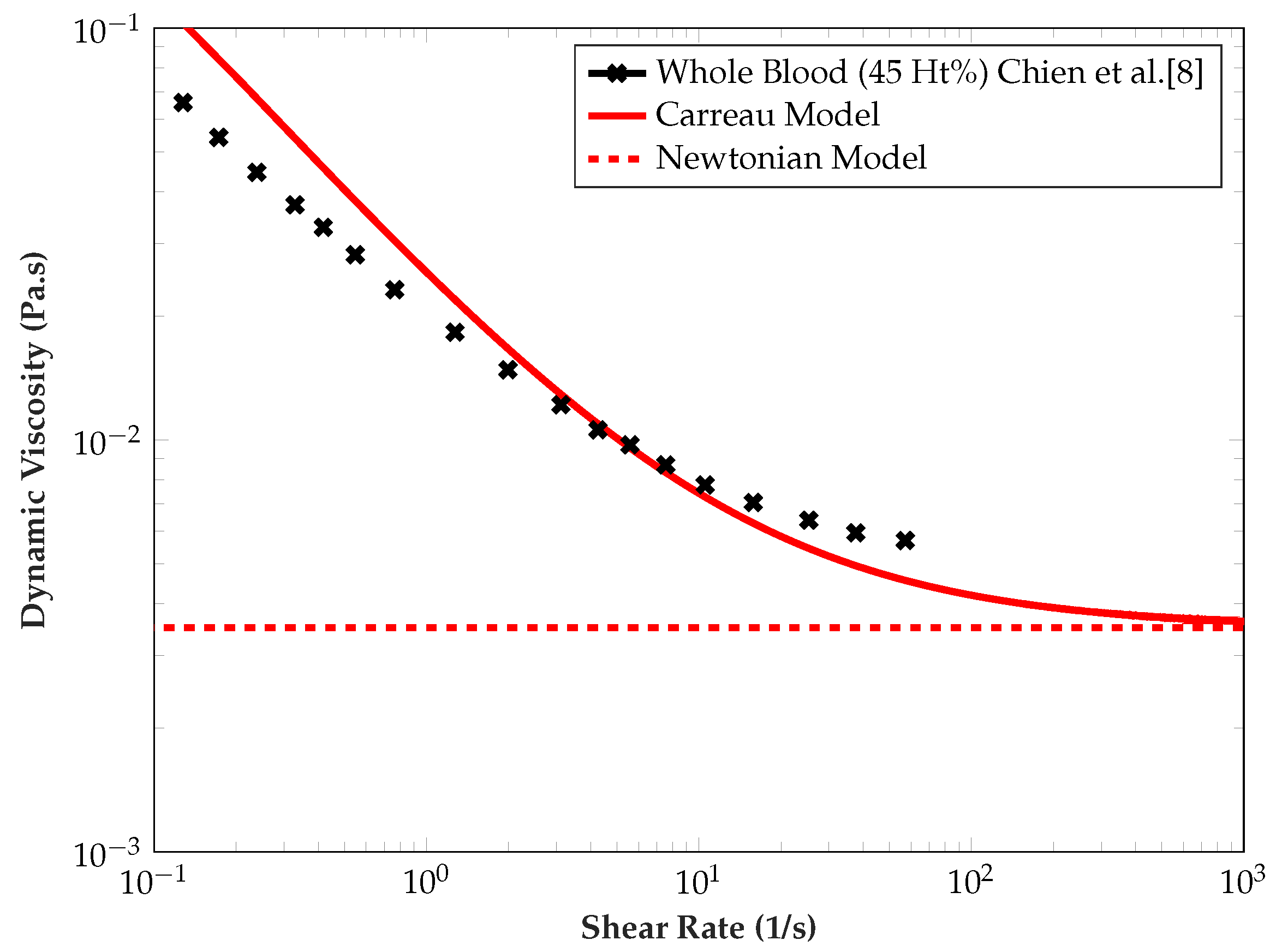
2.5. Rheological Models
2.6. Solution of Equations
2.7. Parallel Processing
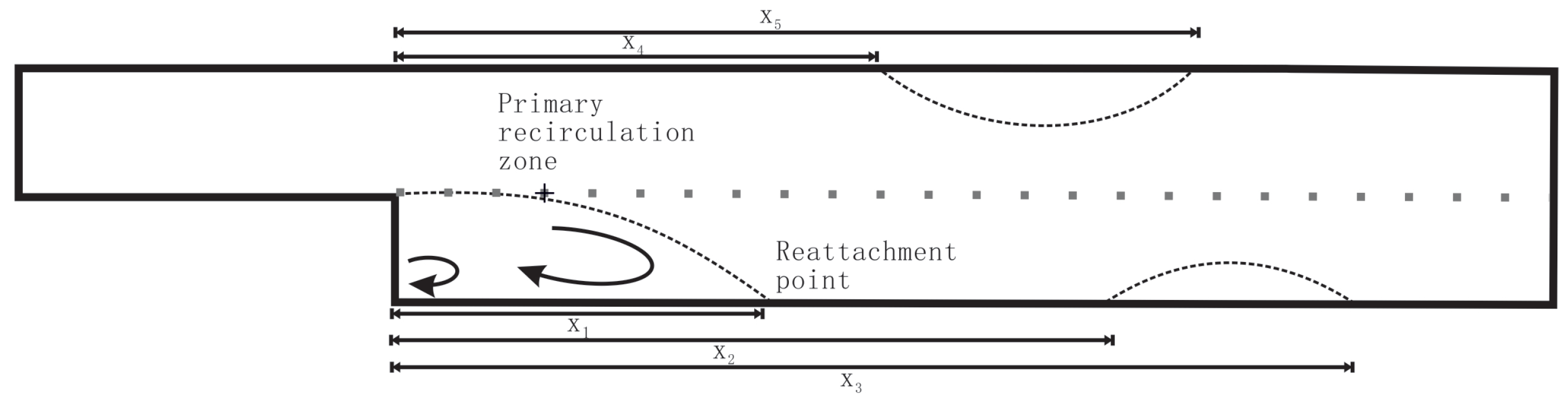
2.8. Analysis of Recirculating Flow Regions
3. Results
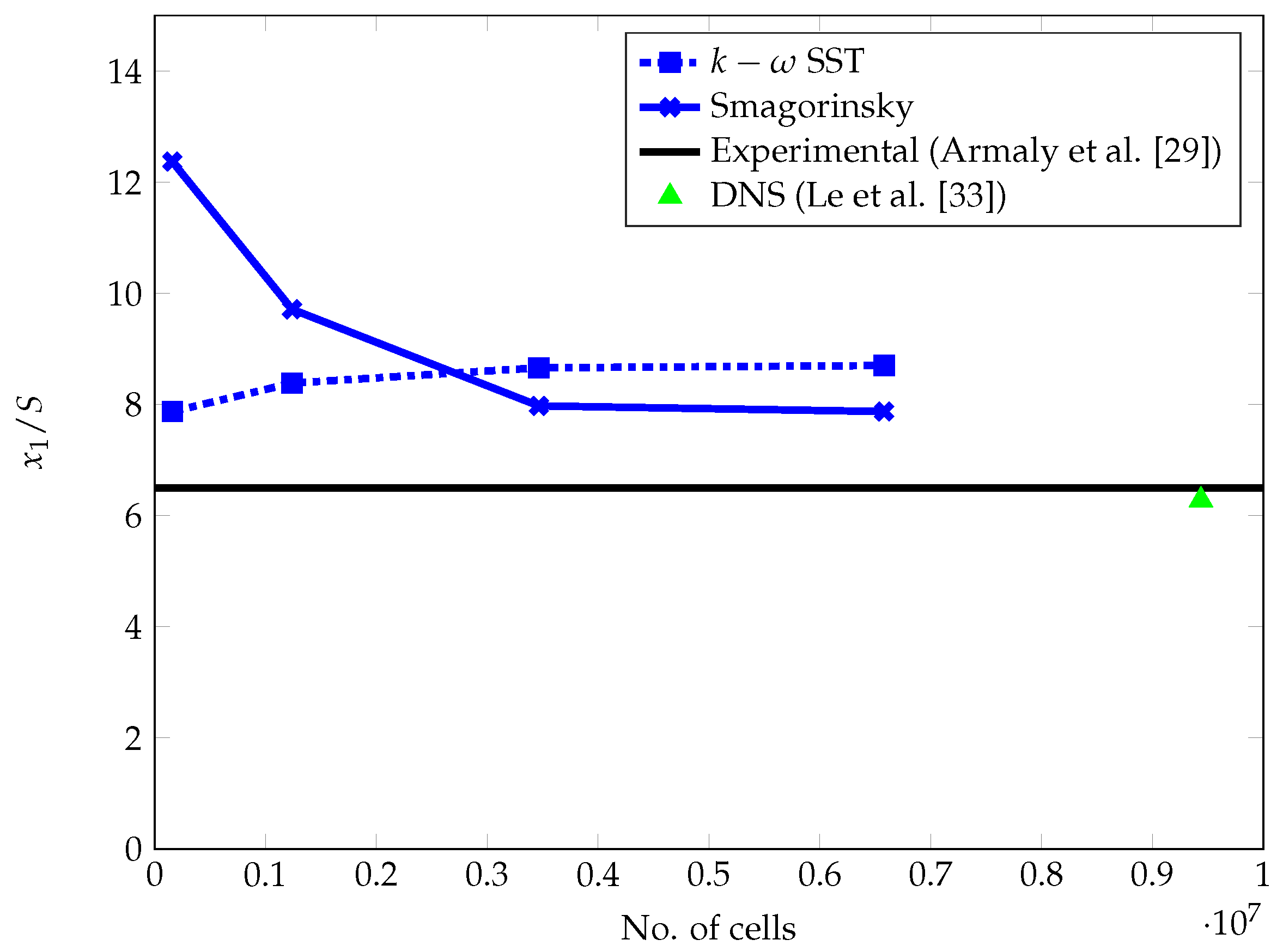
3.1. Mesh Independence Study
3.2. Validation Study
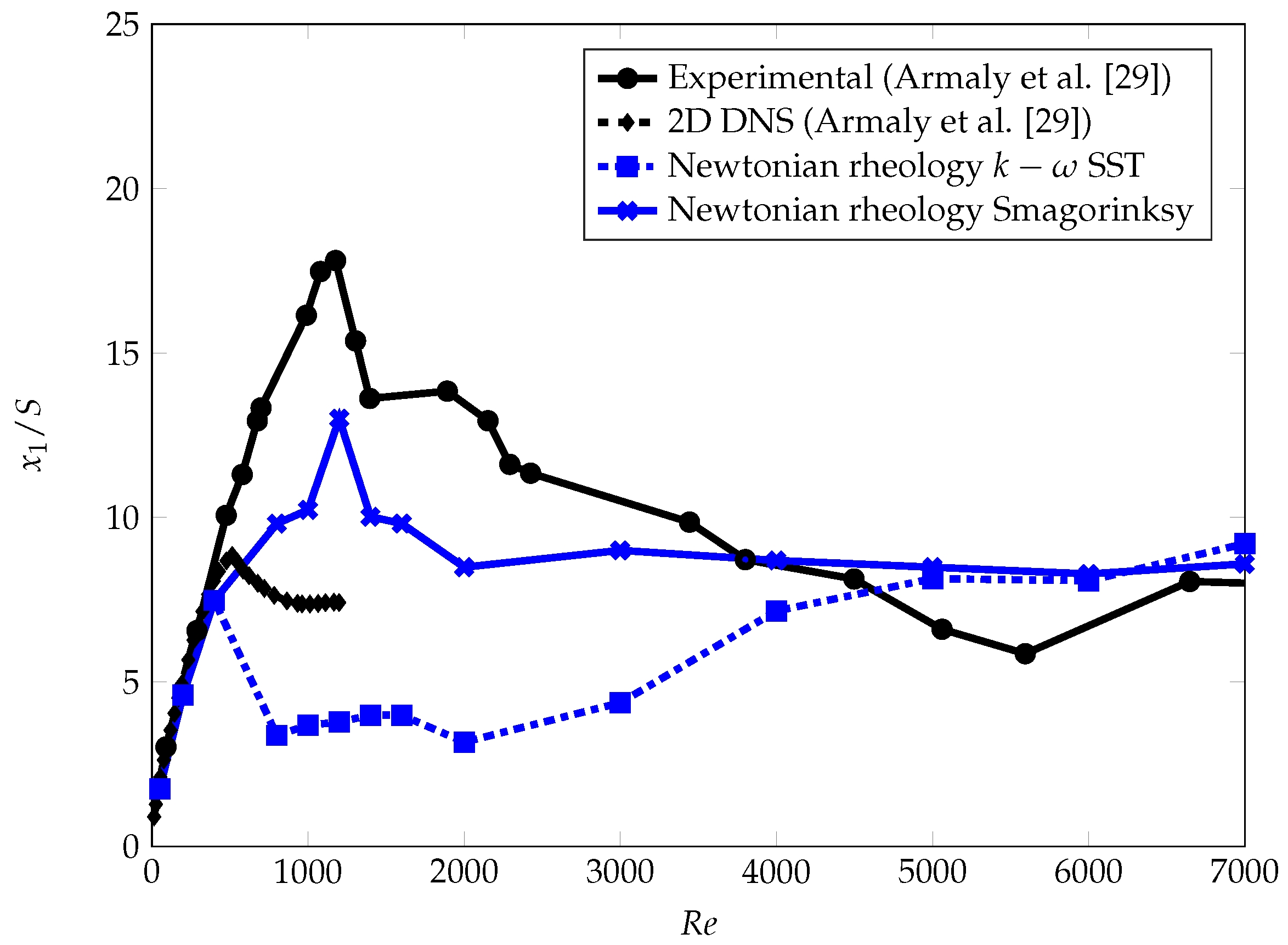
3.2.1. Validation of Recirculation Zone Length for Newtonian Blood Rheology
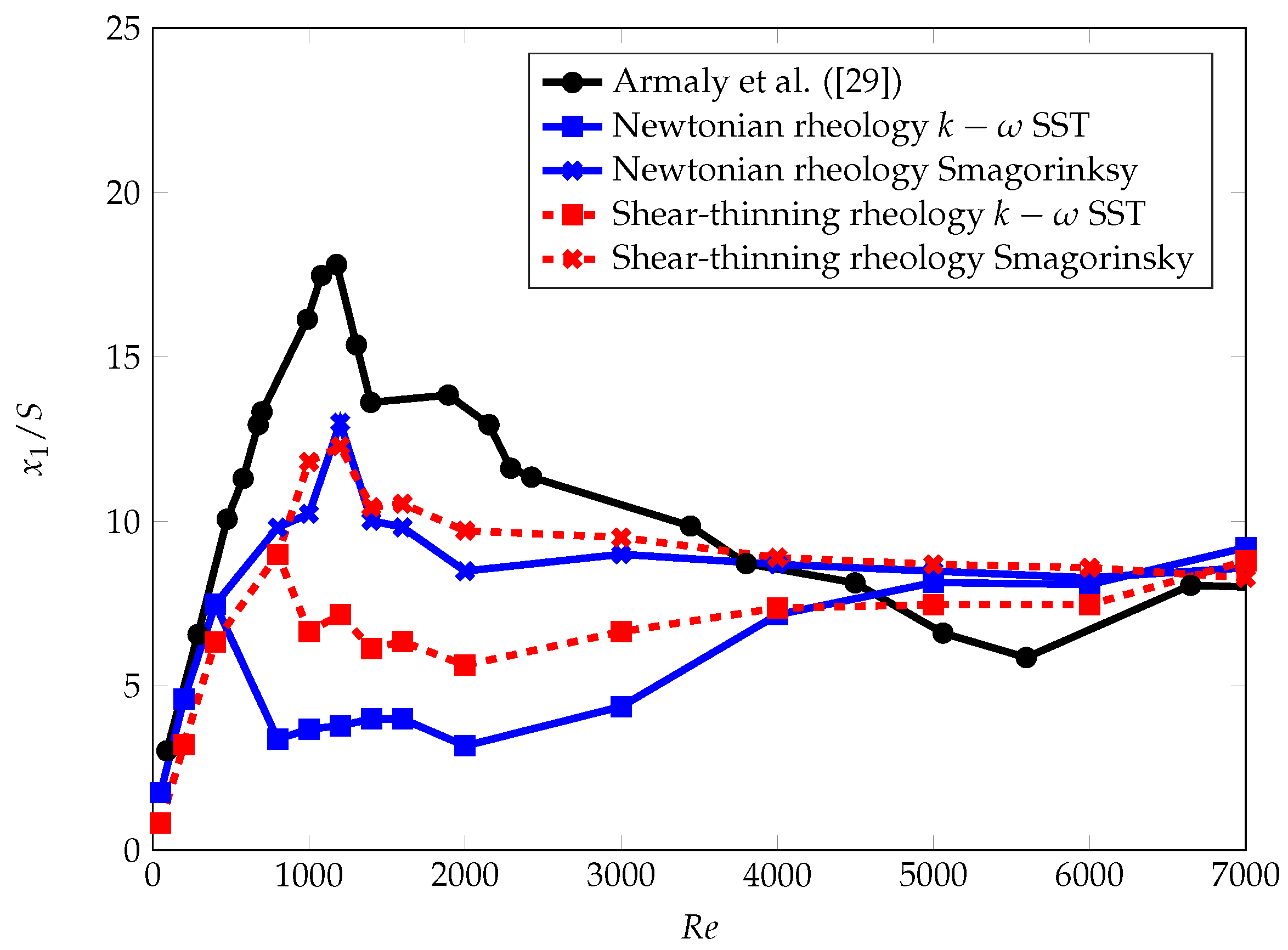
3.2.2. Validation of Recirculation Zone Length for Shear-Thinning Rheology
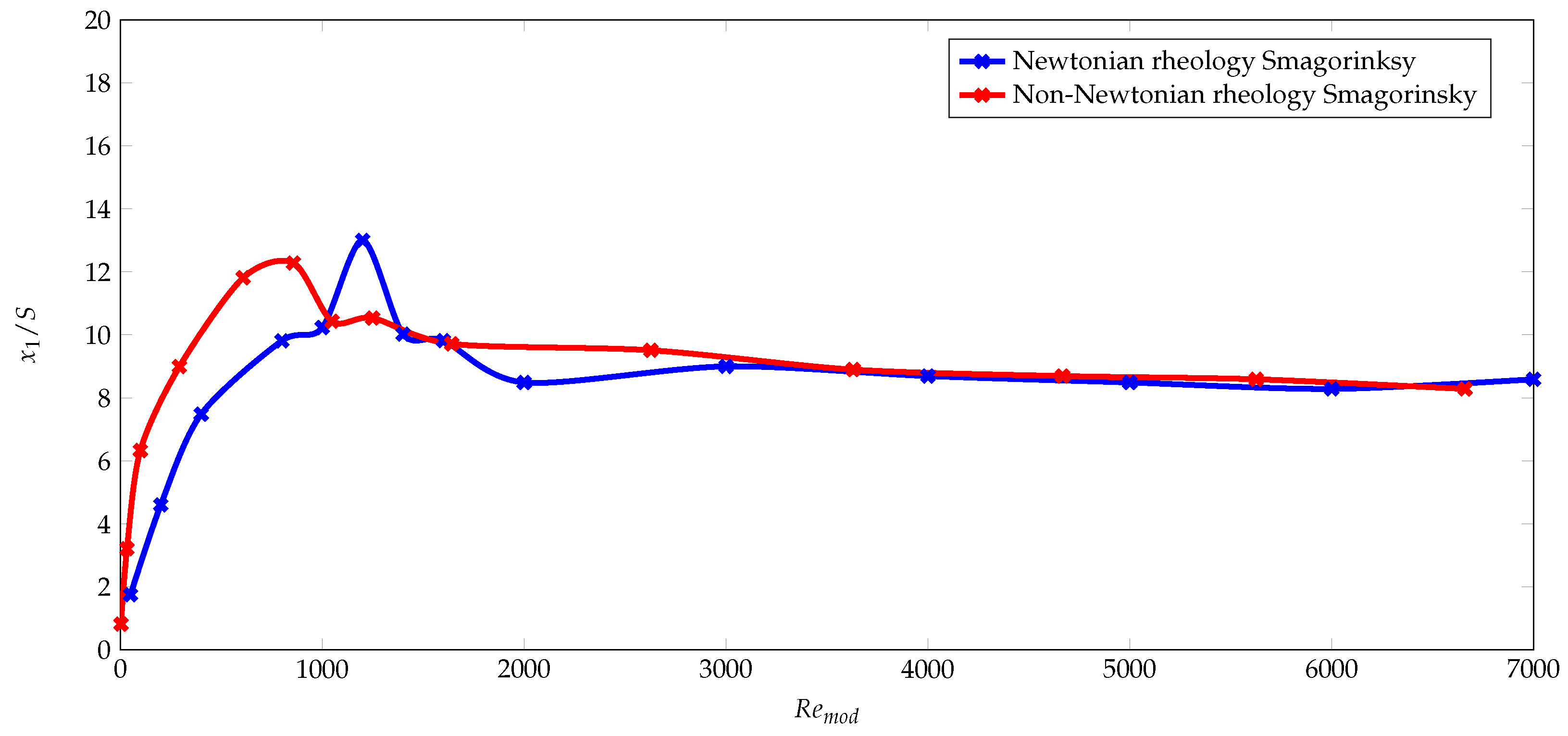
3.3. Impact of Newtonian vs. Shear-Thinning Blood Rheology on Recirculation Zone Length for All
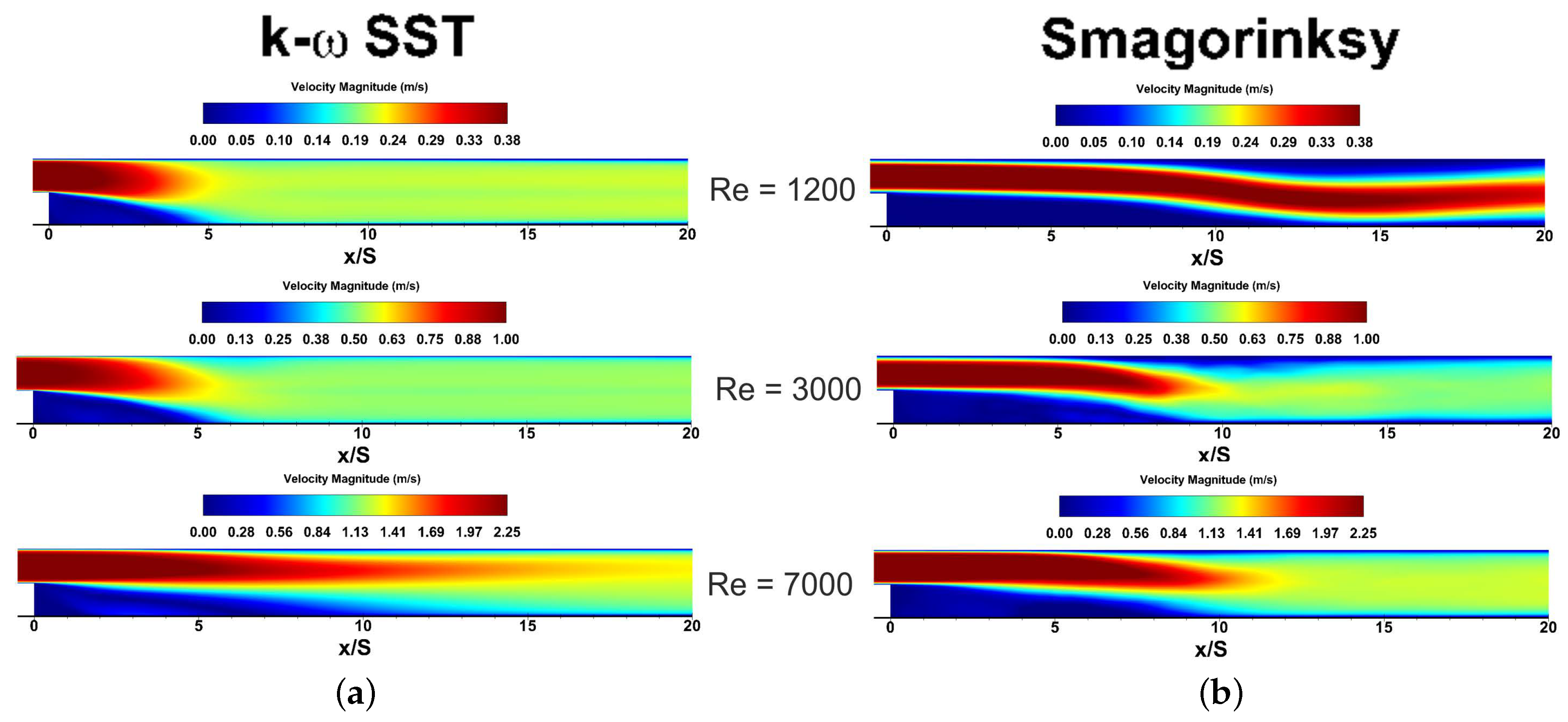
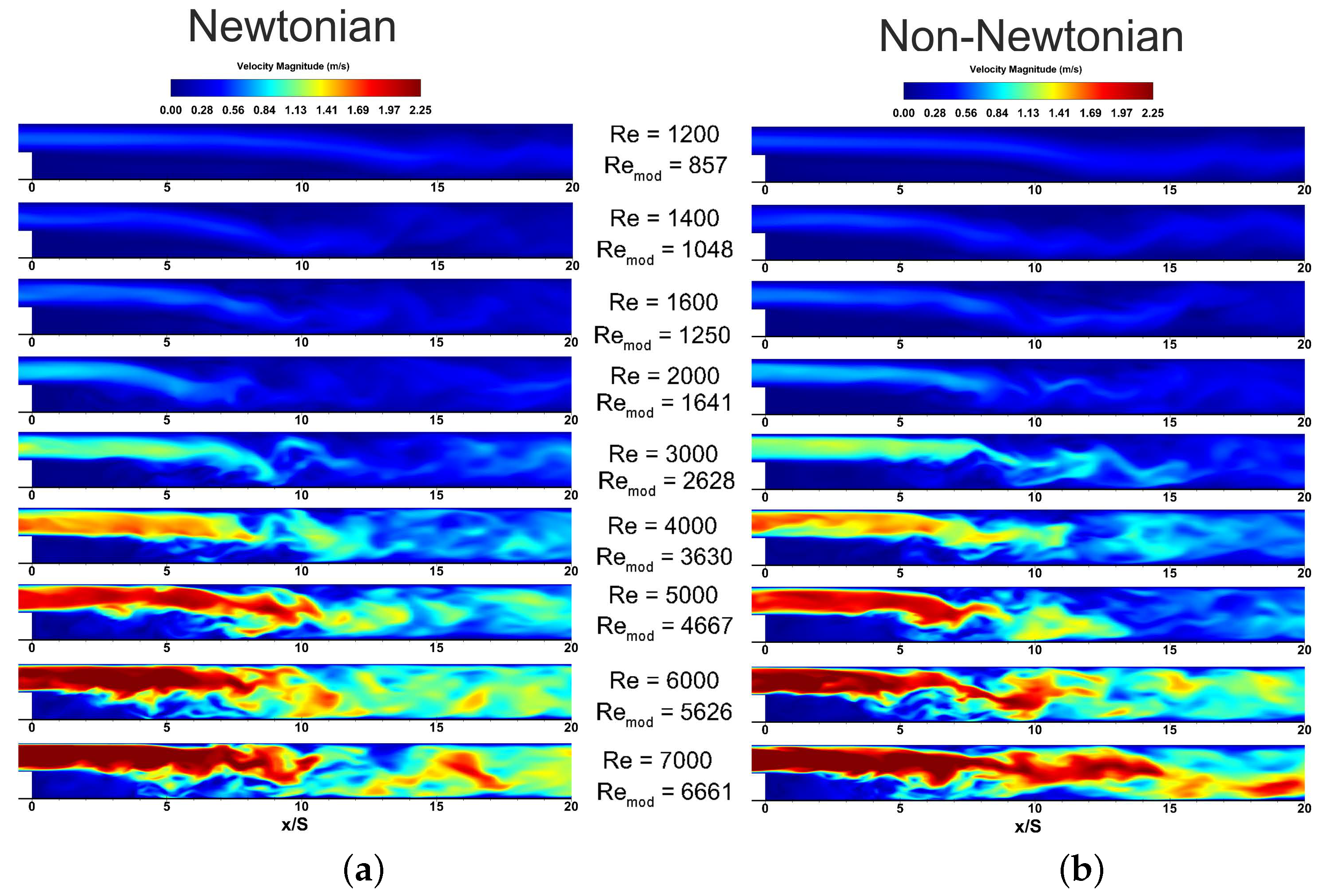
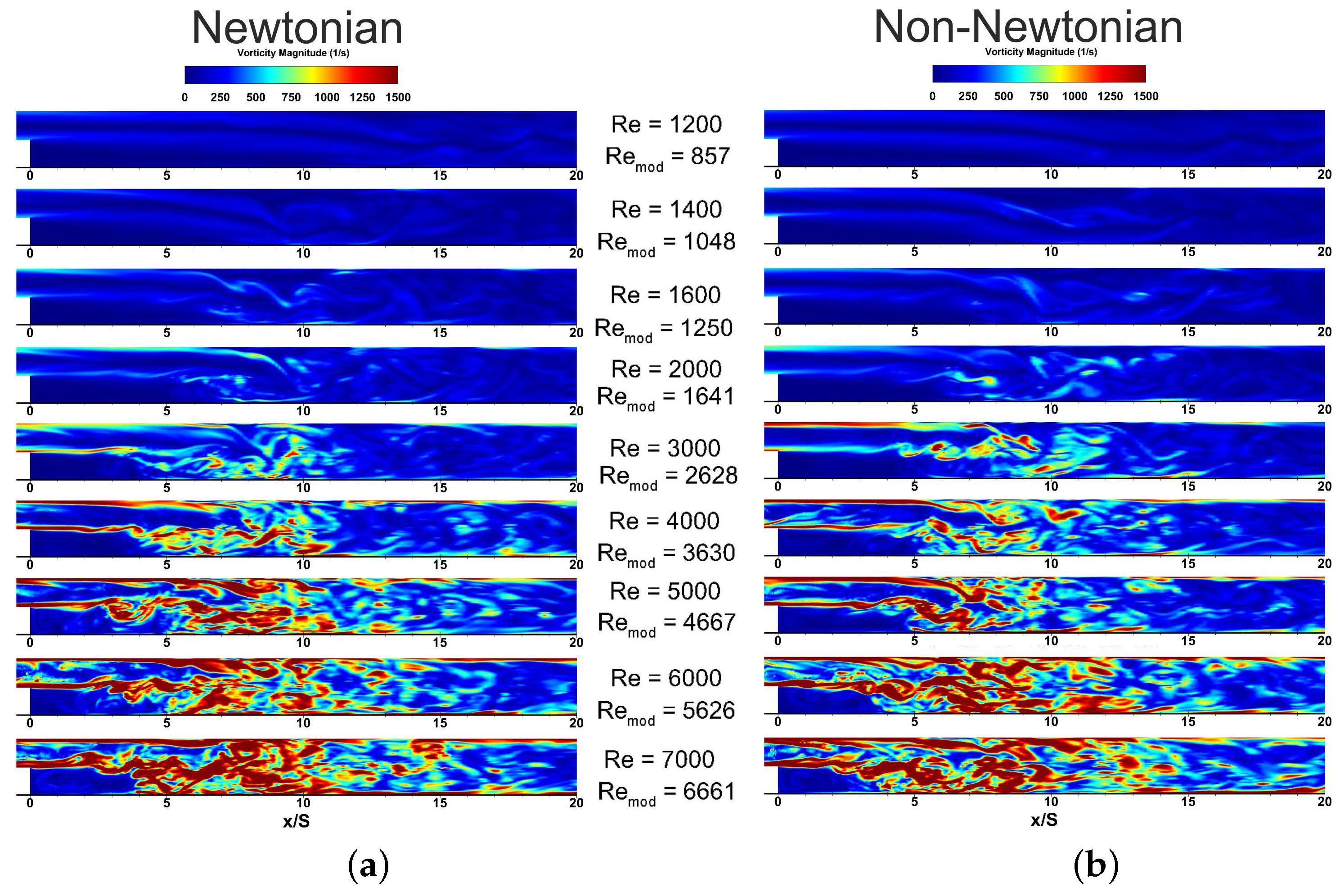
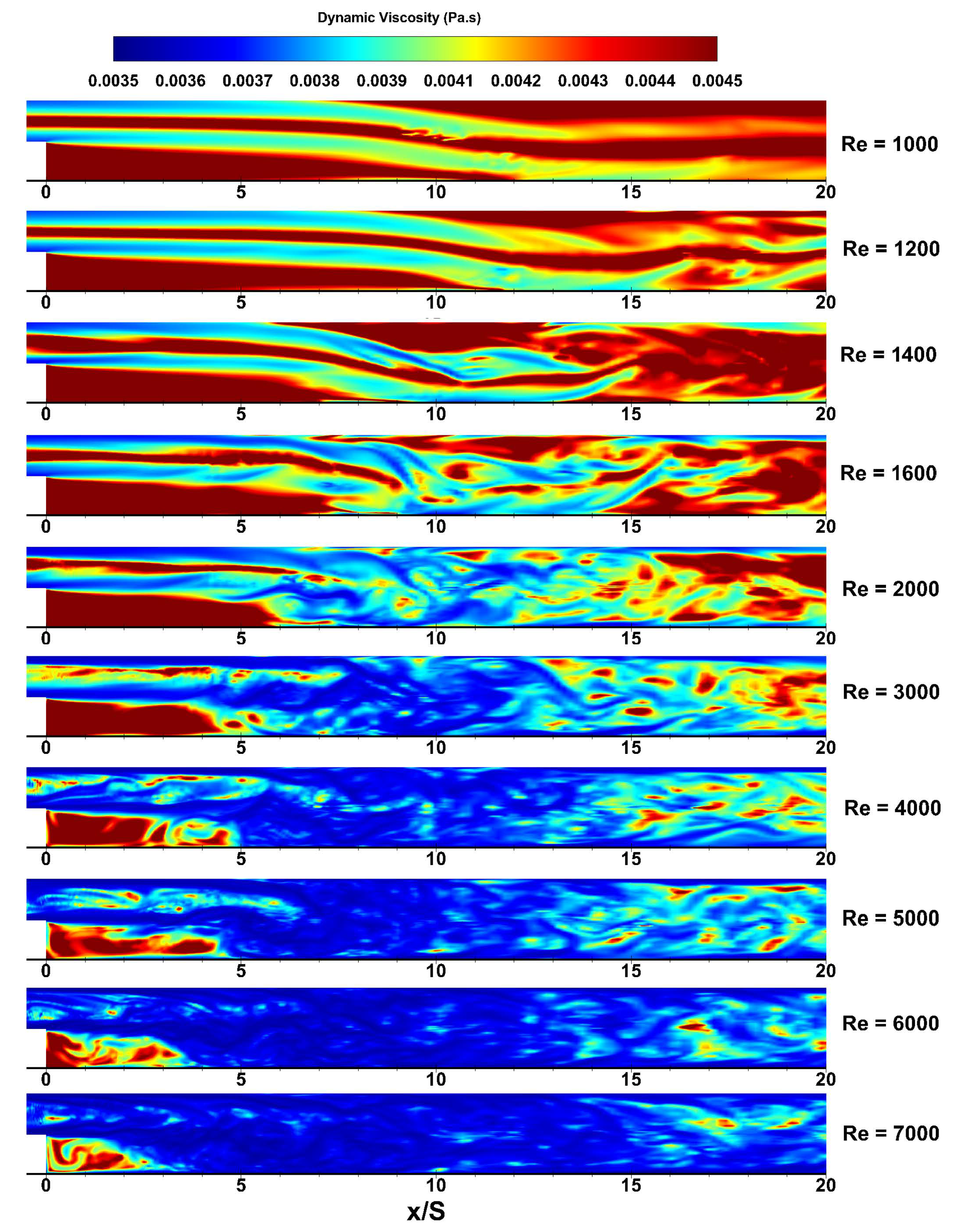
3.4. Velocity and Vorticity Flow Fields
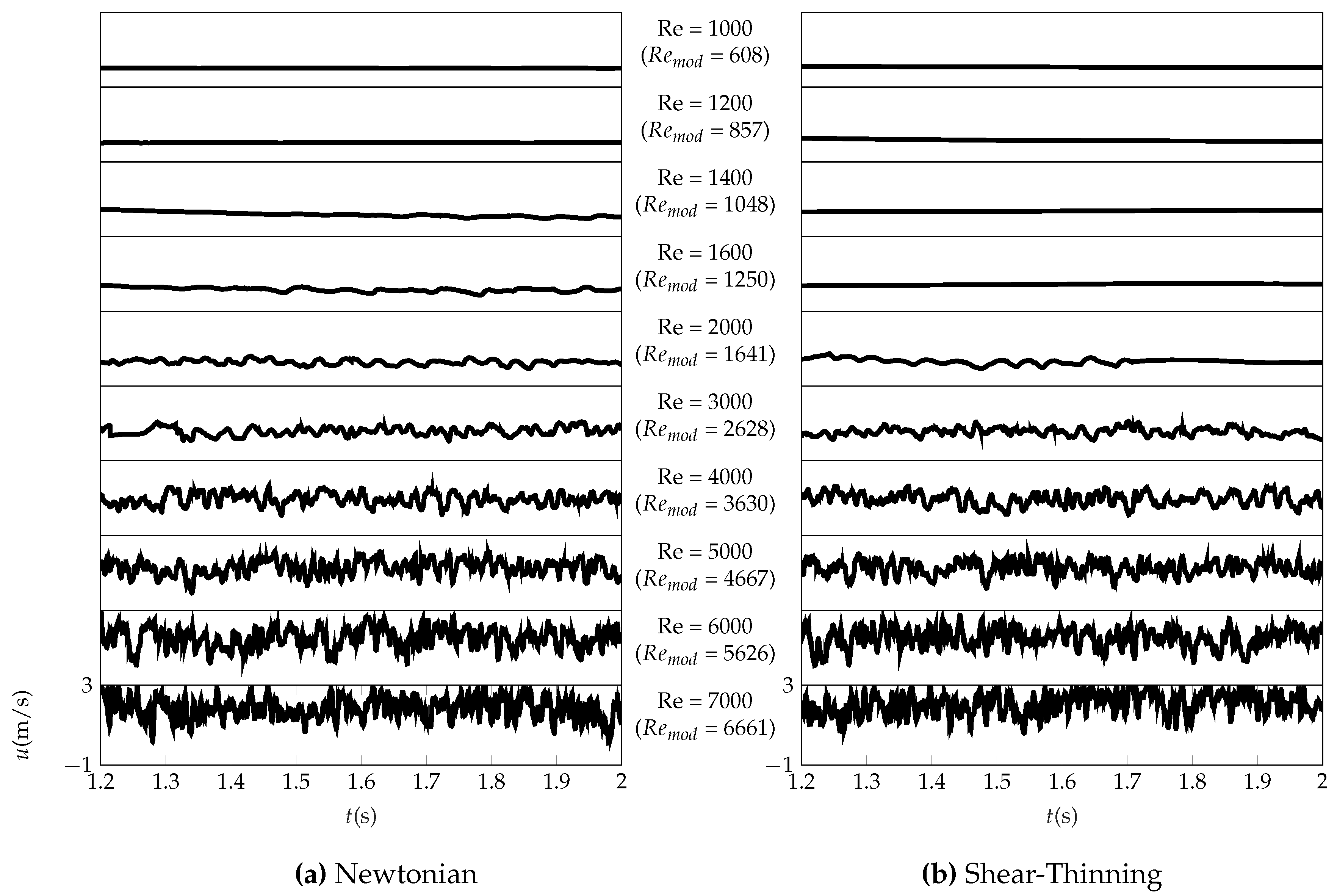
3.5. Temporal Flow Analysis
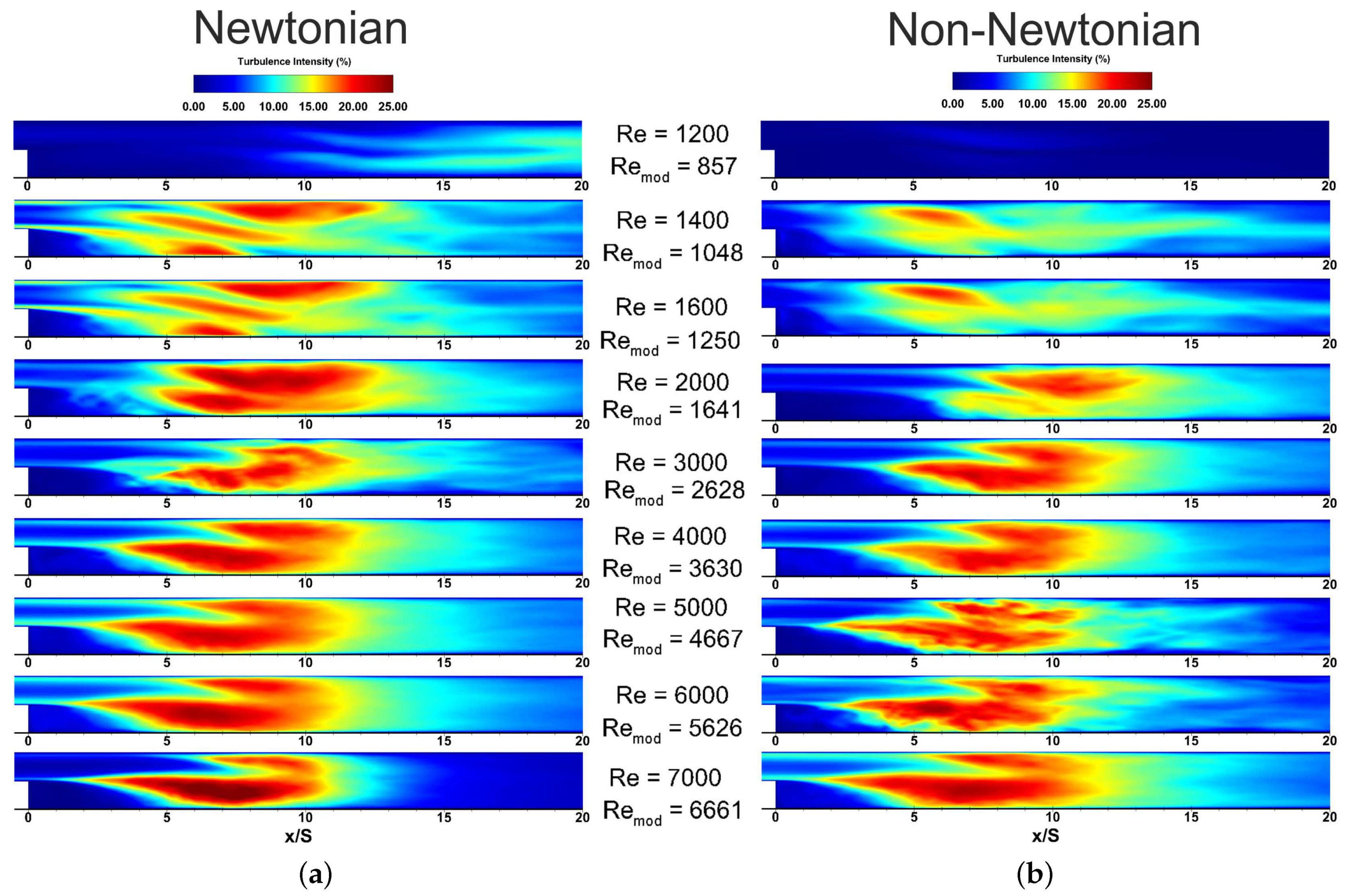
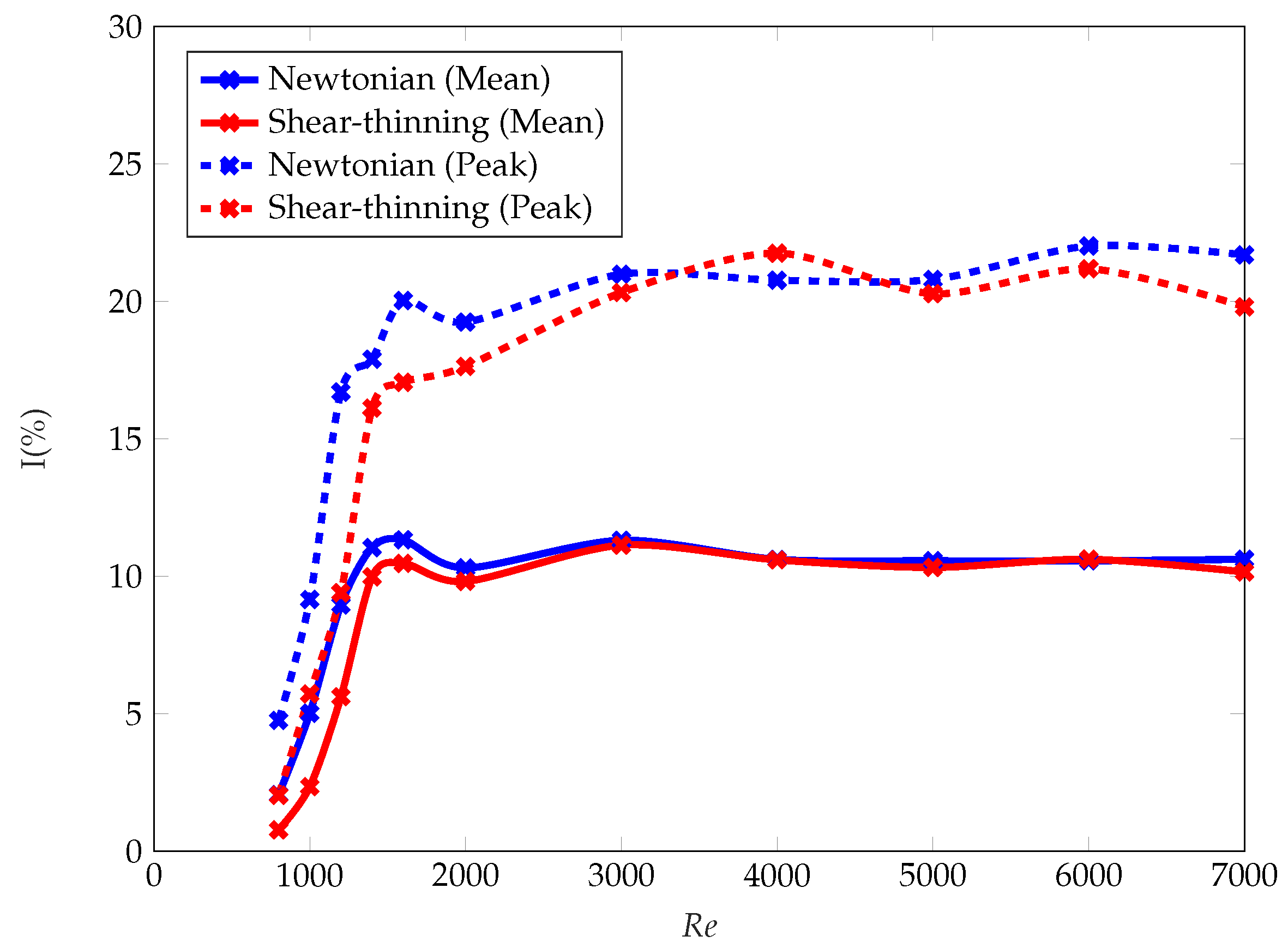
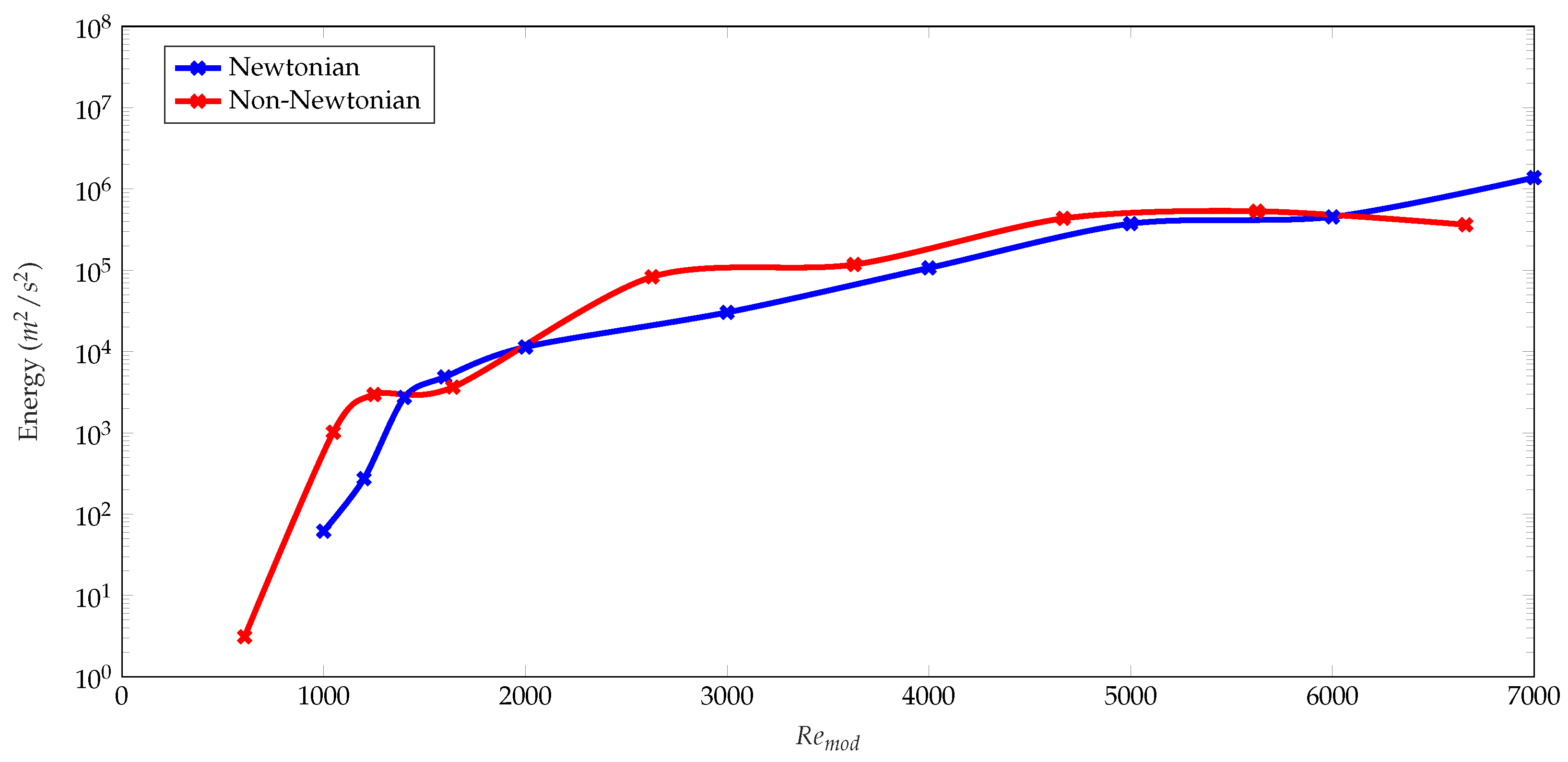
3.5.1. Turbulence Intensity
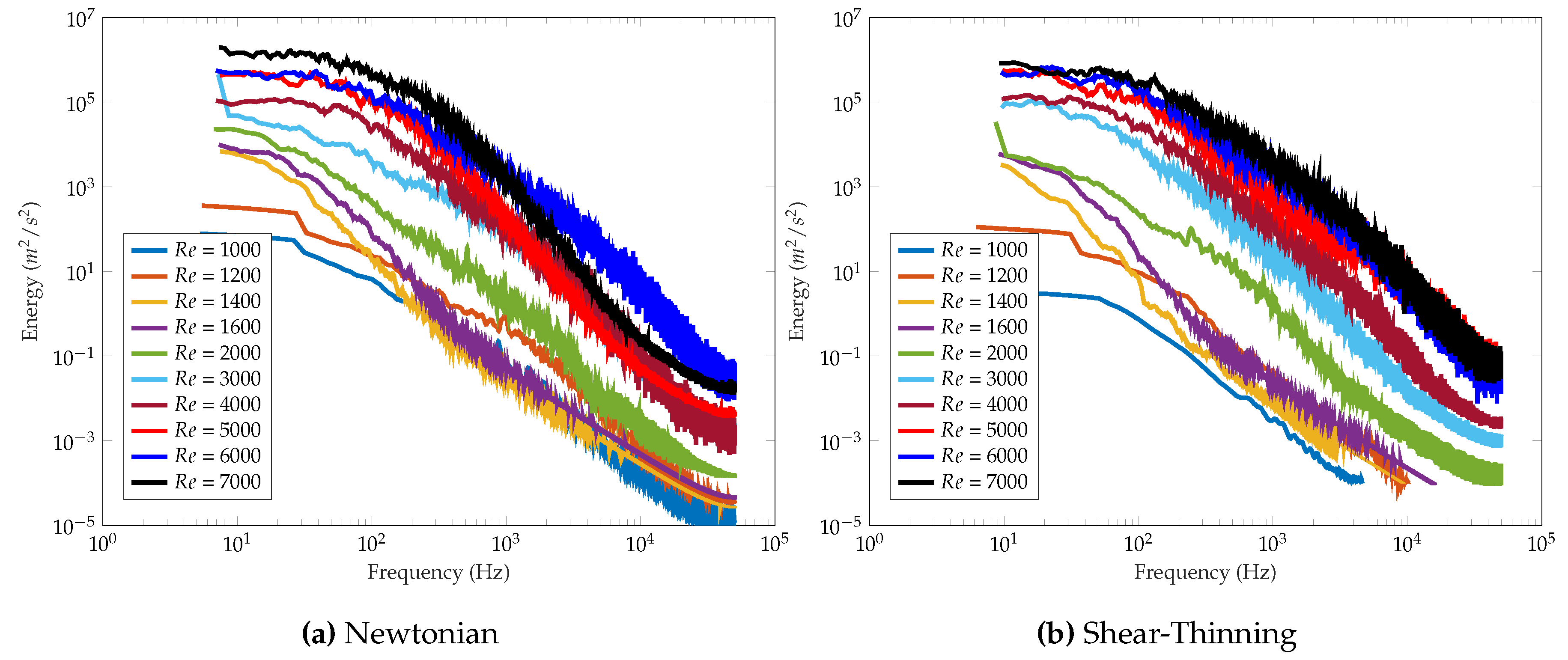
3.5.2. Turbulent Kinetic Energy Frequency Spectra
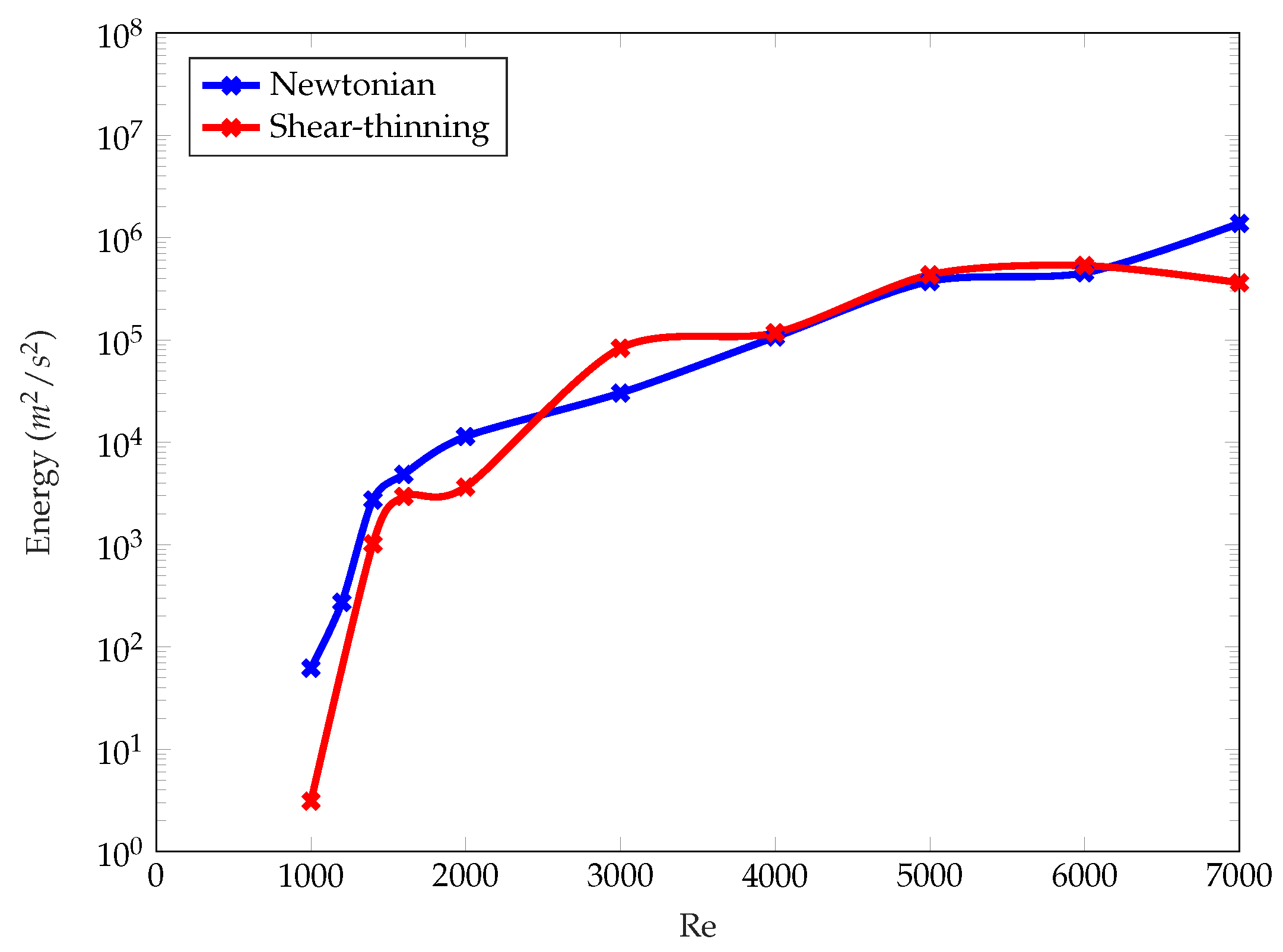
3.6. Impact of Shear-Thinning Blood Rheology
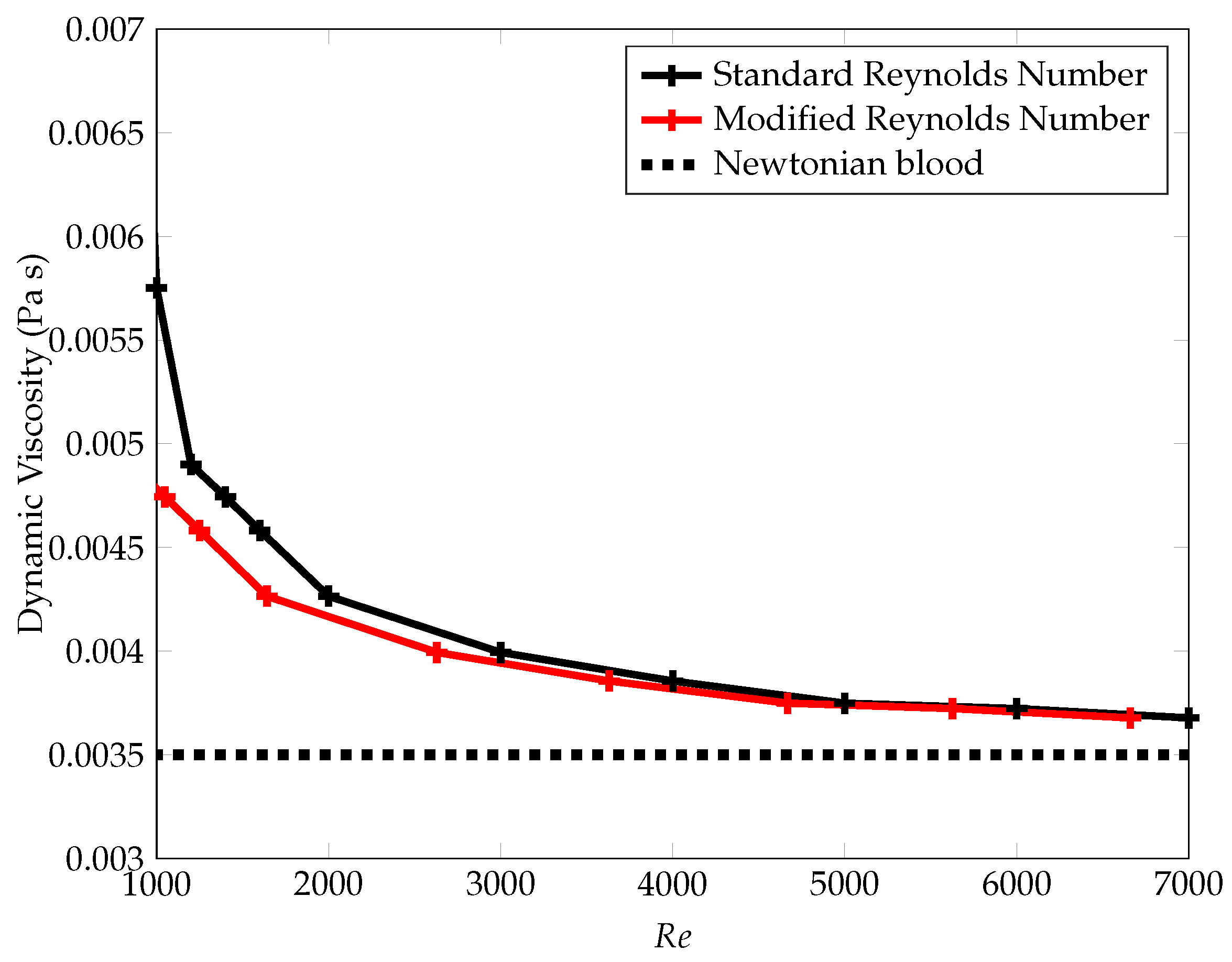
3.7. Effect of Shear-Thinning Viscosity on Reynolds Number
4. Discussion
4.1. Recirculation Zone Development
4.2. Evaluation of Laminar-Turbulent Transition
4.3. Definition of Reynolds Number on Shear-Thinning Rheology
4.4. Limitations and Future Perspectives
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| LES | Large Eddy Simulation |
| URANS | Unsteady Reynolds averaged Navier Stokes |
| DNS | Direct numerical simulation |
| SGS | Subgrid scale |
| GS | Grid scale |
| TKE | Turbulent kinetic energy |
| MHV | Mechanical heart valve |
| VAD | Ventricular assist device |
| CFD | Computational fluid dynamics |
| BFS | Backward facing step |
| RMS | Root mean square |
| TI | Turbulence intensity |
| RBC | Red blood cell |
| Reynolds number | |
| Critical Reynolds number | |
| Modified Reynolds number |
References
- Dewey, C.F.; Bussolari, S.R.; Gimbrone, M.A.; Davies, P.F. The Dynamic Response of Vascular Endothelial Cells to Fluid Shear Stress. J. Biomech. Eng. 1981, 103, 177. [Google Scholar] [CrossRef]
- Chiu, J.J.; Usami, S.; Chien, S. Vascular endothelial responses to altered shear stress: Pathologic implications for atherosclerosis. Ann. Med. 2009, 41, 19–28. [Google Scholar] [CrossRef] [PubMed]
- Einav, S.; Bluestein, D. Dynamics of blood flow and platelet transport in pathological vessels. Ann. N. Y. Acad. Sci. 2004, 1015, 351–366. [Google Scholar] [CrossRef] [PubMed]
- Stein, P.D.; Sabbah, H.N. Turbulent Blood-Flow in Ascending Aorta of Humans with Normal and Diseased Aortic Valves. Circ. Res. 1976, 39, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Ha, H.; Ziegler, M.; Welander, M.; Bjarnegård, N.; Carlhäll, C.J.; Lindenberger, M.; Länne, T.; Ebbers, T.; Dyverfeldt, P. Age-related vascular changes affect turbulence in aortic blood flow. Front. Physiol. 2018, 9, 36. [Google Scholar] [CrossRef]
- Kameneva, M.V.; Burgreen, G.W.; Kono, K.; Repko, B.; Antaki, J.F.; Umezu, M. Effects of Turbulent Stresses upon Mechanical Hemolysis: Experimental and Computational Analysis. ASAIO J. 2004, 50, 418–423. [Google Scholar] [CrossRef]
- Luckraz, H.; Woods, M.; Large, S.R. In addition, hemolysis goes on: Ventricular assist device in combination with veno-venous hemofiltration. Ann. Thorac. Surg. 2002, 73, 546–548. [Google Scholar] [CrossRef]
- Chien, S.; Usami, S.; Taylor, H.M.; Lundberg, J.L.; Gregersen, M.I. Effects of hematocrit and plasma proteins on human blood rheology at low shear rates. J. Appl. Physiol. 1966, 21, 81–87. [Google Scholar] [CrossRef]
- Goldsmith, H.L. The microrheology of red blood cell suspensions. J. Gen. Physiol. 1968, 52, 5–28. [Google Scholar] [CrossRef]
- Dintenfass, L. Thixotropy of blood and proneness to thrombus formation. J. Am. Heart Res. 1962, XI, 233–239. [Google Scholar] [CrossRef]
- Merrill, E.W.; Gilliland, E.R.; Cokelet, G.; Shin, H.; Britten, A.; Wells, R.E. Rheology of Human Blood, near and at Zero Flow: Effects of Temperature and Hematocrit Level. Biophys. J. 1963, 3, 199–213. [Google Scholar] [CrossRef]
- Thurston, G. Viscoelasticity of Human Blood. Biophys. J. 1972, 12, 1205–1217. [Google Scholar] [CrossRef]
- Chien, S.; King, R.G.; Skalak, R.; Usami, S.; Copley, A.L. Viscoelastic Properties of Human Blood and Red Cell Suspensions. Biorheology 1975, 12, 341–346. [Google Scholar] [CrossRef] [PubMed]
- Coulter, N.A., Jr.; Pappenheimer, J.R. Development of turbulence in flowing blood. Am. J. Physiol. 1949, 159, 401–408. [Google Scholar] [CrossRef]
- Nerem, R.M.; Seed, W.A.; Wood, N.B. An experimental study of the velocity distribution and transition to turbulence in the aorta. J. Fluid Mech. 1972, 52, 137–161. [Google Scholar] [CrossRef]
- Biswas, D.; Casey, D.M.; Crowder, D.C.; Steinman, D.A.; Yun, Y.H.; Loth, F. Characterization of Transition to Turbulence for Blood in a Straight Pipe Under Steady Flow Conditions. J. Biomech. Eng. 2016, 138, 071001. [Google Scholar] [CrossRef]
- Sherwin, S.J.; Blackburn, H.M. Three-dimensional instabilities and transition of steady and pulsatile axisymmetric stenotic flows. J. Fluid Mech. 2005, 533, 297–327. [Google Scholar] [CrossRef]
- Khan, M.O.; Valen-Sendstad, K.; Steinman, D.A. Direct Numerical Simulation of Laminar-Turbulent Transition in a Non-Axisymmetric Stenosis Model for Newtonian vs. Shear-Thinning Non-Newtonian Rheologies. Flow Turbul. Combust. 2018, 102, 43–72. [Google Scholar] [CrossRef]
- Escudier, M.P.; Poole, R.J.; Presti, F.; Dales, C.; Nouar, C.; Desaubry, C.; Graham, L.; Pullum, L. Observations of asymmetrical flow behaviour in transitional pipe flow of yield-stress and other shear-thinning liquids. J. Non-Newton. Fluid Mech. 2005, 127, 143–155. [Google Scholar] [CrossRef]
- Güzel, B.; Burghelea, T.; Frigaard, I.A.; Martinez, D.M. Observation of laminar-turbulent transition of a yield stress fluid in Hagen-Poiseuille flow. J. Fluid Mech. 2009, 627, 97–128. [Google Scholar] [CrossRef]
- Bahrani, S.A.; Nouar, C. Intermittency in the transition to turbulence for a shear-thinning fluid in hagen-poiseuille flow. J. Appl. Fluid Mech. 2014, 7, 1–6. [Google Scholar]
- Peixinho, J.; Nouar, C.; Desaubry, C.; Théron, B. Laminar transitional and turbulent flow of yield stress fluid in a pipe. J. Non-Newton. Fluid Mech. 2005, 128, 172–184. [Google Scholar] [CrossRef]
- Escudier, M.P.; Presti, F.; Smith, S. Drag reduction in the turbulent pipe flow of polymers. J. Non-Newton. Fluid Mech. 1998, 81, 197–213. [Google Scholar] [CrossRef]
- Pozarlik, A.K.; Kok, J.B.W. Numerical Simulation of a Turbulent Flow Over a Backward Facing Step with Heated Wall: Effect of Pulsating Velocity and Oscillating Wall. J. Therm. Sci. Eng. Appl. 2012, 4, 041005. [Google Scholar] [CrossRef]
- Pearce, B.W.; Brandner, P.A.; Foster, S.J. Ventilated cavity flow over a backward-facing step. J. Phys. Conf. Ser. 2015, 656, 012164. [Google Scholar] [CrossRef]
- Truskey, G.A.; Barber, K.M.; Robey, T.C.; Olivier, L.A.; Combs, M.P. Characterization of a Sudden Expansion Flow Chamber to Study the Response of Endothelium to Flow Recirculation. J. Biomech. Eng. 1995, 117, 203–210. [Google Scholar] [CrossRef] [PubMed]
- Gijsen, F.J.H.; Van De Vosse, F.N.; Janssen, J.D. Wall shear stress in backward-facing step flow of a red blood cell suspension. Biorheology 1998, 35, 263–279. [Google Scholar] [CrossRef]
- Choi, H.W.; Barakat, A.I. Numerical study of the impact of non-Newtonian blood behavior on flow over a two-dimensional backward facing step. Biorheology 2005, 42, 493–509. [Google Scholar]
- Armaly, B.F.; Durst, F.; Pereira, J.C.F.; Schönung, B. Experimental and theoretical investigation of backward-facing step flow. J. Fluid Mech. 1983, 127, 473. [Google Scholar] [CrossRef]
- Schäfer, F.; Breuer, M.; Durst, F. The dynamics of the transitional flow over a backward-facing step. J. Fluid Mech. 2009, 623, 85–119. [Google Scholar] [CrossRef]
- Rani, H.P.; Sheu, T.W.; Tsai, E.S. Eddy structures in a transitional backward-facing step flow. J. Fluid Mech. 2007, 588, 43–58. [Google Scholar] [CrossRef]
- Kaiktsis, L.; Karniadakis, G.M.; Orszag, S.A. Onset of three-dimensionality, equibria and early transition in flow over a backward-facing step. J. Fluid Mech. 1991, 231, 501–528. [Google Scholar] [CrossRef]
- Le, H.; Moin, P.; Kim, J. Direct Numerical Simulation of Turbulent Flow over a Backward-Facing Step. J. Fluid Mech. 1997, 330, 349–374. [Google Scholar] [CrossRef]
- DePaola, N.; Gimbrone, M.A.; Davies, P.F.; Dewey, C.F. Vascular endothelium responds to fluid shear stress gradients [published erratum appears in Arterioscler Thromb 1993 Mar;13(3):465]. Arterioscler. Thromb. Vasc. Biol. 1992, 12, 1254–1257. [Google Scholar] [CrossRef] [PubMed]
- Driver, D.M.; Seegmiller, H.L. Features of a reattaching turbulent shear layer in divergent channelflow. AIAA J. 1985, 23, 163–171. [Google Scholar] [CrossRef]
- Poole, R.J.; Escudier, M.P. Turbulent flow of non-Newtonian liquids over a backward-facing step Part I. A thixotropic and shear-thinning liquid. J. Non-Newton. Fluid Mech. 2003, 109, 177–191. [Google Scholar] [CrossRef]
- Poole, R.J.; Escudier, M.P. Turbulent flow of non-Newtonian liquids over a backward-facing step Part II. Viscoelastic and shear-thinning liquids. J. Non-Newton. Fluid Mech. 2003, 109, 193–230. [Google Scholar] [CrossRef]
- Barri, M.; Khoury, G.K.E.; Andersson, H.I.; Pettersen, B. DNS of backward-facing step flow with fully turbulent inflow. Int. J. Numer. Methods Fluids 2009. [Google Scholar] [CrossRef]
- Kopera, M.A.; Kerr, R.M.; Blackburn, H.M.; Barkley, D. Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 2014, in press. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Robertson, A.M.; Kameneva, M.V. Hemorheology. In Hemodynamical Flows. Oberwolfach Seminars; Birkhuser: Basel, Switzerland, 2008; Volume 37, pp. 63–120. [Google Scholar]
- Cho, Y.I.; Kensey, K.R. Effects of the non-Newtonian viscosity of blood on flows in a diseased arterial vessel. Part 1: Steady flows. Biorheology 1991, 28, 241–262. [Google Scholar] [CrossRef] [PubMed]
- Balena HPC Cluster. Available online: https://www.bath.ac.uk/corporate-information/balena-hpc-cluster/ (accessed on 21 April 2020).
- Cirrus Powered by EPCC. Available online: http://www.cirrus.ac.uk/ (accessed on 21 April 2020).
- Braunmüller, S.; Schmid, L.; Sackmann, E.; Franke, T. Hydrodynamic deformation reveals two coupled modes/time scales of red blood cell relaxation. Soft Matter 2012, 8, 11240–11248. [Google Scholar] [CrossRef]
- Capoccia, M.; Bowles, C.T.; Sabashnikov, A.; Simon, A. Recurrent Early Thrombus Formation in HeartMate II Left Ventricular Assist Device. J. Investig. Med. High Impact Case Rep. 2013, 1. [Google Scholar] [CrossRef]
- Hasin, T.; Deo, S.; Maleszewski, J.J.; Topilsky, Y.; Edwards, B.S.; Pereira, N.L.; Stulak, J.M.; Joyce, L.; Daly, R.; Kushwaha, S.S.; et al. The Role of Medical Management for Acute Intravascular Hemolysis in Patients Supported on Axial Flow LVAD. ASAIO J. 2014, 60, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Neofytou, P.; Drikakis, D. Effects of blood models on flows through a stenosis. Int. J. Numer. Methods Fluids 2003, 43, 597–635. [Google Scholar] [CrossRef]
- Pal, A.; Anupindi, K.; Delorme, Y.; Ghaisas, N.; Shetty, D.A.; Frankel, S.H. Large Eddy Simulation of Transitional Flow in an Idealized Stenotic Blood Vessel: Evaluation of Subgrid Scale Models. J. Biomech. Eng. 2014, 136, 071009. [Google Scholar] [CrossRef] [PubMed]
- Varghese, S.S.; Frankel, S.H.; Fischer, P.F. Modeling Transition to Turbulence in Eccentric Stenotic Flows. J. Biomech. Eng. 2008, 130, 014503. [Google Scholar] [CrossRef]
- Tan, F.P.P. Comparison of LES of Steady Transitional Flow in an Idealized Stenosed Axisymmetric Artery Model With a RANS Transitional Model. J. Biomech. Eng. 2011, 133, 051001. [Google Scholar] [CrossRef]
- Premnath, K.N.; Pattison, M.J.; Banerjee, S. An Investigation of the Lattice Boltzmann Method for Large Eddy Simulation of Complex Turbulent Separated Flow. J. Fluids Eng. 2013, 135, 051401. [Google Scholar] [CrossRef]
- Rahgozar, S.; Rival, D.E. On turbulence decay of a shear-thinning fluid. Phys. Fluids 2017, 29, 123101. [Google Scholar] [CrossRef]
- Sayadi, T.; Moin, P. Predicting natural transition using large eddy simulation. In Center for Turbulence Research Annual Research Briefs; Stanford University: Stanford, CA, USA, 2011. [Google Scholar]
- Han, S.I.; Marseille, O.; Gehlen, C.; Blümich, B. Rheology of Blood by NMR. J. Magn. Reson. 2001, 152, 87–94. [Google Scholar] [CrossRef] [PubMed]
- Gallagher, M.; Wain, R.; Dari, S.; Whitty, J.; Smith, D. Non-identifiability of parameters for a class of shear-thinning rheological models, with implications for haematological fluid dynamics. J. Biomech. 2019, 85, 230–238. [Google Scholar] [CrossRef] [PubMed]


| Author (Year) | Numerical/Experimental | Flow Regime | Reynolds Number Definition | Rheology | ER |
|---|---|---|---|---|---|
| Armaly et al. (1983) | Experimental & Numerical | L-TR-T | Newtonian | 1.942 | |
| Driver and Seegmiller (1985) [35] | Experimental & Numerical | T | Newtonian | 1.125 | |
| Le, Moin and Kim (1997) [33] | Numerical | T | Newtonian | 1.2 | |
| Gijsen, Vosse and Janssen (1998) [27] | Experimental & Numerical | L | Newtonian and Shear thinning | 2 | |
| Poole and Escudier (2003) [36] | Experimental | T | Thixotropic/Shear thinning | 1.43 | |
| Poole and Escudier (2003) [37] | Experimental | T | Viscoelastic/Shear thinning | 1.43 | |
| Choi and Barakat (2005) [28] | Numerical | L | Newtonian and Shear thinning | 1.942 | |
| Barri et al. (2009) [38] | Numerical | T | Newtonian | 2 | |
| Schaefer, Breuer and Durst (2009) [30] | Numerical | TR | Newtonian | 1.942 | |
| Kopera et al. (2014) [39] | Numerical | T | Newtonian | 2 | |
| Current Work | Numerical | L-TR-T | Newtonian and Shear thinning | 1.942 |
| Mesh | No. of Cells | ||||
|---|---|---|---|---|---|
| 1 | Coarse | 5.71 | 0.931 | 7.58 | |
| 2 | Medium | 3.28 | 0.464 | 4.19 | |
| 3 | Fine | 2.86 | 0.313 | 2.91 | |
| 4 | Very Fine | 2.30 | 0.270 | 2.21 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kelly, N.S.; Gill, H.S.; Cookson, A.N.; Fraser, K.H. Influence of Shear-Thinning Blood Rheology on the Laminar-Turbulent Transition over a Backward Facing Step. Fluids 2020, 5, 57. https://doi.org/10.3390/fluids5020057
Kelly NS, Gill HS, Cookson AN, Fraser KH. Influence of Shear-Thinning Blood Rheology on the Laminar-Turbulent Transition over a Backward Facing Step. Fluids. 2020; 5(2):57. https://doi.org/10.3390/fluids5020057
Chicago/Turabian StyleKelly, Nathaniel S., Harinderjit S. Gill, Andrew N. Cookson, and Katharine H. Fraser. 2020. "Influence of Shear-Thinning Blood Rheology on the Laminar-Turbulent Transition over a Backward Facing Step" Fluids 5, no. 2: 57. https://doi.org/10.3390/fluids5020057
APA StyleKelly, N. S., Gill, H. S., Cookson, A. N., & Fraser, K. H. (2020). Influence of Shear-Thinning Blood Rheology on the Laminar-Turbulent Transition over a Backward Facing Step. Fluids, 5(2), 57. https://doi.org/10.3390/fluids5020057








