A Review of Topology Optimisation for Fluid-Based Problems
Abstract
1. Introduction
1.1. Definitions for Inclusion
1.1.1. Governing Equations
- Darcy, Forchheimer and Brinkman flow
- Stokes and Navier–Stokes flow
- Homogenised fluid equations
- Kinetic gas theory, Lattice Boltzmann and similar methods based on distributions
- Particle methods
- Species transport, e.g., microfluidic mixers,
- Reaction kinetics, e.g., ion transport in flow batteries,
- Temperature, e.g., heat exchangers,
- Structural mechanics, e.g., fluid–structure interaction.
1.1.2. Literature Search
- fluid flow
- conjugate heat transfer
- convection
- fluid structure interaction
- microstructure
- homogenization
1.1.3. Optimisation Methodology
1.2. Layout of Paper
2. Literature Review
2.1. Fluid Flow
2.1.1. Steady Laminar Flow
2.1.2. Unsteady Flow
2.1.3. Turbulent Flow
2.1.4. Non-Newtonian Fluids
2.2. Species Transport
2.3. Conjugate Heat Transfer
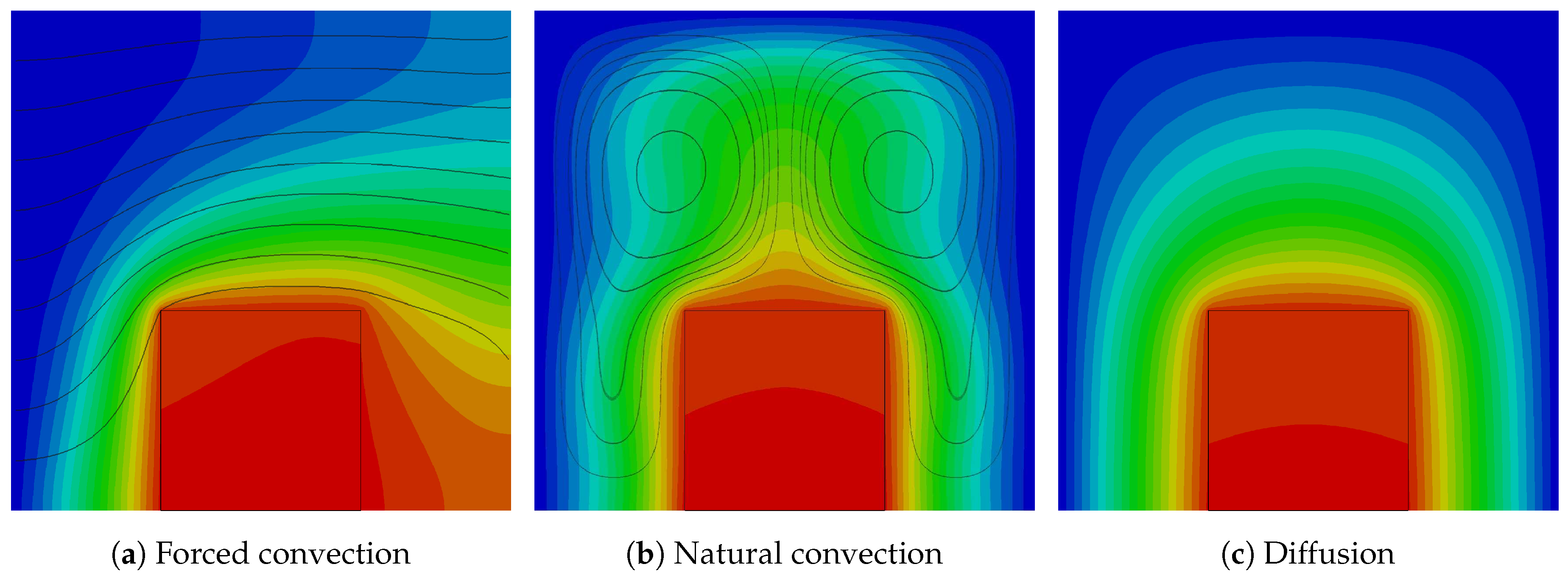
2.3.1. Forced Convection
2.3.2. Natural Convection
2.4. Fluid–Structure Interaction
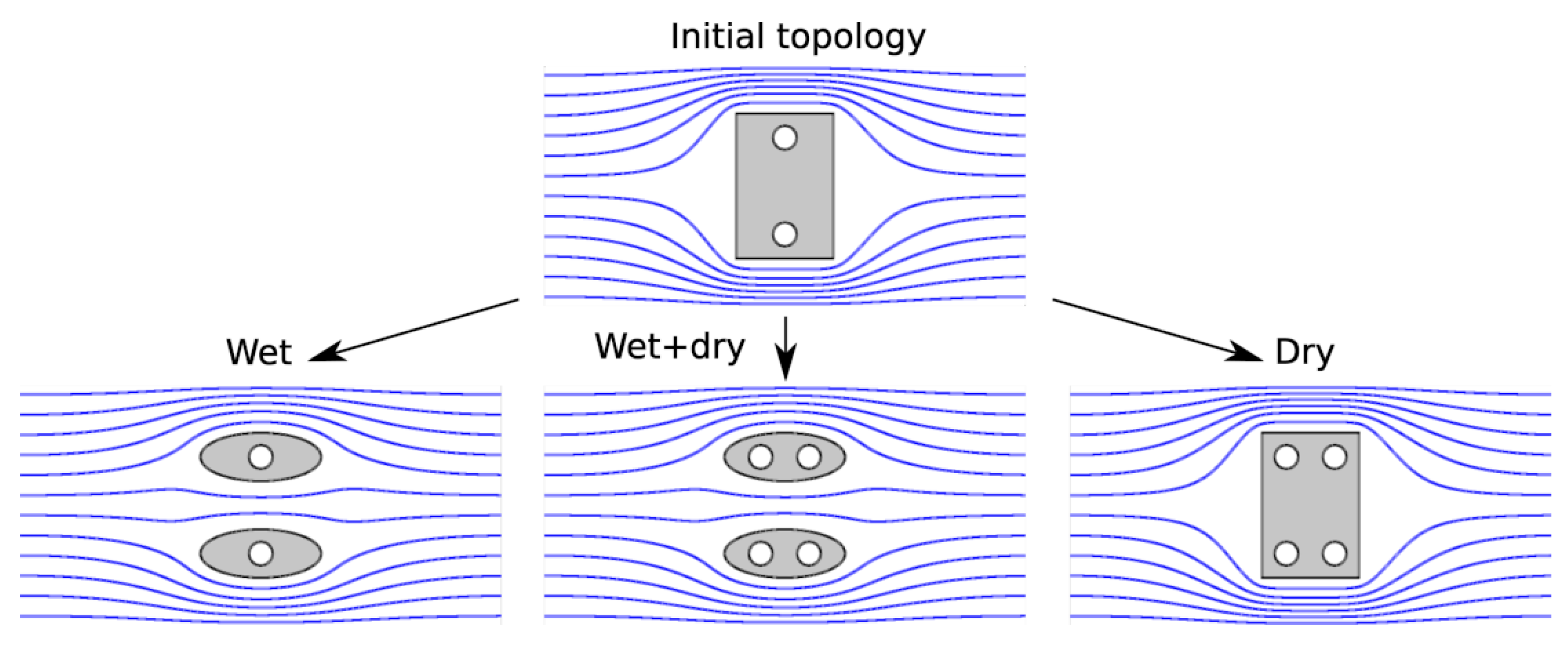
2.5. Microstructure and Porous Media
2.5.1. Material Microstructures
2.5.2. Porous Media
3. Quantitative Analysis
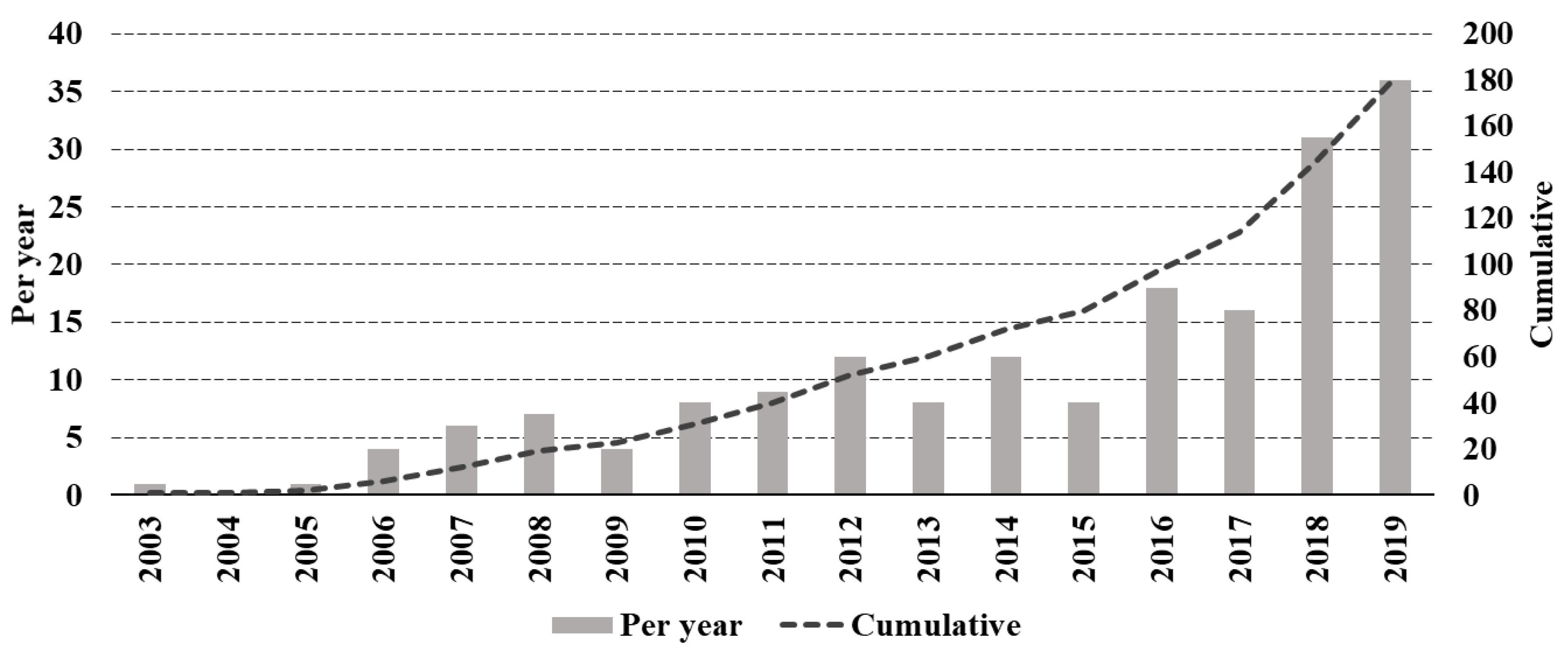
3.1. Total Publications
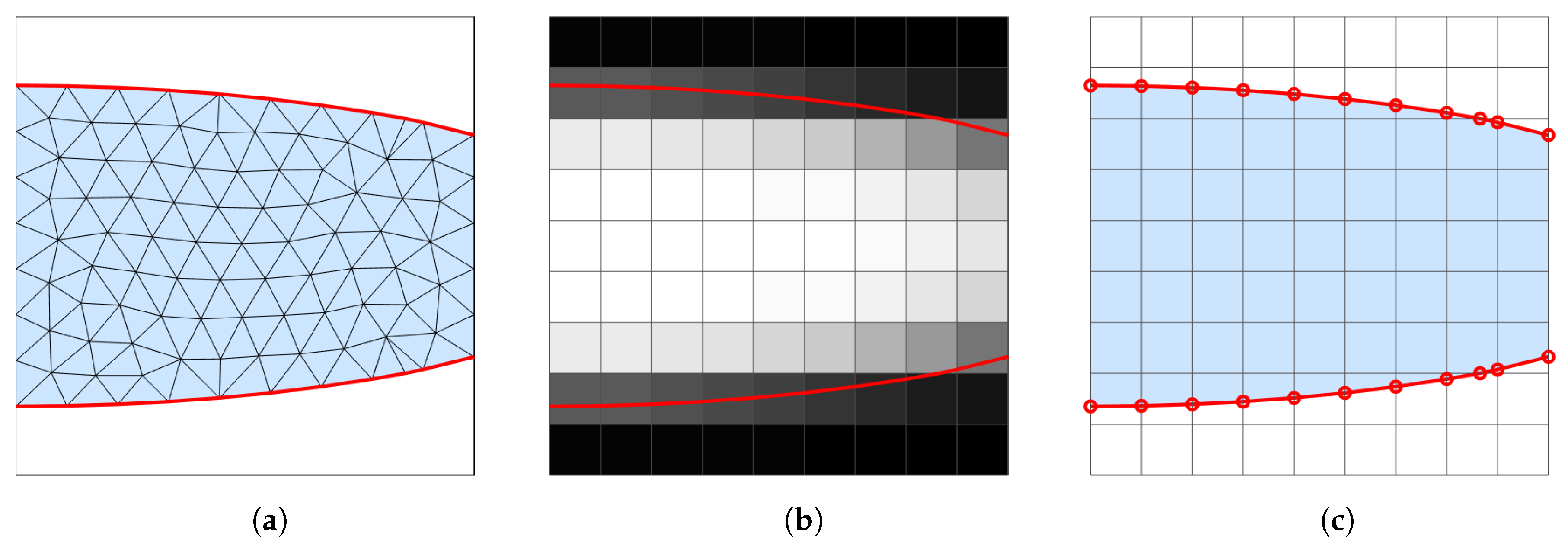
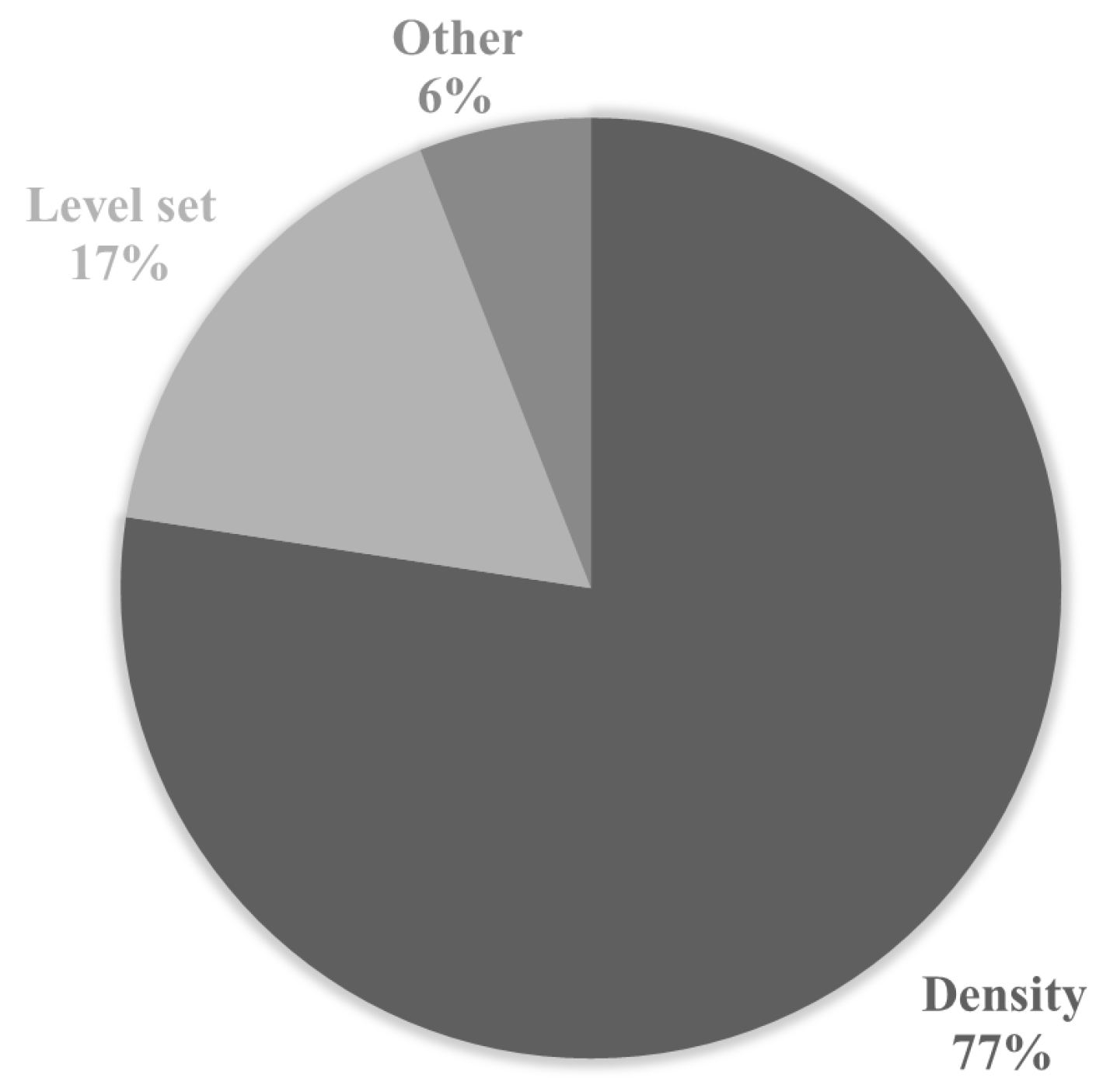
3.2. Design Representations
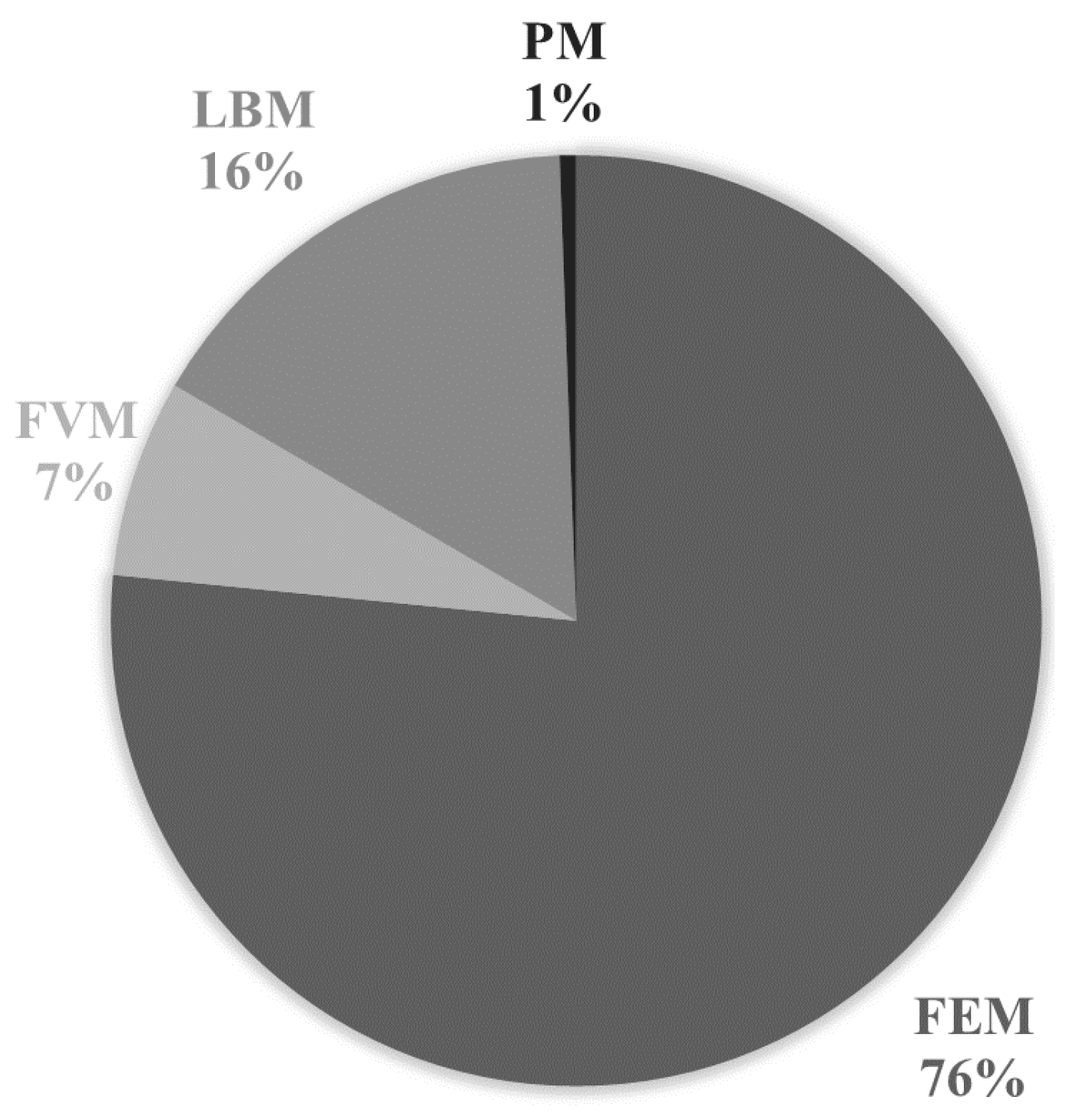
3.3. Discretisation Methods
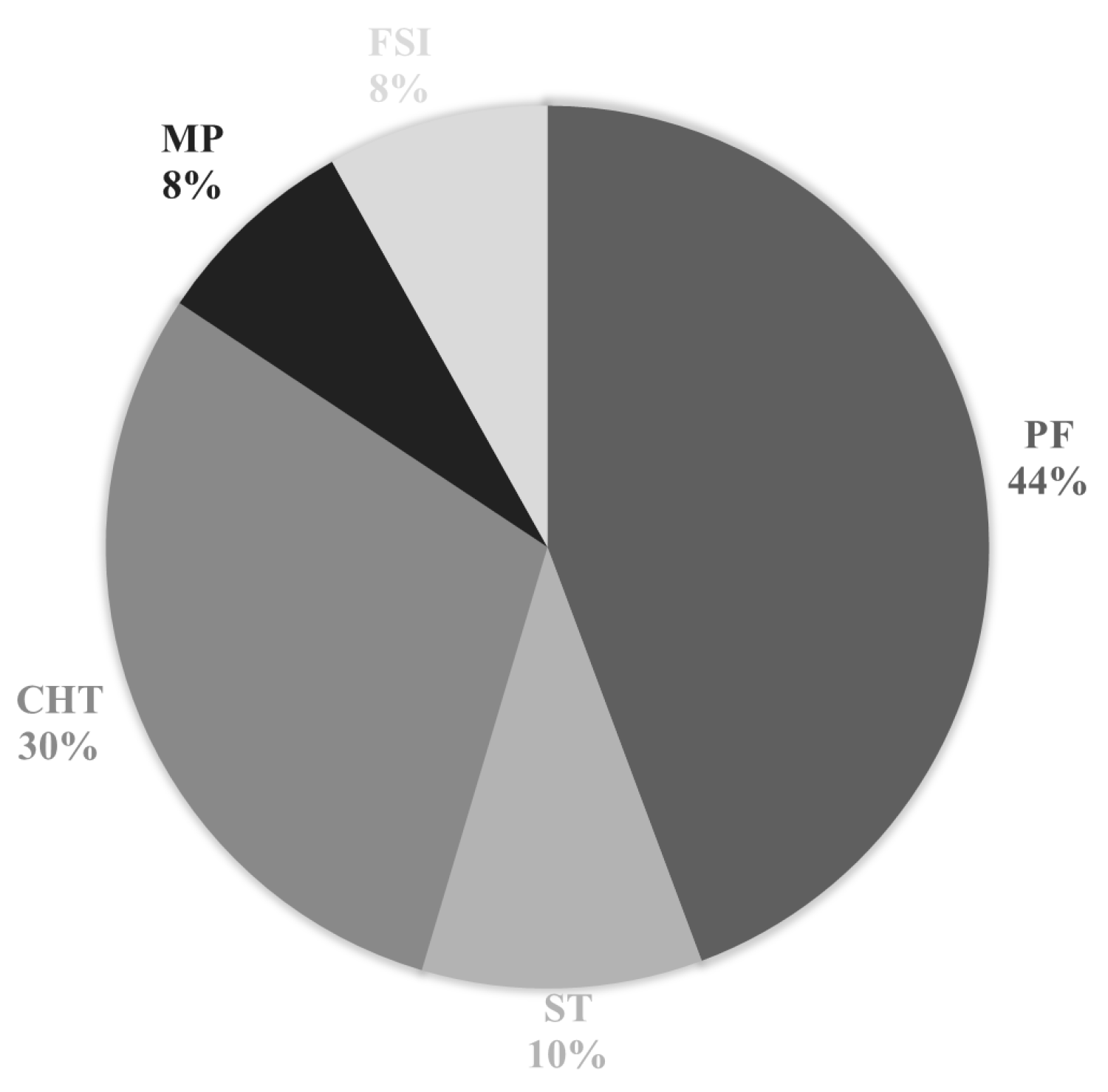
3.4. Problem Types
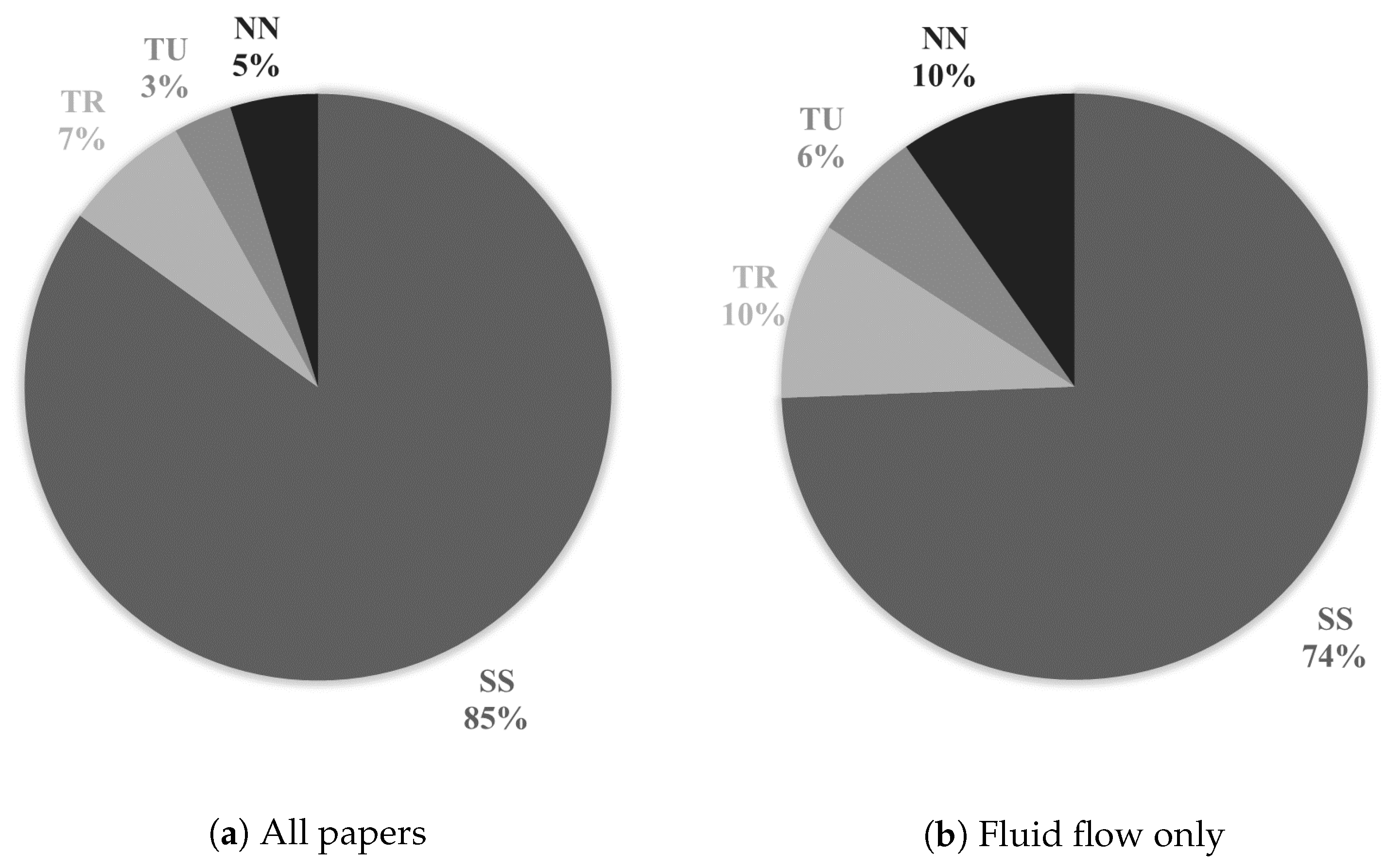
3.5. Flow Types
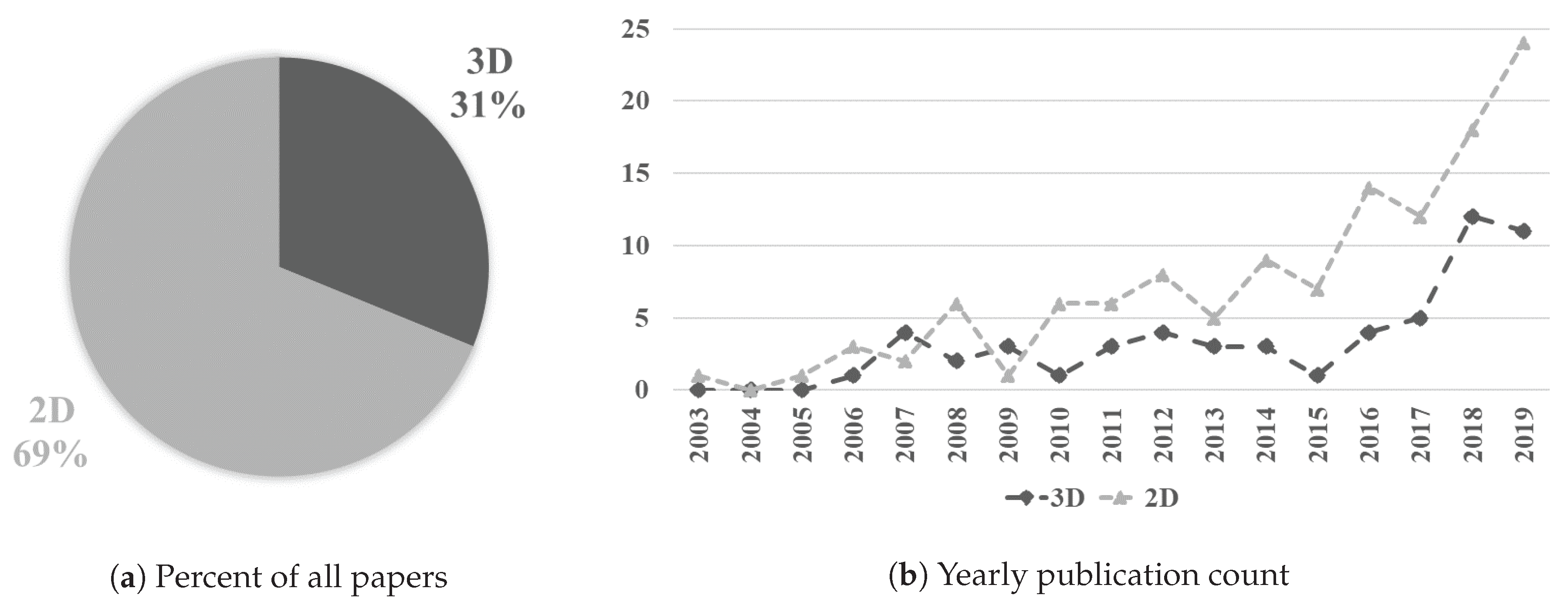
3.6. Three-Dimensional Problems
4. Recommendations
4.1. Optimisation Methods
4.2. Density-Based Approaches
4.3. Level Set-Based Approaches
4.4. Steady-State Laminar Incompressible Flow
4.5. Benchmarking
- accuracy of the geometric representation
- precision of solution and/or optimality
- algorithmic and/or computational efficiency
- parameter robustness and algorithmic stability
4.6. Time-Dependent Problems
4.7. Turbulent Flow
4.8. Compressible Flow
4.9. Fluid–Structure Interaction
4.10. Three-Dimensional Problems
4.11. Simplified Models or Approximations
4.11.1. 2D Simplification of 3D
4.11.2. Simplified Flow Models
4.12. Numerical Verification
4.13. Experimental Validation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology optimization approaches: A comparative review. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Deaton, J.D.; Grandhi, R.V. A survey of structural and multidisciplinary continuum topology optimization: post 2000. Struct. Multidiscip. Optim. 2014, 49, 1–38. [Google Scholar] [CrossRef]
- Chen, X. Topology optimization of microfluidics—A review. Microchem. J. 2016, 127, 52–61. [Google Scholar] [CrossRef]
- Dbouk, T. A review about the engineering design of optimal heat transfer systems using topology optimization. Appl. Therm. Eng. 2017, 112, 841–854. [Google Scholar] [CrossRef]
- van Dijk, N.P.; Maute, K.; Langelaar, M.; van Keulen, F. Level-set methods for structural topology optimization: A review. Struct. Multidiscip. Optim. 2013, 48, 437–472. [Google Scholar] [CrossRef]
- Borrvall, T.; Petersson, J. Topology optimization of fluids in Stokes flow. Int. J. Numer. Methods Fluids 2003, 41, 77–107. [Google Scholar] [CrossRef]
- Gersborg-Hansen, A.; Sigmund, O.; Haber, R.B. Topology optimization of channel flow problems. Struct. Multidiscip. Optim. 2005, 30, 181–192. [Google Scholar] [CrossRef]
- Evgrafov, A. The Limits of Porous Materials in the Topology Optimization of Stokes Flows. Appl. Math. Optim. 2005, 52, 263–277. [Google Scholar] [CrossRef]
- Olesen, L.H.; Okkels, F.; Bruus, H. A high-level programming-language implementation of topology optimization applied to steady-state Navier–Stokes flow. Int. J. Numer. Methods Eng. 2006, 65, 975–1001. [Google Scholar] [CrossRef]
- Guest, J.K.; Prévost, J.H. Topology optimization of creeping fluid flows using a Darcy–Stokes finite element. Int. J. Numer. Methods Eng. 2006, 66, 461–484. [Google Scholar] [CrossRef]
- Evgrafov, A. Topology optimization of slightly compressible fluids. ZAMM 2006, 86, 46–62. [Google Scholar] [CrossRef]
- Wiker, N.; Klarbring, A.; Borrvall, T. Topology optimization of regions of Darcy and Stokes flow. Int. J. Numer. Methods Eng. 2007, 69, 1374–1404. [Google Scholar] [CrossRef]
- Pingen, G.; Evgrafov, A.; Maute, K. Topology optimization of flow domains using the lattice Boltzmann method. Struct. Multidiscip. Optim. 2007, 34, 507–524. [Google Scholar] [CrossRef]
- Aage, N.; Poulsen, T.H.; Gersborg-Hansen, A.; Sigmund, O. Topology optimization of large scale Stokes flow problems. Struct. Multidiscip. Optim. 2007, 35, 175–180. [Google Scholar] [CrossRef]
- Bruns, T.E. Topology optimization by penalty (TOP) method. Comput. Methods Appl. Mech. Eng. 2007, 196, 4430–4443. [Google Scholar] [CrossRef]
- Duan, X.B.; Ma, Y.C.; Zhang, R. Shape-topology optimization for Navier–Stokes problem using variational level set method. J. Comput. Appl. Math. 2008, 222, 487–499. [Google Scholar] [CrossRef]
- Duan, X.B.; Ma, Y.C.; Zhang, R. Shape-topology optimization of Stokes flow via variational level set method. Appl. Math. Comput. 2008, 202, 200–209. [Google Scholar] [CrossRef]
- Duan, X.; Ma, Y.; Zhang, R. Optimal shape control of fluid flow using variational level set method. Phys. Lett. A 2008, 372, 1374–1379. [Google Scholar] [CrossRef]
- Evgrafov, A.; Pingen, G.; Maute, K. Topology optimization of fluid domains: kinetic theory approach. ZAMM 2008, 88, 129–141. [Google Scholar] [CrossRef]
- Othmer, C. A continuous adjoint formulation for the computation of topological and surface sensitivities of ducted flows. Int. J. Numer. Methods Fluids 2008, 58, 861–877. [Google Scholar] [CrossRef]
- Pingen, G.; Evgrafov, A.; Maute, K. A parallel Schur complement solver for the solution of the adjoint steady-state lattice Boltzmann equations: application to design optimisation. Int. J. Comput. Fluid Dyn. 2008, 22, 457–464. [Google Scholar] [CrossRef]
- Zhou, S.; Li, Q. A variational level set method for the topology optimization of steady-state Navier–Stokes flow. J. Comput. Phys. 2008, 227, 10178–10195. [Google Scholar] [CrossRef]
- Pingen, G.; Waidmann, M.; Evgrafov, A.; Maute, K. A parametric level-set approach for topology optimization of flow domains. Struct. Multidiscip. Optim. 2010, 41, 117–131. [Google Scholar] [CrossRef]
- Challis, V.J.; Guest, J.K. Level set topology optimization of fluids in Stokes flow. Int. J. Numer. Methods Eng. 2009, 79, 1284–1308. [Google Scholar] [CrossRef]
- Kreissl, S.; Pingen, G.; Maute, K. An explicit level set approach for generalized shape optimization of fluids with the lattice Boltzmann method. Int. J. Numer. Methods Fluids 2011, 65, 496–519. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, Q.; Zhang, P.; Xuan, M.; Wu, Y. Topology optimization of fluid channels with flow rate equality constraints. Struct. Multidiscip. Optim. 2011, 44, 31–37. [Google Scholar] [CrossRef]
- Okkels, F.; Dufva, M.; Bruus, H. Optimal homogenization of perfusion flows in microfluidic bio-reactors: A numerical study. PLoS ONE 2011, 6, e14574. [Google Scholar] [CrossRef]
- Kondoh, T.; Matsumori, T.; Kawamoto, A. Drag minimization and lift maximization in laminar flows via topology optimization employing simple objective function expressions based on body force integration. Struct. Multidiscip. Optim. 2012, 45, 693–701. [Google Scholar] [CrossRef]
- Kreissl, S.; Maute, K. Levelset based fluid topology optimization using the extended finite element method. Struct. Multidiscip. Optim. 2012, 46, 311–326. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Z.; Wu, Y. Topology optimization of steady and unsteady incompressible Navier–Stokes flows driven by body forces. Struct. Multidiscip. Optim. 2013, 47, 555–570. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Z.; Wu, J.; Wu, Y. Topology optimization of steady Navier–Stokes flow with body force. Comput. Methods Appl. Mech. Eng. 2013, 255, 306–321. [Google Scholar] [CrossRef]
- Aage, N.; Lazarov, B.S. Parallel framework for topology optimization using the method of moving asymptotes. Struct. Multidiscip. Optim. 2013, 47, 493–505. [Google Scholar] [CrossRef]
- Evgrafov, A. State space Newton’s method for topology optimization. Comput. Methods Appl. Mech. Eng. 2014, 278, 272–290. [Google Scholar] [CrossRef]
- Romero, J.S.; Silva, E.C.N. A topology optimization approach applied to laminar flow machine rotor design. Comput. Methods Appl. Mech. Eng. 2014, 279, 268–300. [Google Scholar] [CrossRef]
- Yaji, K.; Yamada, T.; Yoshino, M.; Matsumoto, T.; Izui, K.; Nishiwaki, S. Topology optimization using the lattice Boltzmann method incorporating level set boundary expressions. J. Comput. Phys. 2014, 274, 158–181. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, G.; Geier, M.; Krafczyk, M.; Chen, T. Discrete adjoint sensitivity analysis for fluid flow topology optimization based on the generalized lattice Boltzmann method. Comput. Math. Appl. 2014, 68, 1374–1392. [Google Scholar] [CrossRef]
- Yonekura, K.; Kanno, Y. A flow topology optimization method for steady state flow using transient information of flow field solved by lattice Boltzmann method. Struct. Multidiscip. Optim. 2015, 51, 159–172. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, B.; Sun, J. An improved implicit re-initialization method for the level set function applied to shape and topology optimization of fluid. J. Comput. Appl. Math. 2015, 281, 207–229. [Google Scholar] [CrossRef]
- Duan, X.B.; Li, F.F.; Qin, X.Q. Adaptive mesh method for topology optimization of fluid flow. Appl. Math. Lett. 2015, 44, 40–44. [Google Scholar] [CrossRef]
- Evgrafov, A. On Chebyshev’s method for topology optimization of Stokes flows. Struct. Multidiscip. Optim. 2015, 51, 801–811. [Google Scholar] [CrossRef]
- Garcke, H.; Hecht, C. Shape and Topology Optimization in Stokes Flow with a Phase Field Approach. Appl. Math. Optim. 2016, 73, 23–70. [Google Scholar] [CrossRef]
- Lin, S.; Zhao, L.; Guest, J.K.; Weihs, T.P.; Liu, Z. Topology Optimization of Fixed-Geometry Fluid Diodes. J. Mech. Des. 2015, 137, 081402. [Google Scholar] [CrossRef]
- Garcke, H.; Hecht, C.; Hinze, M.; Kahle, C. Numerical Approximation of Phase Field Based Shape and Topology Optimization for Fluids. SIAM J. Sci. Comput. 2015, 37, A1846–A1871. [Google Scholar] [CrossRef]
- Duan, X.; Qin, X.; Li, F. Topology optimization of Stokes flow using an implicit coupled level set method. Appl. Math. Model. 2016, 40, 5431–5441. [Google Scholar] [CrossRef]
- Sá, L.F.N.; Amigo, R.C.R.; Novotny, A.A.; Silva, E.C.N. Topological derivatives applied to fluid flow channel design optimization problems. Struct. Multidiscip. Optim. 2016, 54, 249–264. [Google Scholar] [CrossRef]
- Yoshimura, M.; Shimoyama, K.; Misaka, T.; Obayashi, S. Topology optimization of fluid problems using genetic algorithm assisted by the Kriging model. Int. J. Numer. Methods Eng. 2017, 109, 514–532. [Google Scholar] [CrossRef]
- Pereira, A.; Talischi, C.; Paulino, G.H.; Menezes, I.F.M.; Carvalho, M.S. Fluid flow topology optimization in PolyTop: stability and computational implementation. Struct. Multidiscip. Optim. 2016, 54, 1345–1364. [Google Scholar] [CrossRef]
- Duan, X.; Li, F.; Qin, X. Topology optimization of incompressible Navier–Stokes problem by level set based adaptive mesh method. Comput. Math. Appl. 2016, 72, 1131–1141. [Google Scholar] [CrossRef]
- Kubo, S.; Yaji, K.; Yamada, T.; Izui, K.; Nishiwaki, S. A level set-based topology optimization method for optimal manifold designs with flow uniformity in plate-type microchannel reactors. Struct. Multidiscip. Optim. 2017, 55, 1311–1327. [Google Scholar] [CrossRef]
- Jang, G.W.; Lee, J.W. Topology optimization of internal partitions in a flow-reversing chamber muffler for noise reduction. Struct. Multidiscip. Optim. 2016, 55, 2181–2196. [Google Scholar] [CrossRef]
- Koch, J.R.L.; Papoutsis-Kiachagias, E.M.; Giannakoglou, K.C. Transition from adjoint level set topology to shape optimization for 2D fluid mechanics. Comput. Fluids 2017, 150, 123–138. [Google Scholar] [CrossRef]
- Sato, Y.; Yaji, K.; Izui, K.; Yamada, T.; Nishiwaki, S. Topology optimization of a no-moving-part valve incorporating Pareto frontier exploration. Struct. Multidiscip. Optim. 2017, 56, 839–851. [Google Scholar] [CrossRef]
- Sá, N.L.F.; Novotny, A.A.; Romero, J.S.; Silva, E.C.N. Design optimization of laminar flow machine rotors based on the topological derivative concept. Struct. Multidiscip. Optim. 2017, 56, 1013–1026. [Google Scholar] [CrossRef]
- Yonekura, K.; Kanno, Y. Topology optimization method for interior flow based on transient information of the lattice Boltzmann method with a level-set function. Jpn. J. Ind. Appl. Math. 2017, 34, 611–632. [Google Scholar] [CrossRef]
- Dai, X.; Zhang, C.; Zhang, Y.; Gulliksson, M. Topology optimization of steady Navier–Stokes flow via a piecewise constant level set method. Struct. Multidiscip. Optim. 2018, 57, 2193–2203. [Google Scholar] [CrossRef]
- Shen, C.; Hou, L.; Zhang, E.; Lin, J. Topology optimization of three-phase interpolation models in Darcy–Stokes flow. Struct. Multidiscip. Optim. 2018, 57, 1663–1677. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Z.; Wu, Y. Topology Optimization of Capillary, Two-Phase Flow Problems. Commun. Comput. Phys. 2017, 22, 1413–1438. [Google Scholar] [CrossRef]
- Garcke, H.; Hinze, M.; Kahle, C.; Lam, K.F. A phase field approach to shape optimization in Navier–Stokes flow with integral state constraints. Adv. Comput. Math. 2018, 44, 1345–1383. [Google Scholar] [CrossRef]
- Alonso, D.H.; de Sá, L.F.N.; Saenz, J.S.R.; Silva, E.C.N. Topology optimization applied to the design of 2D swirl flow devices. Struct. Multidiscip. Optim. 2018, 58, 2341–2364. [Google Scholar] [CrossRef]
- Jensen, K.E. Topology optimization of Stokes flow on dynamic meshes using simple optimizers. Comput. Fluids 2018, 174, 66–77. [Google Scholar] [CrossRef]
- Sá, L.F.N.; Romero, J.S.; Horikawa, O.; Silva, E.C.N. Topology optimization applied to the development of small scale pump. Struct. Multidiscip. Optim. 2018, 57, 2045–2059. [Google Scholar] [CrossRef]
- Zhou, M.; Lian, H.; Sigmund, O.; Aage, N. Shape morphing and topology optimization of fluid channels by explicit boundary tracking. Int. J. Numer. Methods Fluids 2018, 88, 296–313. [Google Scholar] [CrossRef]
- Shin, S.; Jeong, J.H.; Lim, D.K.; Kim, E.S. Design of SFR fluidic diode axial port using topology optimization. Nucl. Eng. Des. 2018, 338, 63–73. [Google Scholar] [CrossRef]
- Yonekura, K.; Kanno, Y. A Heuristic Method Using Hessian Matrix for Fast Flow Topology Optimization. J. Optim. Theory Appl. 2019, 180, 671–681. [Google Scholar] [CrossRef]
- Behrou, R.; Ranjan, R.; Guest, J.K. Adaptive topology optimization for incompressible laminar flow problems with mass flow constraints. Comput. Methods Appl. Mech. Eng. 2019, 346, 612–641. [Google Scholar] [CrossRef]
- Alonso, D.H.; de Sá, L.F.N.; Saenz, J.S.R.; Silva, E.C.N. Topology optimization based on a two-dimensional swirl flow model of Tesla-type pump devices. Comput. Math. Appl. 2019, 77, 2499–2533. [Google Scholar] [CrossRef]
- Lim, D.K.; Song, M.S.; Chae, H.; Kim, E.S. Topology optimization on vortex-type passive fluidic diode for advanced nuclear reactors. Nucl. Eng. Technol. 2019, 51, 1279–1288. [Google Scholar] [CrossRef]
- Sato, A.; Yamada, T.; Izui, K.; Nishiwaki, S.; Takata, S. A topology optimization method in rarefied gas flow problems using the Boltzmann equation. J. Comput. Phys. 2019, 395, 60–84. [Google Scholar] [CrossRef]
- Gaymann, A.; Montomoli, F.; Pietropaoli, M. Fluid topology optimization: Bio-inspired valves for aircraft engines. Int. J. Heat Fluid Flow 2019, 79, 108455. [Google Scholar] [CrossRef]
- Gaymann, A.; Montomoli, F. Deep Neural Network and Monte Carlo Tree Search applied to fluid–structure Topology Optimization. Sci. Rep. 2019, 9, 15916. [Google Scholar] [CrossRef] [PubMed]
- Kreissl, S.; Pingen, G.; Maute, K. Topology optimization for unsteady flow. Int. J. Numer. Methods Eng. 2011, 87, 1229–1253. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Z.; Zhang, P.; Liu, Y.; Wu, Y. Topology optimization of unsteady incompressible Navier–Stokes flows. J. Comput. Phys. 2011, 230, 6688–6708. [Google Scholar] [CrossRef]
- Abdelwahed, M.; Hassine, M. Topology Optimization of Time Dependent Viscous Incompressible Flows. Abstr. Appl. Anal. 2014, 2014, 923016. [Google Scholar] [CrossRef]
- Nørgaard, S.; Sigmund, O.; Lazarov, B. Topology optimization of unsteady flow problems using the lattice Boltzmann method. J. Comput. Phys. 2016, 307, 291–307. [Google Scholar] [CrossRef]
- Villanueva, C.H.; Maute, K. CutFEM topology optimization of 3D laminar incompressible flow problems. Comput. Methods Appl. Mech. Eng. 2017, 320, 444–473. [Google Scholar] [CrossRef]
- Chen, C.; Yaji, K.; Yamada, T.; Izui, K.; Nishiwaki, S. Local-in-time adjoint-based topology optimization of unsteady fluid flows using the lattice Boltzmann method. Mech. Eng. J. 2017, 4, 17-00120. [Google Scholar] [CrossRef]
- Nørgaard, S.A.; Sagebaum, M.; Gauger, N.R.; Lazarov, B.S. Applications of automatic differentiation in topology optimization. Struct. Multidiscip. Optim. 2017, 56, 1135–1146. [Google Scholar] [CrossRef]
- Sasaki, Y.; Sato, Y.; Yamada, T.; Izui, K.; Nishiwaki, S. Topology optimization for fluid flows using the MPS method incorporating the level set method. Comput. Fluids 2019, 188, 86–101. [Google Scholar] [CrossRef]
- Kontoleontos, E.A.; Papoutsis-Kiachagias, E.M.; Zymaris, A.S.; Papadimitriou, D.I.; Giannakoglou, K.C. Adjoint-based constrained topology optimization for viscous flows, including heat transfer. Eng. Optim. 2013, 45, 941–961. [Google Scholar] [CrossRef]
- Yoon, G.H. Topology optimization for turbulent flow with Spalart–Allmaras model. Comput. Methods Appl. Mech. Eng. 2016, 303, 288–311. [Google Scholar] [CrossRef]
- Dilgen, S.B.; Dilgen, C.B.; Fuhrman, D.R.; Sigmund, O.; Lazarov, B.S. Density based topology optimization of turbulent flow heat transfer systems. Struct. Multidiscip. Optim. 2018, 57, 1905–1918. [Google Scholar] [CrossRef]
- Yoon, G.H. Topology optimization method with finite elements based on the k-ϵ turbulence model. Comput. Methods Appl. Mech. Eng. 2020, 361, 112784. [Google Scholar] [CrossRef]
- Pingen, G.; Maute, K. Optimal design for non-Newtonian flows using a topology optimization approach. Comput. Math. Appl. 2010, 59, 2340–2350. [Google Scholar] [CrossRef]
- Ejlebjerg Jensen, K.; Szabo, P.; Okkels, F. Topology optimization of viscoelastic rectifiers. Appl. Phys. Lett. 2012, 100, 234102. [Google Scholar] [CrossRef]
- Jensen, K.E.; Szabo, P.; Okkels, F. Optimization of bistable viscoelastic systems. Struct. Multidiscip. Optim. 2014, 49, 733–742. [Google Scholar] [CrossRef][Green Version]
- Hyun, J.; Wang, S.; Yang, S. Topology optimization of the shear thinning non-Newtonian fluidic systems for minimizing wall shear stress. Comput. Math. Appl. 2014, 67, 1154–1170. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, X. Topology optimization study of arterial bypass configurations using the level set method. Struct. Multidiscip. Optim. 2015, 51, 773–798. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, X.; Sun, J. Topology optimization design of non-Newtonian roller-type viscous micropumps. Struct. Multidiscip. Optim. 2016, 53, 409–424. [Google Scholar] [CrossRef]
- Romero, J.S.; Silva, E.C.N. Non-newtonian laminar flow machine rotor design by using topology optimization. Struct. Multidiscip. Optim. 2017, 55, 1711–1732. [Google Scholar] [CrossRef]
- Dong, X.; Liu, X. Bi-objective topology optimization of asymmetrical fixed-geometry microvalve for non-Newtonian flow. Microsyst. Technol. 2019, 25, 2471–2479. [Google Scholar] [CrossRef]
- Okkels, F.; Bruus, H. Scaling behavior of optimally structured catalytic microfluidic reactors. Phys. Rev. E 2007, 75, 016301. [Google Scholar] [CrossRef]
- Andreasen, C.S.; Gersborg, A.R.; Sigmund, O. Topology optimization of microfluidic mixers. Int. J. Numer. Methods Fluids 2009, 61, 498–513. [Google Scholar] [CrossRef]
- Gregersen, M.M.; Okkels, F.; Bazant, M.Z.; Bruus, H. Topology and shape optimization of induced-charge electro-osmotic micropumps. New J. Phys. 2009, 11, 075019. [Google Scholar] [CrossRef]
- Schäpper, D.; Lencastre Fernandes, R.; Lantz, A.E.; Okkels, F.; Bruus, H.; Gernaey, K.V. Topology optimized microbioreactors. Biotechnol. Bioeng. 2011, 108, 786–796. [Google Scholar] [CrossRef]
- Kim, C.; Sun, H. Topology optimization of gas flow channel routes in an automotive fuel cell. Int. J. Automot. Technol. 2012, 13, 783–789. [Google Scholar] [CrossRef]
- Makhija, D.; Pingen, G.; Yang, R.; Maute, K. Topology optimization of multi-component flows using a multi-relaxation time lattice Boltzmann method. Comput. Fluids 2012, 67, 104–114. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Z.; Zhang, P.; Liu, Y.; Gao, Q.; Wu, Y. A flexible layout design method for passive micromixers. Biomed. Microdevices 2012, 14, 929–945. [Google Scholar] [CrossRef]
- Makhija, D.; Maute, K. Level set topology optimization of scalar transport problems. Struct. Multidiscip. Optim. 2014, 51, 267–285. [Google Scholar] [CrossRef]
- Oh, S.; Wang, S.; Park, M.; Kim, J.H. Novel spacer design using topology optimization in a reverse osmosis channel. J. Fluids Eng. Trans. ASME 2014, 136, 021201. [Google Scholar] [CrossRef]
- Chen, X.; Li, T. A novel design for passive misscromixers based on topology optimization method. Biomed. Microdevices 2016, 18, 57. [Google Scholar] [CrossRef]
- Hyun, J.c.; Hyun, J.; Wang, S.; Yang, S. Improved pillar shape for deterministic lateral displacement separation method to maintain separation efficiency over a long period of time. Sep. Purif. Technol. 2017, 172, 258–267. [Google Scholar] [CrossRef]
- Andreasen, C.S. Topology optimization of inertia driven dosing units. Struct. Multidiscip. Optim. 2016, 55, 1301–1309. [Google Scholar] [CrossRef]
- Yaji, K.; Yamasaki, S.; Tsushima, S.; Suzuki, T.; Fujita, K. Topology optimization for the design of flow fields in a redox flow battery. Struct. Multidiscip. Optim. 2018, 57, 535–546. [Google Scholar] [CrossRef]
- Guo, Y.; Xu, Y.; Deng, Y.; Liu, Z. Topology Optimization of Passive Micromixers Based on Lagrangian Mapping Method. Micromachines 2018, 9, 137. [Google Scholar] [CrossRef]
- Behrou, R.; Pizzolato, A.; Forner-Cuenca, A. Topology optimization as a powerful tool to design advanced PEMFCs flow fields. Int. J. Heat Mass Transf. 2019, 135, 72–92. [Google Scholar] [CrossRef]
- Chen, C.H.; Yaji, K.; Yamasaki, S.; Tsushima, S.; Fujita, K. Computational design of flow fields for vanadium redox flow batteries via topology optimization. J. Energy Storage 2019, 26, 100990. [Google Scholar] [CrossRef]
- Dugast, F.; Favenne, Y.; Josset, C. Reactive fluid flow topology optimization with the multi-relaxation time lattice Boltzmann method and a level-set function. J. Comput. Phys. 2020, 109252. [Google Scholar] [CrossRef]
- Alexandersen, J.; Aage, N.; Andreasen, C.S.; Sigmund, O. Topology optimisation for natural convection problems. Int. J. Numer. Methods Fluids 2014, 76, 699–721. [Google Scholar] [CrossRef]
- Dede, E.M. Multiphysics Topology Optimization of Heat Transfer and Fluid Flow Systems. In Proceedings of the COMSOL Conference 2009, Boston, MA, USA, 8–10 October 2009. [Google Scholar]
- Yoon, G.H. Topological design of heat dissipating structure with forced convective heat transfer. J. Mech. Sci. Technol. 2010, 24, 1225–1233. [Google Scholar] [CrossRef]
- Dede, E.M. Optimization and design of a multipass branching microchannel heat sink for electronics cooling. J. Electron. Packag. Trans. ASME 2012, 134, 041001. [Google Scholar] [CrossRef]
- McConnell, C.; Pingen, G. Multi-Layer, Pseudo 3D Thermal Topology Optimization of Heat Sinks. In Proceedings of the ASME 2012 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 9–15 November 2012; pp. 2381–2392. [Google Scholar] [CrossRef]
- Matsumori, T.; Kondoh, T.; Kawamoto, A.; Nomura, T. Topology optimization for fluid–thermal interaction problems under constant input power. Struct. Multidiscip. Optim. 2013, 47, 571–581. [Google Scholar] [CrossRef]
- Marck, G.; Nemer, M.; Harion, J.L. Topology Optimization of Heat and Mass Transfer Problems: Laminar Flow. Numer. Heat Transf. Part B Fundam. 2013, 63, 508–539. [Google Scholar] [CrossRef]
- Koga, A.A.; Lopes, E.C.C.; Villa Nova, H.F.; Lima, C.R.d.; Silva, E.C.N. Development of heat sink device by using topology optimization. Int. J. Heat Mass Transf. 2013, 64, 759–772. [Google Scholar] [CrossRef]
- Yaji, K.; Yamada, T.; Kubo, S.; Izui, K.; Nishiwaki, S. A topology optimization method for a coupled thermal–fluid problem using level set boundary expressions. Int. J. Heat Mass Transf. 2015, 81, 878–888. [Google Scholar] [CrossRef]
- Yaji, K.; Yamada, T.; Yoshino, M.; Matsumoto, T.; Izui, K.; Nishiwaki, S. Topology optimization in thermal-fluid flow using the lattice Boltzmann method. J. Comput. Phys. 2016, 307, 355–377. [Google Scholar] [CrossRef]
- Łaniewski Wołłk, L.; Rokicki, J. Adjoint Lattice Boltzmann for topology optimization on multi-GPU architecture. Comput. Math. Appl. 2016, 71, 833–848. [Google Scholar] [CrossRef]
- Qian, X.; Dede, E.M. Topology optimization of a coupled thermal-fluid system under a tangential thermal gradient constraint. Struct. Multidiscip. Optim. 2016, 54, 531–551. [Google Scholar] [CrossRef]
- Haertel, J.H.K.; Nellis, G.F. A fully developed flow thermofluid model for topology optimization of 3D-printed air-cooled heat exchangers. Appl. Therm. Eng. 2017, 119, 10–24. [Google Scholar] [CrossRef]
- Pietropaoli, M.; Ahlfeld, R.; Montomoli, F.; Ciani, A.; D’Ercole, M. Design for Additive Manufacturing: Internal Channel Optimization. J. Eng. Gas Turbines Power 2017, 139, 102101. [Google Scholar] [CrossRef]
- Zhao, X.; Zhou, M.; Sigmund, O.; Andreasen, C.S. A “poor man’s approach” to topology optimization of cooling channels based on a Darcy flow model. Int. J. Heat Mass Transf. 2018, 116, 1108–1123. [Google Scholar] [CrossRef]
- Qian, S.; Wang, W.; Ge, C.; Lou, S.; Miao, E.; Tang, B. Topology optimization of fluid flow channel in cold plate for active phased array antenna. Struct. Multidiscip. Optim. 2018, 57, 2223–2232. [Google Scholar] [CrossRef]
- Sato, Y.; Yaji, K.; Izui, K.; Yamada, T.; Nishiwaki, S. An Optimum Design Method for a Thermal-Fluid Device Incorporating Multiobjective Topology Optimization With an Adaptive Weighting Scheme. J. Mech. Des. 2018, 140, 31402. [Google Scholar] [CrossRef]
- Yaji, K.; Ogino, M.; Chen, C.; Fujita, K. Large-scale topology optimization incorporating local-in-time adjoint-based method for unsteady thermal-fluid problem. Struct. Multidiscip. Optim. 2018, 58, 817–822. [Google Scholar] [CrossRef]
- Haertel, J.H.K.; Engelbrecht, K.; Lazarov, B.S.; Sigmund, O. Topology optimization of a pseudo 3D thermofluid heat sink model. Int. J. Heat Mass Transf. 2018, 121, 1073–1088. [Google Scholar] [CrossRef]
- Zeng, S.; Kanargi, B.; Lee, P.S. Experimental and numerical investigation of a mini channel forced air heat sink designed by topology optimization. Int. J. Heat Mass Transf. 2018, 121, 663–679. [Google Scholar] [CrossRef]
- Dilgen, C.B.; Dilgen, S.B.; Fuhrman, D.R.; Sigmund, O.; Lazarov, B.S. Topology optimization of turbulent flows. Comput. Methods Appl. Mech. Eng. 2018, 331, 363–393. [Google Scholar] [CrossRef]
- Ramalingom, D.; Cocquet, P.H.; Bastide, A. A new interpolation technique to deal with fluid-porous media interfaces for topology optimization of heat transfer. Comput. Fluids 2018, 168, 144–158. [Google Scholar] [CrossRef]
- Dugast, F.; Favennec, Y.; Josset, C.; Fan, Y.; Luo, L. Topology optimization of thermal fluid flows with an adjoint Lattice Boltzmann Method. J. Comput. Phys. 2018, 365, 376–404. [Google Scholar] [CrossRef]
- Santhanakrishnan, M.S.; Tilford, T.; Bailey, C. Performance assessment of density and level-set topology optimisation methods for three-dimensional heat sink design. J. Algorithms Comput. Technol. 2018, 12, 273–287. [Google Scholar] [CrossRef]
- Sun, C.; Lewpiriyawong, N.; Khoo, K.L.; Zeng, S.; Lee, P.S. Thermal enhancement of fin and tube heat exchanger with guiding channels and topology optimisation. Int. J. Heat Mass Transf. 2018, 127, 1001–1013. [Google Scholar] [CrossRef]
- Lv, Y.; Liu, S. Topology optimization and heat dissipation performance analysis of a micro-channel heat sink. Meccanica 2018, 53, 3693–3708. [Google Scholar] [CrossRef]
- Pietropaoli, M.; Montomoli, F.; Gaymann, A. Three-dimensional fluid topology optimization for heat transfer. Struct. Multidiscip. Optim. 2019, 59, 801–812. [Google Scholar] [CrossRef]
- Makhija, D.S.; Beran, P.S. Concurrent shape and topology optimization for steady conjugate heat transfer. Struct. Multidiscip. Optim. 2019, 59, 919–940. [Google Scholar] [CrossRef]
- Subramaniam, V.; Dbouk, T.; Harion, J.L. Topology optimization of conjugate heat transfer systems: A competition between heat transfer enhancement and pressure drop reduction. Int. J. Heat Fluid Flow 2019, 75, 165–184. [Google Scholar] [CrossRef]
- Yu, M.; Ruan, S.; Wang, X.; Li, Z.; Shen, C. Topology optimization of thermal–fluid problem using the MMC-based approach. Struct. Multidiscip. Optim. 2019, 60, 151–165. [Google Scholar] [CrossRef]
- Zhang, B.; Gao, L. Topology optimization of convective heat transfer problems for non-Newtonian fluids. Struct. Multidiscip. Optim. 2019, 60, 1821–1840. [Google Scholar] [CrossRef]
- Kobayashi, H.; Yaji, K.; Yamasaki, S.; Fujita, K. Freeform winglet design of fin-and-tube heat exchangers guided by topology optimization. Appl. Therm. Eng. 2019, 161, 114020. [Google Scholar] [CrossRef]
- Zeng, S.; Lee, P.S. Topology optimization of liquid-cooled microchannel heat sinks: An experimental and numerical study. Int. J. Heat Mass Transf. 2019, 142, 118401. [Google Scholar] [CrossRef]
- Jahan, S.; Wu, T.; Shin, Y.; Tovar, A.; El-Mounayri, H. Thermo-fluid Topology Optimization and Experimental Study of Conformal Cooling Channels for 3D Printed Plastic Injection Molds. Procedia Manuf. 2019, 34, 631–639. [Google Scholar] [CrossRef]
- Yan, S.; Wang, F.; Hong, J.; Sigmund, O. Topology optimization of microchannel heat sinks using a two-layer model. Int. J. Heat Mass Transf. 2019, 143, 118462. [Google Scholar] [CrossRef]
- Tawk, R.; Ghannam, B.; Nemer, M. Topology optimization of heat and mass transfer problems in two fluids-one solid domains. Numer. Heat Transf. Part B Fundam. 2019, 76, 130–151. [Google Scholar] [CrossRef]
- Lundgaard, C.; Engelbrecht, K.; Sigmund, O. A density-based topology optimization methodology for thermal energy storage systems. Struct. Multidiscip. Optim. 2019, 60, 2189–2204. [Google Scholar] [CrossRef]
- Li, H.; Ding, X.; Meng, F.; Jing, D.; Xiong, M. Optimal design and thermal modelling for liquid-cooled heat sink based on multi-objective topology optimization: An experimental and numerical study. Int. J. Heat Mass Transf. 2019, 144, 118638. [Google Scholar] [CrossRef]
- Dong, X.; Liu, X. Multi-objective optimal design of microchannel cooling heat sink using topology optimization method. Numeri. Heat Transf. Part A Appl. 2020, 77, 90–104. [Google Scholar] [CrossRef]
- Yaji, K.; Yamasaki, S.; Fujita, K. Multifidelity design guided by topology optimization. Struct. Multidiscip. Optim. 2019, 61, 1071–1085. [Google Scholar] [CrossRef]
- Hu, D.; Zhang, Z.; Li, Q. Numerical study on flow and heat transfer characteristics of microchannel designed using topological optimizations method. Sci. China Technol. Sci. 2020, 63, 105–115. [Google Scholar] [CrossRef]
- Coffin, P.; Maute, K. A level-set method for steady-state and transient natural convection problems. Struct. Multidiscip. Optim. 2016, 53, 1047–1067. [Google Scholar] [CrossRef]
- Alexandersen, J.; Sigmund, O.; Aage, N. Large scale three-dimensional topology optimisation of heat sinks cooled by natural convection. Int. J. Heat Mass Transf. 2016, 100, 876–891. [Google Scholar] [CrossRef]
- Pizzolato, A.; Sharma, A.; Maute, K.; Sciacovelli, A.; Verda, V. Design of effective fins for fast PCM melting and solidification in shell-and-tube latent heat thermal energy storage through topology optimization. Appl. Energy 2017, 208, 210–227. [Google Scholar] [CrossRef]
- Alexandersen, J.; Sigmund, O.; Meyer, K.E.; Lazarov, B.S. Design of passive coolers for light-emitting diode lamps using topology optimisation. Int. J. Heat Mass Transf. 2018, 122, 138–149. [Google Scholar] [CrossRef]
- Lazarov, B.S.; Sigmund, O.; Meyer, K.E.; Alexandersen, J. Experimental validation of additively manufactured optimized shapes for passive cooling. Appl. Energy 2018, 226, 330–339. [Google Scholar] [CrossRef]
- Lei, T.; Alexandersen, J.; Lazarov, B.S.; Wang, F.; Haertel, J.H.K.; De Angelis, S.; Sanna, S.; Sigmund, O.; Engelbrecht, K. Investment casting and experimental testing of heat sinks designed by topology optimization. Int. J. Heat Mass Transf. 2018, 127, 396–412. [Google Scholar] [CrossRef]
- Saglietti, C.; Schlatter, P.; Wadbro, E.; Berggren, M.; Henningson, D.S. Topology optimization of heat sinks in a square differentially heated cavity. Int. J. Heat Fluid Flow 2018, 74, 36–52. [Google Scholar] [CrossRef]
- Asmussen, J.; Alexandersen, J.; Sigmund, O.; Andreasen, C.S. A “poor man’s” approach to topology optimization of natural convection problems. Struct. Multidiscip. Optim. 2019, 59, 1105–1124. [Google Scholar] [CrossRef]
- Pizzolato, A.; Sharma, A.; Ge, R.; Maute, K.; Verda, V.; Sciacovelli, A. Maximization of performance in multi-tube latent heat storage–Optimization of fins topology, effect of materials selection and flow arrangements. Energy 2019. [Google Scholar] [CrossRef]
- Ramalingom, D.; Cocquet, P.H.; Maleck, R.; Bastide, A. A multi-objective optimization problem in mixed and natural convection for a vertical channel asymmetrically heated. Struct. Multidiscip. Optim. 2019, 60, 2001–2020. [Google Scholar] [CrossRef]
- Pollini, N.; Sigmund, O.; Andreasen, C.S.; Alexandersen, J. A “poor man’s” approach for high-resolution three-dimensional topology design for natural convection problems. Adv. Eng. Softw. 2020, 140, 102736. [Google Scholar] [CrossRef]
- Yoon, G.H. Topology optimization for stationary fluid–structure interaction problems using a new monolithic formulation. Int. J. Numer. Methods Eng. 2010, 82, 591–616. [Google Scholar] [CrossRef]
- Yoon, G.H.; Jensen, J.S.; Sigmund, O. Topology optimization of acoustic–structure interaction problems using a mixed finite element formulation. Int. J. Numer. Methods Eng. 2007, 70, 1049–1075. [Google Scholar] [CrossRef]
- Kreissl, S.; Pingen, G.; Evgrafov, A.; Maute, K. Topology optimization of flexible micro-fluidic devices. Struct. Multidiscip. Optim. 2010, 42, 495–516. [Google Scholar] [CrossRef]
- Yoon, G.H. Topological layout design of electro-fluid-thermal-compliant actuator. Comput. Methods Appl. Mech. Eng. 2012, 209–212, 28–44. [Google Scholar] [CrossRef]
- Yoon, G.H. Stress-based topology optimization method for steady-state fluid–structure interaction problems. Comput. Methods Appl. Mech. Eng. 2014, 278, 499–523. [Google Scholar] [CrossRef]
- Yoon, G.H. Compliant topology optimization for planar passive flap micro valve. J. Nanosci. Nanotechnol. 2014, 14, 7585–7591. [Google Scholar] [CrossRef]
- Jenkins, N.; Maute, K. An immersed boundary approach for shape and topology optimization of stationary fluid–structure interaction problems. Struct. Multidiscip. Optim. 2016, 54, 1191–1208. [Google Scholar] [CrossRef]
- Munk, D.J.; Kipouros, T.; Vio, G.A.; Steven, G.P.; Parks, G.T. Topology optimisation of micro fluidic mixers considering fluid–structure interactions with a coupled Lattice Boltzmann algorithm. J. Comput. Phys. 2017, 349, 11–32. [Google Scholar] [CrossRef]
- Picelli, R.; Vicente, W.M.; Pavanello, R. Evolutionary topology optimization for structural compliance minimization considering design-dependent FSI loads. Finite Elem. Anal. Des. 2017, 135, 44–55. [Google Scholar] [CrossRef]
- Yoon, G.H. Brittle and ductile failure constraints of stress-based topology optimization method for fluid–structure interactions. Comput. Math. Appl. 2017, 74, 398–419. [Google Scholar] [CrossRef]
- Lundgaard, C.; Alexandersen, J.; Zhou, M.; Andreasen, C.S.; Sigmund, O. Revisiting density-based topology optimization for fluid–structure interaction problems. Struct. Multidiscip. Optim. 2018, 58, 969–995. [Google Scholar] [CrossRef]
- Munk, D.J.; Kipouros, T.; Vio, G.A.; Parks, G.T.; Steven, G.P. On the effect of fluid–structure interactions and choice of algorithm in multi-physics topology optimisation. Finite Elem. Anal. Des. 2018, 145, 32–54. [Google Scholar] [CrossRef]
- Munk, D.J.; Kipouros, T.; Vio, G.A. Multi-physics bi-directional evolutionary topology optimization on GPU-architecture. Eng. Comput. 2018, 35, 1059–1079. [Google Scholar] [CrossRef]
- Feppon, F.; Allaire, G.; Bordeu, F.; Cortial, J.; Dapogny, C. Shape optimization of a coupled thermal fluid–structure problem in a level set mesh evolution framework. SeMA J. 2019, 76, 413–458. [Google Scholar] [CrossRef]
- Guest, J.K.; Prévost, J.H. Design of maximum permeability material structures. Comput. Methods Appl. Mech. Eng. 2007, 196, 1006–1017. [Google Scholar] [CrossRef]
- Guest, J.K.; Prévost, J.H. Optimizing multifunctional materials: Design of microstructures for maximized stiffness and fluid permeability. Int. J. Solids Struct. 2006, 43, 7028–7047. [Google Scholar] [CrossRef]
- Hollister, S.J.; Lin, C.Y. Computational design of tissue engineering scaffolds. Comput. Methods Appl. Mech. Eng. 2007, 196, 2991–2998. [Google Scholar] [CrossRef]
- Xu, S.; Cheng, G. Optimum material design of minimum structural compliance under seepage constraint. Struct. Multidiscip. Optim. 2010, 41, 575–587. [Google Scholar] [CrossRef]
- Andreasen, C.S.; Sigmund, O. Saturated poroelastic actuators generated by topology optimization. Struct. Multidiscip. Optim. 2010, 43, 693–706. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, S.; Li, Q. Microstructure design of biodegradable scaffold and its effect on tissue regeneration. Biomaterials 2011, 32, 5003–5014. [Google Scholar] [CrossRef]
- Chen, Y.; Schellekens, M.; Zhou, S.; Cadman, J.; Li, W.; Appleyard, R.; Li, Q. Design Optimization of Scaffold Microstructures Using Wall Shear Stress Criterion Towards Regulated Flow-Induced Erosion. J. Biomech. Eng. 2011, 133, 081008. [Google Scholar] [CrossRef]
- Gonçalves Coelho, P.; Rui Fernandes, P.; Carriço Rodrigues, H. Multiscale modeling of bone tissue with surface and permeability control. J. Biomech. 2011, 44, 321–329. [Google Scholar] [CrossRef]
- Challis, V.J.; Guest, J.K.; Grotowski, J.F.; Roberts, A.P. Computationally generated cross-property bounds for stiffness and fluid permeability using topology optimization. Int. J. Solids Struct. 2012, 49, 3397–3408. [Google Scholar] [CrossRef]
- Andreasen, C.S.; Sigmund, O. Multiscale modeling and topology optimization of poroelastic actuators. Smart Mater. Struct. 2012, 21, 065005. [Google Scholar] [CrossRef][Green Version]
- Andreasen, C.S.; Sigmund, O. Topology optimization of fluid–structure-interaction problems in poroelasticity. Comput. Methods Appl. Mech. Eng. 2013, 258, 55–62. [Google Scholar] [CrossRef]
- Youssef, K.; Mack, J.J.; Iruela-Arispe, M.L.; Bouchard, L.S. Macro-scale topology optimization for controlling internal shear stress in a porous scaffold bioreactor. Biotechnol. Bioeng. 2012, 109, 1844–1854. [Google Scholar] [CrossRef]
- Ha, S.H.; Lee, H.Y.; Hemker, K.J.; Guest, J.K. Topology Optimization of Three-Dimensional Woven Materials Using a Ground Structure Design Variable Representation. J. Mech. Des. 2019, 141. [Google Scholar] [CrossRef]
- Wein, F.; Chen, N.; Iqbal, N.; Stingl, M.; Avila, M. Topology optimization of unsaturated flows in multi-material porous media: Application to a simple diaper model. Commun. Nonlinear Sci. Numer. Simul. 2019, 78, 104871. [Google Scholar] [CrossRef]
- Takezawa, A.; Zhang, X.; Tanaka, T.; Kitamura, M. Topology optimisation of a porous unit cell in a fluid flow considering Forchheimer drag. Int. J. Comput. Fluid Dyn. 2019. [Google Scholar] [CrossRef]
- Lurie, S.A.; Rabinskiy, L.N.; Solyaev, Y.O. Topology optimization of the wick geometry in a flat plate heat pipe. Int. J. Heat Mass Transf. 2019, 128, 239–247. [Google Scholar] [CrossRef]
- Takezawa, A.; Zhang, X.; Kato, M.; Kitamura, M. Method to optimize an additively-manufactured functionally-graded lattice structure for effective liquid cooling. Addit. Manuf. 2019, 28, 285–298. [Google Scholar] [CrossRef]
- Takezawa, A.; Zhang, X.; Kitamura, M. Optimization of an additively manufactured functionally graded lattice structure with liquid cooling considering structural performances. Int. J. Heat Mass Transf. 2019, 143, 118564. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Takizawa, K.; Tezduyar, T.E. New directions and challenging computations in fluid dynamics modeling with stabilized and multiscale methods. Math. Models Methods Appl. Sci. 2015, 25, 2217–2226. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Takizawa, K.; Tezduyar, T.E. Computational analysis methods for complex unsteady flow problems. Math. Models Methods Appl. Sci. 2019, 29, 825–838. [Google Scholar] [CrossRef]
- Sigmund, O. On the usefulness of non-gradient approaches in topology optimization. Struct. Multidiscip. Optim. 2011, 43, 589–596. [Google Scholar] [CrossRef]
- Alexandersen, J. Topology Optimisation for Coupled Convection Problems. Master’s Thesis, Technical University of Denmark (DTU), Kongens Lyngby, Denmark, 2013. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexandersen, J.; Andreasen, C.S. A Review of Topology Optimisation for Fluid-Based Problems. Fluids 2020, 5, 29. https://doi.org/10.3390/fluids5010029
Alexandersen J, Andreasen CS. A Review of Topology Optimisation for Fluid-Based Problems. Fluids. 2020; 5(1):29. https://doi.org/10.3390/fluids5010029
Chicago/Turabian StyleAlexandersen, Joe, and Casper Schousboe Andreasen. 2020. "A Review of Topology Optimisation for Fluid-Based Problems" Fluids 5, no. 1: 29. https://doi.org/10.3390/fluids5010029
APA StyleAlexandersen, J., & Andreasen, C. S. (2020). A Review of Topology Optimisation for Fluid-Based Problems. Fluids, 5(1), 29. https://doi.org/10.3390/fluids5010029




