Energy Transport by Kelvin-Helmholtz Instability at the Magnetopause
Abstract
1. Introduction
2. Numerical Method
3. Simulation Results
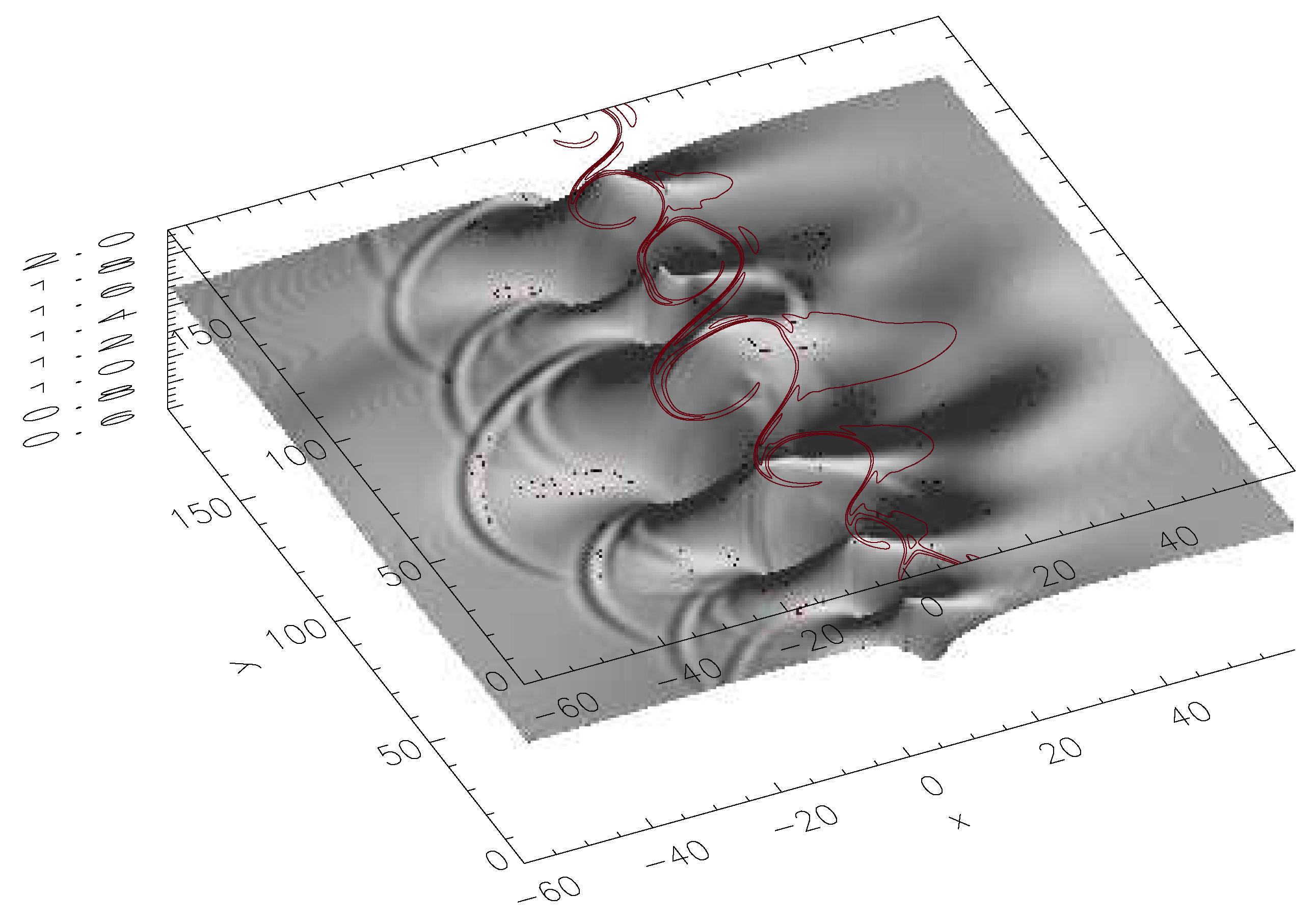
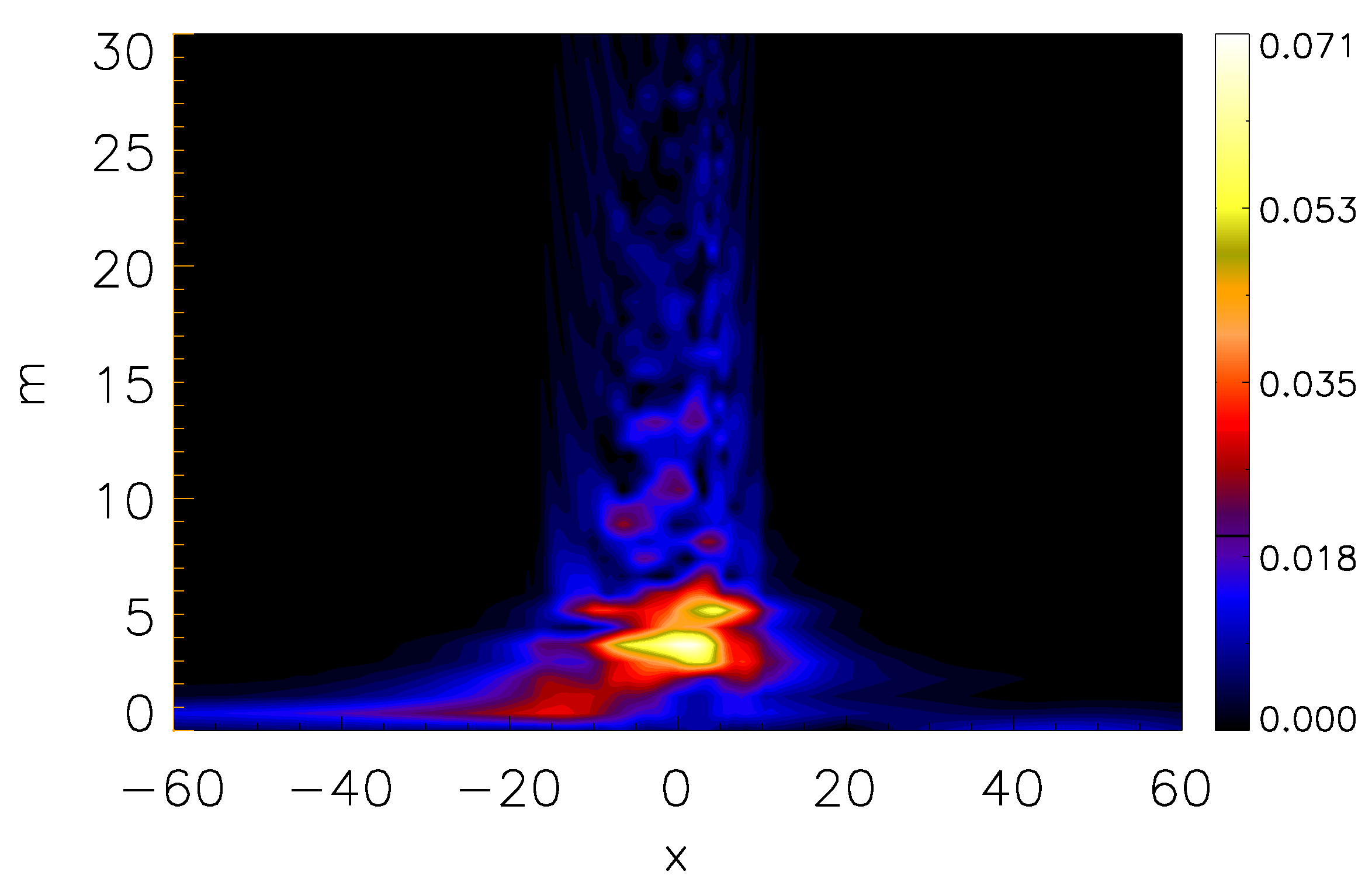
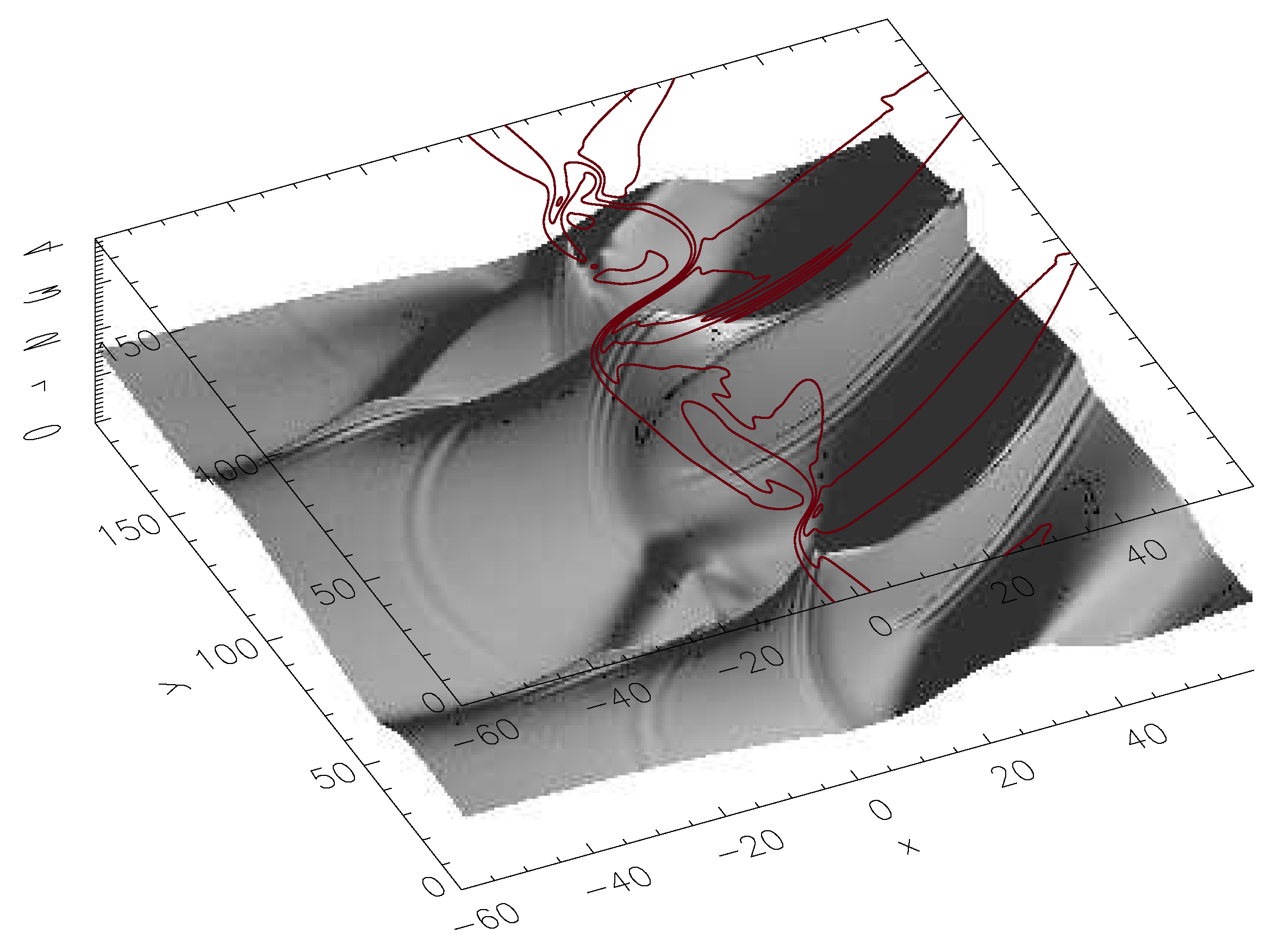
3.1. Plasma Configuration
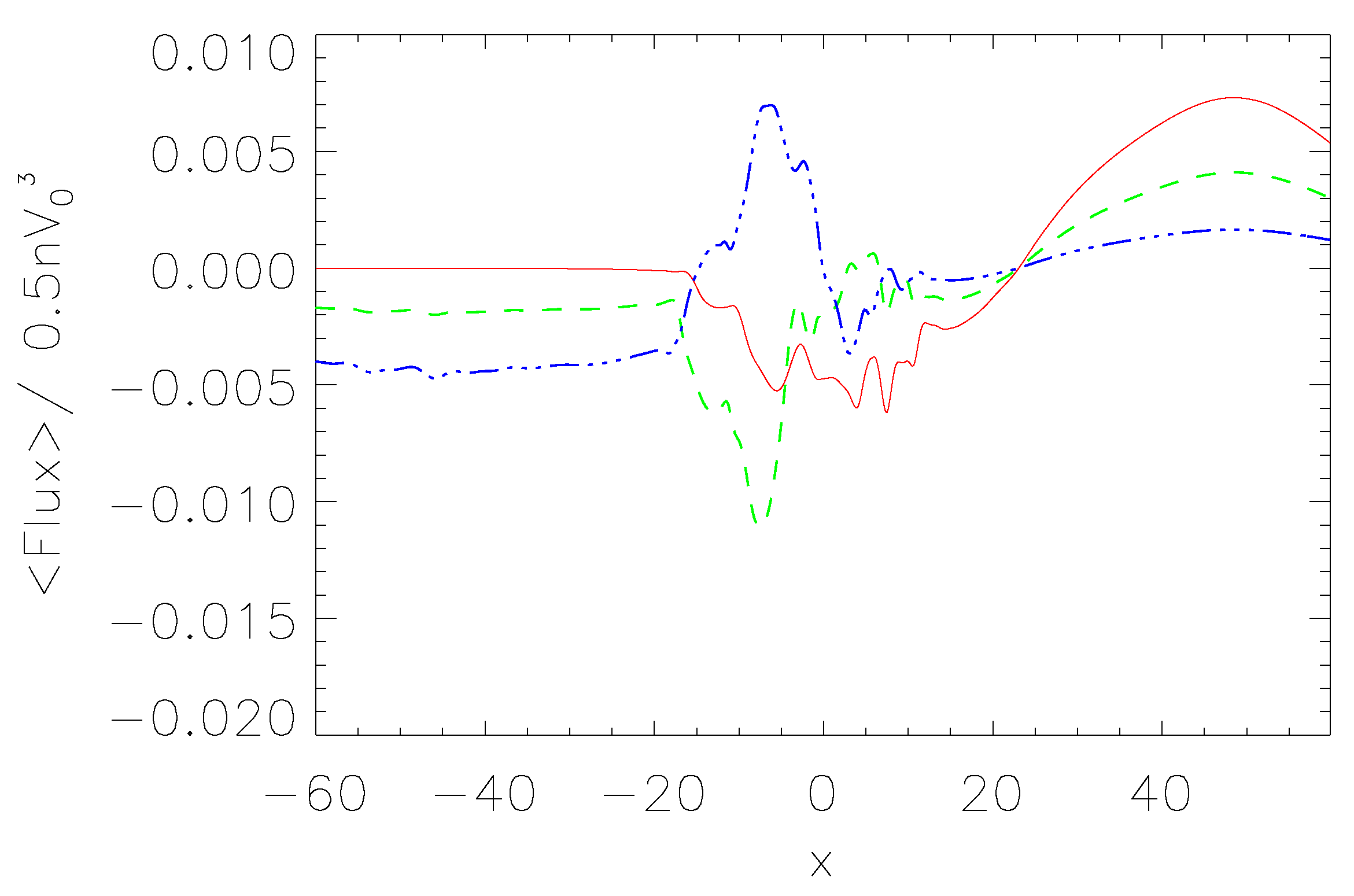
3.2. Energy Flux by Kelvin Helmholtz (KH) Instability
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Song, P.; Elphic, R.C.; Russell, C.T. ISEE 1 & 2 observations of the oscillating magnetopause. Geophys. Res. Lett. 1988, 15, 744–747. [Google Scholar]
- Yagodkina, O.I.; Vorobjev, V.G. Daytime high latitude pulsations associated with solar wind dynamic pressure impulses and flux transfer events. J. Geophys. Res. 1997, 102, 57–67. [Google Scholar] [CrossRef]
- Lee, S.H.; Zhang, H.; Zong, Q.G.; Wang, Y.; Otto, A.; Réme, H.; Glassmeier, K.H. Asymmetric ionospheric outflow observed at the dayside magnetopause. J. Geophys. Res. Space Phys. 2015, 120, 3564–3573. [Google Scholar] [CrossRef]
- Ofman, L.; Thompson, B.J. Observation of Kelvin Helmholtz instability in the solar corona. Astrophys. J. Lett. 2011, 734, L11. [Google Scholar] [CrossRef]
- Rogers, B.N.; Dorland, W.; Kotschenreuther, M. Generation and Stability of Zonal Flows in Ion-Temperature- Gradient Mode Turbulence. Phys. Rev. Lett. 2000, 85, 5336. [Google Scholar] [CrossRef] [PubMed]
- Palermo, F.; Garbet, X.; Ghizzo, A.; Cartier-Michaud, T.; Ghendrih, P.; Grandgirard, V.; Sarazin, Y. Shear flow instabilities induced by trapped ion modes in collisionless temperature gradient turbulence. Phys. Plasmas 2015, 22, 042304. [Google Scholar] [CrossRef]
- Ghizzo, A.; Palermo, F. Shear-flow trapped-ion-mode interaction revisited. I. Influence of low-frequency zonal flow on ion-temperature-gradient driven turbulence. Phys. Plasmas 2015, 22, 082303. [Google Scholar] [CrossRef]
- Palermo, F.; Garbet, X.; Ghizzo, A. Bicoherence analysis of streamer dynamics induced by trapped ion modes. Europ. Phys. J. D 2015, 69, 8. [Google Scholar] [CrossRef]
- Axford, W.I.; Hincs, C.O. A unifying theory of high-latitude. Geophysical phenomena and geomagnetic storms. Can. J. Phys. 1961, 39, 1433–1464. [Google Scholar] [CrossRef]
- Lemaire, J.; Roth, M. Penetration of the solar wind plasma elements into the magnetosphere. J. Atmos. Terr. Phys. 1978, 40, 331–335. [Google Scholar] [CrossRef]
- Miura, A.; Pritchett, P. Nonlocal stability analysis of the MHD Kelvin-Helmholtz instability in a compressible plasma. J. Geophys. Res. 1982, 87, 7431–7444. [Google Scholar] [CrossRef]
- Miura, A. Anomalous transport by magnetohydrodynamic Kelvin-Helmholtz instabilities in the solar wind-magnetosphere interaction. J. Geophys. Res. 1984, 89, 801–848. [Google Scholar] [CrossRef]
- Miura, A. Simulation of Kelvin-Helmholtz Instability at the Magnetospheric Boundary. J. Geophys. Res. 1987, 97, 3195–3206. [Google Scholar] [CrossRef]
- Hasegawa, H.; Fujimoto, M.; Phan, T.D.; Réme, H.; Balogh, A.; Dunlop, M.W.; Hashimoto, C.; TanDokoro, R. Transport of solar wind into Earth’s magnetosphere through rolled-up Kelvin-Helmholtz vortices. Nature 2004, 430, 755. [Google Scholar] [CrossRef]
- Nishino, M.N.; Hasegawa, H.; Fujimoto, M.; Saito, Y.; Mukai, T.; Dandouras, I.; Reme, H.; Retino, A.; Nakamura, R.; Lucek, E.; et al. A case study of Kelvin–Helmholtz vortices on both flanks of the Earth’s magnetotail. Planet. Space Sci. 2011, 59, 502–509. [Google Scholar] [CrossRef]
- Otto, A.; Fairfield, D.H. Kelvin-Helmholtz instability at the magnetotail boundary: MHD simulation and comparison with Geotail observations. J. Geophys. Res. 2000, 105, 21175–21190. [Google Scholar] [CrossRef]
- Palermo, F.; Califano, F.; Pegoraro, F.; Le Contel, O. Possible magnetospheric Kelvin-Helmholtz vortex signatures near the post-noon magnetopause. Mem. Soc. Astron. Ital. Suppl. 2010, 14, 189. [Google Scholar]
- Faganello, M.; Califano, F.; Pegoraro, F.; Retino, A. Kelvin-Helmholtz vortices and doublemid-latitude reconnection at the Earth’smagnetopause: Comparison between observations and simulations. Eur. Phys. J. 2014, 107, 19001. [Google Scholar]
- Matsumoto, Y.; Hoshino, M. Onset of turbulence induced by a Kelvin-Helmholtz vortex. Geophys. Res. Lett. 2004, 31, L02807. [Google Scholar] [CrossRef]
- Faganello, M.; Califano, F.; Pegoraro, F. Competing mechanisms of plasma transport in inhomogeneous configurations with velocity shear: The solar-wind interaction with Earth’s magnetosphere. Phys. Rev. Lett. 2008, 100, 015001. [Google Scholar] [CrossRef]
- Fadanelli, S.; Faganello, M.; Califano, F.; Cerri, S.S.; Pegoraro, F.; Lavraud, B. North-South Asymmetric Kelvin-Helmholtz Instability and Induced Reconnection at the Earth’s Magnetospheric Flanks. J. Geophys. Res. 2018, 123, 9340–9356. [Google Scholar] [CrossRef]
- Leroy, M.H.J.; Keppens, R. On the influence of environmental parameters on mixing and reconnection caused by the Kelvin-Helmholtz instability at the magnetopause. Phys. Plasmas 2017, 24, 012906. [Google Scholar] [CrossRef]
- Ma, X.; Delamere, P.; Antonius Otto, A.; Burkholder, B. Plasma Transport Driven by the Three-Dimensional Kelvin-Helmholtz Instability. J. Geophys. Res. 2017, 122, 10382–10395. [Google Scholar] [CrossRef]
- Leroy, M.H.J.; Ripperda, B.; Keppens, R. Particle Orbits at the Magnetopause: Kelvin-Helmholtz Induced Trapping. J. Geophys. Res. 2019, 124, 6715–6729. [Google Scholar] [CrossRef]
- Blumen, W. Shear layer instability of an inviscid compressible fluid. J. Fluid Mech. 1970, 40, 769–781. [Google Scholar] [CrossRef]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability; Cambridge University Press: Cambridge, UK, 1977. [Google Scholar]
- Pu, Z.Y.; Kivelson, M.G. Kelvin-Helmholtz Instability at the Magnetopause’ Energy Flux Into the Magnetosphere. J. Geoph. Res. 1983, 88, 853–861. [Google Scholar] [CrossRef]
- Fairfield, D.H.; Otto, A.; Mukai, T.; Kokubun, S.; Lepping, R.P.; Steinberg, J.T.; Lazarus, A.J.; Yamamoto, T. Geotail observations of the Kelvin-Helmholtz instability at the equatorial magnetotail boundary for parallel northward fields. J. Geophys. Res. 2000, 105, 21159–21173. [Google Scholar] [CrossRef]
- Spreiter, J.R.; Summers, A.L.; Alksne, A.Y. Hydromagnetic flow around the magnetosphere. Planet. Space Sci. 1966, 14, 223–253. [Google Scholar] [CrossRef]
- Chen, S.H.; Kivelson, M.G.; Gosling, J.T.; Walker, R.J.; Lazarus, A.J. Anomalous aspects of magnetosheath flow and of the shape and oscillations of the magnetopause during an interval of strongly northward interplanetary magnetic field. J. Geophys. Res. 1993, 98, 5727–5742. [Google Scholar] [CrossRef]
- Lai, S.H.; Lyu, L.H. A simulation and theoretical study of energy transport in the event of MHD Kelvin-Helmholtz instability. J. Geophys. Res. 2010, 115, A10215. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Kato, M.; Nakamura, K.T.A.; Nakamura, T.K.M.; Fujimoto, M. The structure of Kelvin-Helmholtz vortices with super-sonic flow. Adv. Space Res. 2008, 41, 1325–1330. [Google Scholar] [CrossRef]
- Miura, A. Kelvin-Helmholtz instability for supersonic shear flow at the magnetospheric boundary. Geophys. Res. Lett. 1990, 17, 749–752. [Google Scholar] [CrossRef]
- Miura, A. Kelvin-Helmholtz instability at the magnetospheric boundary: Dependence on the magnetosheath sonic Mach number. J. Geophys. Res. 1992, 97, 10655–10675. [Google Scholar] [CrossRef]
- Miura, A. Nonlinear evolution of the magnetohydrodynamic Kelvin-Helmholtz instability. Phys. Rev. Lett. 1982, 49, 779. [Google Scholar] [CrossRef]
- Palermo, F.; Faganello, M.; Califano, F.; Pegoraro, F.; le Contel, O. Compressible Kelvin-Helmholtz instability in supermagnetosonic regimes. J. Geoph. Res. 2011, 116, A04223. [Google Scholar] [CrossRef]
- Palermo, F.; Faganello, M.; Califano, F.; Pegoraro, F.; Le Contel, O. The Role of the magnetosonic mach number on the evolution of Kelvin Helmholtz vortices. Europ. Conf. Lab. Astroph. 2012, 58, 91–94. [Google Scholar] [CrossRef]
- Palermo, F.; Faganello, M.; Califano, F.; Pegoraro, F.; Le Contel, O. Kelvin-Helmholtz vortices and secondary instabilities in super-magnetosonic regimes. Ann. Geophys. 2011, 29, 1169–1178. [Google Scholar] [CrossRef]
- Valentini, F.; Trávníček, P.; Califano, F.; Hellinger, P.; Mangeney, A. A hybrid-Vlasov model based on the current advance method for the simulation of collisionless magnetized plasma. J. Comp. Phys. 2007, 225, 753–770. [Google Scholar] [CrossRef]
- Faganello, M.; Califano, F.; Pegoraro, F. Being on time in magnetic reconnection. New J. Phys. 2009, 11, 063008. [Google Scholar] [CrossRef]
- Lele, S.K. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]




© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palermo, F. Energy Transport by Kelvin-Helmholtz Instability at the Magnetopause. Fluids 2019, 4, 189. https://doi.org/10.3390/fluids4040189
Palermo F. Energy Transport by Kelvin-Helmholtz Instability at the Magnetopause. Fluids. 2019; 4(4):189. https://doi.org/10.3390/fluids4040189
Chicago/Turabian StylePalermo, Francesco. 2019. "Energy Transport by Kelvin-Helmholtz Instability at the Magnetopause" Fluids 4, no. 4: 189. https://doi.org/10.3390/fluids4040189
APA StylePalermo, F. (2019). Energy Transport by Kelvin-Helmholtz Instability at the Magnetopause. Fluids, 4(4), 189. https://doi.org/10.3390/fluids4040189




