Lubrication Approximation for Fluids with Shear-Dependent Viscosity
Abstract
:1. Introduction
2. Formulation of the Problem
2.1. Lubrication Approximation
- the flow takes place between two almost parallel surfaces situated at and ;
- the lubricating film is thin, that is, , where denotes a small non-dimensional parameter;
- the flow is slow enough or the viscosity high enough so that ;
- the power-law parameter will have to be such that or .
2.2. Formal Asymptotic Analysis
2.2.1. Case
2.2.2. Case
3. Examples
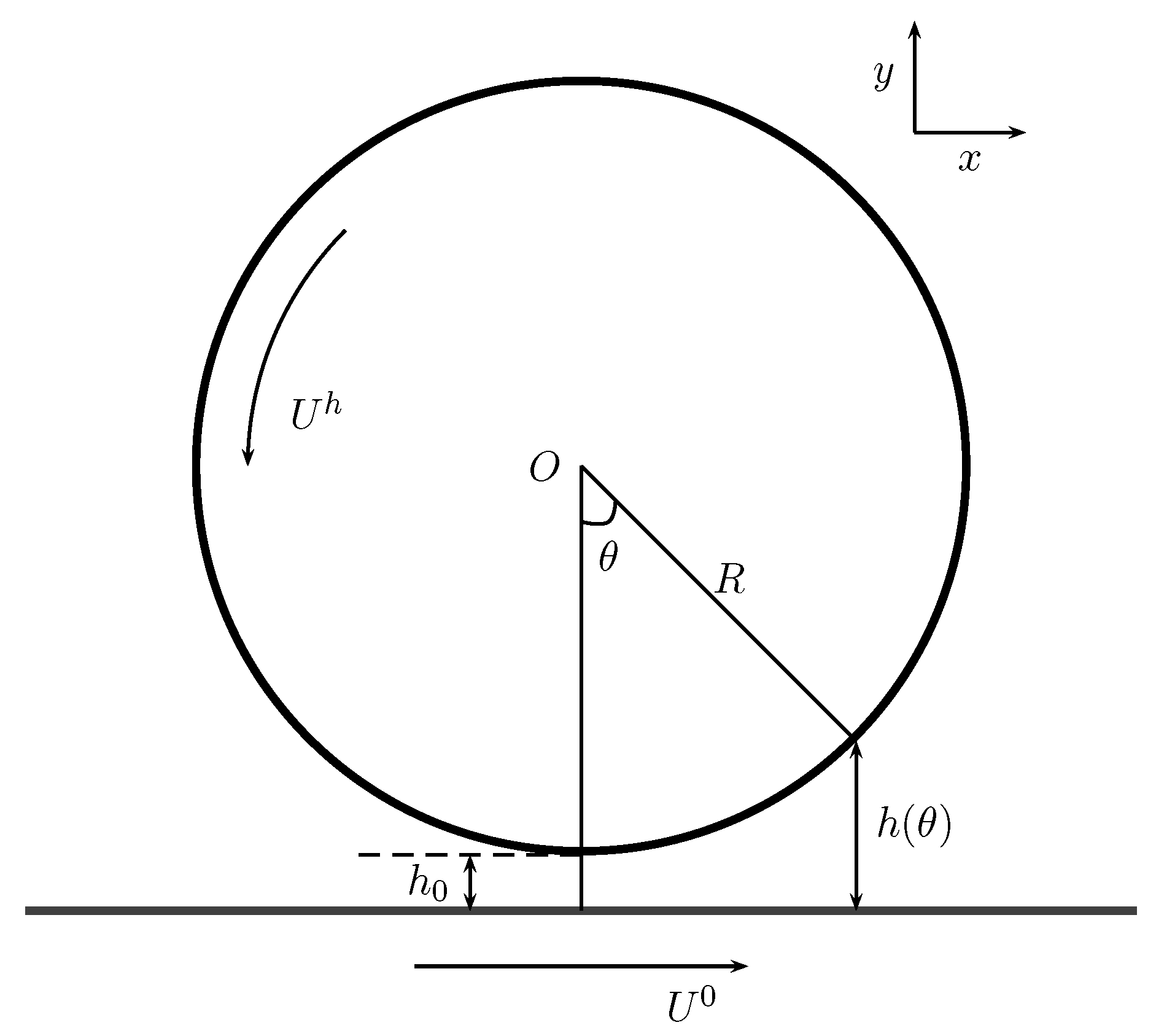
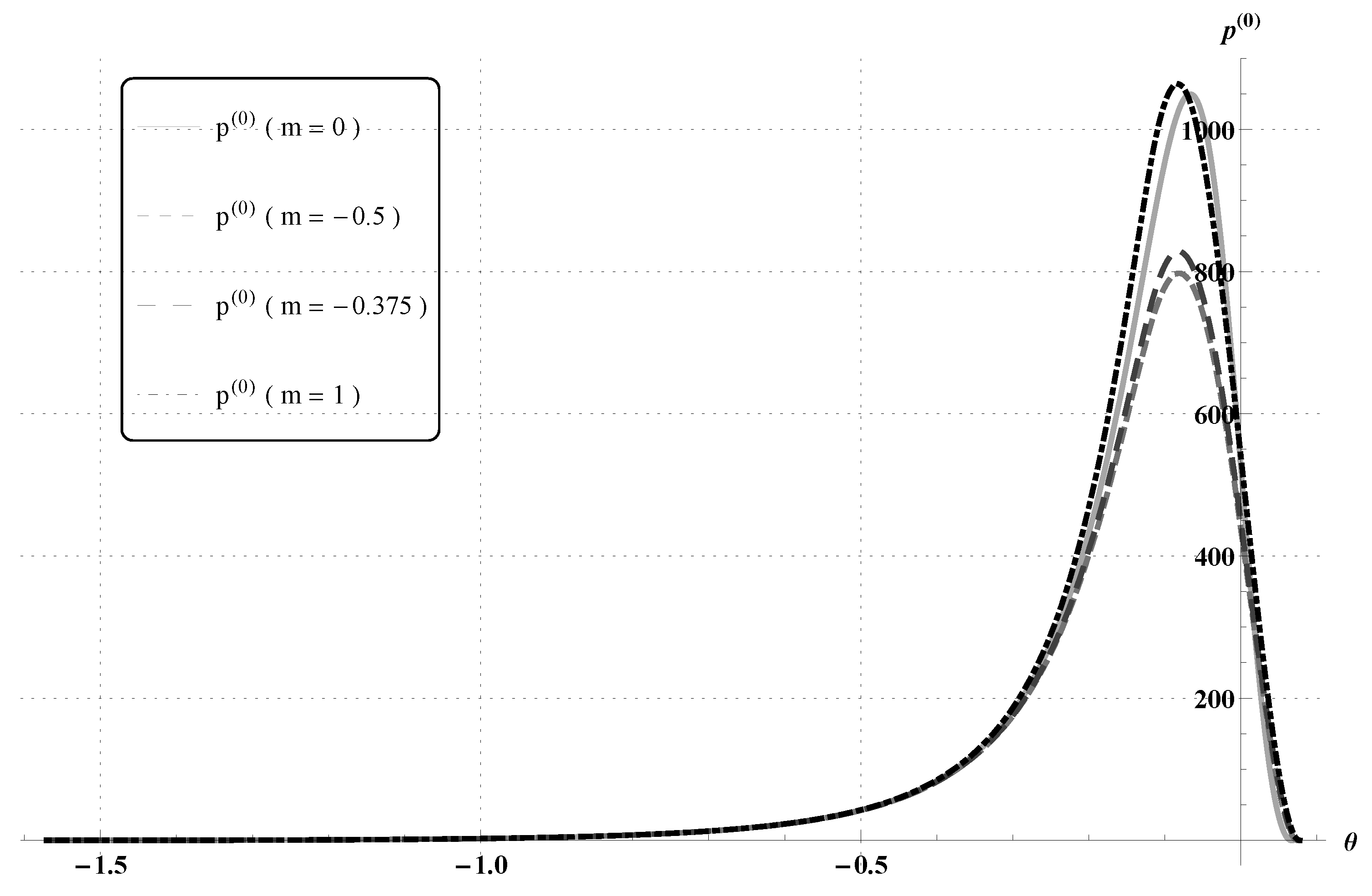
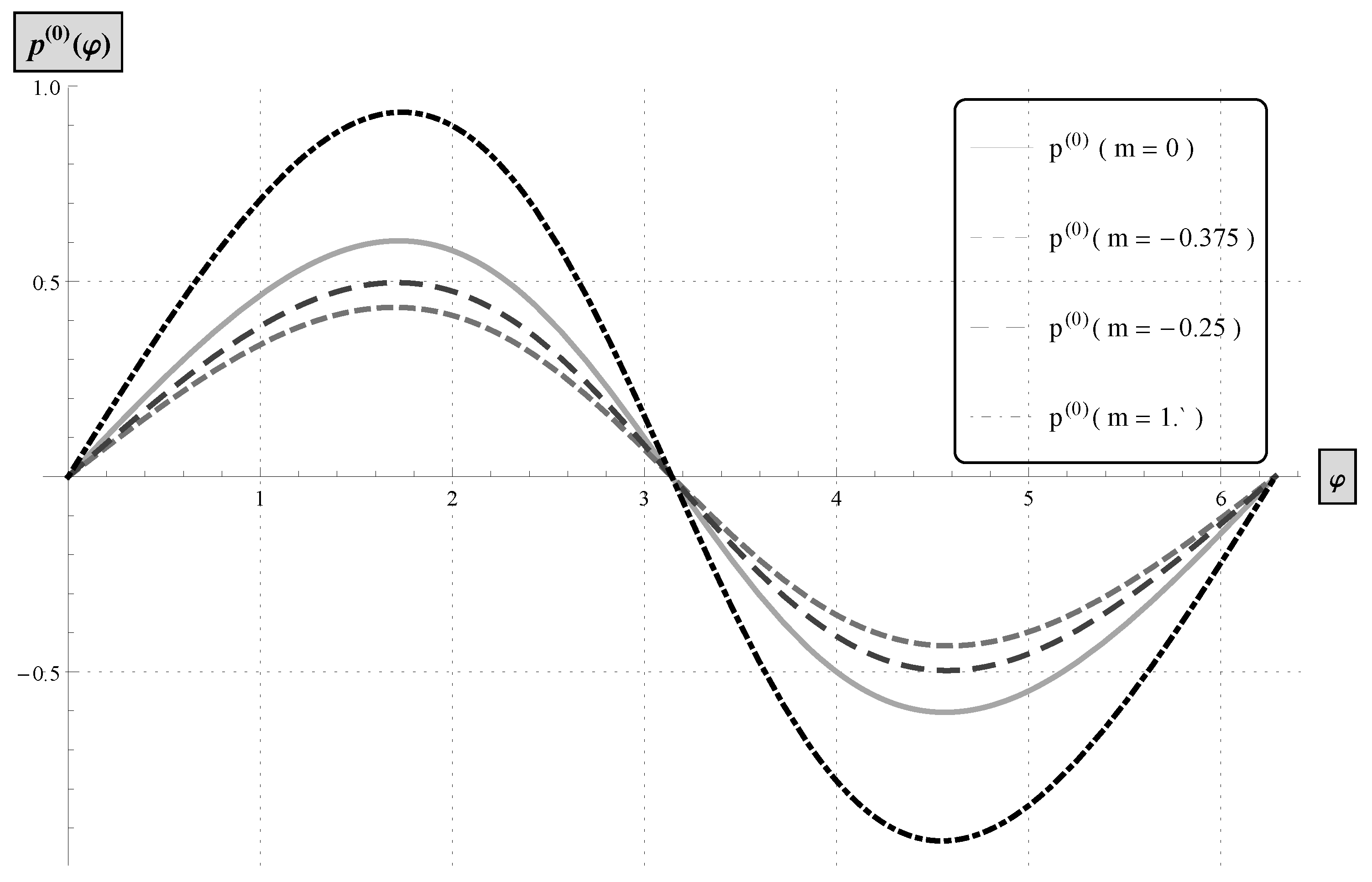
3.1. Rolling Cylinder
3.1.1.
3.1.2.
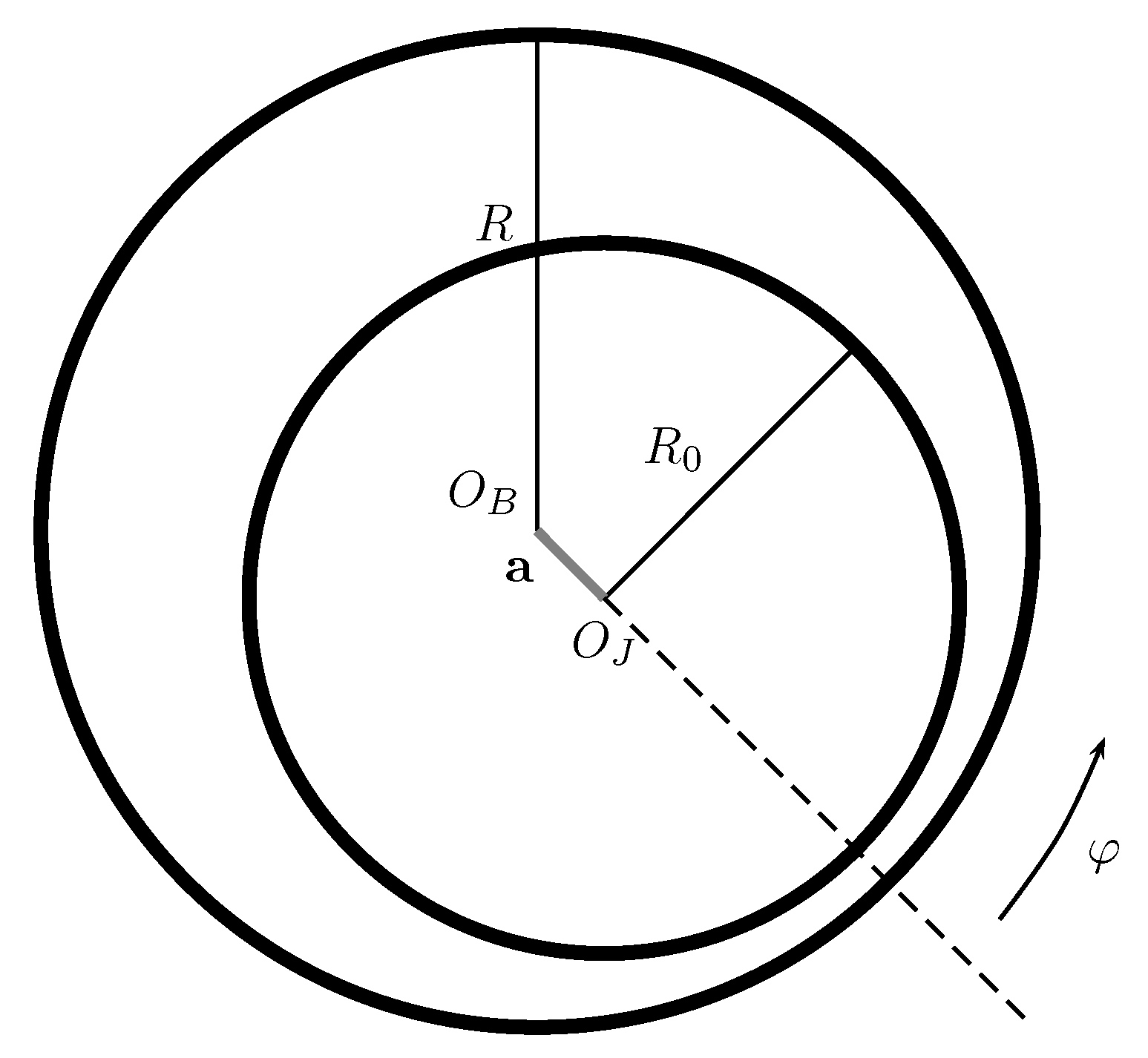
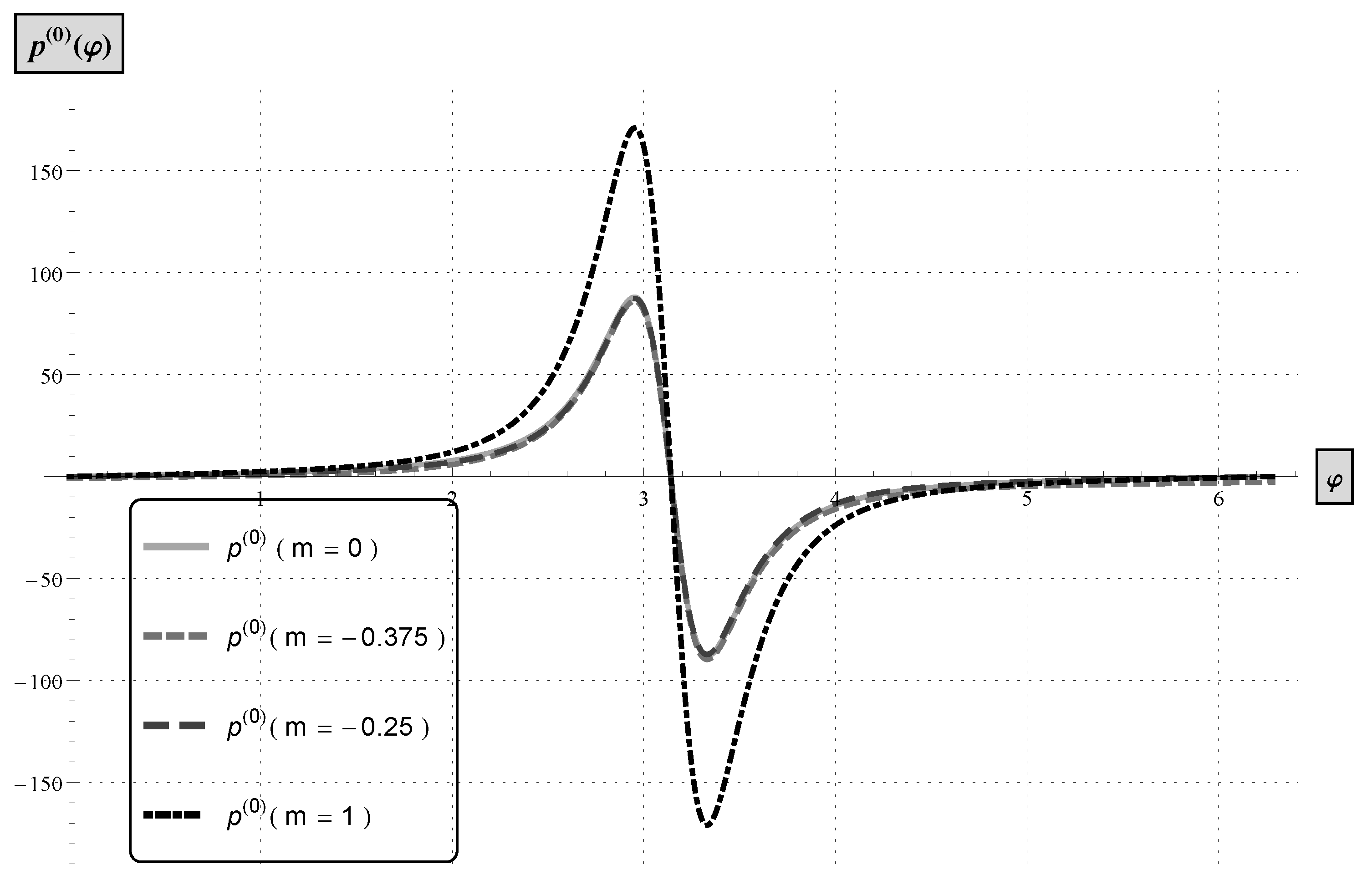
3.2. Journal Bearing
3.2.1.
3.2.2.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Reynolds, O. On the theory of lubrication and its application to Mr Tower’s experiments. Philos. Trans. R. Soc. Lond. 1886, 177, 159–209. [Google Scholar]
- Szeri, A.Z. Fluid Film Lubrication, 2nd ed.; Cambridge University Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Bair, S.; Khonsari, M.M. Reynolds equations for common generalized Newtonian models and an approximate Reynolds–Carreau equation. Proc. Inst. Mech. Eng. Part J J. Eng. 2006, 220, 365–374. [Google Scholar] [CrossRef]
- Myers, T.G. Application of non-Newtonian models to thin film flow. Phys. Rev. E 2005, 72, 066302. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Huang, P.; Fang, Y. A novel Reynolds equation of non-Newtonian fluid for lubrication simulation. Tribol. Int. 2016, 94, 458–463. [Google Scholar] [CrossRef]
- Shukla, J.B.; Prasad, K.R.; Chandra, P. Effects of consistency variation of power law lubricants in squeeze film. Wear 1982, 76, 299–319. [Google Scholar] [CrossRef]
- Park, O.O.; Kwon, M.H. Study on the lubrication approximation of power law fluid. Korean J. Chem. Eng. 1989, 6, 150–153. [Google Scholar] [CrossRef]
- Johnson, M.W., Jr.; Mangkoesoebroto, S. Analysis of lubrication theory for the power law fluid. J. Tribol. 1993, 115, 71–77. [Google Scholar] [CrossRef]
- Bourgin, P. Fluid-Film Flows of Differential Fluids of Complexity n Dimensional Approach—Applications to Lubrication Theory. ASME J. Lubr. Technol. 1979, 101, 140–144. [Google Scholar] [CrossRef]
- Kacou, A.; Rajagopal, K.R.; Szeri, A.Z. A thermodynamic analysis of journal bearings lubricated by non-Newtonian fluids. J. Tribol. 1998, 110, 414–428. [Google Scholar] [CrossRef]
- Harnoy, A. Three dimensional analysis of the elastico-viscous lubrication in short journal bearings. Rheol. Acta 1977, 16, 51–60. [Google Scholar] [CrossRef]
- Ballal, B.Y.; Rivlin, R.S. Flow of a Newtonian fluid between eccentric rotating cylinders: Inertial effects. Arch. Ration. Mech. Anal. 1976, 62, 237–294. [Google Scholar] [CrossRef]
- Andres, A.S.; Szeri, A.Z. Flow between Eccentric Rotating Cylinders. J. Appl. Mech. 1984, 51, 869–878. [Google Scholar] [CrossRef]
- Cal, F.S.; Dias, G.A.S.; Pereira, B.M.M.; Pires, G.E.; Rajagopal, K.R.; Videman, J.H. On the lubrication approximation for a class of viscoelastic fluids. Int. J. Nonlinear Mech. 2016, 87, 30–37. [Google Scholar] [CrossRef]
- Barus, C. Isothermals, isopiestics and isometrics relative to viscosity. Am. J. Sci. 1893, 45, 87–96. [Google Scholar] [CrossRef]
- Bair, S. High Pressure Rheology for Quantitative Elastohydrodynamics; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Rajagopal, K.R.; Szeri, A. On an inconsistency in the derivation of the equations of elastohydrodynamic lubrication. Proc. R. Soc. Lond. A Math. Phys. Sci. 2003, 459, 2771–2786. [Google Scholar] [CrossRef]
- Gustafsson, T.; Rajagopal, K.R.; Stenberg, R.; Videman, J. Nonlinear Reynolds equation for hydrodynamic lubrication. Appl. Math. Model. 2015, 39, 5299–5309. [Google Scholar] [CrossRef]
- Fusi, L.; Farina, A.; Rosso, F.; Roscani, S. Pressure driven lubrication flow of a Bingham fluid in a channel: A novel approach. J. Non-Newton. Fluid Mech. 2015, 221, 66–75. [Google Scholar] [CrossRef]
- Rajagopal, K.R. Implicit constitutive relations for fluids. J. Fluid Mech. 2006, 550, 243–249. [Google Scholar] [CrossRef]
- Rajagopal, K.R.; Srinivasa, A.R. A Gibbs-potential-based formulation for obtaining the response functions for a class of viscoelastic materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 2011, 467, 39–58. [Google Scholar] [CrossRef]
- Nazarov, S.A.; Videman, J.H. A modified nonlinear Reynolds equation for thin viscous flows in lubrication. Asymptot. Anal. 2007, 52, 1–36. [Google Scholar]
- Rajagopal, K.R. Remarks on the notion of “pressure”. Int. J. Nonlinear Mech. 2015, 71, 165–172. [Google Scholar] [CrossRef]
- Málek, J. Mathematical properties of flows of incompressible power-law-like fluids that are described by implicit constitutive relations. Electron. Trans. Numer. Anal. 2008, 31, 110–125. [Google Scholar]
- Málek, J.; Rajagopal, K.R.; Ruzicka, M. Existence and regularity of solutions and stability of the rest state for fluids with shear dependent viscosity. Math. Model. Methods Appl. Sci. 1995, 6, 789–812. [Google Scholar] [CrossRef]
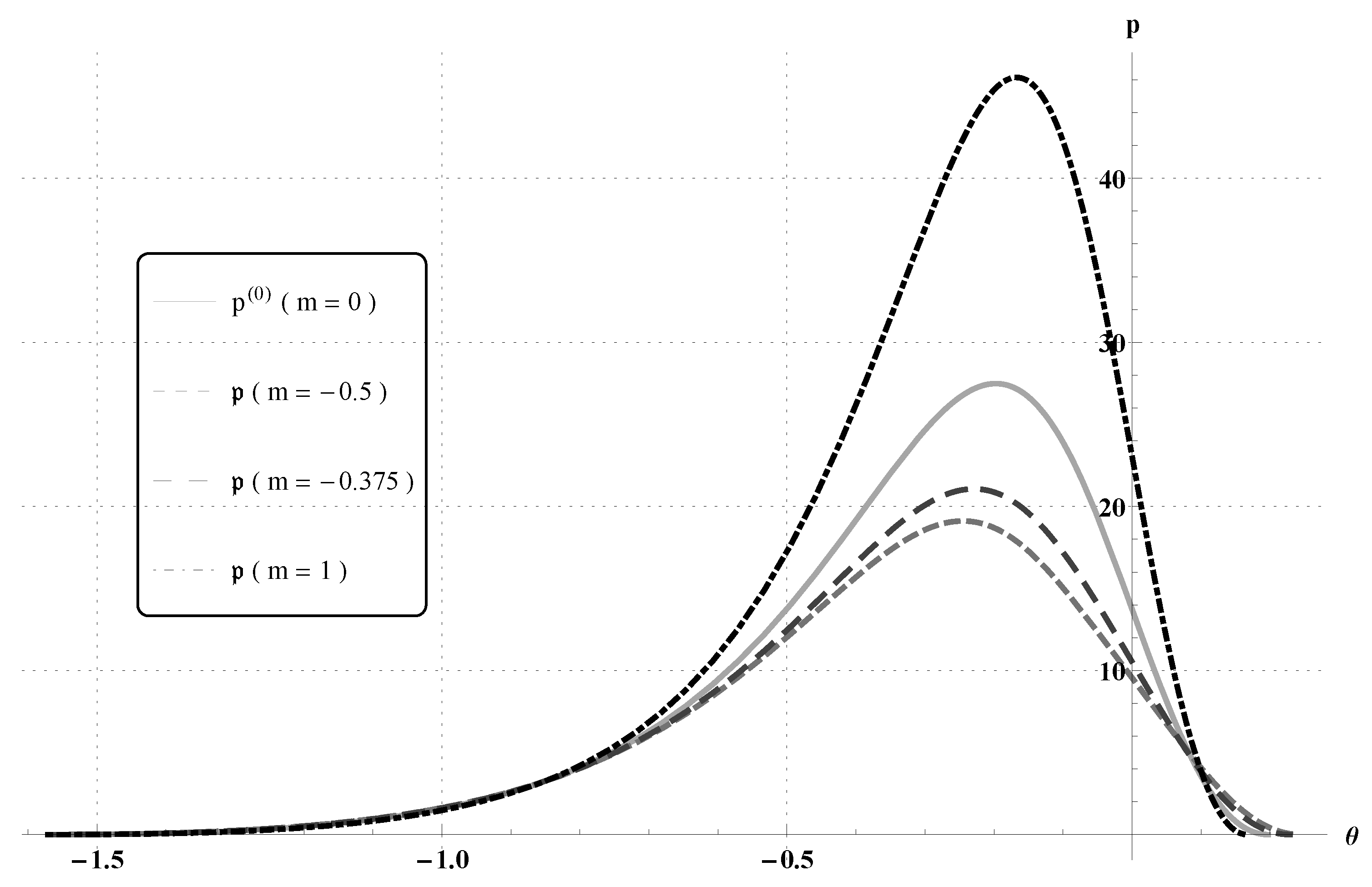
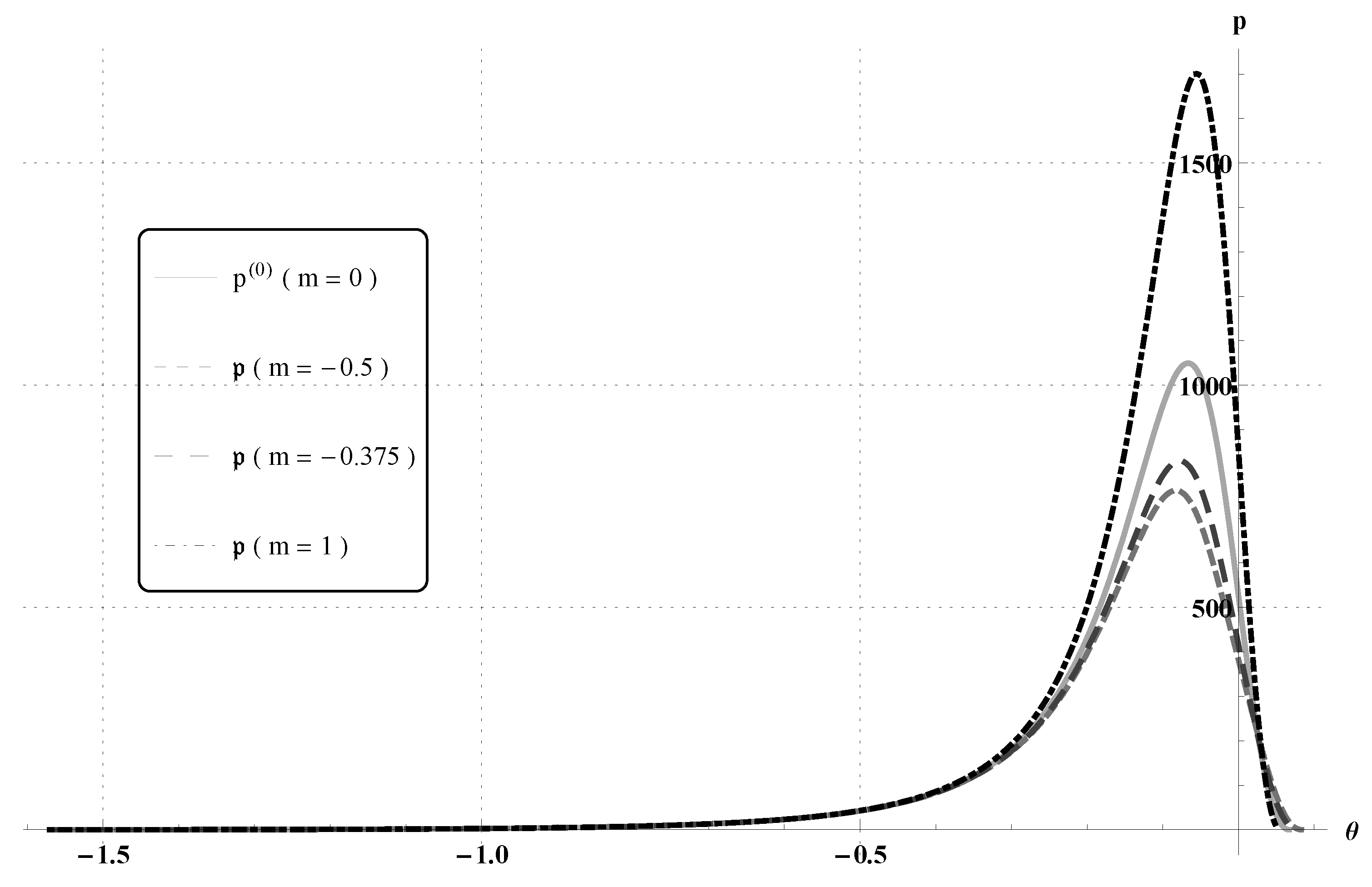
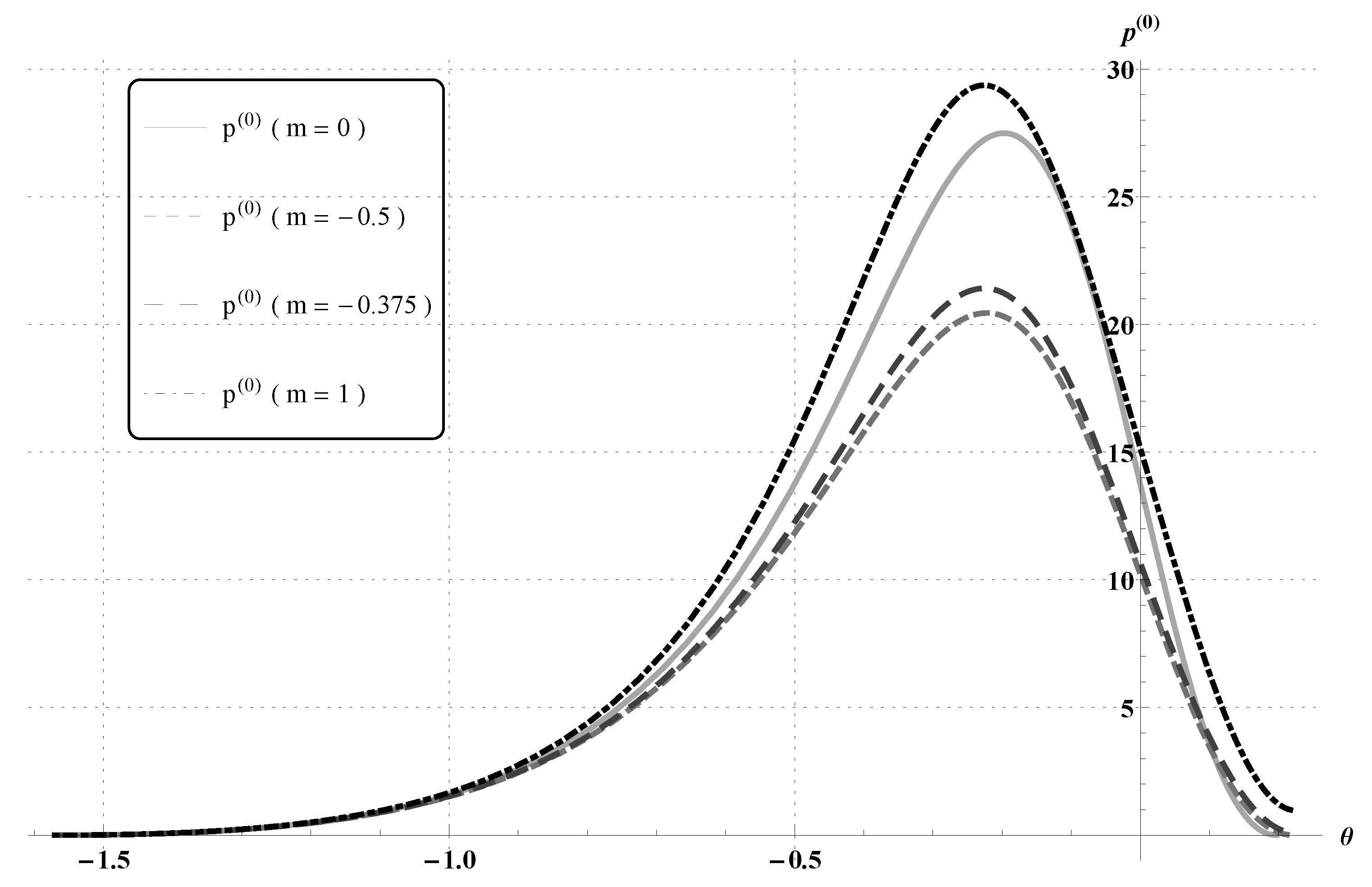

| m | (rad) | |
|---|---|---|
| −0.5 | 0.245119 | 10.7558 |
| −0.375 | 0.229178 | 11.5351 |
| 1 | 0.167257 | 20.8097 |
| m | (rad) | |
|---|---|---|
| −0.5 | 0.0827747 | 181.54 |
| −0.375 | 0.077616 | 191.168 |
| 1 | 0.0553576 | 306.272 |
| m | (rad) | |
|---|---|---|
| −0.5 | 0.221825 | 11.105 |
| −0.375 | 0.225363 | 11.5739 |
| 0 | 0.197408 | 13.985 |
| 1 | 0.227645 | 15.2337 |
| m | (rad) | |
|---|---|---|
| −0.5 | 0.0747584 | 189.875 |
| −0.375 | 0.0760101 | 194.649 |
| 0 | 0.0666264 | 221.456 |
| 1 | 0.0774216 | 233.142 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, B.M.M.; Dias, G.A.S.; Cal, F.S.; Rajagopal, K.R.; Videman, J.H. Lubrication Approximation for Fluids with Shear-Dependent Viscosity. Fluids 2019, 4, 98. https://doi.org/10.3390/fluids4020098
Pereira BMM, Dias GAS, Cal FS, Rajagopal KR, Videman JH. Lubrication Approximation for Fluids with Shear-Dependent Viscosity. Fluids. 2019; 4(2):98. https://doi.org/10.3390/fluids4020098
Chicago/Turabian StylePereira, Bruno M.M., Gonçalo A.S. Dias, Filipe S. Cal, Kumbakonam R. Rajagopal, and Juha H. Videman. 2019. "Lubrication Approximation for Fluids with Shear-Dependent Viscosity" Fluids 4, no. 2: 98. https://doi.org/10.3390/fluids4020098
APA StylePereira, B. M. M., Dias, G. A. S., Cal, F. S., Rajagopal, K. R., & Videman, J. H. (2019). Lubrication Approximation for Fluids with Shear-Dependent Viscosity. Fluids, 4(2), 98. https://doi.org/10.3390/fluids4020098





