Application of a Projection Method for Simulating Flow of a Shear-Thinning Fluid
Abstract
1. Introduction
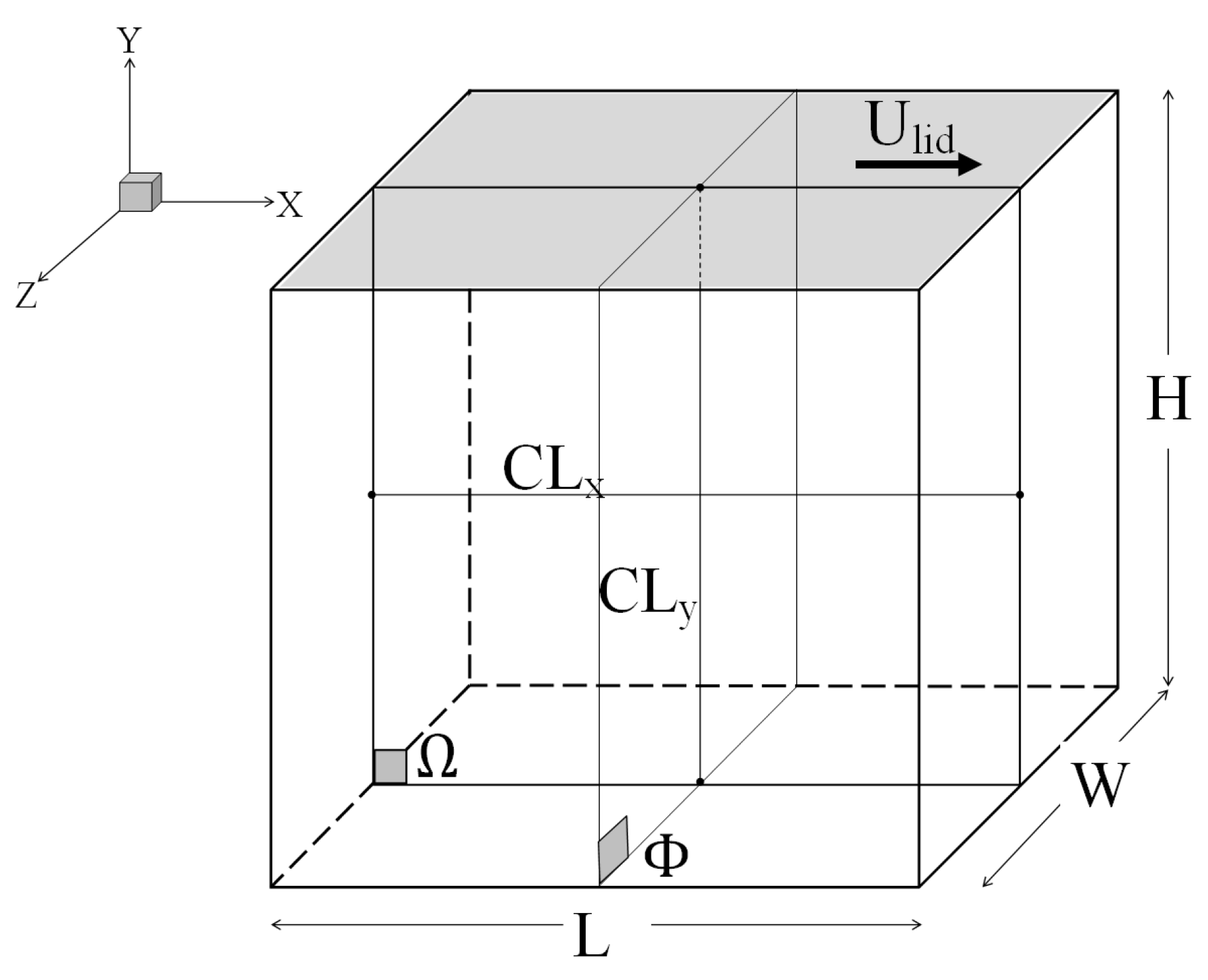
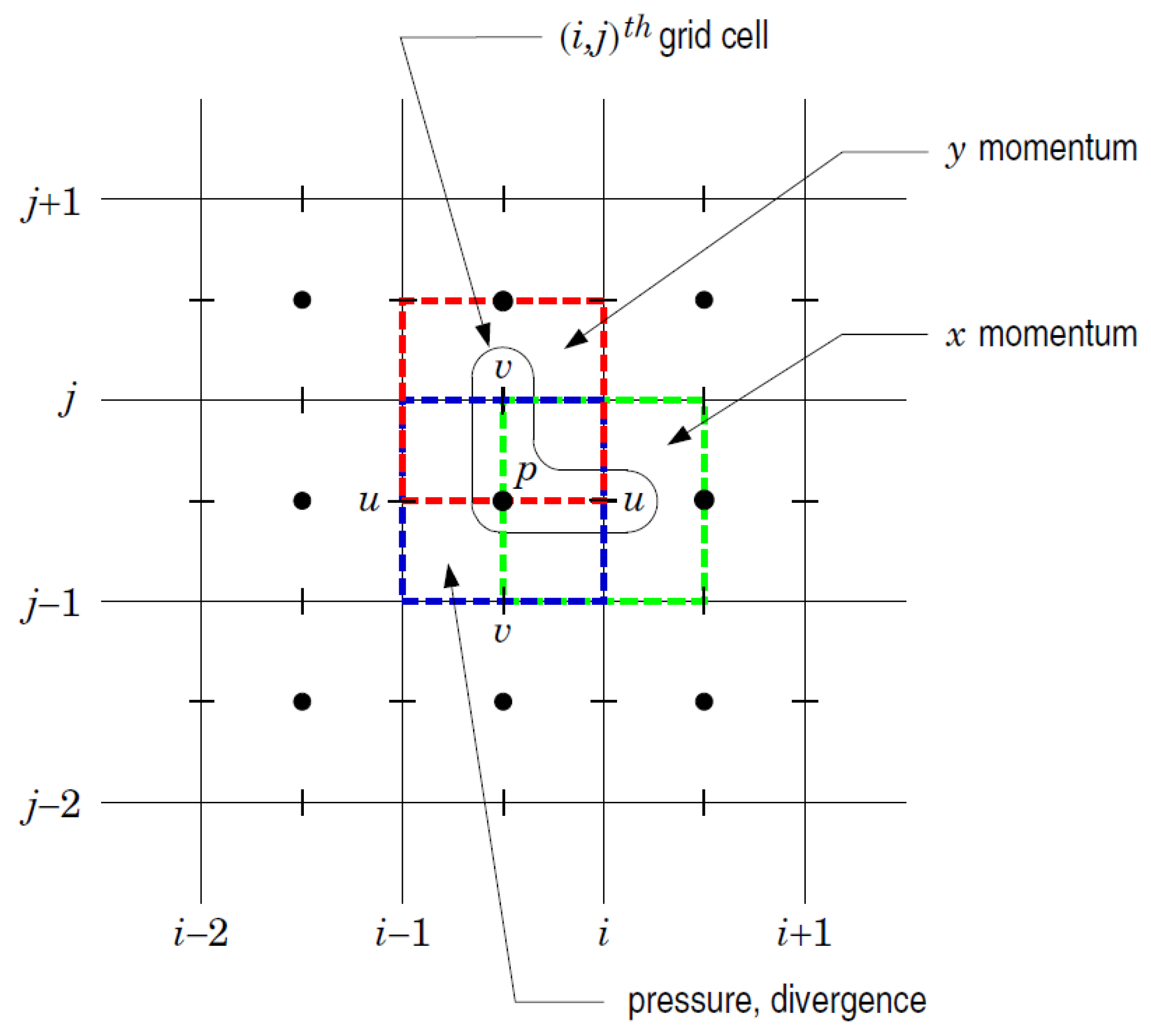
2. Mathematical Model
3. Results and Discussion
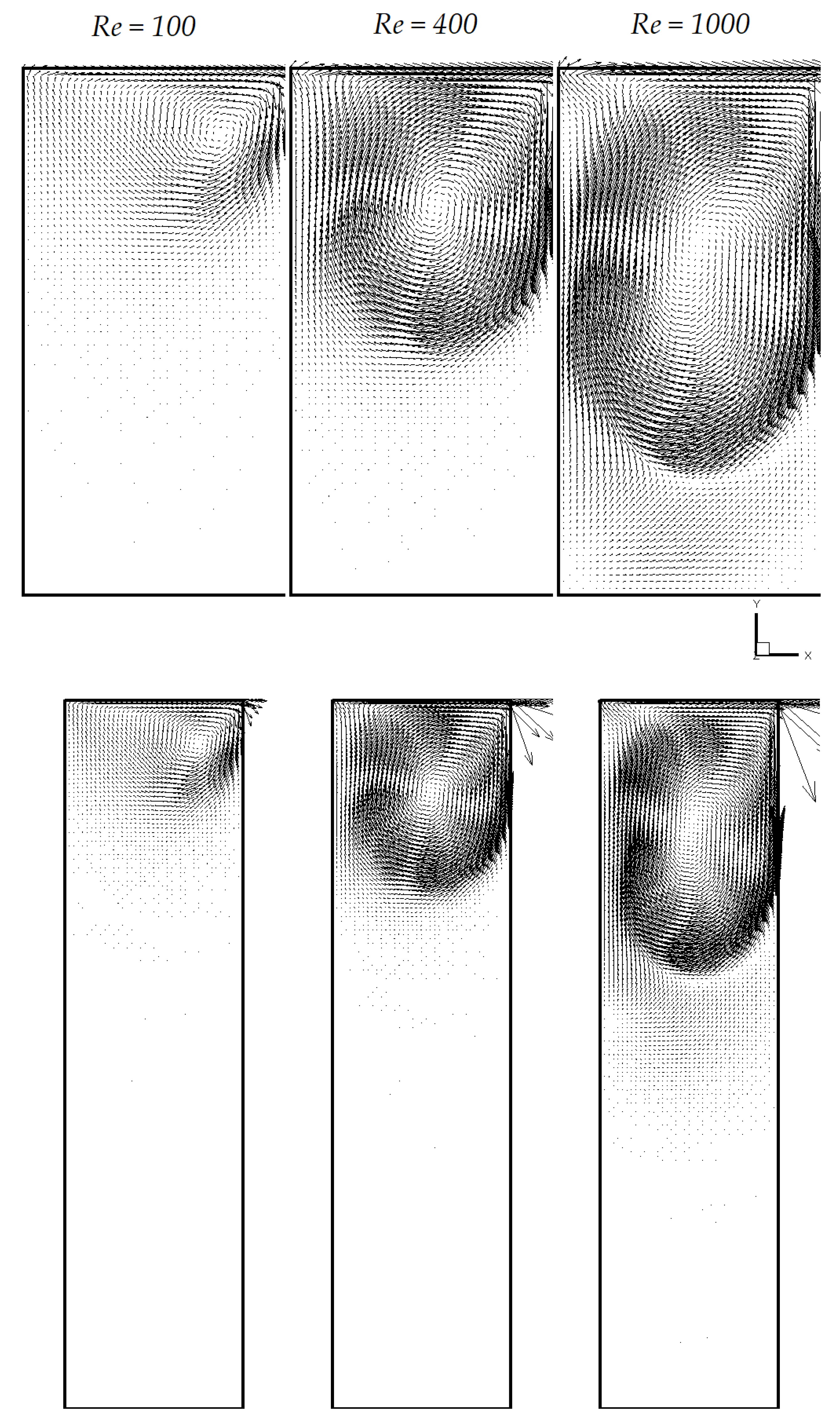
3.1. Code Validation for Newtonian Fluid
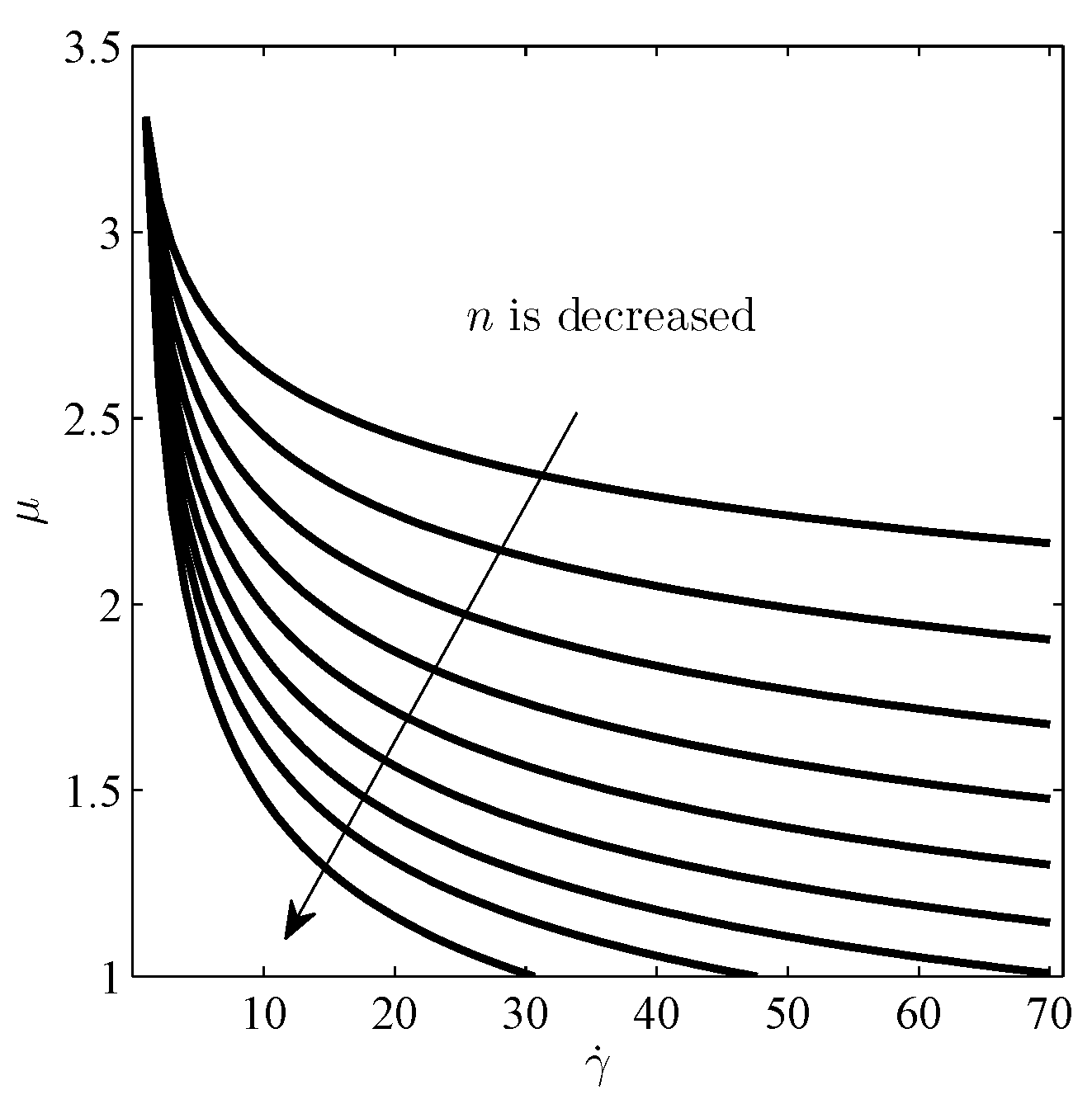
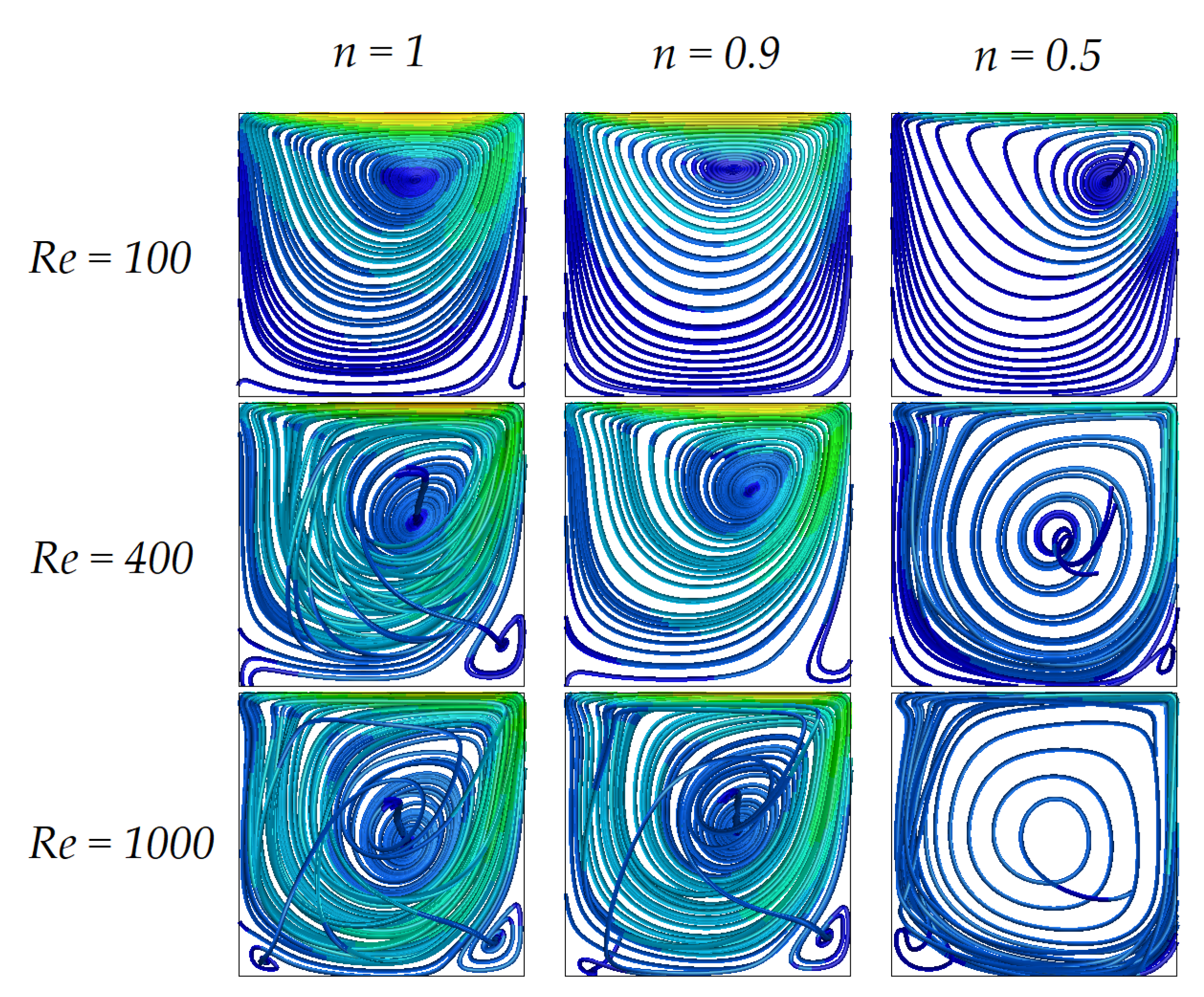
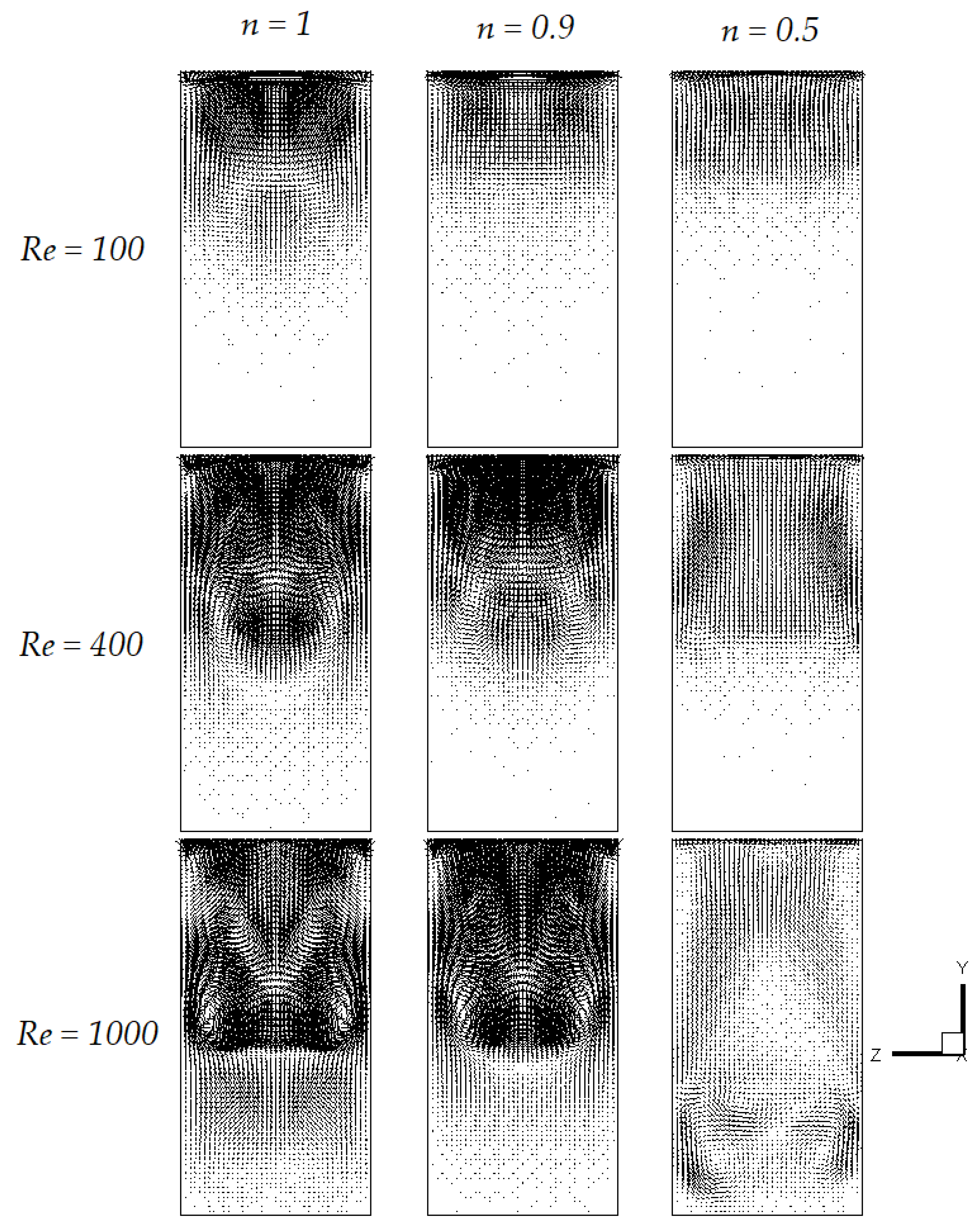
3.2. Shear-Thinning Fluid
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shankar, P.; Deshpande, M. Fluid Mechanics in the Driven Cavity. Annu. Rev. Fluid Mech. 2000, 32, 93–136. [Google Scholar] [CrossRef]
- Shuja, S.; Yilbas, B.; Iqbal, M. Mixed Convection in a Square Cavity due to Heat Generating Rectangular Body: Effect of Cavity Exit Port Locations. Int. J. Numer. Methods Heat Fluid Flow 2000, 10, 824–841. [Google Scholar] [CrossRef]
- Wong, J.C.F. Numerical Simulation of Two-dimensional Laminar Mixed-convection in a Lid-driven Cavity Using the Mixed Finite Element Consistent Splitting Scheme. Int. J. Numer. Methods Heat Fluid Flow 2007, 17, 46–93. [Google Scholar] [CrossRef]
- Aidun, C.K.; Triantafillopoulos, N.; Benson, J. Global Stability of a Lid-driven Cavity with Throughflow: Flow Visualization Studies. Phys. Fluids A 1991, 3, 2081–2091. [Google Scholar] [CrossRef]
- Jana, S.C.; Metcalfe, G.; Ottino, J. Experimental and Computational Studies of Mixing in Complex Stokes Flows: The Vortex Mixing Flow and Multicellular Cavity Flows. J. Fluid Mech. 1994, 269, 199–246. [Google Scholar] [CrossRef]
- Alleborn, N.; Raszillier, H.; Durst, F. Lid-driven Cavity with Heat and Mass Transport. Int. J. Heat Mass Trans. 1999, 42, 833–853. [Google Scholar] [CrossRef]
- Mills, R.D. On the Closed Motion of a Fluid in a Square Cavity. J. R. Aeronaut. Soc. 1965, 69, 116–120. [Google Scholar] [CrossRef]
- Pan, F.; Acrivos, A. Steady flows in rectangular cavities. J. Fluid Mech. 1967, 28, 643–655. [Google Scholar] [CrossRef]
- Koseff, J.; Street, R. Visualization Studies of a Shear Driven Three-dimensional Recirculating Flow. J. Fluid Eng. 1984, 106, 21–27. [Google Scholar] [CrossRef]
- Koseff, J.; Street, R. The lid-driven cavity flow: A synthesis of qualitative and quantitative observations. J. Fluid Eng. 1984, 106, 390–398. [Google Scholar] [CrossRef]
- de Vahl Davis, G.; Mallinson, G. An Evaluation of Upwind and Central Difference Approximations by a Study of Recirculating Flow. Comput. Fluids 1976, 4, 29–43. [Google Scholar] [CrossRef]
- Schreiber, R.; Keller, H.B. Driven Cavity Flows by Efficient Numerical Techniques. J. Comput. Phys. 1983, 49, 310–333. [Google Scholar] [CrossRef]
- Ku, H.C.; Hirsh, R.S.; Taylor, T.D. A Pseudospectral Method for Solution of the Three-dimensional Incompressible Navier–Stokes Equations. J. Comput. Phys. 1987, 70, 439–462. [Google Scholar] [CrossRef]
- Iwatsu, R.; Ishii, K.; Kawamura, T.; Kuwahara, K.; Hyun, J.M. Numerical Simulation of Three-dimensional Flow structure in a Driven Cavity. Fluid Dyn. Res. 1989, 5, 173. [Google Scholar] [CrossRef]
- Chiang, T.; Sheu, W.; Hwang, R.R. Effect of Reynolds Number on the Eddy Structure in a Lid-driven Cavity. Int. J. Numer Methods Fluids 1998, 26, 557–579. [Google Scholar] [CrossRef]
- Ghia, U.; Ghia, K.N.; Shin, C. High-Re Solutions for Incompressible Flow Using the Navier–Stokes Equations and a Multigrid Method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]
- Albensoeder, S.; Kuhlmann, H.; Rath, H. Three-dimensional Centrifugal-flow Instabilities in the Lid-driven-cavity Problem. Phys. Fluids 2001, 13, 121–135. [Google Scholar] [CrossRef]
- Leriche, E.; Gavrilakis, S. Direct Numerical Simulation of the Flow in a Lid-driven Cubical Cavity. Phys. Fluids 2000, 12, 1363–1376. [Google Scholar] [CrossRef]
- De, S.; Nagendra, K.; Lakshmisha, K. Simulation of Laminar Flow in a Three-dimensional Lid-driven Cavity by Lattice Boltzmann Method. Int. J. Numer. Method Heat Fluid Flow 2009, 19, 790–815. [Google Scholar] [CrossRef]
- Tanner, R.I.; Walters, K. Rheology: An Historical Perspective; Elsevier: Amsterdam, The Netherlands, 1998; Volume 7. [Google Scholar]
- Reid, R.C.; Prausnitz, J.M.; Poling, B.E. The Properties of Gases and Liquids; McGraw Hill Book Co.: New York, NY, USA, 1987. [Google Scholar]
- Blackery, J.; Mitsoulis, E. Creeping Motion of a Sphere in Tubes Filled with a Bingham Plastic Material. J. Non-Newton. Fluid Mech. 1997, 70, 59–77. [Google Scholar] [CrossRef]
- Beaulne, M.; Mitsoulis, E. Creeping Motion of a Sphere in Tubes Filled with Herschel-Bulkley Fluids. J. Non-Newton. Fluid Mech. 1997, 72, 55–71. [Google Scholar] [CrossRef]
- Mitsoulis, E. Numerical Simulation of Confined Flow of Polyethylene Melts Around a Cylinder in a Planar Channel. J. Non-Newton. Fluid Mech. 1998, 76, 327–350. [Google Scholar] [CrossRef]
- Missirlis, K.; Assimacopoulos, D.; Mitsoulis, E.; Chhabra, R. Wall Effects for Motion of Spheres in Power-law Fluids. J. Non-Newton. Fluid Mech. 2001, 96, 459–471. [Google Scholar] [CrossRef]
- Mitsoulis, E.; Zisis, T. Flow of Bingham Plastics in a Lid-driven Square Cavity. J. Non-Newton. Fluid Mech. 2001, 101, 173–180. [Google Scholar] [CrossRef]
- Chatzimina, M.; Xenophontos, C.; Georgiou, G.; Argyropaidas, I.; Mitsoulis, E. Cessation of Annular Poiseuille Flows of Bingham Plastics. J. Non-Newton. Fluid Mech. 2007, 142, 135–142. [Google Scholar] [CrossRef]
- Mitsoulis, E.; Hatzikiriakos, S. Steady Flow Simulations of Compressible PTFE Paste Extrusion Under Severe Wall Slip. J. Non-Newton. Fluid Mech. 2009, 157, 26–33. [Google Scholar] [CrossRef]
- Muravleva, L.; Muravleva, E.; Georgiou, G.; Mitsoulis, E. Numerical Simulations of Cessation Flows of a Bingham Plastic with the Augmented Lagrangian Method. J. Non-Newton. Fluid Mech. 2010, 165, 544–550. [Google Scholar] [CrossRef]
- Jabbari, M.; Bulatova, R.; Hattel, J.; Bahl, C. Quasi–steady State Power Law Model for the Flow of (La0.85Sr0.15)0.9MnO3 Ceramic Slurry in Tape Casting. Mater. Sci. Technol. 2013, 29, 1080–1087. [Google Scholar] [CrossRef]
- Jabbari, M.; Hattel, J. Numerical Modeling of the Side Flow in Tape Casting of a Non-Newtonian Fluid. J. Am. Ceram. Soc. 2013, 96, 1414–1420. [Google Scholar] [CrossRef]
- Jabbari, M.; Bulatova, R.; Hattel, J.; Bahl, C. An Evaluation of Interface Capturing Methods in a VOF Based Model for Multiphase Flow of a Non-Newtonian Ceramic in Tape Casting. App. Math. Model. 2014, 38, 3222–3232. [Google Scholar] [CrossRef]
- Jabbari, M.; Spangenberg, J.; Hattel, J. Particle Migration Using Local Variation of the Viscosity (LVOV) Model in Flow of a Non-Newtonian Fluid for Ceramic Tape Casting. Chem. Eng. Res. Des. 2016, 109, 226–233. [Google Scholar] [CrossRef]
- Pakdel, P.; Spiegelberg, S.; McKinley, G. Cavity Flows of Elastic Liquids: Two-dimensional Flows. Phys. Fluids 1997, 9, 3123–3140. [Google Scholar] [CrossRef]
- Pakdel, P.; McKinley, G. Cavity Flows of Elastic Liquids: Purely Elastic Instabilities. Phys. Fluids 1998, 10, 1058–1070. [Google Scholar] [CrossRef]
- Yapici, K.; Karasozen, B.; Uludag, Y. Finite Volume Simulation of Viscoelastic Laminar Flow in a Lid-driven Cavity. J. Non-Newton. Fluid Mech. 2009, 164, 51–65. [Google Scholar] [CrossRef]
- Rafiee, A. Modelling of Generalized Newtonian Lid-Driven Cavity Flow Using An SPH Method. ANZIAM J. 2008, 49, 411–422. [Google Scholar] [CrossRef]
- Shamekhi, A.; Sadeghy, K. Cavity Flow Simulation of Carreau-Yasuda Non-Newtonian Fluids Using PIM Meshfree Method. Appl. Math. Model. 2009, 33, 4131–4145. [Google Scholar] [CrossRef]
- Shamekhi, A.; Sadeghy, K. A Numerical Method for Solving Incompressible Viscous Flow Problems. Appl. Math. Model. 1967, 2, 12–26. [Google Scholar]
- Bell, J.; Colella, P.; Glaz, H. A Second-Order Projection Method for the Incompressible Navier–Stokes Equations. J. Comput. Phys. 1989, 85, 257–283. [Google Scholar] [CrossRef]
- Gresho, P. On the Theory of Semi-implicit Projection Methods for Viscous Incompressible Flow and its Implementation via a Finite Element Method that also Introduces a Nearly Consistent Mass Matrix. Part 1: Theory. Int. J. Numer. Methods Fluids 1990, 11, 587–620. [Google Scholar] [CrossRef]
- Douglas, J.; Gunn, J. A General Formulation of Alternating Direction Method Part I. Parabolic and Hyperbolic Problems. Numer. Math. 1964, 6, 428–453. [Google Scholar] [CrossRef]
- Foias, C.; Manley, O.; Rosa, R.; Temam, R. Navier–Stokes Equations and Turbulence; Cambridge University Press: Cambridge, UK, 2001; Volume 83. [Google Scholar]
- McDonough, J.M. Lectures in Computational Fluid Dynamics of Incompressible Flow: Mathematics, Algorithms and Implementations; Lecture Notes for ME 691; Department of Mechanical Engineering, University of Kentucky: Lexington, KY, USA, 2013. [Google Scholar]
- Gnedin, N.; Semenov, V.; Kravtsov, A. Enforcing the Courant–Friedrichs–Lewy Condition in Explicitly Conservative Local Time Stepping Schemes. J. Comput. Phys. 2018, 359, 93–105. [Google Scholar] [CrossRef]
- Mitsoulis, E. Flows of Viscoplastic Materials: Models and Computations. Rheol. Rev. 2007, 2007, 135–178. [Google Scholar]
- Albensoeder, S.; Kuhlmann, H. Accurate Three-dimensional Lid-driven Cavity Flow. J. Comput. Phys. 2005, 206, 536–558. [Google Scholar] [CrossRef]
- Neofytou, P. A 3rd Order Upwind Finite Volume Method for Generalised Newtonian Fluid Flows. Adv. Eng. Softw. 2005, 36, 664–680. [Google Scholar] [CrossRef]
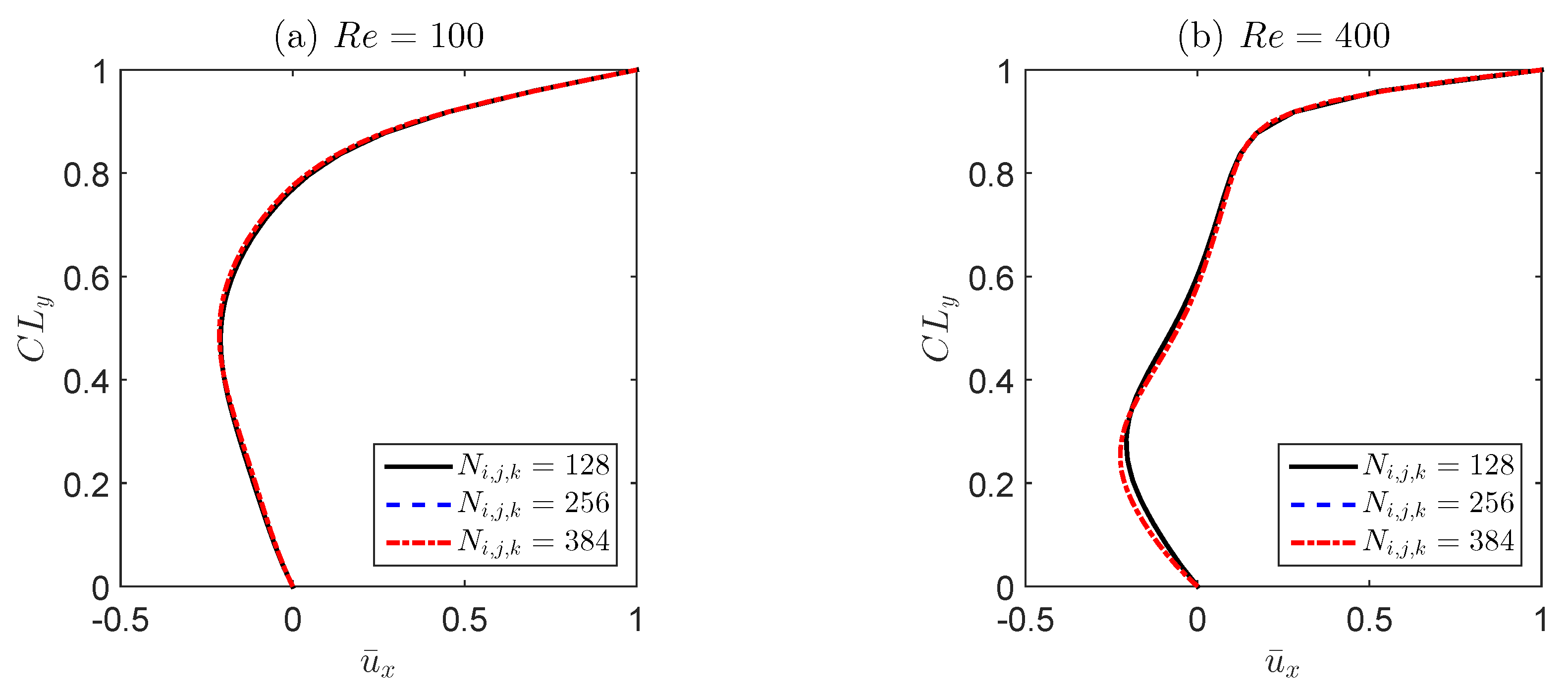
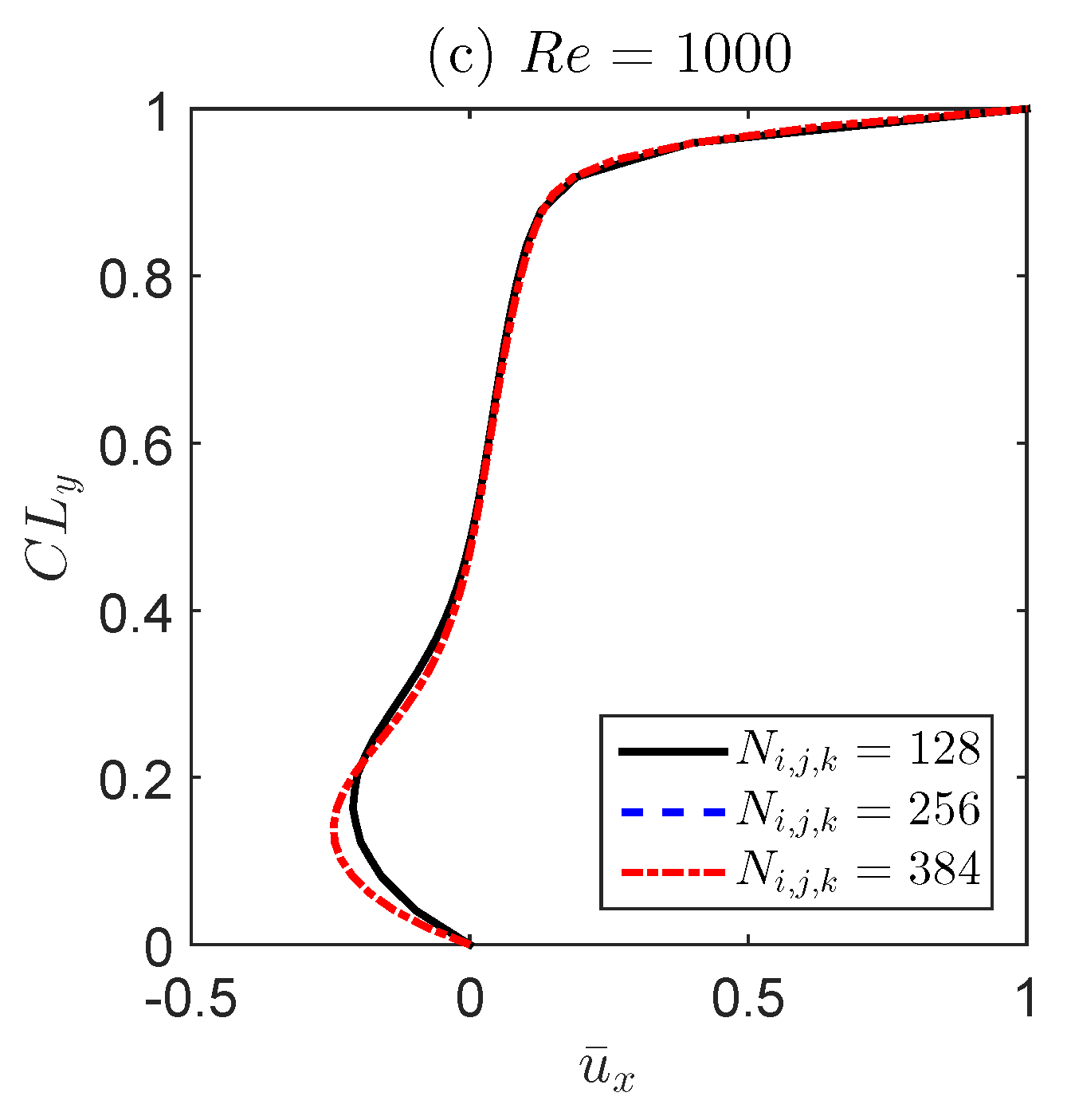
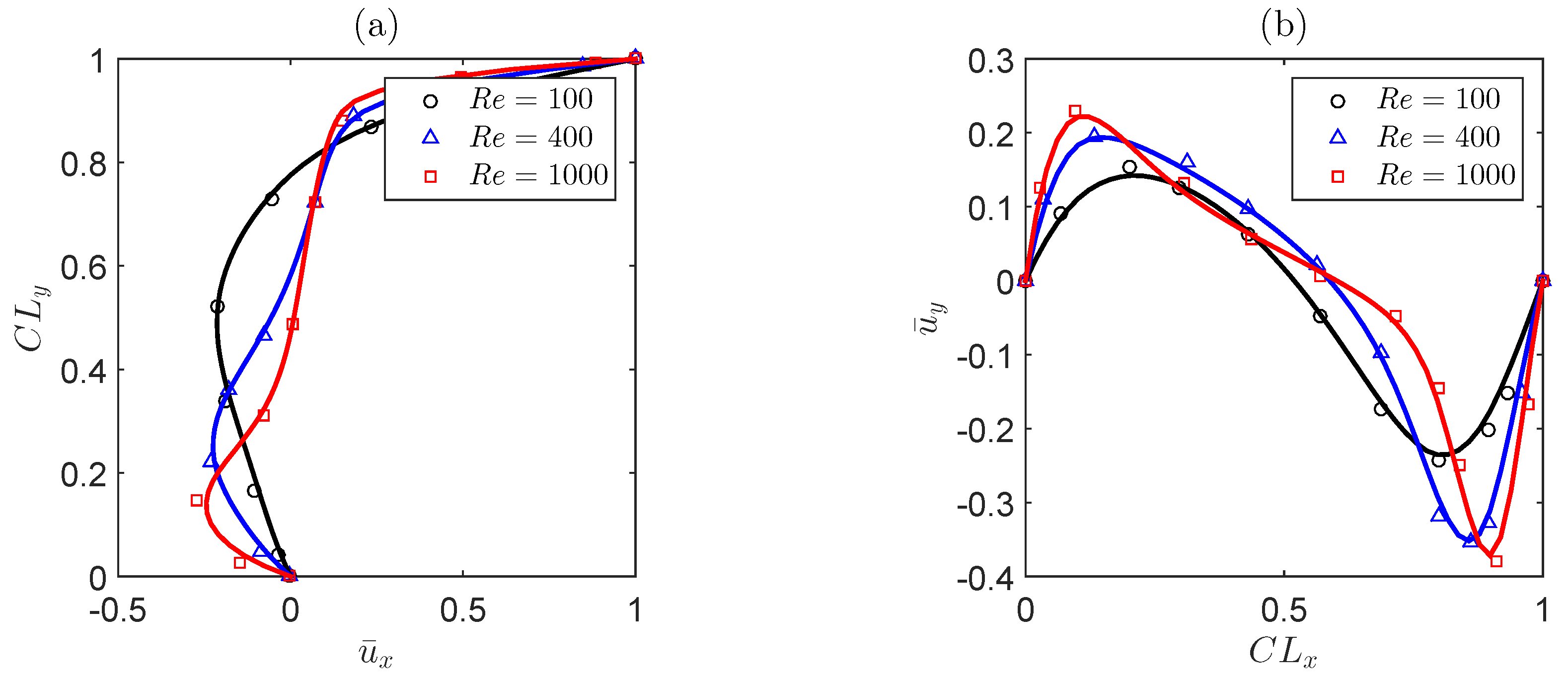
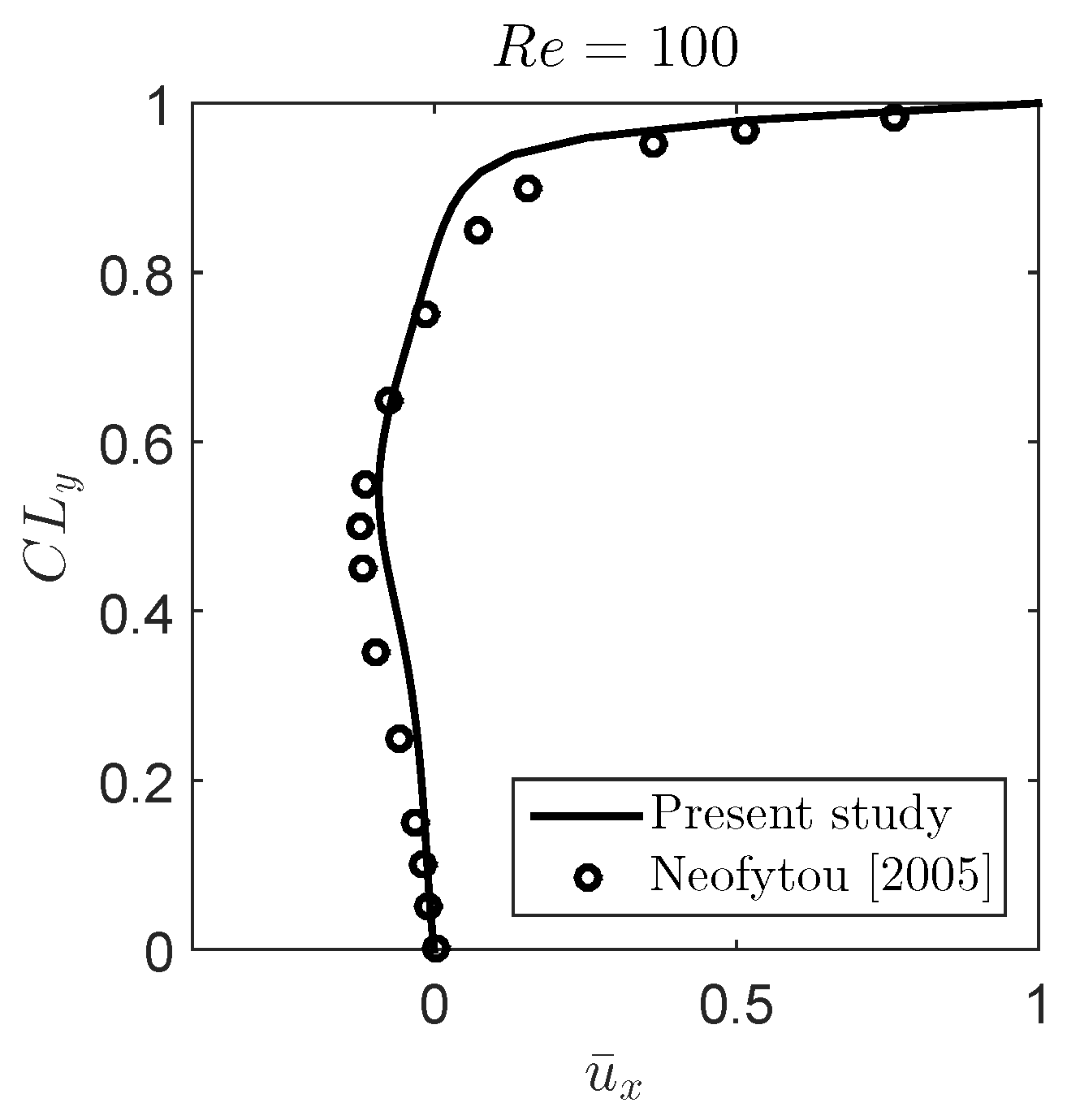

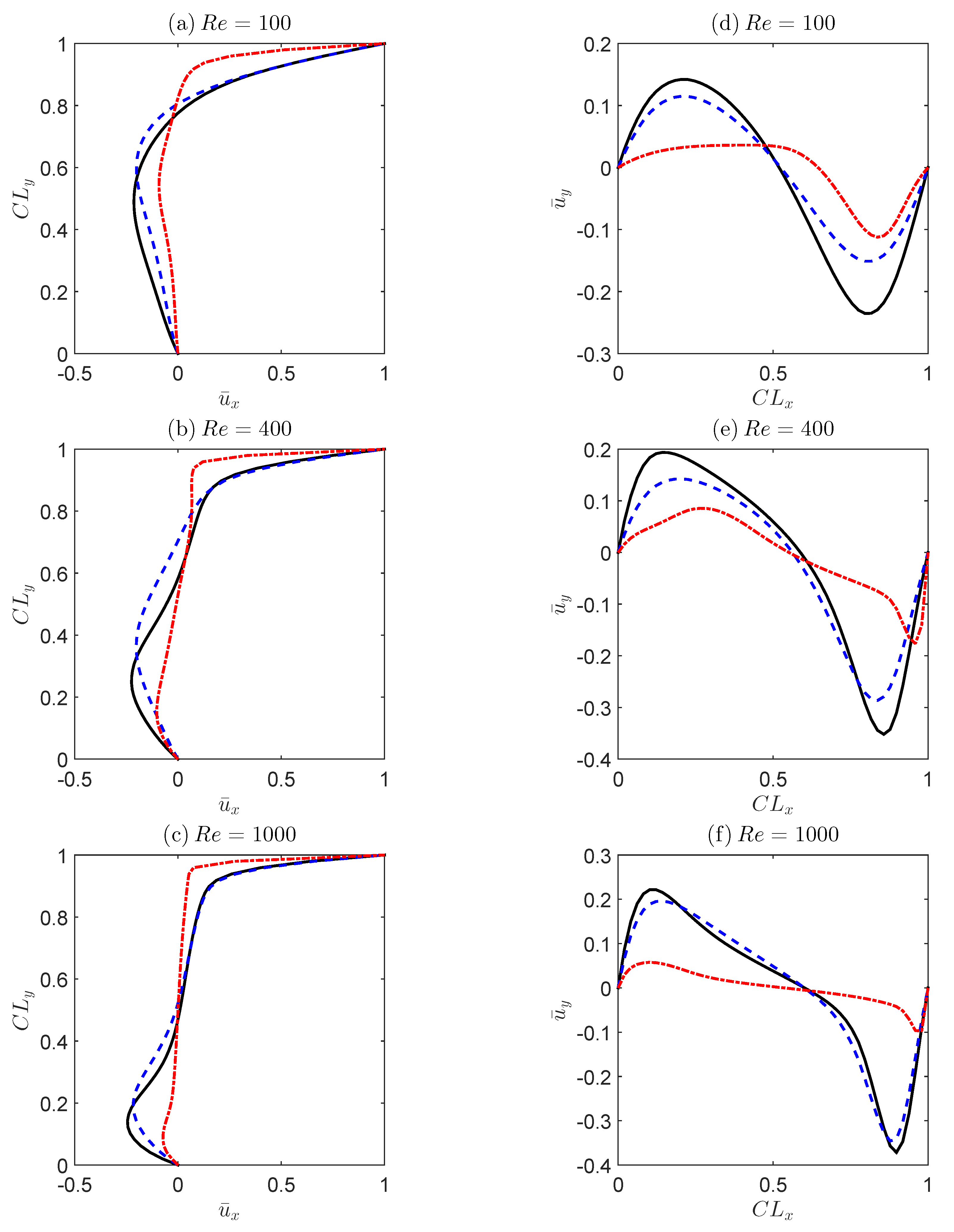

| = 100 | |||
| = 400 | |||
| = 1000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jabbari, M.; McDonough, J.; Mitsoulis, E.; Hattel, J.H. Application of a Projection Method for Simulating Flow of a Shear-Thinning Fluid. Fluids 2019, 4, 124. https://doi.org/10.3390/fluids4030124
Jabbari M, McDonough J, Mitsoulis E, Hattel JH. Application of a Projection Method for Simulating Flow of a Shear-Thinning Fluid. Fluids. 2019; 4(3):124. https://doi.org/10.3390/fluids4030124
Chicago/Turabian StyleJabbari, Masoud, James McDonough, Evan Mitsoulis, and Jesper Henri Hattel. 2019. "Application of a Projection Method for Simulating Flow of a Shear-Thinning Fluid" Fluids 4, no. 3: 124. https://doi.org/10.3390/fluids4030124
APA StyleJabbari, M., McDonough, J., Mitsoulis, E., & Hattel, J. H. (2019). Application of a Projection Method for Simulating Flow of a Shear-Thinning Fluid. Fluids, 4(3), 124. https://doi.org/10.3390/fluids4030124





