Quantum Mechanical and Optical Analogies in Surface Gravity Water Waves
Abstract
1. Introduction
2. Mathematical Introduction
2.1. Governing Equations
2.2. The Schrödinger Equation Describing the Evolution of Linear Wavepackets of Various Physical Nature
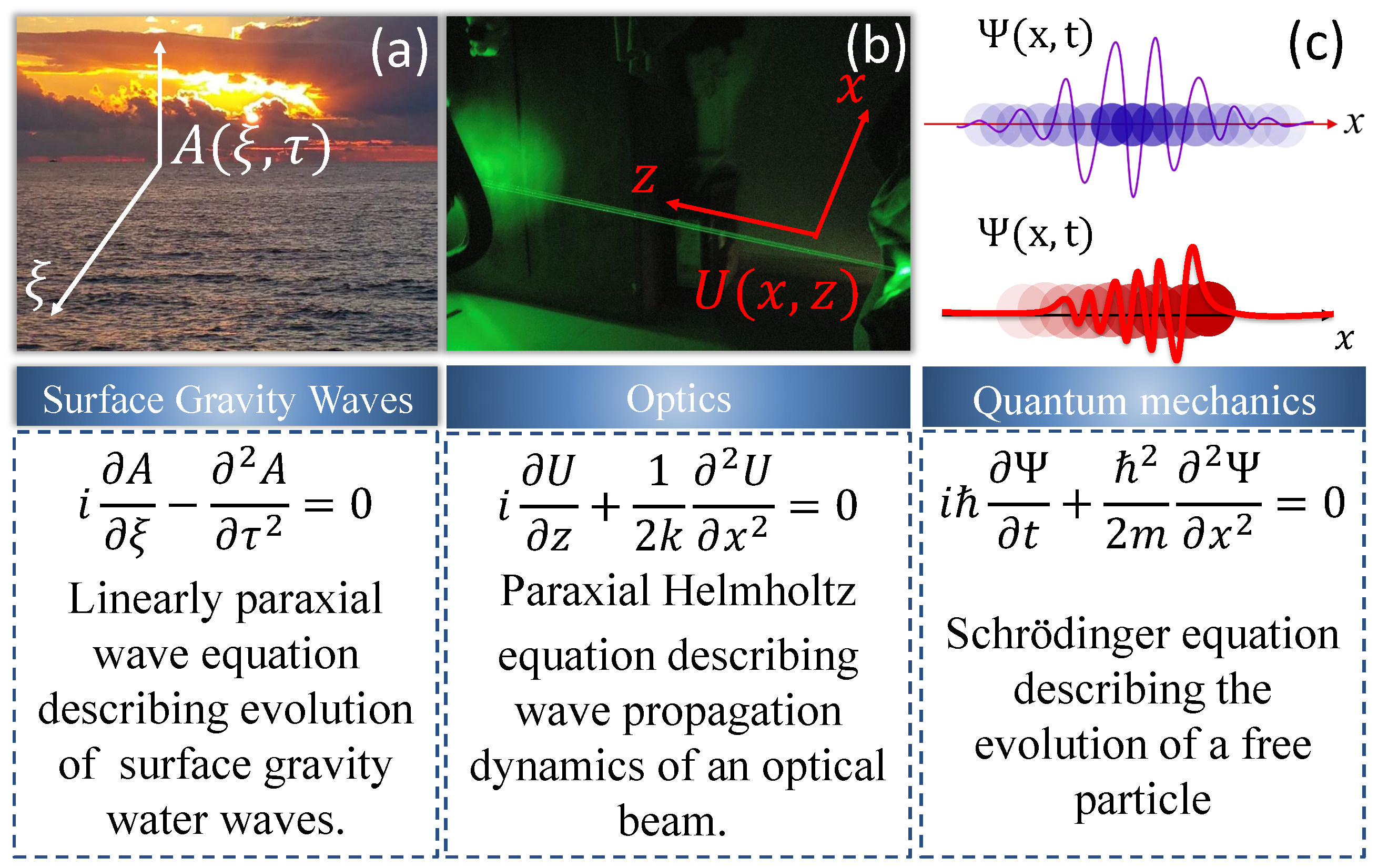
2.2.1. The Schrödinger Equation in Quantum Mechanics
2.2.2. The Schrödinger Equation in Optics
2.2.3. Linear Schrödinger Equation For Narrow-Banded Surface Gravity Waves
2.3. Wavepackets
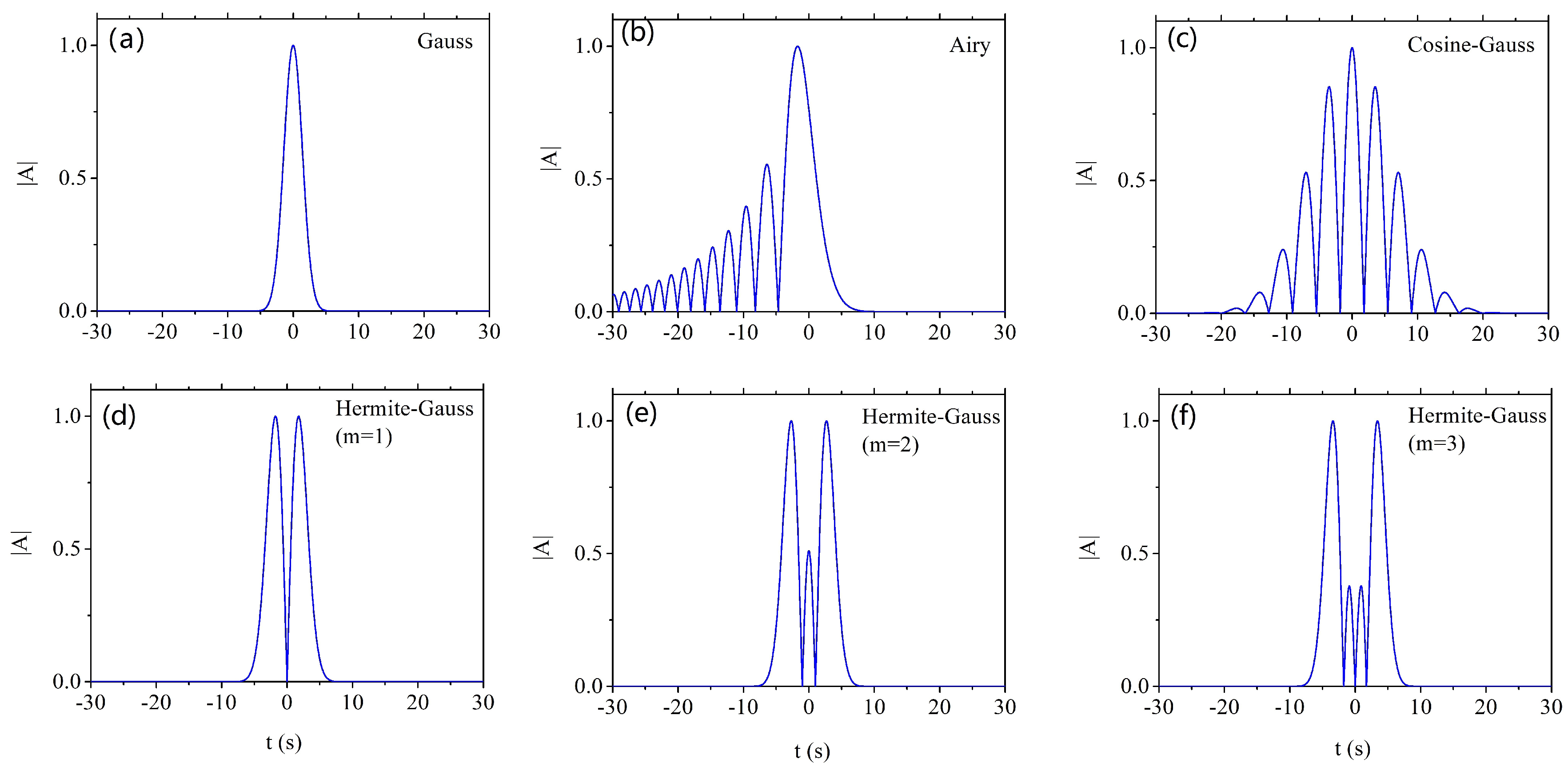
2.3.1. Gaussian Wavepackets
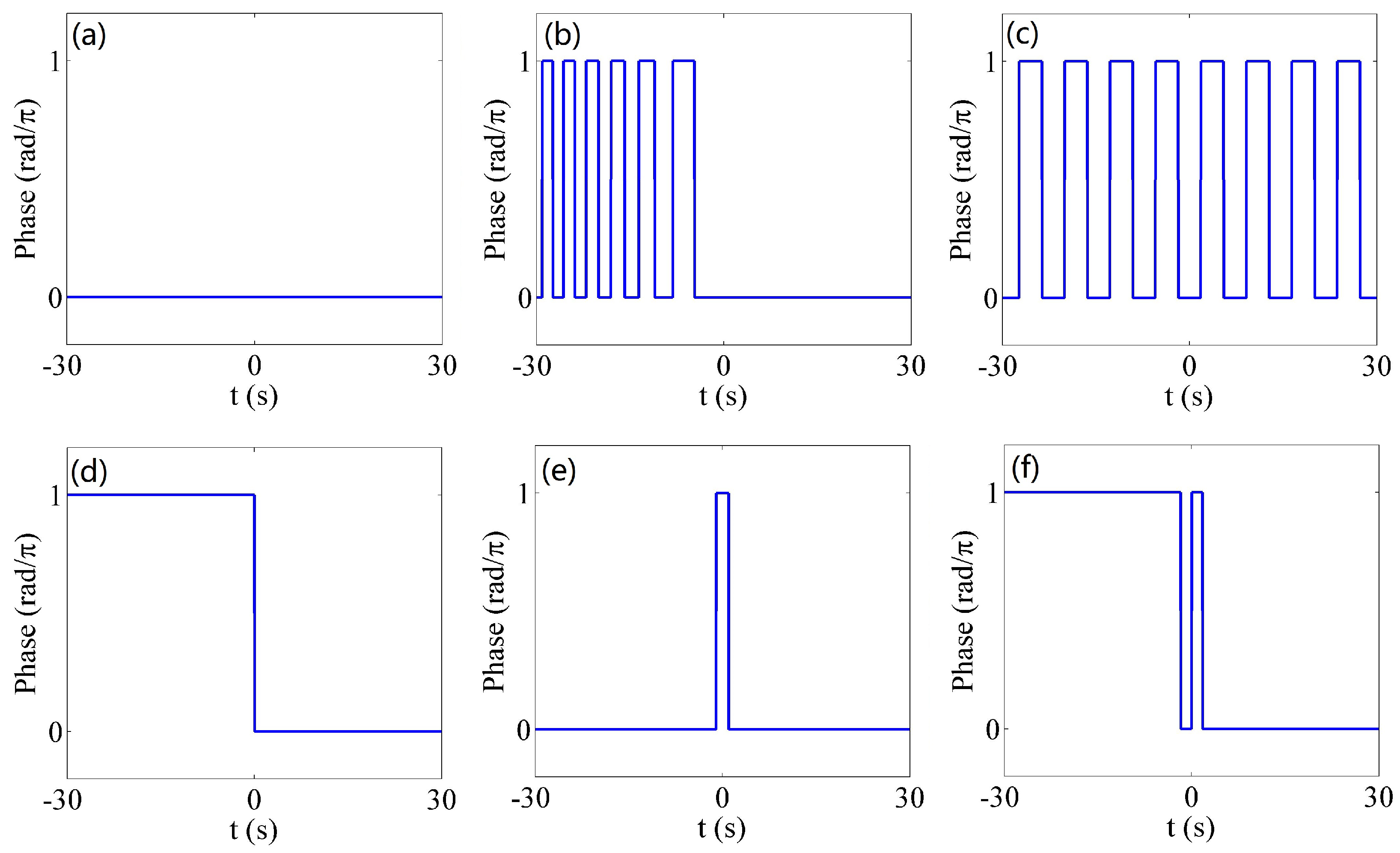
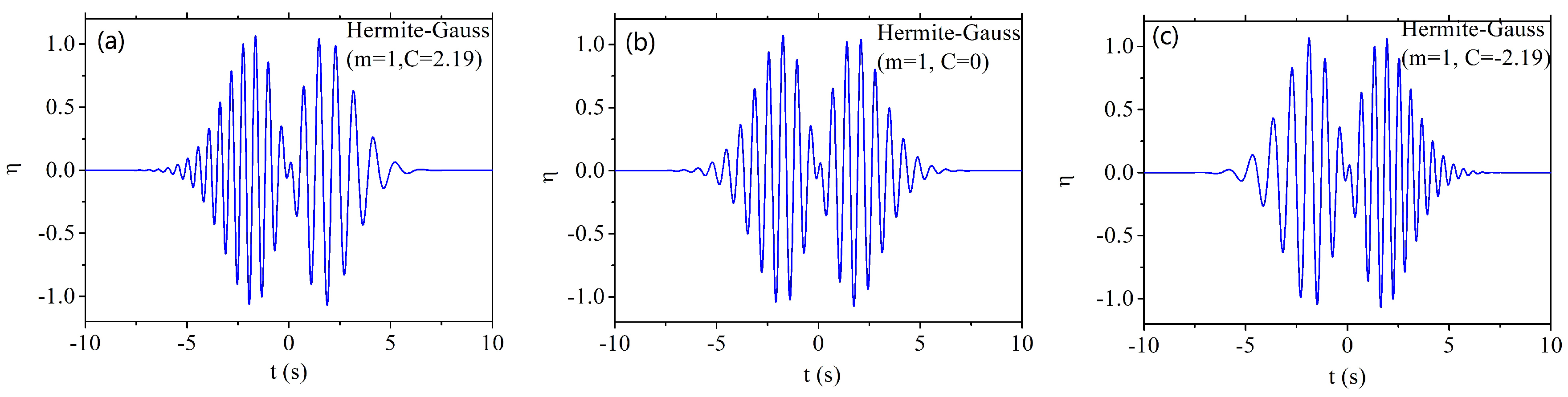
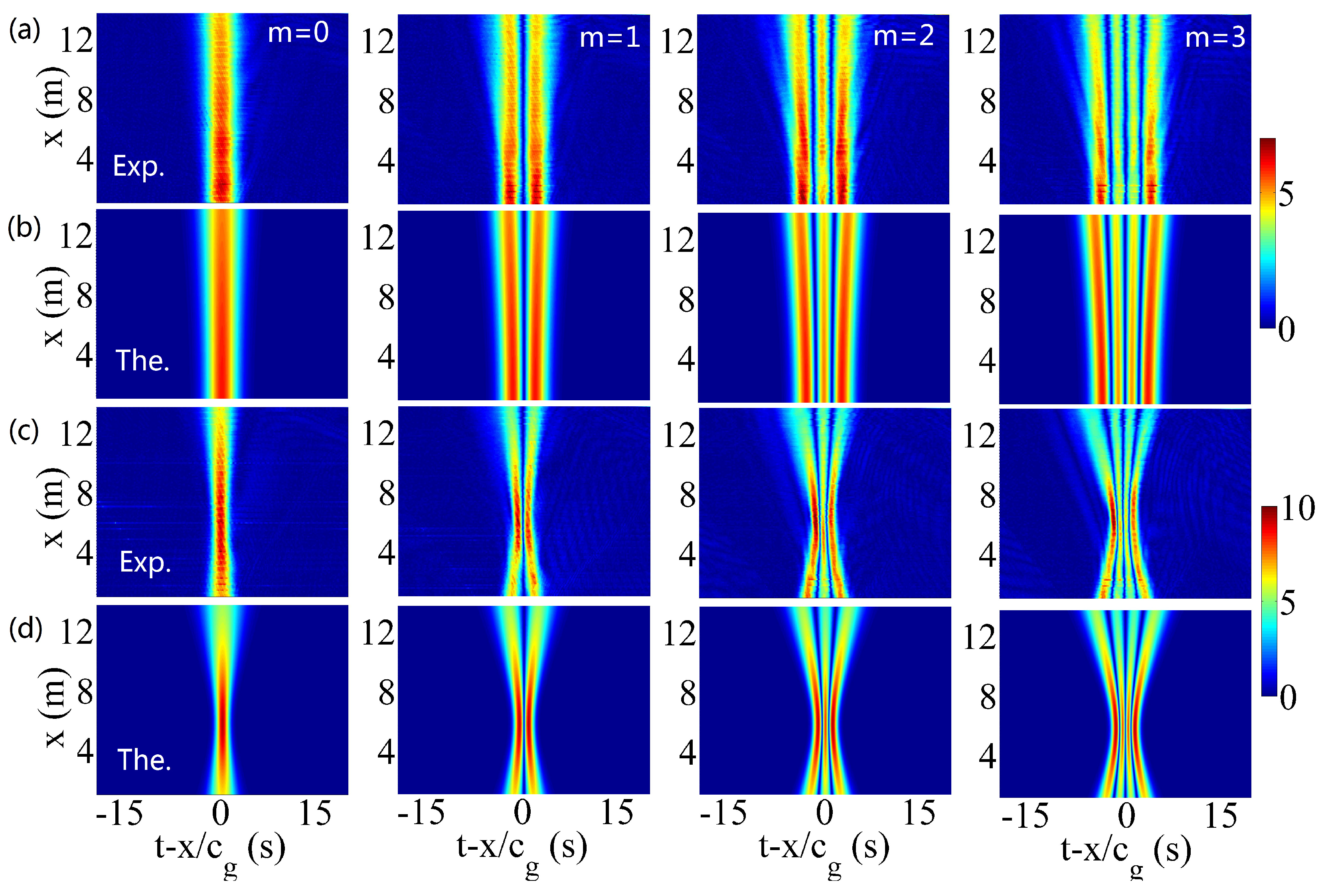
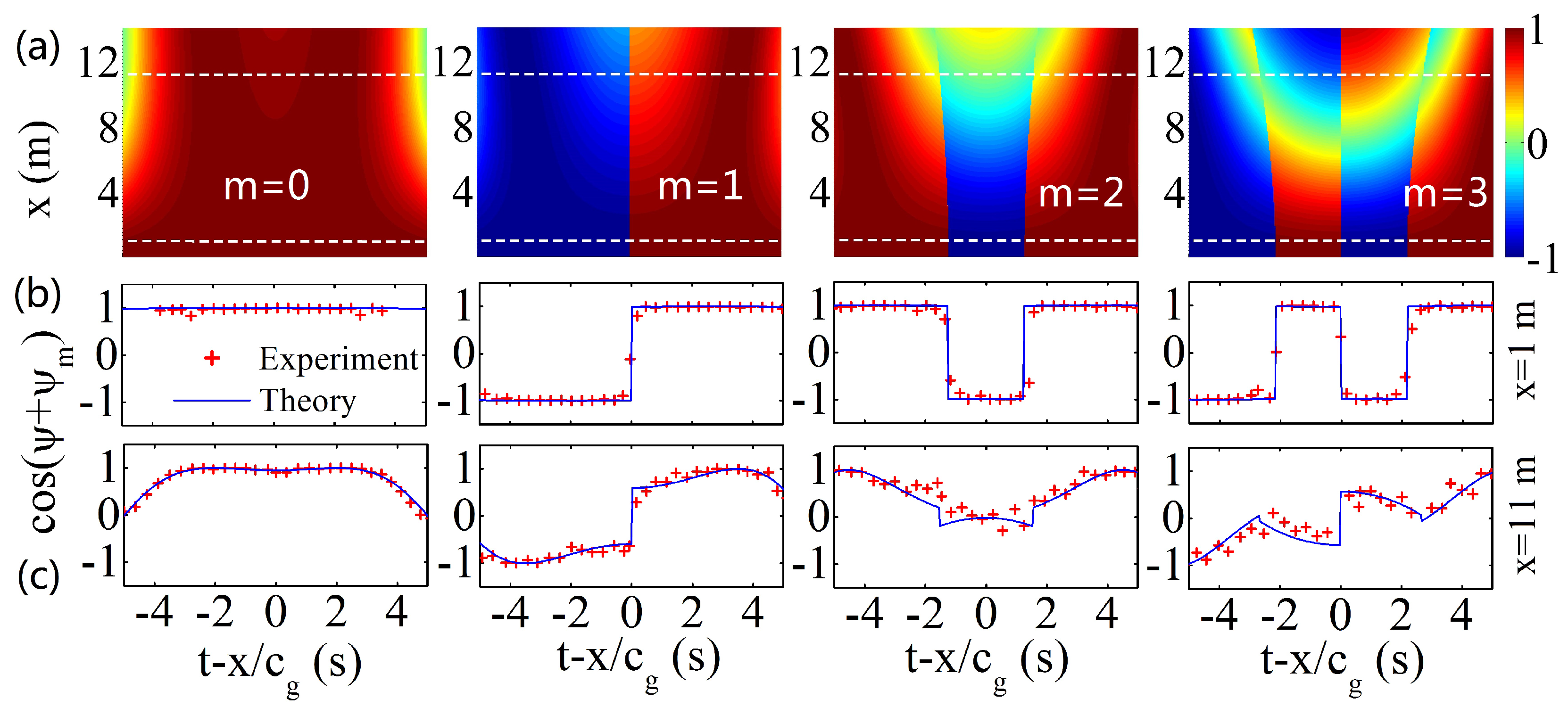
2.3.2. Hermite-Gauss Wavepackets
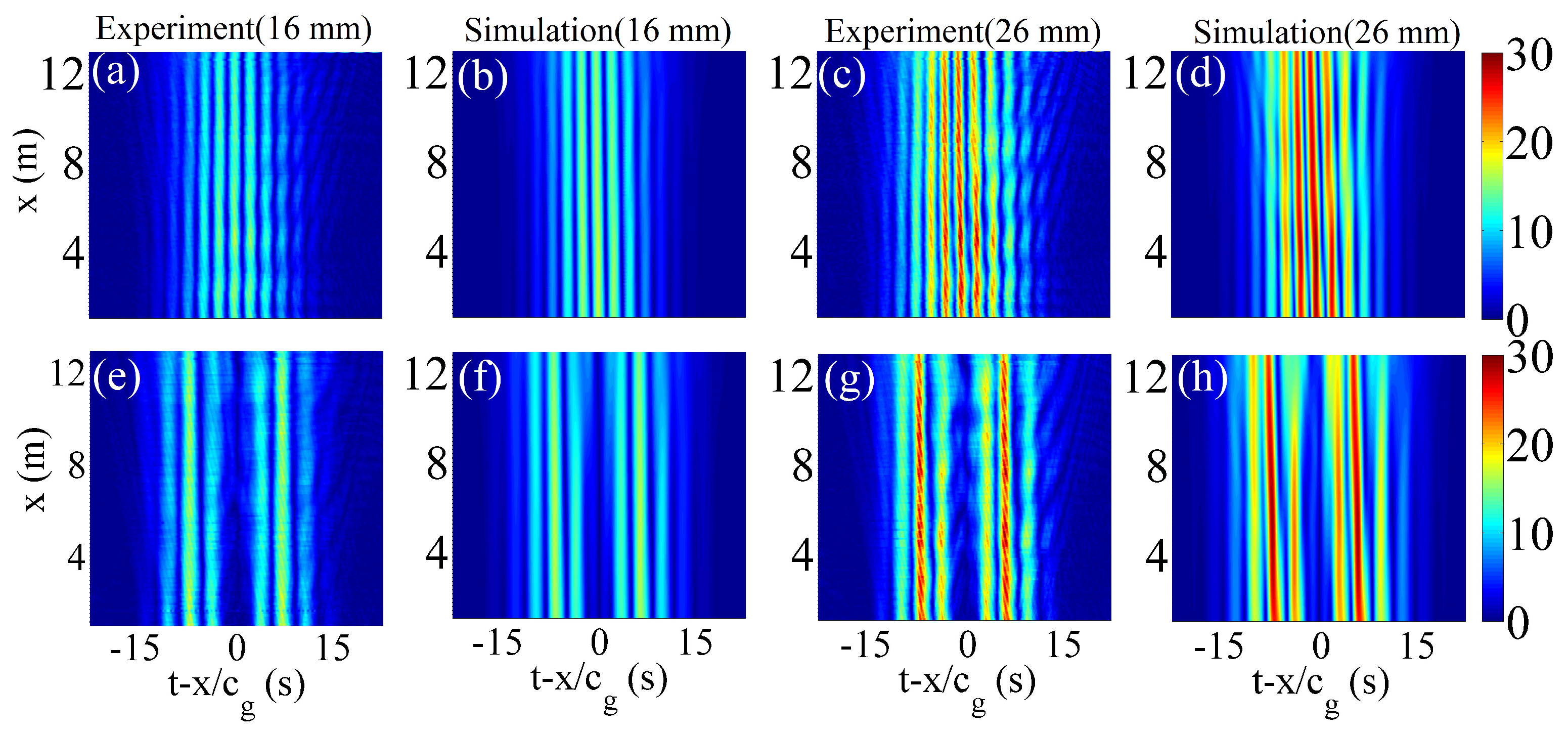
2.3.3. Cosine-Gauss Wavepackets
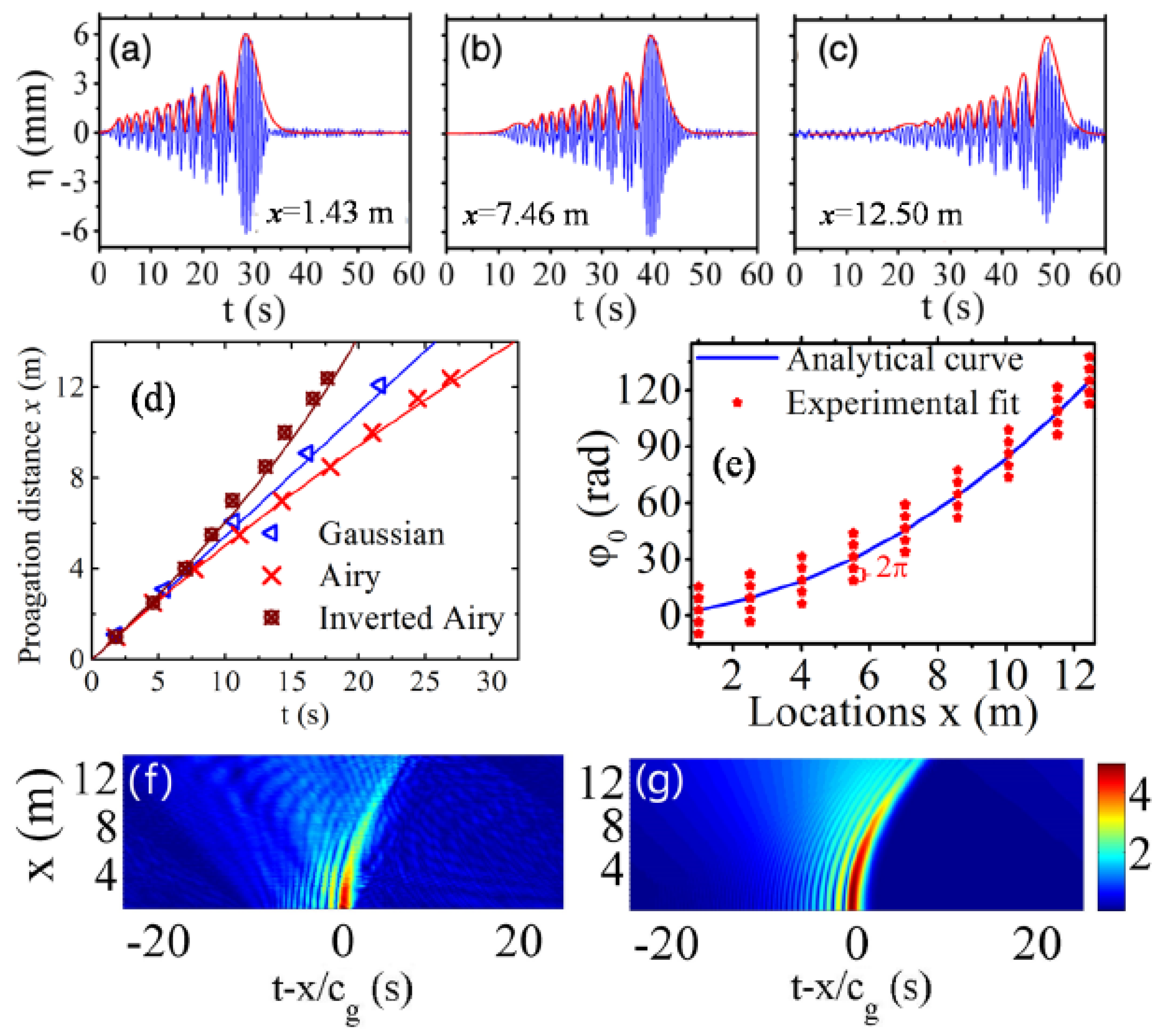
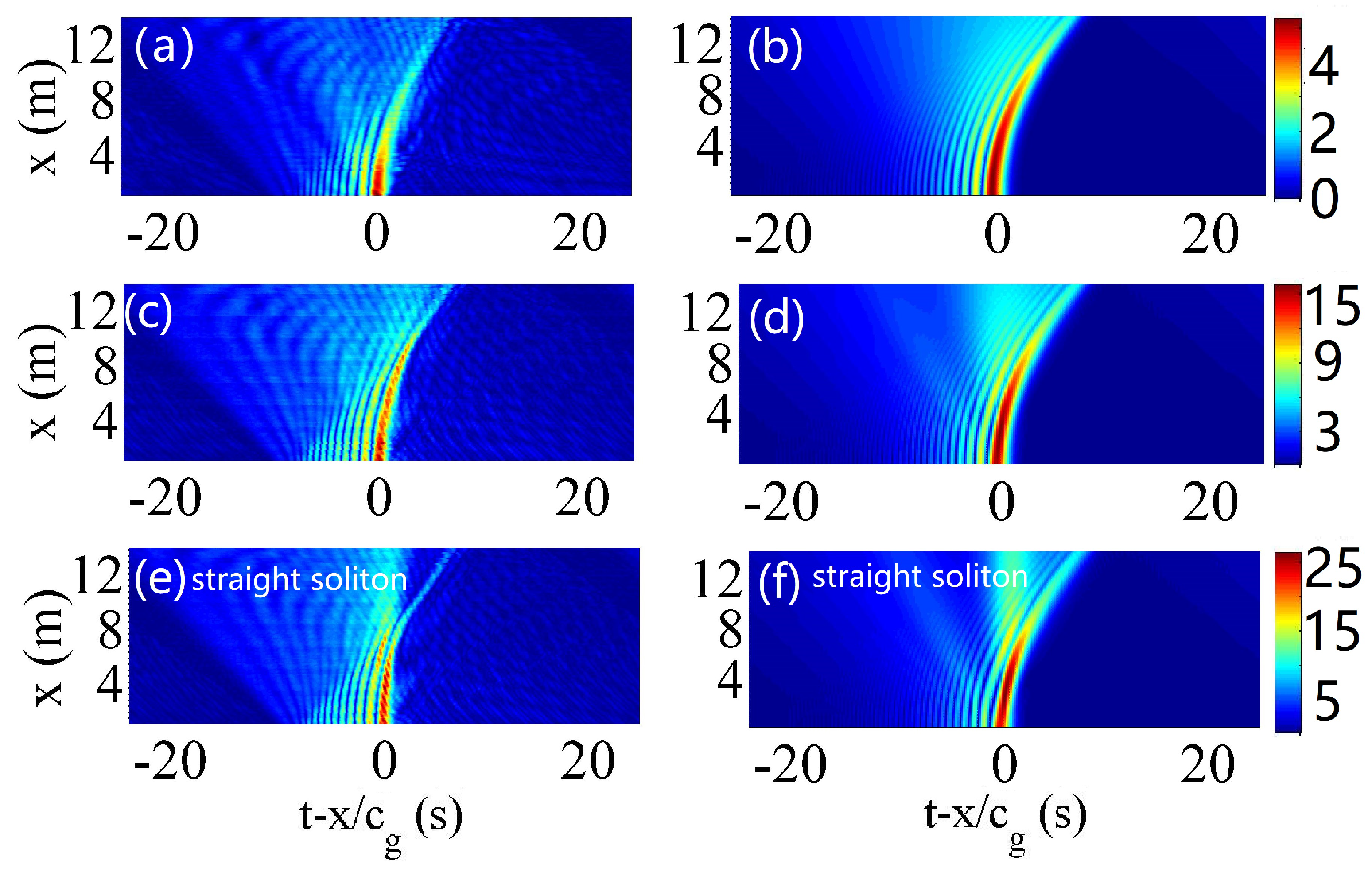
2.3.4. Airy Wavepackets
2.3.5. The Temporal Slit
3. Experiments on Water-Wave Packets
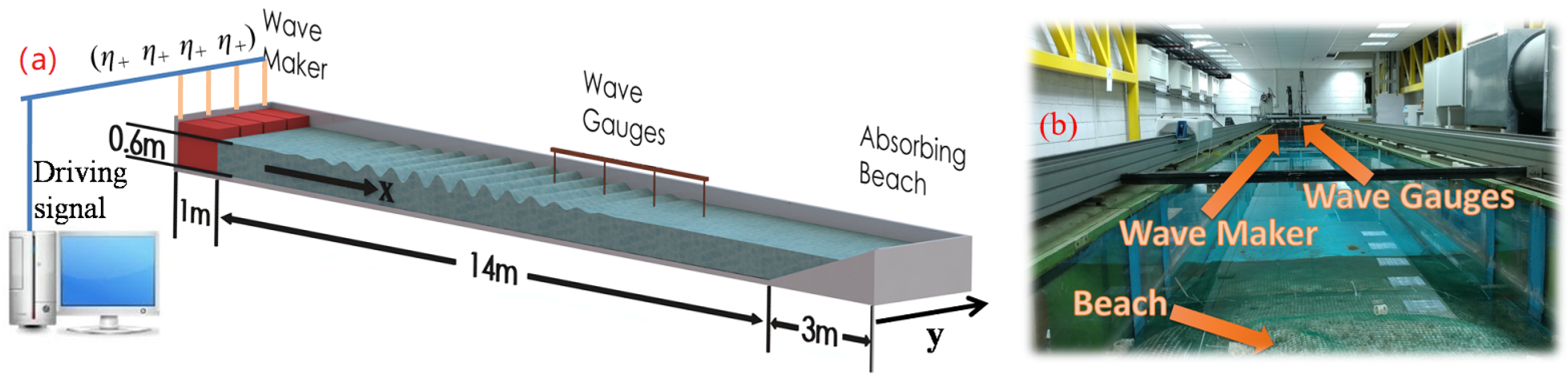
3.1. Experimental Facility and Procedure
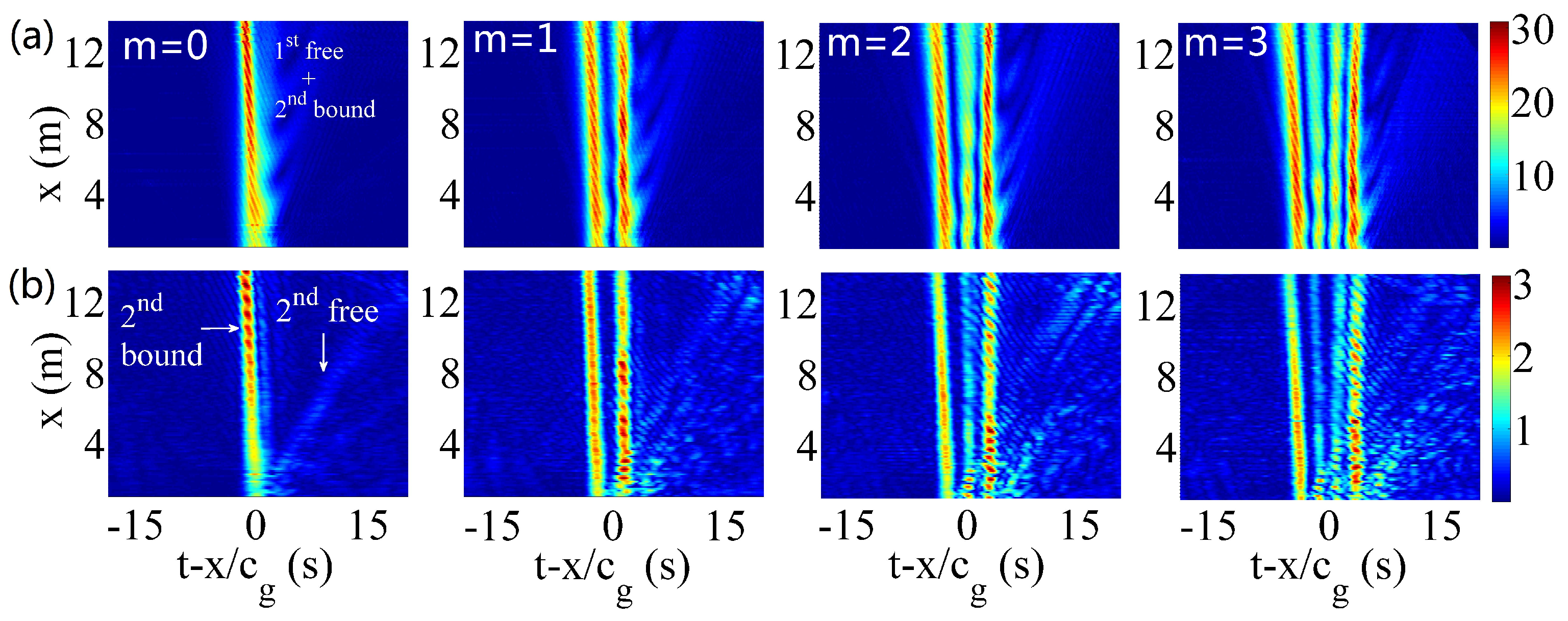
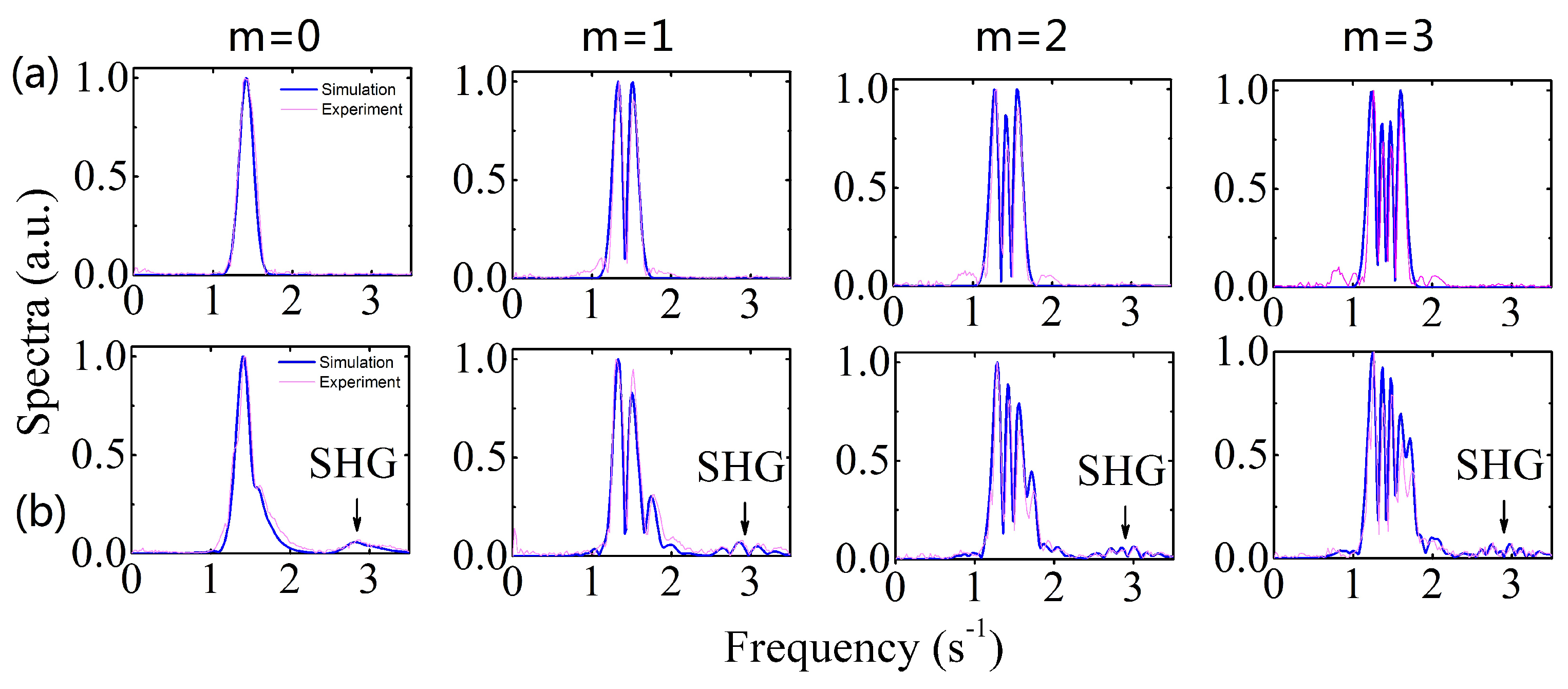
3.2. Linear Dynamics
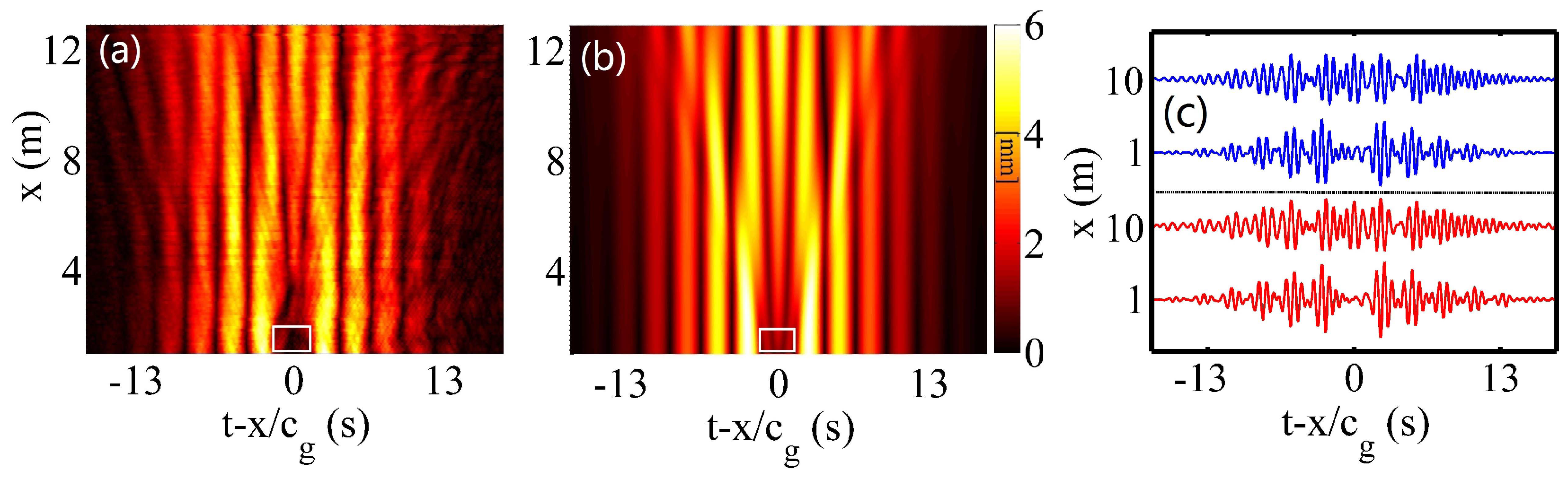
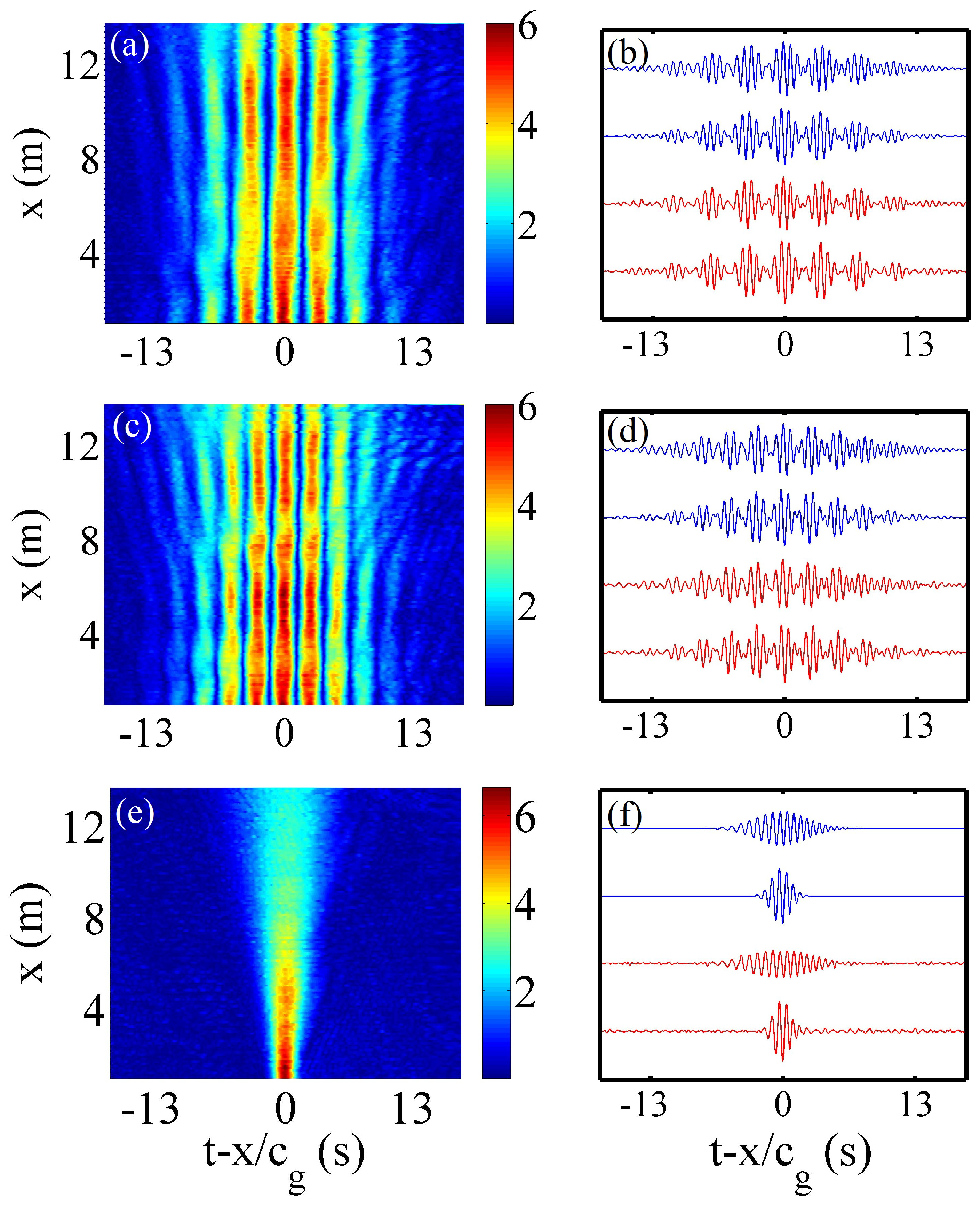
3.3. Nonlinear Dynamics
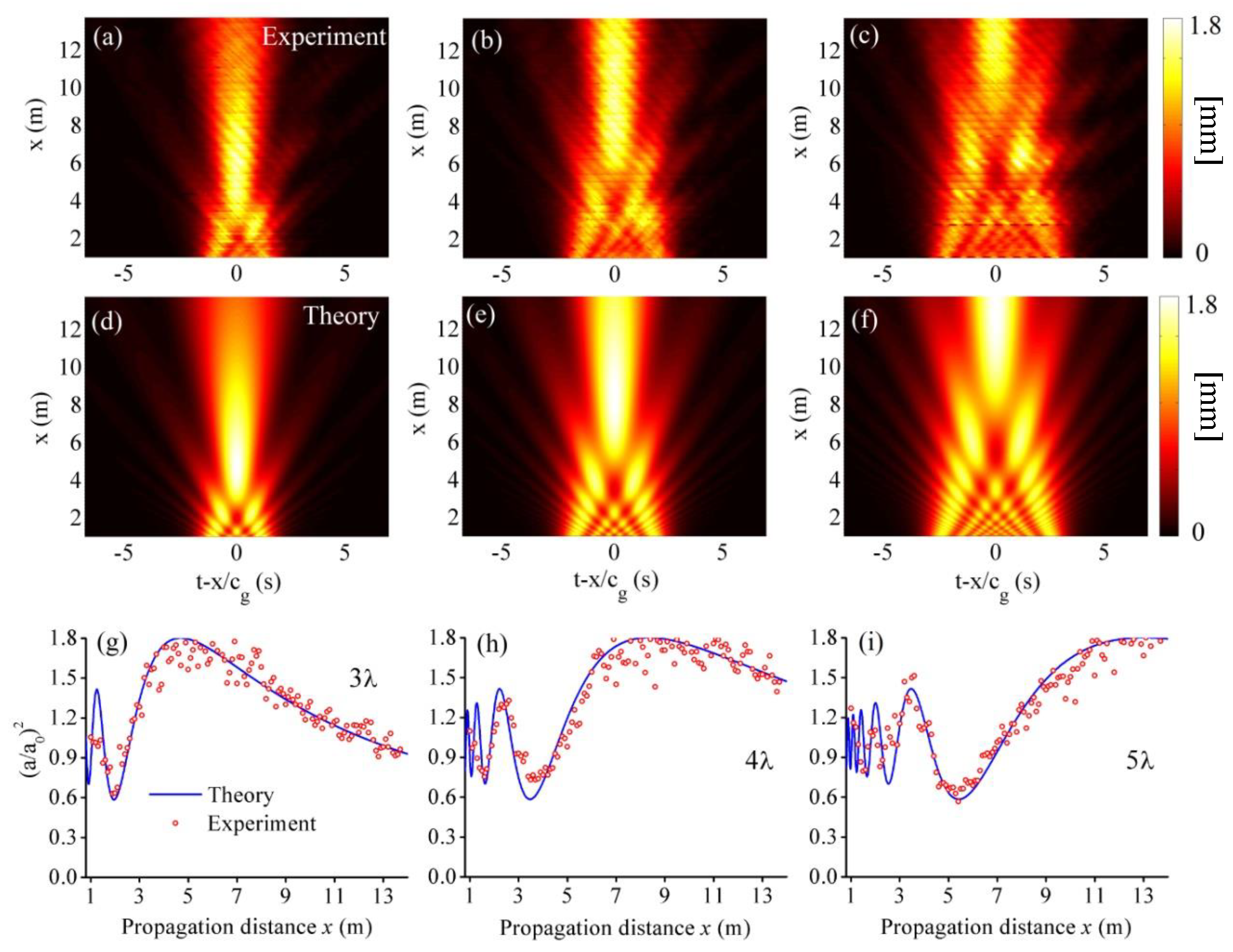
3.4. Diffractive Focusing
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pain, H.J. The Physics of Vibrations and Waves, 6th ed.; Wiley: Hoboken, NJ, USA, 2006; ISBN 0471985422. [Google Scholar]
- Faber, T. Fluid Dynamics for Physicists; Cambridge University Press: Cambridge, UK, 1995; ISBN 9780511806735. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: Hoboken, NJ, USA, 1998; ISBN 9780471309321. [Google Scholar]
- Griffiths, D.J. Introduction to Quantum Mechanics; Wiley: Hoboken, NJ, USA, 1998; ISBN 9780471309321. [Google Scholar]
- Danon, J.; Nazarov, Y. Advanced Quantum Mechanics: A Practical Guide; Cambridge University Press: Cambridge, UK, 2013; ISBN 9780521761505. [Google Scholar]
- Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures on Physics, Vol. I: The New Millennium Edition: Mainly Mechanics, Radiation, and Heat; Wiley: Hoboken, NJ, USA, 1998; ISBN 9780471309321. [Google Scholar]
- Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures on Physics, Vol. II: The New Millennium Edition: Mainly Electromagnetism and Matter (Feynman Lectures on Physics); Wiley: Hoboken, NJ, USA, 1998; ISBN 0465024165. [Google Scholar]
- Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures on Physics, Vol. III: The New Millennium Edition: Quantum Mechanics (Feynman Lectures on Physics); Wiley: Hoboken, NJ, USA, 1998; ISBN 9780465025015. [Google Scholar]
- Fu, S.; Tsur, Y.; Zhou, J.; Shemer, L.; Arie, A. Propagation Dynamics of Airy Water-Wave Pulses. Phys. Rev. Lett. 2015, 115, 034501. [Google Scholar] [CrossRef]
- Fu, S.; Tsur, Y.; Zhou, J.; Shemer, L.; Arie, A. Propagation Dynamics of Nonspreading Cosine-Gauss Water-Wave Pulses. Phys. Rev. Lett. 2015, 115, 254501. [Google Scholar] [CrossRef]
- Fu, S.; Tsur, Y.; Zhou, J.; Shemer, L.; Arie, A. Self-similar propagation of Hermite-Gauss water-wave pulses. Phys. Rev. E 2016, 93, 013127. [Google Scholar] [CrossRef]
- Berry, M.V.; Chambers, R.G.; Large, M.D.; Upstill, C.; Walmsley, J.C. Wavefront Dislocations in the Aharonov-Bohm Effect and its Water Wave Analogue. Eur. J. Phys. 1980, 1, 154. [Google Scholar] [CrossRef]
- Bar-Ziv, U.; Postan, A.; Segev, M. Observation of Shape-preserving Accelerating Underwater Acoustic Beams. Phys. Rev. B. 2015, 92, 100301. [Google Scholar] [CrossRef]
- Chabchoub, A.; Kibler, B.; Finot, C.; Millot, G.; Onorato, M.; Dudley, J.M.; Babanin, A.V. The Nonlinear Schrödinger Equation and the Propagation of Weakly Nonlinear Waves in Optical Fibers and on the Water Surface. Ann. Phys. 2015, 361, 490–500. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.P.; Akhmediev, N. Rogue Wave Observation in a Water Wave Tank. Phys. Rev. Lett. 2011, 106, 204502. [Google Scholar] [CrossRef] [PubMed]
- Dudley, J.M.; Erkintalo, M.; Genty, G. Rogue-wave-like Characteristics in Femtosecond Supercontinuum Qeneration. Opt. Photonics News 2015, 26, 34–41. [Google Scholar] [CrossRef]
- Dudley, J.M.; Dias, F.; Erkintalo, M.; Genty, G. Instabilities, Breathers and Rogue Waves in Optics. Nat. Photonics 2014, 8, 755. [Google Scholar] [CrossRef]
- Rozenman, G.G.; Zimmermann, M.; Efremov, M.A.; Schleich, W.P.; Shemer, L.; Arie, A. Amplitude and Phase of Wavepackets in Linear Potential. Phys. Rev. Lett. 2019, 122, 124302. [Google Scholar] [CrossRef]
- Bush, J.W.; Couder, Y.; Gilet, T.; Milewski, P.A.; Nachbin, A. Chaos: An Interdisciplinary. J. Nonlinear Sci. 2018, 28, 096001. [Google Scholar]
- Bush, J.W. Pilot-Wave Hydrodynamics. Annu. Rev. Fluid Mech. 2015, 47, 269–292. [Google Scholar] [CrossRef]
- Milewski, A.P.; Wang, Z. Self-focusing Dynamics of Patches of Ripples. Phys. Nonlinear Phenom. 2016, 333, 235–242. [Google Scholar] [CrossRef]
- Mei, C.C. Theory and Applications of Ocean Surface Waves; World Scientific: Singapore, 2005; ISBN 9789812388933. [Google Scholar]
- Sutherland, B.R. Internal Gravity Waves; Wiley: Hoboken, NJ, USA, 2010; ISBN 9780521839150. [Google Scholar]
- Zakharov, V.E. Stability of Periodic Waves of Finite Amplitude on the Surface of a Deep Fluid. J. Appl. Mech. Tech. Phys. 1968, 9, 190–194. [Google Scholar] [CrossRef]
- Dysthe, K.B. Note on a Modification to the Nonlinear Schrödinger Equation for Application to Deep Water Waves. Proc. R. Soc. A 1979, 369, 105–114. [Google Scholar] [CrossRef]
- Lo, E.; Mei, C.C. A Numerical Study of Water-wave Modulation Based on a Higher-order Nonlinear Schrödinger Equation. J. Fluid Mech. 1985, 150, 395–416. [Google Scholar] [CrossRef]
- Shemer, L.; Dorfman, B. Experimental and Numerical Study of Spatial and Temporal Evolution of Nonlinear Wave Groups. Nonlin. Process. Geophys. 2008, 15, 931–942. [Google Scholar] [CrossRef]
- Blokhintsev, D.I. Foundations of Quantum Mechanics; Springer: Berlin, Germany, 1964; ISBN 978-94-010-9711-6. [Google Scholar]
- Saleh, B.E.A.; Teich, M.C. Fundementals of Photonics; Wiley: Hoboken, NJ, USA, 1993; ISBN 9780471839651. [Google Scholar]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Da Silva, H.J.A.; O’Reilly, J.J. Optical Pulse Modeling with Hermite-Gaussian Functions. Opt. Lett. 1989, 14, 526–528. [Google Scholar] [CrossRef]
- Bouchal, Z. Nondiffracting Optical Beams: Physical Properties, Experiments, and Applications. Czeck Phys. 2003, 53, 537–578. [Google Scholar] [CrossRef]
- Lin, J.; Dellinger, J.; Genevet, P.; Cluzel, B.; de Fornel, F.; Capasso, F. Cosine-Gauss Plasmon beam: A Localized Long-range Nondiffracting Surface wave. Phys. Rev. Lett. 2012, 109, 093904. [Google Scholar] [CrossRef]
- Li, L.; Li, T.; Wang, S.M.; Zhu, S.N. Plasmonic Airy Beam Generated by In-Plane Diffraction. Phys. Rev. Lett. 2013, 110, 046807. [Google Scholar] [CrossRef]
- Berry, M.V.; Balazs, N.L. Nonspreading Wave Packets. Am. J. Phys. 1979, 47, 264–267. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of Accelerating Airy Beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef]
- Baumgartl, J.; Mazilu, M.; Dholakia, K. Optically Mediated Particle Clearing Using Airy wavepackets. Nat. Photonics 2008, 2, 675. [Google Scholar] [CrossRef]
- Polynkin, P.; Kolesik, M.; Moloney, J.V.; Siviloglou, G.A.; Christodoulides, D.N. Curved Plasma Channel Generation Using Ultraintense Airy beams. Christodoulides. Science 2009, 324, 229–232. [Google Scholar] [CrossRef]
- Rose, P.; Diebel, F.; Boguslawski, M.; Denz, C. Broadband Acoustic Focusing by Airy-like Beams Based on Acoustic Metasurfaces. Appl. Phys. Lett. 2013, 102, 101101. [Google Scholar] [CrossRef]
- Jia, S.; Vaughan, J.C.; Zhuang, X. Isotropic 3D Super-resolution Imaging With a Self-bending Point Spread Function. Nat. Photonics 2014, 8, 302. [Google Scholar] [CrossRef] [PubMed]
- Ellenbogen, T.; Bloch, N.V.; Padowicz, A.G.; Arie, A. Nonlinear Generation and Manipulation of Airy Beams. Nat. Photonics 2009, 3, 395. [Google Scholar] [CrossRef]
- Dolev, I.; Kaminer, I.; Shapira, A.; Segev, M.; Arie, A. Experimental Observation of Self-Accelerating Beams in Quadratic Nonlinear Media. Phys. Rev. Lett. 2012, 108, 113903. [Google Scholar] [CrossRef]
- Kaminer, I.; Segev, M.; Christodoulides, D.N. Self-Accelerating Self-Trapped Optical Beams. Phys. Rev. Lett. 2011, 106, 213903. [Google Scholar] [CrossRef]
- Gonçalves, M.R.; Case, W.B.; Arie, A.; Schleich, W.P. Single-slit Focusing and Its Representations. Appl. Phys. B 2017, 123, 121. [Google Scholar] [CrossRef]
- Weisman, D.; Fu, S.; Goncalves, M.; Shemer, L.; Zhou, J.; Schleich, W.P.; Arie, A. Diffractive Focusing of Waves in Time and in Space. Phys. Rev. Lett. 2017, 118, 154301. [Google Scholar] [CrossRef]
- Kennard, E.H. Zur Quantenmechanik einfacher Bewegungstypen. Zeitschrift für Physik 1927, 44, 326–352. [Google Scholar] [CrossRef]
- Zimmermann, M.; Efremov, M.A.; Roura, A.; Schleich, W.P.; DeSavage, S.A.; Davis, J.P.; Srinivasan, A.; Narducci, F.A.; Werner, S.A.; Rasel, E.M. T3-interferometer for Atoms. Appl. Phys. B 2017, 123, 102. [Google Scholar] [CrossRef]
- Vega, J.C.G.; Bandres, M.A. Helmholtz–Gauss Waves. J. Opt. Soc. Am. A 2005, 22, 289–298. [Google Scholar] [CrossRef]
- Epstein, I.; Lilach, Y.; Arie, A. Shaping Plasmonic Light Beams with Near-field Plasmonic Holograms. J. Opt. Soc. Am. B 2014, 31, 1642–1647. [Google Scholar] [CrossRef]
- Saghafi, S.; Sheppard, C.J.R.; Piper, J.A. Characterising Elegant and Standard Hermite–Gaussian Beam Modes. Opt. Commun. 2001, 191, 173–179. [Google Scholar] [CrossRef]
- Gouy, L.G. Sur la propagation anomale des ondes. Ann. Chim. Phys. Ser. 1891, 24, 145. [Google Scholar]
- Boyd, R. Nonlinear Optics, 3rd ed.; Academic Press: Cambridge, MA, USA, 2008; ISBN 9780123694706. [Google Scholar]
- Fu, S.; Zhou, J.; Li, Y.; Shemer, L.; Arie, A. Dispersion Management of Propagating Waveguide Modes on the Water Surface. Phys. Rev. Lett. 2017, 118, 144501. [Google Scholar] [CrossRef]
- Porat, G.; Dolev, I.; Barlev, O.; Arie, A. Airy Beam Laser. Opt. Lett. 2011, 36, 4119–4121. [Google Scholar] [CrossRef]
- Epstein, I.; Remez, R.; Tsur, Y.; Arie, A. Generation of intensity-controlled Two-dimensional Shape-preserving Beams in Plasmonic Lossy Media. Optica 2016, 3, 15–19. [Google Scholar] [CrossRef]
- Shemer, L. Advantages and Limitations Of the Nonlinear Schrodinger Equation in Describing the Evolution of Nonlinear Water-wave Groups. Proc. Estonian Acad. Sci. 2015, 64, 356. [Google Scholar] [CrossRef]
- Fermann, M.E.; Kruglov, V.I.; Thomsen, B.C.; Dudley, J.M.; Harvey, J.D. Self-Similar Propagation and Amplification of Parabolic Pulses in Optical Fibers. Phys. Rev. Lett. 2000, 84, 6010. [Google Scholar] [CrossRef] [PubMed]
- Anderson, D.; Desaix, M.; Karlsson, M.; Lisak, M.; Quiroga-Teixeiro, M.L. Wave-breaking-free Pulses in Nonlinear-optical Fibers. J. Opt. Soc. Am. B 1993, 10, 1185–1190. [Google Scholar] [CrossRef]
- Shemer, L.; Goulitski, K.; Kit, E. Evolution of Wide-spectrum Unidirectional Wave Groups in a Tank: An Experimental and Numerical Study. Eur. J. Mech. B Fluids 2007, 26, 193–219. [Google Scholar] [CrossRef]
- Shemer, L.; Jiao, H.; Kit, E.; Agnon, Y. Evolution of a Nonlinear Wave Field Along a tank: Experiments and Numerical Simulations Based on the Spatial Zakharov Equation. J. Fluid Mech. 2001, 427, 107–129. [Google Scholar] [CrossRef]
- Vitrant, G.; Zaiba, S.; Vineeth, B.Y.; Kouriba, T.; Ziane, O.; Stéphan, O.; Bosson, J.; Baldeck, P.L. Obstructive Micro Diffracting Structures as an Alternative to Plasmonics Nano slits for Making Efficient Microlenses. Opt. Express 2012, 20, 26542. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rozenman, G.G.; Fu, S.; Arie, A.; Shemer, L. Quantum Mechanical and Optical Analogies in Surface Gravity Water Waves. Fluids 2019, 4, 96. https://doi.org/10.3390/fluids4020096
Rozenman GG, Fu S, Arie A, Shemer L. Quantum Mechanical and Optical Analogies in Surface Gravity Water Waves. Fluids. 2019; 4(2):96. https://doi.org/10.3390/fluids4020096
Chicago/Turabian StyleRozenman, Georgi Gary, Shenhe Fu, Ady Arie, and Lev Shemer. 2019. "Quantum Mechanical and Optical Analogies in Surface Gravity Water Waves" Fluids 4, no. 2: 96. https://doi.org/10.3390/fluids4020096
APA StyleRozenman, G. G., Fu, S., Arie, A., & Shemer, L. (2019). Quantum Mechanical and Optical Analogies in Surface Gravity Water Waves. Fluids, 4(2), 96. https://doi.org/10.3390/fluids4020096






