Baropycnal Work: A Mechanism for Energy Transfer across Scales
Abstract
1. Introduction
- (I)
- Barotropic and baroclinic generation of strain, , from gradients of pressure and density, :,
- (II)
- Baroclinic generation of vorticity, :,
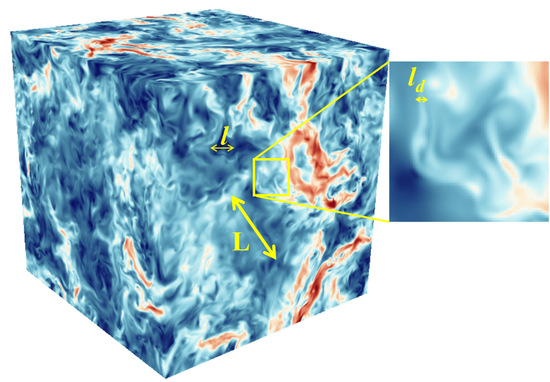
2. Multi-Scale Dynamics
Variable Density Flows
3. The Mechanism of Baropycnal Work
4. Simulations
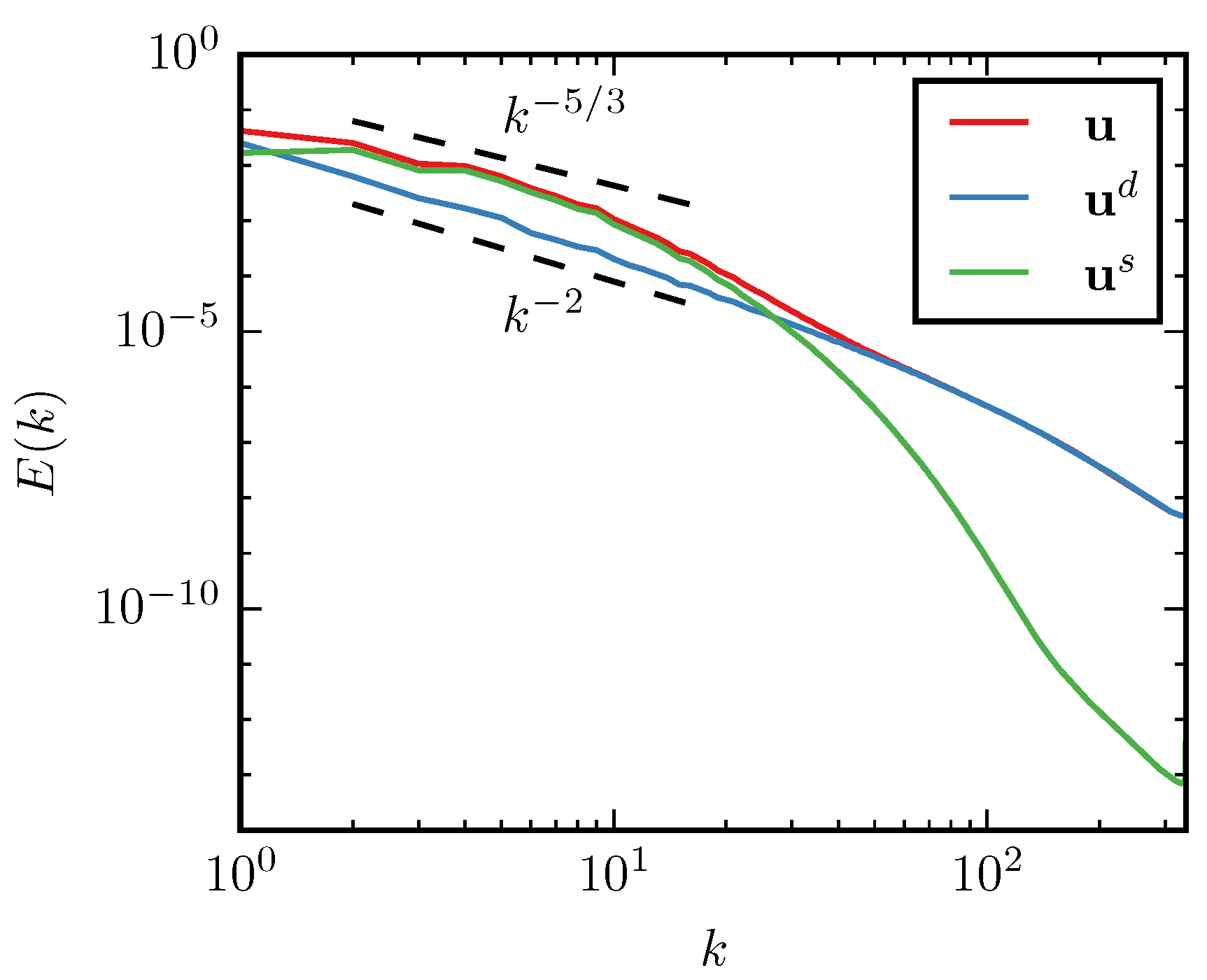
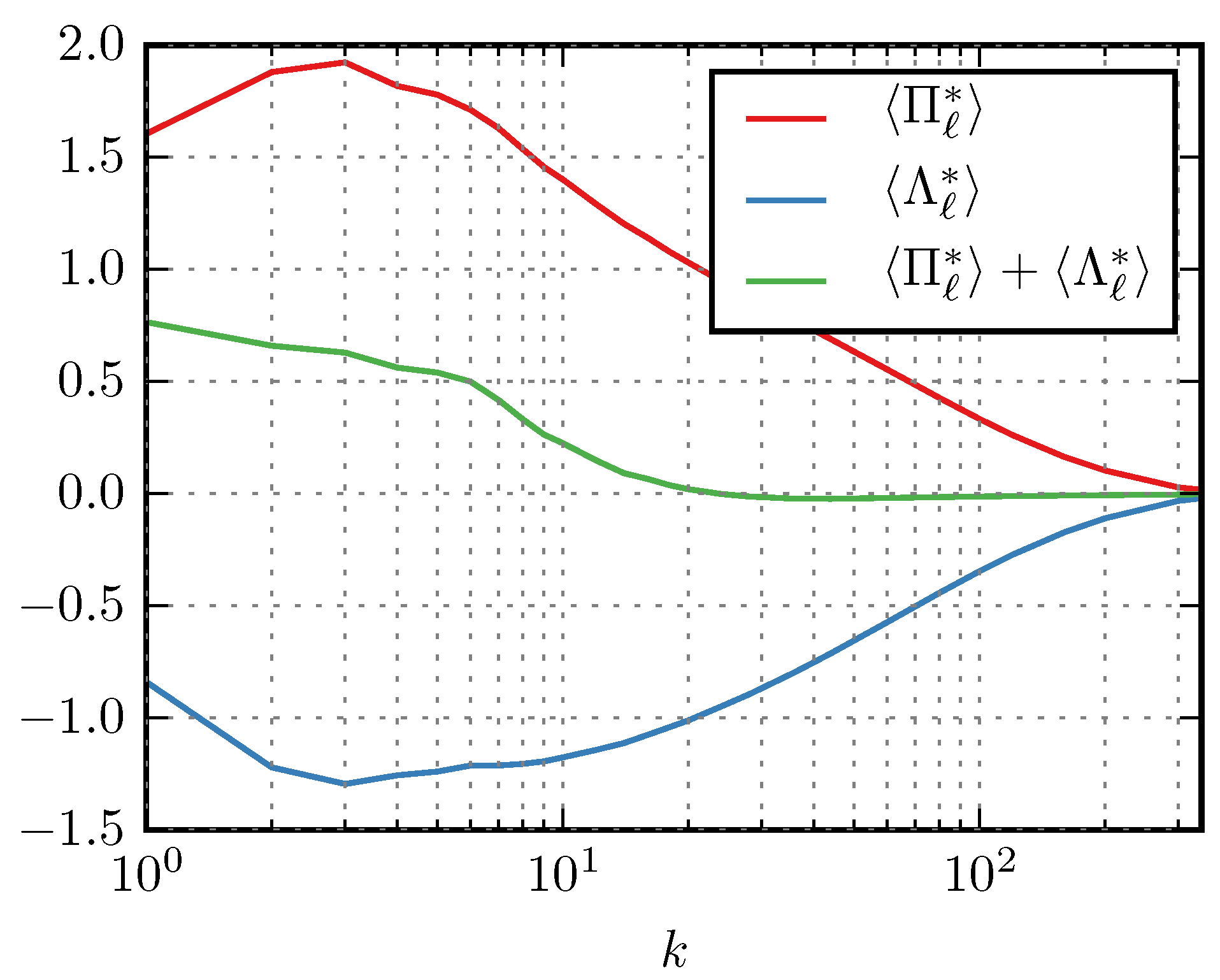
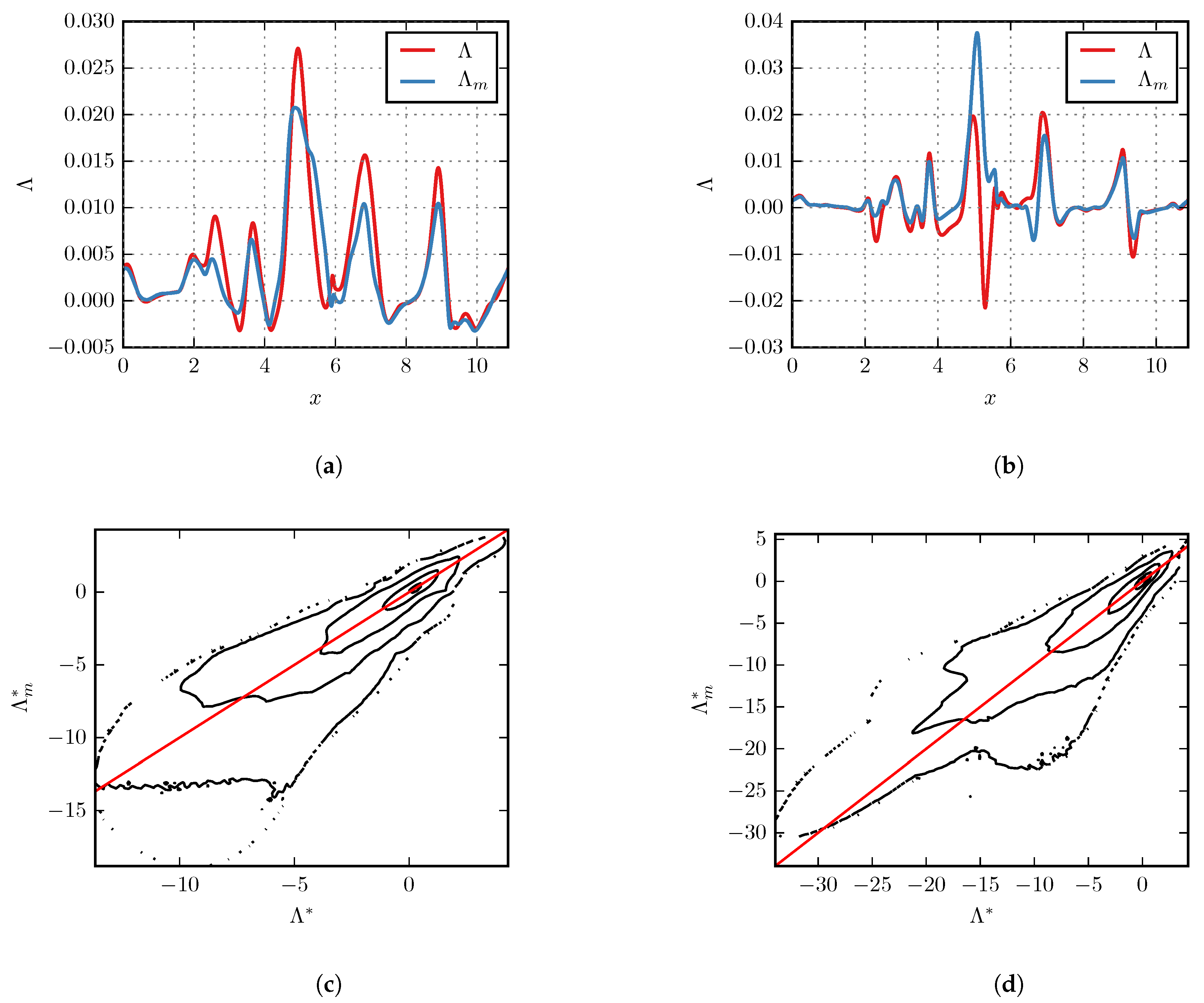
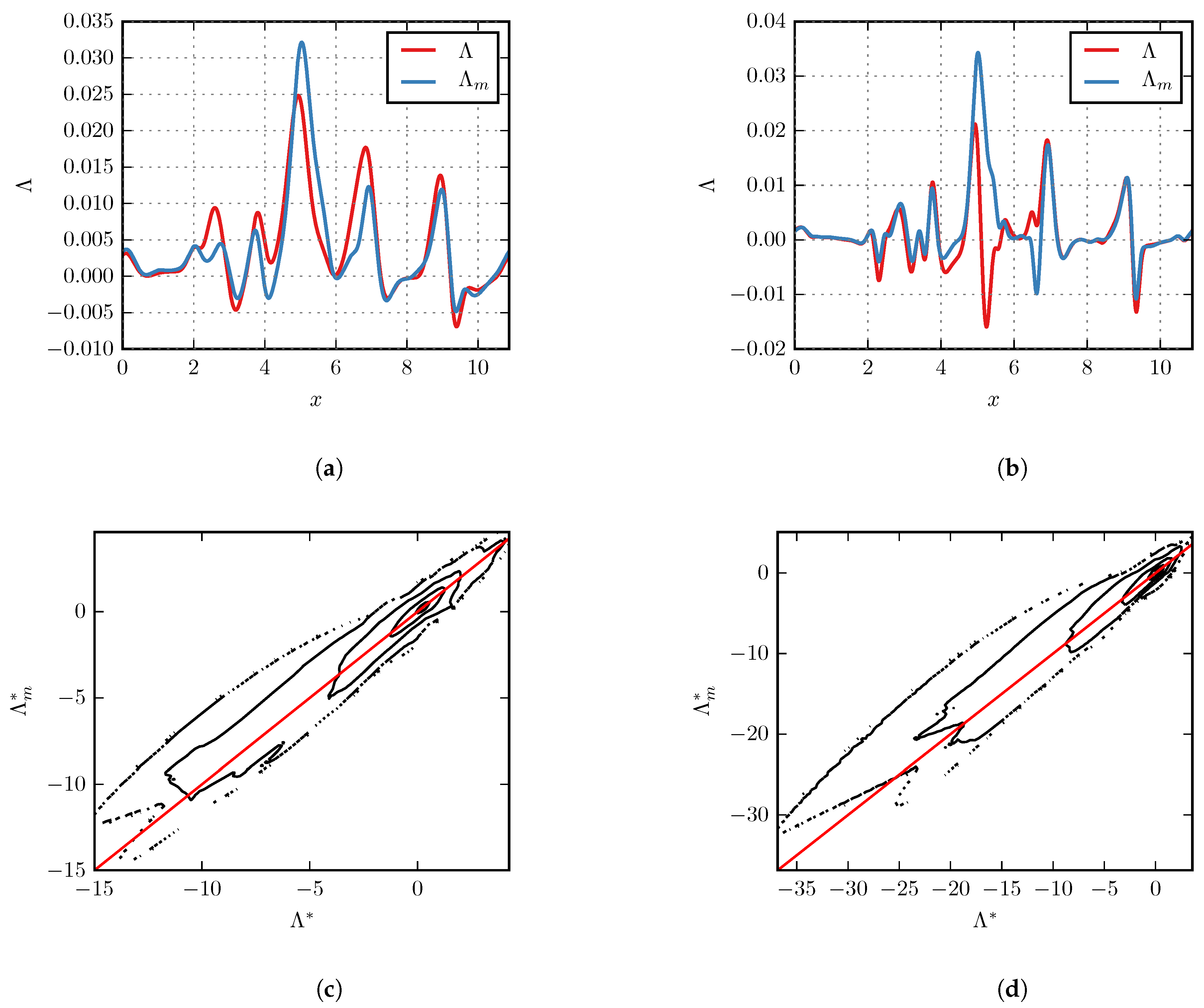
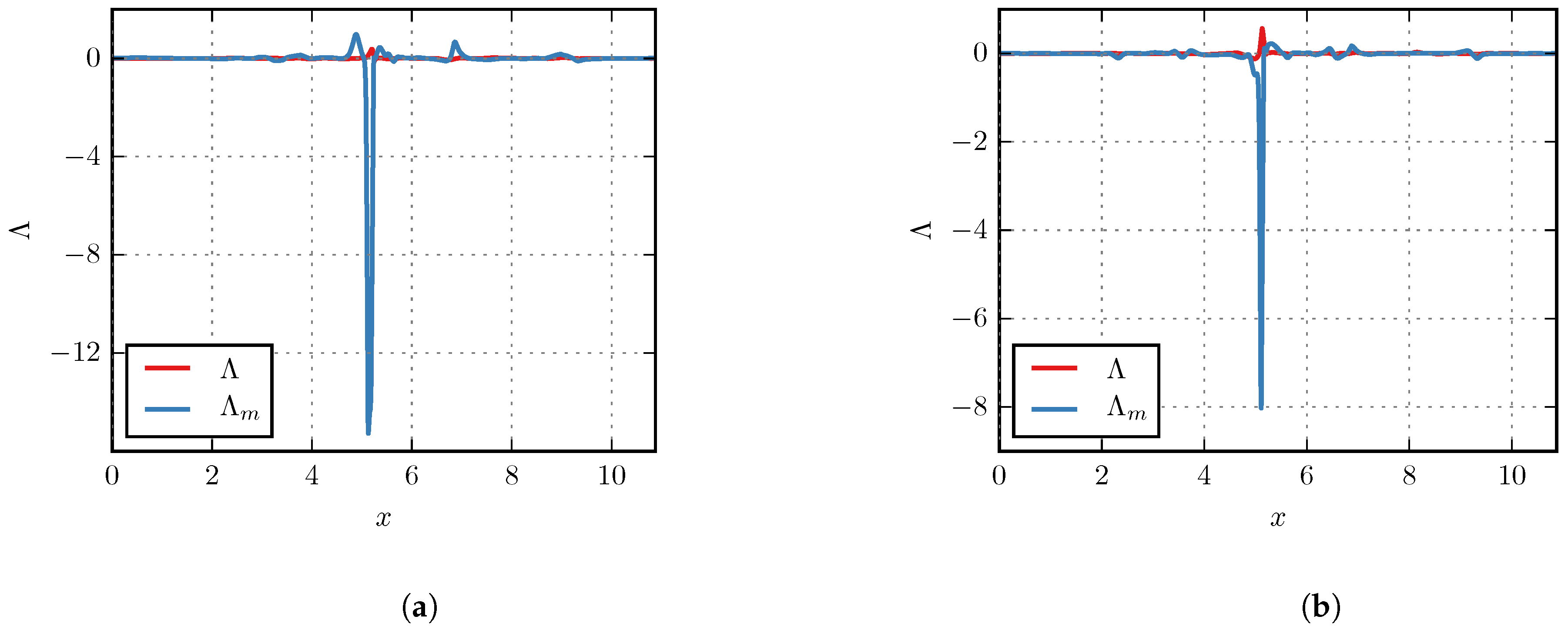
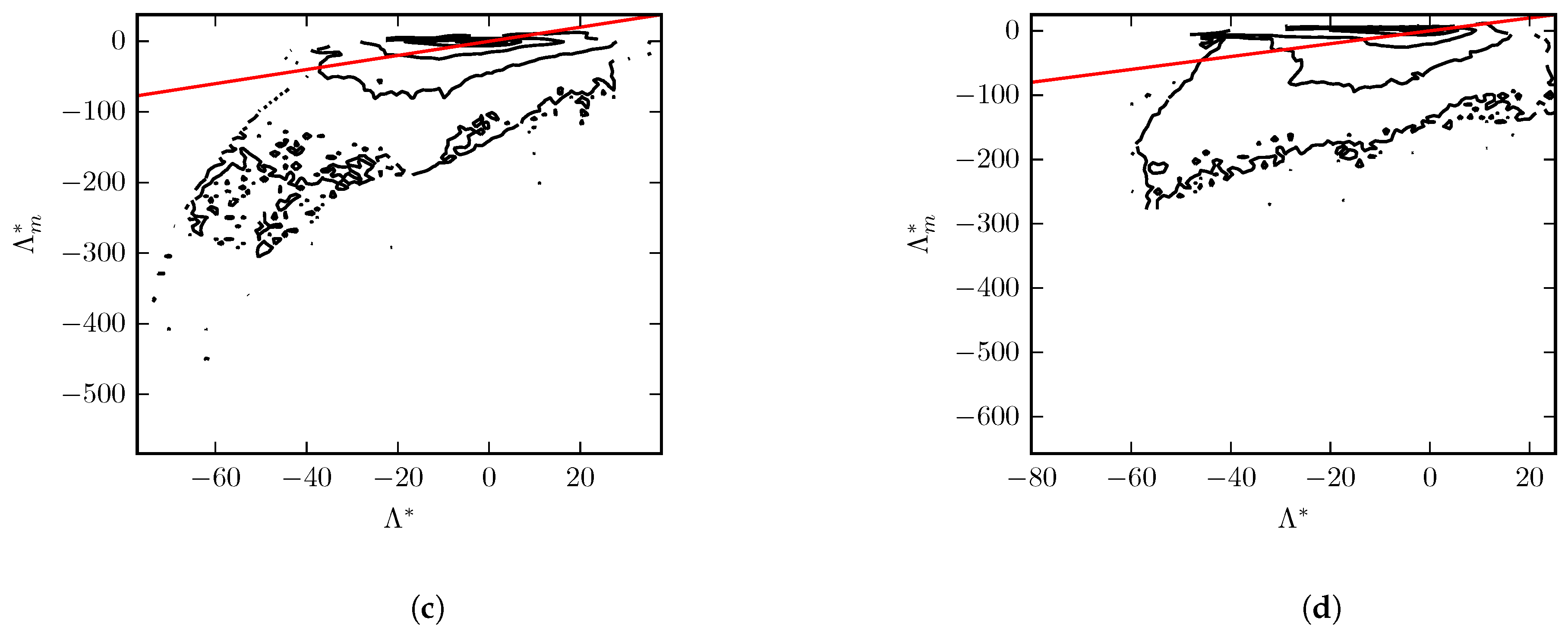
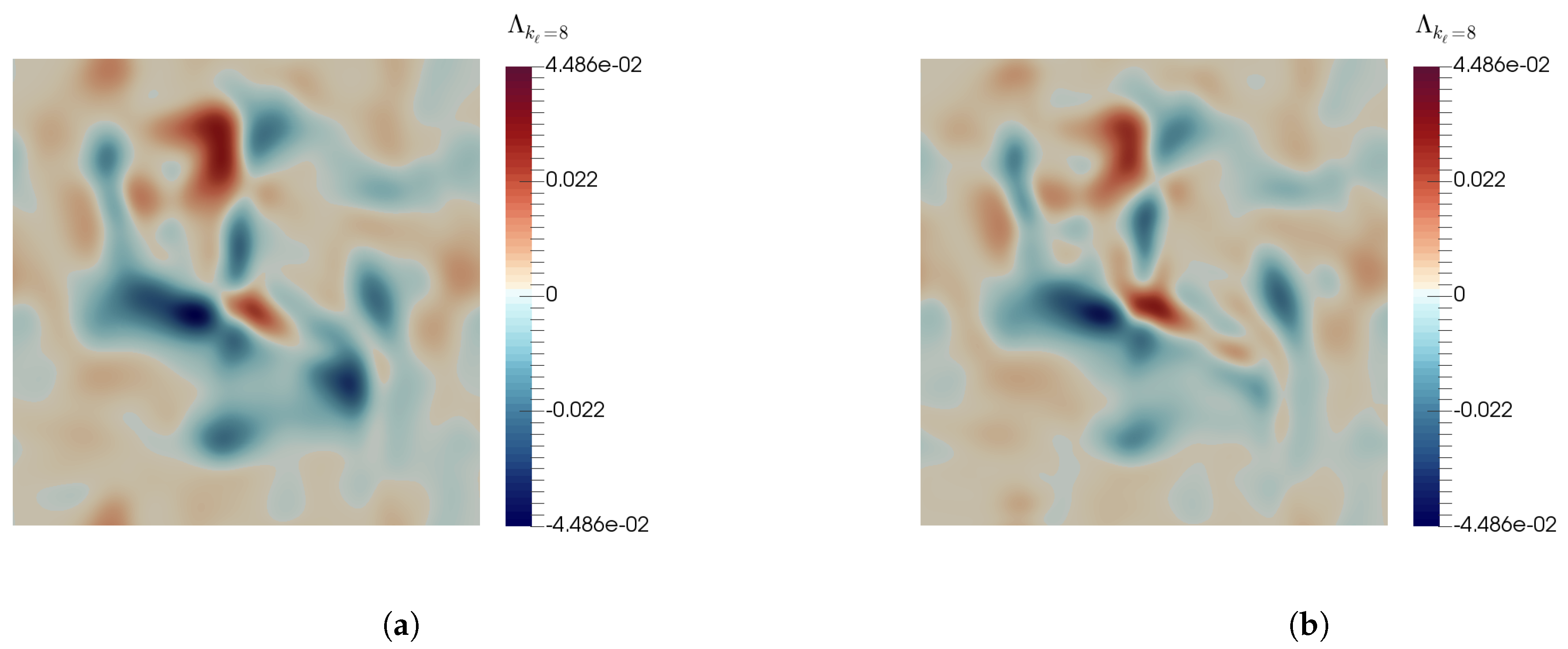
5. Numerical Results
6. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; The MIT Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Alexakis, A.; Biferale, L. Cascades and transitions in turbulent flows. Phys. Rep. 2018, 767–769, 1–101. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Frisch, U. Turbulence. The Legacy of A. N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Alexakis, A.; Mininni, P.D.; Pouquet, A. Imprint of large-scale flows on turbulence. Phys. Rev. Lett. 2005, 95, 264503. [Google Scholar] [CrossRef] [PubMed]
- Mininni, P.D.; Alexakis, A.; Pouquet, A. Large-scale flow effects, energy transfer, and self-similarity on turbulence. Phys. Rev. E 2006, 74, 016303. [Google Scholar] [CrossRef]
- Borue, V.; Orszag, S.A. Local energy flux and subgrid-scale statistics in three-dimensional turbulence. J. Fluid Mech. 1998, 366, 1–31. [Google Scholar] [CrossRef]
- Eyink, G.L. Cascade of circulations in fluid turbulence. Phys. Rev. E 2006, 74, 066302. [Google Scholar] [CrossRef] [PubMed]
- Eyink, G.L. Dissipative anomalies in singular Euler flows. Phys. D Nonlinear Phenom. 2008, 237, 1956–1968. [Google Scholar] [CrossRef]
- Xu, H.; Pumir, A.; Bodenschatz, E. The pirouette effect in turbulent flows. Nat. Phys. 2011, 7, 709–712. [Google Scholar] [CrossRef]
- Taylor, G.I.; Green, A.E. Mechanism of the production of small eddies from large ones. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1937, 158, 499–521. [Google Scholar]
- Taylor, G.I. Production and dissipation of vorticity in a turbulent fluid. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1938, 164, 15–23. [Google Scholar]
- Aluie, H. Compressible Turbulence: The Cascade and its Locality. Phys. Rev. Lett. 2011, 106, 174502. [Google Scholar] [CrossRef]
- Aluie, H.; Li, S.; Li, H. Conservative Cascade of Kinetic Energy in Compressible Turbulence. Astrophys. J. Lett. 2012, 751, L29. [Google Scholar] [CrossRef]
- Aluie, H. Scale decomposition in compressible turbulence. Phys. D Nonlinear Phenom. 2013, 247, 54–65. [Google Scholar] [CrossRef]
- Kritsuk, A.G.; Wagner, R.; Norman, M.L. Energy cascade and scaling in supersonic isothermal turbulence. J. Fluid Mech. 2013, 729, R1. [Google Scholar] [CrossRef][Green Version]
- Wang, J.; Yang, Y.; Shi, Y.; Xiao, Z.; He, X.T.; Chen, S. Cascade of Kinetic Energy in Three-Dimensional Compressible Turbulence. Phys. Rev. Lett. 2013, 110, 214505. [Google Scholar] [CrossRef] [PubMed]
- Eyink, G.L.; Drivas, T.D. Cascades and Dissipative Anomalies in Compressible Fluid Turbulence. Phys. Rev. X 2018, 8, 011022. [Google Scholar] [CrossRef]
- Favre, A. Statistical equations of turbulent gases. In Problems of Hydrodynamic and Continuum Mechanics; SIAM: Philadelphia, PA, USA, 1969; pp. 231–266. [Google Scholar]
- Lele, S.K. Compressibility effects on turbulence. Annu. Rev. Fluid Mech. 1994, 26, 211–254. [Google Scholar] [CrossRef]
- Garnier, E.; Adams, N.; Sagaut, P. Large Eddy Simulation for Compressible Flows; Springer: Amsterland, The Netherlands, 2009. [Google Scholar]
- O’Brien, J.; Urzay, J.; Ihme, M.; Moin, P.; Saghafian, A. Subgrid-scale backscatter in reacting and inert supersonic hydrogen–air turbulent mixing layers. J. Fluid Mech. 2014, 743, 554–584. [Google Scholar] [CrossRef]
- Mukherjee, S.; Zarghami, A.; Haringa, C.; van As, K.; Kenjereš, S.; Van den Akker, H.E. Simulating liquid droplets: A quantitative assessment of lattice Boltzmann and Volume of Fluid methods. Int. J. Heat Fluid Flow 2018, 70, 59–78. [Google Scholar] [CrossRef]
- Kritsuk, A.G.; Norman, M.L.; Padoan, P.; Wagner, R. The statistics of supersonic isothermal turbulence. Astrophys. J. 2007, 665, 416–431. [Google Scholar] [CrossRef]
- Federrath, C.; Roman-Duval, J.; Klessen, R.S.; Schmidt, W.; Mac Low, M.M. Comparing the statistics of interstellar turbulence in simulations and observations. Astron. Astrophys. 2010, 512, A81. [Google Scholar] [CrossRef]
- Pan, L.; Padoan, P.; Haugbølle, T.; Nordlund, Å. Supernova Driving. II. Compressive Ratio In Molecular-Cloud Turbulence. Astrophys. J. Lett. 2016, 825, 30. [Google Scholar] [CrossRef]
- Yan, R.; Betti, R.; Sanz, J.; Aluie, H.; Liu, B.; Frank, A. Three-dimensional single-mode nonlinear ablative Rayleigh-Taylor instability. Phys. Plasmas 2016, 23, 022701. [Google Scholar] [CrossRef]
- Zhang, H.; Betti, R.; Gopalaswamy, V.; Yan, R.; Aluie, H. Nonlinear excitation of the ablative Rayleigh-Taylor instability for all wave numbers. Phys. Rev. E 2018, 97, 011203. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Betti, R.; Yan, R.; Zhao, D.; Shvarts, D.; Aluie, H. Self-Similar Multimode Bubble-Front Evolution of the Ablative Rayleigh-Taylor Instability in Two and Three Dimensions. Phys. Rev. Lett. 2018, 121, 185002. [Google Scholar] [CrossRef] [PubMed]
- Larsson, J.; Laurence, S.; Bermejo-Moreno, I.; Bodart, J.; Karl, S.; Vicquelin, R. Incipient thermal choking and stable shock-train formation in the heat-release region of a scramjet combustor. Part II: Large eddy simulations. Combust. Flame 2015, 162, 907–920. [Google Scholar] [CrossRef]
- Urzay, J. Supersonic Combustion in Air-Breathing Propulsion Systems for Hypersonic Flight. Annu. Rev. Fluid Mech. 2018, 50, 593–627. [Google Scholar] [CrossRef]
- Emanuel, K.A. An air-sea interaction theory for tropical cyclones. Part I: Steady-state maintenance. J. Atmos. Sci. 1986, 43, 585–605. [Google Scholar] [CrossRef]
- Bourassa, M.A.; Rodriguez, E.; Chelton, D. Winds and currents mission: Ability to observe mesoscale AIR/SEA coupling. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 7392–7395. [Google Scholar]
- Deike, L.; Melville, W.K.; Popinet, S. Air entrainment and bubble statistics in breaking waves. J. Fluid Mech. 2016, 801, 91–129. [Google Scholar] [CrossRef]
- Renault, L.; McWilliams, J.C.; Masson, S. Satellite observations of imprint of oceanic current on wind stress by air-sea coupling. Sci. Rep. 2017, 7, 17747. [Google Scholar] [CrossRef]
- Meneveau, C.; Katz, J. Scale-Invariance and Turbulence Models for Large-Eddy Simulation. Annu. Rev. Fluid Mech. 2000, 32, 1–32. [Google Scholar] [CrossRef]
- Eyink, G.L. Locality of turbulent cascades. Physica D 2005, 207, 91–116. [Google Scholar] [CrossRef]
- Strichartz, R.S. A Guide to Distribution Theory and Fourier Transforms; World Scientific Publishing Company: Singapore, 2003. [Google Scholar]
- Evans, L.C. Partial Differential Equations; American Mathematical Society: Providence, RI, USA 2010. [Google Scholar]
- Leonard, A. Energy Cascade in Large-Eddy Simulations of Turbulent Fluid Flows. Adv. Geophys. 1974, 18, A237. [Google Scholar]
- Germano, M. Turbulence: The filtering approach. J. Fluid Mech. 1992, 238, 325–336. [Google Scholar] [CrossRef]
- Eyink, G.L. Local energy flux and the refined similarity hypothesis. J. Stat. Phys. 1995, 78, 335–351. [Google Scholar] [CrossRef]
- Eyink, G.L. Exact Results on Scaling Exponents in the 2D Enstrophy Cascade. Phys. Rev. Lett. 1995, 74, 3800–3803. [Google Scholar] [CrossRef] [PubMed]
- Eyink, G.; Aluie, H. Localness of energy cascade in hydrodynamic turbulence. I. Smooth coarse graining. Phys. Fluids 2009, 21, 115107. [Google Scholar] [CrossRef]
- Piomelli, U.; Cabot, W.H.; Moin, P.; Lee, S. Subgrid-scale backscatter in turbulent and transitional flows. Phys. Fluids A Fluid Dyn. 1991, 3, 1766–1771. [Google Scholar] [CrossRef]
- Vreman, B.; Geurts, B.; Kuerten, H. Realizability conditions for the turbulent stress tensor in large-eddy simulation. J. Fluid Mech. 1994, 278, 351–362. [Google Scholar] [CrossRef]
- Aluie, H.; Eyink, G. Localness of energy cascade in hydrodynamic turbulence. II. Sharp spectral filter. Phys. Fluids 2009, 21, 115108. [Google Scholar] [CrossRef]
- Buzzicotti, M.; Linkmann, M.; Aluie, H.; Biferale, L.; Brasseur, J.; Meneveau, C. Effect of filter type on the statistics of energy transfer between resolved and subfilter scales from a-priori analysis of direct numerical simulations of isotropic turbulence. J. Turbul. 2018, 19, 167–197. [Google Scholar] [CrossRef]
- Rivera, M.K.; Daniel, W.B.; Chen, S.Y.; Ecke, R.E. Energy and Enstrophy Transfer in Decaying Two-Dimensional Turbulence. Phys. Rev. Lett. 2003, 90, 104502. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Ecke, R.E.; Eyink, G.L.; Wang, X.; Xiao, Z. Physical Mechanism of the Two-Dimensional Enstrophy Cascade. Phys. Rev. Lett. 2003, 91, 214501. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Meneveau, C.; Katz, J. Scale interactions of turbulence subjected to a straining relaxation destraining cycle. J. Fluid Mech. 2006, 562, 123–150. [Google Scholar] [CrossRef]
- Kelley, D.H.; Ouellette, N.T. Spatiotemporal persistence of spectral fluxes in two-dimensional weak turbulence. Phys. Fluids 2011, 23, 5101. [Google Scholar] [CrossRef]
- Rivera, M.K.; Aluie, H.; Ecke, R.E. The direct enstrophy cascade of two-dimensional soap film flows. Phys. Fluids 2014, 26, 055105. [Google Scholar] [CrossRef]
- Liao, Y.; Ouellette, N.T. Long-range ordering of turbulent stresses in two-dimensional flow. Phys. Rev. E 2015, 91, 063004. [Google Scholar] [CrossRef]
- Fang, L.; Ouellette, N.T. Advection and the Efficiency of Spectral Energy Transfer in Two-Dimensional Turbulence. Phys. Rev. Lett. 2016, 117, 104501. [Google Scholar] [CrossRef]
- Liu, S.; Meneveau, C.; Katz, J. On the properties of similarity subgrid-scale models as deduced from measurements in a turbulent jet. J. Fluid Mech. 1994, 275, 83–119. [Google Scholar] [CrossRef]
- Meneveau, C. Statistics of Turbulence Subgrid-Scale Stresses: Necessary Conditions and Experimental Tests. Phys. Fluids 1994, 6, 815–833. [Google Scholar] [CrossRef]
- Tao, B.; Katz, J.; Meneveau, C. Statistical geometry of subgrid-scale stresses determined from holographic particle image velocimetry measurements. J. Fluid Mech. 2002, 457, 35–78. [Google Scholar] [CrossRef]
- Bai, K.; Meneveau, C.; Katz, J. Experimental study of spectral energy fluxes in turbulence generated by a fractal, tree-like object. Phys. Fluids 2013, 25, 110810. [Google Scholar] [CrossRef]
- Chow, Y.C.; Uzol, O.; Katz, J.; Meneveau, C. Decomposition of the spatially filtered and ensemble averaged kinetic energy, the associated fluxes and scaling trends in a rotor wake. Phys. Fluids 2005, 17, 085102. [Google Scholar] [CrossRef]
- Akbari, G.; Montazerin, N. On the role of anisotropic turbomachinery flow structures in inter-scale turbulence energy flux as deduced from SPIV measurements. J. Turbul. 2013, 14, 44–70. [Google Scholar] [CrossRef]
- Aluie, H.; Kurien, S. Joint downscale fluxes of energy and potential enstrophy in rotating stratified Boussinesq flows. EPL Europhys. Lett. 2011, 96, 44006. [Google Scholar] [CrossRef]
- Aluie, H.; Hecht, M.; Vallis, G.K. Mapping the Energy Cascade in the North Atlantic Ocean: The Coarse- Graining Approach. J. Phys. Oceanogr. 2018, 48, 225–244. [Google Scholar] [CrossRef]
- Buzzicotti, M.; Aluie, H.; Biferale, L.; Linkmann, M. Energy transfer in turbulence under rotation. Phys. Rev. Fluids 2018, 3, 291. [Google Scholar] [CrossRef]
- Aluie, H.; Eyink, G. Scale Locality of Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 2010, 104, 081101. [Google Scholar] [CrossRef]
- Aluie, H. Coarse-grained incompressible magnetohydrodynamics: Analyzing the turbulent cascades. New J. Phys. 2017, 19, 025008. [Google Scholar] [CrossRef]
- Sadek, M.; Aluie, H. Extracting the spectrum of a flow by spatial filtering. Phys. Rev. Fluids 2018, 3, 124610. [Google Scholar] [CrossRef]
- Chassaing, P. An alternative formulation of the equations of turbulent motion for a fluid of variable density. J. Mec. Theor. Appl. 1985, 4, 375–389. [Google Scholar]
- Bodony, D.J.; Lele, S.K. On using large-eddy simulation for the prediction of noise from cold and heated turbulent jets. Phys. Fluids 2005, 17, 085103. [Google Scholar] [CrossRef]
- Burton, G.C. Study of ultrahigh Atwood-number Rayleigh–Taylor mixing dynamics using the nonlinear large-eddy simulation method. Phys. Fluids 2011, 23, 045106. [Google Scholar] [CrossRef]
- Karimi, M.; Girimaji, S.S. Influence of orientation on the evolution of small perturbations in compressible shear layers with inflection points. Phys. Rev. E 2017, 95, 033112. [Google Scholar] [CrossRef] [PubMed]
- Kida, S.; Orszag, S.A. Energy and spectral dynamics in forced compressible turbulence. J. Sci. Comput. 1990, 5, 85–125. [Google Scholar] [CrossRef]
- Cook, A.W.; Zhou, Y. Energy transfer in Rayleigh-Taylor instability. Phys. Rev. E 2002, 66, 026312. [Google Scholar] [CrossRef] [PubMed]
- Grete, P.; O’Shea, B.W.; Beckwith, K.; Schmidt, W.; Christlieb, A. Energy transfer in compressible magnetohydrodynamic turbulence. Phys. Plasmas 2017, 24, 092311. [Google Scholar] [CrossRef]
- Zhao, D.; Aluie, H. Inviscid criterion for decomposing scales. Phys. Rev. Fluids 2018, 3, 054603. [Google Scholar] [CrossRef]
- Hesselberg, T. Die Gesetze der ausgeglichenen atmosphärischen Bewegungen. Beiträge Zur Phys. Der Freien Atmosphäre 1926, 12, 141–160. [Google Scholar]
- Favre, A.; Gaviglio, J.; Dumas, R. Further space-time correlations of velocity in a turbulent boundary layer. J. Fluid Mech. 1958, 3, 344–356. [Google Scholar] [CrossRef]
- Drivas, T.D.; Eyink, G.L. An Onsager singularity theorem for turbulent solutions of compressible Euler equations. Commun. Math. Phys. 2018, 359, 733–763. [Google Scholar] [CrossRef]
- Eyink, G.L. Multi-scale gradient expansion of the turbulent stress tensor. J. Fluid Mech. 2006, 549, 159–190. [Google Scholar] [CrossRef]
- Bardina, J.; Ferziger, J.H.; Reynolds, W.C. Improved subgrid-scale models for large-eddy simulation. In Proceedings of the 13th Fluid and Plasma Dynamics Conference, Snowmass, CO, USA, 14–16 July 1980. [Google Scholar]
- Sharp, D.H. An overview of Rayleigh-Taylor instability. Phys. D Nonlinear Phenom. 1984, 12, 3–18. [Google Scholar] [CrossRef]
- Kundu, P.K.; Cohen, I.M. Fluid Mechanics; Academic Press: Oxford, UK, 2008. [Google Scholar]
- Federrath, C.; Klessen, R.S.; Schmidt, W. The Density Probability Distribution in Compressible Isothermal Turbulence: Solenoidal versus Compressive Forcing. Astrophys. J. Lett. 2008, 688, L79. [Google Scholar] [CrossRef]
- Eswaran, V.; Pope, S. An examination of forcing in direct numerical simulations of turbulence. Comput. Fluids 1988, 16, 257–278. [Google Scholar] [CrossRef]
- Jagannathan, S.; Donzis, D.A. Reynolds and Mach number scaling in solenoidally-forced compressible turbulence using high-resolution direct numerical simulations. J. Fluid Mech. 2016, 789, 669–707. [Google Scholar] [CrossRef]
- Wang, J.; Wang, L.P.; Xiao, Z.; Shi, Y.; Chen, S. A hybrid numerical simulation of isotropic compressible turbulence. J. Comput. Phys. 2010, 229, 5257–5279. [Google Scholar] [CrossRef]
- Petersen, M.R.; Livescu, D. Forcing for statistically stationary compressible isotropic turbulence. Phys. Fluids 2010, 22, 116101. [Google Scholar] [CrossRef]
- Livescu, D.; Ristorcelli, J.R.; Gore, R.A.; Dean, S.H.; Cabot, W.H.; Cook, A.W. High-Reynolds number Rayleigh-Taylor turbulence. J. Turbul. 2009, 10, 1–32. [Google Scholar] [CrossRef]
- Zhao, D.; Betti, R.; Aluie, H. The cascade in compressible Rayleigh-Taylor turbulence. 2019. in preparation. [Google Scholar]
- Kritsuk, A.G.; Ustyugov, S.D.; Norman, M.L.; Padoan, P. Self-organization in Turbulent Molecular Clouds: Compressional Versus Solenoidal Modes. In Numerical Modeling of Space Plasma Flows, Astronum-2009; Pogorelov, N.V., Audit, E., Zank, G.P., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2010; Volume 429, p. 15. [Google Scholar]
- Sarkar, S.; Erlebacher, G.; Hussaini, M.Y.; Kreiss, H.O. The analysis and modelling of dilatational terms in compressible turbulence. J. Fluid Mech. 1991, 227, 473–493. [Google Scholar] [CrossRef]
- Shivamoggi, B.K. Equilibrium statistical mechanics of compressible isotropic turbulence. Europhys. Lett. 1997, 38, 657–662. [Google Scholar] [CrossRef]

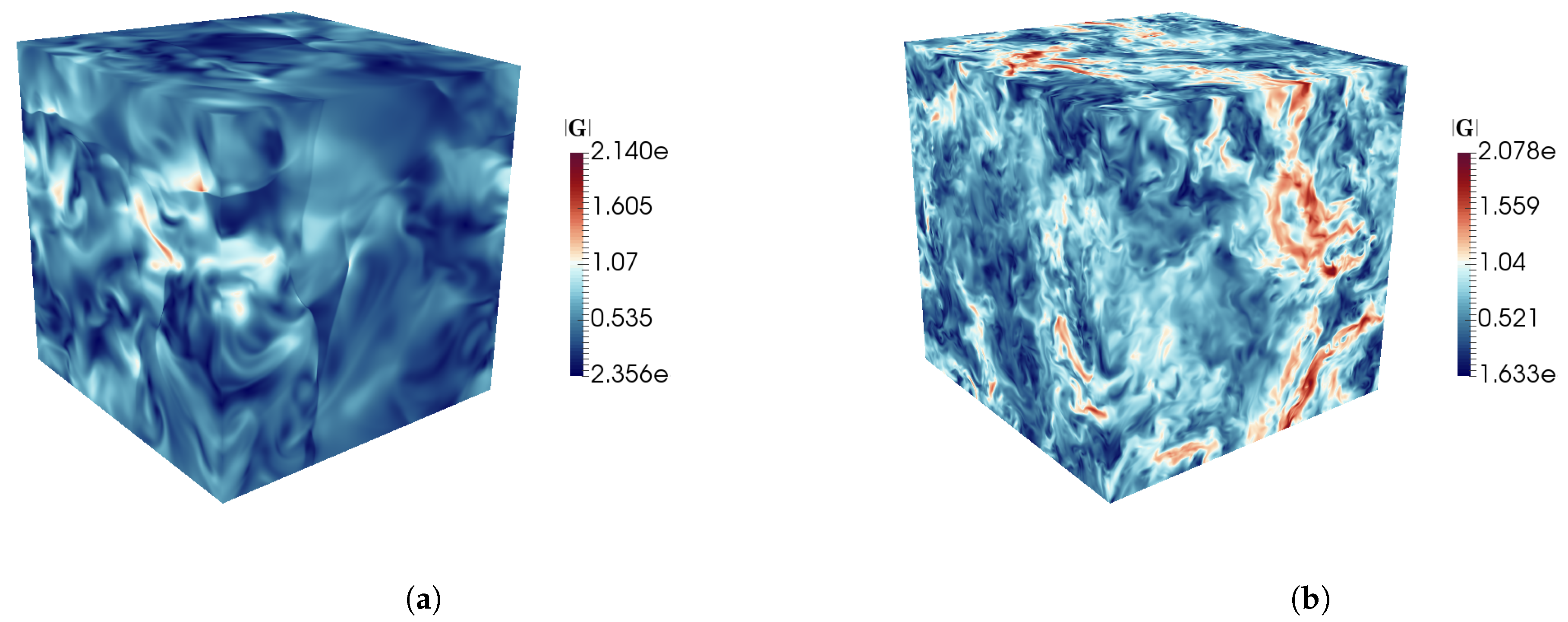
| Run | N | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1024 | 0.01 | 0.23 | 65 | 0.50 | 0.74 | 0.23 | ||
| 2 | 512 | 0.01 | 0.22 | 33 | 0.46 | 0.51 | 0.28 | ||
| 3 | 512 | 0.6 | 0.33 | 206 | 0.05 | 0.02 | 1.78 | ||
| 4 | 256 | 0.01 | 0.21 | 18 | 0.54 | 0.56 | 0.25 | ||
| 5 | 256 | 0.6 | 0.42 | 150 | 0.04 | 0.01 | 2.1 | ||
| 6 | 256 | 1.0 | 0.46 | 175 | 0.03 | 0.003 | 2.2 | ||
| 7 | 128 | 0.01 | 0.20 | 10 | 0.65 | 0.80 | 0.24 | ||
| 8 | 128 | 0.6 | 0.50 | 105 | 0.05 | 0.01 | 2.3 | ||
| 9 | 128 | 1.0 | 0.40 | 95 | 0.03 | 0.01 | 2.0 |
| Filter Type | Kernel | ||
|---|---|---|---|
| Box | 0.93 | 0.94 | |
| Gaussian | 0.97 | 0.97 | |
| Sharp spectral | 0.27 | 0.28 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lees, A.; Aluie, H. Baropycnal Work: A Mechanism for Energy Transfer across Scales. Fluids 2019, 4, 92. https://doi.org/10.3390/fluids4020092
Lees A, Aluie H. Baropycnal Work: A Mechanism for Energy Transfer across Scales. Fluids. 2019; 4(2):92. https://doi.org/10.3390/fluids4020092
Chicago/Turabian StyleLees, Aarne, and Hussein Aluie. 2019. "Baropycnal Work: A Mechanism for Energy Transfer across Scales" Fluids 4, no. 2: 92. https://doi.org/10.3390/fluids4020092
APA StyleLees, A., & Aluie, H. (2019). Baropycnal Work: A Mechanism for Energy Transfer across Scales. Fluids, 4(2), 92. https://doi.org/10.3390/fluids4020092