Time-Reversal Analogy by Nonlinear Acoustic–Gravity Wave Triad Resonance
Abstract
1. Introduction
2. Preliminaries
3. Linear Solution
4. Nonlinear Triad Resonance
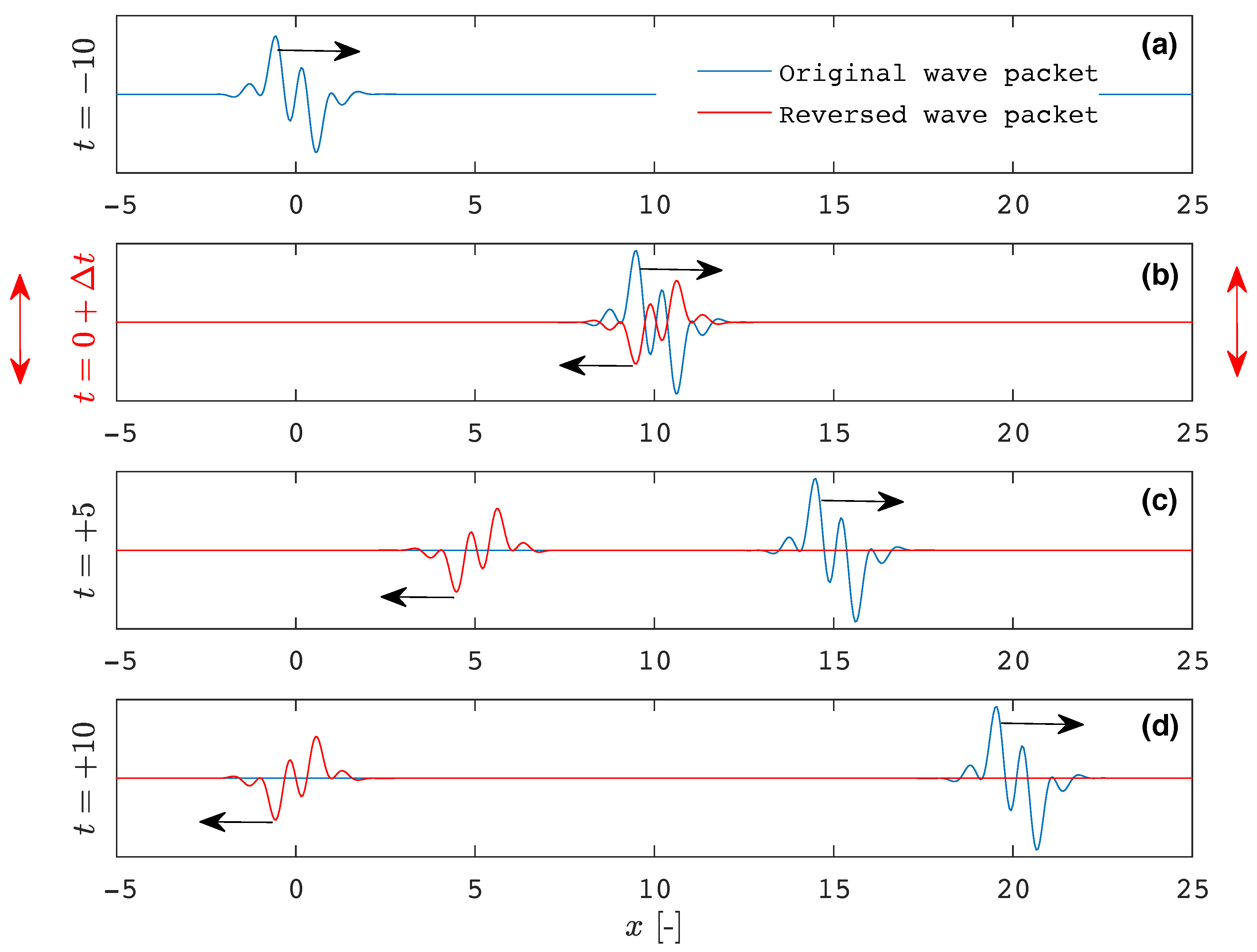
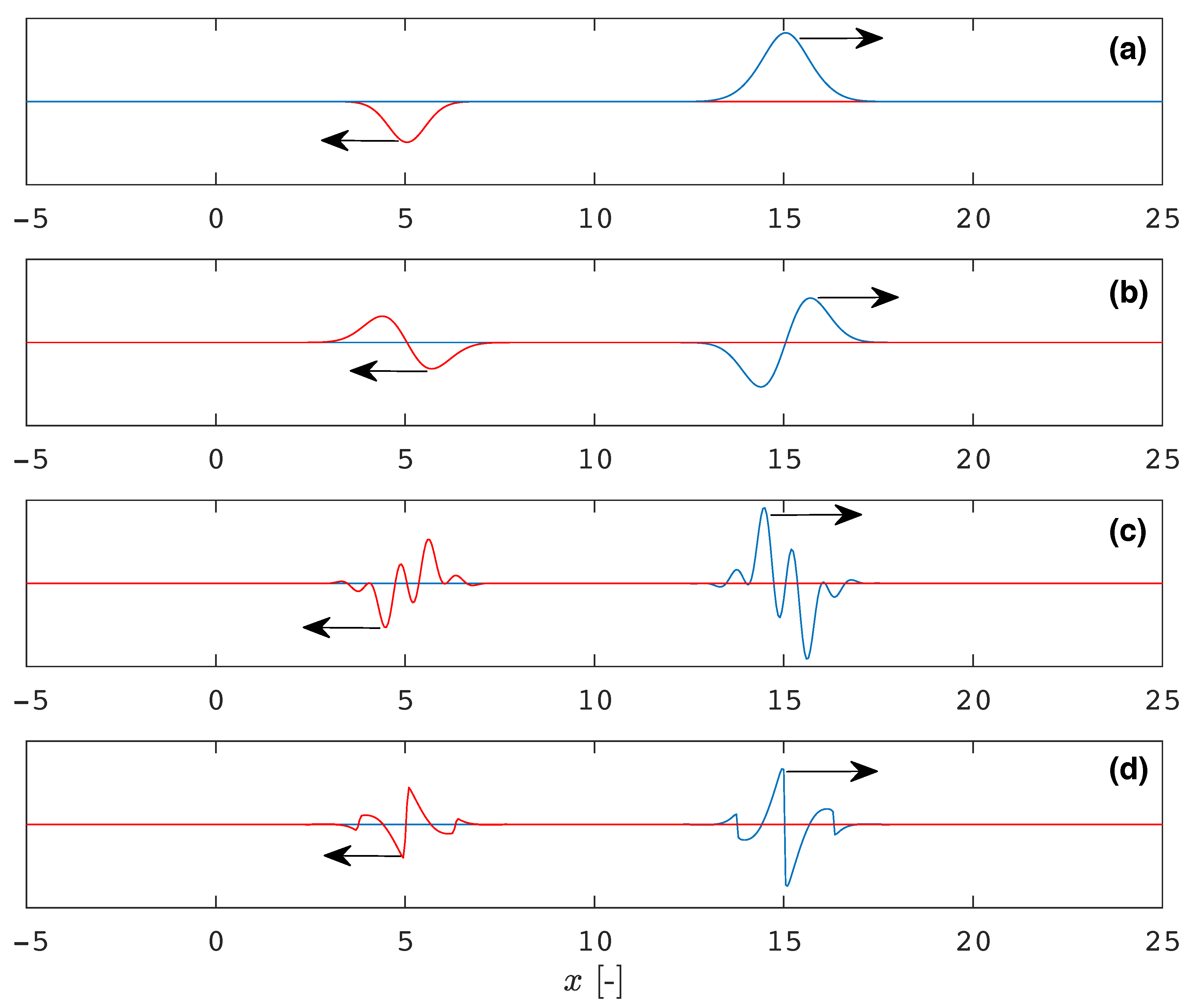
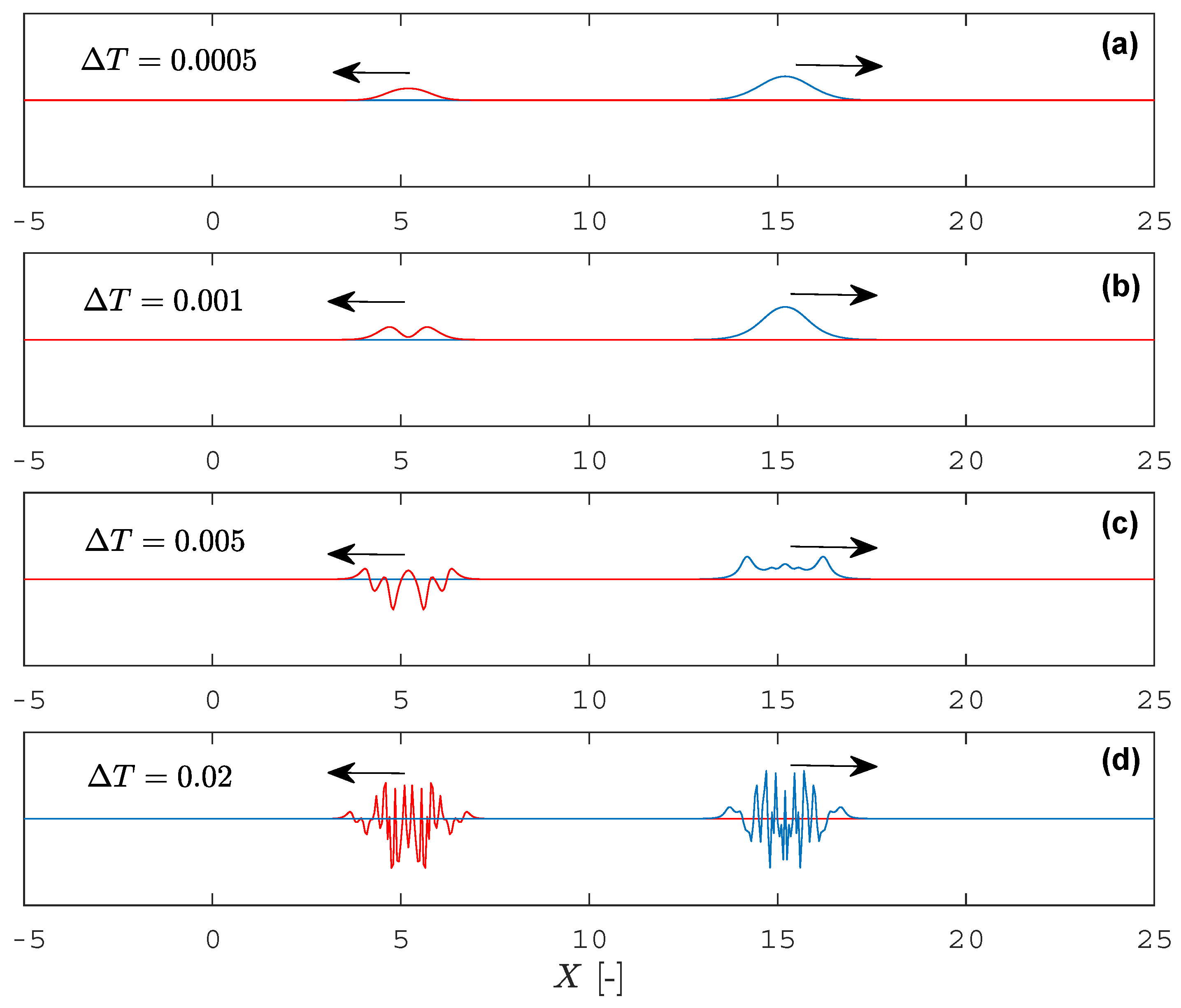
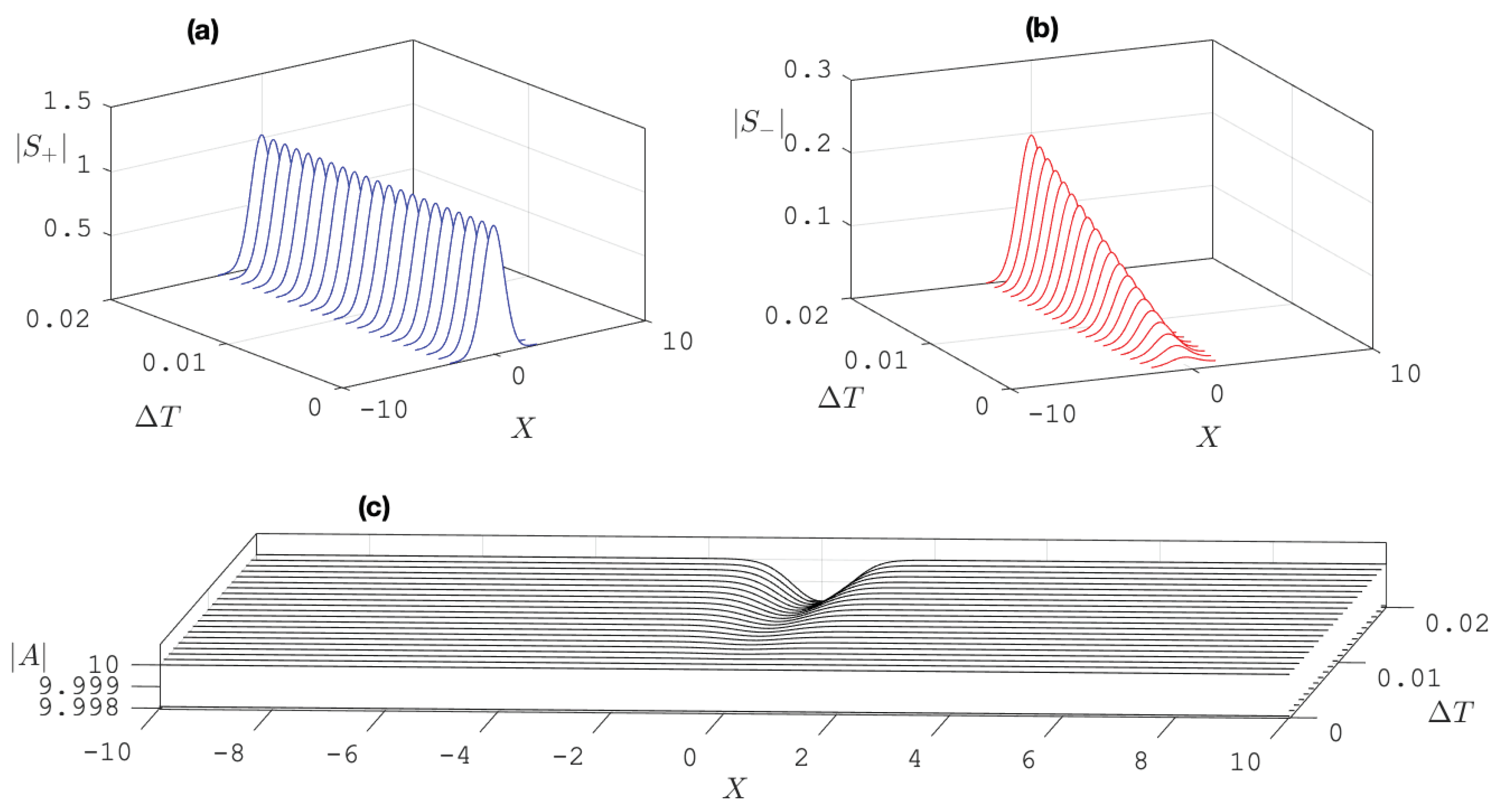
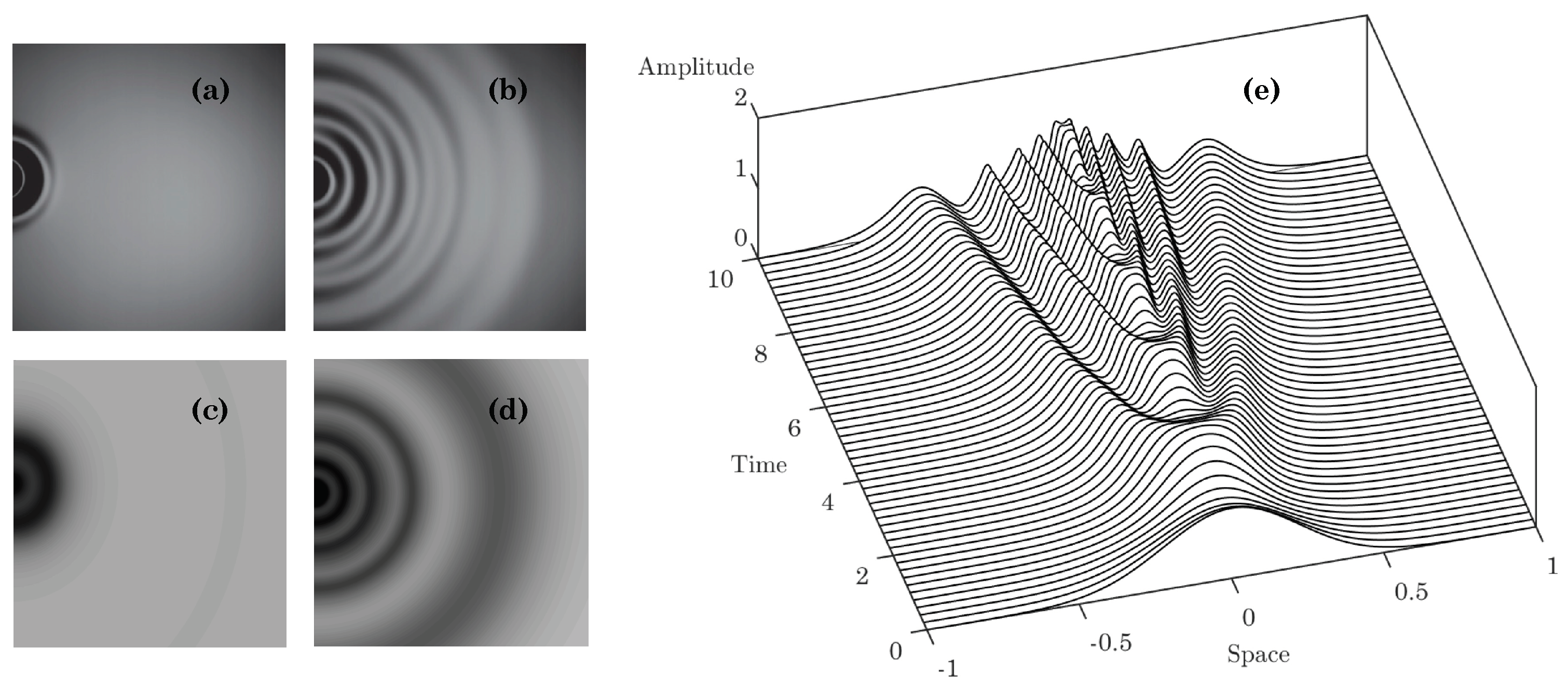
5. Results and Discussion
A Note on the Evolution of Faraday-Type Waves
Funding
Conflicts of Interest
References
- Bacot, V.; Labousse, M.; Eddi, A.; Fink, M.; Fort, E. Time reversal and holography with spacetime transformations. Nat. Phys. 2016, 12, 972–977. [Google Scholar] [CrossRef]
- Fink, M.; Fort, E. From the time-reversal mirror to the instantaneous time mirror. Eur. Phys. J. Spec. Top. 2017, 226, 1477–1486. [Google Scholar] [CrossRef]
- Przadka, A.; Feat, S.; Petitjeans, P.; Pagneux, V.; Maurel, A.; Fink, M. Time reversal of water waves. Phys. Rev. Lett. 2012, 109, 064501. [Google Scholar] [CrossRef] [PubMed]
- Chabchoub, A.; Fink, M. Time-reversal generation of rogue waves. Phys. Rev. Lett. 2014, 112, 124101. [Google Scholar] [CrossRef] [PubMed]
- Fink, M. Time reversal of ultrasonic fields. I. Basic principles. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1992, 39, 555–566. [Google Scholar] [CrossRef] [PubMed]
- Fink, M. Time-reversal waves and super resolution. J. Phys. 2008, 124, 012004. [Google Scholar] [CrossRef]
- Draeger, C.; Fink, M. One-channel time reversal of elastic waves in a chaotic 2D-silicon cavity. Phys. Rev. Lett. 1997, 79, 407–410. [Google Scholar] [CrossRef]
- Lerosey, G.; De Rosny, J.; Tourin, A.; Derode, A.; Montaldo, G.; Fink, M. Time reversal of electromagnetic waves. Phys. Rev. Lett. 2004, 92, 193904. [Google Scholar] [CrossRef] [PubMed]
- Longuet-Higgins, M.S. A theory of the origin of microseisms. Philos. Trans. R. Soc. Lond. 1950, 243, 1–35. [Google Scholar] [CrossRef]
- Kadri, U.; Stiassnie, M. Generation of an acoustic-gravity wave by two gravity waves, and their subsequent mutual interaction. J. Fluid Mech. 2013, 735, R6. [Google Scholar] [CrossRef]
- Kadri, U.; Akylas, T.R. On resonant triad interactions of acoustic–gravity waves. J. Fluid Mech. 2016, 788, R1. [Google Scholar] [CrossRef]
- Eyov, E.; Klar, A.; Kadri, U.; Stiassnie, M. Progressive waves in a compressible ocean with elastic bottom. Wave Motion 2013, 50, 929–939. [Google Scholar] [CrossRef]
- Gabor, D. A new microscopic principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef] [PubMed]
- Bojarski, N. A survey of the near-field far-field inverse scattering inverse source integral equation. IEEE Trans. Antenna Propag. 1982, 30, 975–979. [Google Scholar] [CrossRef]
- Eddi, A.; Sultan, E.; Moukhtar, J.; Fort, E.; Rossi, M.; Couder, Y. Information stored in Faraday waves: The origin of a path memory. J. Fluid Mech. 2011, 674, 433–463. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kadri, U. Time-Reversal Analogy by Nonlinear Acoustic–Gravity Wave Triad Resonance. Fluids 2019, 4, 91. https://doi.org/10.3390/fluids4020091
Kadri U. Time-Reversal Analogy by Nonlinear Acoustic–Gravity Wave Triad Resonance. Fluids. 2019; 4(2):91. https://doi.org/10.3390/fluids4020091
Chicago/Turabian StyleKadri, Usama. 2019. "Time-Reversal Analogy by Nonlinear Acoustic–Gravity Wave Triad Resonance" Fluids 4, no. 2: 91. https://doi.org/10.3390/fluids4020091
APA StyleKadri, U. (2019). Time-Reversal Analogy by Nonlinear Acoustic–Gravity Wave Triad Resonance. Fluids, 4(2), 91. https://doi.org/10.3390/fluids4020091



