An Experimental and Computational Study on Inverted Flag Dynamics for Simultaneous Wind–Solar Energy Harvesting
Abstract
1. Introduction
2. Materials and Methods
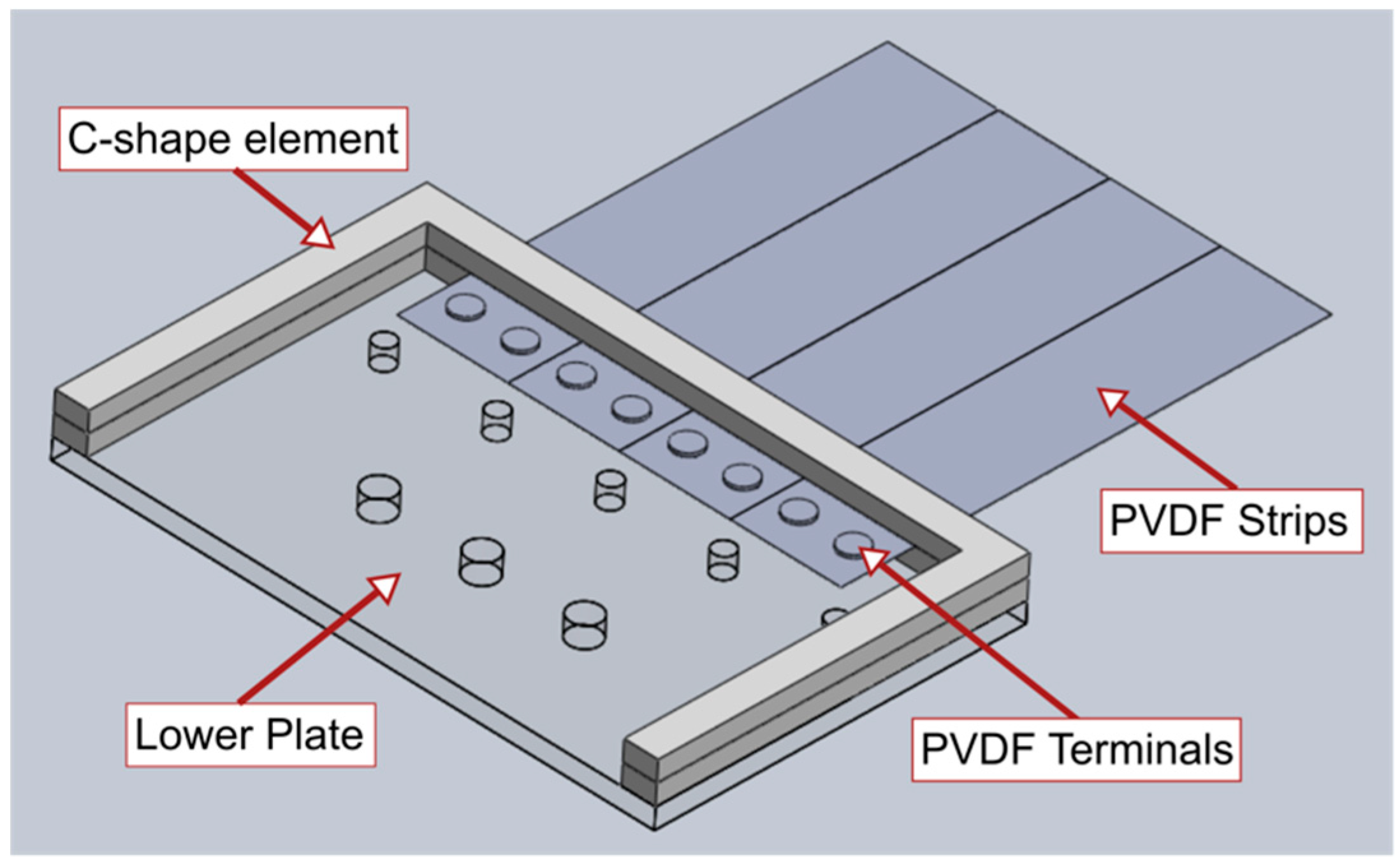
2.1. Piezo-Solar Inverted Flag Harvester
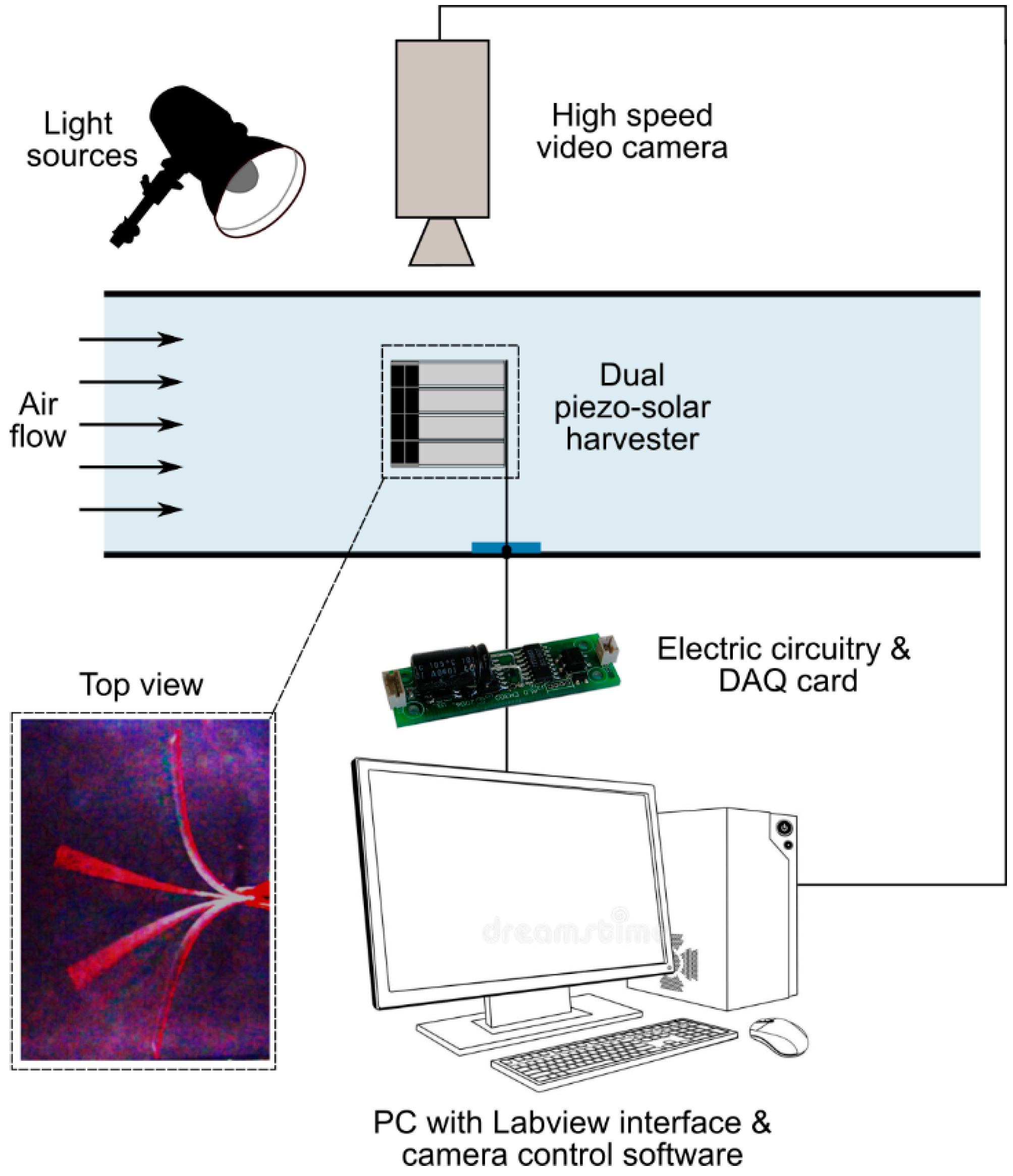
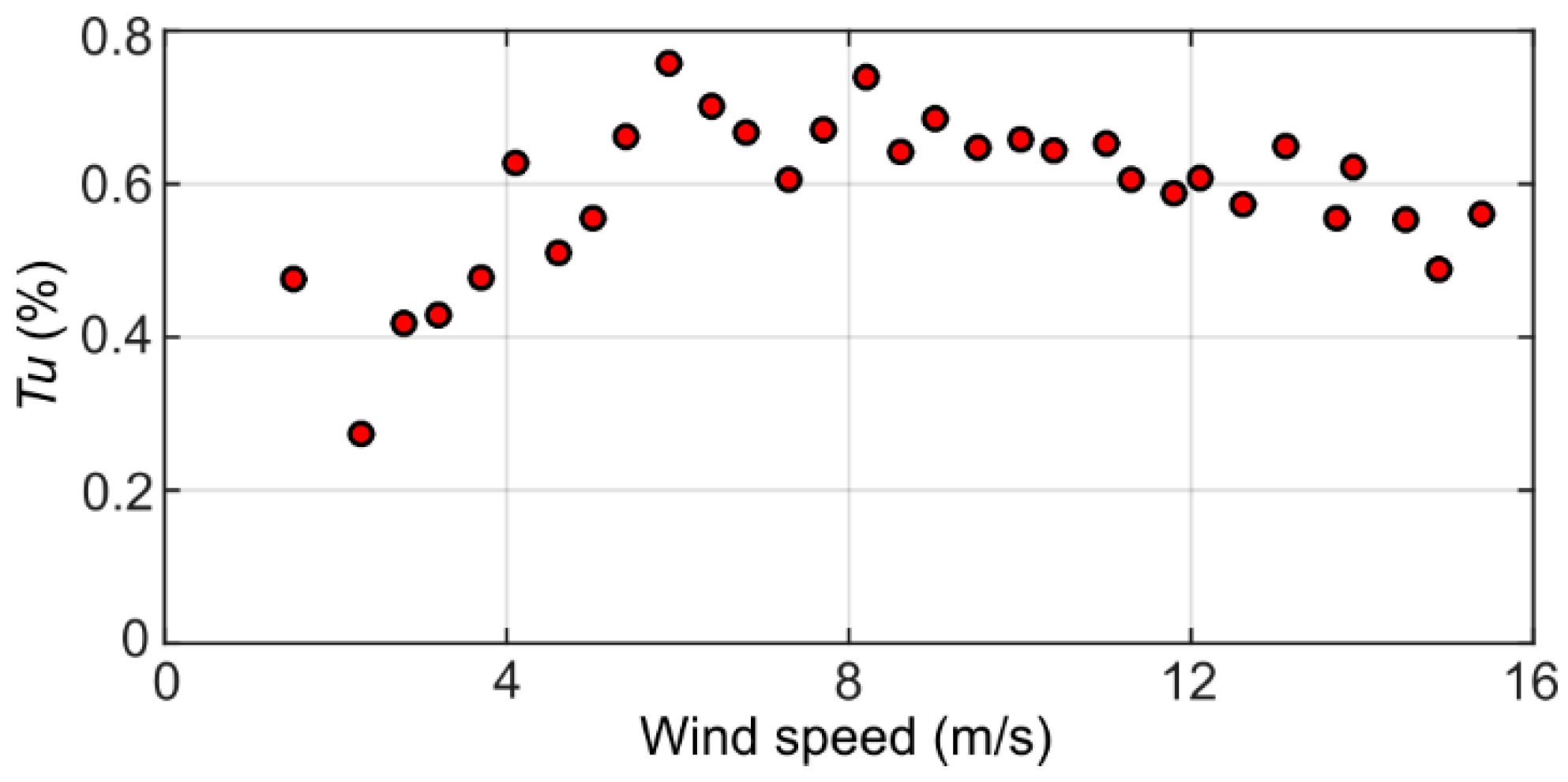
2.2. Experimental Set-Up and Methodology
2.3. Numerical Model
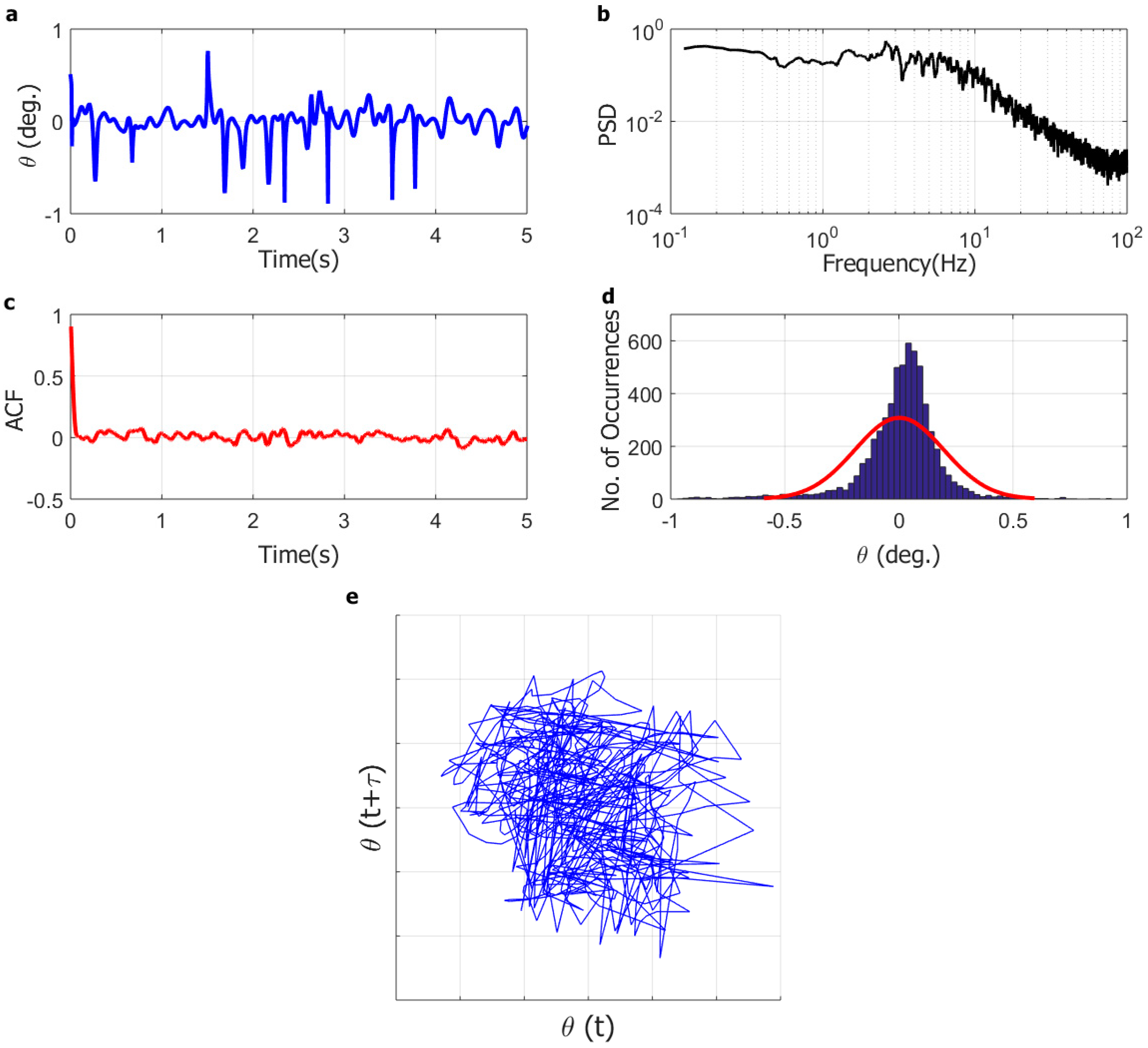
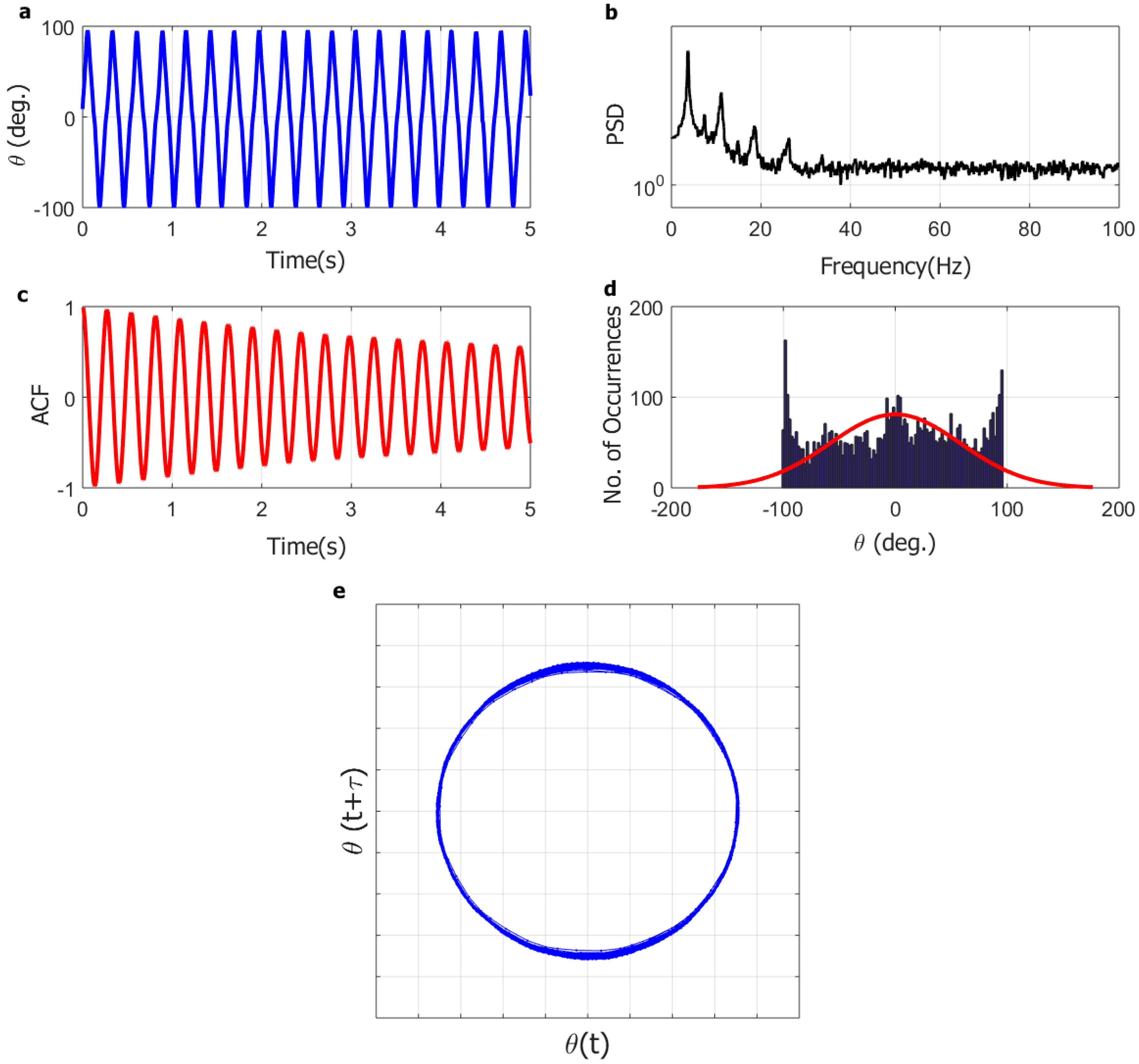
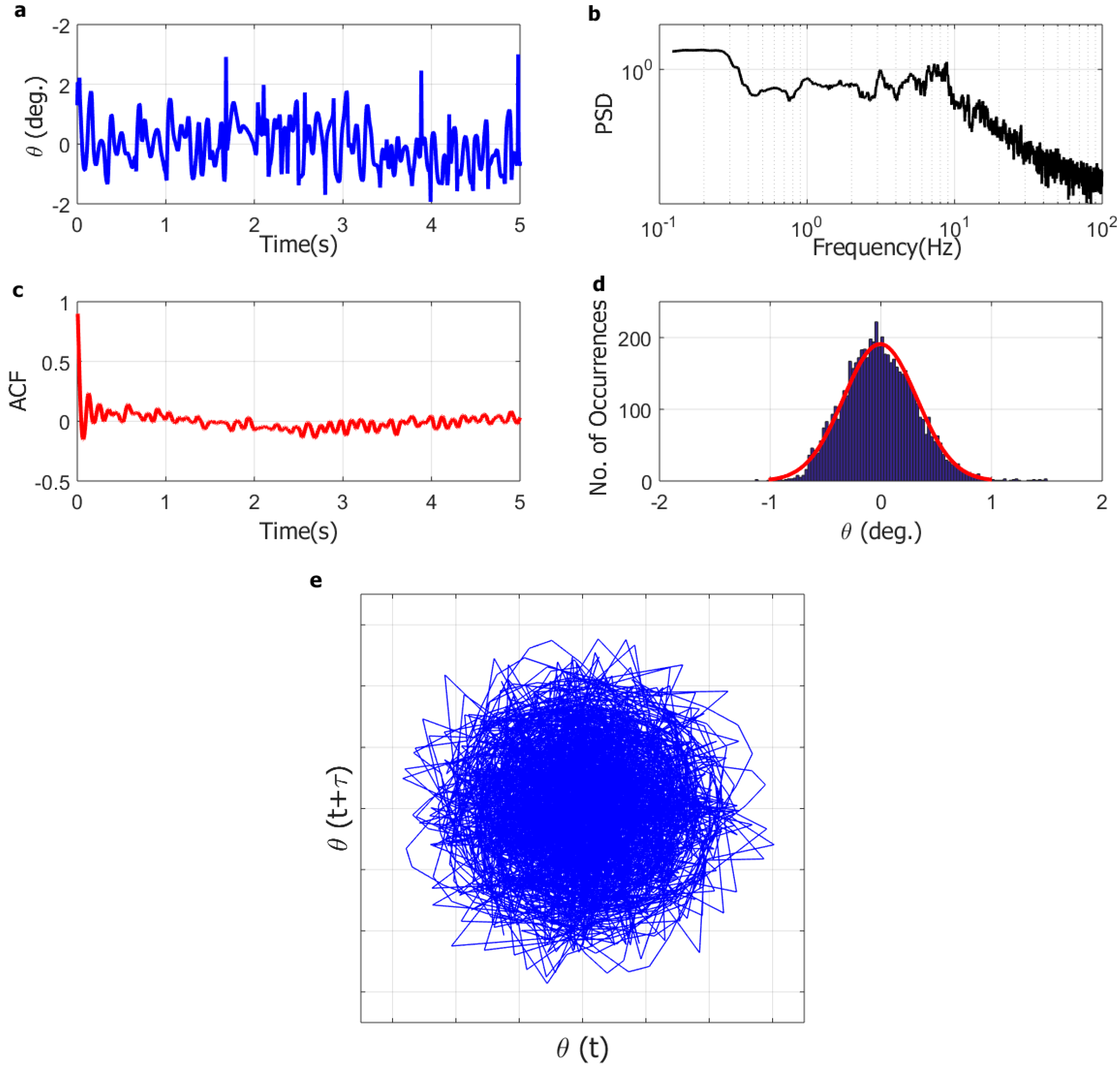
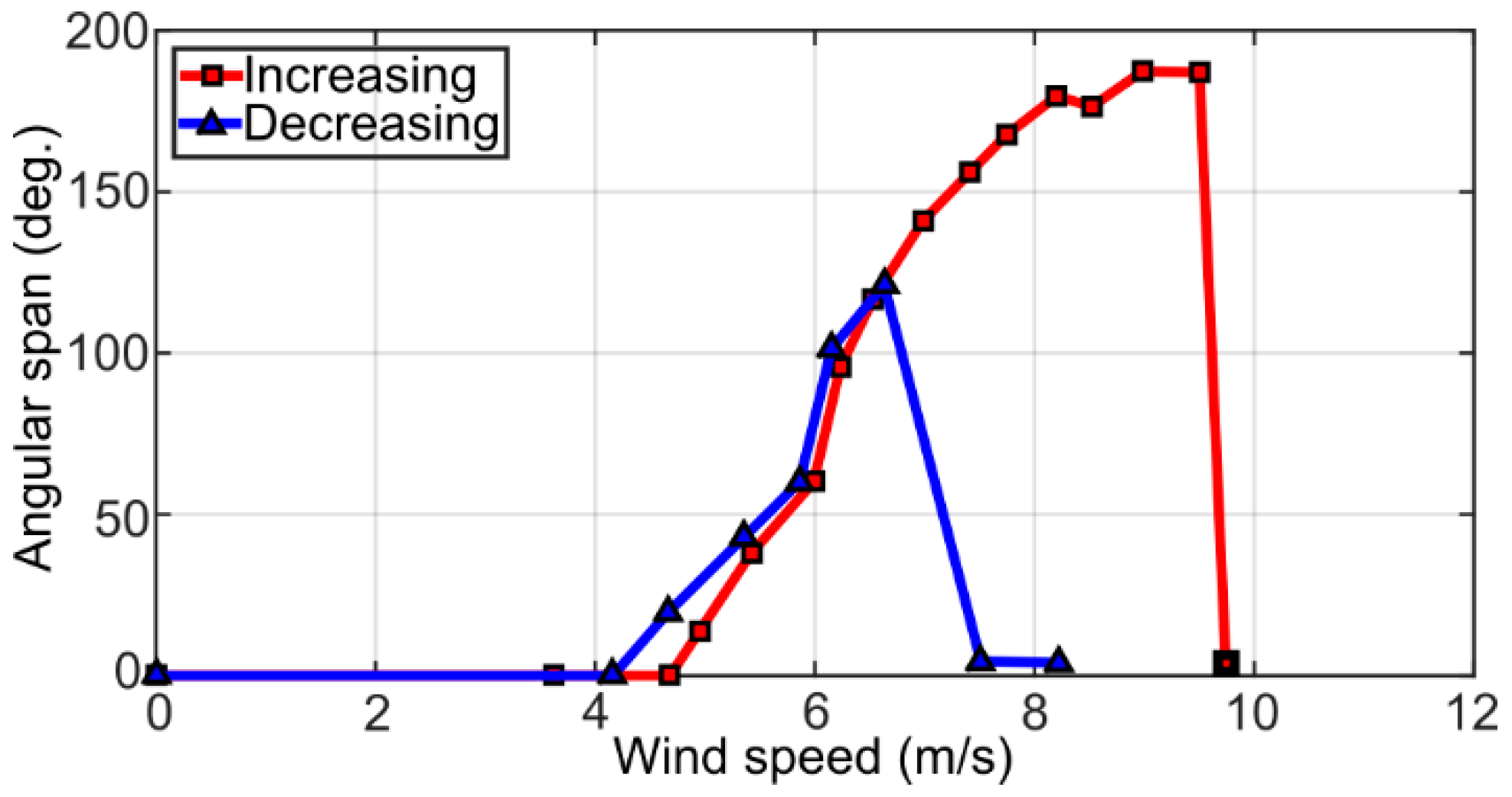
3. Results and Discussion
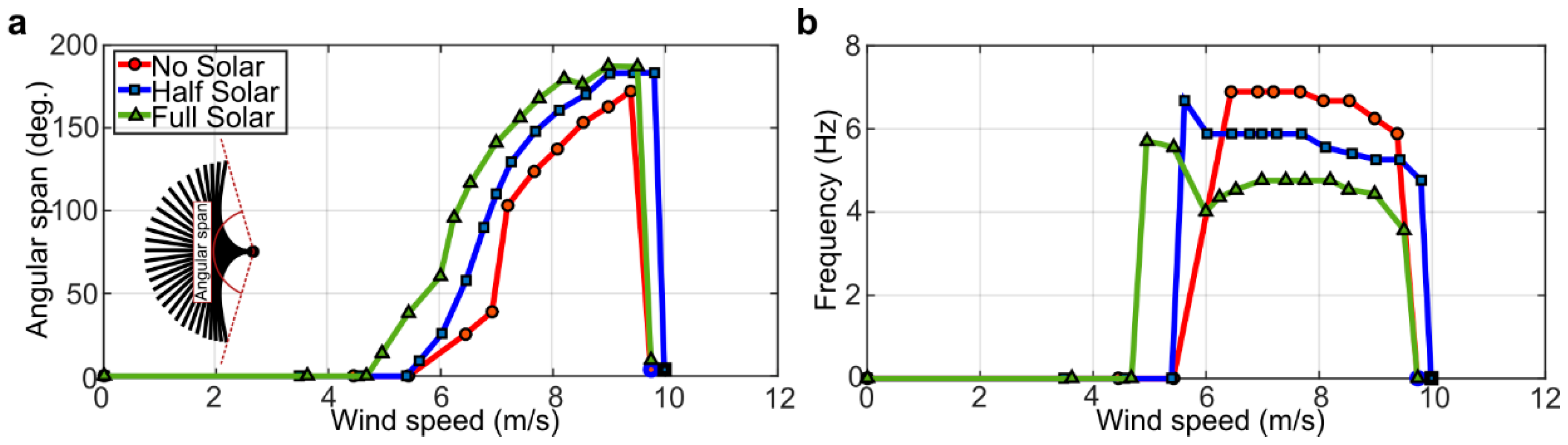
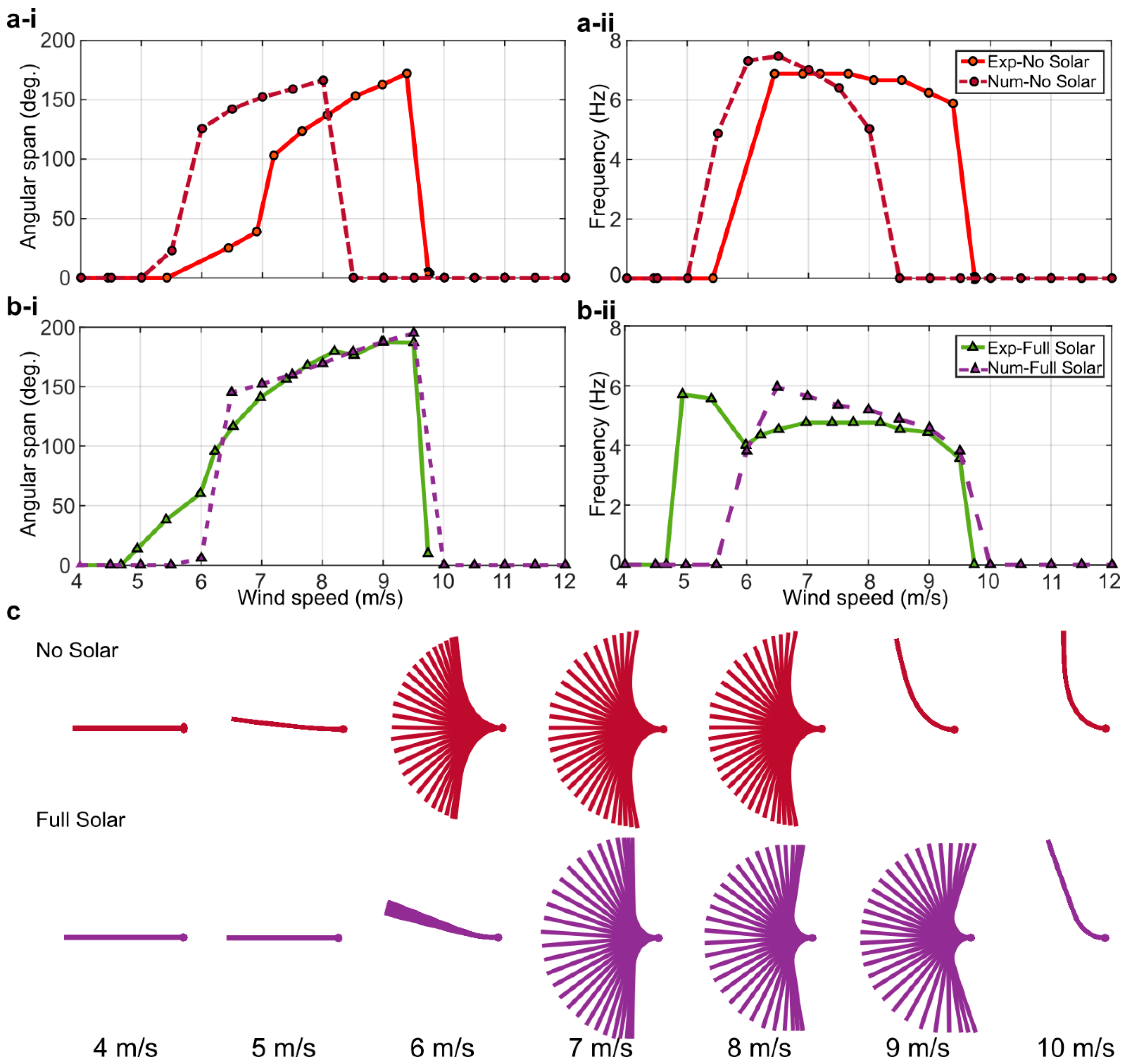
3.1. Inverted Flag Dynamics
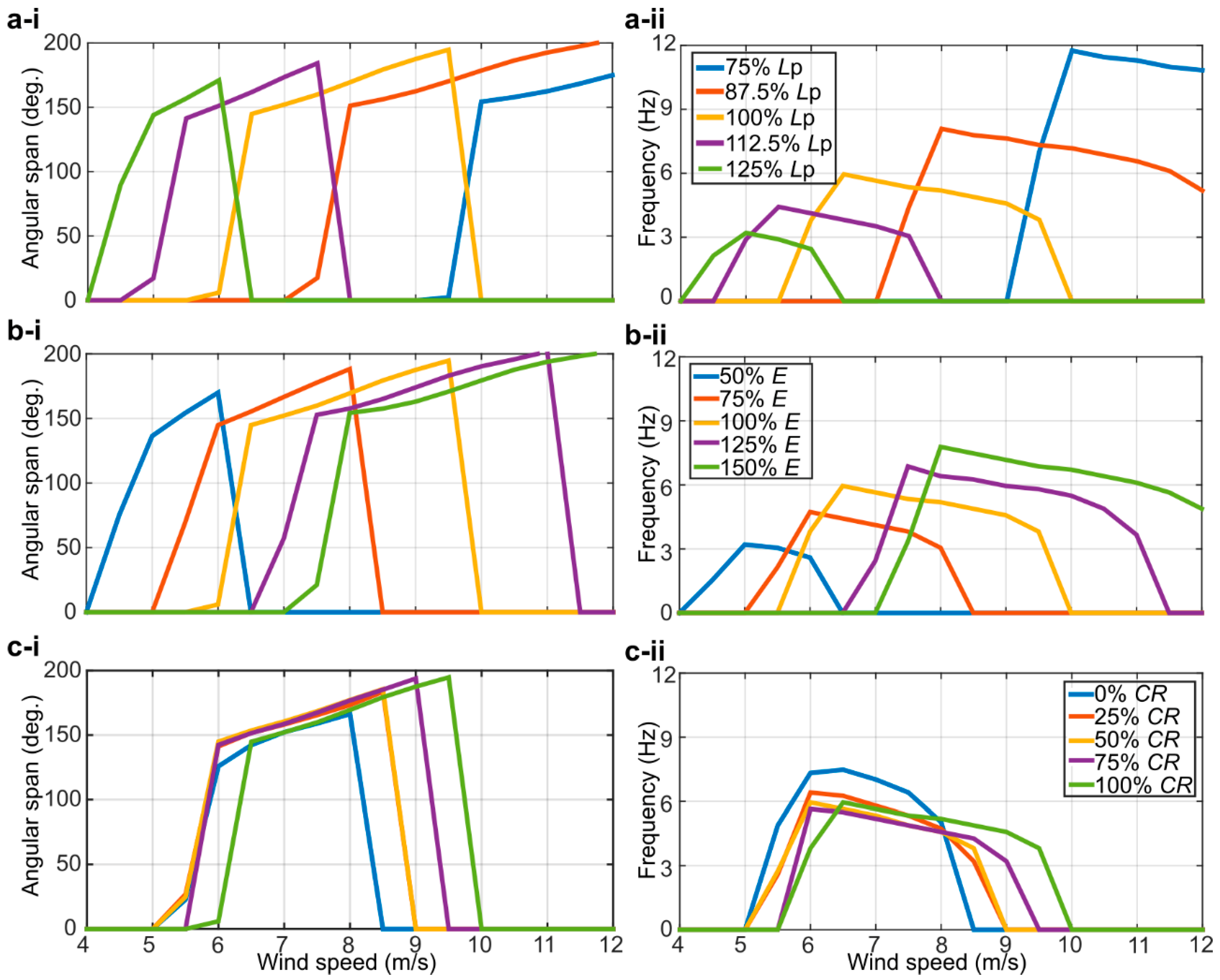
3.2. Numerical Simulations
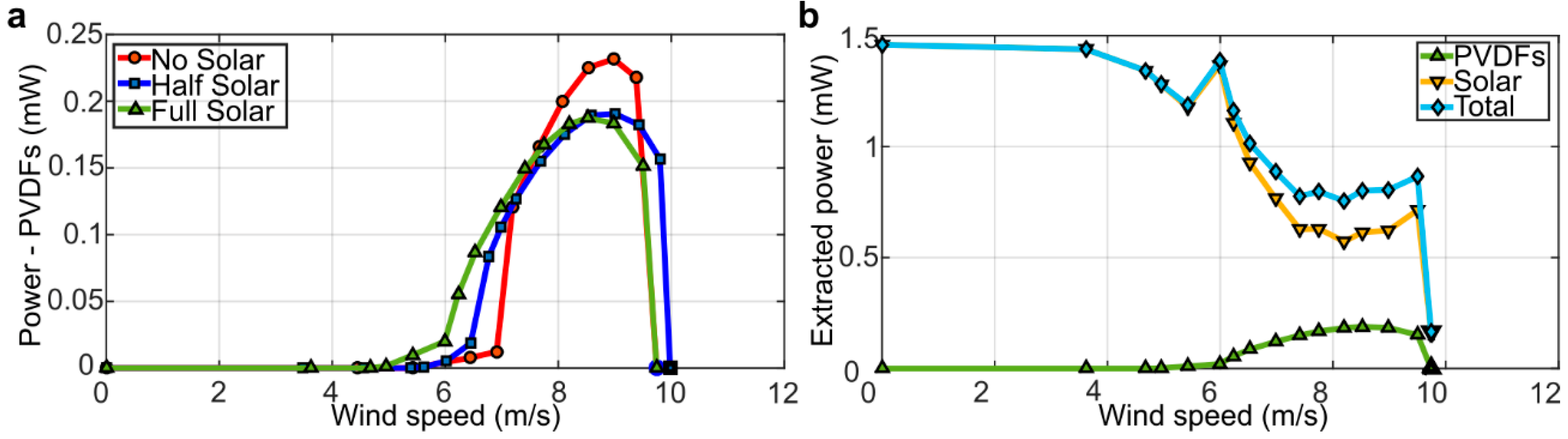
3.3. Power Generation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Paradiso, J.A.; Starner, T. Energy scavenging for mobile and wireless electronics. IEEE Pervasive Comput. 2005, 4, 18–27. [Google Scholar] [CrossRef]
- Mathúna, C.Ó.; O’Donnell, T.; Martinez-Catala, R.V.; Rohan, J.; O’Flynn, B. Energy scavenging for long-term deployable wireless sensor networks. Talanta 2008, 75, 613–623. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, Y.; Xu, C.; Lin, L.; Snyder, R.L.; Wang, Z.L. Self-powered system with wireless data transmission. Nano Lett. 2011, 11, 2572–2577. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L.; Zhu, G.; Yang, Y.; Wang, S.; Pan, C. Progress in nanogenerators for portable electronics. Mater. Today 2012, 15, 532–543. [Google Scholar] [CrossRef]
- Gubbi, J.; Buyya, R.; Marusic, S.; Palaniswami, M. Internet of Things (IoT): A vision, architectural elements, and future directions. Future Gener. Comput. Syst. 2013, 29, 1645–1660. [Google Scholar] [CrossRef]
- Hancke, G.P.; de Carvalho e Silva, B.; Hanche, G.P. The role of advanced sensing in Smart Cities. Sensors 2013, 13, 393–425. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar] [CrossRef]
- Renno, J.M.; Daqaq, M.F.; Inman, D.J. On the optimal energy harvesting from a vibration source. J. Sound Vib. 2009, 320, 386–405. [Google Scholar] [CrossRef]
- Stanton, S.C.; Erturk, A.; Mann, B.P.; Inman, D.J. Nonlinear piezoelectricity in electro-elastic energy harvesters: Modelling and experimental identification. J. Appl. Phys. 2010, 108, 074903. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Najar, F.; Nayfeh, A.H.; Ayed, S.B. An energy harvester using piezoelectric cantilever beams undergoing coupled bending–torsion vibrations. Smart Mater. Struct. 2011, 20, 115007. [Google Scholar] [CrossRef]
- Doaré, O.; Michelin, S. Piezoelectric coupling in energy-harvesting fluttering flexible plates: Linear stability analysis and conversion efficiency. J. Fluids Struct. 2011, 27, 1357–1375. [Google Scholar] [CrossRef]
- Michelin, S.; Doaré, O. Energy harvesting efficiency of piezoelectric flags in axial flows. J. Fluid Mech. 2013, 714, 489–504. [Google Scholar] [CrossRef]
- Hobeck, J.D.; Inman, D.J. A distributed parameter electromechanical and statistical model for energy harvesting from turbulence-induced vibration. Smart Mater. Struct. 2014, 23, 115003. [Google Scholar] [CrossRef]
- Nabawy, M.R.A.; Parslew, B.; Crowther, W.J. Dynamic performance of unimorph piezoelectric bending actuators. Proc. Inst. Mech. Eng. I J. Syst. Control Eng. 2015, 229, 118–129. [Google Scholar] [CrossRef]
- McCarty, J.M.; Watkins, S.; Deivasigamani, A.; John, S.J. Fluttering energy harvesters in the wind: A review. J. Sound Vib. 2016, 361, 355–377. [Google Scholar] [CrossRef]
- Nabavi, S.; Zhang, L. Portable wind energy harvesters for low-power applications: A survey. Sensors 2016, 16, 1101. [Google Scholar] [CrossRef] [PubMed]
- Nabawy, M.R.A.; Crowther, W.J. Dynamic electromechanical coupling of piezoelectric bending actuators. Micromachines 2016, 7, 12. [Google Scholar] [CrossRef]
- Shoele, K.; Mittal, R. Flutter instability of a thin flexible plate in a channel. J. Fluid Mech. 2016, 786, 29–46. [Google Scholar] [CrossRef]
- Shoele, K.; Mittal, R. Energy harvesting by flow-induced flutter in a simple model of an inverted piezoelectric flag. J. Fluid Mech. 2016, 790, 582–606. [Google Scholar] [CrossRef]
- Vatansever, D.; Hadimani, R.L.; Shah, T.; Siores, E. An investigation of energy harvesting from renewable sources with PVDF and PZT. Smart Mater. Struct. 2011, 20, 055019. [Google Scholar] [CrossRef]
- Kim, D.; Cossé, J.; Huertas Cerdeira, C.; Gharib, M. Flapping dynamics of an inverted flag. J. Fluid Mech. 2013, 736, R1. [Google Scholar] [CrossRef]
- Cossé, J.; Sader, J.; Kim, D.; Huertas Cerdeira, C.; Gharib, M. The effect of aspect ratio and angle of attack on the transition regions of the inverted flag instability. In Proceedings of the ASME 2014 Pressure Vessels & Piping Conference, Anaheim, CA, USA, 20–24 July 2014. PVP2014-28445. [Google Scholar]
- Orrego, S.; Shoele, K.; Ruas, A.; Doran, K.; Caggiano, B.; Mittal, R.; Kang, S.H. Harvesting ambient wind energy with an inverted piezoelectric flag. Appl. Energy 2017, 194, 212–222. [Google Scholar] [CrossRef]
- Li, S.; Yuan, J.; Lipson, H. Ambient wind energy harvesting using cross-flow fluttering. J. Appl. Phys. 2011, 109, 026104. [Google Scholar] [CrossRef]
- McCarty, J.M.; Deivasigamani, A.; John, S.J.; Watkins, S.; Coman, F.; Petersen, P. Downstream flow structures of a fluttering piezoelectric energy harvester. Exp. Them. Fluid Sci. 2013, 51, 279–290. [Google Scholar] [CrossRef]
- McCarty, J.M.; Deivasigamani, A.; Watkins, S.; John, S.J.; Coman, F.; Petersen, P. On the visualisation of flow structures downstream of fluttering piezoelectric energy harvesters in a tandem configuration. Exp. Them. Fluid Sci. 2014, 57, 407–419. [Google Scholar] [CrossRef]
- Hobeck, J.D.; Inman, D.J. Artificial piezoelectric grass for energy harvesting from turbulence-induced vibration. Smart Mater. Struct. 2012, 21, 105024. [Google Scholar] [CrossRef]
- Shi, S.; New, T.H.; Liu, Y. Flapping dynamics of a low aspect-ratio energy-harvesting membrane immersed in a square cylinder wake. Exp. Them. Fluid Sci. 2013, 46, 151–161. [Google Scholar] [CrossRef]
- Shi, S.; New, T.H.; Liu, Y. Effects of aspect-ratio on the flapping behaviour of energy-harvesting membrane. Exp. Them. Fluid Sci. 2014, 52, 339–346. [Google Scholar] [CrossRef]
- Erturk, A.; Delporte, G. Underwater thrust and power generation using flexible piezoelectric composites: An experimental investigation toward self-powered swimmer-sensor platforms. Smart Mater. Struct. 2011, 20, 125013. [Google Scholar] [CrossRef]
- Haji, M.N.; Kluger, J.M.; Sapsis, T.P.; Slocum, A.H. A symbiotic approach to the design of offshore wind turbines with other energy harvesting systems. Ocean Eng. 2018, 169, 673–681. [Google Scholar] [CrossRef]
- Iqbal, M.; Khan, F.U. Hybrid vibration and wind energy harvesting using combined piezoelectric and electromagnetic conversion for bridge health monitoring applications. Energy Convers. Manag. 2018, 172, 611–618. [Google Scholar] [CrossRef]
- Deivasigamani, A.; McCarthy, J.M.; John, S.; Watkins, S.; Coman, F. Investigation of asymmetrical configurations for piezoelectric energy harvesting from fluid flow. In Proceedings of the ASME 2014 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, New Port, RI, USA, 8–10 September 2014. [Google Scholar]
- Cioncolini, A.; Silva-Leon, J.; Cooper, D.; Quinn, M.K.; Iacovides, H. Axial-flow-induced vibration experiments on cantilevered rods for nuclear reactor applications. Nucl. Eng. Des. 2018, 338, 102–118. [Google Scholar] [CrossRef]
- Silva-Leon, J.; Cioncolini, A.; Filippone, A.; Domingos, M. Flow-induced motions of flexible filaments hanging in cross-flow. Exp. Therm. Fluid Sci. 2018, 97, 254–269. [Google Scholar] [CrossRef]
- Silva-Leon, J.; Cioncolini, A. Modulation of flexible filament dynamics due to attachment angle relative to the flow. Exp. Therm. Fluid Sci. 2019, 102, 232–244. [Google Scholar] [CrossRef]
- Bradley, E.; Kantz, H. Non-linear time-series analysis revisited. Chaos 2015, 25, 097610. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Doolen, G. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Shi, B. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 2002, 65, 046308. [Google Scholar] [CrossRef]
- He, X.; Luo, L. A priori derivation of the lattice Boltzmann equation. Phys. Rev. E 1997, 55, R6333. [Google Scholar] [CrossRef]
- Shan, X.; He, X. Discretization of the velocity space in the solution of the Boltzmann equation. Phys. Rev. Lett. 1998, 80, 65–68. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2014. [Google Scholar]
- Zienkiewicz, O.J.; Taylor, R.L.; Fox, D. The Finite Element Method for Solid and Structural Mechanics, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Mittal, R.; Iaccarino, G. Immersed boundary methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef]
- Pinelli, A.; Naqavi, I.Z.; Piomelli, U.; Favier, J. Immersed-boundary methods for general finite-difference and finite-volume Navier-Stokes solvers. J. Comput. Phys. 2010, 229, 9073–9091. [Google Scholar] [CrossRef]
- Li, Z.; Favier, J.; D’Ortona, U.; Poncet, S. An immersed boundary-lattice Boltzmann method for single- and multi-component fluid flows. J. Comput. Phys. 2016, 304, 424–440. [Google Scholar] [CrossRef]
- Kuttler, U.; Wall, W.A. Fixed-point fluid-structure interaction solvers with dynamic relaxation. Comput. Mech. 2008, 43, 61–72. [Google Scholar] [CrossRef]
- Harwood, A.R.G.; O’Connor, J.; Munoz, J.S.; Santasmasas, M.C.; Revell, A.J. LUMA: A many-core, fluid-structure interaction solver based on the lattice-Boltzmann method. SoftwareX 2018, 7, 88–94. [Google Scholar] [CrossRef]
- Zhu, L.; Peskin, C. Simulation of a flapping flexible filament in a flowing soap film by the immersed boundary method. J. Comput. Phys. 2002, 179, 452–468. [Google Scholar] [CrossRef]
- Ryu, J.; Park, S.; Kim, B.; Sung, H. Flapping dynamics of an inverted flag in a uniform flow. J. Fluids Struct. 2015, 57, 159–169. [Google Scholar] [CrossRef]
- De Rosis, A.; Lévêque, E. Central-moment lattice Boltzmann schemes with fixed and moving immersed boundaries. Comput. Math. Appl. 2016, 72, 1616–1628. [Google Scholar] [CrossRef]
- Latt, J.; Chopard, B.; Malaspinas, O.; Deville, M.; Michler, A. Straight velocity boundaries in the lattice Boltzmann method. Phys. Rev. E 2008, 77, 056703. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z. Lattice Boltzmann outflow treatments: Convective conditions and others. Comput. Math. Appl. 2013, 65, 160–171. [Google Scholar] [CrossRef]
- Silva-Leon, J.; Cioncolini, A.; Nabawy, M.N.A.; Revell, A.; Kennaugh, A. Simultaneous wind and solar energy harvesting with inverted flags. Appl. Energy 2019, 239, 846–858. [Google Scholar] [CrossRef]
- Eloy, C.; Souilliez, C.; Schouveiler, L. Flutter of a rectangular plate. J. Fluids Struct. 2007, 23, 904–919. [Google Scholar] [CrossRef]
- Sader, J.E.; Huertas-Cerdeira, C.; Gharib, M. Stability of slender inverted flags and rods in uniform steady flow. J. Fluid Mech. 2016, 809, 873–894. [Google Scholar] [CrossRef]
- Tavallaeinejad, M.; Païdoussis, M.P.; Legrand, M. Nonlinear static response of low-aspect-ratio inverted flags subjected to a steady flow. J. Fluid Struct. 2018, 83, 413–428. [Google Scholar] [CrossRef]

| Reference | PVDF Model | Power Density (mW/cm3) | Wind Speed (m/s) |
|---|---|---|---|
| Vatansever et al. [20] | LDT4-028K/L | 0.16 | 10 |
| Li et al. [24] | LDT2-028K/L | 0.871 | 8 |
| Hobeck and Inman [27] | LDT4-028K/L | 0.0051 | 7 |
| Present study: no-solar flag | LDT4-028K/L | 0.27 | 8.5 |
| Present study: full-solar flag | LDT4-028K/L | 0.48 | 8.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cioncolini, A.; Nabawy, M.R.A.; Silva-Leon, J.; O’Connor, J.; Revell, A. An Experimental and Computational Study on Inverted Flag Dynamics for Simultaneous Wind–Solar Energy Harvesting. Fluids 2019, 4, 87. https://doi.org/10.3390/fluids4020087
Cioncolini A, Nabawy MRA, Silva-Leon J, O’Connor J, Revell A. An Experimental and Computational Study on Inverted Flag Dynamics for Simultaneous Wind–Solar Energy Harvesting. Fluids. 2019; 4(2):87. https://doi.org/10.3390/fluids4020087
Chicago/Turabian StyleCioncolini, Andrea, Mostafa R.A. Nabawy, Jorge Silva-Leon, Joseph O’Connor, and Alistair Revell. 2019. "An Experimental and Computational Study on Inverted Flag Dynamics for Simultaneous Wind–Solar Energy Harvesting" Fluids 4, no. 2: 87. https://doi.org/10.3390/fluids4020087
APA StyleCioncolini, A., Nabawy, M. R. A., Silva-Leon, J., O’Connor, J., & Revell, A. (2019). An Experimental and Computational Study on Inverted Flag Dynamics for Simultaneous Wind–Solar Energy Harvesting. Fluids, 4(2), 87. https://doi.org/10.3390/fluids4020087








