On the Asymmetric Spectral Broadening of a Hydrodynamic Modulated Wave Train in the Optical Regime
Abstract
1. Introduction
2. Hydrodynamic and Optical Rogue Waves
2.1. Nonlinear Schrödinger Equation (NLSE)
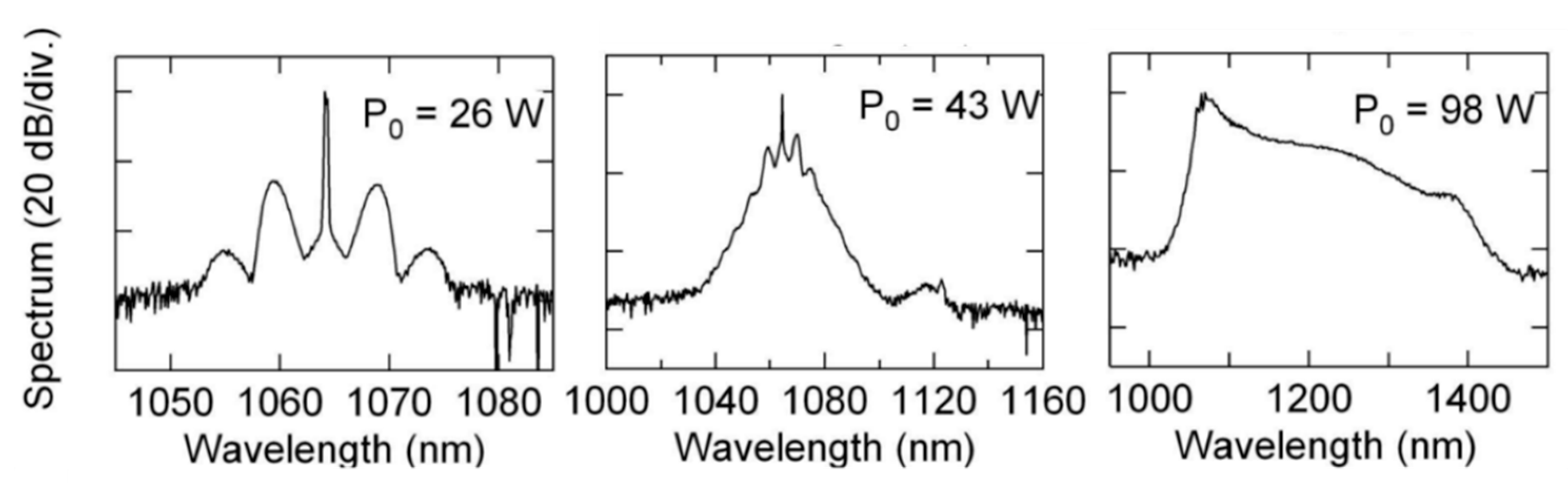
2.2. Hydrodynamic and Optic Rogue Wave Experiments in Literature
3. Broadband Hydrodynamic Numerical Simulation
3.1. Higher-Order Spectral Model
3.2. Modulated Wave Train
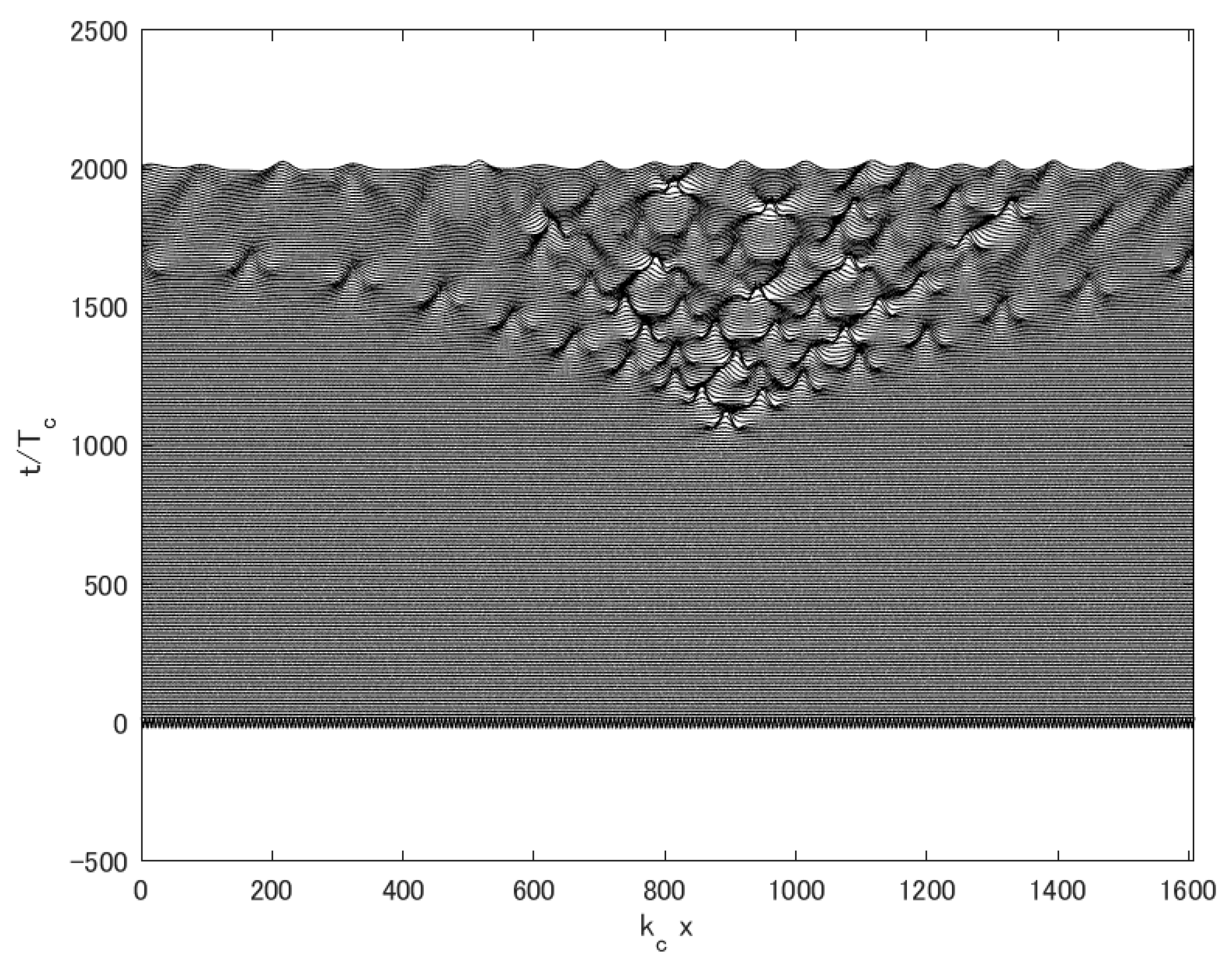
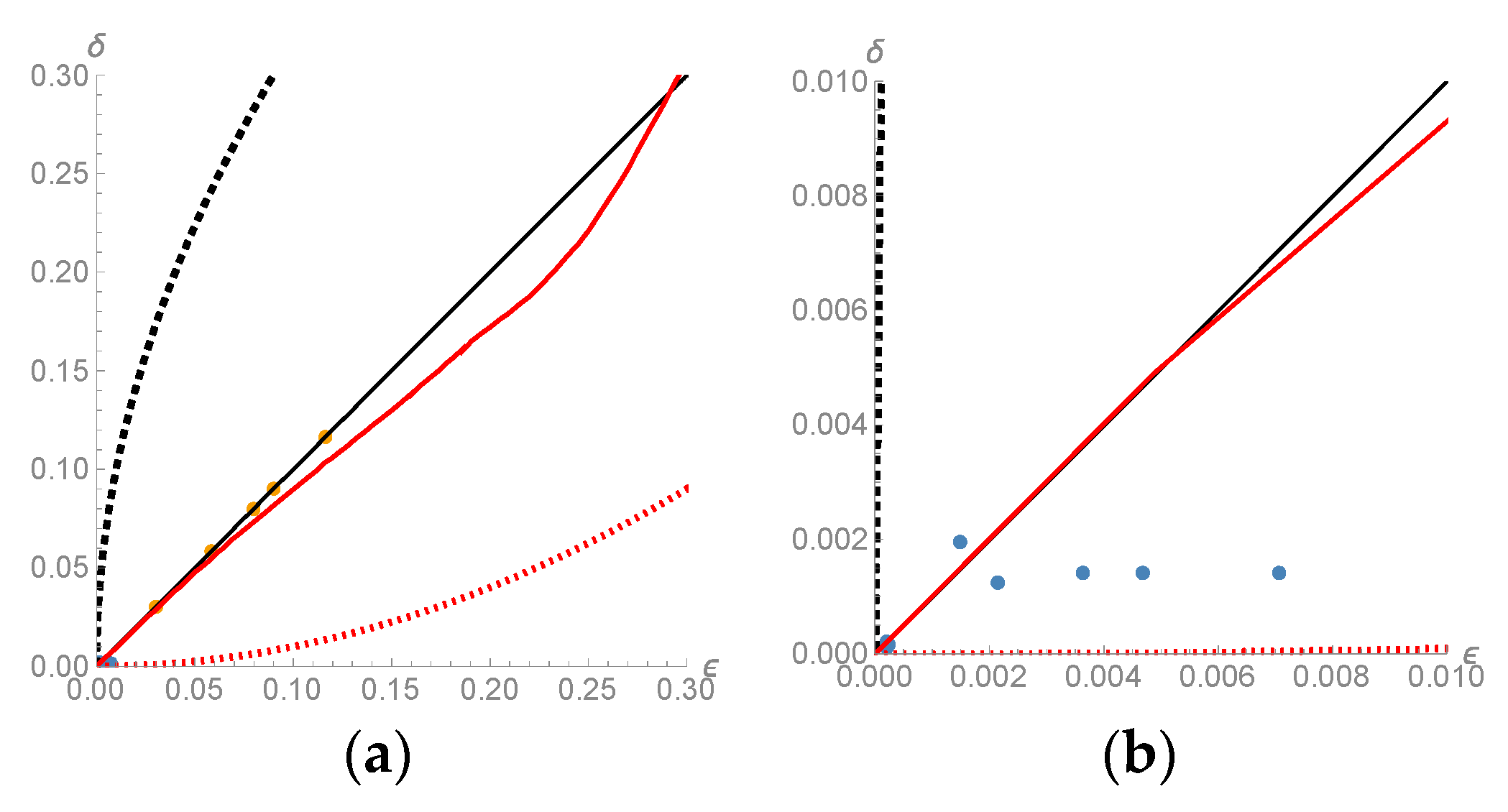
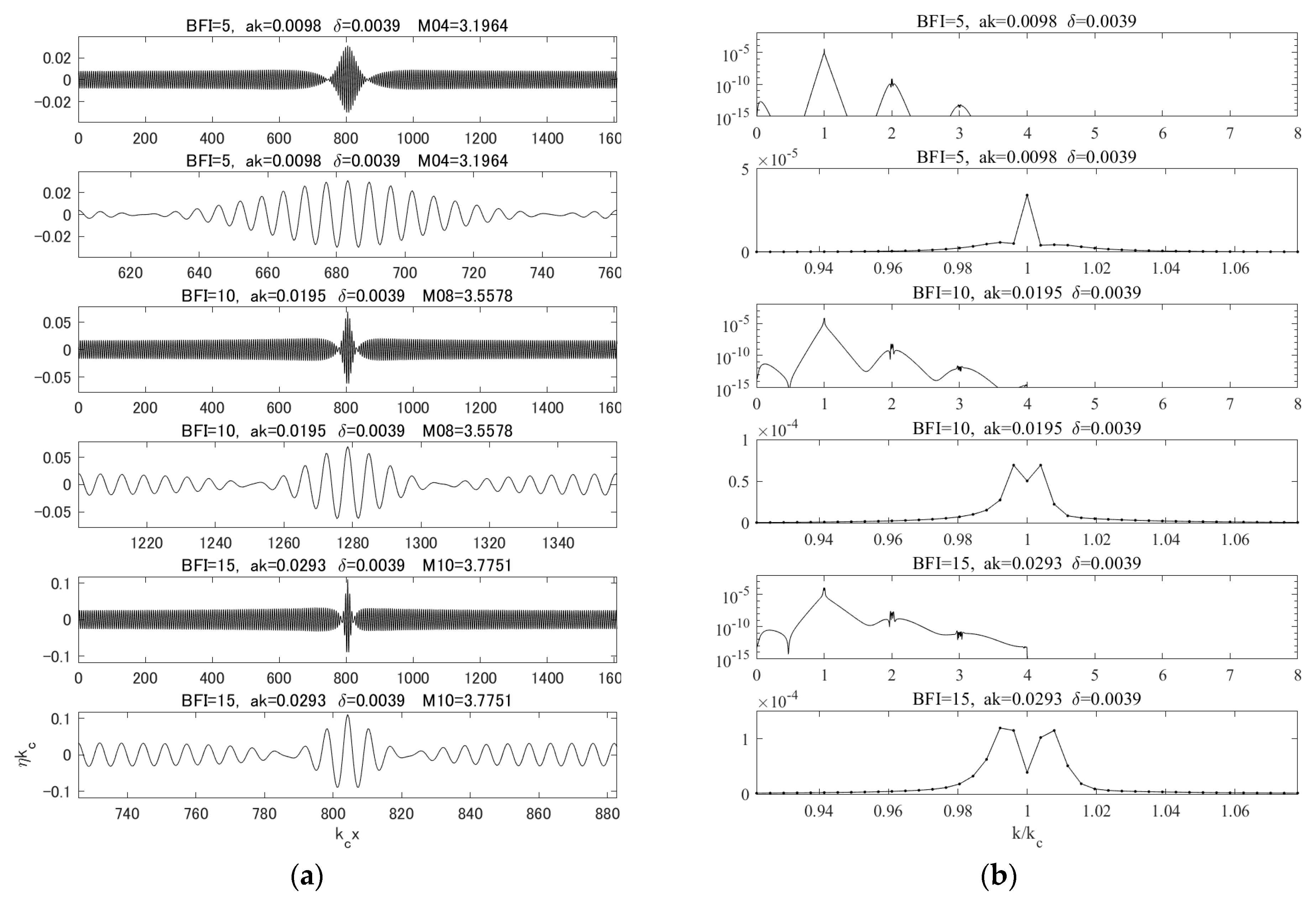
4. Results
4.1. Cases 1–4; ()
4.2. Cases 5–7; ()
5. Discussion
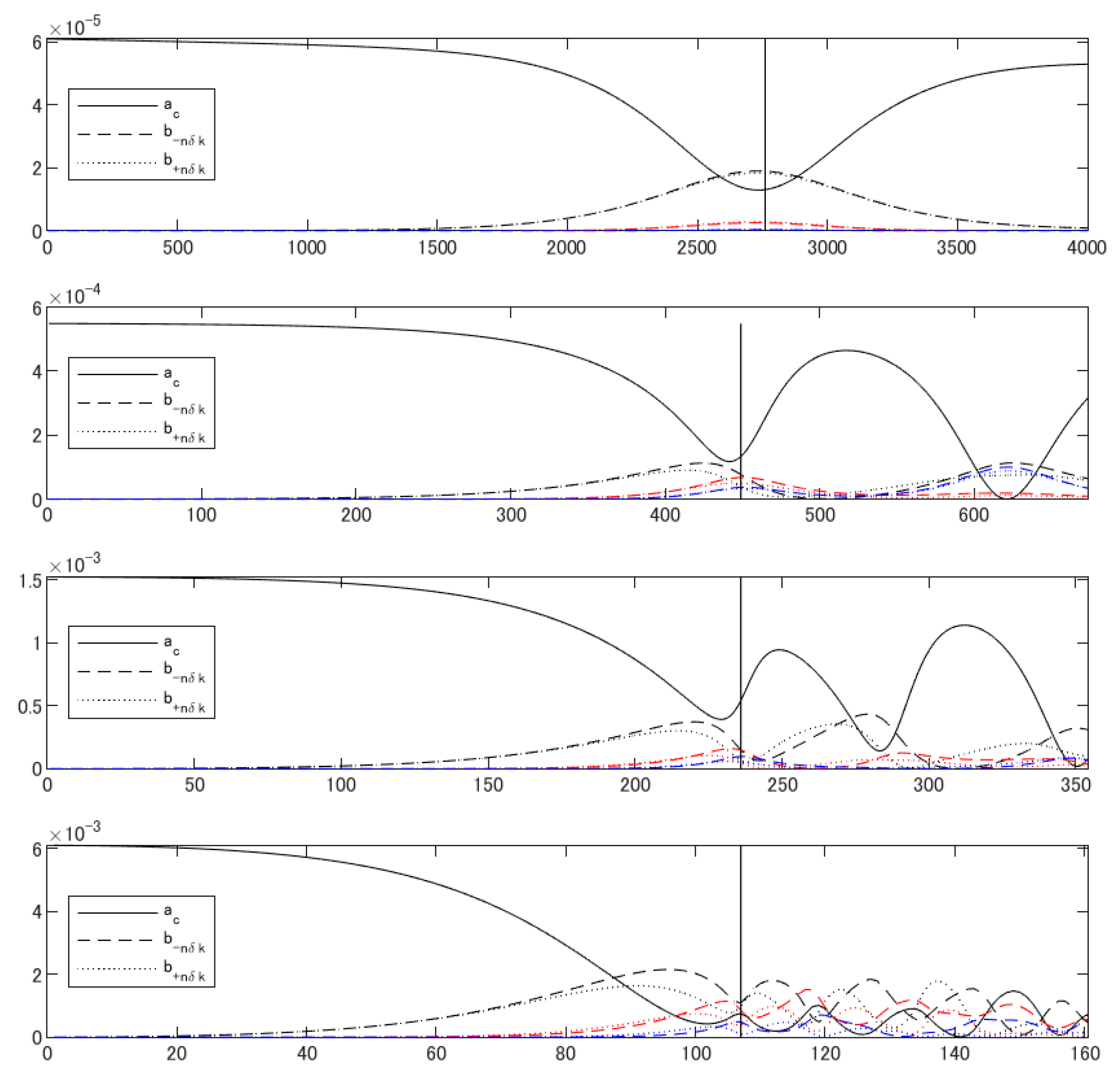
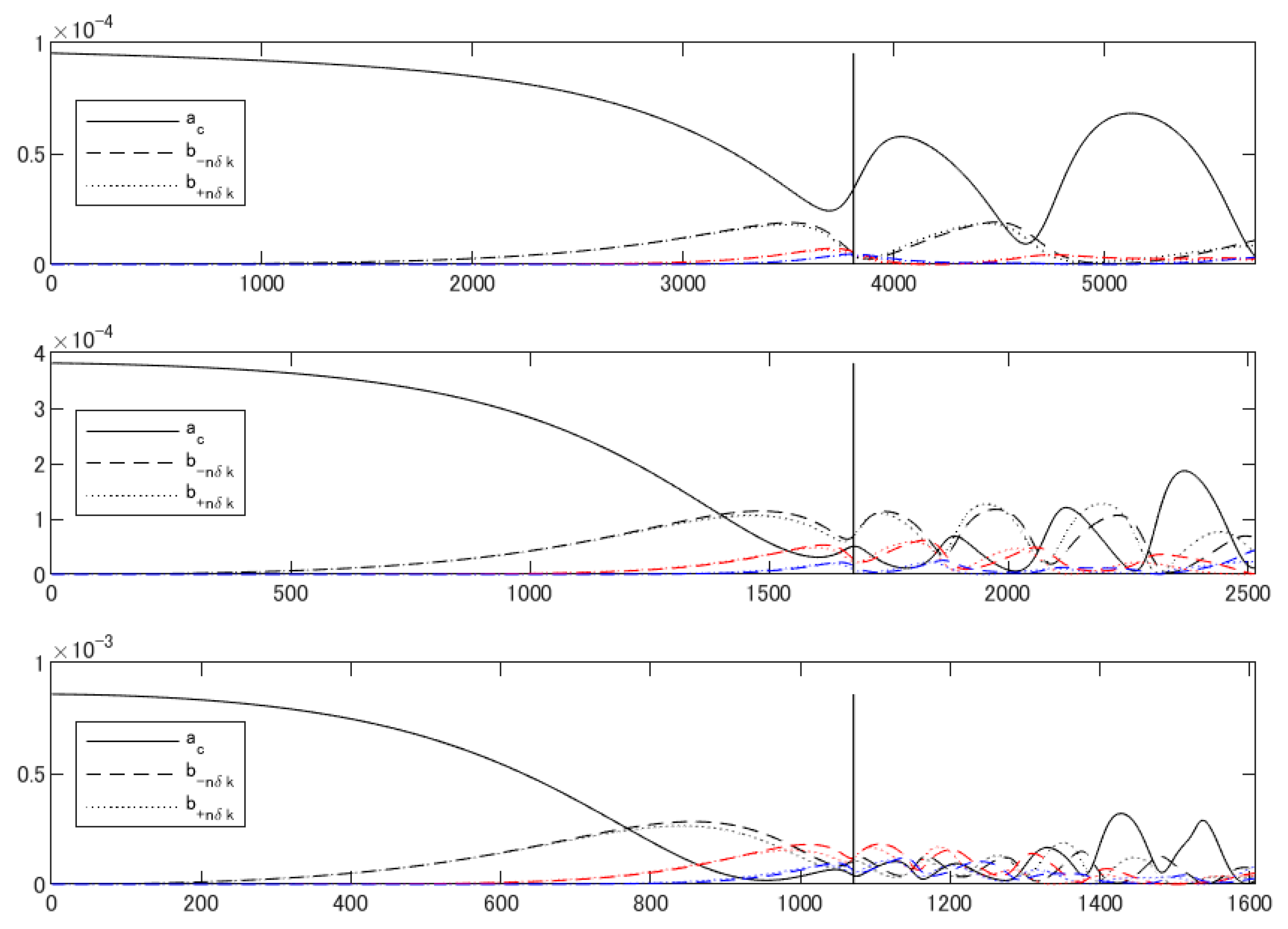
5.1. Spectral Mode Evolutions
5.2. Spectral Broadening Due to Fast Envelope Variation
5.3. Limitation of the Use of Hydrodynamic Equation in the Optical Regime
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Optical Fiber | Deepwater Waves | |
|---|---|---|
| Dispersion parameter | where | |
| Nonlinear parameter | ||
| Steepness | ||
| Spectral bandwidth | ||
| Optical Rogue Waves | Chabchoub et al. 2015 [38] Solli et al. 2007 [25] | Dudley et al. 2009 Simulation [31] | Dudley et al. 2009 Experiment [31] |
|---|---|---|---|
| Case | Akhmediev breather | Akhmediev breather | |
| 1.2153 | |||
| 30.0 | |||
| , , | |||
| - | 289 | ||
| - | |||
| - | 1.0 | , , | |
| - | 25.8648 | 42.5, 48.2, 59.2 | |
| L = Fiber length (m) | - | ~500 m | ~ 300 m |
| - | 7200.7829 | 3742, 6189, 14106 | |
| Kibler et al. (2010) [26] | Kibler et al. (2012) [27] | Frisquet et al. (2014) [28] | |
| Case | Peregrine soliton | Kuznetsov-Ma soliton | High-order Akhmediev breather |
| 192670 | 192920 | 193410 | |
| 0.7 | 0.513 | ||
| 241 | 30.5 | ||
| 37.0764 | 97.628 | 136.3499, 68.1717 | |
| L = Fiber length (m) | 900 | 5300 | 3800 |
| 2676.2 | 194.0162 | 96.8620 | |
Appendix B
References
- Kharif, C.; Pelinovsky, E.; Slunyaev, A. Quasi-Linear Wave Focusing. In Rogue Waves in the Ocean; Springer: Berlin/Heidelberg, Germany, 2009; pp. 63–89. [Google Scholar]
- Toffoli, A.; Lefevre, J.M.; Bitner-Gregersen, E.; Monbaliu, J. Towards the identification of warning criteria: Analysis of a ship accident database. Appl. Ocean Res. 2005, 27, 281–291. [Google Scholar] [CrossRef]
- Waseda, T.; Tamura, H.; Kinoshita, T. Freakish sea index and sea states during ship accidents. J. Mar. Sci. Technol. 2012, 17, 305–314. [Google Scholar] [CrossRef]
- Haver, S. A possible freak wave event measured at the Draupner Jacket January 1 1995. Rogue Waves. 2004, Volume 2004, pp. 1–8. Available online: http://aircrewremembered.com/PDF/draupner-wave.pdf (accessed on 18 February 2019).
- Magnusson, A.K.; Donelan, M.A. The Andrea wave characteristics of a measured North Sea rogue wave. J. Offshore Mech. Arctic Eng. 2013, 135, 031108. [Google Scholar] [CrossRef]
- Dias, F.; Brennan, J.; de León, S.P.; Clancy, C.; Dudley, J. Local analysis of wave fields produced from hindcasted rogue wave sea states. In ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Fedele, F.; Brennan, J.; Ponce de León, S.; Dudley, J.; Dias, F. Real world ocean rogue waves explained without the modulational instability. Sci. Rep. 2016, 6, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Trulsen, K.; Nieto Borge, J.C.; Gramstad, O.; Aouf, L.; Lefèvre, J.M. Crossing sea state and rogue wave probability during the Prestige accident. J. Geophys. Res. Ocean 2015, 120, 7113–7136. [Google Scholar] [CrossRef]
- Onorato, M.; Waseda, T.; Toffoli, A.; Cavaleri, L.; Gramstad, O.; Janssen, P.A.E.M.; Kinoshita, T.; Monbaliu, J.; Mori, N.; Osborne, A.R. Statistical properties of directional ocean waves: The role of the modulational instability in the formation of extreme events. Phys. Rev. Lett. 2009, 102, 114502. [Google Scholar] [CrossRef] [PubMed]
- Onorato, M.; Cavaleri, L.; Fouques, S.; Gramstad, O.; Janssen, P.A.; Monbaliu, J.; Osborne, A.R.; Pakozdi, C.; Serio, M.; Stansberg, C.T.; et al. Statistical properties of mechanically generated surface gravity waves: A laboratory experiment in a three-dimensional wave basin. J. Fluid Mech. 2009, 627, 235–257. [Google Scholar] [CrossRef]
- Waseda, T.; Kinoshita, T.; Tamura, H. Evolution of a random directional wave and freak wave occurrence. J. Phys. Oceanogr. 2009, 39, 621–639. [Google Scholar] [CrossRef]
- Mori, N.; Onorato, M.; Janssen, P.A. On the estimation of the kurtosis in directional sea states for freak wave forecasting. J. Phys. Oceanogr. 2011, 41, 1484–1497. [Google Scholar] [CrossRef]
- Fujimoto, W.; Waseda, T.; Webb, A. Impact of the four-wave quasi-resonance on freak wave shapes in the ocean. Ocean Dyn. 2019, 69, 101–121. [Google Scholar] [CrossRef]
- Kokorina, A.; Slunyaev, A. Lifetimes of rogue wave events in direct numerical simulations of deep-water irregular sea waves. Fluids 2019, 4, 70. [Google Scholar] [CrossRef]
- Zakharov, V.E. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 1968, 9, 190–194. [Google Scholar] [CrossRef]
- Yuen, H.C.; Lake, B.M. Nonlinear deep water waves: Theory and experiment. Phys. Fluids 1975, 18, 956–960. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Feir, J.E. The disintegration of wave trains on deep water Part 1. Theory. J. Fluid Mech. 1967, 27, 417–430. [Google Scholar] [CrossRef]
- Akhmediev, N.N.; Korneev, V.I. Modulation instability and periodic solutions of the nonlinear Schrödinger equation. Theor. Math. Phys. 1986, 69, 1089–1093. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.P.; Akhmediev, N. Rogue wave observation in a water wave tank. Phys. Rev. Lett. 2011, 106, 204502. [Google Scholar] [CrossRef] [PubMed]
- Chabchoub, A.; Hoffmann, N.; Onorato, M.; Akhmediev, N. Super rogue waves: Observation of a higher-order breather in water waves. Phys. Rev. X 2012, 2, 011015. [Google Scholar] [CrossRef]
- Chabchoub, A.; Kibler, B.; Dudley, J.M.; Akhmediev, N. Hydrodynamics of periodic breathers. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20140005. [Google Scholar] [CrossRef]
- Perić, R.; Hoffmann, N.; Chabchoub, A. Initial wave breaking dynamics of Peregrine-type rogue waves: A numerical and experimental study. Eur. J. Mech.-B/Fluids 2015, 49, 71–76. [Google Scholar] [CrossRef]
- Shemer, L.; Ee, B.K. Steep Unidirectional Wave Groups: Fully Nonlinear Simulations vs Experiments. In ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Shemer, L. Quantitative Analysis of Nonlinear Water-Waves: A Perspective of an Experimentalist. In New Approaches to Nonlinear Waves; Springer: Cham, Switzerland, 2016; pp. 211–293. [Google Scholar]
- Solli, D.R.; Ropers, C.; Koonath, P.; Jalali, B. Optical rogue waves. Nature 2007, 450, 1054. [Google Scholar] [CrossRef]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Dias, F.; Genty, G.; Akhmediev, N.; Dudley, J.M. The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 2010, 6, 790. [Google Scholar] [CrossRef]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Genty, G.; Wetzel, B.; Akhmediev, N.; Dias, F.; Dudley, J.M. Observation of Kuznetsov-Ma soliton dynamics in optical fibre. Sci. Rep. 2012, 2, 463. [Google Scholar] [CrossRef]
- Frisquet, B.; Chabchoub, A.; Fatome, J.; Finot, C.; Kibler, B.; Millot, G. Two-stage linear-nonlinear shaping of an optical frequency comb as rogue nonlinear-Schrödinger-equation-solution generator. Phys. Rev. A 2014, 89, 023821. [Google Scholar] [CrossRef]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G. Experiments on breathers in nonlinear fibre optics. In Rogue and Shock Waves in Nonlinear Dispersive Media; Springer: Cham, Switzerland, 2016; pp. 89–115. [Google Scholar]
- Travers, J.C. Blue extension of optical fibre supercontinuum generation. J. Opt. 2010, 12, 113001. [Google Scholar] [CrossRef]
- Dudley, J.M.; Genty, G.; Dias, F.; Kibler, B.; Akhmediev, N. Modulation instability, Akhmediev Breathers and continuous wave supercontinuum generation. Opt. Express 2009, 17, 21497–21508. [Google Scholar] [CrossRef]
- Peregrine, D.H. Water waves, nonlinear Schrödinger equations and their solutions. ANZIAM J. 1983, 25, 16–43. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A.; Soto-Crespo, J.M.; Dudley, J.M. Rogue wave early warning through spectral measurements? Phys. Lett. A 2011, 375, 541–544. [Google Scholar] [CrossRef]
- Dysthe, K.B. Note on a modification to the nonlinear Schrödinger equation for application to deep water waves. Proc. R. Soc. Lond. A 1979, 369, 105–114. [Google Scholar] [CrossRef]
- Yan, Z. Generalized method and its application in the higher-order nonlinear Schrödinger equation in nonlinear optical fibres. Chaos Solitons Fractals 2003, 16, 759–766. [Google Scholar] [CrossRef]
- Amiranashvili, S. Hamiltonian framework for short optical pulses. In New Approaches to Nonlinear Waves; Springer: Cham, Switzerland, 2016; pp. 153–196. [Google Scholar]
- Conforti, M.; Marini, A.; Tran, T.X.; Faccio, D.; Biancalana, F. Interaction between optical fields and their conjugates in nonlinear media. Opt. Express 2013, 21, 31239–31252. [Google Scholar] [CrossRef] [PubMed]
- Chabchoub, A.; Kibler, B.; Finot, C.; Millot, G.; Onorato, M.; Dudley, J.M.; Babanin, A.V. The nonlinear Schrödinger equation and the propagation of weakly nonlinear waves in optical fibers and on the water surface. Ann. Phys. 2015, 361, 490–500. [Google Scholar] [CrossRef]
- Stiassnie, M.; Kroszynski, U.I. Long-time evolution of an unstable water-wave train. J. Fluid Mech. 1982, 116, 207–225. [Google Scholar] [CrossRef]
- Tulin, M.P.; Waseda, T. Laboratory observations of wave group evolution, including breaking effects. J. Fluid Mech. 1999, 378, 197–232. [Google Scholar] [CrossRef]
- Janssen, P.A. Nonlinear four-wave interactions and freak waves. J. Phys. Oceanogr. 2003, 33, 863–884. [Google Scholar] [CrossRef]
- Stiassnie, M. Note on the modified nonlinear Schrödinger equation for deep water waves. Wave Motion 1984, 6, 431–433. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.; Onorato, M.; Genty, G.; Dudley, J.M.; Akhmediev, N. Hydrodynamic supercontinuum. Phys. Rev. Lett. 2013, 111, 054104. [Google Scholar] [CrossRef]
- Trulsen, K.; Dysthe, K.B. A modified nonlinear Schrödinger equation for broader bandwidth gravity waves on deep water. Wave Motion 1996, 24, 281–289. [Google Scholar] [CrossRef]
- Chabchoub, A.; Kibler, B.; Dudley, J.M.; Akhmediev, N. Hydrodynamics of periodic breathers. Philos. Trans. R. Soc. A 2014, 372, 20140005. [Google Scholar] [CrossRef]
- West, B.J.; Brueckner, K.A.; Janda, R.S.; Milder, D.M.; Milton, R.L. A new numerical method for surface hydrodynamics. J. Geophys. Res. Oceans 1987, 92, 11803–11824. [Google Scholar] [CrossRef]
- Toffoli, A.; Bitner-Gregersen, E.; Onorato, M.; Babanin, A.V. Wave crest and trough distributions in a broad-banded directional wave field. Ocean Eng. 2008, 35, 1784–1792. [Google Scholar] [CrossRef]
- Dommermuth, D. The initialization of nonlinear waves using an adjustment scheme. Wave Motion 2000, 32, 307–317. [Google Scholar] [CrossRef]
- Tanaka, M. A method of studying nonlinear random field of surface gravity waves by direct numerical simulation. Fluid Dyn. Res. 2001, 28, 41. [Google Scholar] [CrossRef]
- Onorato, M.; Osborne, A.R.; Serio, M. On the relation between two numerical methods for the computation of random surface gravity waves. Eur. J. Mech. B/Fluids 2007, 26, 43–48. [Google Scholar] [CrossRef]
- Erkintalo, M.; Genty, G.; Wetzel, B.; Dudley, J.M. Akhmediev breather evolution in optical fiber for realistic initial conditions. Phys. Lett. A 2011, 375, 2029–2034. [Google Scholar] [CrossRef]
- Armaroli, A.; Brunetti, M.; Kasparian, J. Recurrence in the high-order nonlinear Schrödinger equation: A low-dimensional analysis. Phys. Rev. E 2017, 96, 012222. [Google Scholar] [CrossRef] [PubMed]
- Yuen, H.C.; Lake, B.M. Nonlinear dynamics of deep-water gravity waves. In Advances in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 1982; Volume 22, pp. 67–229. [Google Scholar]
- Erkintalo, M.; Hammani, K.; Kibler, B.; Finot, C.; Akhmediev, N.; Dudley, J.M.; Genty, G. Higher-order modulation instability in nonlinear fiber optics. Phys. Rev. Lett. 2011, 107, 253901. [Google Scholar] [CrossRef]
- Kimmoun, O.; Hsu, H.C.; Kibler, B.; Chabchoub, A. Nonconservative higher-order hydrodynamic modulation instability. Phys. Rev. E 2017, 96, 022219. [Google Scholar] [CrossRef] [PubMed]
- Armaroli, A.; Conti, C.; Biancalana, F. Rogue solitons in optical fibers: A dynamical process in a complex energy landscape? Optica 2015, 2, 497–504. [Google Scholar] [CrossRef]
- Grimshaw, R.H.J.; Tovbis, A. Rogue waves: Analytical predictions. Proc. R. Soc. A 2013, 469, 20130094. [Google Scholar] [CrossRef]
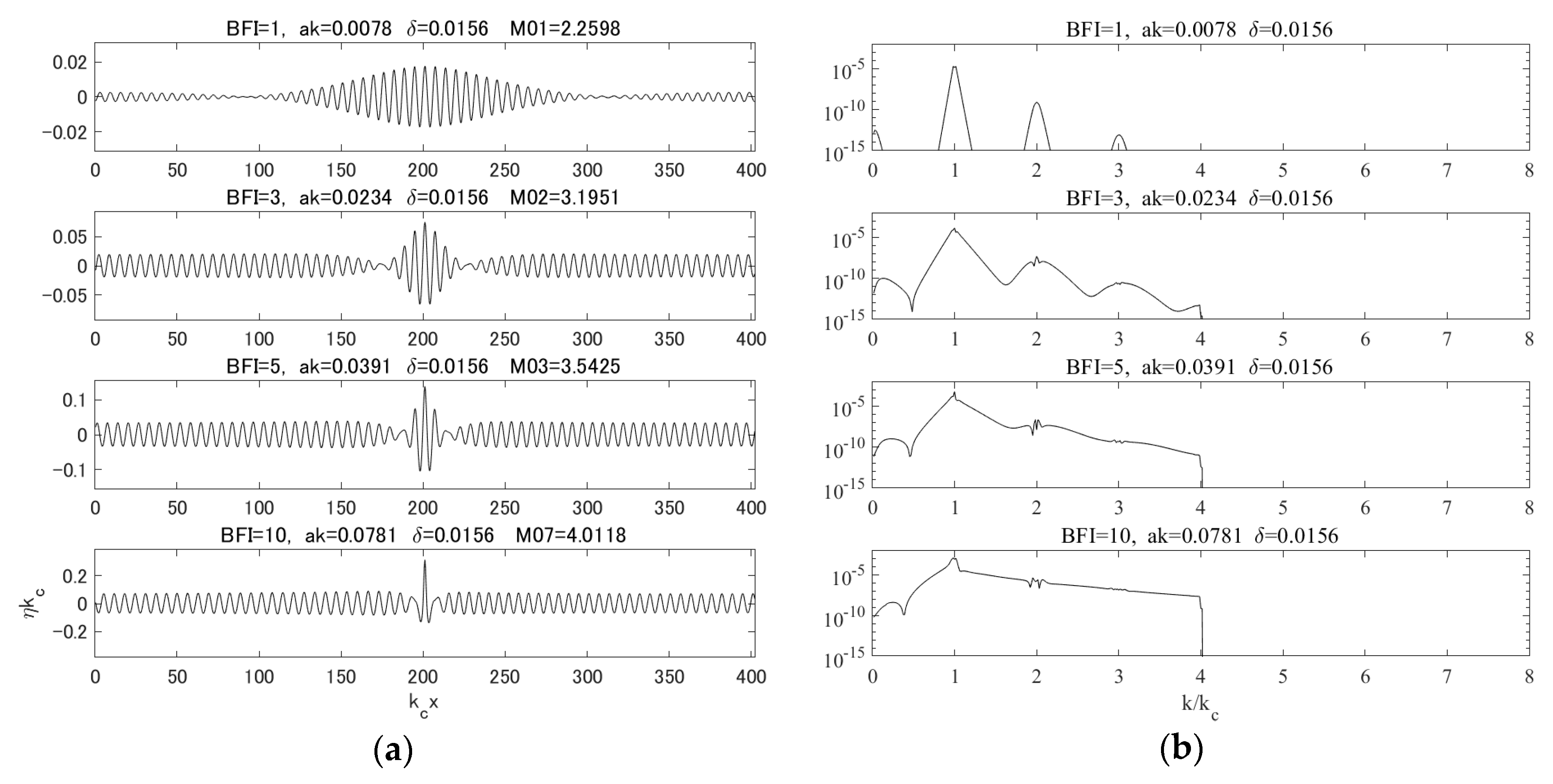
| Case 1 | 64 | 1 | 0.0156 | 0.0078 | 1024 |
| Case 2 | 64 | 3 | 0.0156 | 0.0234 | 1024 |
| Case 3 | 64 | 5 | 0.0156 | 0.0391 | 1024 |
| Case 4 | 64 | 10 | 0.0156 | 0.0781 | 1024 |
| Case 5 | 256 | 5 | 0.0039 | 0.0098 | 4096 |
| Case 6 | 256 | 10 | 0.0039 | 0.0195 | 4096 |
| Case 7 | 256 | 15 | 0.0039 | 0.0293 | 4096 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waseda, T.; Fujimoto, W.; Chabchoub, A. On the Asymmetric Spectral Broadening of a Hydrodynamic Modulated Wave Train in the Optical Regime. Fluids 2019, 4, 84. https://doi.org/10.3390/fluids4020084
Waseda T, Fujimoto W, Chabchoub A. On the Asymmetric Spectral Broadening of a Hydrodynamic Modulated Wave Train in the Optical Regime. Fluids. 2019; 4(2):84. https://doi.org/10.3390/fluids4020084
Chicago/Turabian StyleWaseda, Takuji, Wataru Fujimoto, and Amin Chabchoub. 2019. "On the Asymmetric Spectral Broadening of a Hydrodynamic Modulated Wave Train in the Optical Regime" Fluids 4, no. 2: 84. https://doi.org/10.3390/fluids4020084
APA StyleWaseda, T., Fujimoto, W., & Chabchoub, A. (2019). On the Asymmetric Spectral Broadening of a Hydrodynamic Modulated Wave Train in the Optical Regime. Fluids, 4(2), 84. https://doi.org/10.3390/fluids4020084







