Abstract
We numerically investigate pairwise collisions of solitary wave structures on the surface of deep water—breathers. These breathers are spatially localised coherent groups of surface gravity waves which propagate so that their envelopes are stable and demonstrate weak oscillations. We perform numerical simulations of breather mutual collisions by using fully nonlinear equations for the potential flow of ideal incompressible fluid with a free surface written in conformal variables. The breather collisions are inelastic. However, the breathers can still propagate as stable localised wave groups after the interaction. To generate initial conditions in the form of separate breathers we use the reduced model—the Zakharov equation. We present an explicit expression for the four-wave interaction coefficient and third order accuracy formulas to recover physical variables in the Zakharov model. The suggested procedure allows the generation of breathers of controlled phase which propagate stably in the fully nonlinear model, demonstrating only minor radiation of incoherent waves. We perform a detailed study of breather collision dynamics depending on their relative phase. In 2018 Kachulin and Gelash predicted new effects of breather interactions using the Dyachenko–Zakharov equation. Here we show that all these effects can be observed in the fully nonlinear model. Namely, we report that the relative phase controls the process of energy exchange between breathers, level of energy loses, and space positions of breathers after the collision.
1. Introduction
Solitary wave groups have been known as solutions of different weakly nonlinear models of water surface dynamics for a long time. Among them the most important are the exact soliton solutions of the Korteweg–de Vries (KdV) equation and the focusing one-dimensional nonlinear Schrödinger equation (NLSE), which describe propagation of localised wave groups on the surface of shallow and deep water correspondingly. To a certain wave steepness, these solutions can be reproduced in fully nonlinear models and experiments. For example, solitons of the NLSE demonstrate stable propagation in numerical simulations of the fully nonlinear equations describing ideal deep water [1,2] and in experimental water wave tanks [3]. Here we study propagation and interactions of solitary wave groups in framework of the well-known fully nonlinear system of equations describing 1D waves of the surface of ideal deep water: the Laplace equation for hydrodynamic velocity potential of 2D water and kinematic and dynamic boundary conditions at water free surface—see Equation (1) in the next section. For the sake of simplicity, we refer this system of equations just as fully nonlinear equations/model.
The existence of strongly nonlinear (i.e., having high steepness) solitary type solutions of the fully nonlinear equations—breathers—was demonstrated numerically by Dyachenko and Zakharov [4]. Later, propagation and interactions of these breathers were studied numerically and in water tank experiments by Slunyaev and coauthors [5,6,7]. In these works the strongly nonlinear breathers were generated by using the following methodology. At the first step exact soliton solution of the NLSE having high steepness is used as initial condition for numerical simulations in the framework of the fully nonlinear model. The soliton propagates and radiates incoherent waves which are absorbed at the boundary of simulation region by a specially design damping. The radiation decreases in time so that, after certain propagation soliton transforms to a stable wave group having weakly oscillating envelope—breather.
In the present work we improve method of numerical finding of the strongly nonlinear breathers in the fully nonlinear model. More precisely, we use the well known reduced Hamiltonian model for deep water surface waves—the Zakharov equation [8], see also [9,10], written in canonical variables. The range of applicability of the Zakharov equation is far beyond the NLSE model, though solitary type solutions no longer can be found analytically. We find breather solutions of the Zakharov equation by using the numerical Petviashvili method [11]. Then we use the transformation from the canonical variables to the physical one (free surface elevation and velocity potential on it) with third order of accuracy by wave steepness. All these steps allows us to generate breathers which stably propagate in the fully nonlinear model demonstrating only minor radiation.
Solitary type solutions of the high order and fully nonlinear models have fundamental difference when compared to exact soliton solutions of integrable equations, such as the NLSE. In the latter case, solitons interact elastically and after collision completely restore their initial shape. In the other case, solitary wave groups interact inelastically and radiate incoherent waves during collision. After the interaction they can still propagate in the form of stable localised wave groups.
The main aim of this work is to verify in the fully nonlinear model the effects of breather interactions predicted recently by Kachulin and Gelash [12] by using a modification of the Zakharov model—the so called super compact Dyachenko–Zakharov equation (see [13,14,15] and also [16,17,18]). The work [12] focuses on how the breather interaction dynamics depends on their relative phase. In addition to the previously known data about interactions of strongly nonlinear breathers [7], the work [12] predicts that the relative phase controls the process of energy exchange between breathers, level of energy loses and space positions of breathers after the collision. More precisely, the energy exchange between breathers results in increase or decrease of their amplitudes depending on the relative phase. The level of energy loses increases with certain synchronisation of the breather phase. Most interesting, the space position of a breather after the collision can be either further or nearer to the interaction area, than where it would have been if the breather had been traveling alone. Note, that both terms “solitons” and “breathers” are used in the literature to describe solitary wave group solutions of the high order and fully nonlinear models. We use the term “breather” following the works [4,19].
In this work we observe and study in details all these effects using the fully nonlinear model which indicates, that our theoretical picture of the interactions of strongly nonlinear coherent structures is universal and can be observed in laboratory experiments.
2. Theoretical Formalism
2.1. Fully Nonlinear Equations for Ideal Deep Fluid
The fully nonlinear 2D equations describing gravity waves on the surface of ideal deep fluid are well know and can be written as:
Here x and y are the horizontal and vertical coordinates, t is time, g is the free-fall acceleration, is the shape of the surface, is the hydrodynamic potential inside the fluid. The first equation in (1) is the Laplace equation for the hydrodynamic potential, while the second and third equations are kinematic and dynamic conditions at the fluid surface.
Following the work [20] we perform conformal mapping of the free surface liquid domain confined by a free boundary onto a half-plane of the new complex variable having a fixed boundary . This transformation can be written in the following form:
Then we use the following variables suggested by Dyachenko [21]:
We define the functions U and B using the Hilbert operator and the projection operator as:
Here and below the asterisks stands for complex conjugation. In the new variables (3) the Equation (1) have the following form:
with the boundary conditions:
2.2. Zakharov Equation
Gravity waves on the surface of ideal deep fluid can be also studied using reduced nonlinear models favourable for both numerical simulations and analytical analysis. As well known, one-dimensional potential flow of an ideal fluid of infinite depth in the presence of gravity is a Hamiltonian system. As was shown by Zakharov [8], the surface elevation and the velocity potential at the surface of the fluid are canonically conjugated variables and satisfy the following Hamilton’s equations:
Here H is the Hamiltonian, i.e., total energy of the fluid:
The reduced Hamiltonian equations of the fluid motion can be derived from (6) in the assumption of small wave steepness. In this case the Hamiltonian can be represented as the infinite series where the first order terms are:
Here the operator means multiplication by in k-space.
The equations of motion (6) with the truncated Hamiltonian (8) can be used for efficient numerical simulations of water surface dynamics [22], meanwhile for purposes of analytical analysis they are not optimal. In this work we use the so called Zakharov equation, which can be obtained from (6) after appropriate canonical transformation to the variables —see the work [14] and the monograph [23] for all details.
First we introduce the so called normal variables , see [8]:
Here, is the dispersion law for the gravity waves, and the Fourier transformations , are defined as follows:
In the new variables , the Hamiltonian includes quadratic, cubic, and quartic terms:
The exact expressions for the Hamiltonian in terms of the variables can be found in the references [24,25]. The Hamiltonian (9) contains nonresonant three-wave and four-wave interactions. Then, following [23], we perform additional canonical transformation , which aims at eliminating all non-resonant cubic and quartic terms in the new Hamiltonian:
The exact expressions for the coefficients of the transformation (10) can be found in [25]. After that we can write Zakharov equation in the variables in the following form:
where the Hamiltonian is:
The Equation (11) is a standard form of the Hamiltonian equation of motion written in normal variables. The resulting Hamiltonian (12) consist of only diagonal and resonance four-wave interaction terms.
We find that in the case of k-resonance: (i.e., when the argument of delta function in (12) is zero), the four-wave interaction coefficient has the following form:
where the expression means that in this case each of the wave numbers is positive or each of the wave numbers is negative. The coefficient is:
The term means the minimum of the four values: . In the case of k-resonance this term takes the form:
As one can see from Equation (13), when the product , the coefficient of four-wave interactions vanishes: . It means that a system initially consisting of unidirectional waves (in variables ) retains this property during its evolution. In this case it is possible to further simplify the Hamiltonian and the equation of motion, that can be done by applying an additional canonical transformation which replaces the initial four-wave interaction coefficient by the more simple one keeping its diagonal part the same. It allows to derive Zakharov equation in the so called compact [9] and super compact [13,14] forms. However, as we just mentioned, it demands one additional complex transformation of the variables, that is not convenient for the purpose of this work. Namely, below we use the Zakharov model to generate breather solutions of strong nonlinearity in variables and then transform them to the physical variables and with third order accuracy. The additional canonical transformation would make this procedure cumbersome, that is why here we use the Zakharov equation which corresponds to the original coefficient of four-wave interactions (17).
Now if we consider only the waves moving in one direction, i.e., , then the four-wave interaction coefficient takes the form:
After the following simple change of variable:
made by using the Heaviside step function , we obtain the Zakharov equation, which in x-space has the following form:
with the Hamiltonian
The transformation of a solution of the Zakharov equation to physical variables and is not trivial and can be written as power series of wave steepness:
The first and second order terms in these series are well known, see e.g., [14]. In the x-space the first order of the transformation can be written as:
Here the operator is multiplication by in Fourier space. The second order of the transformation in the x-space is:
Note that the eigenvalue of the Hilbert transform operator is .
Here we focus on detailed investigation of the breather dynamics in the fully nonlinear equations and we need to restore shape of the breather in the physical variables as much precise as possible. For this purpose we derive the third order accuracy term of the transformation to physical variables:
Unfortunately, presence of the term does not allow to write the expression (22) in the x-space similar to (20) and (21). Moreover, here we present the third order term (22) only for the case of unidirectional waves: . Since the functions and are real valued, their Fourier transforms obey the following relations:
The expression (22) can be easily generalised to the case using the Equation (23).
3. Numerical Methods
3.1. Breather Solution of the Zakharov Equation
The Equation (17) has a breather solution:
where is a carrier wavenumber, is a group velocity in the laboratory frame of reference and is a nonlinear frequency close to . In Fourier space this solution has the following form:
where
In the Formula (25) instead of we use the new frequency parameter :
Breather solutions can be found numerically by the Petviashvili method [11]. Namely, the solution can be found numerically by the iterations:
Here is the breather solution on the n-th iteration and
The symbol denotes the nonlinear part of the Equation (17) on the n-th iteration in the x-space:
and is the discrete Fourier transform of . The breather solution is determined by two independent parameters: the group velocity V and the frequency . The value of the first parameter defines the carrier wave number (and the carrier wave length ) of the solitary group. The second parameter has the value close to (or , see Formula (27)) and implicitly defines shape and amplitude of the breather.
The method of Petviashvili is one of the most well known and efficient numerical approaches developed to find solitary wave solutions of nonlinear wave equations. Proposed initially for the scalar equations with power-law nonlinearity by Petviashvili in 1976 [11], this approach was later generalised to vector equations with arbitrary form of nonlinear term [26]. Simple time dependence of the solitary solution allows to find an envelope of the wave group by fixed-point iterations approach. The key improvement of the Petviashvili method in comparison to standard fixed-point iterations scheme is introducing a stabilizing factor providing convergence of the iteration process. The right hand term of the iteration Equation (28) consists of the standard fixed-point iteration term and the stabilizing factor (the term in big square brackets). The latter is derived using the general expression suggested by Petviashvili, applied for the particular case of the Equation (17). We refer to the monograph [27] for more general information about the Petviashvili approach, and to our previous works [12,14] for more details about its application to the Zakharov equation.
The breather amplitude is not an independent parameter of the solution. To find the breather with the given velocity V and amplitude we vary the parameter (27). The breather solutions found by Petviashvili method (28) are determined up to an arbitrary phase factor .
3.2. Numerical Integration of the Fully Nonlinear Equations
We use the pseudo-spectral Fourier method and the fourth-order Runge–Kutta method for numerical simulation of the exact nonlinear equations in conformal variables (4). We generate initial conditions (functions R and V) for simulations in the Equation (4) by the known functions and using the algorithm described below.
The conformal mapping described in the Section 2.1 satisfies the following equation:
which can be solved by the iterative procedure:
Here the index n stands for the step of the iteration. After the conformal mapping is found by the use of (32), we compute the function R simply using its definition (3). In order to find the function V also by its definition (3) we need to know the potential in conformal variables. The potential in conformal variables can be found using the Fourier transform and the known spectrum of the potential on the free surface as:
where N is the number of grid points.
4. Results of Numerical Simulations
4.1. Generation of Stable Breather in the Fully Nonlinear Model
In this section we show how we generate breathers in the fully nonlinear model (1) and demonstrate the advantages of using the third-order transformation (22) in comparison with the first and second order transformations (20) and (21).
First we find numerically an exact breather solution of the Zakharov Equation (17) as described in the Section 3.1. Here and below we use the characteristic wavelength meters and the length of computational domain km, so the characteristic wavenumber and the characteristic wave period s.
In this section we first choose the amplitude and the velocity . The corresponding steepness of the generated breather . We determine steepness as the maximum of derivative of the surface elevation:
Then we restore the physical wave fields and using Formulas (20)–(22). We use the wave fields and restored with first (i.e., and ), second ( and ), and third order accuracy ( and ) as initial conditions for numerical simulation in the framework of the fully nonlinear equations as described in the Section 3.2. In the Figure 1, Figure 2 and Figure 3 we show the evolution of the obtained breather in the fully nonlinear model for all three variants of initial conditions. Note that in the whole paper we consider breathers in the frame moving with the velocity .
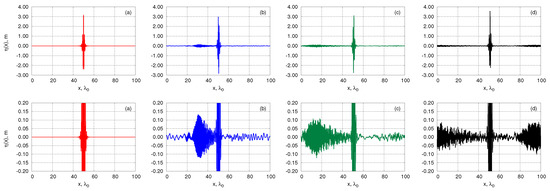
Figure 1.
Propagation of single breather with the wave steepness in the fully nonlinear model. The initial condition in physical variables was restored with the first order accuracy from variables of the Zakharov equation. (Top) row: the surface elevation at different subsequent moments of time. Panel (a) shows the initial surface profile (at ); panel (b) corresponds to ; thepanel (c) corresponds to ; and thepanel (d) corresponds to (Bottom) row: zoom of the top row pictures.
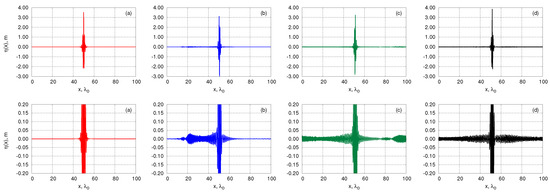
Figure 2.
Propagation of single breather with the wave steepness in the fully nonlinear model. The initial condition in physical variables was restored with the second order accuracy from variables of the Zakharov equation. (Top) row: the surface elevation at different subsequent moments of time. Panel (a) shows the initial surface profile (at ); panel (b) corresponds to ; panel (c) corresponds to ; and panel (d) corresponds to (Bottom) row: zoom of the top row pictures.
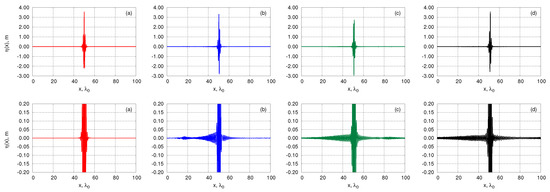
Figure 3.
Propagation of single breather with the wave steepness in the fully nonlinear model. The initial condition in physical variables was restored with the third order accuracy from variables of the Zakharov equation. (Top) row: the surface elevation at different subsequent moments of time. Panel (a) shows the initial surface profile (at ); panel (b) corresponds to ; panel (c) corresponds to ; and panel (d) corresponds to (Bottom) row: zoom of the top row pictures.
When an initial condition is restored only with the first order accuracy, the corresponding breather radiates incoherent waves of significant amplitude during initial stage of its propagation—see Figure 1. The radiation of incoherent waves changes shape of the breather and makes parameters of the final stable solitary wave group hardly controllable. In particular, it is difficult to generate stable breather with certain phase, what is important for our work. That is why here we suggest to use the high order accuracy transformations (21) and (22) when generating an initial condition.
In Figure 2 and Figure 3 we show evolution of the breather restored with the second and the third order accuracy correspondingly. The characteristic amplitude of the radiating waves now significantly less that in the case of the first order transformation and shape of the breather almost does not change in time (except evolution of the breather phase, of course). In the next sections we will study the cases of less steeper breathers, so amplitude of the radiated incoherent waves even smaller that we observe in Figure 3. Thereby here we do not need to use damping of the radiation, as was done in the previous works [4,5,6,7], where single soliton solutions of the NLSE were used as initial conditions.
The phase of the fully nonlinear breather evolves, during its propagation, similar to the phase of breather in Zakharov model (24)—see the changes in the surface elevation with time in Figure 1, Figure 2 and Figure 3. It can be also seen as oscillations in time of the maximum value of surface elevation of the breathers wave field shown in Figure 4a,c.
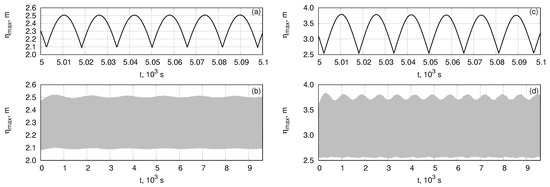
Figure 4.
Behaviour of the maximum value of the surface elevation , when single breathers with the wave steepnesses (a,b) and (c,d) propagate in the fully nonlinear model. The upper row pictures are zoom of the lower row pictures. The fast oscillations of the function caused by evolution of the breather phase can be seen in the upper row pictures, which have small time scale. In the large time scale lower row pictures, these oscillations cannot be distinguished, but instead of that, one can see the effect of oscillations of maximum value of the surface elevation function.
In contrast to the Zakharov model where the envelope of breather (i.e., ) does not change in time at all, the amplitude of the breather envelope in the fully nonlinear model weakly oscillate [4]. Here we do not reconstruct the envelope of the surface elevation of the breather. However, the oscillations of the envelope can be seen from large time behaviour of —see Figure 4b,d. The amplitude and characteristic frequency of these oscillations increase when we increase wave steepness of the breather—see again Figure 4b,d.
We do not observe significant changes of character of the surface elevation oscillations at the long time evolution, that is in agreement with the results of the work [4].
4.2. Breather Collisions
In the following two sections we present results of our study of breather collision dynamics in the framework of the Equation (1). As was noted in the Introduction, the main aim of these numerical experiments is to verify that the phase-dependent effects of breather interactions predicted recently by Kachulin and Gelash [12] can be observed in the fully nonlinear model. For this purpose, similar to the work [12], we examine overtaking collisions of breathers depending on their relative phase and wave steepness. In addition we also study three different cases of the relative velocity between breathers.
Remember that we consider the gravity wave dynamics in the frame moving with the velocity . We study interactions of two breathers having (in the laboratory reference frame) close unidirectional velocities and equal amplitudes. More precisely, following the Section 3.1 we find the exact single breather solutions of Zakharov Equation (17) with velocities , , and amplitudes . Then we restore the physical wave fields and for each of the breathers as described in the Section 3.2. We place the breathers in the computational domain of the size , where , so that at the initial time the breathers are located at and . We label the breather that was initially located at the left (i.e., at ) and the right breather by the indexes 1 and 2 respectively. After that we run simulations in the fully nonlinear model as described in the Section 3.2. The total simulation time is .
We perform three series of experiments (Exp. 1, 2, and 3) with two–breather interactions, each of them corresponds to different values of breather amplitudes (and steepness correspondingly). In each experiment we study three different cases of the relative breather velocity. In addition, we perform the Exp. 4 with the breathers having so high steepness that at certain parameters we observe wave breaking. In the Exp. 4 we confine ourselves only to one case of relative velocities of the breathers.
All parameters of the breathers studied in our experiments are summarised in Table 1 for further references in the text. We provide information about the amplitude and the relative difference of velocities , which we take to generate breathers in the Zakharov model. We also show the values of the maximum amplitude of breathers in terms of surface elevation and maximum wave steepness. We compute the maximum value of at the initial moment of time for the phase of the breather (i.e., when the function achieves its maximum). The presented value of wave steepness is the maximum value which is detected during the propagation of single breather—see the Section 4.1 where this propagation is described in details.

Table 1.
Parameters of left (subscript 1) and right (subscript 2) placed breathers for which we study the collision dynamics.
The relative phase of two colliding breathers is not invariant in time. Indeed, using the Formulas (24) and (27), we find the dependence of the breather phase at its center on time in the framework of Zakharov model:
Then, the relative phase of the breathers having different parameters , and velocities is given by the following time-dependent expression:
Similar to the work [12] we define the phase difference of the breathers at the moment of time as:
We use this definition of the relative phase in the further part of the work.
4.3. Breather Collisions: Amplitude Amplification and Energy Loss
First we study the phase-dependent behaviour of the maximum amplitude of the wave field formed during the whole collision process of the breathers. We use the following function of maximum amplitude amplification normalized on the maximum amplitudes of the breathers:
In Figure 5 we show the amplitude amplification function computed for the experiments 1, 2, 3, and 4 (see Table 1) in the fully nonlinear model. We study how the function changes with wave steepness of the breathers as well as with their relative velocity. In the NLS model the amplitude amplification function does not exceed unity. The maximum value is achieved when the phase difference between the colliding NLS solitons is equal to zero: (see e.g., [28]). As was found in [7] and later in [12], the maximum of the function can exceed unity in the fully nonlinear and the Zakharov models respectively.
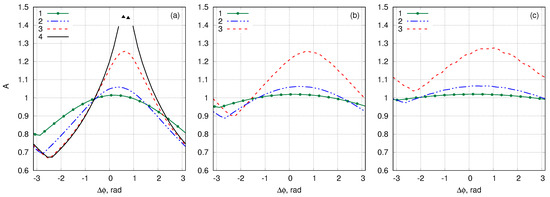
Figure 5.
The maximum amplification A of the wave field amplitude of colliding breathers depending on the relative phase for the all four numerical experiments performed in this work. The green solid curves 1 with dots corresponds to experiment 1, the blue dash-dotted curves 2 with dots—experiment 2, the red dashed curves 3 with dots—experiment 3, the black solid curve 4—experiment 4. The black triangles mark the wave breaking. Panels (a–c) correspond to the three different values of the relative velocities of the breathers in ascending order. The values of all parameters are listed in the Table 1.
In our experiments, similar to the work [12], we observe that when steepness of the breathers is small (experiment 1), the maximum of the amplitude amplification function is observed at (i.e., again similar to the NLS case [12])—see the green solid lines with dots in the Figure 5. At larger values of wave steepness the position of maximum of is shifted from more significantly. As was proposed in [12], the shift of the maximum of can be compensated by choosing a more precise definition of the breather phase difference (37), that is unsolved problem so far.
As we will see later, all other strongly nonlinear effects are also enhanced at the same values of the relative phase at which we observe the maximum of the amplitude amplification function, which has a simple explanation. The maximum amplitude amplification is accompanied by the formation of the wave profile of high steepness, that is why the high order nonlinear effects become much more pronounced. For the sake of simplicity, we call this situation as phase synchronisation between the colliding breathers. In contrast, the situation when the amplitude amplification function achieves its minimum, we call as phase desynchronisation. As can be seen from Figure 5, the phase desynchronisation corresponds to in the cases of small wave steepness (again similar to the NLS model) and is shifted from these values when when the steepness has significant value.
For experiment 3 with the maximum value of amplitude amplification exceeds by ≈. The evolution of the surface elevation profile, corresponding to this case of phase synchronization, is shown in Figure 6, while Figure 7 demonstrates the same experiment but in the case of minimum amplification (i.e., phase desynchronization).
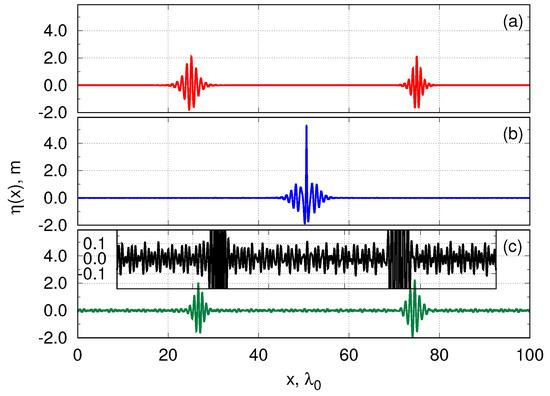
Figure 6.
Collision of breathers studied in experiment 3 with the relative velocity and the phase difference . Snapshots show the surface elevation function at the initial moment of simulation (snapshot (a)); at the moment of maximum amplitude amplification (snapshot (b)) and at the final moment of simulation (snapshot (c)). Zoom of the final amplitude profile is shown in the inset of the snapshot (c).
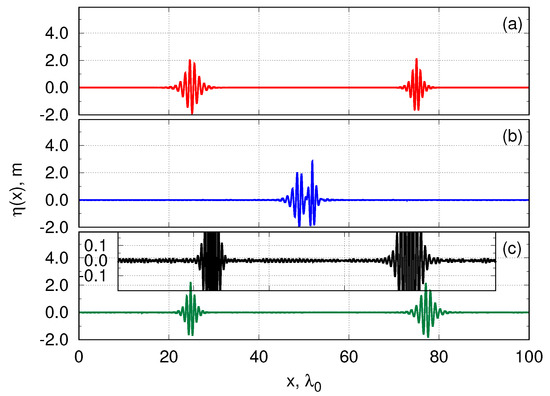
Figure 7.
Collision of breathers studied in experiment 3 with the relative velocity and the phase difference . Snapshots show the surface elevation function at the initial moment of simulation (snapshot (a)); at the moment of maximum amplitude amplification (snapshot (b)) and at the final moment of simulation (snapshot (c)). Zoom of the final amplitude profile is shown in the inset of the snapshot (c).
The further increase of the breather amplitudes leads to appearance of wave breaking during their collisions—see the amplitude amplification function corresponding to experiment 4 in Figure 5. The wave breaking first appears for the breathers with synchronised phases at the moment of interaction, when wave steepness reaches very high value. In Figure 8 we show the wave profile of the colliding breathers right before the wave breaking. Note, that in this work we do not use any special procedure (like adding a dissipation to numerical scheme) to avoid or mitigate wave breaking. This effect appears naturally as a result of high increase of wave steepness at certain moment of breather collision and we expect that similar situation can be observed in laboratory experiments. Once our numerical scheme detects wave breaking, it stops the simulation.
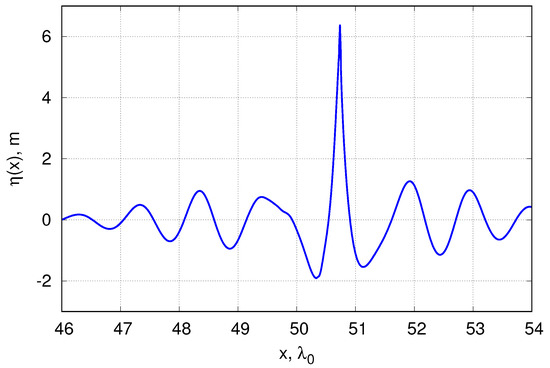
Figure 8.
Surface elevation function at the moment of breather collisions right before wave breaking. Parameters of the breathers correspond to experiment 4 with .
The interactions of the breathers are inelastic, as can be seen in Figure 6 and Figure 7 where the radiation of the incoherent waves after the collision is demonstrated. Similar to the work [12], here we quantitatively study the dependence of breather energy losses on the relative phase . We find the energy of the breathers initially located at the left and right ( and respectively) after the collision computed in the specially chosen window where the breather is localised. We denote the values of energy change of each of the breathers after collision as and . For all details of this procedure we refer to the work [12]. We define the total energy losses caused by the radiation of incoherent waves relatively to the total energy of the system:
where E is computed as the total value of the Hamiltonian
in the whole numerical interval.
Figure 9 shows the energy losses as a function of the relative phase for experiment 3 with . The value of the energy losses can exceed when phases of the breathers are synchronised and is negligible in the desynchronised case.
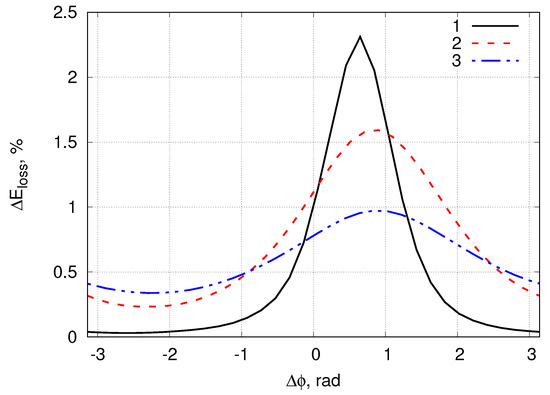
Figure 9.
The total energy losses (in percent—see Formula (39)) of breathers after their collision depending on the relative phase . The picture corresponds to experiment 3 with the relative velocity .
4.4. Breather Collisions: Energy Interchange and Spatial Positions after Collision
Now we describe individual changes of the breathers after collision. We measure the energy changes of the left and right breather relative to their individual energies:
Similar to the work [12] we observe that breathers exchange energy with each other. Each of the breathers can gain or lose the energy after collision in dependence on the relative phase —see Figure 10. The energy exchange results in changing of the amplitudes of the breathers after the collision—see Figure 11.
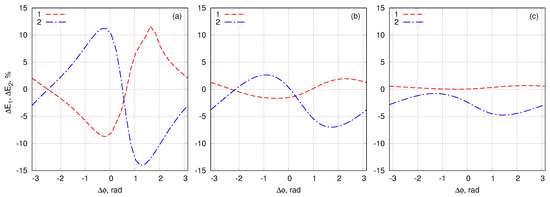
Figure 10.
The individual energy change (in percent—see Formula (41)) of breathers after their collision depending on the relative phase in experiment 3. The dashed red curve 1 shows dependence of the energy change for the left breather while the blue dash-dotted curve 2 corresponds to dependence of the energy change for the right breather . Panels (a–c) correspond to the three different values of the relative velocities of the breathers in ascending order.
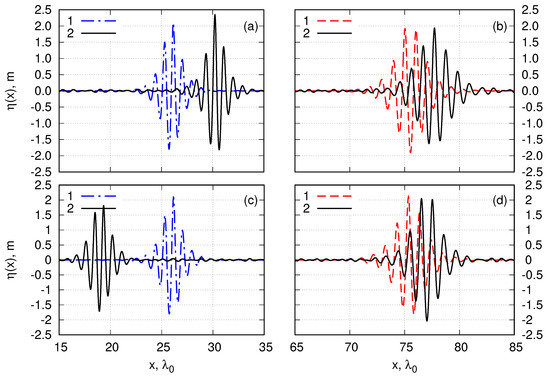
Figure 11.
Comparison of the breathers after mutual collision and the same breathers propagated without interaction in experiment 3 with relative velocity . The considered moment of time is . The pictures (a,b) correspond to the relative phase and the pictures (c,d) to the relative phase of the colliding breathers. The black solid curves 2 show surface elevation after collision of breathers. The red dashed curves 1 show the left breather propagated in the absence of right breather. The blue dash-dotted curves 1 show the right breather propagated in the absence of the left breather.
Finally we study location of the breathers at the end of our simulations. We compare the space position of the breather after the collision with than where it would have been if the breather had been traveling alone. We denote the difference in this position of the first and second breather as and . In the NLS model the soliton always acquires positive space shifts as a results of collision and appears farther that in the case of free propagation. Here we find that the interaction results in either positive and negative shift of the breather position at the end of the simulations as illustrated by Figure 11. The phase dependency of this effect is demonstrated in the Figure 12 and Figure 13 for different steepness and relative velocity of the breathers. The possible explanations of this effect are discussed in the Section 5.
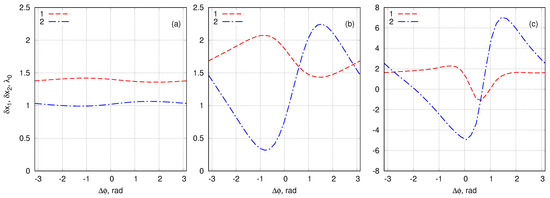
Figure 12.
Space shifts of the breathers depending on the relative phase for different wave steepnesses and the relative velocity . Panels (a–c) correspond to experiment 1, experiment 2, and experiment 3, respectively.
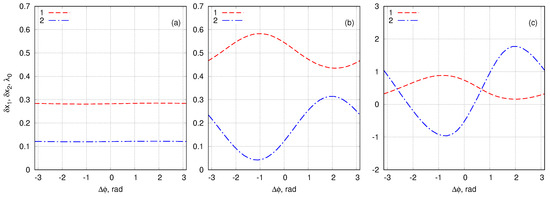
Figure 13.
Space shifts of the breathers depending on the relative phase for different wave steepnesses and the relative velocity . Panels (a–c) correspond to experiment 1, experiment 2, and experiment 3, respectively.
5. Discussion
In this work we verify in the fully nonlinear model the effects of overtaking collisions of breathers predicted recently by Kachulin and Gelash [12] in the framework of the super compact Dyachenko–Zakharov equation.
We suggest alternative approach to find stably propagating breathers in the fully nonlinear equations. In the previous works such breathers were generated using soliton solutions of the NLSE as initial conditions [4,5,6,7]. The transformation from the variables of the NLSE to the physical variables was performed with second order accuracy and in the approximation of narrow band breather spectrum (the latter is implied in the NLS model). Here we use exact numerical breather solutions of the Zakharov equation computed without any assumptions about spectral width of the breathers and transformed to physical variables with third order accuracy. The suggested approach can be especially useful for the works with breathers of extremely high steepness. The presence of minor radiation is explained by the fact that we use solutions of the reduced model as initial conditions. The low level of this radiation allows us to say that these solutions are very close to the stationary propagating solitary wave groups obtained previously in [4,5] and neglect the radiation when their interactions are studied. The results of the works [4,5] demonstrate that the radiation decays at long times and the remaining structures live hundreds and even thousands of characteristic time periods. Nevertheless, the fundamental question remains open—whether such solitary wave groups are quasi-stationary structures having extremely long life times or are exact solutions (or a good approximation of them) of the fully nonlinear model.
The results of our numerical simulations of the breather collision dynamics in the framework of the fully nonlinear equations written in conformal variables demonstrate that the relative phase of the breathers controls the process of energy exchange between breathers, level of energy losses, and space positions of breathers after the collision (compare with results of the work [12]). We also report that the maximum of the wave field can significantly exceed the sum of the breather amplitudes that was observed in the Dyachenko–Zakharov model in [12] and previously in the fully nonlinear model and experiments in water wave tank in [7].
The phase dependence of space positions of breathers after the collision, observed here in the framework of the fully nonlinear model and previously in Dyachenko–Zakharov equation [12], needed further studies. On one hand this effect can be caused by changing of the space shifts acquiring by solitary wave groups directly during their collision. On the other hand the process of energy exchange between solitary wave groups can results not only in changing of solitary wave group amplitudes, as illustrated by Figure 11, but also in changing of solitary wave group velocities, that in turn can influence their space positions. In the latter case the space shifts, studied here and in the work [12] for a certain moment in time, will also depend on the distance of breather propagation. We believe that it is most probable we observe the combination of the mentioned above two effects.
The pairwise collisions of solitary wave groups play an important role in the formation of wave field statistics when considered in integrable models (see the works [29,30] devoted to the KdV equation). As we demonstrate here and previously in [12] the nonlinear effects caused by high order energy exchange between solitary wave groups is significantly stronger than the energy losses. It means that we are able to observe several nontrivial (i.e., beyond the NLS approximation) interactions before destruction of solitary groups. That is why we believe that the results presented here and previously in [12] can be used for the developing a similar statistical approach for the Zakharov model and even for the the fully nonlinear one to the works in [29,30].
We believe that the effect of energy exchange between breathers and shifts of breather positions may be clearly observed in experiments with surface waves. We demonstrate that these effects are especially well pronounced when the relative velocity of the breathers is not high, i.e., collision occurs slowly. The latter provides a restriction on the minimum length of the breathers propagation distance needed to observe this effect in experiments, which should be taken into account in the further studies. We provide results of numerical simulations of water surface dynamics for a wide range of initial parameters of breathers up to such “critical” values, when wave breaking occurs. The obtained values of the breather parameters, at which we predict the wave breaking during collision, are to be verified in laboratory experiments.
Author Contributions
Investigation, writing—review and editing, D.K., A.D., A.G.; software and visualisation, D.K.; writing—original draft preparation, A.G.
Funding
The most part of the work was supported by the Russian Science Foundation (Grant No. 18-71-00079 to D.K.). The study reported in the Section 2.2 was additionally founded by state assignment “Dynamics of the complex materials” (to A.D.). The study reported in the Section 4.4 was additionally founded by Russian Foundation for Basic Research (RFBR) (Grant No. 18-02-00042 to A.G.).
Acknowledgments
Simulations were performed at the Novosibirsk Supercomputer Center of Novosibirsk State University. The authors thank the anonymous referees for their helpful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviation is used in this manuscript:
| NLSE | nonlinear Schrödinger equation |
References
- West, B.J.; Brueckner, K.A.; Janda, R.S.; Milder, D.M.; Milton, R.L. A new numerical method for surface hydrodynamics. J. Geophys. Res. Ocean. 1987, 92, 11803–11824. [Google Scholar]
- Zakharov, V.; Dyachenko, A.; Prokofiev, A. Freak waves as nonlinear stage of Stokes wave modulation instability. Eur. J. Mech. B Fluids 2006, 25, 677–692. [Google Scholar] [CrossRef]
- Yuen, H.C.; Lake, B.M. Nonlinear deep water waves: Theory and experiment. Phys. Fluids 1975, 18, 956–960. [Google Scholar]
- Dyachenko, A.; Zakharov, V. On the formation of freak waves on the surface of deep water. JETP Lett. 2008, 88, 307. [Google Scholar] [CrossRef]
- Slunyaev, A. Numerical simulation of “limiting” envelope solitons of gravity waves on deep water. J. Exp. Theor. Phys. 2009, 109, 676. [Google Scholar]
- Slunyaev, A.; Clauss, G.F.; Klein, M.; Onorato, M. Simulations and experiments of short intense envelope solitons of surface water waves. Phys. Fluids 2013, 25, 067105. [Google Scholar] [CrossRef]
- Slunyaev, A.; Klein, M.; Clauss, G. Laboratory and numerical study of intense envelope solitons of water waves: Generation, reflection from a wall, and collisions. Phys. Fluids 2017, 29, 047103. [Google Scholar] [CrossRef]
- Zakharov, V.E. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 1968, 9, 190–194. [Google Scholar]
- Dyachenko, A.; Zakharov, V.E. Compact equation for gravity waves on deep water. JETP Lett. 2011, 93, 701–705. [Google Scholar] [CrossRef]
- Dyachenko, A.; Zakharov, V. A dynamic equation for water waves in one horizontal dimension. Eur. J. Mech. B Fluids 2012, 32, 17–21. [Google Scholar]
- Petviashvili, V. Equation of an extraordinary soliton(ion acoustic wave packet dispersion in plasma). Sov. J. Plasma Phys. 1976, 2, 257. [Google Scholar]
- Kachulin, D.; Gelash, A. On the phase dependence of the soliton collisions in the Dyachenko–Zakharov envelope equation. Nonlinear Process. Geophys. 2018, 25, 553–563. [Google Scholar] [CrossRef]
- Dyachenko, A.; Kachulin, D.; Zakharov, V. About compact equations for water waves. Nat. Hazards 2016, 84, 529–540. [Google Scholar] [CrossRef]
- Dyachenko, A.; Kachulin, D.; Zakharov, V. Super compact equation for water waves. J. Fluid Mech. 2017, 828, 661–679. [Google Scholar] [CrossRef]
- Dyachenko, A.; Kachulin, D.; Zakharov, V. Envelope equation for water waves. J. Ocean Eng. Mar. Energy 2017, 3, 409–415. [Google Scholar]
- Fedele, F.; Dutykh, D. Solitary wave interaction in a compact equation for deep-water gravity waves. JETP Lett. 2012, 95, 622–625. [Google Scholar]
- Dyachenko, A.; Kachulin, D.; Zakharov, V.E. On the nonintegrability of the free surface hydrodynamics. JETP Lett. 2013, 98, 43–47. [Google Scholar] [CrossRef]
- Fedele, F.; Dutykh, D. Special solutions to a compact equation for deep-water gravity waves. J. Fluid Mech. 2012, 712, 646–660. [Google Scholar] [CrossRef]
- Zakharov, V.; Dyachenko, A. About shape of giant breather. Eur. J. Mech. B Fluids 2010, 29, 127–131. [Google Scholar] [CrossRef]
- Dyachenko, A.; Kuznetsov, E.; Spector, M.; Zakharov, V. Analytical description of the free surface dynamics of an ideal fluid (canonical formalism and conformal mapping). Phys. Lett. A 1996, 221, 73–79. [Google Scholar] [CrossRef]
- Dyachenko, A.I. On the Dynamics of an Ideal Fluid with a Free Surface. Dokl. Math. 2001, 63, 115–117. [Google Scholar]
- Korotkevich, A.; Pushkarev, A.; Resio, D.; Zakharov, V.E. Numerical verification of the weak turbulent model for swell evolution. Eur. J. Mech. B Fluids 2008, 27, 361–387. [Google Scholar] [CrossRef]
- Zakharov, V.E.; L’vov, V.S.; Falkovich, G. Kolmogorov Spectra of Turbulence 1. Wave Turbulence; Springer: Berlin, Germany, 1992. [Google Scholar]
- Zakharov, V. Statistical theory of gravity and capillary waves on the surface of a finite-depth fluid. Eur. J. Mech. B Fluids 1999, 18, 327. [Google Scholar] [CrossRef]
- Dyachenko, A.I.; Kachulin, D.I.; Zakharov, V.E. Freak-Waves: Compact Equation Versus Fully Nonlinear One. In Extreme Ocean Waves; Pelinovsky, E., Kharif, C., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 23–44. [Google Scholar]
- Lakoba, T.I.; Yang, J. A generalized Petviashvili iteration method for scalar and vector Hamiltonian equations with arbitrary form of nonlinearity. J. Comput. Phys. 2007, 226, 1668–1692. [Google Scholar] [CrossRef][Green Version]
- Jianke, Y. Nonlinear Waves in Integrable and Nonintegrable Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010; Volume 16. [Google Scholar]
- Antikainen, A.; Erkintalo, M.; Dudley, J.; Genty, G. On the phase-dependent manifestation of optical rogue waves. Nonlinearity 2012, 25, R73. [Google Scholar] [CrossRef]
- Pelinovsky, E.N.; Shurgalina, E.; Sergeeva, A.; Talipova, T.G.; El, G.; Grimshaw, R.H. Two-soliton interaction as an elementary act of soliton turbulence in integrable systems. Phys. Lett. A 2013, 377, 272–275. [Google Scholar] [CrossRef]
- Shurgalina, E.; Pelinovsky, E. Nonlinear dynamics of a soliton gas: Modified Korteweg–de Vries equation framework. Phys. Lett. A 2016, 380, 2049–2053. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).