Interactions of Coherent Structures on the Surface of Deep Water
Abstract
1. Introduction
2. Theoretical Formalism
2.1. Fully Nonlinear Equations for Ideal Deep Fluid
2.2. Zakharov Equation
3. Numerical Methods
3.1. Breather Solution of the Zakharov Equation
3.2. Numerical Integration of the Fully Nonlinear Equations
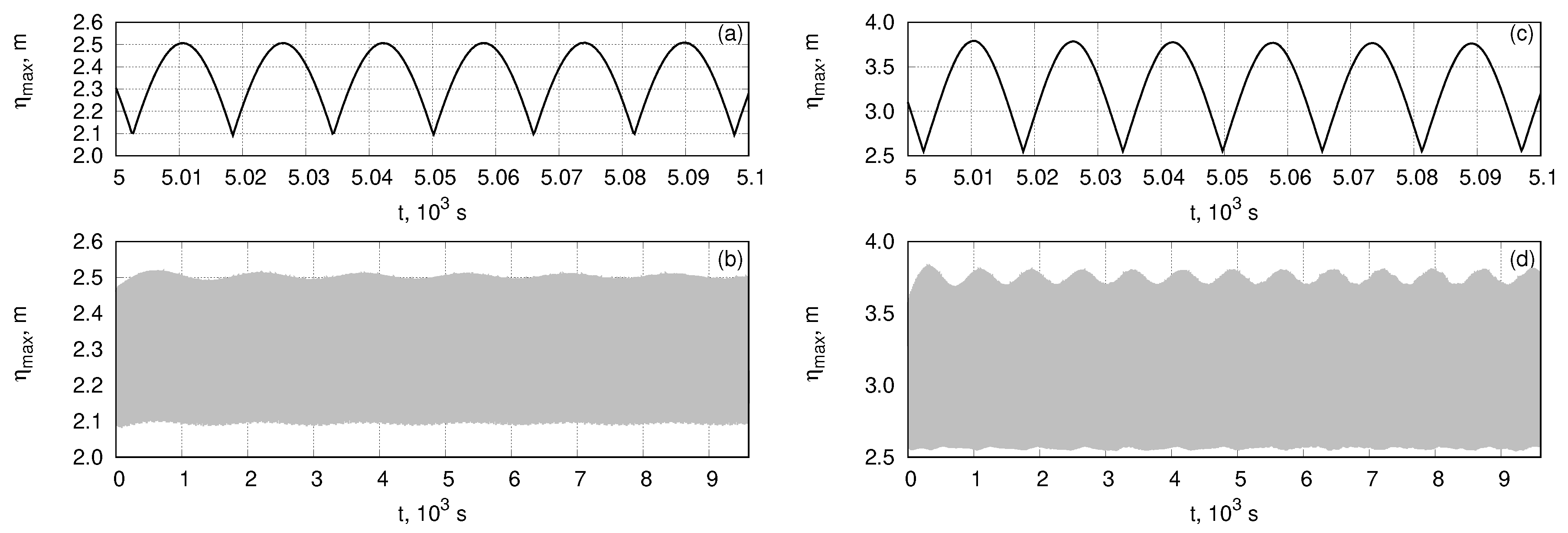
4. Results of Numerical Simulations
4.1. Generation of Stable Breather in the Fully Nonlinear Model
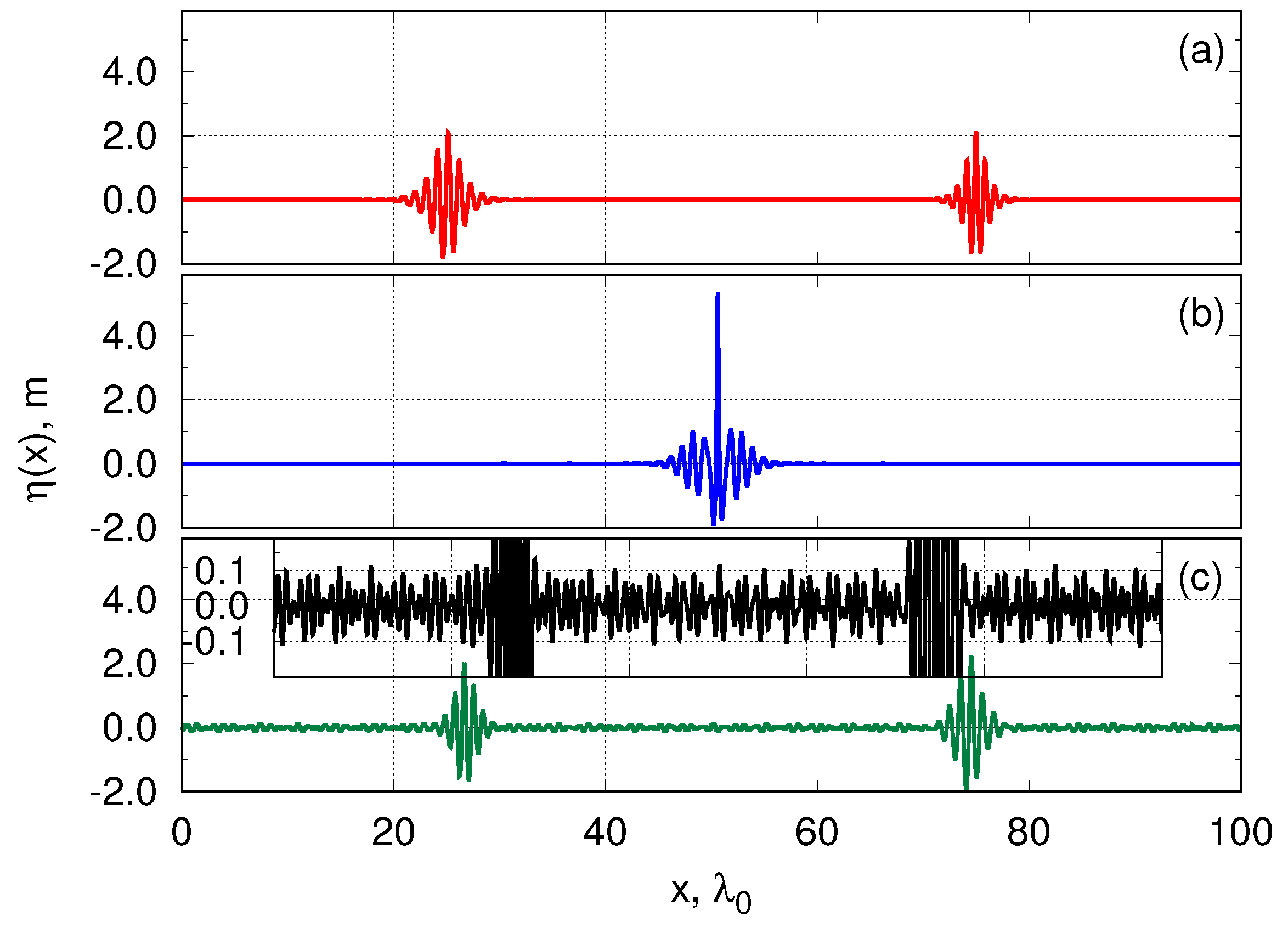
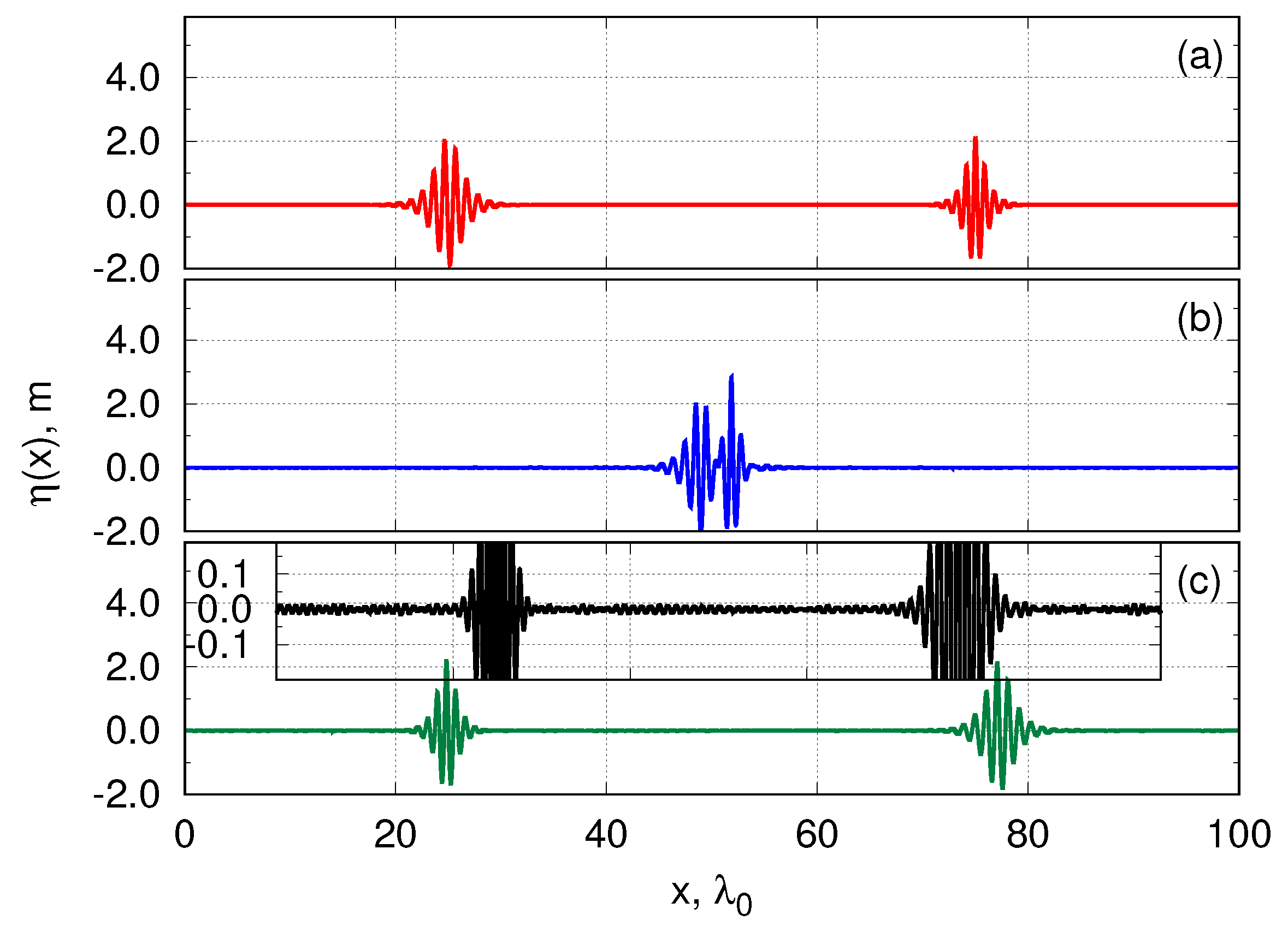
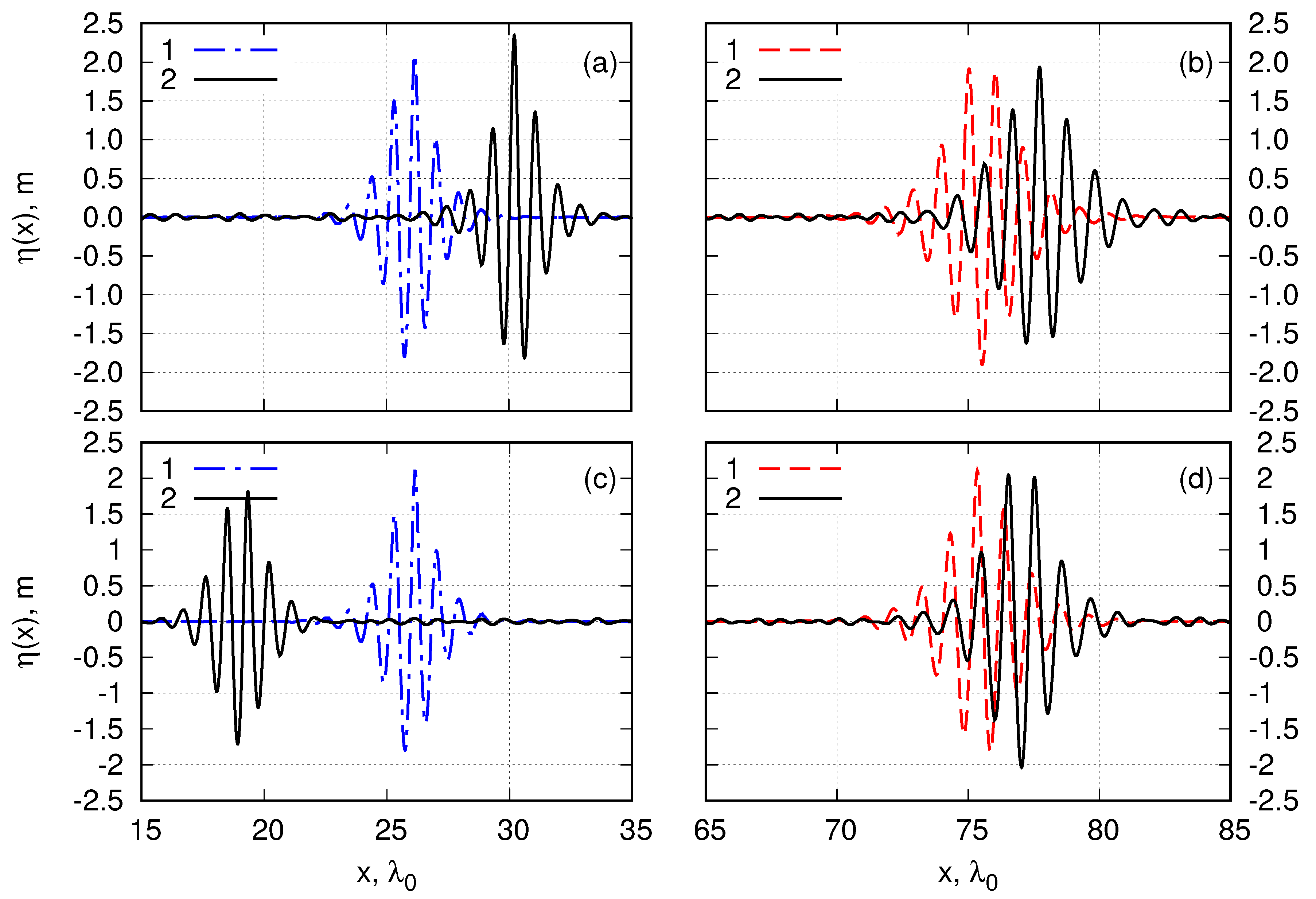
4.2. Breather Collisions
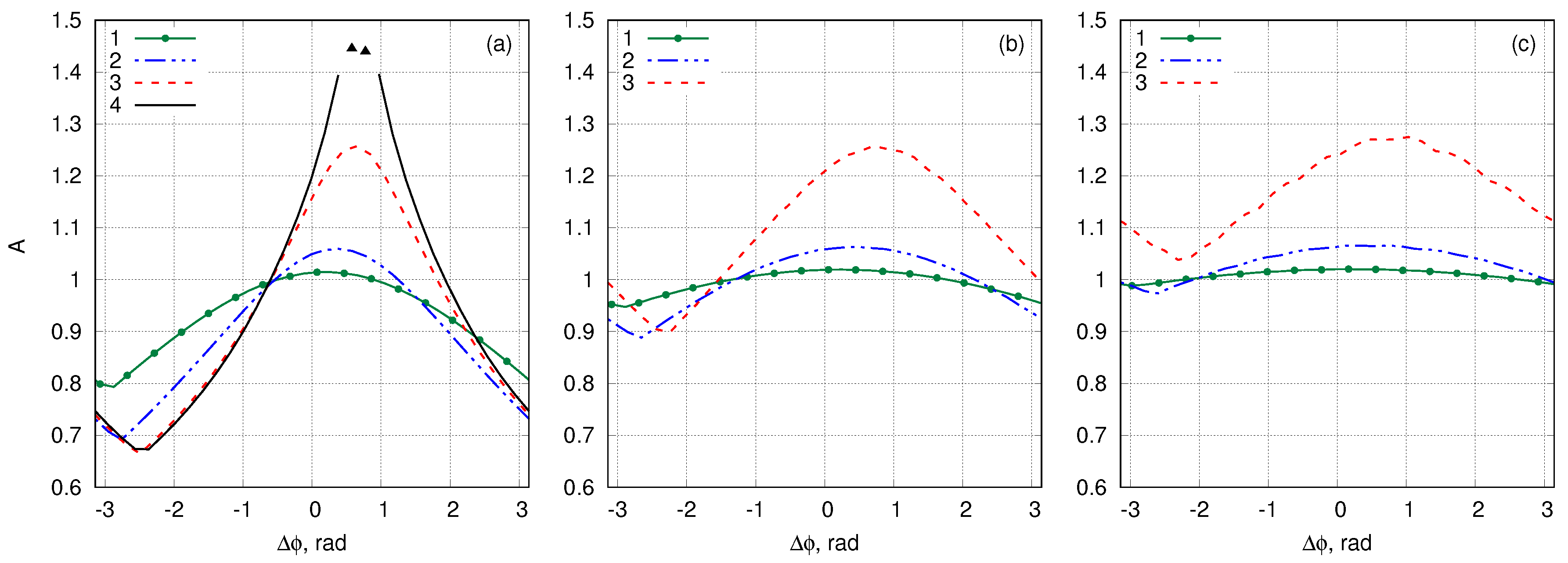
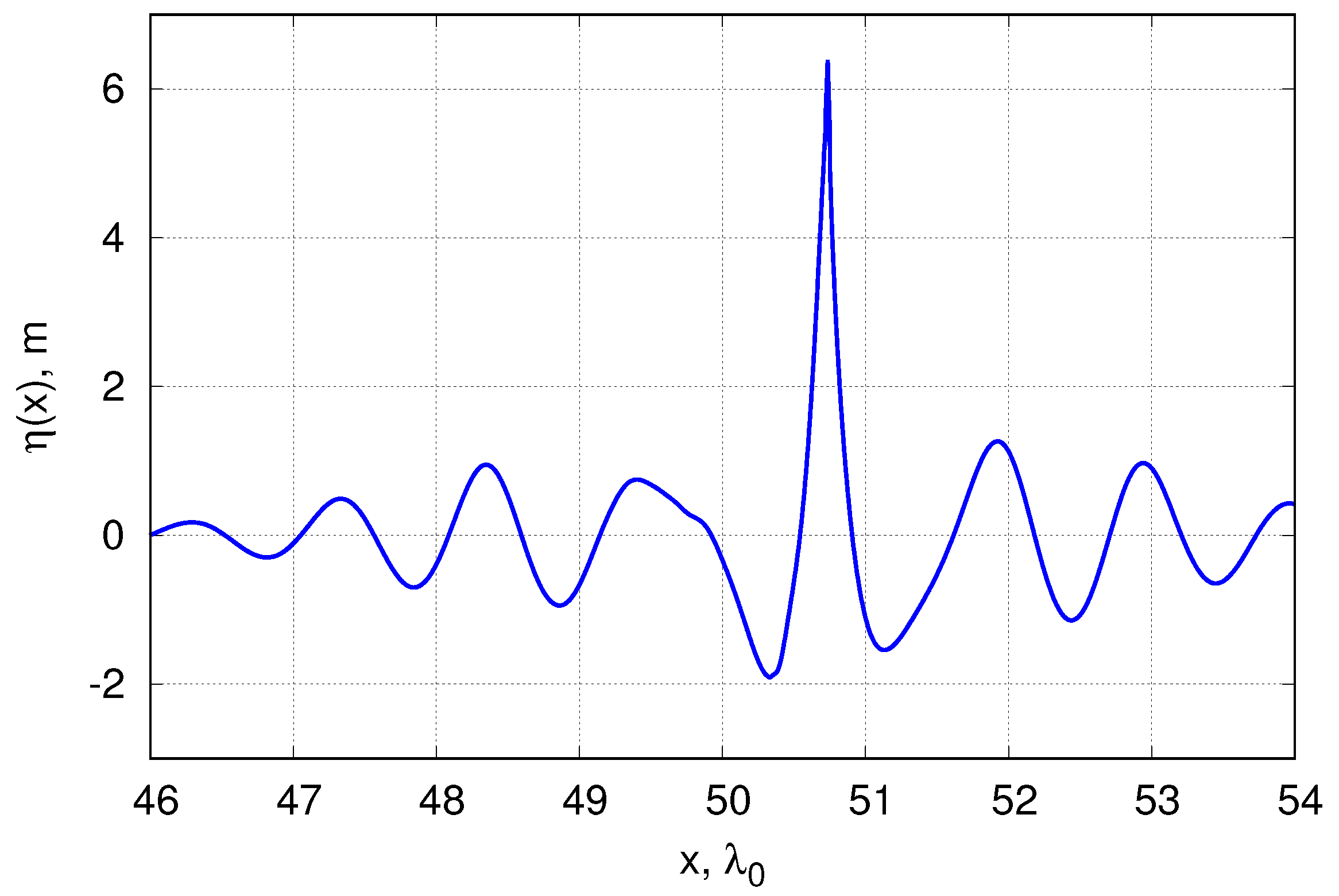
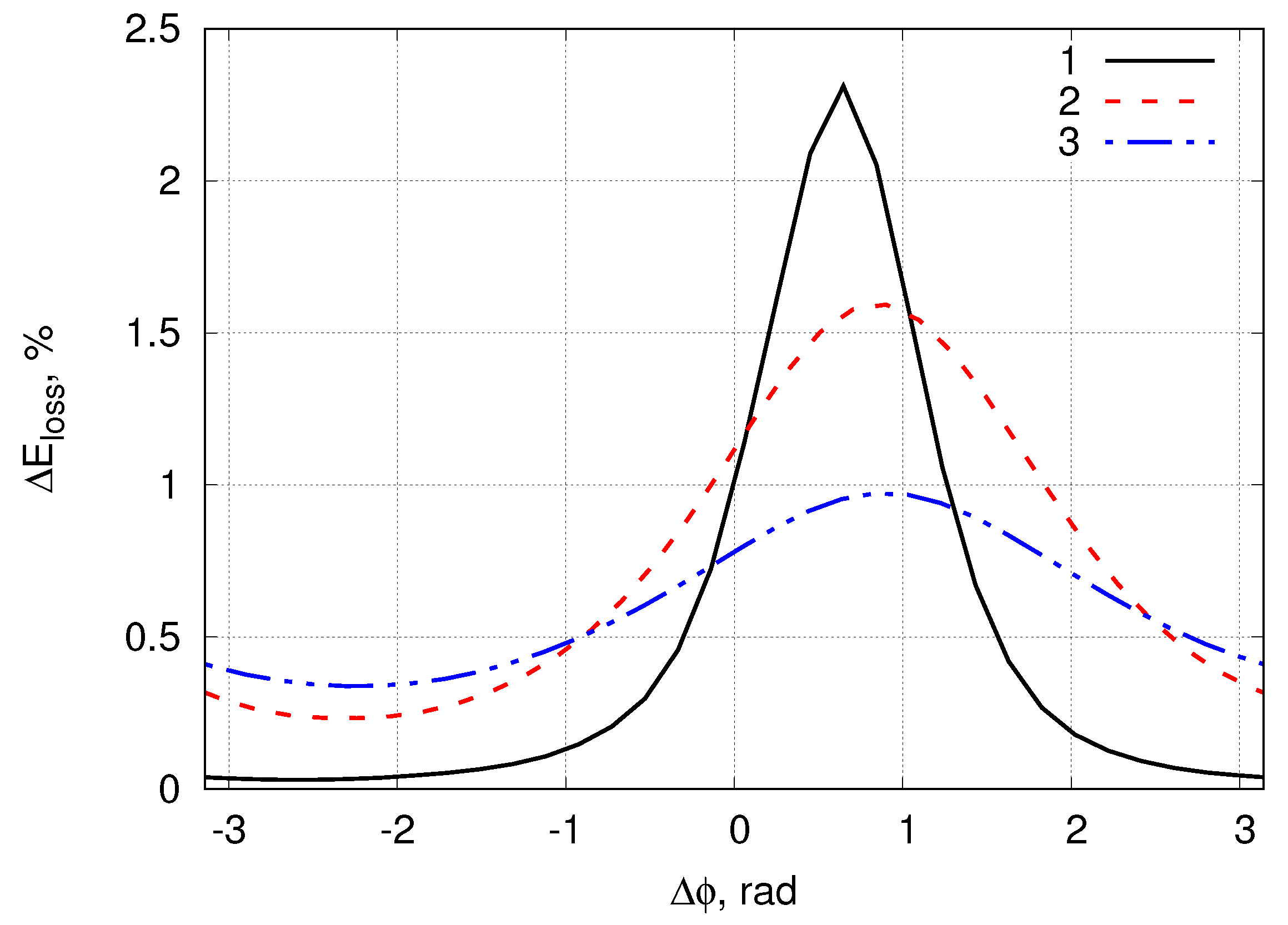
4.3. Breather Collisions: Amplitude Amplification and Energy Loss
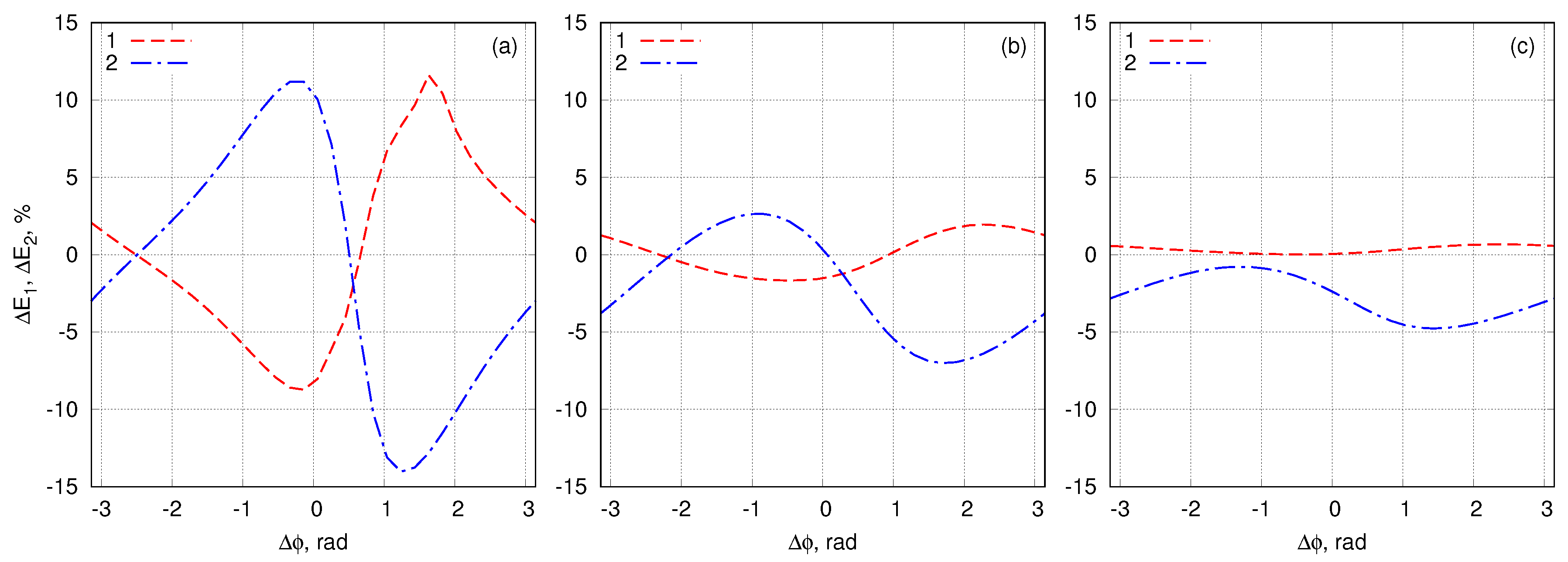
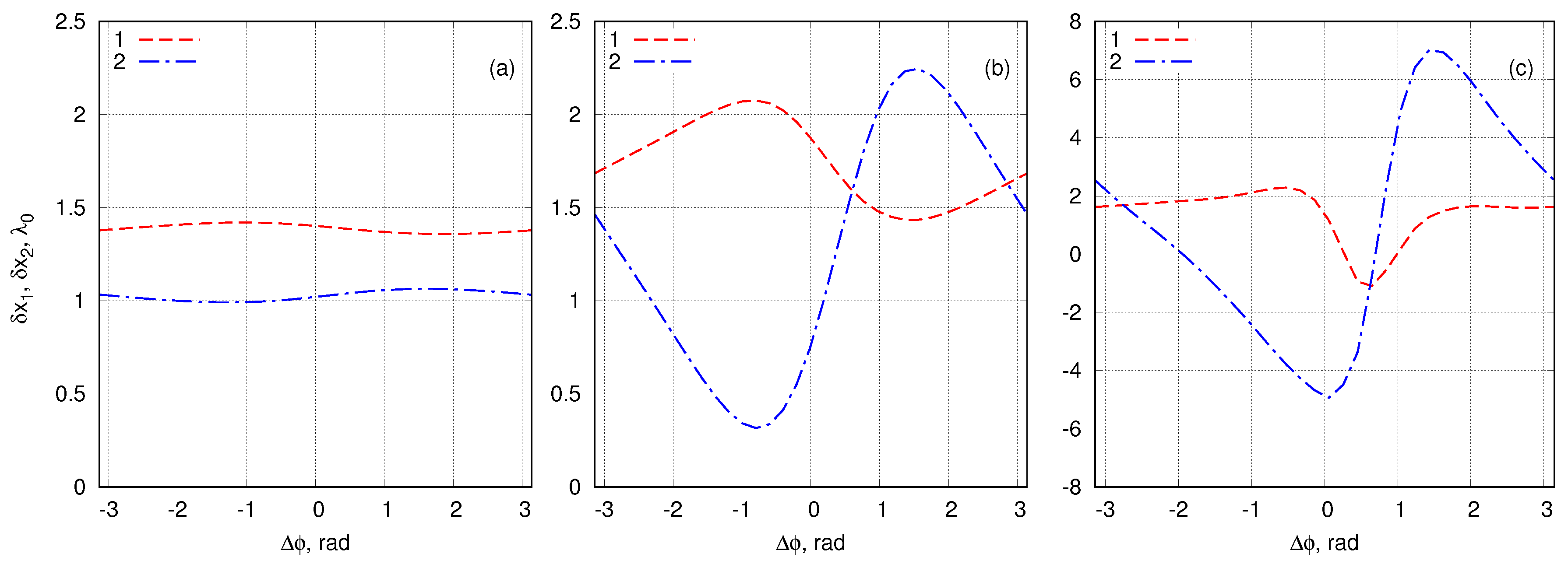
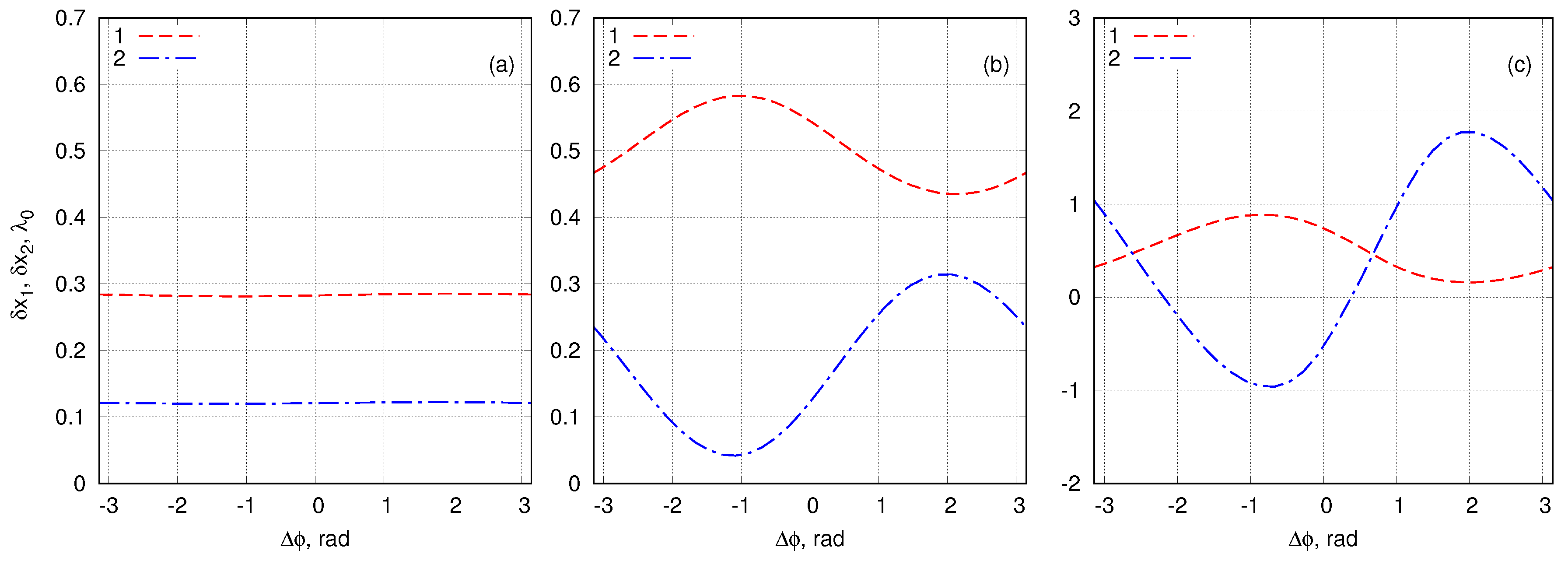
4.4. Breather Collisions: Energy Interchange and Spatial Positions after Collision
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| NLSE | nonlinear Schrödinger equation |
References
- West, B.J.; Brueckner, K.A.; Janda, R.S.; Milder, D.M.; Milton, R.L. A new numerical method for surface hydrodynamics. J. Geophys. Res. Ocean. 1987, 92, 11803–11824. [Google Scholar]
- Zakharov, V.; Dyachenko, A.; Prokofiev, A. Freak waves as nonlinear stage of Stokes wave modulation instability. Eur. J. Mech. B Fluids 2006, 25, 677–692. [Google Scholar] [CrossRef]
- Yuen, H.C.; Lake, B.M. Nonlinear deep water waves: Theory and experiment. Phys. Fluids 1975, 18, 956–960. [Google Scholar]
- Dyachenko, A.; Zakharov, V. On the formation of freak waves on the surface of deep water. JETP Lett. 2008, 88, 307. [Google Scholar] [CrossRef]
- Slunyaev, A. Numerical simulation of “limiting” envelope solitons of gravity waves on deep water. J. Exp. Theor. Phys. 2009, 109, 676. [Google Scholar]
- Slunyaev, A.; Clauss, G.F.; Klein, M.; Onorato, M. Simulations and experiments of short intense envelope solitons of surface water waves. Phys. Fluids 2013, 25, 067105. [Google Scholar] [CrossRef]
- Slunyaev, A.; Klein, M.; Clauss, G. Laboratory and numerical study of intense envelope solitons of water waves: Generation, reflection from a wall, and collisions. Phys. Fluids 2017, 29, 047103. [Google Scholar] [CrossRef]
- Zakharov, V.E. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 1968, 9, 190–194. [Google Scholar]
- Dyachenko, A.; Zakharov, V.E. Compact equation for gravity waves on deep water. JETP Lett. 2011, 93, 701–705. [Google Scholar] [CrossRef]
- Dyachenko, A.; Zakharov, V. A dynamic equation for water waves in one horizontal dimension. Eur. J. Mech. B Fluids 2012, 32, 17–21. [Google Scholar]
- Petviashvili, V. Equation of an extraordinary soliton(ion acoustic wave packet dispersion in plasma). Sov. J. Plasma Phys. 1976, 2, 257. [Google Scholar]
- Kachulin, D.; Gelash, A. On the phase dependence of the soliton collisions in the Dyachenko–Zakharov envelope equation. Nonlinear Process. Geophys. 2018, 25, 553–563. [Google Scholar] [CrossRef]
- Dyachenko, A.; Kachulin, D.; Zakharov, V. About compact equations for water waves. Nat. Hazards 2016, 84, 529–540. [Google Scholar] [CrossRef]
- Dyachenko, A.; Kachulin, D.; Zakharov, V. Super compact equation for water waves. J. Fluid Mech. 2017, 828, 661–679. [Google Scholar] [CrossRef]
- Dyachenko, A.; Kachulin, D.; Zakharov, V. Envelope equation for water waves. J. Ocean Eng. Mar. Energy 2017, 3, 409–415. [Google Scholar]
- Fedele, F.; Dutykh, D. Solitary wave interaction in a compact equation for deep-water gravity waves. JETP Lett. 2012, 95, 622–625. [Google Scholar]
- Dyachenko, A.; Kachulin, D.; Zakharov, V.E. On the nonintegrability of the free surface hydrodynamics. JETP Lett. 2013, 98, 43–47. [Google Scholar] [CrossRef]
- Fedele, F.; Dutykh, D. Special solutions to a compact equation for deep-water gravity waves. J. Fluid Mech. 2012, 712, 646–660. [Google Scholar] [CrossRef]
- Zakharov, V.; Dyachenko, A. About shape of giant breather. Eur. J. Mech. B Fluids 2010, 29, 127–131. [Google Scholar] [CrossRef]
- Dyachenko, A.; Kuznetsov, E.; Spector, M.; Zakharov, V. Analytical description of the free surface dynamics of an ideal fluid (canonical formalism and conformal mapping). Phys. Lett. A 1996, 221, 73–79. [Google Scholar] [CrossRef]
- Dyachenko, A.I. On the Dynamics of an Ideal Fluid with a Free Surface. Dokl. Math. 2001, 63, 115–117. [Google Scholar]
- Korotkevich, A.; Pushkarev, A.; Resio, D.; Zakharov, V.E. Numerical verification of the weak turbulent model for swell evolution. Eur. J. Mech. B Fluids 2008, 27, 361–387. [Google Scholar] [CrossRef]
- Zakharov, V.E.; L’vov, V.S.; Falkovich, G. Kolmogorov Spectra of Turbulence 1. Wave Turbulence; Springer: Berlin, Germany, 1992. [Google Scholar]
- Zakharov, V. Statistical theory of gravity and capillary waves on the surface of a finite-depth fluid. Eur. J. Mech. B Fluids 1999, 18, 327. [Google Scholar] [CrossRef]
- Dyachenko, A.I.; Kachulin, D.I.; Zakharov, V.E. Freak-Waves: Compact Equation Versus Fully Nonlinear One. In Extreme Ocean Waves; Pelinovsky, E., Kharif, C., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 23–44. [Google Scholar]
- Lakoba, T.I.; Yang, J. A generalized Petviashvili iteration method for scalar and vector Hamiltonian equations with arbitrary form of nonlinearity. J. Comput. Phys. 2007, 226, 1668–1692. [Google Scholar] [CrossRef][Green Version]
- Jianke, Y. Nonlinear Waves in Integrable and Nonintegrable Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010; Volume 16. [Google Scholar]
- Antikainen, A.; Erkintalo, M.; Dudley, J.; Genty, G. On the phase-dependent manifestation of optical rogue waves. Nonlinearity 2012, 25, R73. [Google Scholar] [CrossRef]
- Pelinovsky, E.N.; Shurgalina, E.; Sergeeva, A.; Talipova, T.G.; El, G.; Grimshaw, R.H. Two-soliton interaction as an elementary act of soliton turbulence in integrable systems. Phys. Lett. A 2013, 377, 272–275. [Google Scholar] [CrossRef]
- Shurgalina, E.; Pelinovsky, E. Nonlinear dynamics of a soliton gas: Modified Korteweg–de Vries equation framework. Phys. Lett. A 2016, 380, 2049–2053. [Google Scholar] [CrossRef]
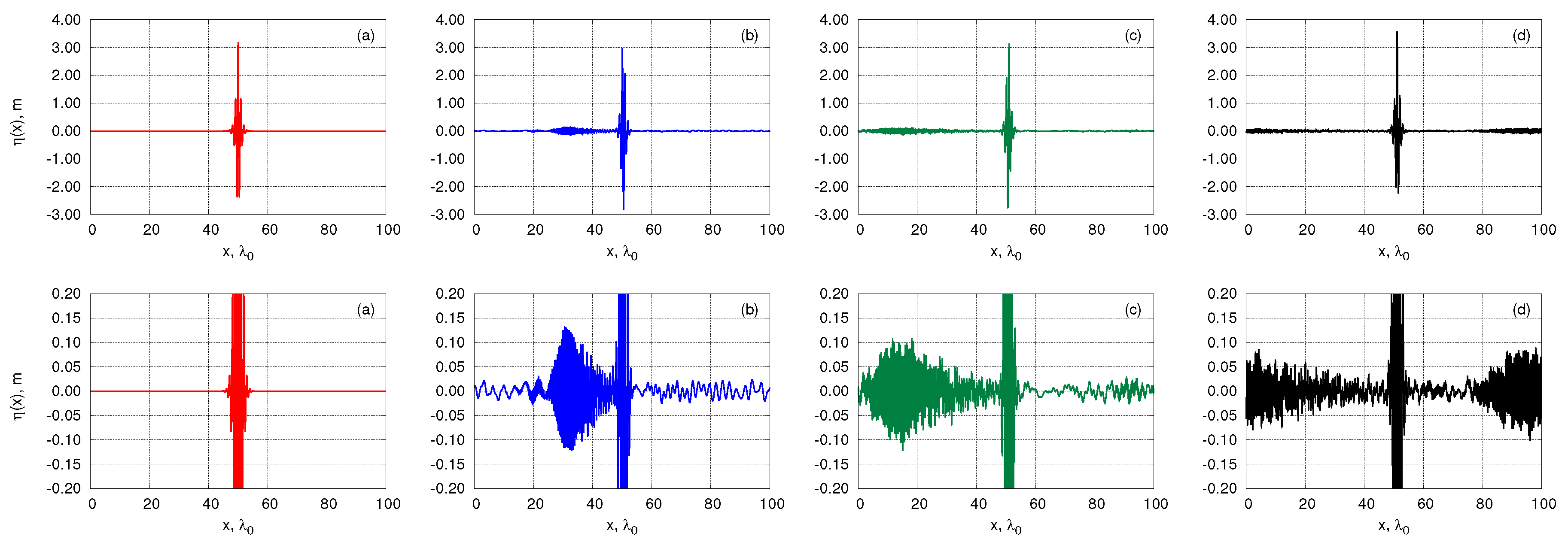
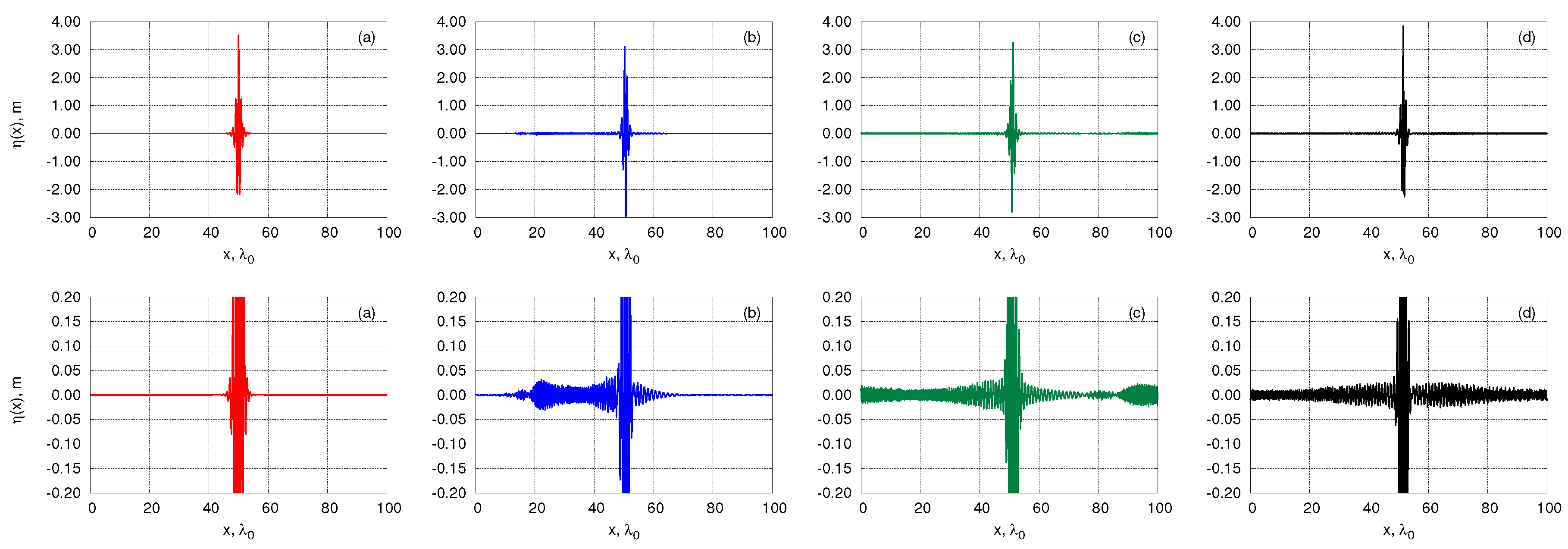
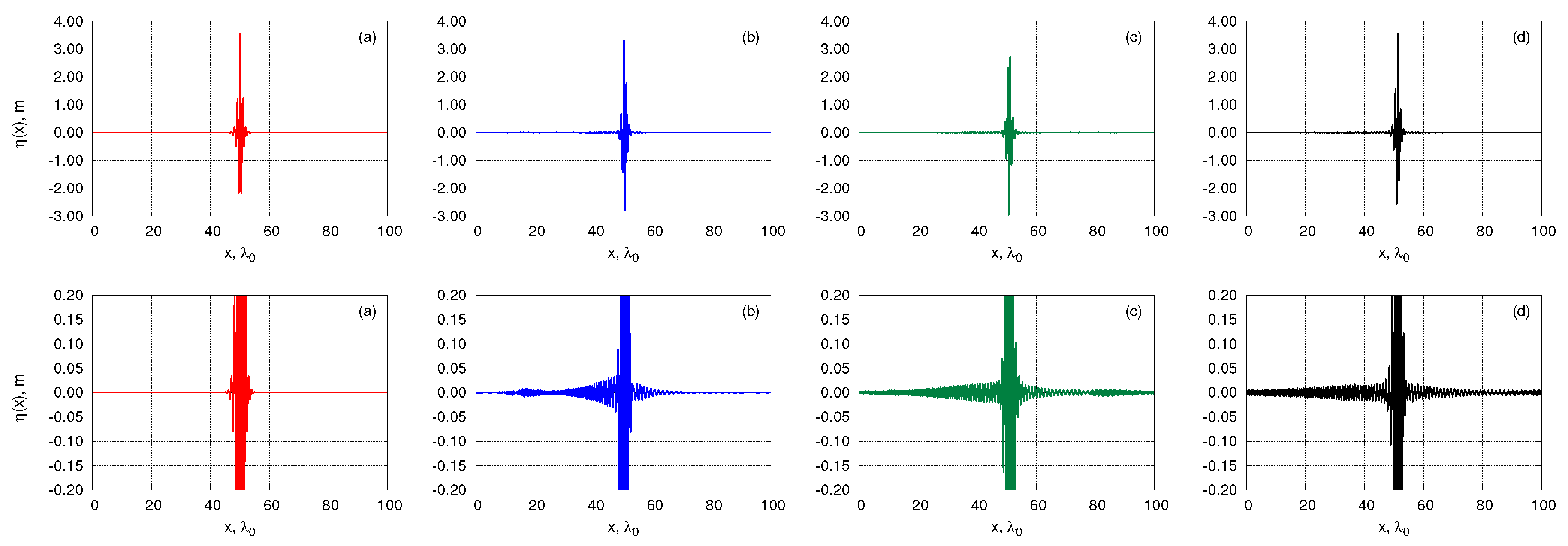
| Exp. 1 | |||
| m m | m m | m m | |
| Exp. 2 | |||
| m m | m m | m m | |
| Exp. 3 | |||
| m m | m m | m m | |
| Exp. 4 | |||
| m m | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kachulin, D.; Dyachenko, A.; Gelash, A. Interactions of Coherent Structures on the Surface of Deep Water. Fluids 2019, 4, 83. https://doi.org/10.3390/fluids4020083
Kachulin D, Dyachenko A, Gelash A. Interactions of Coherent Structures on the Surface of Deep Water. Fluids. 2019; 4(2):83. https://doi.org/10.3390/fluids4020083
Chicago/Turabian StyleKachulin, Dmitry, Alexander Dyachenko, and Andrey Gelash. 2019. "Interactions of Coherent Structures on the Surface of Deep Water" Fluids 4, no. 2: 83. https://doi.org/10.3390/fluids4020083
APA StyleKachulin, D., Dyachenko, A., & Gelash, A. (2019). Interactions of Coherent Structures on the Surface of Deep Water. Fluids, 4(2), 83. https://doi.org/10.3390/fluids4020083




