Assessment of Piezoelectric Sensors for the Acquisition of Steady Melt Pressures in Polymer Extrusion
Abstract
1. Introduction
2. Experimental
2.1. Materials
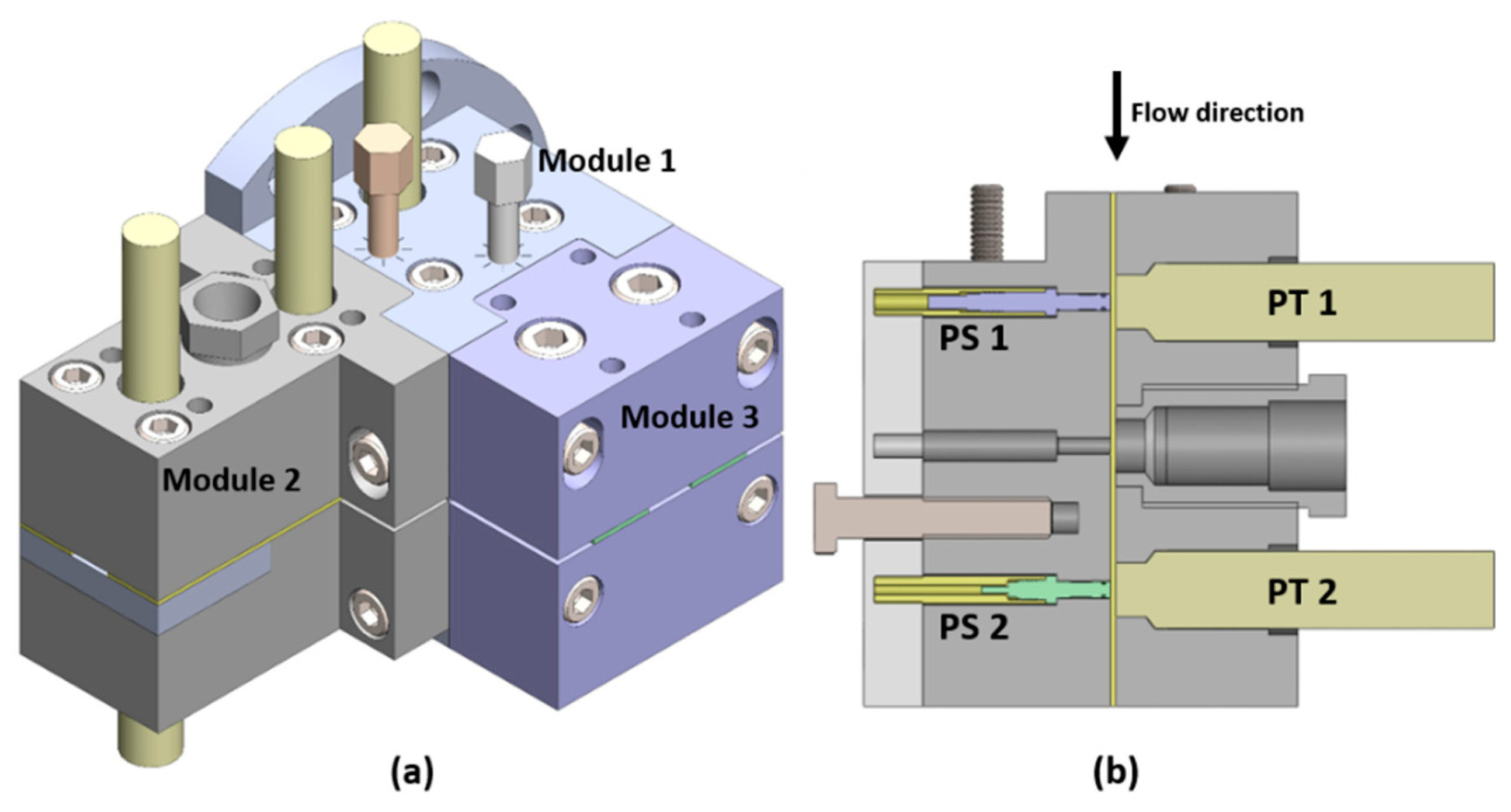
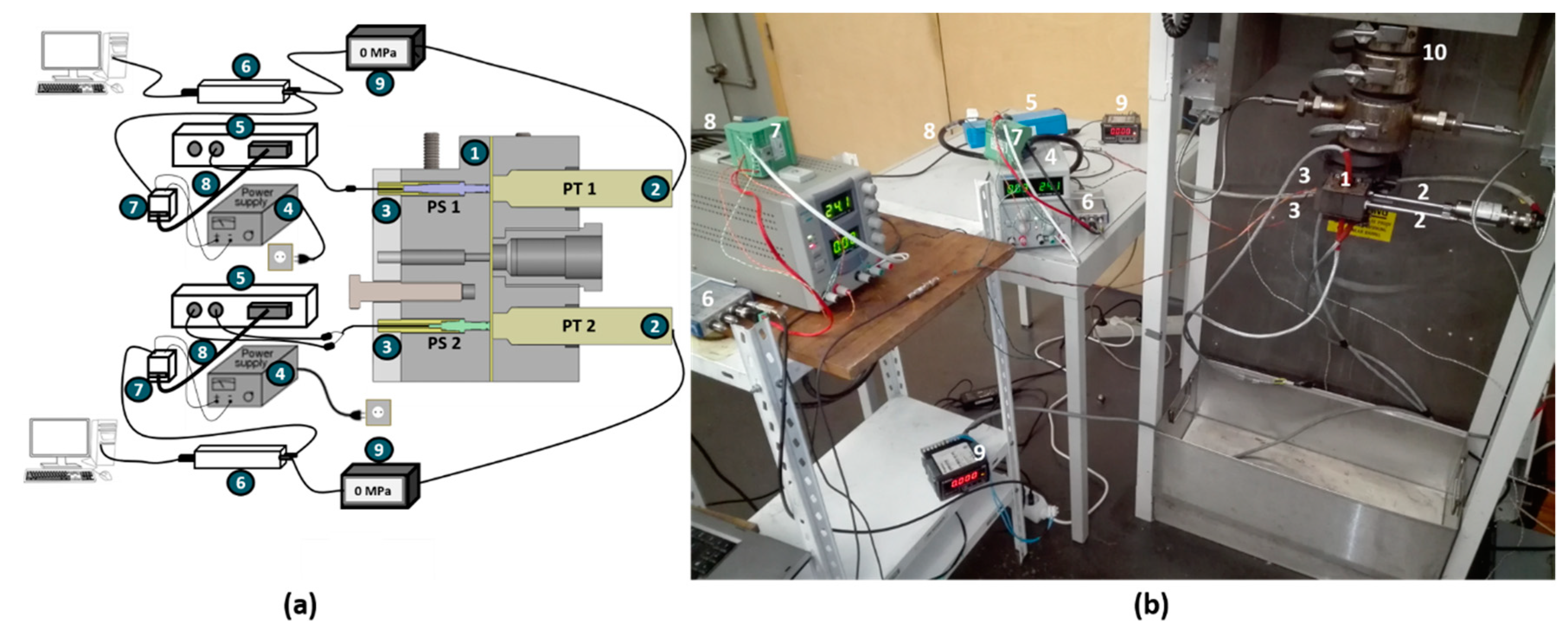
2.2. Experimental Set-Up
- -
- Two charge amplifiers, a Kistler 5155A 2241 for PS 1 and a Kistler 5155A 22A1 (with separate channels to acquire pressure and temperature) for PS 2. Two amplification ranges are available which depend on the maximum charge delivered by the transducer, namely up to 20000 pC (which corresponds to 10 V in Range I) and up to 5000 pC (which corresponds to 10 V in Range II for larger amplification).
- -
- Two power supplies (Matrix MPS-5LK-2, delivering a voltage between 18–30 V DC) to feed the amplifiers and command functions.
- -
- -
- Two DIN-Rail Mount Terminal Blocks for 25-Pin D-SUB Modules and two 25-Pin Shielded D-SUB cables (from National Instruments, Austin, TX, USA) in order to interface the power supply, the amplifier, and the ADC.
2.3. Experimental Procedure
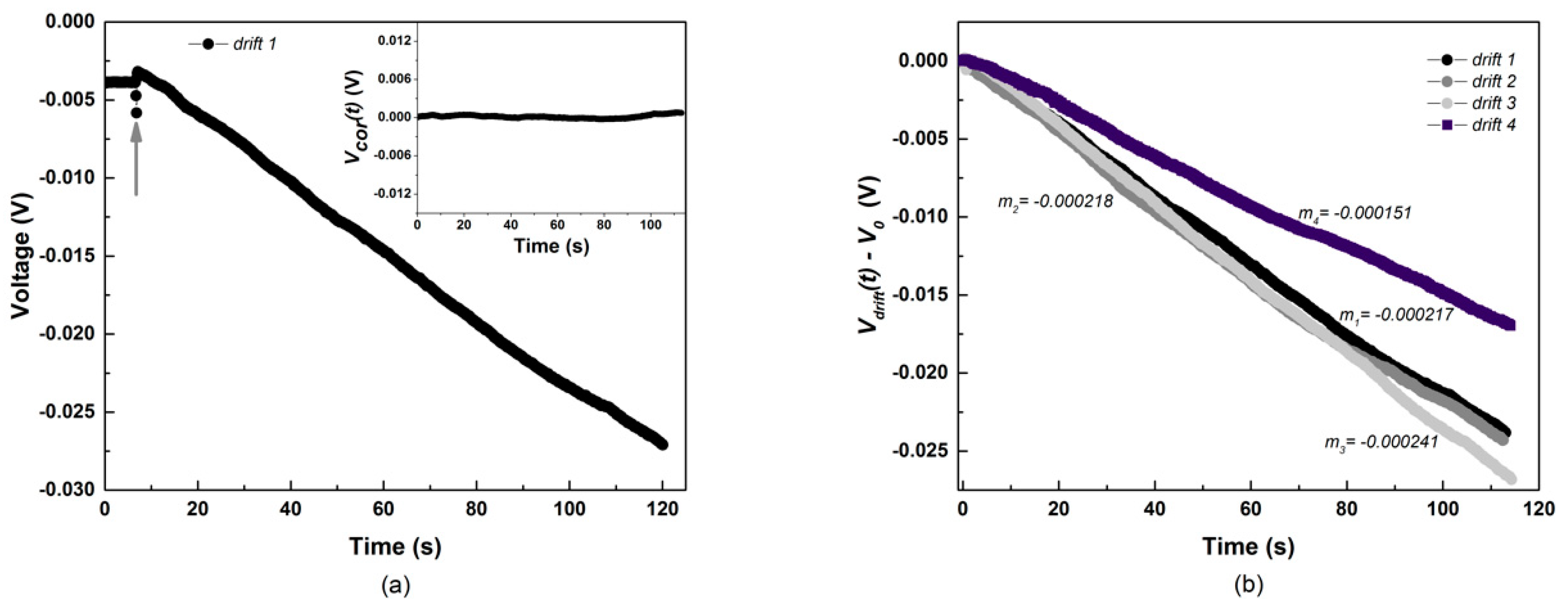
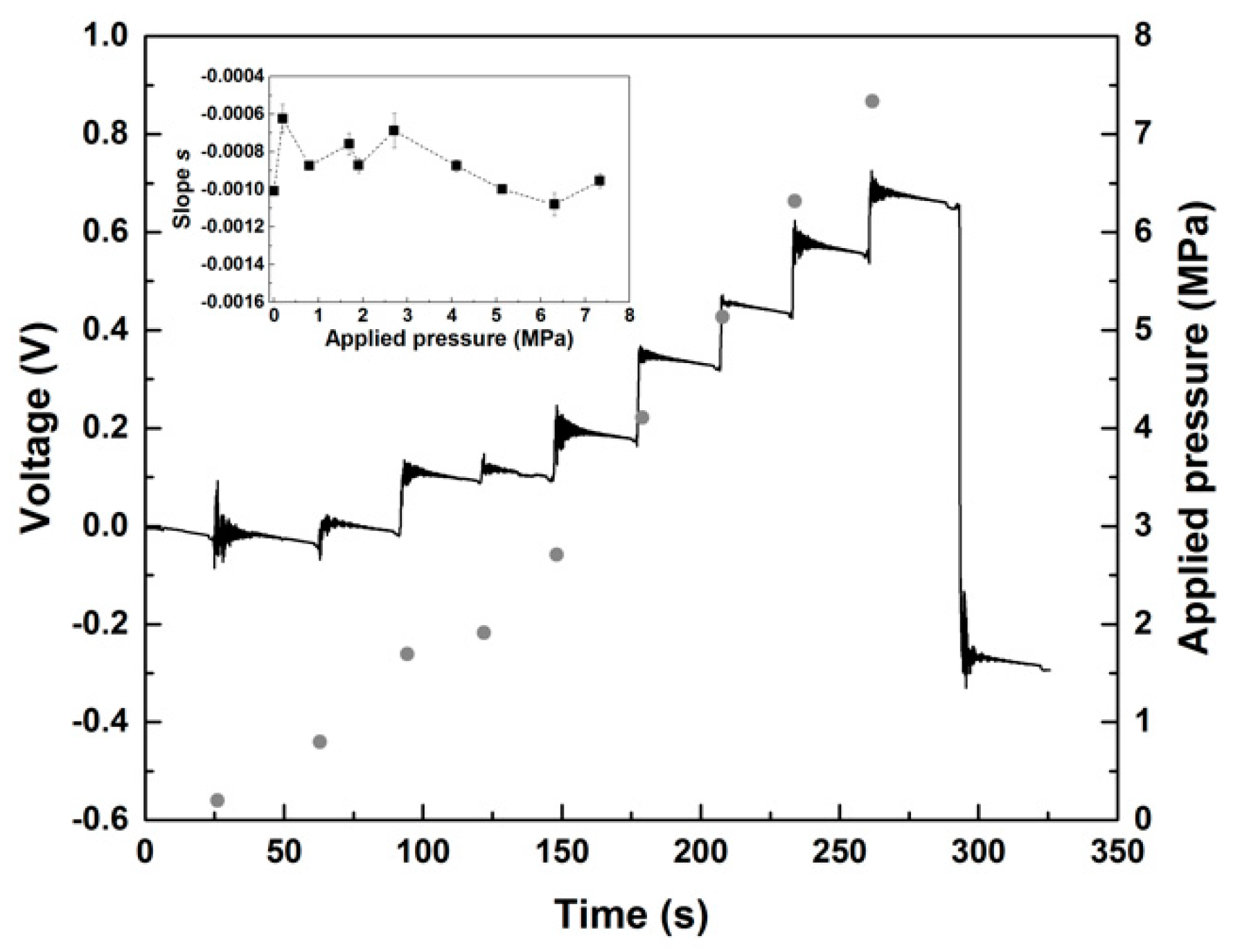
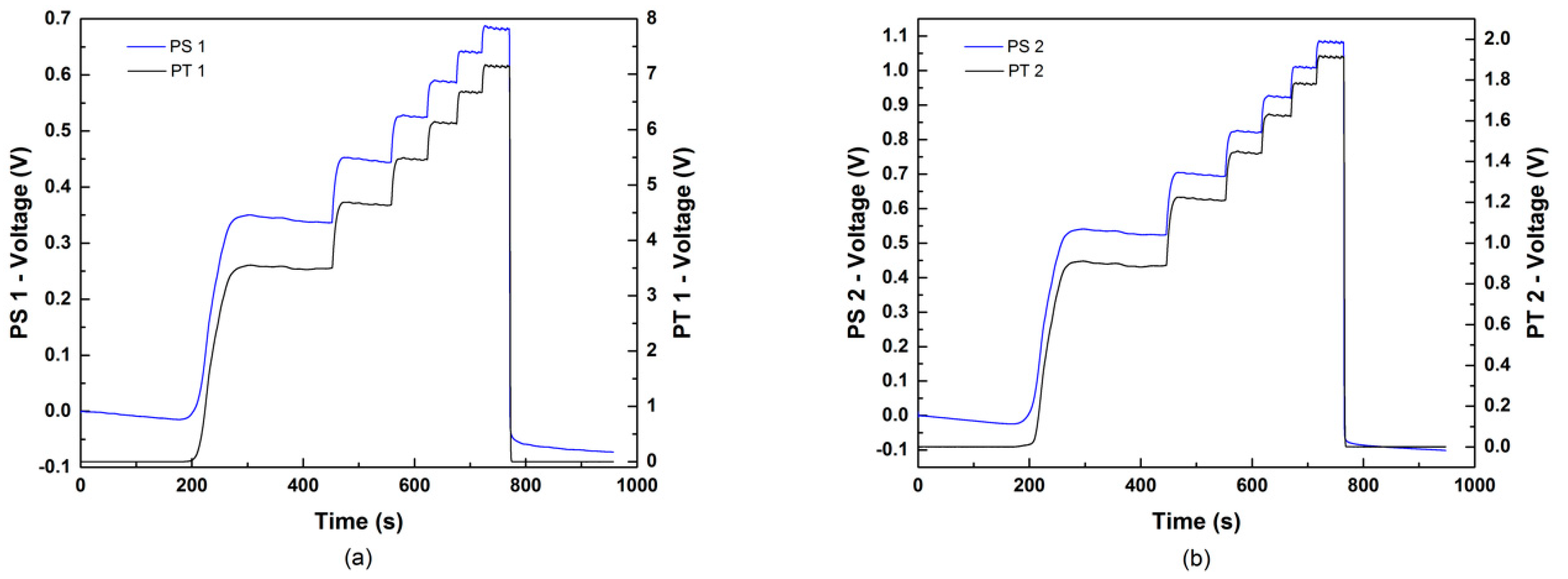
2.3.1. Calibrations
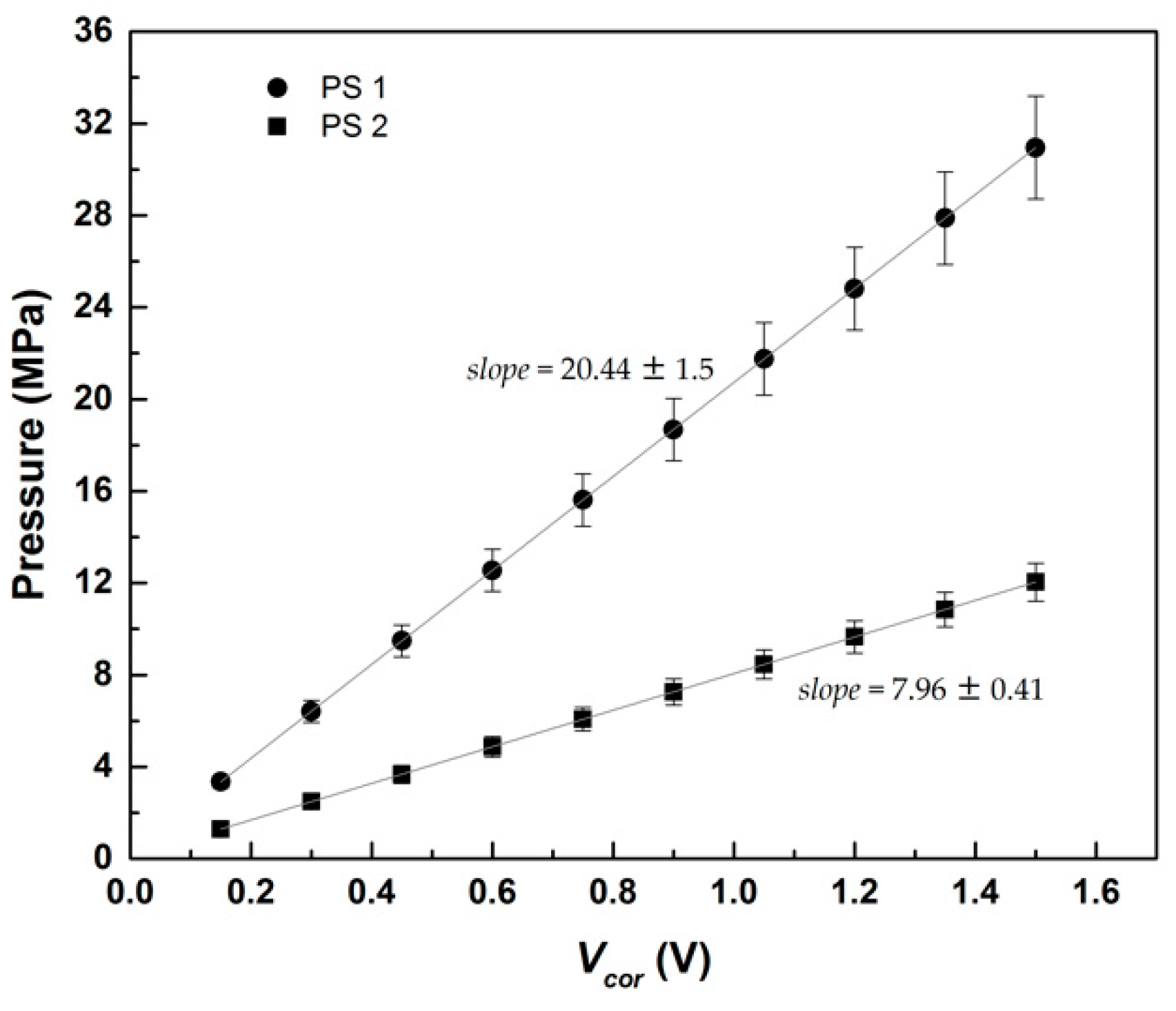
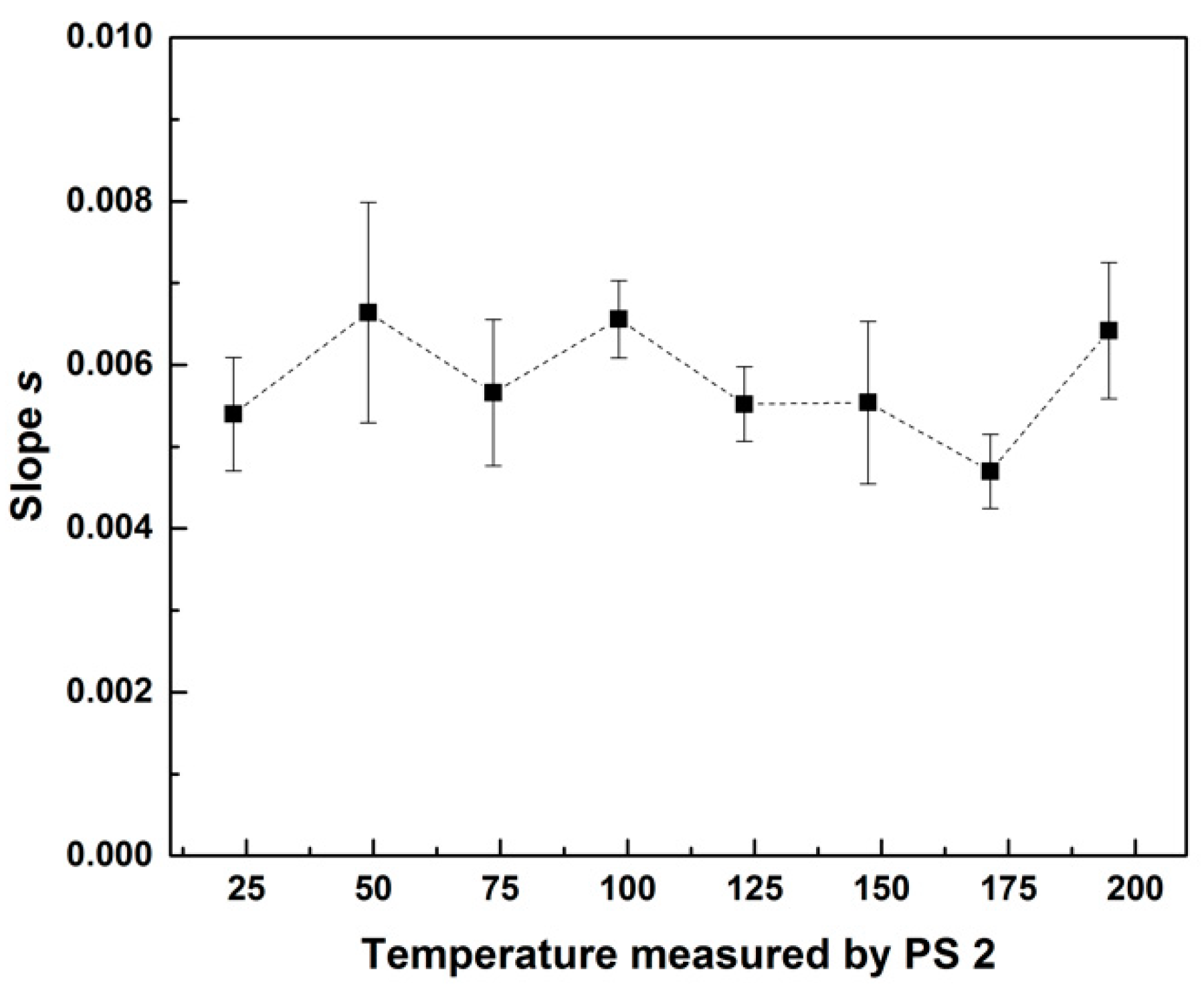
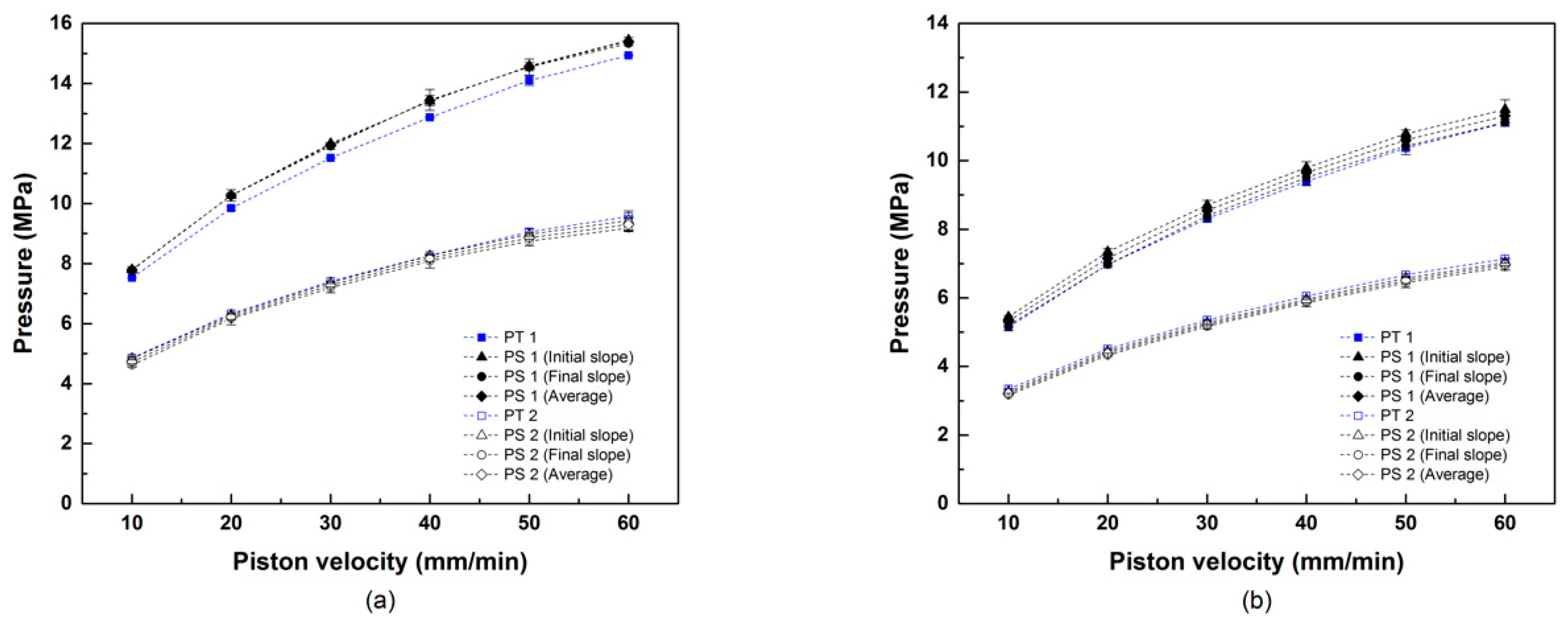
2.3.2. Pressure Measurements and Flow Curves
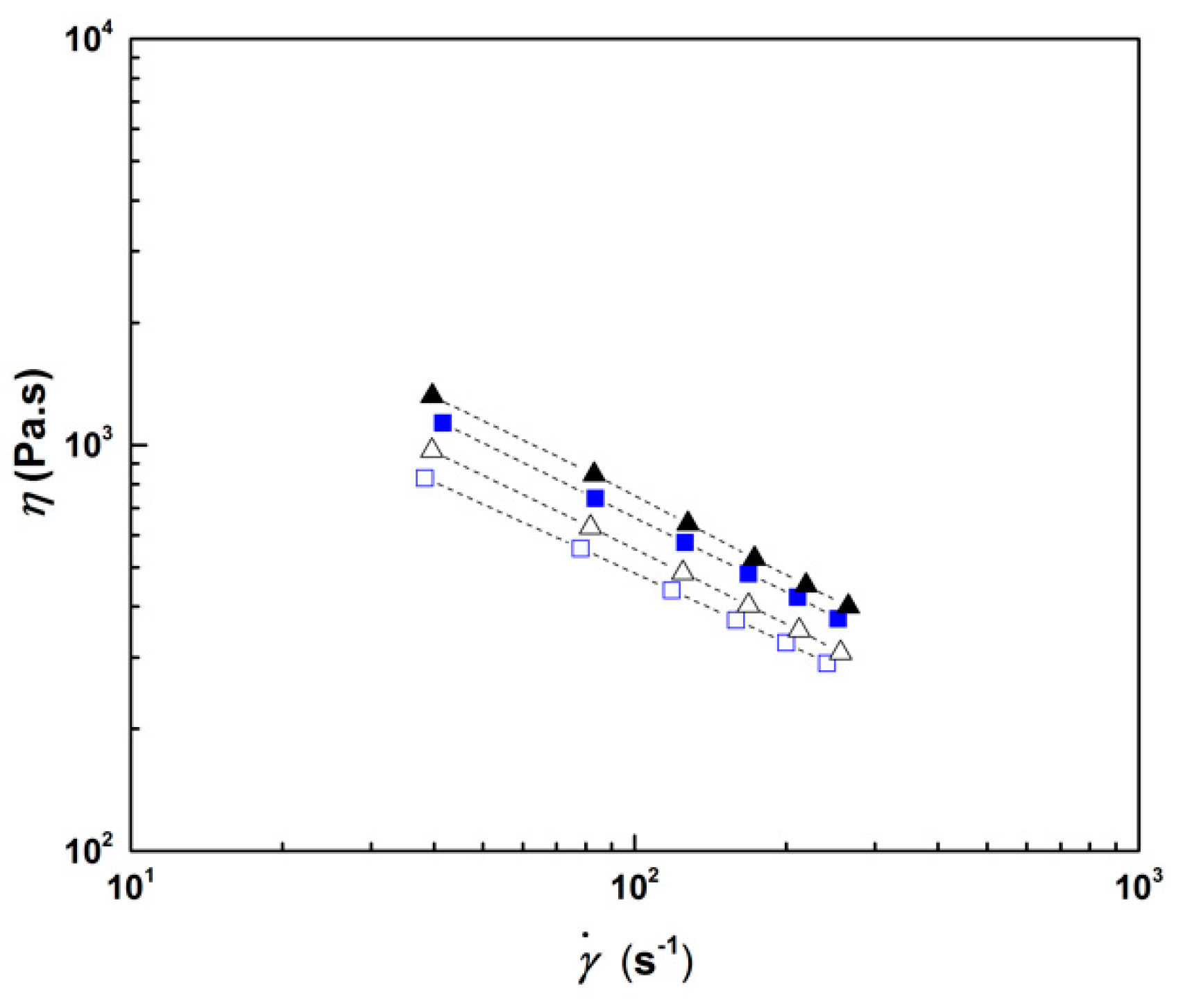
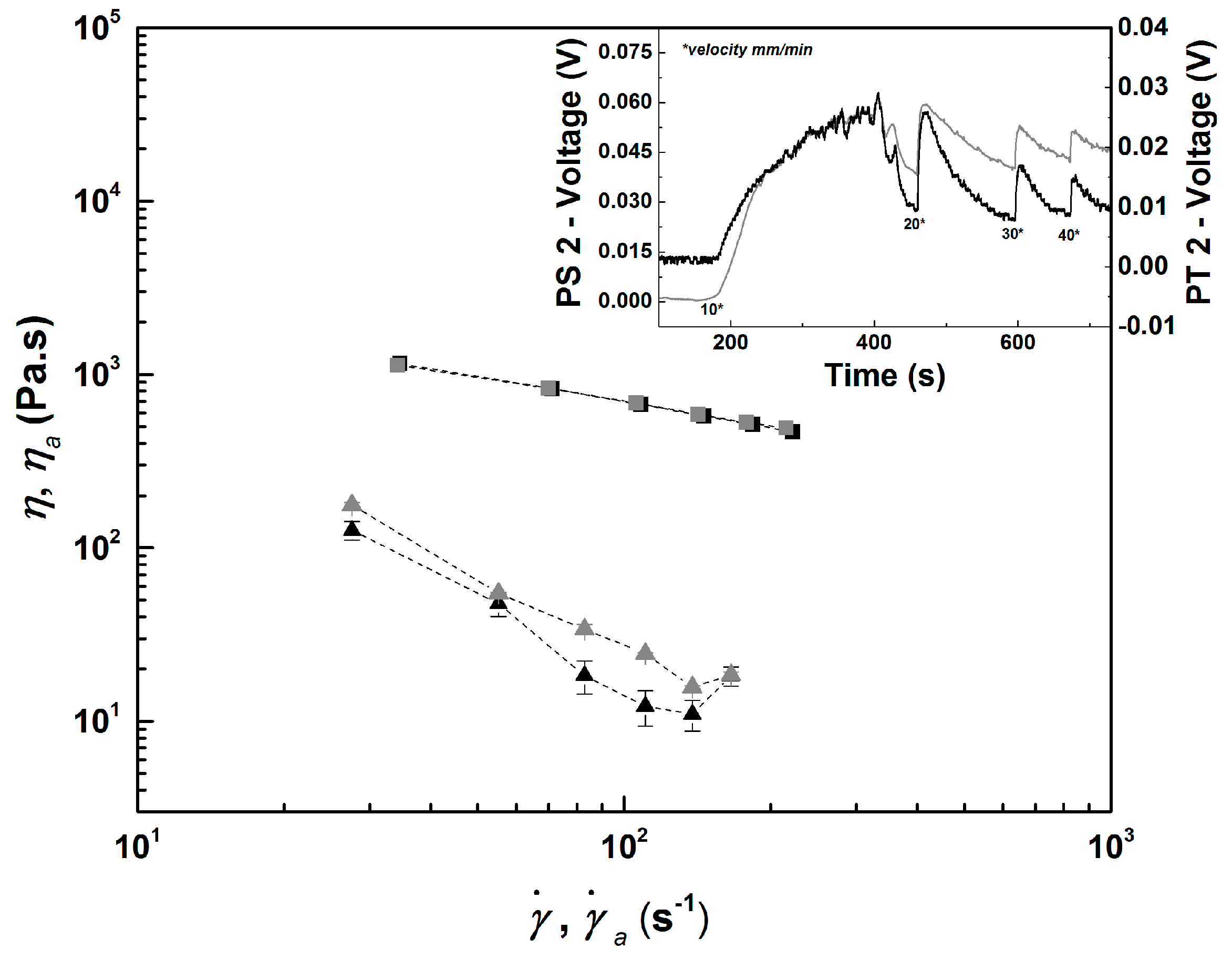
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Macosko, C.W. Principles, Measurements and Applications; VCH: New York, NY, USA, 1994. [Google Scholar]
- Teixeira, P.F.; Fernandes, S.N.; Canejo, J.; Godinho, M.H.; Covas, J.A.; Leal, C.; Hilliou, L. Rheo-optical characterization of liquid crystalline acetoxypropylcellulose melt undergoing large shear flow and relaxation after flow cessation. Polymer 2015, 71, 102–112. [Google Scholar] [CrossRef]
- den Doelder, J.; Koopmans, R.; Dees, M.; Mangnus, M. Pressure oscillations and periodic extrudate distortions of long-chain branched polyolefins. J. Rheol. 2005, 49, 113–126. [Google Scholar] [CrossRef]
- Filipe, S.; Becker, A.; Barroso, V.C.; Wilhelm, M. Evaluation of melt flow instabilities of high-density polyethylenes via an optimised method for detection and analysis of the pressure fluctuations in capillary rheometry. Appl. Rheol. 2009, 19, 23345. [Google Scholar]
- Kádár, R.; Naue, I.F.; Wilhelm, M. First normal stress difference and in-situ spectral dynamics in a high sensitivity extrusion die for capillary rheometry via the ‘hole effect’. Polymer 2016, 104, 193–203. [Google Scholar] [CrossRef]
- Naue, I.F.; Kádár, R.; Wilhelm, M. A new high sensitivity system to detect instabilities during the extrusion of polymer melts. Macromol. Mater. Eng. 2015, 300, 1141–1152. [Google Scholar] [CrossRef]
- Palza, H.; Filipe, S.; Naue, I.F.; Wilhelm, M. Correlation between polyethylene topology and melt flow instabilities by determining in-situ pressure fluctuations and applying advanced data analysis. Polymer 2010, 51, 522–534. [Google Scholar] [CrossRef]
- Palza, H.; Naue, I.; Wilhelm, M.; Filipe, S.; Becker, A.; Sunder, J.; Goettfert, A. On-line detection of polymer melt flow instabilities in a capillary rheometer. Kgk. Kautsch. GummiKunstst. 2010, 63, 456–461. [Google Scholar]
- Palza, H.; Naue, I.F.; Wilhelm, M. In situ pressure fluctuations of polymer melt flow instabilities: Experimental evidence about their origin and dynamics. Macromol. Rapid Commun. 2009, 30, 1799–1804. [Google Scholar] [CrossRef]
- Cyriac, F.; Covas, J.A.; Hilliou, L.H.G.; Vittorias, I. Predicting extrusion instabilities of commercial polyethylene from non-linear rheology measurements. Rheol. Acta 2014, 53, 817–829. [Google Scholar] [CrossRef]
- Hruska, C.K. Least-squares estimates of the nonlinear constants of piezoelectric crystals. J. Appl. Phys. 1992, 72, 2432–2439. [Google Scholar] [CrossRef]
- Mullen, A.J. Temperature variation of the piezoelectric constant of quartz. J. Appl. Phys. 1969, 40, 1693–1696. [Google Scholar] [CrossRef]
- Broadbent, J.M.; Kaye, A.; Lodge, A.S.; Vale, D.G. Possible systematic error in measurement of normal stress differences in polymer solutions in steady shear flow. Nature 1968, 217, 55–56. [Google Scholar] [CrossRef]
- Teixeira, P.F.; Hilliou, L.; Covas, J.A.; Maia, J.M. Assessing the practical utility of the hole-pressure method for the in-line rheological characterization of polymer melts. Rheol. Acta 2013, 52, 661–672. [Google Scholar] [CrossRef]
- Teixeira, P.F.; Ferrás, L.L.; Hilliou, L.; Covas, J.A. A new double-slit rheometrical die for in-process characterization and extrusion of thermo-mechanically sensitive polymer systems. Polym. Test. 2018, 66, 137–145. [Google Scholar] [CrossRef]
- Wilhelm, M.; Reinheimer, P.; Ortseifer, M. High sensitivity fourier-transform rheology. Rheol. Acta 1999, 38, 349–356. [Google Scholar] [CrossRef]
- Wilhelm, M. Fourier-transform rheology. Macromol. Mater. Eng. 2002, 287, 83–105. [Google Scholar] [CrossRef]
- Hilliou, L.; van Dusschoten, D.; Wilhelm, M.; Burhin, H.; Rodger, E.R. Increasing the force torque transducer sensitivity of an rpa 2000 by a factor 5–10 via advanced data acquisition. Rubber Chem. Technol. 2004, 77, 192–200. [Google Scholar] [CrossRef]
- Mack, O. New procedures to characterize drift and non-linear effects of piezoelectric force sensors. In Proceedings of the IMEKO TC3 Conference, Istanbul, Turkey, 17–21 September 2001. [Google Scholar]
- Laun, H.M. Capillary rheometry for polymer melts revisited. Rheol. Acta 2004, 43, 509–528. [Google Scholar] [CrossRef]
- Marquardt, W.; Nijmann, J. Experimental errors when using rotational rheometers. Appl. Rheol. 1993, 3, 120. [Google Scholar]
- Laun, M.; Auhl, D.; Brummer, R.; Dijkstra, D.J.; Gabriel, K.; Mangnus, M.A.; Rullmann, M.; Zoetelief, W.; Handge, U.A. Guidelines for checking performance and verifying accuracy of rotational rheometers: viscosity measurements in steady and oscillatory shear (IUPAC Technical Report). Pure Appl. Chem. 2014, 86, 1945–1968. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Arakawa, K. Effect of thermal degradation on rheological properties for poly (3-hydroxybutyrate). Eur. Polym. J. 2006, 42, 1479–1486. [Google Scholar] [CrossRef]
- Ramkumar, D.; Bhattacharya, M. Steady shear and dynamic properties of biodegradable polyesters. Polym. Eng. Sci. 1998, 38, 1426–1435. [Google Scholar] [CrossRef]
- Cunha, M.; Fernandes, B.; Covas, J.A.; Vicente, A.A.; Hilliou, L. Film blowing of phbv blends and phbv-based multilayers for the production of biodegradable packages. J. Appl. Polym. Sci. 2016, 133. [Google Scholar] [CrossRef]
| Characteristics | Kistler 6182 B | Kistler 6189A | PT422A |
|---|---|---|---|
| Front diameter | 2.5 (mm) | 2.5 (mm) | 7.8 (mm) |
| Range | 0–200 (MPa) | 0–200 (MPa) | 0–21 (MPa) |
| Sensibility, x | −2.5 (pC/bar) | −6.6 (pC/bar) | 0.5% |
| Operating temperature range: | |||
| Sensor, cable, connector box | 0–00 (°C) | 0–200 (°C) | |
| At the front of the sensor | < 450 (°C) | < 450 (°C) | 0–400 (°C) |
| Temperature | Sensors | Initial Slope | Final Slope | Average Slope | |||
|---|---|---|---|---|---|---|---|
| Pressure | Viscosity | Pressure | Viscosity | Pressure | Viscosity | ||
| 150 °C | PT 1 vs. PS 1 | 2.4–3.0% | 6.7–9.3% | 1.9–3.1% | 9.1–11% | 2.2–3.0% | 8.0–10% |
| PT 2 vs. PS 2 | 0.4–1.0% | 1.6–3.6% | 0.8–2.0% | ||||
| 180 °C | PT 1 vs. PS 1 | 2.5–4.0% | 6.7–12% | 0.0–0.8% | 5.0–7.1% | 1.3–2.3% | 5.6–9.2% |
| PT 2 vs. PS 2 | 1.0–1.5% | 2.3–3.9% | 1.7–2.7% | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, S.; Teixeira, P.F.; Covas, J.A.; Hilliou, L. Assessment of Piezoelectric Sensors for the Acquisition of Steady Melt Pressures in Polymer Extrusion. Fluids 2019, 4, 66. https://doi.org/10.3390/fluids4020066
Costa S, Teixeira PF, Covas JA, Hilliou L. Assessment of Piezoelectric Sensors for the Acquisition of Steady Melt Pressures in Polymer Extrusion. Fluids. 2019; 4(2):66. https://doi.org/10.3390/fluids4020066
Chicago/Turabian StyleCosta, Sónia, Paulo F. Teixeira, José A. Covas, and Loic Hilliou. 2019. "Assessment of Piezoelectric Sensors for the Acquisition of Steady Melt Pressures in Polymer Extrusion" Fluids 4, no. 2: 66. https://doi.org/10.3390/fluids4020066
APA StyleCosta, S., Teixeira, P. F., Covas, J. A., & Hilliou, L. (2019). Assessment of Piezoelectric Sensors for the Acquisition of Steady Melt Pressures in Polymer Extrusion. Fluids, 4(2), 66. https://doi.org/10.3390/fluids4020066







