Longevity of Enhanced Geothermal Systems with Brine Circulation in Hydraulically Fractured Hydrocarbon Wells
Abstract
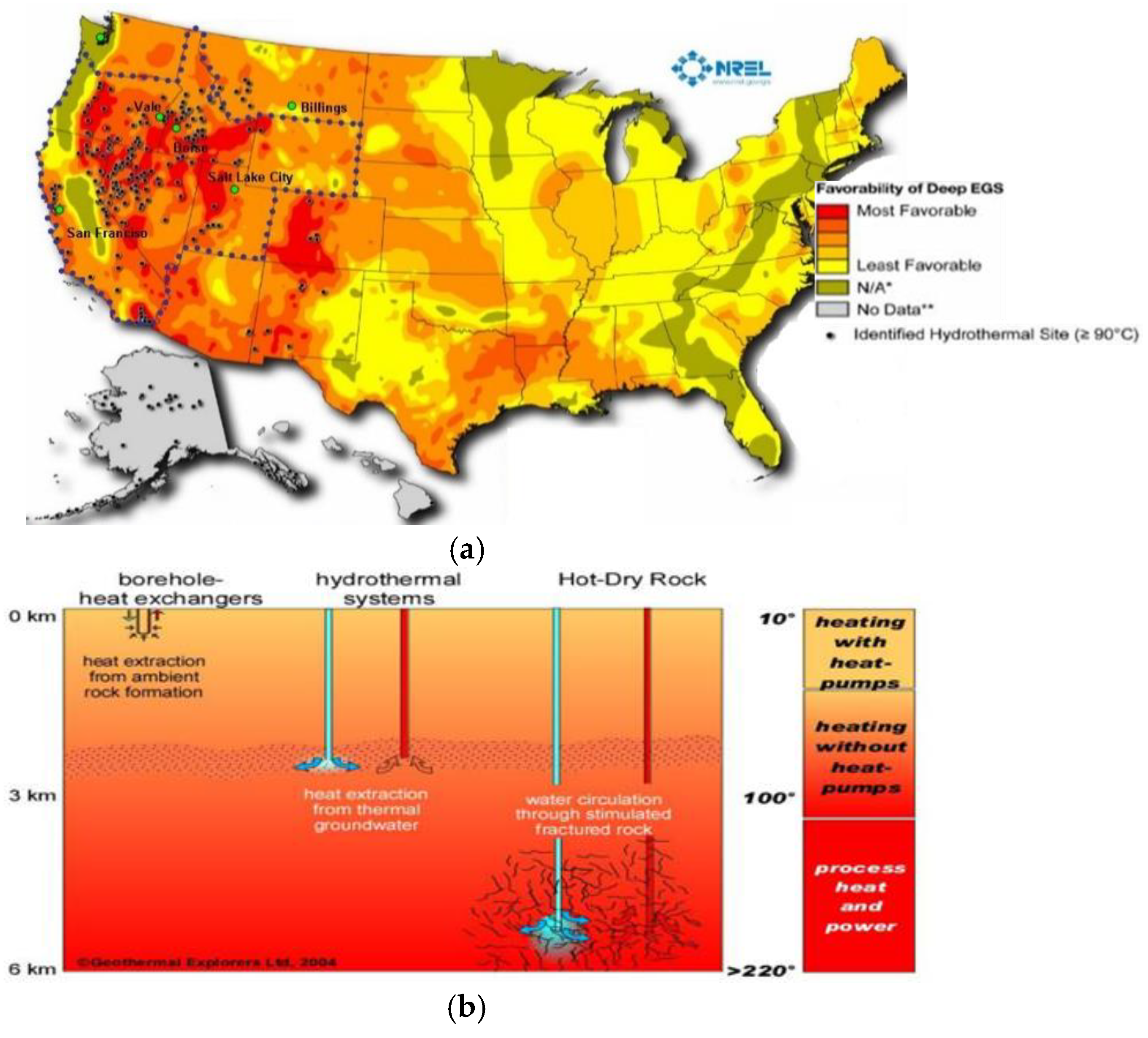
:1. Introduction
2. Prior Work and Model Design
2.1. Generic Models and Case Studies
2.2. Analytical Models
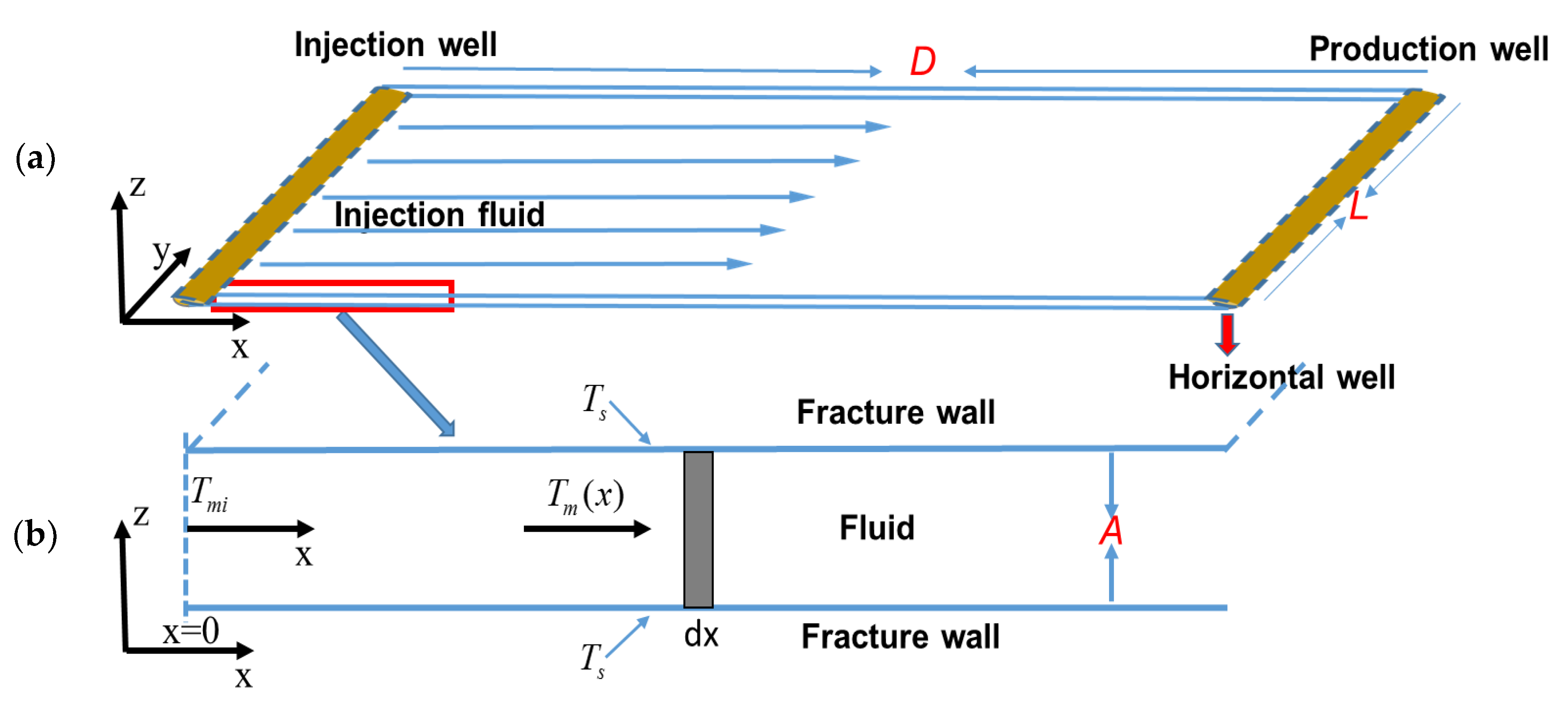
2.3. Model Design Used in This Study
- Mechanism 1: Heating of the cold injection brine when passing along a hotter fracture wall;
- Mechanism 2: Cooling of the hot rock due to the passing of a colder brine;
- Mechanism 3: The integrated effects of brine-heating and fracture-wall cooling;
- Mechanism 4: Recovery of the cooled fracture wall by “self-heating” via the adjacent deeper, still hot rock, once the injection of the cold brine is (temporarily) halted.
- The fracture plane is horizontal with variable finite length and width; channel flow is assumed within the fracture.
- Flow distance needed to reach a certain temperature is calculated analytically (Equation (7)) for fixed fracture wall temperature.
- Thermal conduction in the rock interior adjacent to the fracture wall cooled by the circulating brine is analytically solved (Equation (12)), which gives the rock temperature profile versus rock depth.
- Rock temperature recovery after the fluid circulation stops is calculated explicitly using Fourier transform (Equation (15)).
- Heat transfer between the cooler brine and the hotter wall rock of the fracture is integrated using a semi-analytical method.
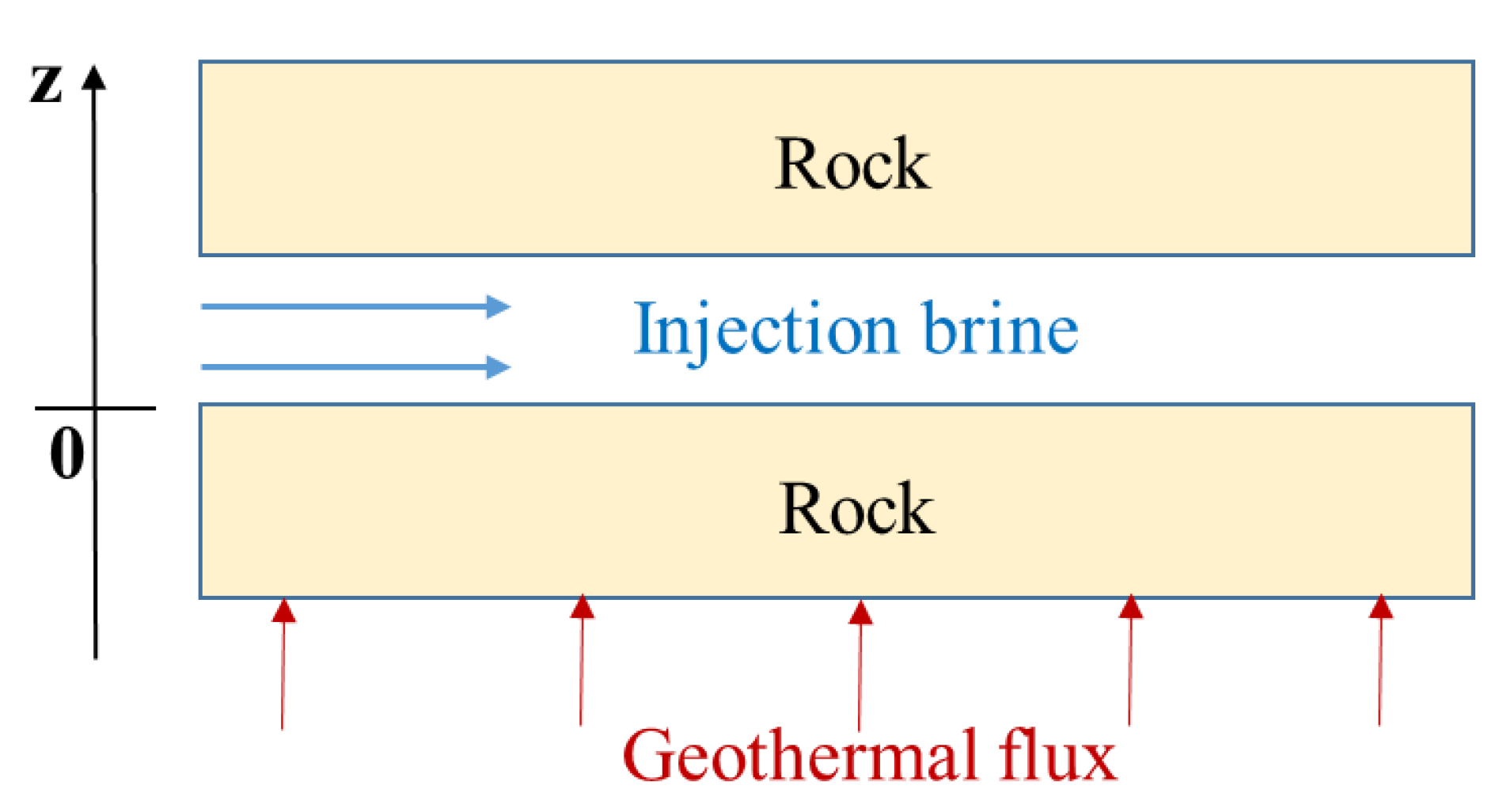
2.4. Heat Flow Recharge of EGS Reservoirs
3. Assessment of Heat Transfer Mechanisms
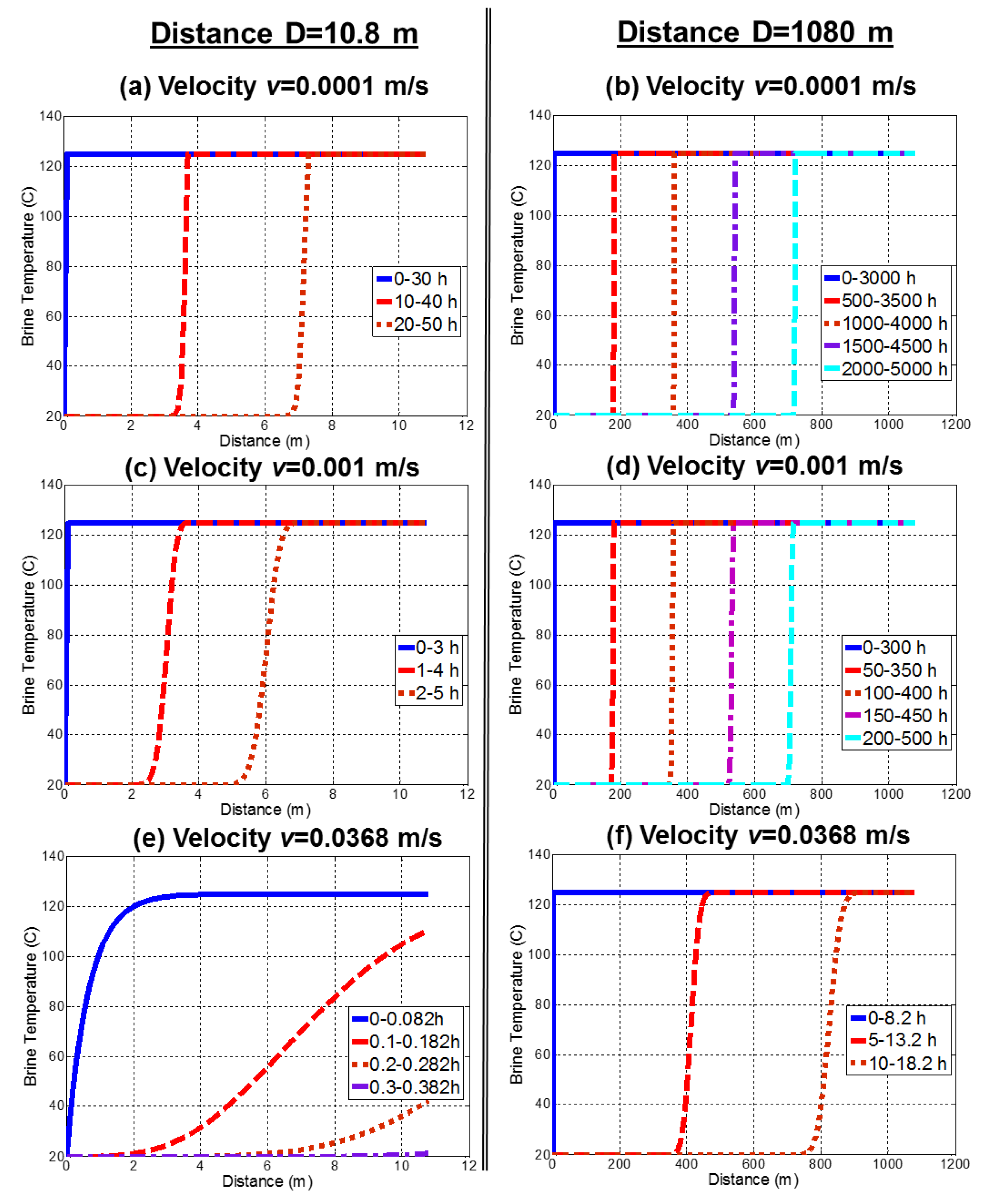
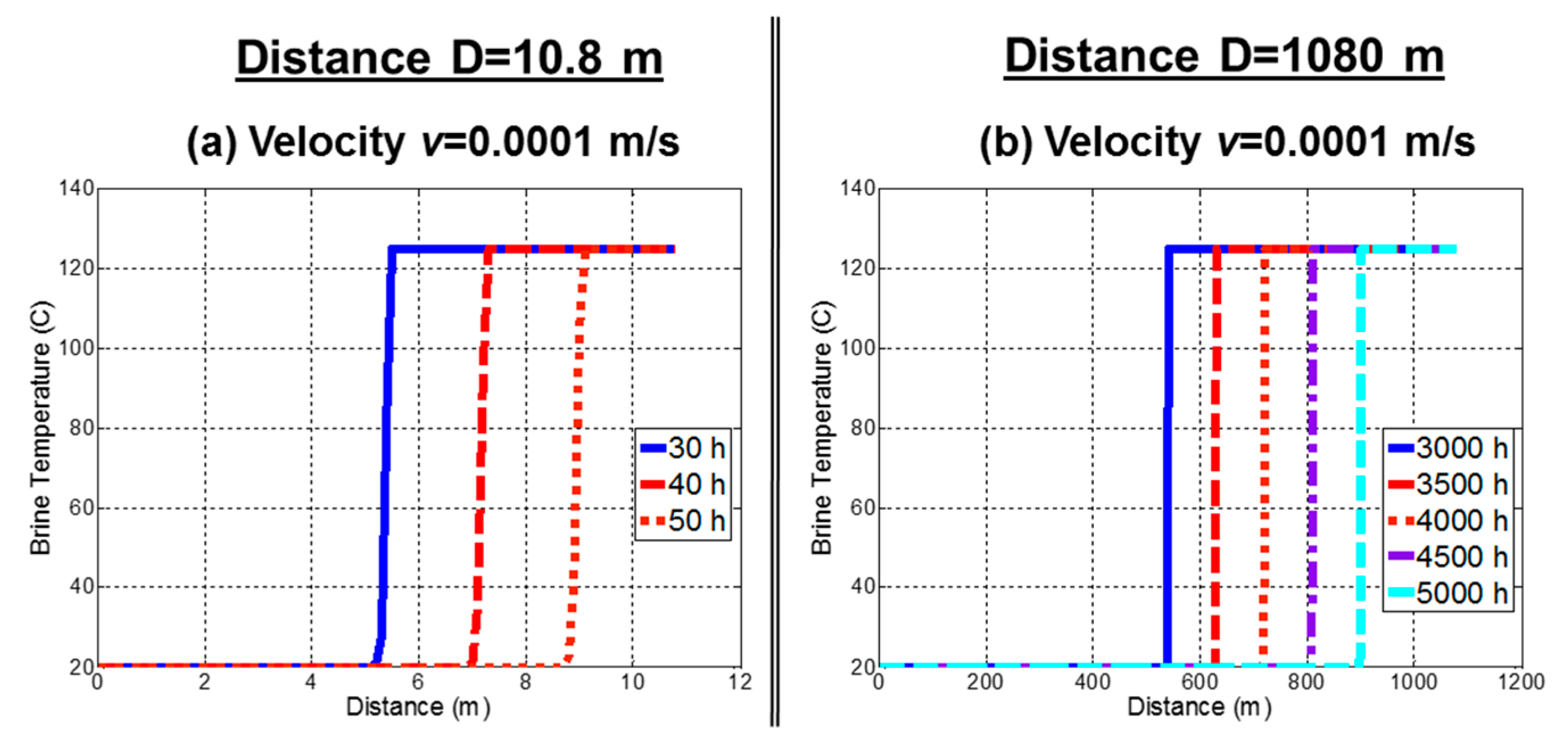
3.1. Mechanism 1: Heating of the Cold Injection Brine When Passing Along a Hotter Fracture Wall
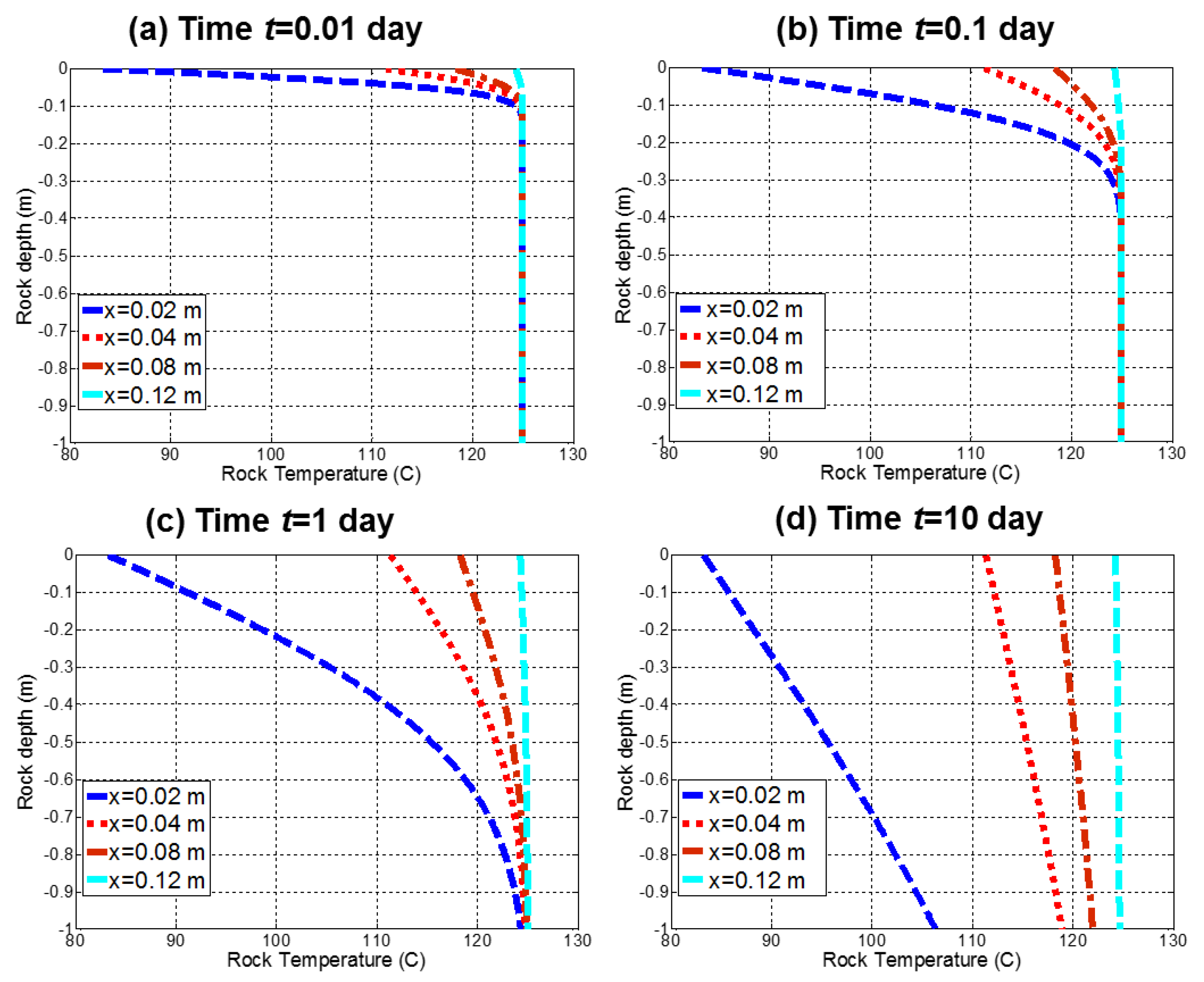
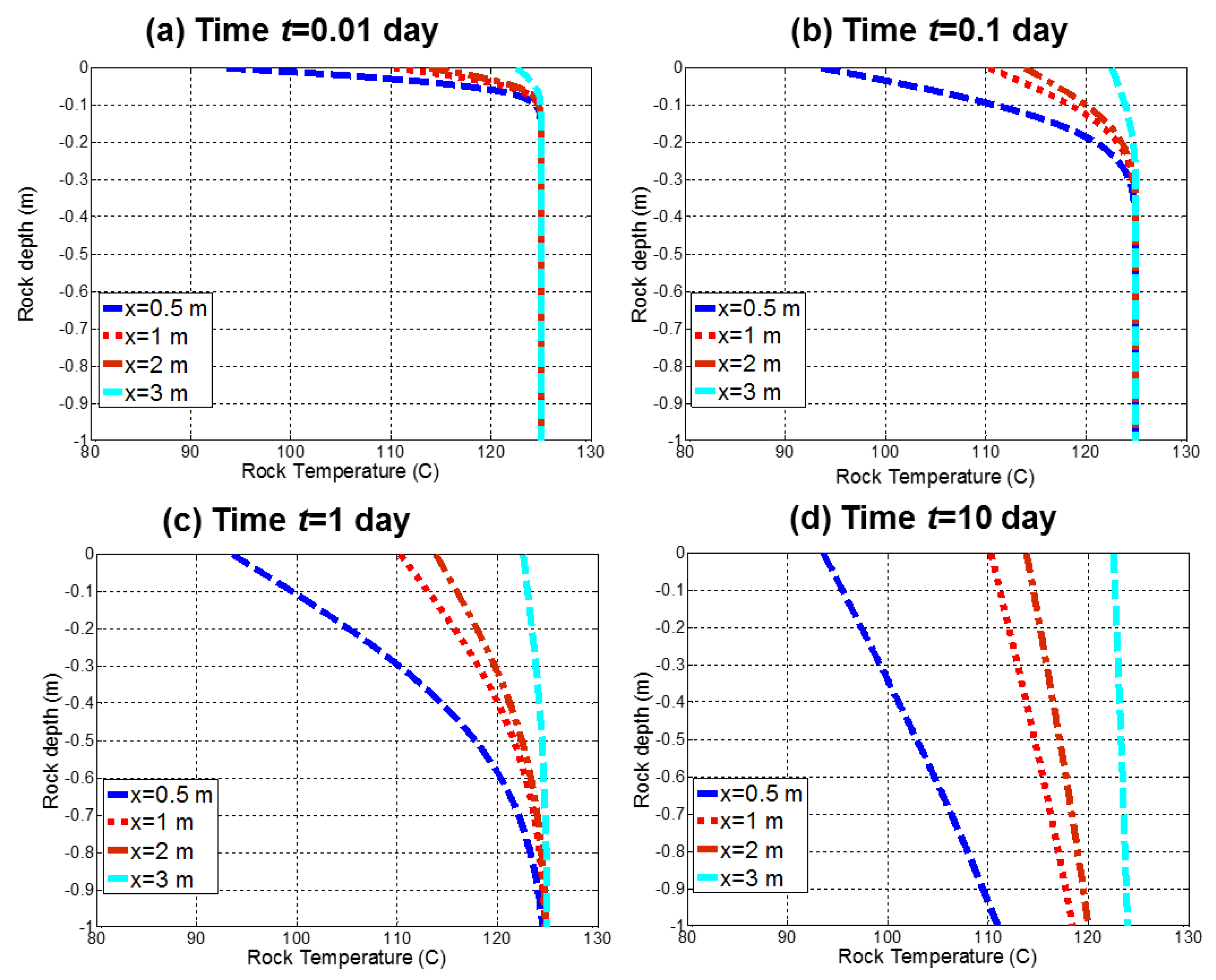
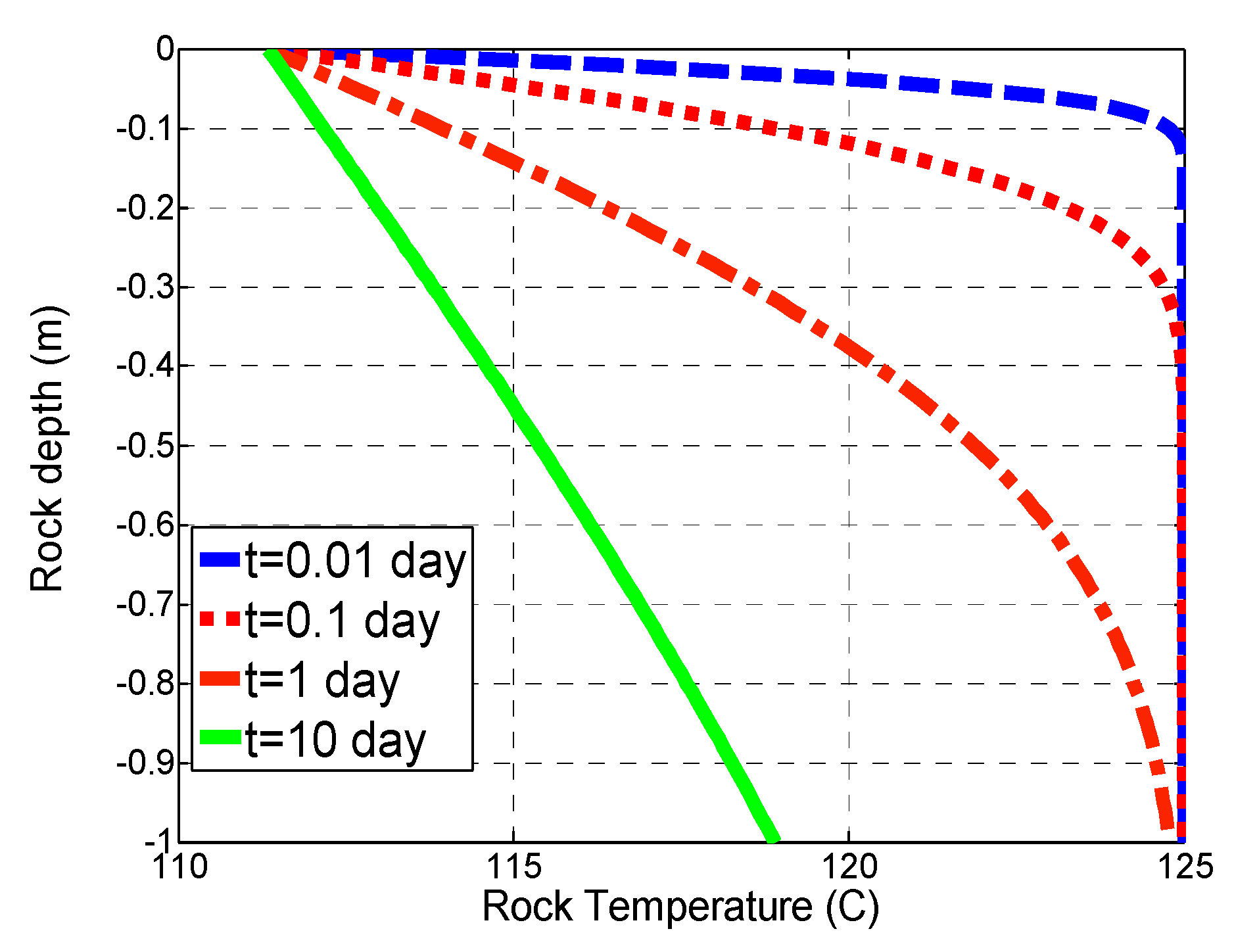
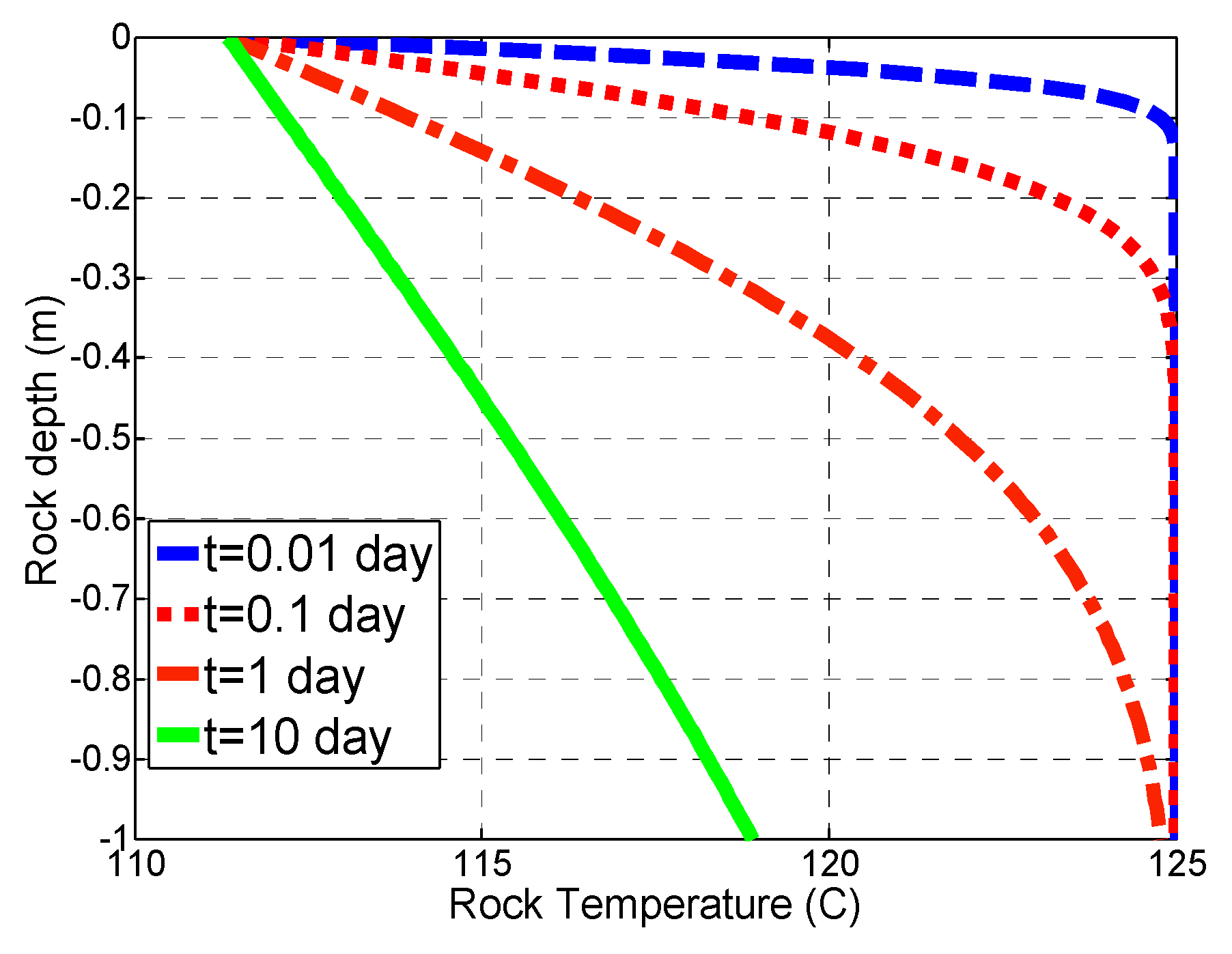
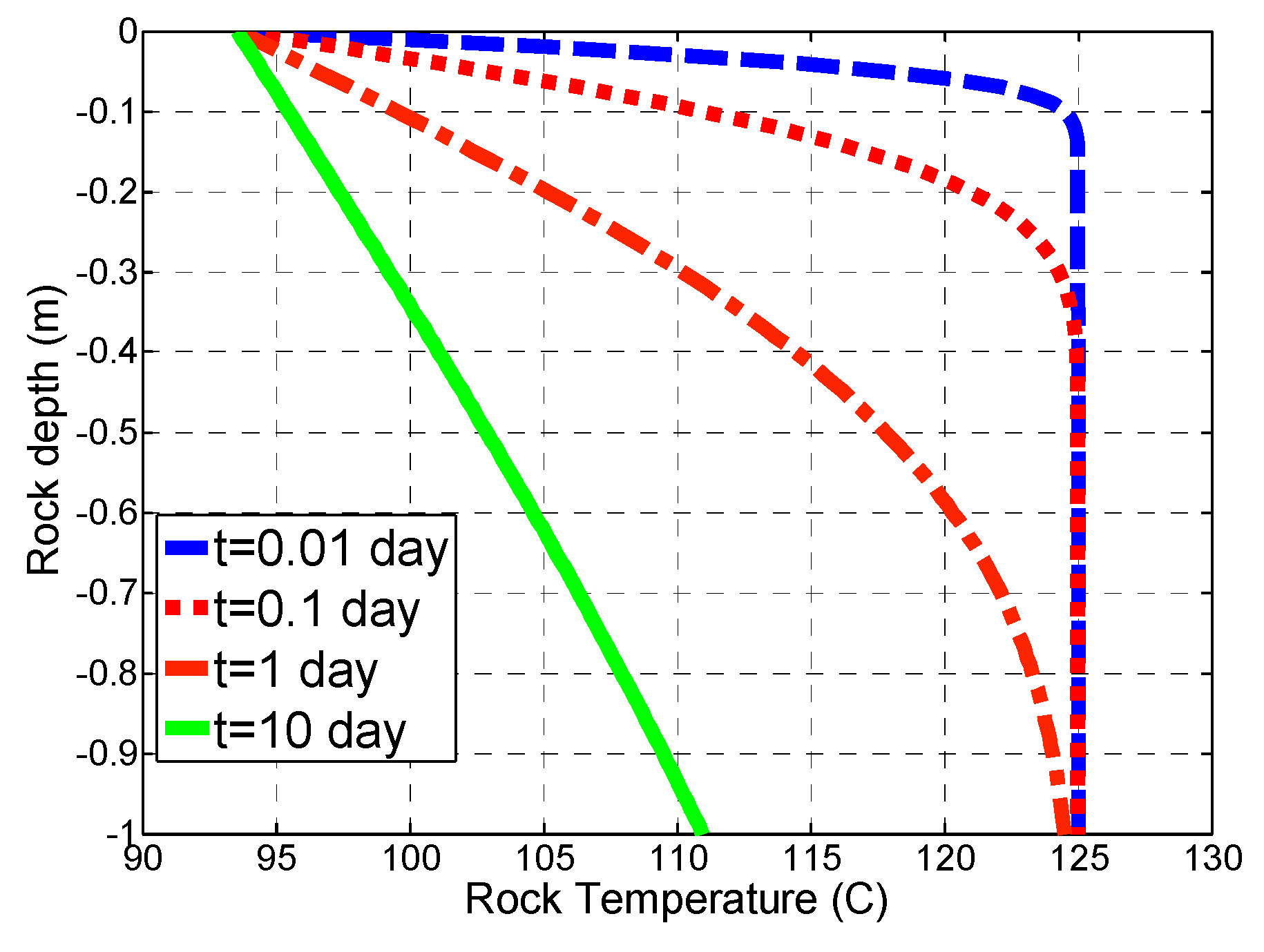
3.2. Mechanism 2: Cooling of the Hot Fracture due to the Passing of a Colder Brine
3.3. Mechanism 3: Combination of Fluid Heating and Fracture Wall Cooling
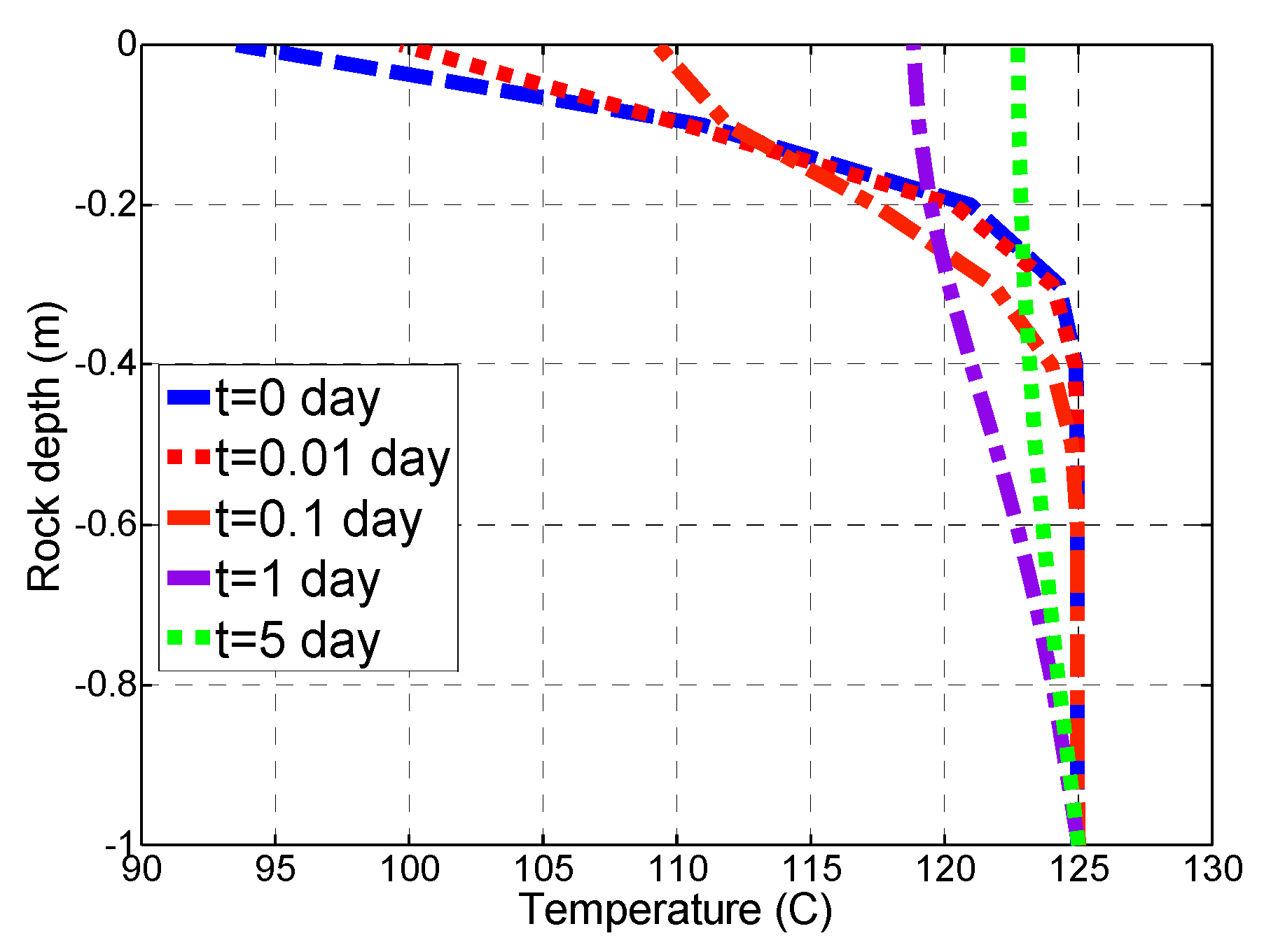
3.4. Mechanism 4: Recovery of the Cooled Fracture Wall by “Self-Heating"
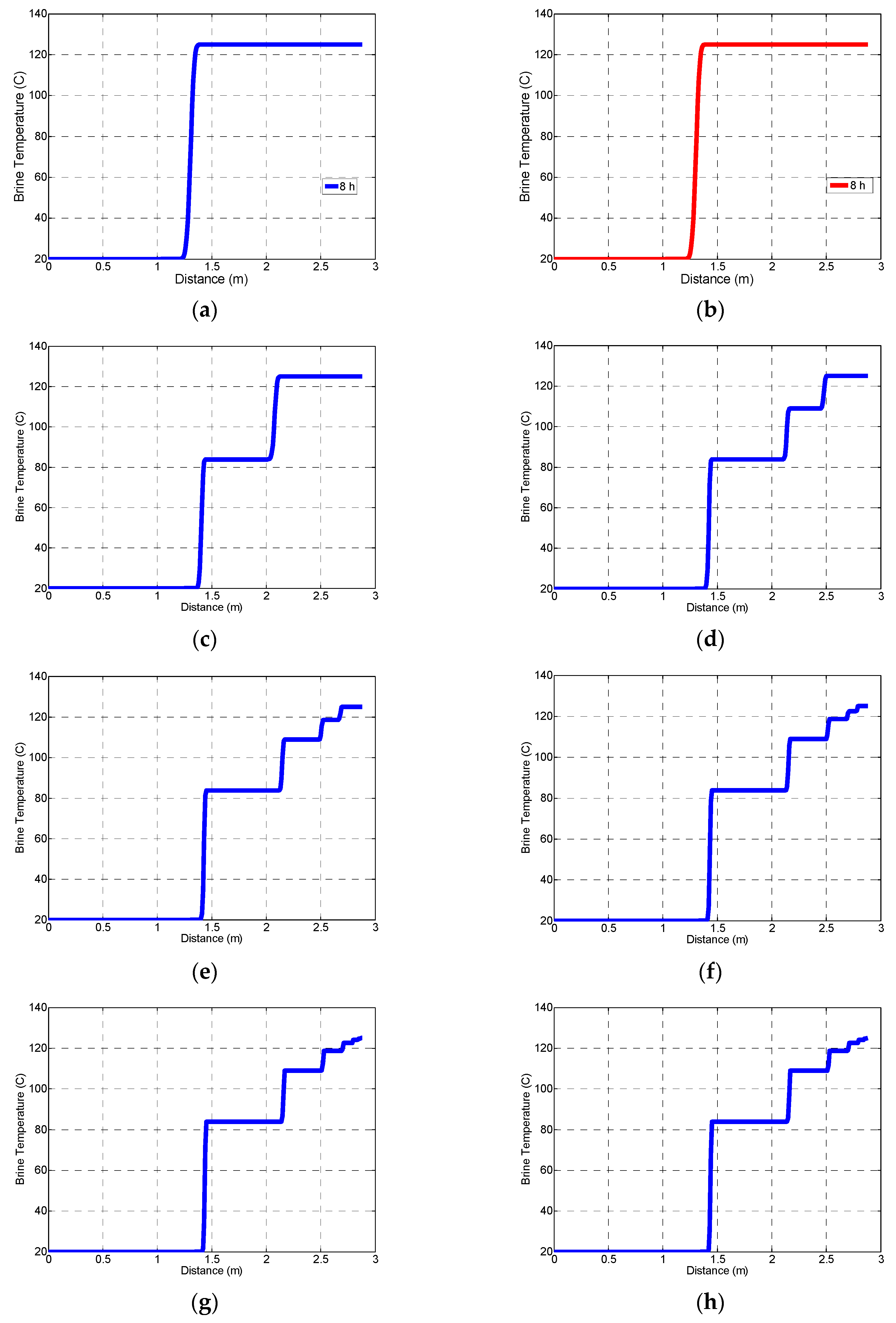
4. Discussions and Intermittent Production Model
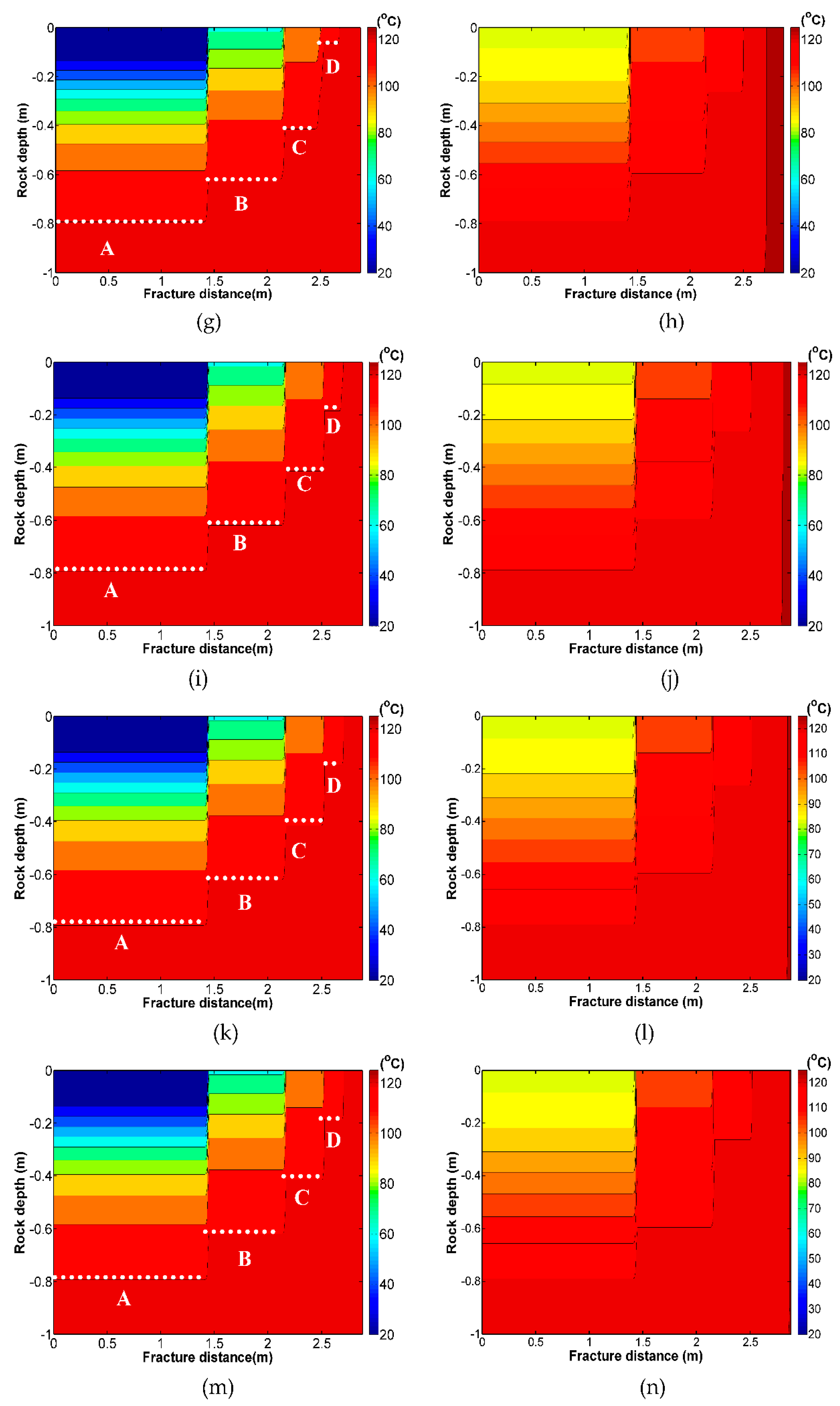
4.1. Principle Outcomes of Simple Heat Transfer Model (Mechanisms 1–4)
4.2. Integrated Model for Longevity of Heat Extraction
4.3. Generic Insights
4.4. Limitations of the Model
5. Conclusions
- A continuous fluid circulation in EGS reservoirs with limited fracture-matrix surface contact area will quickly quench the effective transfer of heat due to rapid cooling of the fracture wall rock. The fracture wall temperature for the region close to the injection point will equalize to the temperature of the cold injection brine in about three days in the cases studied.
- A steady-state extraction of geothermal energy cannot be achieved over longer time scales due to the rapid decline in the heat transfer rate at the fracture wall.
- A periodic circulation plan, proposed here to remedy the situation, could lead to a quasi-steady state of the extracted fluid temperature. The fracture wall is cooled by periodic injection of cold brine but will heat up fast enough after well shut-in to restore the temperature of the cooled fracture wall such that heat transfer is possible again after brine injection resumes. Our models show how fast after shut-in of the injection well the fracture rock wall interior will restore to the initial temperature.
- The temperature history of the injection brine was calculated accounting for four heat transfer mechanisms. The temperature of the cold brine requires a certain travel distance to reach a required temperature for economic production, which is scaled for the specific reservoir conditions studied here.
- The injection brine is heated faster for slower running brine and for smaller fracture aperture; however, the volumetric production is inversely proportional to the fluid velocity in the fracture space.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Methodology for Brine Temperature Computation
Appendix B. Derivation of Rock Heat Recovery
References
- Turcotte, D.L.; Schubert, G. Geodynamics: Applications of Continuum Physics to Geological Problems; John Wiley & Sons: New York, NY, USA, 1982. [Google Scholar]
- GEA Geothermal Energy Association. 2016 Annual, U.S. & Global Geothermal Power Production Report. 2016. Available online: http://www.geo-energy.org/ (accessed on 1 September 2017).
- Electric Power Annual 2013; Independent Statistics & Analysis; U.S. Energy Information Administration: Washington, DC, USA, 2013.
- Blackwell, D.D.; Richards, M. Geothermal Map of North America, AAPG Map, scale 1:6,500,000, Product Code 423; SMU Geothermal Laboratory: Dallas, TX, USA, 2004. [Google Scholar]
- Williams, C.F.; Reed, M.J.; Mariner, R.H. A Review of Methods Applied by the U.S. Geological Survey in the Assessment of Identified Geothermal Resources; U.S. Department of the Interior, U.S. Geological Survey, Open-File Report 2008–1296; U.S. Department of the Interior: Washington, DC, USA, 2008; Volume 27.
- Blackwell, D.; Richards, M.; Stepp, P. Final Report, Texas Geothermal Assessment for the I35 Corridor East; Prepared for Texas State Energy Conservation Office. Contract CM709; Southern Methodist University: Dallas, TX, USA, 29 March 2010. [Google Scholar]
- Anderson, B.J. Recovery Act: Analysis of Low-Temperature Utilization of Geothermal Resources; Final Technical Report; Department of Energy: Washington, DC, USA.
- NREL. Available online: http://www.nrel.gov/gis/geothermal.html (accessed on 12 April 2017).
- Geo Explorers. Available online: www.geoexplorers.ch/eng/vision.html (accessed on 12 April 2017).
- Fox, D.B.; Sutter, D.; Tester, J.W. The thermal spectrum of low-temperature energy use in the United States. Energy Environ. Sci. 2011, 4, 3731–3740. [Google Scholar] [CrossRef]
- Weijermars, R.; Burnett, D.; Claridge, D.; Noynaert, S.; Pate, M.; Westphal, D.; Yu, W.; Zuo, L. Redeveloping Depleted Hydrocarbon Wells in an Enhanced Geothermal System (EGS) for s University Campus: Progress Report of a Real-Asset-Based Feasibility Study. Energy Strategy Rev. 2018, 21, 191–203. [Google Scholar] [CrossRef]
- DOE (U.S. Department of Energy). Geothermal Technologies Program. Multi-Year Research, Development and Demonstration Plan, 2009–2015 with Program Activities to 2025, U.S., Energy Efficiency & RenewableEnergy Office. 2015. Available online: http://www.eere.energy.gov/geothermal/plans.htm. (accessed on 10 August 2017).
- Potter, R.M.; Robison, E S.; Smith, M. Method of Extracting Heat from Dry Geothermal Reservoirs. U.S. Patent 3786858, 27 March 1972. [Google Scholar]
- Brown, D. The US Hot Dry Rock Program-20 Years of Experience in Reservoir Testing. In Proceedings of the World Geothermal Congress, Florence, Italy, 1 January 1995. [Google Scholar]
- Weijermars, R.; Zuo, L.; Warren, I. Modeling reservoir circulation and economic performance of the Neal Hot Springs Geothermal power plant (Oregon, U.S.): An integrated Case Study. Geothermics 2017, 70, 155–172. [Google Scholar] [CrossRef]
- Fox, D.B.; Sutter, D.; Beckers, K.F.; Lukawski, M.J.; Koch, D.L.; Anderson, B.J.; Tester, J.W. Sustainable heat farming: Modeling extraction and recovery in discretely fractured geothermal reservoirs. Geothermics 2013, 46, 42–54. [Google Scholar] [CrossRef]
- Baujard, C.; Genter, A.; Graff, J.J.; Maurer, V.; Dalmais, E. ECOGI, a New Deep EGS Project in Alsace, Rhine Graben, France. In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 19–25 April 2015. [Google Scholar]
- Vidal, J.; Genter, A.; Schmittbuhl, J. Pre-and post-stimulation characterization of geothermal well GRT-1, Rittershoffen, France: Insight form acoustic image logs of hard fractured rock. Geophys. J. Int. 2016, 845–860. [Google Scholar] [CrossRef]
- Heuer, N.; Kupper, T.; Windelberg, D. Mathematical model of a Hot Dry Rock system. Geophys. J. Int. 1991, 105, 659–664. [Google Scholar] [CrossRef]
- Cheng, A.H.D.; Ghassemi, A.; Detournay, E. Integral equation solution of heat extraction from a fracture in hot dry rock. Int. J. Numer. Anal. Meth. Geomech. 2001, 25, 1327–1338. [Google Scholar] [CrossRef]
- Hori, Y.; Kitano, K.; Kaieda, H.; Kiho, K. Present status of the Ogachi HDR Project, Japan, and future plans. Geothermics 1999, 28, 637–645. [Google Scholar] [CrossRef]
- Brown, D.W.; Duchane, D.V.; Heiken, G.; Hriscu, V.T. Mining the Earth’s Heat: Hot Dry Rock Geothermal Energy; Springer: Berlin, Germany, 2012. [Google Scholar]
- Goldstein, R.J.; Ibele, W.E.; Patankar, S.V.; Simon, T.W.; Kuehn, T.H.; Strykowski, P.J.; Tamma, K.K.; Heberlein, J.V.R.; Davidson, J.H.; Bischof, J.; et al. Heat transfer-A review of 2005 literature. Int. J. Heat Mass Transf. 2010, 53, 4397–4447. [Google Scholar] [CrossRef]
- Luchko, Y.; Rundell, W.; Yamamoto, M.; Zuo, L. Uniqueness and reconstruction of an unknown semilinear term in a time-fractional reaction-diffusion equation. Inverse Probl. 2013, 29, 1–17. [Google Scholar] [CrossRef]
- Rundell, W.; Xu, X.; Zuo, L. Determination of an unknown boundary condition in a fractional diffusion equation. Appl. Anal. 2013, 92, 1511–1526. [Google Scholar] [CrossRef]
- Luchko, Y.; Zuo, L. Theta-function method for a time-fractional reaction-diffusion equation. J. Alger. Math. Soc. 2014, 1, 1–15. [Google Scholar]
- Moridis, G.J. A New Set of Direct and Iterative Solvers for the TOUGH2 Family of Codes; LBL Report No. 37066; USDOE: Washington, DC, USA, 1995.
- Moridis, G.J.; Pruess, K. T2SOLV: An Enhanced Package of Solvers for the TOUGH2 Family of Codes; LBNL Report No. 39496; Lawrence Berkeley National Lab.: Berkeley, CA, USA, 1997.
- Pruess, K.; Simmons, A.; Wu, Y.S.; Moridis, G.J. TOUGH2 Software Qualification; LBL Report No. 38383; U.S. Department of Energy: Washington, DC, USA, 1996.
- Pruess, K.; Oldenburg, C.; Moridis, G.; Finsterle, S. Water Injection into Vapor- and Liquid-Dominated Reservoirs: Modeling of Heat Transfer and Mass Transport; LBNL Report No. 40120; USDOE: Washington, DC, USA, 1997.
- Gringarten, A.C.; Witherspoon, P.A.; Ohnishi, Y. Theory of Heat Extraction from Fractured Hot Dry Rock. J. Geophys. Res. 1975, 80, 1120–1124. [Google Scholar] [CrossRef]
- Martinez, A.R.; Roubinet, D.; Tartakovsky, D.M. Analytical models of heat conduction in fractured rocks. J. Geophys. Res. Solid Earth 2014, 119, 83–98. [Google Scholar] [CrossRef]
- Fox, D.B.; Koch, D.L.; Tester, J.F. An analytical thermohydraulic model for discretely fractured geothermal reservoirs. Water Resour. Res. 2016, 52, 6792–6817. [Google Scholar] [CrossRef]
- Hawkins, A.J.; Becker, M.W.; Tsoflias, P.T. Evaluation of inert tracers in a bedrock fracture using ground penetrating radar and thermal sensors. Geothermics 2017, 67, 86–94. [Google Scholar] [CrossRef]
- Blackwell, D.; Richards, M.C.; Frone, Z.S.; Batir, J.F.; Williams, M.A.; Ruzo, A.A.; Dingwall, R.K. SMU Geothermal Laboratory Heat Flow Map of the Conterminous United States; SMU Geothermal Laboratory: Dallas, TX, USA, 2011. [Google Scholar]
- Jaeger, J.C.; Cook, N.G.; Zimmerman, R. Fundamentals of Rock Mechanics, 4th ed.; Wiley-Blackwell: Oxford, UK, 2007; ISBN 978-0-632-05759-7. [Google Scholar]
- Jiji, L.M. Heat Convection; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Westphal, D.; Weijermars, R. Economic Appraisal and Scoping of Geothermal Enrgy Extraction Projects using Depleted Hydrocarbon Wells. Energy Strategy Rev. 2018, 22, 348–364. [Google Scholar] [CrossRef]
- USclimatedata. Available online: http://www.usclimatedata.com/climate/texas/united-states/3213 (accessed on 19 July 2017).
- Rohsenow, W.M.; Hartnett, J.P.; Cho, Y.I. Handbook of Heat Transfer, 3rd ed.; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Burmeister, L.C. Convective Heat Transfer, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 1993; p. 107. ISBN 0-471-57709-X, 9780471577096. [Google Scholar]
- Weijermars, R.; van Harmelen, A. Breakdown of doublet re-circulation and direct line drives by far-field flow: Implications for geothermal and hydrocarbon well placement. Geophys. J. Int. 2016, 206, 19–47. [Google Scholar] [CrossRef]
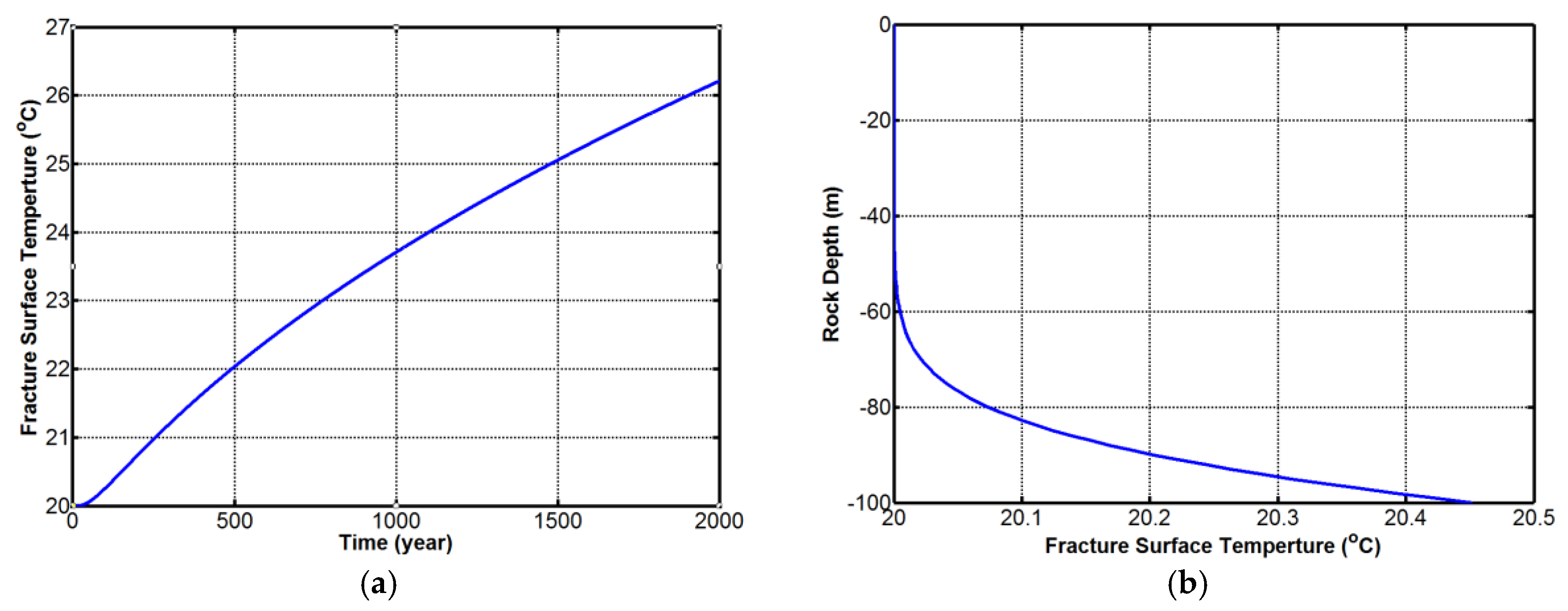
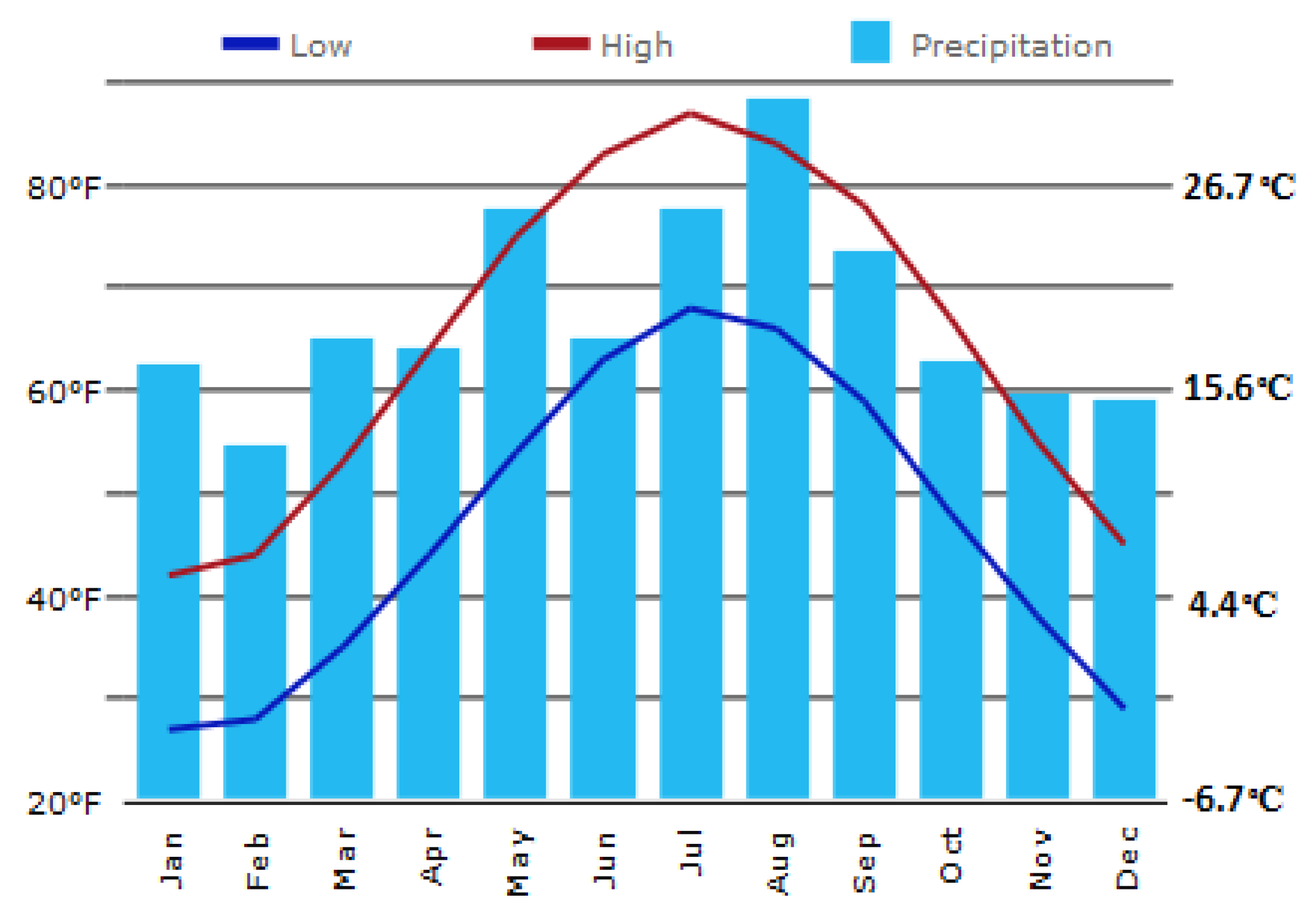
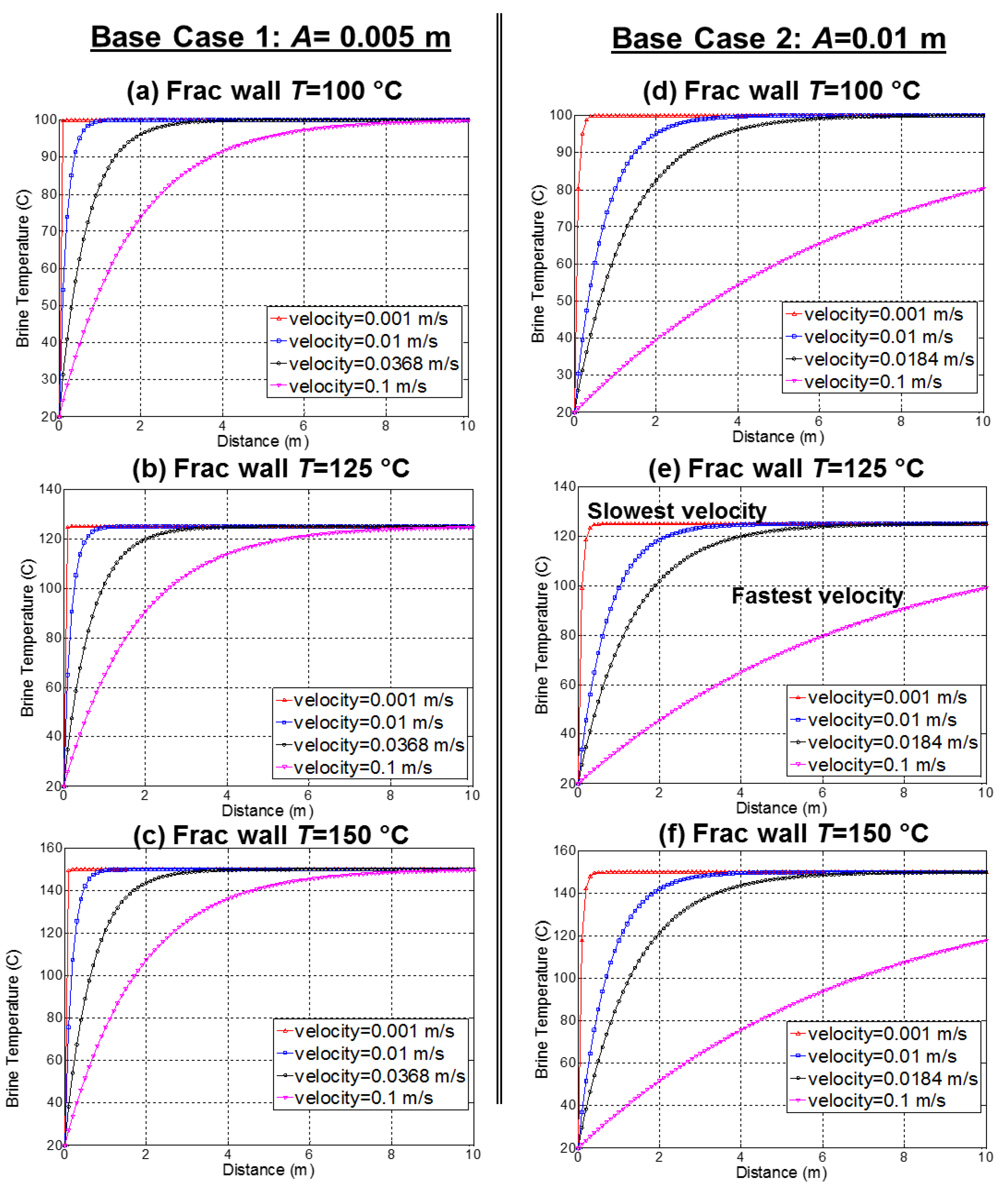

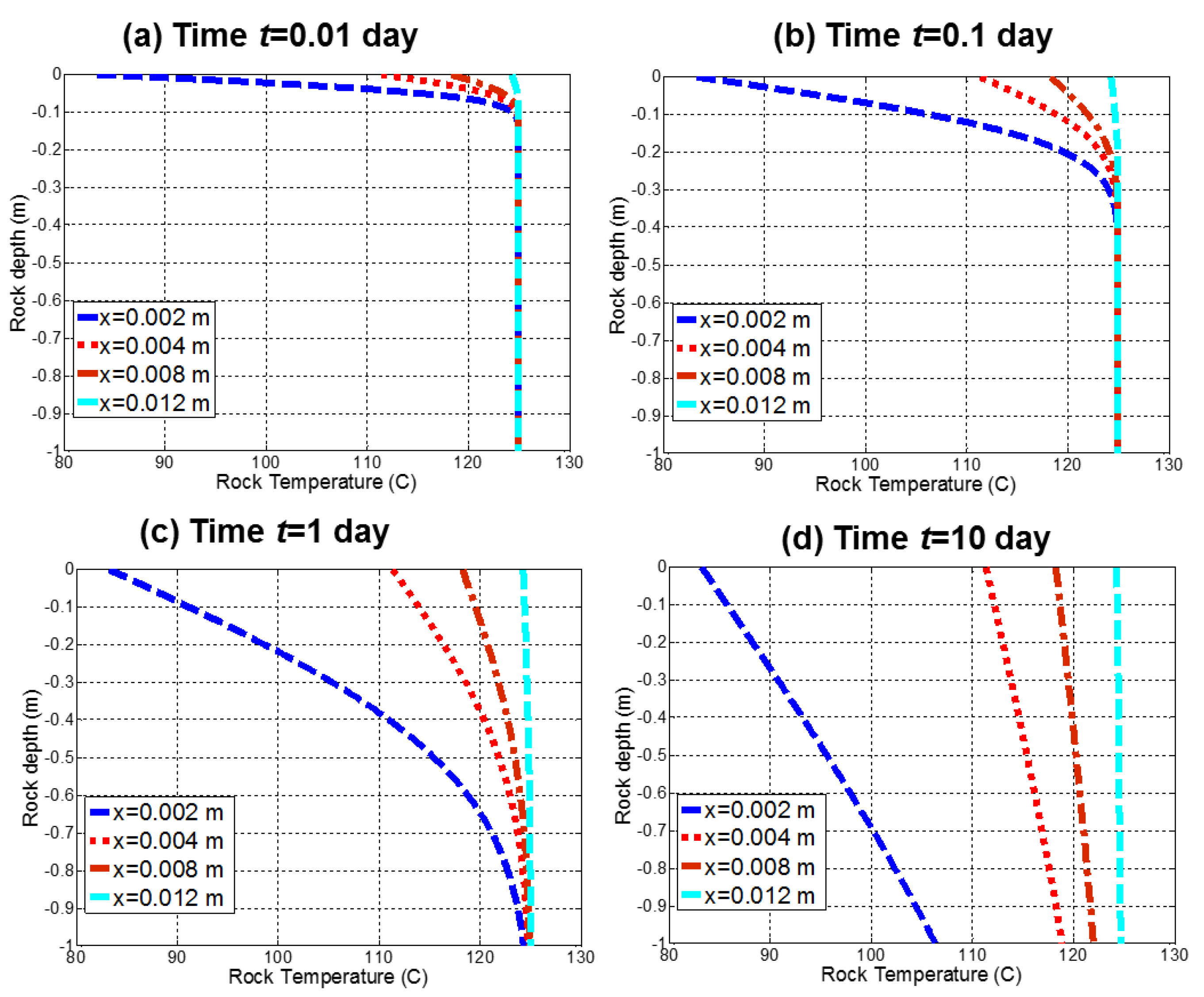


| Fracture Parameters | Notation | Value | Unit |
| Length (of Well) | L | 1000 | m |
| Inter-well Distance | D | 100–1200 m | m |
| Aperture | A | 0.005–0.01 | m |
| Fracture wall temperature | Ts | 100/125/150 (212/257/302) | °C (°F) |
| Brine Parameters | Notation | Value | Unit |
| Initial temperature | Tmi | 20 (70) | °C (°F) |
| Density | ρ | 1 | kg/m3 |
| Heat capacity | c | 4186 | J/(kg·K) |
| Thermal conductivity | k | 0.8 | W/(m K) |
| Heat transfer coefficient | h | 0.0029 | W/(m2 K) |
| Velocity | υ | 0.0001–0.0368 | m/s |
| Nusselt number | Nu | 3.657 | - |
| (a) | ||||
| Velocity (m/s) | m3/s | bbl/day | gpm | L/s |
| 0.1 | 0.5 | 271,720 | 7925 | 500 |
| 0.0368 | 0.184 | 100,000 | 2917 | 184 |
| 0.01 | 0.05 | 27,172 | 793 | 50 |
| 0.001 | 0.005 | 2717 | 79 | 5 |
| 0.0001 | 0.0005 | 271.7 | 7.9 | 0.5 |
| (b) | ||||
| Velocity (m/s) | m3/s | bbl/day | gpm | L/s |
| 0.1 | 1 | 543,440 | 15,850 | 1000 |
| 0.0184 | 0.184 | 100,000 | 2917 | 184 |
| 0.01 | 0.1 | 54,344 | 1585 | 100 |
| 0.001 | 0.01 | 5434 | 159 | 10 |
| 0.0001 | 0.001 | 543.4 | 15.9 | 1 |
| (a) | |||||
| Fracture Aperture 0.005 m | Fracture Aperture 0.01 m | ||||
| Velocity (m/s) | Flux (bbl/day) | Distance (m) | Velocity (m/s) | Flux (bbl/day) | Distance (m) |
| 0.1 | 271,720 | 7.44 | 0.1 | 543,440 | 29.75 |
| 0.0368 | 100,000 | 2.74 | 0.0184 | 100,000 | 5.47 |
| 0.01 | 27,172 | 0.74 | 0.01 | 54,344 | 2.98 |
| 0.001 | 2717 | 0.07 | 0.001 | 5434 | 0.30 |
| (b) | |||||
| Fracture Aperture 0.005 m | Fracture Aperture 0.01 m | ||||
| Velocity (m/s) | Flux (bbl/day) | Distance (m) | Velocity (m/s) | Flux (bbl/day) | Distance (m) |
| 0.1 | 271,720 | 7.61 | 0.1 | 543,440 | 30.45 |
| 0.0368 | 100,000 | 2.80 | 0.0184 | 100,000 | 5.60 |
| 0.01 | 27,172 | 0.76 | 0.01 | 54,344 | 3.05 |
| 0.001 | 2717 | 0.08 | 0.001 | 5434 | 0.30 |
| (c) | |||||
| Fracture Aperture 0.005 m | Fracture Aperture 0.01 m | ||||
| Velocity (m/s) | Flux (bbl/day) | Distance (m) | Velocity (m/s) | Flux (bbl/day) | Distance (m) |
| 0.1 | 271,720 | 7.72 | 0.1 | 543,440 | 30.90 |
| 0.0368 | 100,000 | 2.84 | 0.0184 | 100,000 | 5.69 |
| 0.01 | 27,172 | 0.77 | 0.01 | 54,344 | 3.09 |
| 0.001 | 2717 | 0.08 | 0.001 | 5434 | 0.31 |
| Rock Parameters | Notation | Value | Unit |
|---|---|---|---|
| Surface temperature | 125 (257 °F) | °C | |
| Density | 2650 (quartz) | kg/m3 | |
| Heat capacity | c | 710 (quartz) | J/(kg·K) |
| Thermal conductivity | k | 1.88 (limestone) | W/(mK) |
| Thermal diffusivity | 10−6 | m2/s | |
| Heat transfer coefficient | h | 0.0029 | W/(m2 K) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, L.; Weijermars, R. Longevity of Enhanced Geothermal Systems with Brine Circulation in Hydraulically Fractured Hydrocarbon Wells. Fluids 2019, 4, 63. https://doi.org/10.3390/fluids4020063
Zuo L, Weijermars R. Longevity of Enhanced Geothermal Systems with Brine Circulation in Hydraulically Fractured Hydrocarbon Wells. Fluids. 2019; 4(2):63. https://doi.org/10.3390/fluids4020063
Chicago/Turabian StyleZuo, Lihua, and Ruud Weijermars. 2019. "Longevity of Enhanced Geothermal Systems with Brine Circulation in Hydraulically Fractured Hydrocarbon Wells" Fluids 4, no. 2: 63. https://doi.org/10.3390/fluids4020063
APA StyleZuo, L., & Weijermars, R. (2019). Longevity of Enhanced Geothermal Systems with Brine Circulation in Hydraulically Fractured Hydrocarbon Wells. Fluids, 4(2), 63. https://doi.org/10.3390/fluids4020063






