Equation Discovery Using Fast Function Extraction: a Deterministic Symbolic Regression Approach
Abstract
1. Introduction
2. Methodology
2.1. FFX Problem Statement
- Construct a large library of linear and nonlinear basis functions. This step is known as basis function expansion or feature construction in ML.
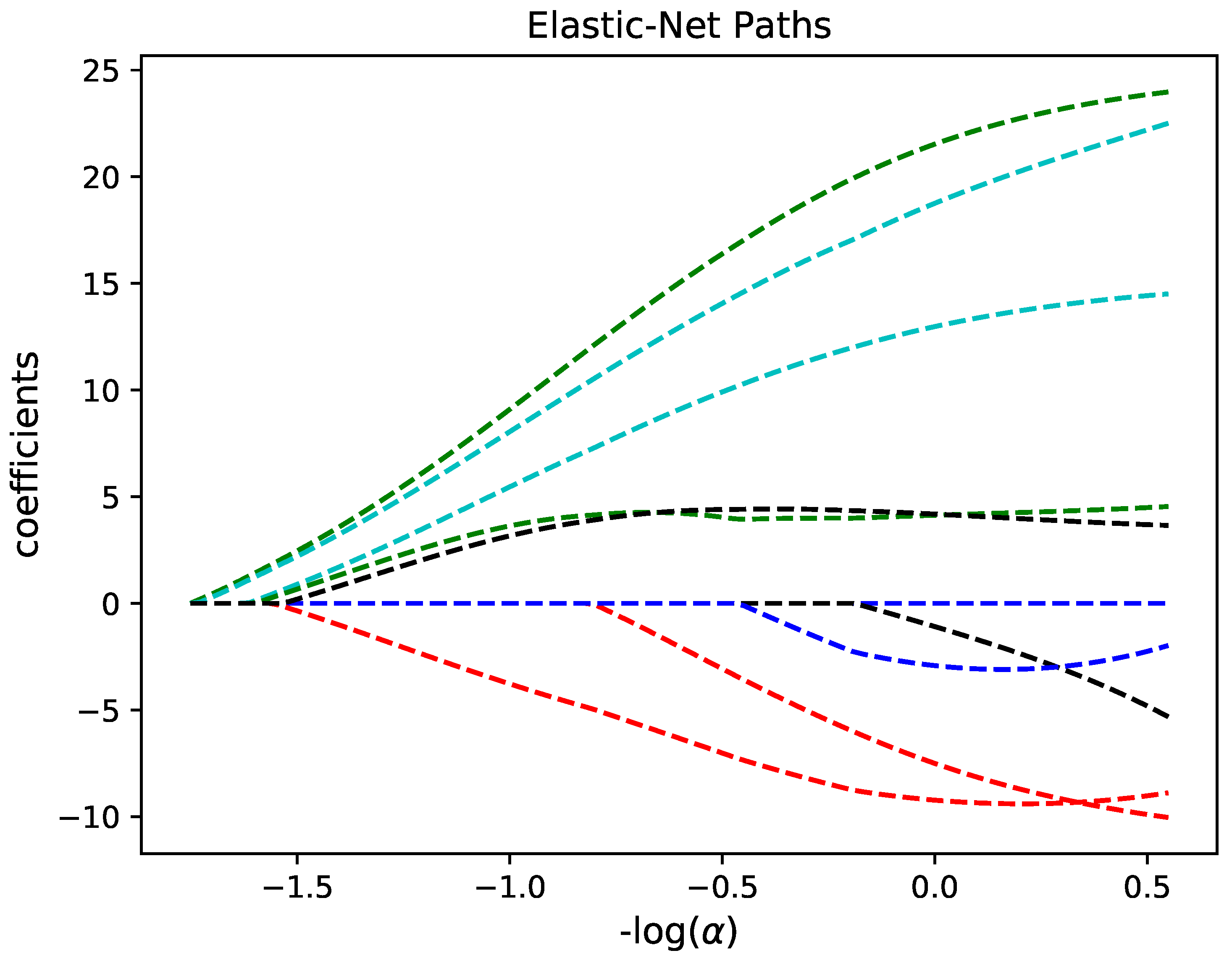
- Use regularized least square algorithm to regress the coefficients and simultaneously select basis functions mapping to target model. FFX uses pathwise regularized learning also known as elastic net algorithm to get the vector of coefficients and corresponding bases that best fit the data. This step is termed as model building.
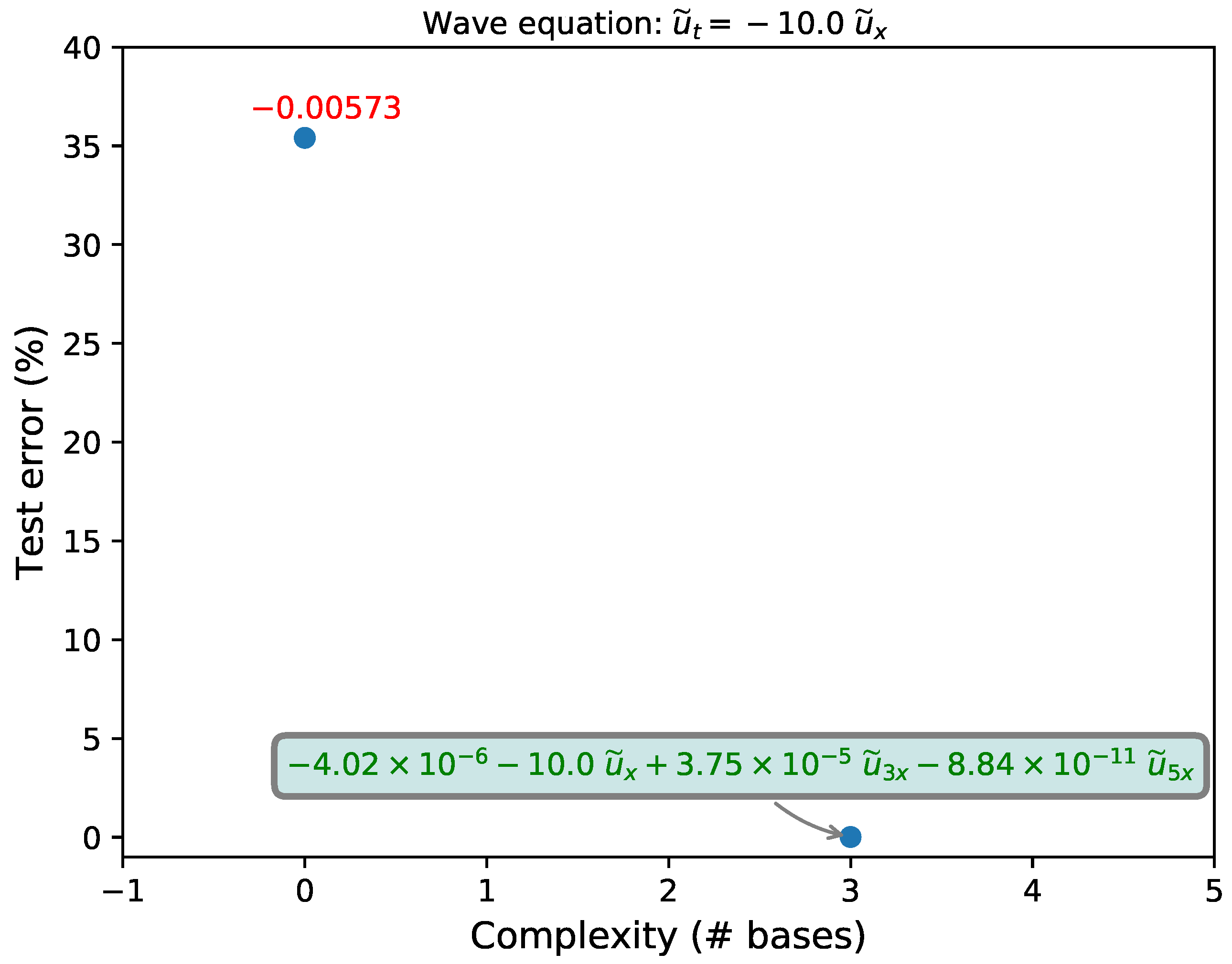
- Avoid over fitting using non-dominated filter (Pareto front analysis) with respect to model complexity (number of bases) versus the testing error. Final step is called model selection.
2.2. Basis Function Expansion (Feature Construction)
| Algorithm 1: Generate interacting variable bases limiting to quadratic nonlinearity |
 |
2.3. Model Building
| Algorithm 2: Pathwise learning algorithm |
 |
2.4. Model Selection
| Algorithm 3: Non-dominated filter |
 |
3. Numerical Experiments
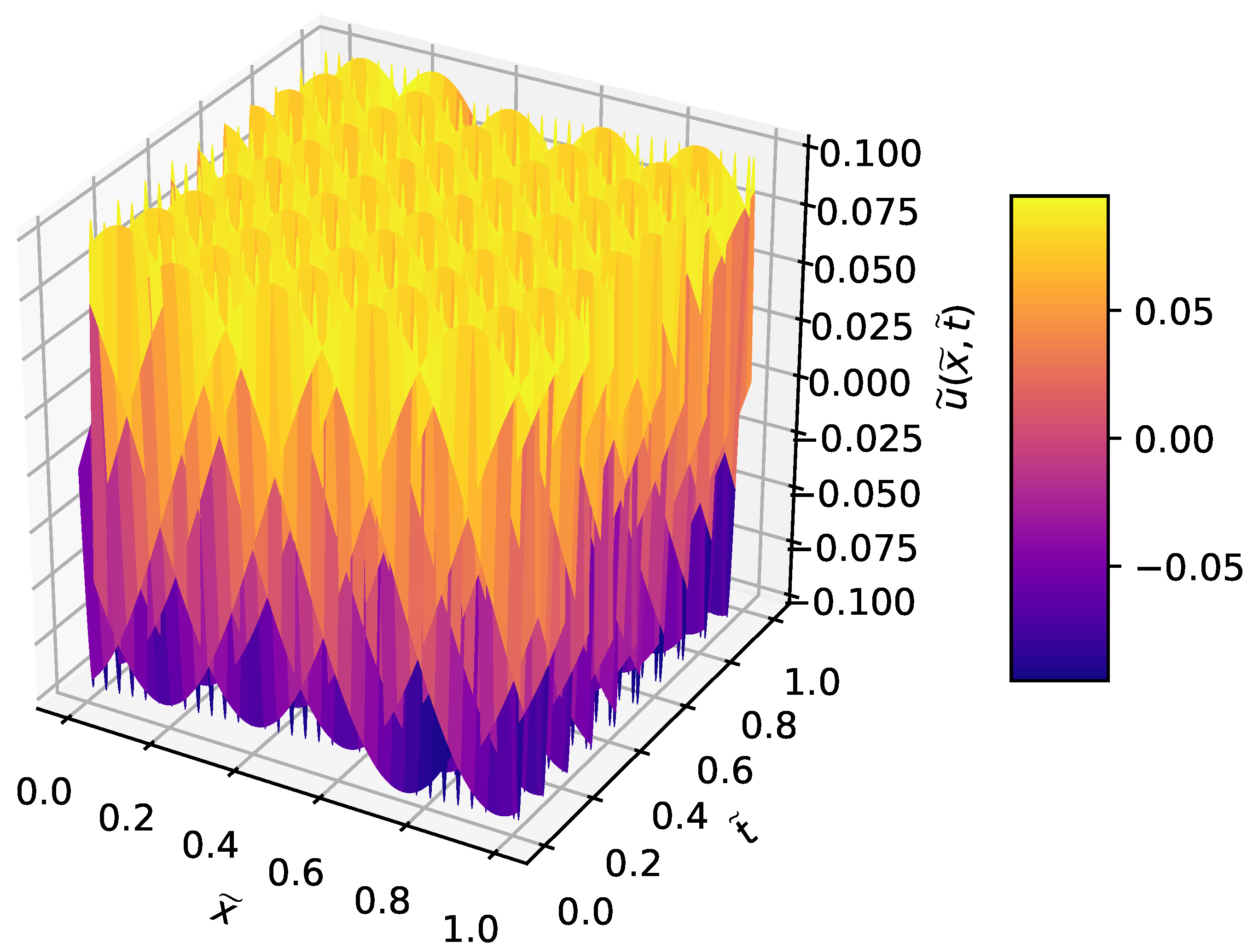
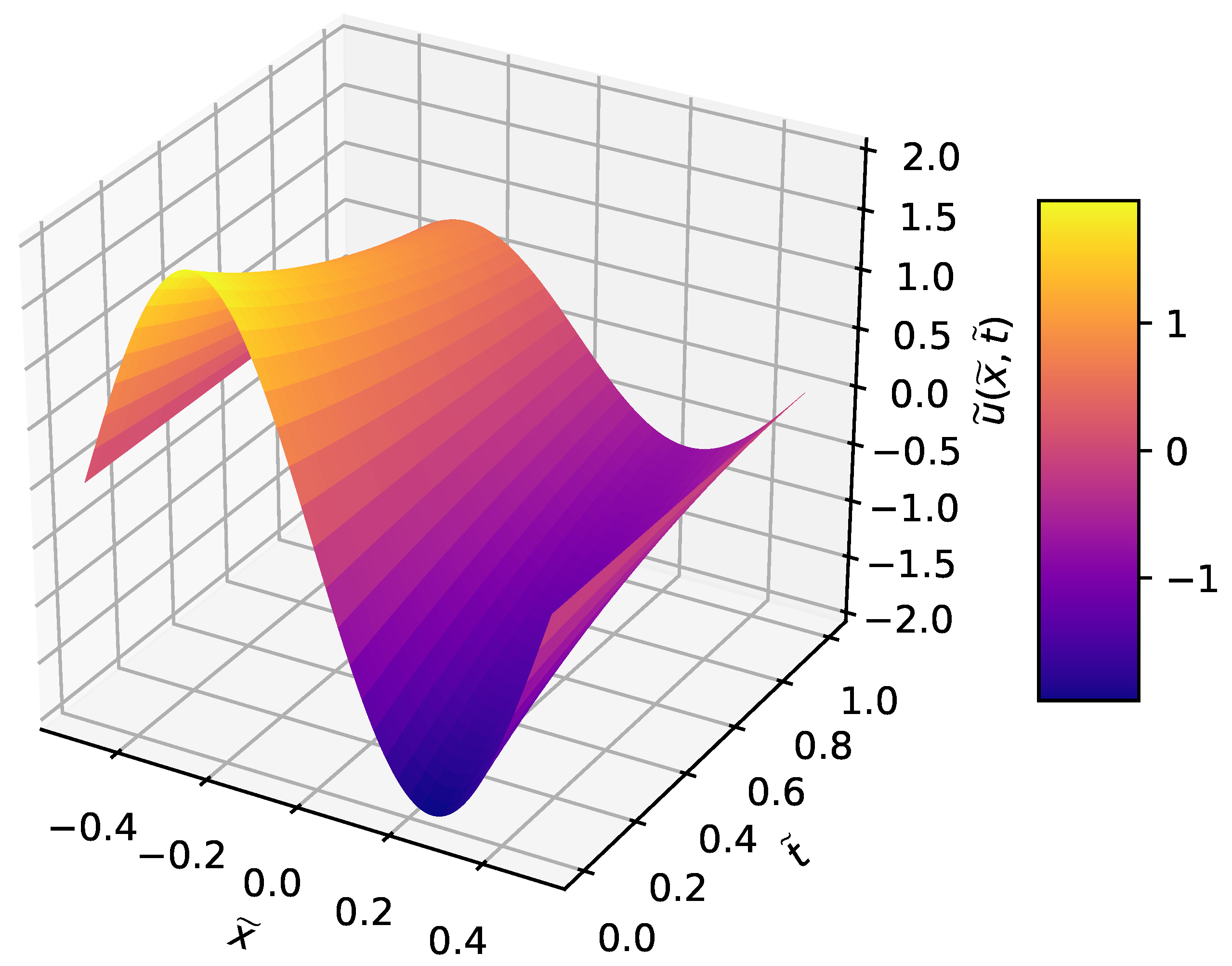
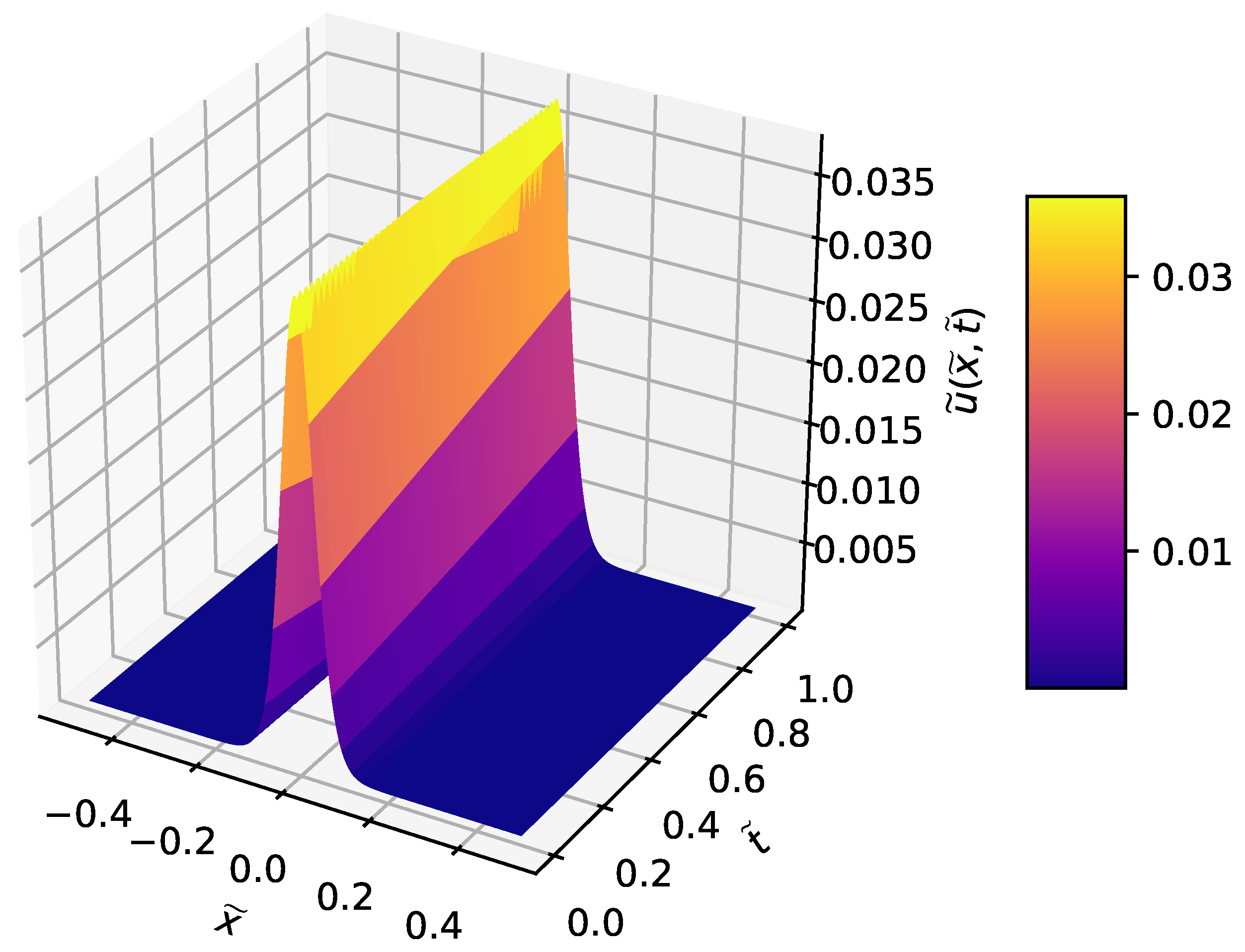
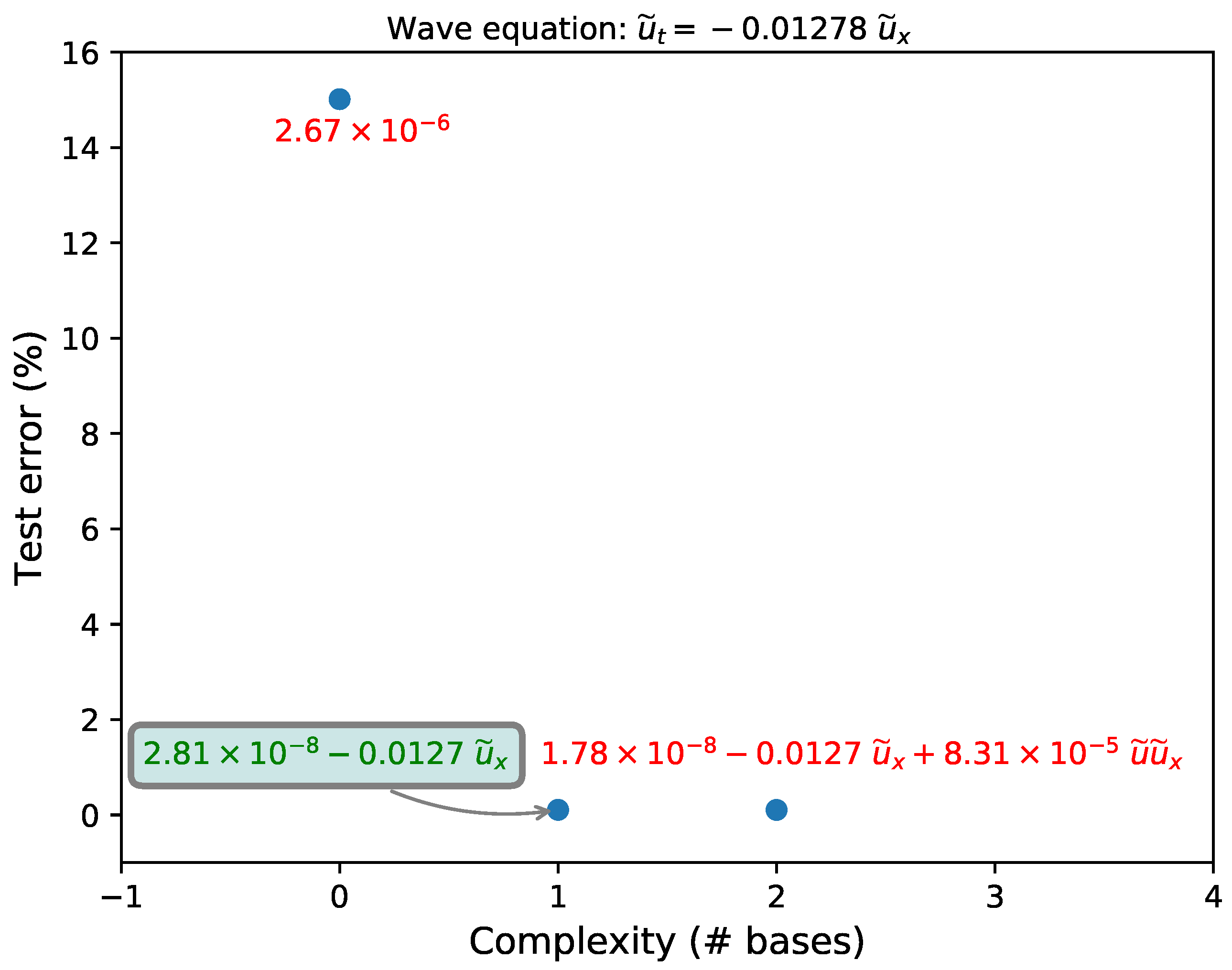
3.1. Wave Equation
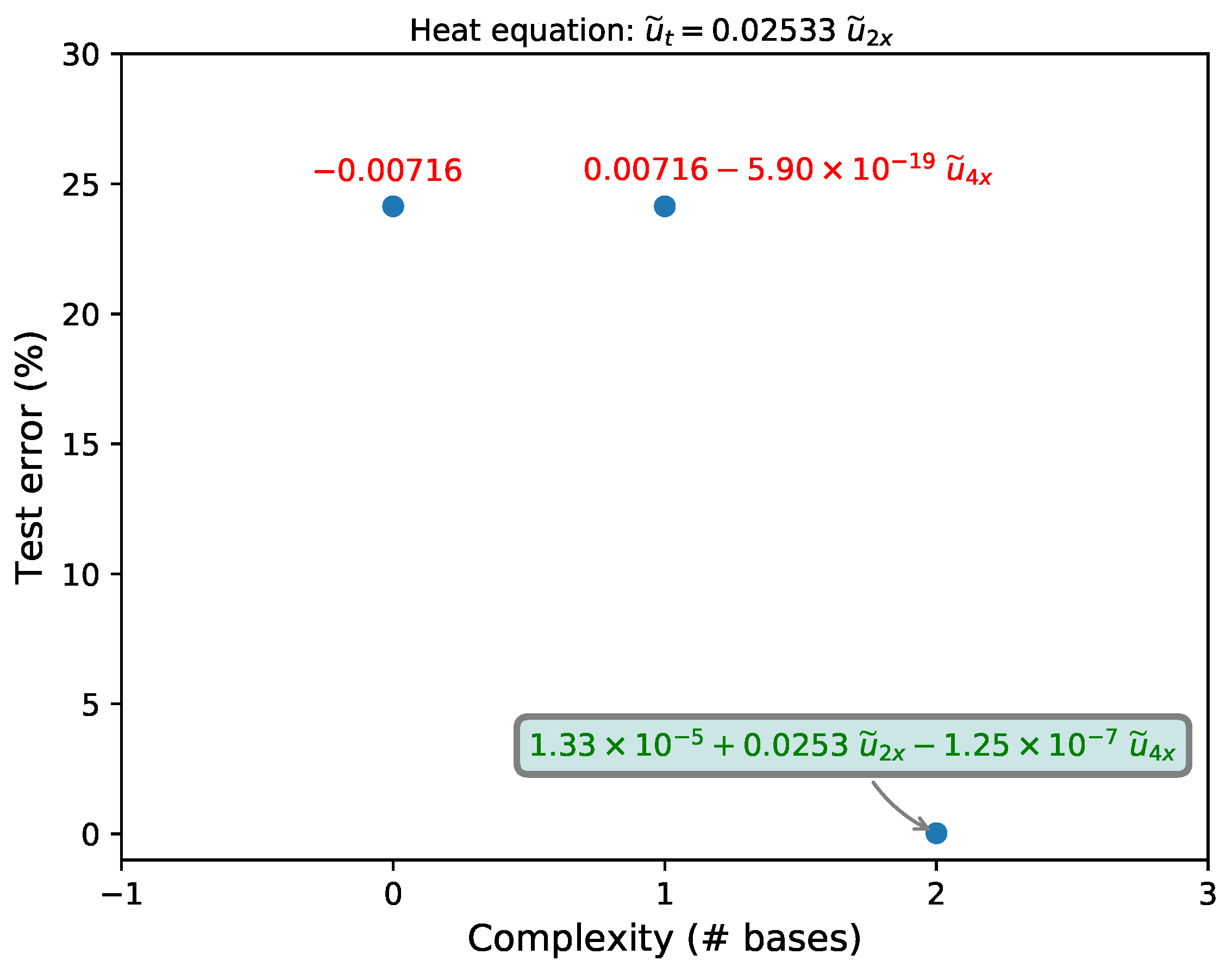
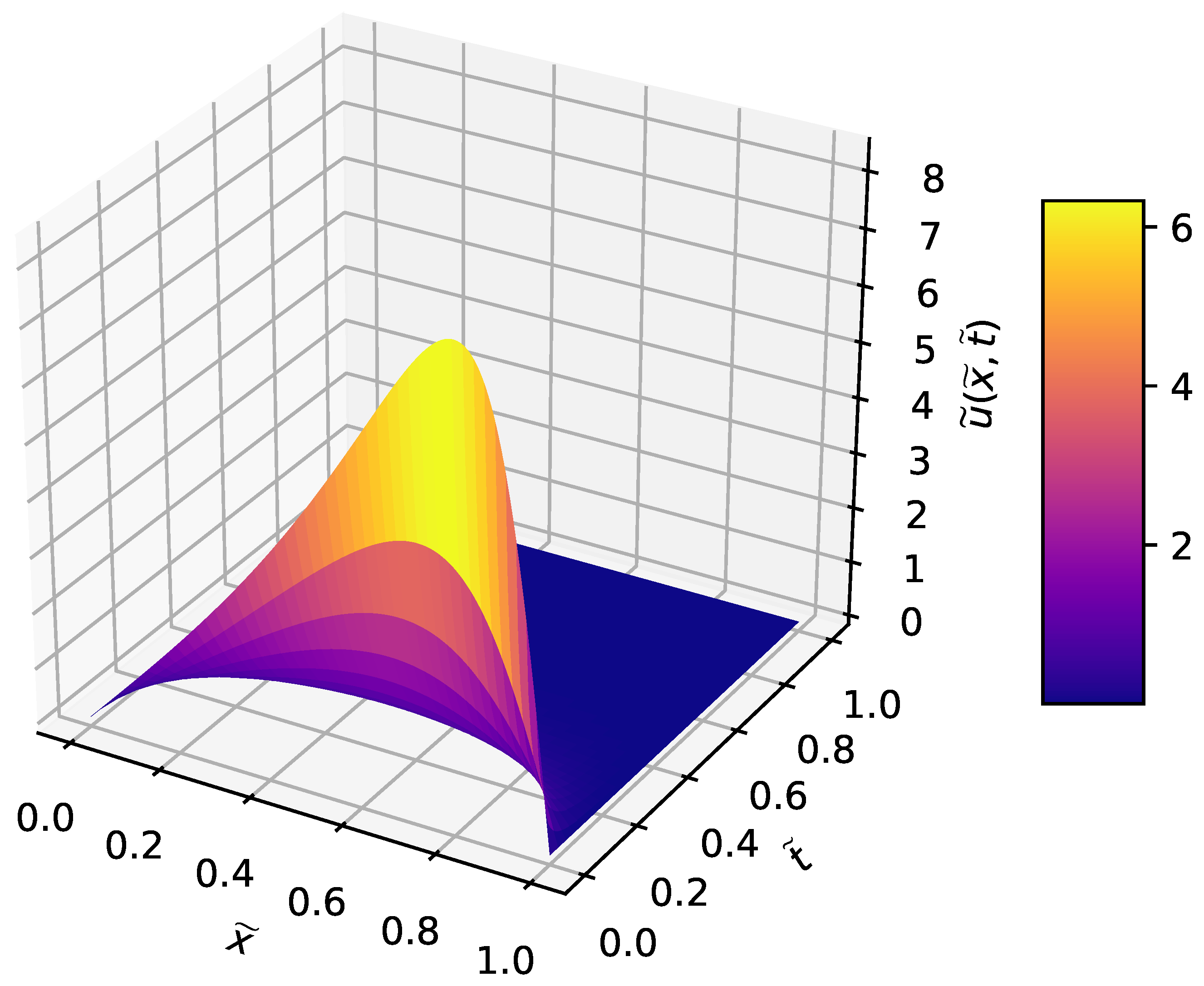
3.2. Heat Equation
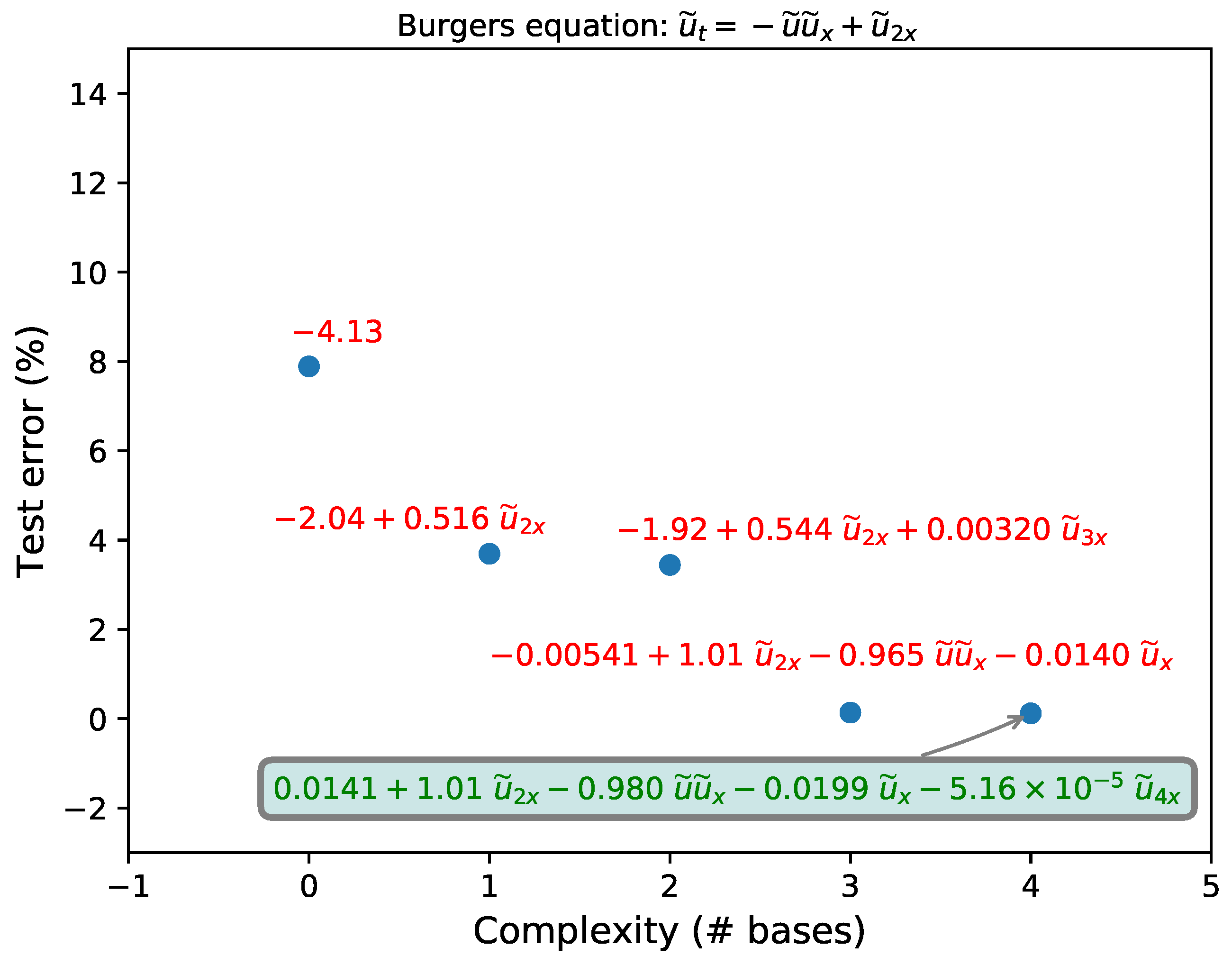
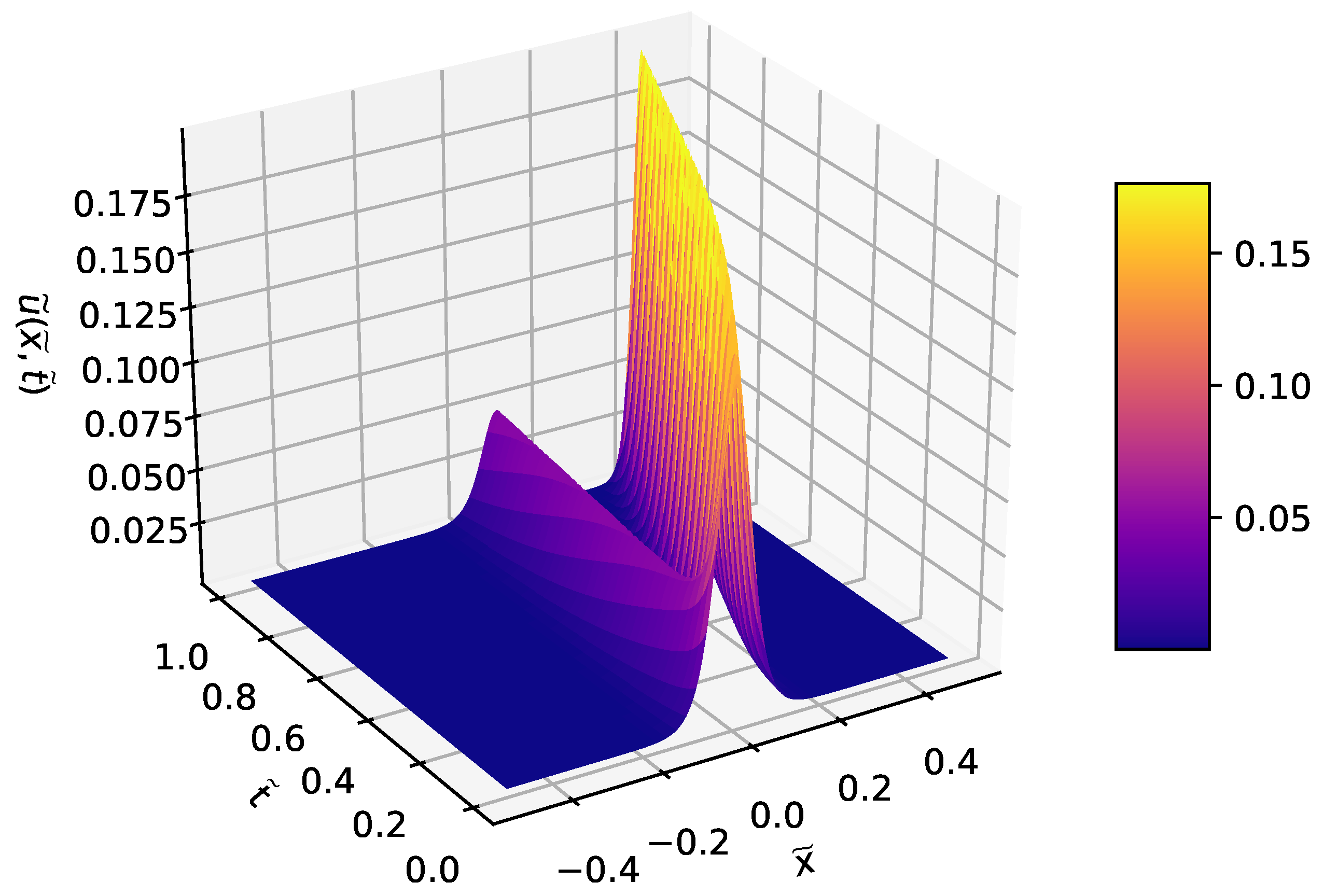
3.3. Burgers Equation
3.4. Korteweg–de Vries Equation
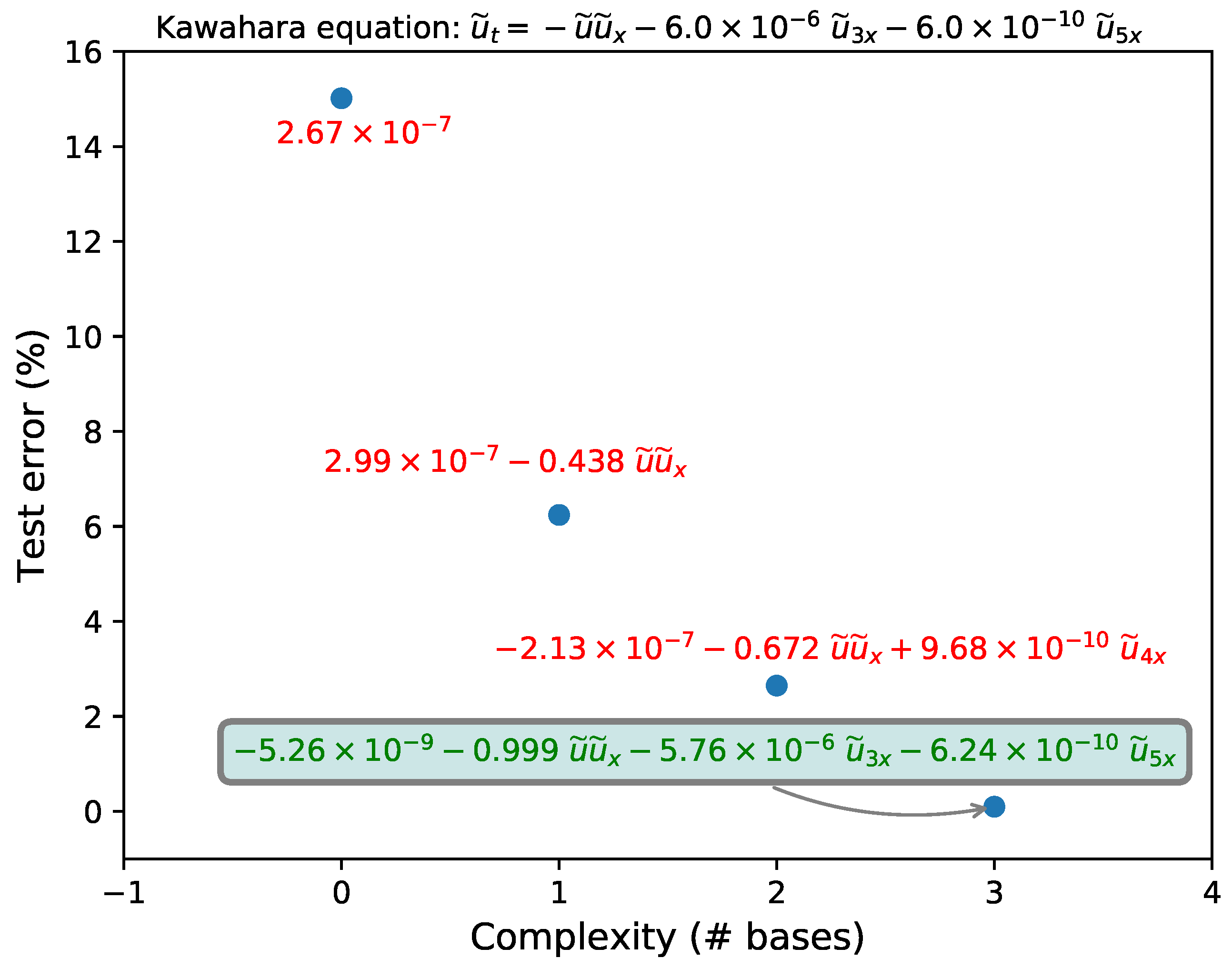
3.5. Kawahara Equation
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Marx, V. Biology: The big challenges of big data. Nature 2013, 498, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Ciregan, D.; Meier, U.; Schmidhuber, J. Multi-column deep neural networks for image classification. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3642–3649. [Google Scholar]
- Karpathy, A.; Fei-Fei, L. Deep visual-semantic alignments for generating image descriptions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3128–3137. [Google Scholar]
- Sallab, A.E.; Abdou, M.; Perot, E.; Yogamani, S. Deep reinforcement learning framework for autonomous driving. Electron. Imaging 2017, 2017, 70–76. [Google Scholar] [CrossRef]
- Al Mamun, S.; Lu, C.; Jayaraman, B. Extreme learning machines as encoders for sparse reconstruction. Fluids 2018, 3, 88. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the LASSO. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer Science + Business Media: New York, NY, USA, 2013; Volume 112. [Google Scholar]
- Rauhut, H. Compressive sensing and structured random matrices. Theor. Found. Numer. Methods Sparse Recovery 2010, 9, 1–92. [Google Scholar]
- Tibshirani, R.; Wainwright, M.; Hastie, T. Statistical Learning with Sparsity: The LASSO and Generalizations; Chapman and Hall/CRC: Boca Raton, FL, USA, 2015. [Google Scholar]
- Candes, E.J.; Romberg, J.K.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. J. Issued Courant Inst. Math. Sci. 2006, 59, 1207–1223. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1. [Google Scholar] [CrossRef] [PubMed]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [PubMed]
- Rudy, S.H.; Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Data-driven discovery of partial differential equations. Sci. Adv. 2017, 3, e1602614. [Google Scholar] [CrossRef] [PubMed]
- Schaeffer, H.; Caflisch, R.; Hauck, C.D.; Osher, S. Sparse dynamics for partial differential equations. Proc. Natl. Acad. Sci. USA 2013, 110, 6634–6639. [Google Scholar] [CrossRef]
- Schaeffer, H. Learning partial differential equations via data discovery and sparse optimization. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20160446. [Google Scholar] [CrossRef]
- Tran, G.; Ward, R. Exact recovery of chaotic systems from highly corrupted data. Multiscale Model. Simul. 2017, 15, 1108–1129. [Google Scholar] [CrossRef]
- Schaeffer, H.; Tran, G.; Ward, R. Extracting sparse high-dimensional dynamics from limited data. SIAM J. Appl. Math. 2018, 78, 3279–3295. [Google Scholar] [CrossRef]
- Mangan, N.M.; Kutz, J.N.; Brunton, S.L.; Proctor, J.L. Model selection for dynamical systems via sparse regression and information criteria. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20170009. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992; Volume 1. [Google Scholar]
- Ferreira, C. Gene Expression Programming: Mathematical Modeling by an Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2006; Volume 21. [Google Scholar]
- Schmidt, M.; Lipson, H. Distilling free-form natural laws from experimental data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Vazquez, K.; Fleming, P.J. Multi-objective genetic programming for nonlinear system identification. Electron. Lett. 1998, 34, 930–931. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, C.; Soh, C. Force identification of dynamic systems using genetic programming. Int. J. Numer. Methods Eng. 2005, 63, 1288–1312. [Google Scholar] [CrossRef]
- Ferariu, L.; Patelli, A. Multiobjective genetic programming for nonlinear system identification. In Proceedings of the International Conference on Adaptive and Natural Computing Algorithms, Kuopio, Finland, 23–25 April 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 233–242. [Google Scholar]
- Brunton, S.L.; Noack, B.R. Closed-loop turbulence control: Progress and challenges. Appl. Mech. Rev. 2015, 67, 050801. [Google Scholar] [CrossRef]
- Gautier, N.; Aider, J.L.; Duriez, T.; Noack, B.; Segond, M.; Abel, M. Closed-loop separation control using machine learning. J. Fluid Mech. 2015, 770, 442–457. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, S.L. Parse-matrix evolution for symbolic regression. Eng. Appl. Artif. Intell. 2012, 25, 1182–1193. [Google Scholar] [CrossRef]
- Brameier, M.F.; Banzhaf, W. Linear Genetic Programming; Springe: New York, NY, USA, 2007. [Google Scholar]
- Weatheritt, J.; Sandberg, R. A novel evolutionary algorithm applied to algebraic modifications of the RANS stress–strain relationship. J. Comput. Phys. 2016, 325, 22–37. [Google Scholar] [CrossRef]
- Schoepplein, M.; Weatheritt, J.; Sandberg, R.; Talei, M.; Klein, M. Application of an evolutionary algorithm to LES modelling of turbulent transport in premixed flames. J. Comput. Phys. 2018, 374, 1166–1179. [Google Scholar] [CrossRef]
- McConaghy, T. FFX: Fast, scalable, deterministic symbolic regression technology. In Genetic Programming Theory and Practice IX; Springer: New York, NY, USA, 2011; pp. 235–260. [Google Scholar]
- Nelder, J.A.; Wedderburn, R.W. Generalized linear models. J. R. Stat. Soc. Ser. A 1972, 135, 370–384. [Google Scholar] [CrossRef]
- Quade, M.; Abel, M.; Shafi, K.; Niven, R.K.; Noack, B.R. Prediction of dynamical systems by symbolic regression. Phys. Rev. E 2016, 94, 012214. [Google Scholar] [CrossRef]
- Chen, C.; Luo, C.; Jiang, Z. Elite bases regression: A real-time algorithm for symbolic regression. In Proceedings of the 2017 13th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Guilin, China, 29–31 July 2017; pp. 529–535. [Google Scholar]
- Worm, T.; Chiu, K. Prioritized grammar enumeration: Symbolic regression by dynamic programming. In Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation, Amsterdam, The Netherlands, 6–10 July 2013; pp. 1021–1028. [Google Scholar]
- Ng, A.Y. Feature selection, L 1 vs. L 2 regularization, and rotational invariance. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; p. 78. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Blumer, A.; Ehrenfeucht, A.; Haussler, D.; Warmuth, M.K. Occam’s razor. Inf. Process. Lett. 1987, 24, 377–380. [Google Scholar] [CrossRef]
- Berger, J.O.; Jefferys, W.H. The application of robust Bayesian analysis to hypothesis testing and Occam’s razor. J. Ital. Stat. Soc. 1992, 1, 17–32. [Google Scholar] [CrossRef]
- Ozis, T.; Ozer, S. A simple similarity-transformation-iterative scheme applied to Korteweg–de Vries equation. Appl. Math. Comput. 2006, 173, 19–32. [Google Scholar]
- Lamb, G.L., Jr. Elements of Soliton Theory; Wiley-Interscience: New York, NY, USA, 1980. [Google Scholar]
- Kawahara, T. Oscillatory solitary waves in dispersive media. J. Phys. Soc. Jpn. 1972, 33, 260–264. [Google Scholar] [CrossRef]
- Kawahara, T.; Sugimoto, N.; Kakutani, T. Nonlinear interaction between short and long capillary-gravity waves. J. Phys. Soc. Jpn. 1975, 39, 1379–1386. [Google Scholar] [CrossRef]
- Hunter, J.K.; Scheurle, J. Existence of perturbed solitary wave solutions to a model equation for water waves. Phys. D Nonlinear Phenom. 1988, 32, 253–268. [Google Scholar] [CrossRef]
- Sirendaoreji. New exact travelling wave solutions for the Kawahara and modified Kawahara equations. Chaos Solitons Fract. 2004, 19, 147–150. [Google Scholar] [CrossRef]

| PDE | Dimensional Equation | Domain | Discretization n (Spatial), m (Temporal) | |
|---|---|---|---|---|
| 1. | Wave eq. | a | ||
| 2. | Heat eq. | |||
| 3. | Burgers eq. | |||
| 4. | Korteweg–de Vries (KdV) eq. | 6 | ||
| 5. | Kawahara eq. |
| PDE | Non-Dimensional Equation | Length Scale (L), Time Scale (T) | |
|---|---|---|---|
| 1. | Wave eq. | a | |
| 2. | Heat eq. | ||
| 3. | Burgers eq. | ||
| 4. | Korteweg–de Vries (KdV) eq. | ||
| 5. | Kawahara eq. |
| Parameter | Value/Setting |
|---|---|
| Basis function expansion | Interacting—variable bases |
| Elastic net | L ratio () = 0.95 Number of different values = 1000 Train error = Number of maximum bases = 250 |
| Model | Non-Dimensional PDE | Test Error (%) |
|---|---|---|
| True | ||
| Recovered (clean) | 0.01 | |
| Recovered (1% noise) | 5.36 | |
| Recovered (5% noise) | 11.85 | |
| Recovered (10% noise) | 13.74 | |
| Recovered (15% noise) | 14.49 | |
| Recovered (20% noise) | 14.89 | |
| Recovered (25% noise) | 15.07 | |
| Recovered (30% noise) | – |
| Model | Non-Dimensional PDE | Test Error (%) |
|---|---|---|
| True | ||
| Recovered (clean) | 0.01 | |
| Recovered (1% noise) | 5.16 | |
| Recovered (5% noise) | – |
| Model | Non-Dimensional PDE | Test Error (%) |
|---|---|---|
| True | ||
| Recovered (clean) | 0.12 | |
| Recovered (1% noise) | 5.87 | |
| Recovered (5% noise) | – |
| Model | Non-Dimensional PDE | Test Error (%) |
|---|---|---|
| True | ||
| Recovered (clean) | 0.11 | |
| Recovered (1% noise) | 6.75 | |
| Recovered (5% noise) | – |
| Model | Non-Dimensional PDE | Test Error (%) |
|---|---|---|
| True | ||
| Recovered (clean) | 0.18 | |
| Recovered (1% noise) | 6.57 | |
| Recovered (5% noise) | – |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaddireddy, H.; San, O. Equation Discovery Using Fast Function Extraction: a Deterministic Symbolic Regression Approach. Fluids 2019, 4, 111. https://doi.org/10.3390/fluids4020111
Vaddireddy H, San O. Equation Discovery Using Fast Function Extraction: a Deterministic Symbolic Regression Approach. Fluids. 2019; 4(2):111. https://doi.org/10.3390/fluids4020111
Chicago/Turabian StyleVaddireddy, Harsha, and Omer San. 2019. "Equation Discovery Using Fast Function Extraction: a Deterministic Symbolic Regression Approach" Fluids 4, no. 2: 111. https://doi.org/10.3390/fluids4020111
APA StyleVaddireddy, H., & San, O. (2019). Equation Discovery Using Fast Function Extraction: a Deterministic Symbolic Regression Approach. Fluids, 4(2), 111. https://doi.org/10.3390/fluids4020111






