Experimental Observation of Modulational Instability in Crossing Surface Gravity Wavetrains
Abstract
1. Introduction
2. Theoretical Background
2.1. Coupled Nonlinear Schrödinger Equation (CNLSE)
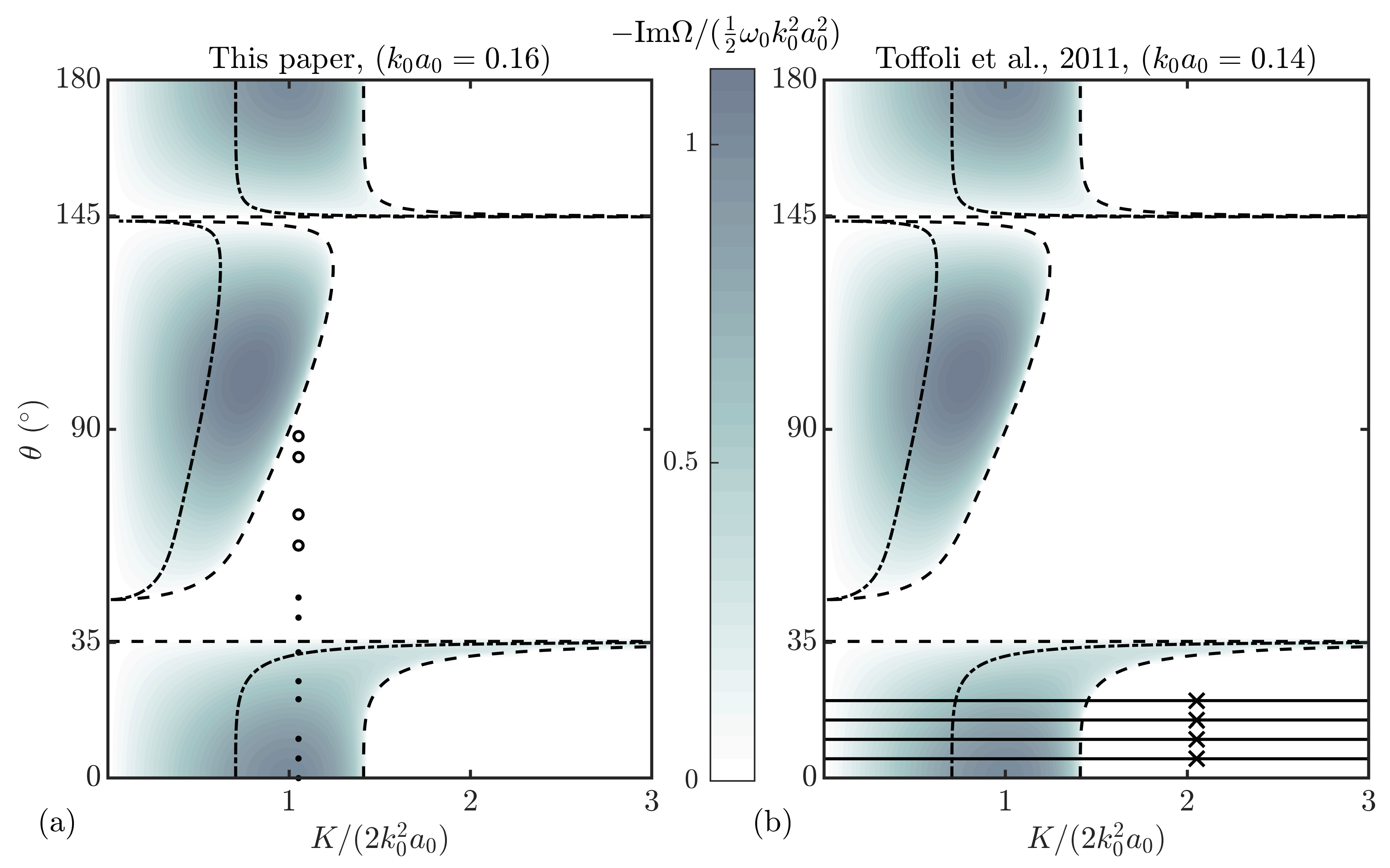
2.2. Linear Stability Analysis
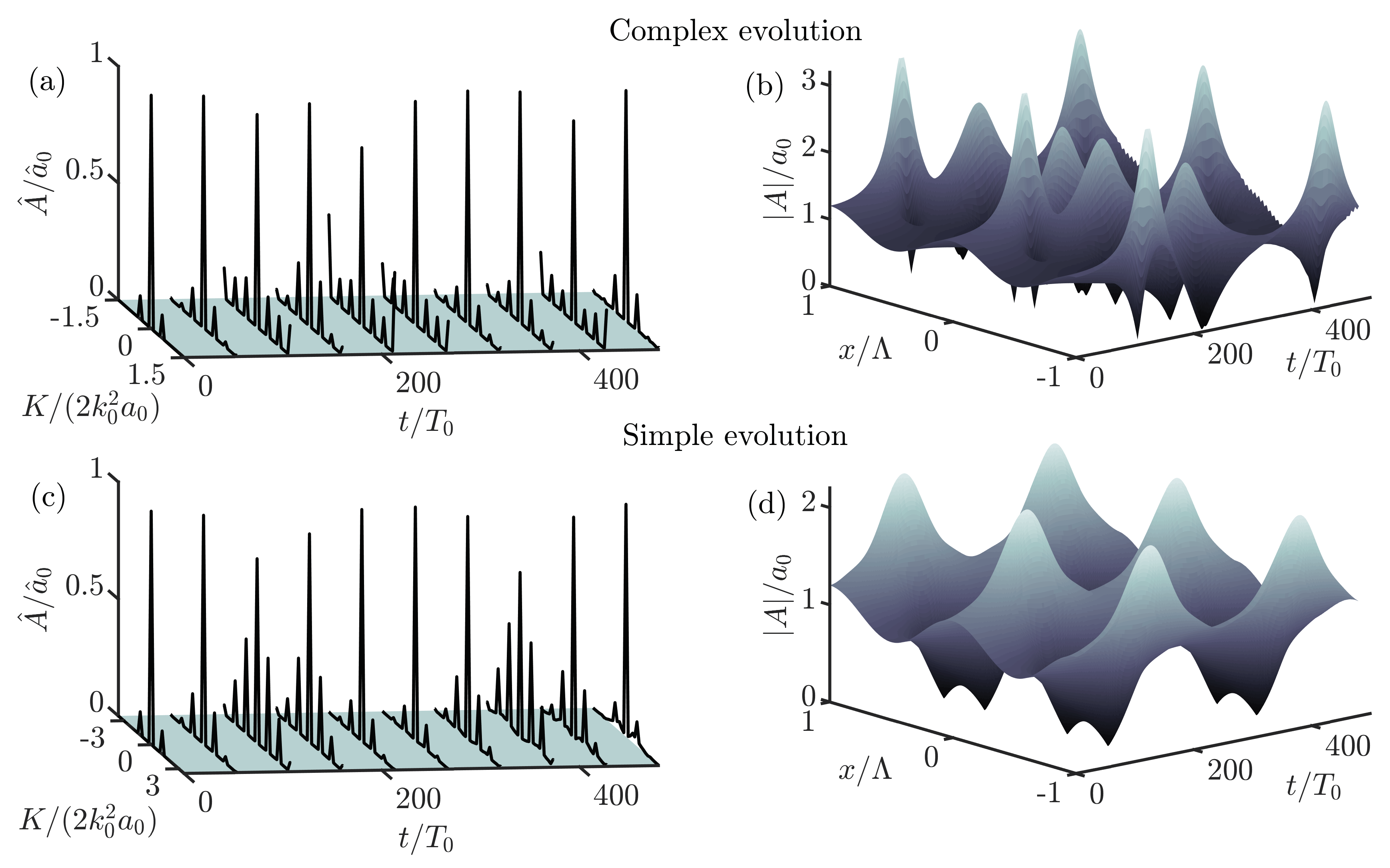
2.3. Characteristics of Modulational Instability: Complex vs. Simple Evolution
3. Experimental Methodology
3.1. Facility
3.2. Matrix of Experiments
3.3. Data Processing
4. Results
4.1. Unidirectional Waves:
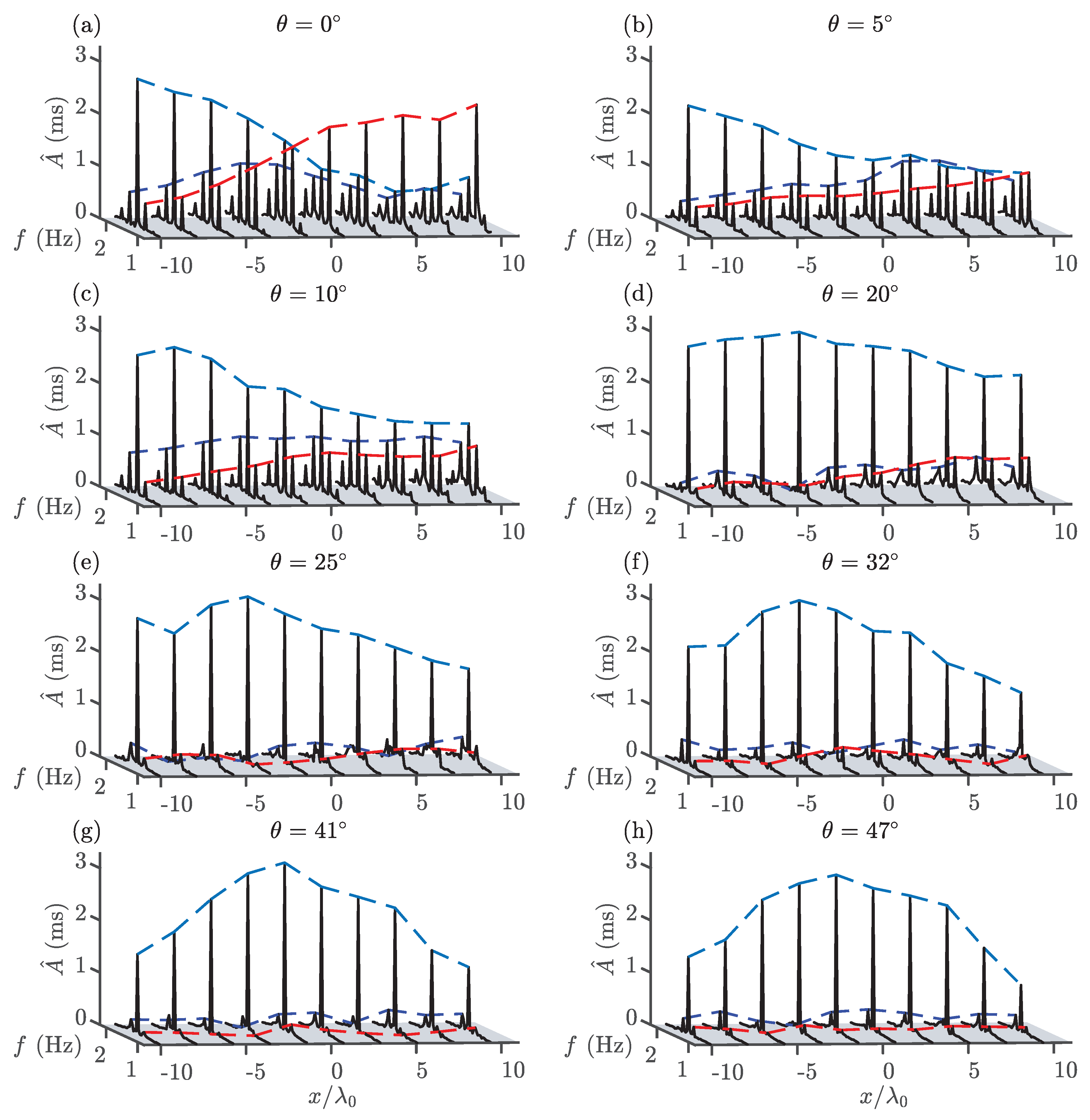
4.2. Crossing Waves:
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Split-Step Time Marching Technique
Appendix B. Experiments 2i–l: 60° ≤ θ ≤ 88°
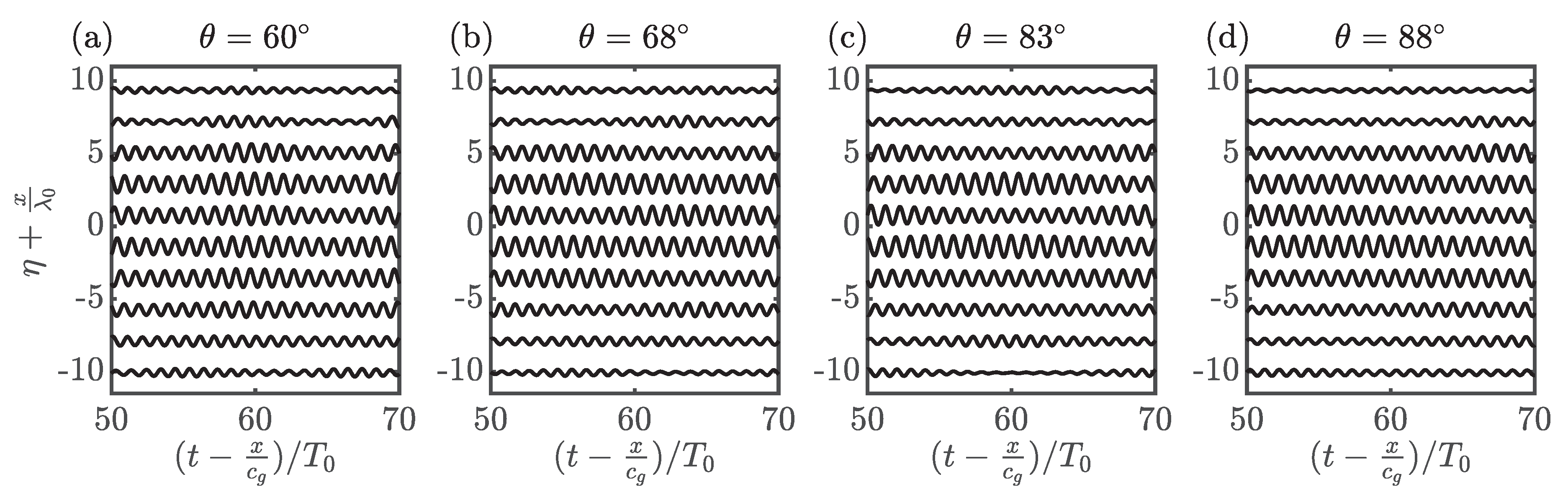
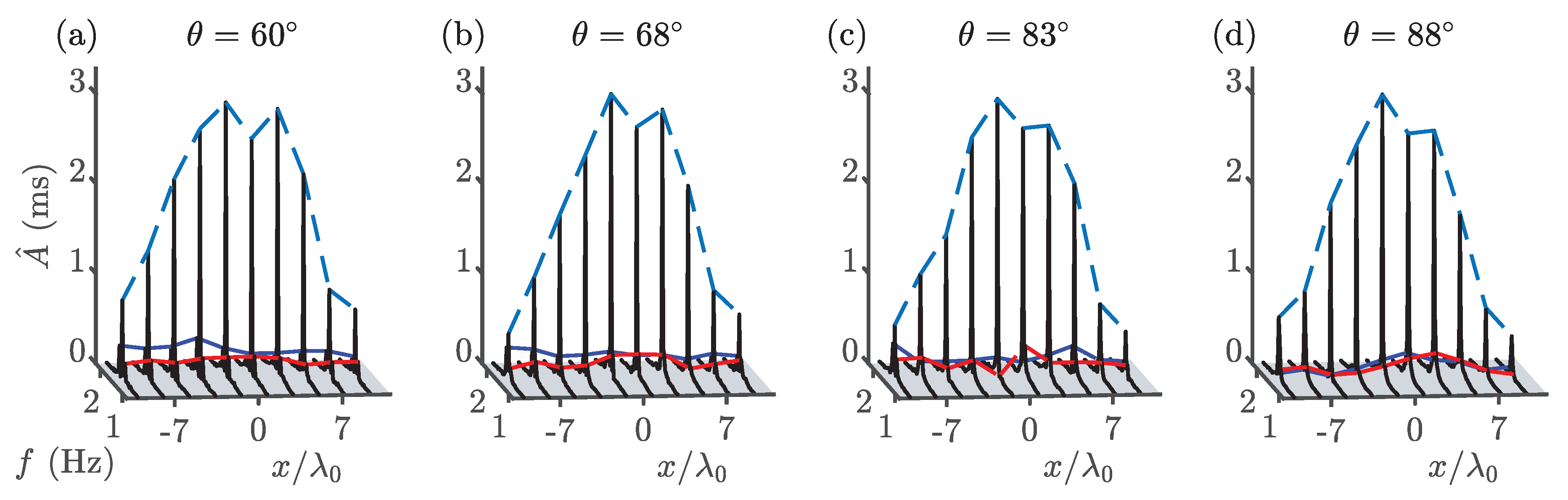
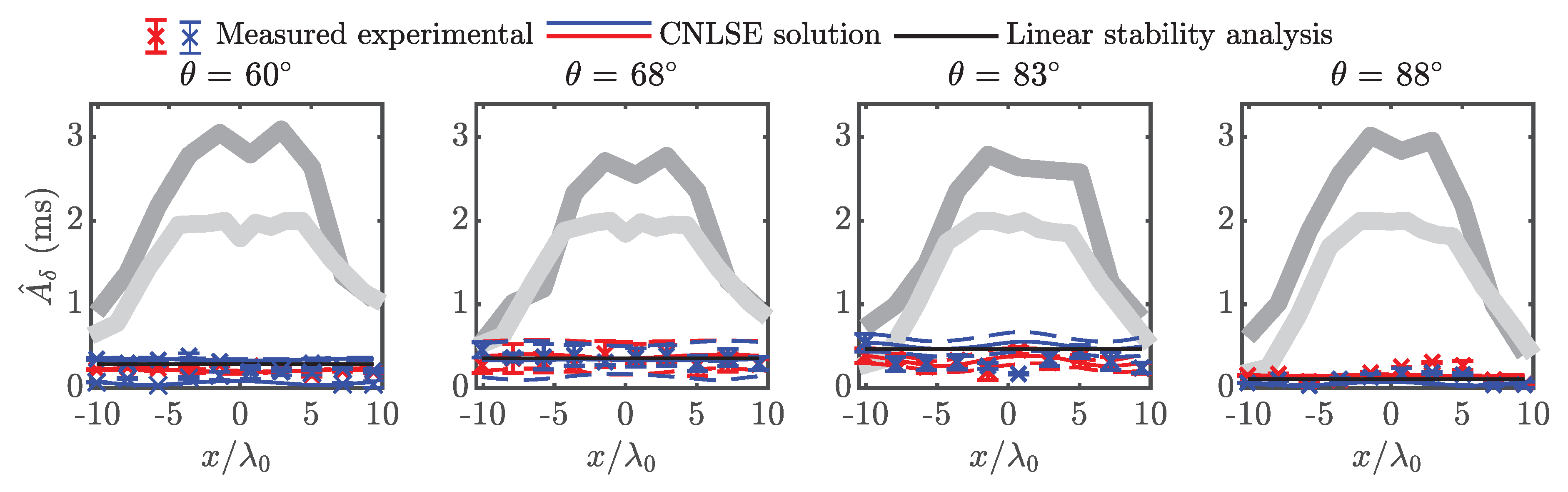
References
- Bitner-Gregersen, E.; Gramstad, O. Rogue waves impact on ships and offshore structures. In Det Norske Veritas Germanischer Lloyd Strategic Research and Innovation Position Paper; DNV GL: Oslo, Norway, 2015. [Google Scholar]
- Cavaleri, L.; Bertotti, L.; Torrisi, L.; Bitner-Gregersen, E.; Serio, M.; Onorato, M. Rogue waves in crossing seas: The Louis Majesty accident. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Kharif, C.; Pelinovsky, E. Physical mechanisms of the rogue wave phenomenon. Eur. J. Mech. B Fluid 2003, 22, 603–634. [Google Scholar] [CrossRef]
- Dysthe, K.; Krogstad, H.E.; Müller, P. Oceanic rogue waves. Annu. Rev. Fluid Mech. 2008, 40, 287–310. [Google Scholar] [CrossRef]
- Onorato, M.; Residori, S.; Bortolozzo, U.; Montina, A.; Arecchi, F. Rogue waves and their generating mechanisms in different physical contexts. Phys. Rep. 2013, 528, 47–89. [Google Scholar] [CrossRef]
- Adcock, T.A.; Taylor, P.H. The physics of anomalous (‘rogue’) ocean waves. Rep. Prog. Phys. 2014, 77, 105901. [Google Scholar] [CrossRef]
- Yuen, H.C.; Lake, B.M. Nonlinear dynamics of deep-water gravity waves. In Advances in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 1982; Volume 22, pp. 67–229. [Google Scholar]
- Benjamin, T.B.; Feir, J. The disintegration of wave trains on deep water Part 1. Theory. J. Fluid Mech. 1967, 27, 417–430. [Google Scholar] [CrossRef]
- Ma, Y.C. The perturbed plane-wave solutions of the cubic Schrödinger equation. Stud. Appl. Math. 1979, 60, 43–58. [Google Scholar] [CrossRef]
- Peregrine, D.H. Water waves, nonlinear Schrödinger equations and their solutions. ANZIAM J. 1983, 25, 16–43. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A.; Taki, M. Waves that appear from nowhere and disappear without a trace. Phys. Lett. A 2009, 373, 675–678. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.; Onorato, M.; Akhmediev, N. Super rogue waves: Observation of a higher-order breather in water waves. Phys. Rev. X 2012, 2, 011015. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.; Akhmediev, N. Rogue wave observation in a water wave tank. Phys. Rev. Lett. 2011, 106, 204502. [Google Scholar] [CrossRef] [PubMed]
- Osborne, A.R.; Resio, D.T.; Costa, A.; de León, S.P.; Chirivì, E. Highly nonlinear wind waves in Currituck Sound: Dense breather turbulence in random ocean waves. Ocean Dyn. 2019, 69, 187–219. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.; Branger, H.; Kharif, C.; Akhmediev, N. Experiments on wind-perturbed rogue wave hydrodynamics using the Peregrine breather model. Phys. Fluids 2013, 25, 101704. [Google Scholar] [CrossRef]
- Lake, B.M.; Yuen, H.C.; Rungaldier, H.; Ferguson, W.E. Nonlinear deep-water waves: Theory and experiment. Part 2. Evolution of a continuous wave train. J. Fluid Mech. 1977, 83, 49–74. [Google Scholar] [CrossRef]
- Fermi, E.; Pasta, P.; Ulam, S.; Tsingou, M. Studies of the Nonlinear Problems; Technical Report; Los Alamos Scientific Lab.: Los Alamos, NM, USA, 1955. [Google Scholar]
- Ford, J. The Fermi-Pasta-Ulam problem: Paradox turns discovery. Phys. Rep. 1992, 213, 271–310. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M. Modulational instability and the Fermi-Pasta-Ulam recurrence. Phys. Fluids 1981, 24, 23–26. [Google Scholar] [CrossRef]
- Chabchoub, A.; Fink, M. Time-reversal generation of rogue waves. Phys. Rev. Lett. 2014, 112, 124101. [Google Scholar] [CrossRef] [PubMed]
- Melville, W. The instability and breaking of deep-water waves. J. Fluid Mech. 1982, 115, 165–185. [Google Scholar] [CrossRef]
- Young, I.; Verhagen, L.; Banner, M. A note on the bimodal directional spreading of fetch-limited wind waves. J. Geophys. Res. Oceans 1995, 100, 773–778. [Google Scholar] [CrossRef]
- Ewans, K.C. Observations of the directional spectrum of fetch-limited waves. J. Phys. Oceanogr. 1998, 28, 495–512. [Google Scholar] [CrossRef]
- Onorato, M.; Osborne, A.R.; Serio, M. Modulational instability in crossing sea states: A possible mechanism for the formation of freak waves. Phys. Rev. Lett. 2006, 96, 014503. [Google Scholar] [CrossRef] [PubMed]
- Zakharov, V.E. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phy. 1968, 9, 190–194. [Google Scholar] [CrossRef]
- Hammack, J.L.; Henderson, D.M.; Segur, H. Progressive waves with persistent two-dimensional surface patterns in deep water. J. Fluid Mech. 2005, 532, 1–52. [Google Scholar] [CrossRef]
- Kundu, S.; Debsarma, S.; Das, K. Modulational instability in crossing sea states over finite depth water. Phys. Fluids 2013, 25, 066605. [Google Scholar] [CrossRef]
- Ruban, V. Giant waves in weakly crossing sea states. J. Exp. Theor. Phys. 2010, 110, 529–536. [Google Scholar] [CrossRef]
- Onorato, M.; Proment, D.; Toffoli, A. Freak waves in crossing seas. Eur. Phys. J. Spec. Top. 2010, 185, 45–55. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Horikis, T.P. Interacting nonlinear wave envelopes and rogue wave formation in deep water. Phys. Fluids 2015, 27, 012107. [Google Scholar] [CrossRef]
- Degasperis, A.; Lombardo, S.; Sommacal, M. Rogue Wave Type Solutions and Spectra of Coupled Nonlinear Schrödinger Equations. Fluids 2019, 4, 57. [Google Scholar] [CrossRef]
- Toffoli, A.; Bitner-Gregersen, E.M.; Osborne, A.R.; Serio, M.; Monbaliu, J.; Onorato, M. Extreme waves in random crossing seas: Laboratory experiments and numerical simulations. Geophys. Res. Lett. 2011, 38, L06605. [Google Scholar] [CrossRef]
- Toffoli, A.; Fernandez, L.; Monbaliu, J.; Benoit, M.; Gagnaire-Renou, E.; Lefevre, J.; Cavaleri, L.; Proment, D.; Pakozdi, C.; Stansberg, C.; et al. Experimental evidence of the modulation of a plane wave to oblique perturbations and generation of rogue waves in finite water depth. Phys. Fluids 2013, 25, 091701. [Google Scholar] [CrossRef]
- Chabchoub, A.; Mozumi, K.; Hoffman, N.; Babanin, A.V.; Toffoli, A.; Steer, J.N.; van den Bremer, T.S.; Akhmediev, N.; Onorato, M.; Waseda, T. Observation of short-crested slanted solitons and breathers. Proc. Natl. Acad. Sci. USA 2019. forthcoming. [Google Scholar]
- Okihiro, M.; Guza, R.T.; Seymour, R.J. Bound infra-gravity waves. J. Geophys. Res. 1992, 97, 453–469. [Google Scholar] [CrossRef]
- Herbers, T.H.C.; Elgar, S.; Guza, R.T. Infragravity-frequency (0.005–0.05 Hz) motions on the shelf. Part I: Forced waves. J. Phys. Oceanogr. 1994, 24, 917–927. [Google Scholar] [CrossRef]
- Toffoli, A.; Onorato, M.; Monbaliu, J. Wave statistics in unimodal and bimodal seas from a second-order model. Eur. J. Mech. B-Fluid 2006, 25, 649–661. [Google Scholar] [CrossRef]
- Christou, M.; Tromans, P.; Vanderschuren, L.; Ewans, K. Second-order crest statistics of realistic sea states. In Proceedings of the 11th International Workshop on Wave Hindcasting and Forecasting, Halifax, NS, Canada, 18–23 October 2009; pp. 18–23. [Google Scholar]
- Hasselmann, K. On the non-linear energy transfer in a gravity-wave spectrum Part 1. General theory. J. Fluid Mech. 1962, 12, 481–500. [Google Scholar] [CrossRef]
- Sharma, J.N.; Dean, R.G. Second-order directional seas and associated wave forces. Soc. Pet. Eng. J. 1981, 21, 129–140. [Google Scholar] [CrossRef]
- Dalzell, J.F. A note on finite depth second-order wave–wave interactions. Appl. Ocean Res. 1999, 21, 105–111. [Google Scholar] [CrossRef]
- Forristall, G.Z. Wave crest distributions: Observations and second-order theory. J. Phys. Oceanogr. 2000, 30, 1931–1943. [Google Scholar] [CrossRef]
- Walker, D.A.G.; Taylor, P.H.; Eatock Taylor, R. The shape of large surface waves on the open sea and the Draupner New Year wave. Appl. Ocean Res. 2004, 26, 73–83. [Google Scholar] [CrossRef]
- Toffoli, A.; Monbaliu, J.; Onorato, M.; Osborne, A.R.; Babanin, A.V.; Bitner-Gregersen, E.M. Second-order theory and setup in surface gravity waves: A comparison with experimental data. J. Phys. Oceanogr. 2007, 37, 2726–2739. [Google Scholar] [CrossRef]
- Santo, H.; Taylor, P.H.; Eatock Taylor, R.; Choo, Y.S. Average properties of the largest waves in Hurricane Camille. J. Offshore Mech. Arct. Eng. 2013, 135, 011602. [Google Scholar] [CrossRef]
- McAllister, M.L.; Adcock, T.A.A.; Taylor, P.H.; van den Bremer, T.S. The set-down and set-up of directionally spread and crossing surface gravity wave groups. J. Fluid Mech. 2018, 835, 131–169. [Google Scholar] [CrossRef]
- Haver, S. A possible freak wave event measured at the Draupner jacket January 1 1995. In Proceedings of the 2004 Rogue Waves, Brest, France, 20–22 October 2004; pp. 1–8. [Google Scholar]
- Adcock, T.; Taylor, P.; Yan, S.; Ma, Q.; Janssen, P. Did the Draupner wave occur in a crossing sea? Proc. R. Soc. A 2011, 467, 3004–3021. [Google Scholar] [CrossRef]
- McAllister, M.L.; Draycott, S.; Adcock, T.A.A.; Taylor, P.H.; van den Bremer, T.S. Laboratory recreation of the Draupner wave and the role of breaking in crossing seas. J. Fluid Mech. 2019, 860, 767–786. [Google Scholar] [CrossRef]
- Fedele, F.; Brennan, J.; De León, S.P.; Dudley, J.; Dias, F. Real world ocean rogue waves explained without the modulational instability. Sci. Rep. 2016, 6, 27715. [Google Scholar] [CrossRef] [PubMed]
- Brennan, J.; Dudley, J.M.; Dias, F. Extreme waves in crossing sea states. Int. J. Ocean Coast. Eng. 2018, 1, 1850001. [Google Scholar] [CrossRef]
- Støle-Hentschel, S.; Trulsen, K.; Rye, L.B.; Raustøl, A. Extreme wave statistics of counter-propagating, irregular, long-crested sea states. Phys. Fluids 2018, 30, 067102. [Google Scholar] [CrossRef]
- Gramstad, O.; Bitner-Gregersen, E.; Trulsen, K.; Nieto Borge, J.C. Modulational instability and rogue waves in crossing sea states. J. Phys. Oceanogr. 2018, 48, 1317–1331. [Google Scholar] [CrossRef]
- Noble, D.R. Combined wave-current scale model testing at FloWave. Ph.D. Thesis, The University of Edinburgh, Edinburgh, UK, August 2017. [Google Scholar]
- Dysthe, K.B.; Trulsen, K.; Krogstad, H.E.; Socquet-Juglard, H. Evolution of a narrow-band spectrum of random surface gravity waves. J. Fluid Mech. 2003, 478, 1–10. [Google Scholar] [CrossRef]
- Weideman, J.; Herbst, B. Split-step methods for the solution of the nonlinear Schrödinger equation. SIAM J. Numer. Anal. 1986, 23, 485–507. [Google Scholar] [CrossRef]
- Taha, T.R.; Ablowitz, M.I. Analytical and numerical aspects of certain nonlinear evolution equations. II. Numerical, nonlinear Schrödinger equation. J. Comput. Phys. 1984, 55, 203–230. [Google Scholar] [CrossRef]



| Part I | Part II | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Expt. | 1a | 1b | 1c | 1d | 2a | 2b | 2c | 2d | 2e | 2f | 2g | 2h | 2i | 2j | 2k | 2l |
| 0 | 30 | 60 | 90 | 0 | 5 | 10 | 20 | 25 | 32 | 41 | 47 | 60 | 68 | 83 | 88 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steer, J.N.; McAllister, M.L.; Borthwick, A.G.L.; van den Bremer, T.S. Experimental Observation of Modulational Instability in Crossing Surface Gravity Wavetrains. Fluids 2019, 4, 105. https://doi.org/10.3390/fluids4020105
Steer JN, McAllister ML, Borthwick AGL, van den Bremer TS. Experimental Observation of Modulational Instability in Crossing Surface Gravity Wavetrains. Fluids. 2019; 4(2):105. https://doi.org/10.3390/fluids4020105
Chicago/Turabian StyleSteer, James N., Mark L. McAllister, Alistair G. L. Borthwick, and Ton S. van den Bremer. 2019. "Experimental Observation of Modulational Instability in Crossing Surface Gravity Wavetrains" Fluids 4, no. 2: 105. https://doi.org/10.3390/fluids4020105
APA StyleSteer, J. N., McAllister, M. L., Borthwick, A. G. L., & van den Bremer, T. S. (2019). Experimental Observation of Modulational Instability in Crossing Surface Gravity Wavetrains. Fluids, 4(2), 105. https://doi.org/10.3390/fluids4020105






