An Accurate Finite Element Method for the Numerical Solution of Isothermal and Incompressible Flow of Viscous Fluid
Abstract
1. Introduction
1.1. Computational Fluid Dynamics (CFD)
1.2. Scope of This Work
2. Variational Formulation
3. Generating the Weak Form
4. Algorithm and Computation
5. Comparative Analysis
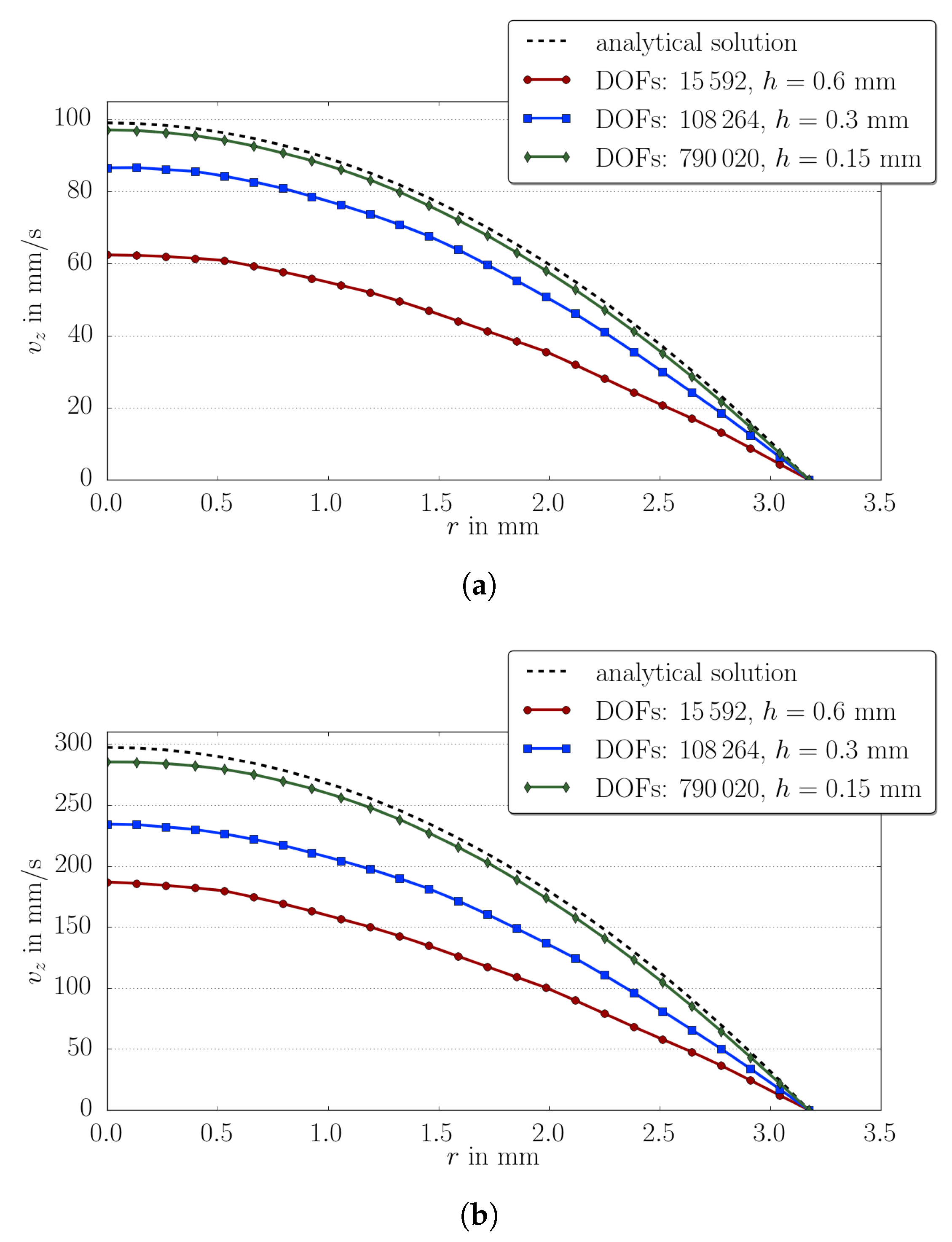
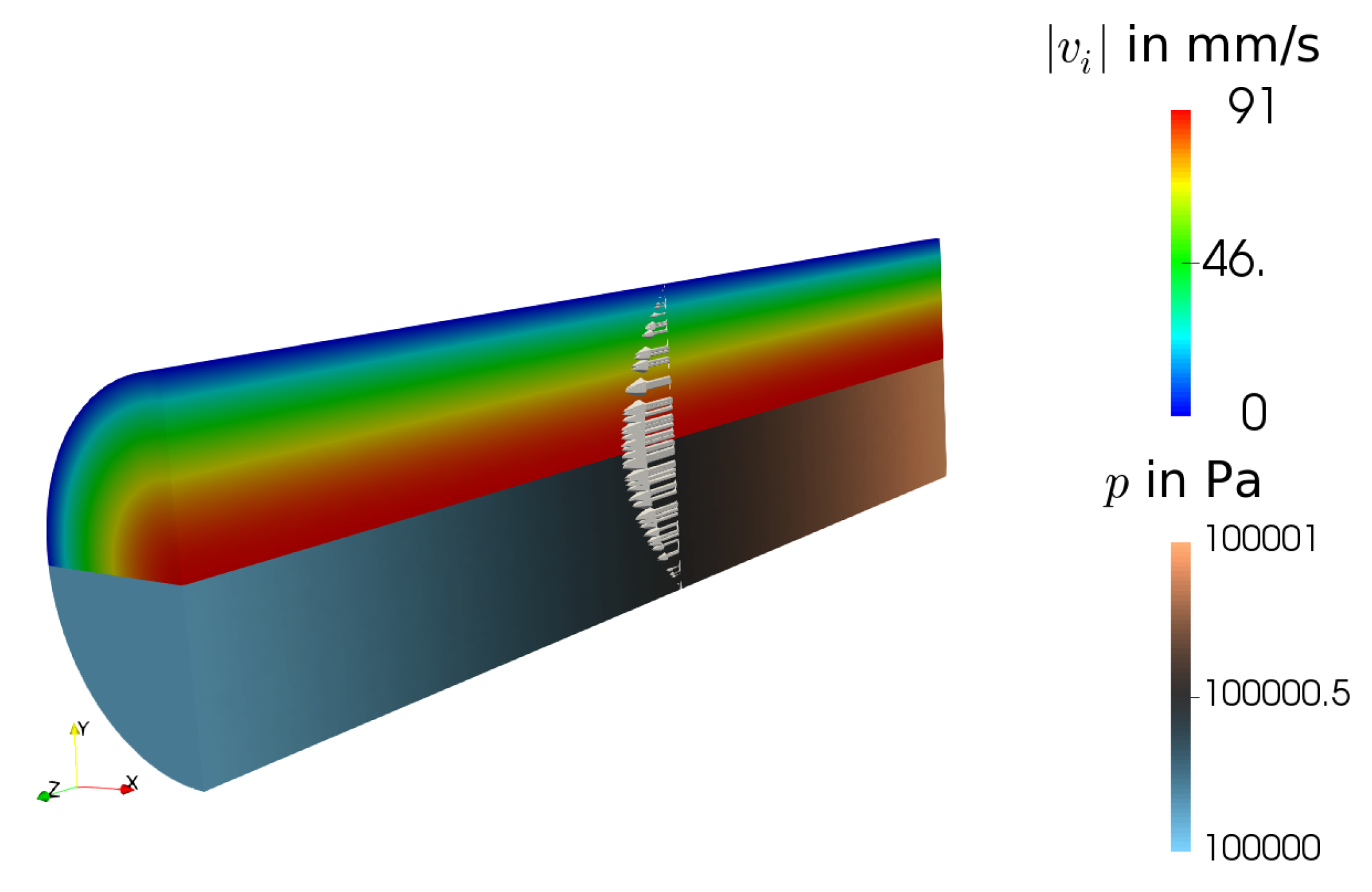
5.1. Steady State Hagen–Poiseuille Flow
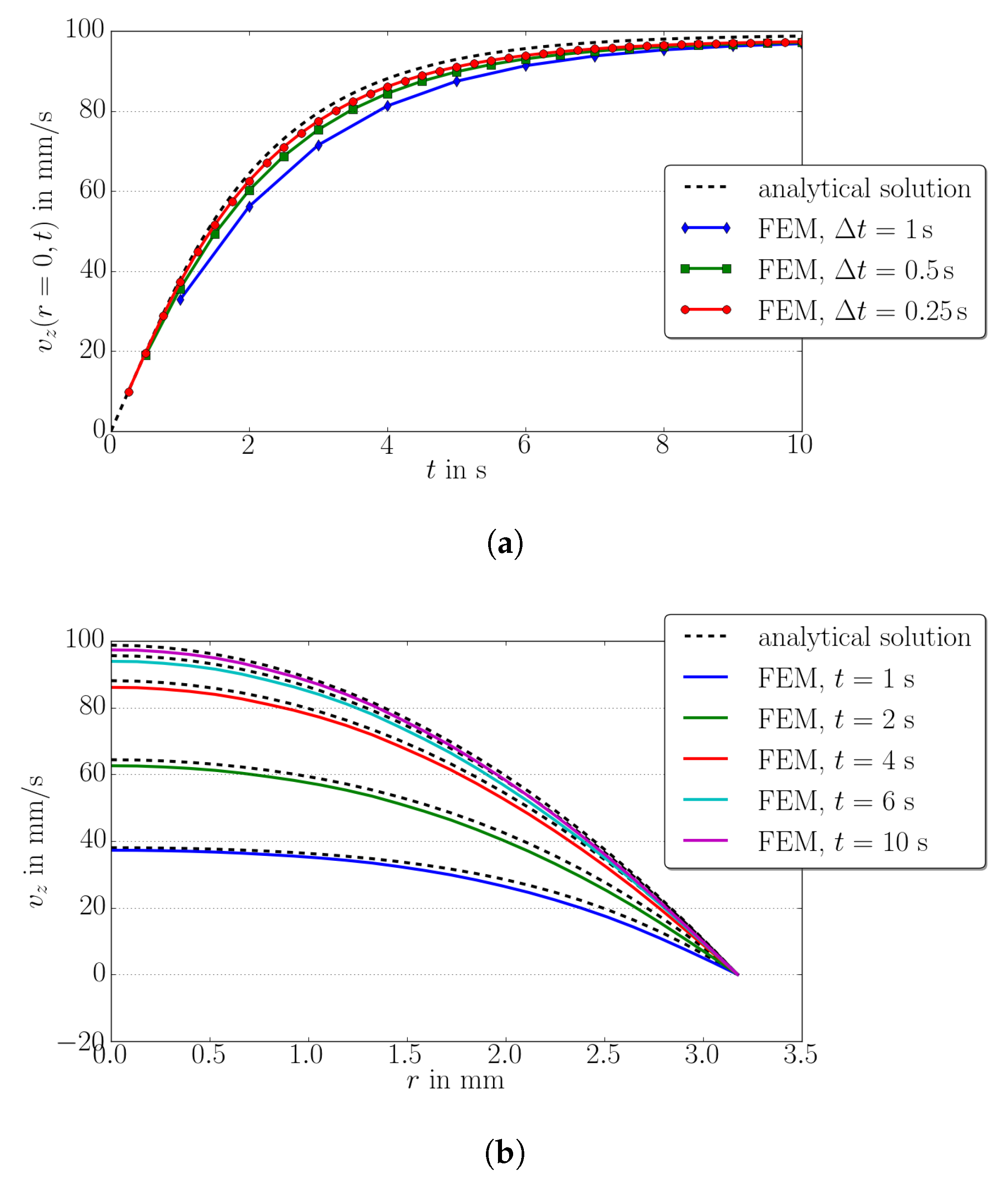
5.2. Starting Hagen–Poiseuille Flow
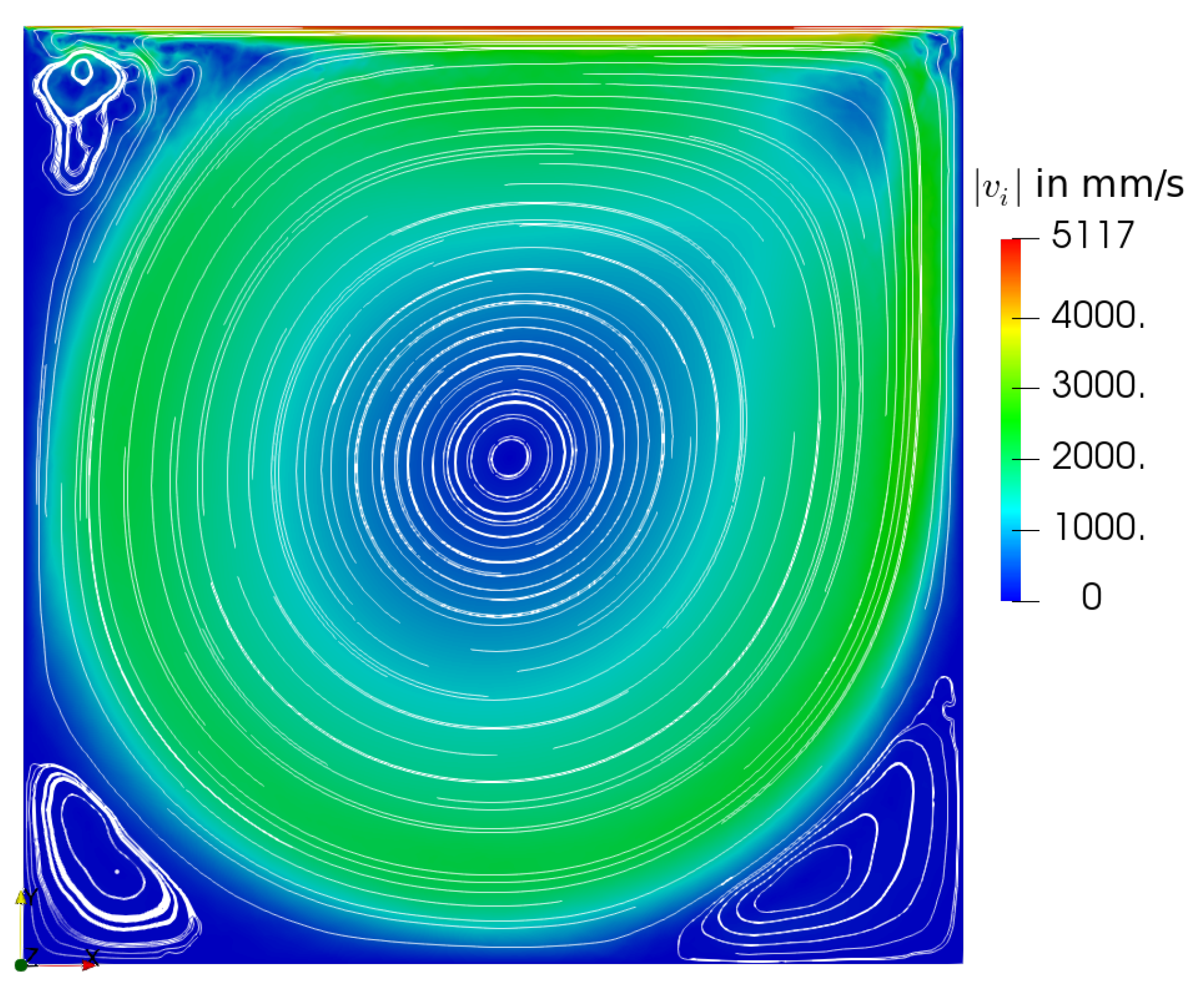
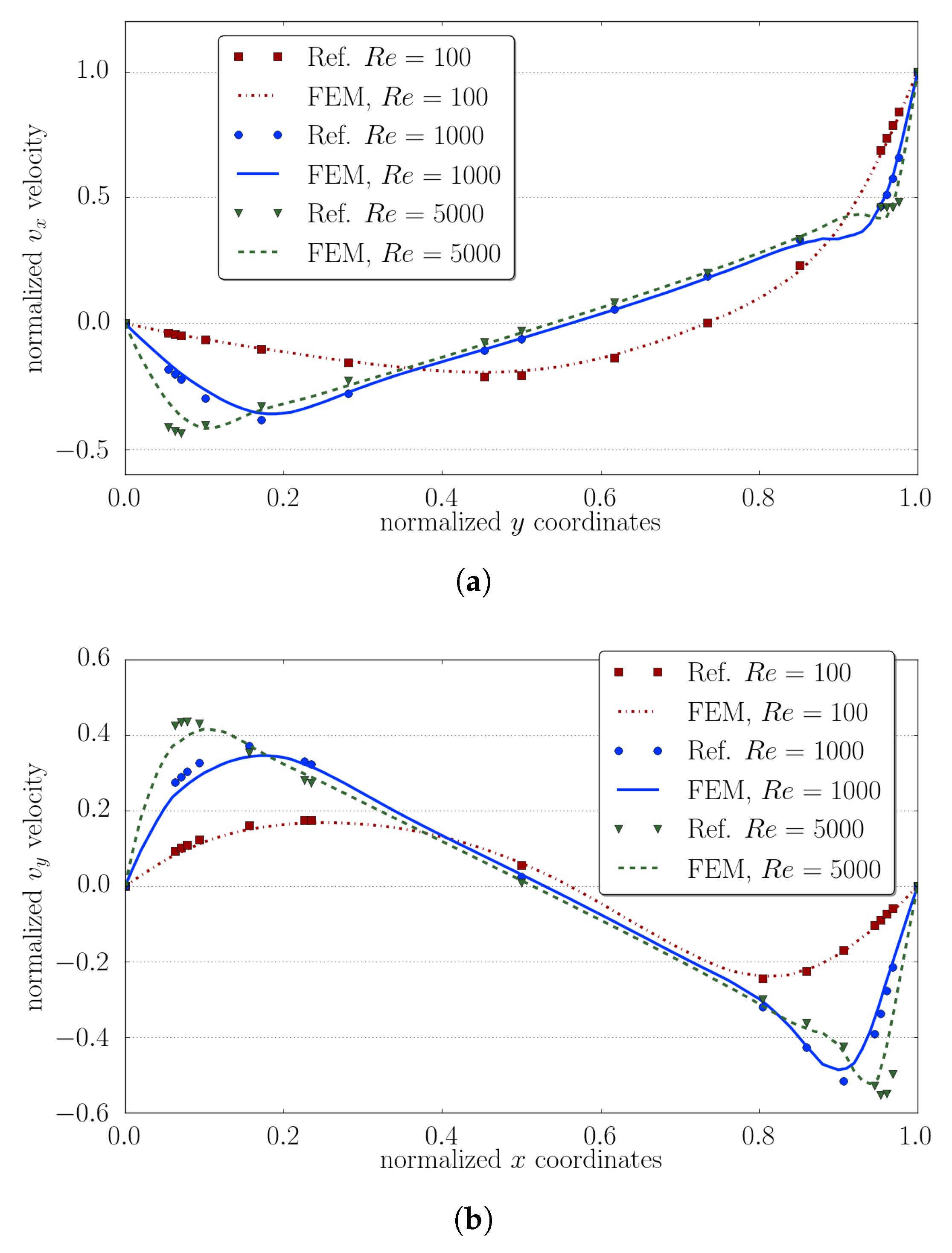
5.3. Lid Driven Cavity
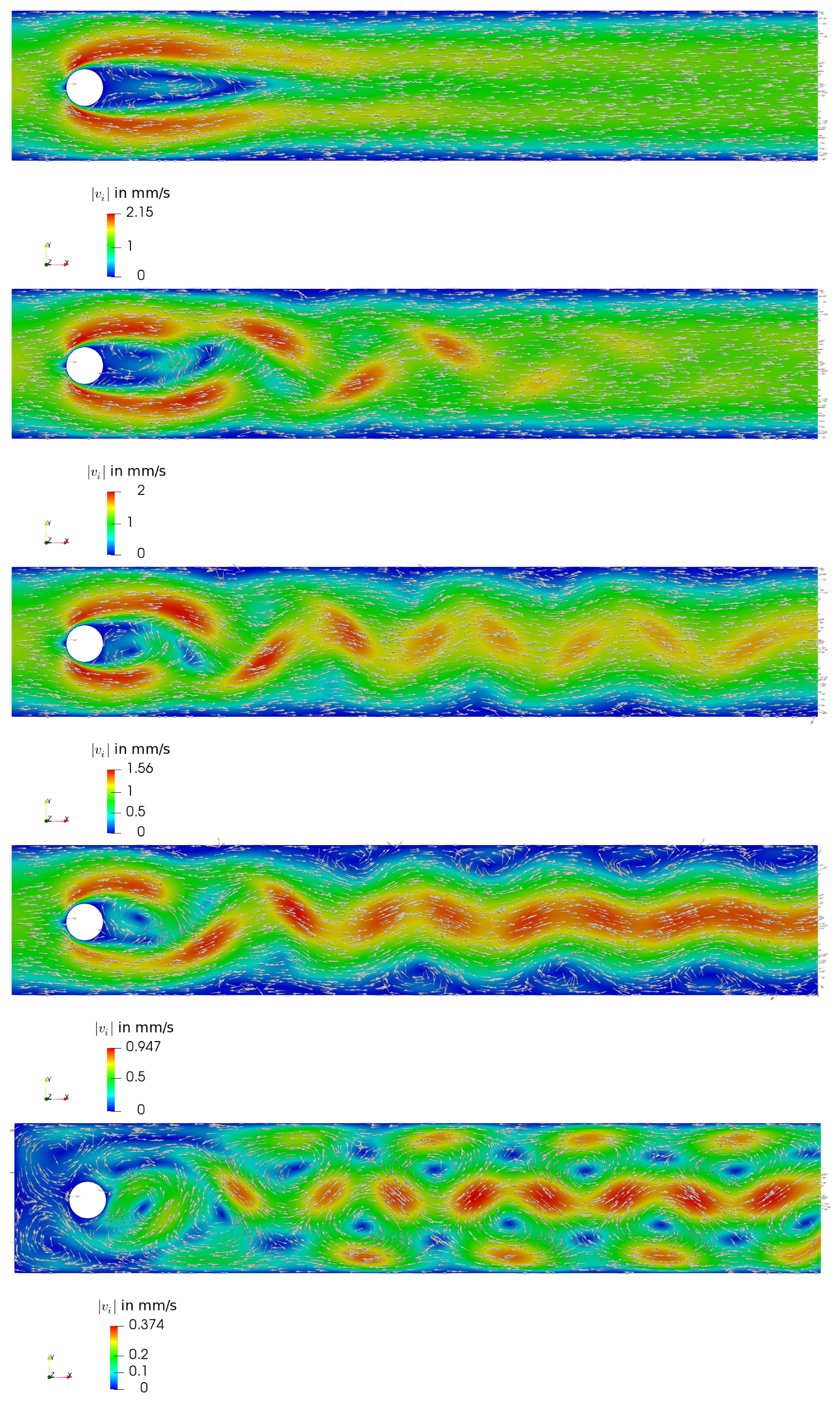
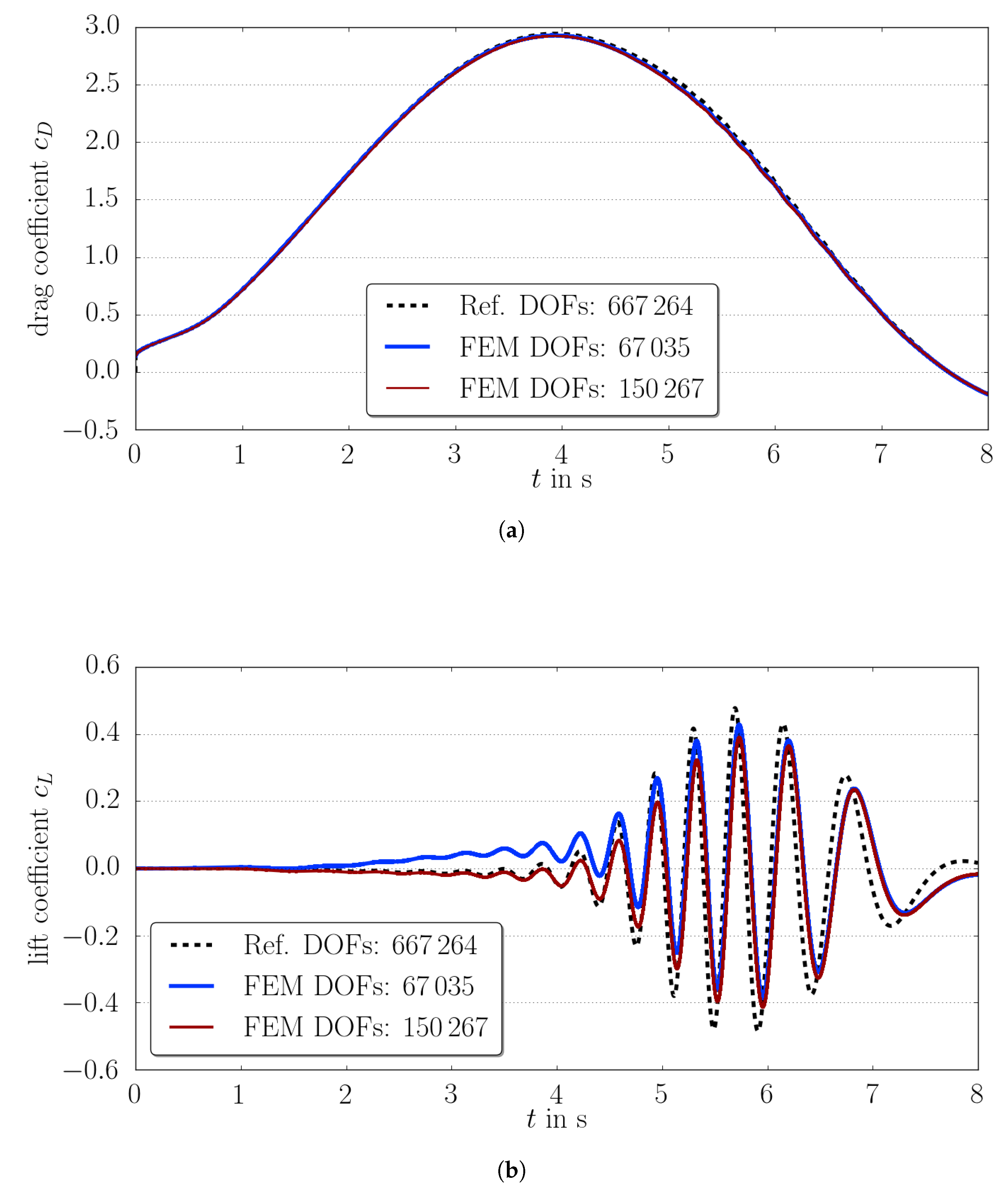
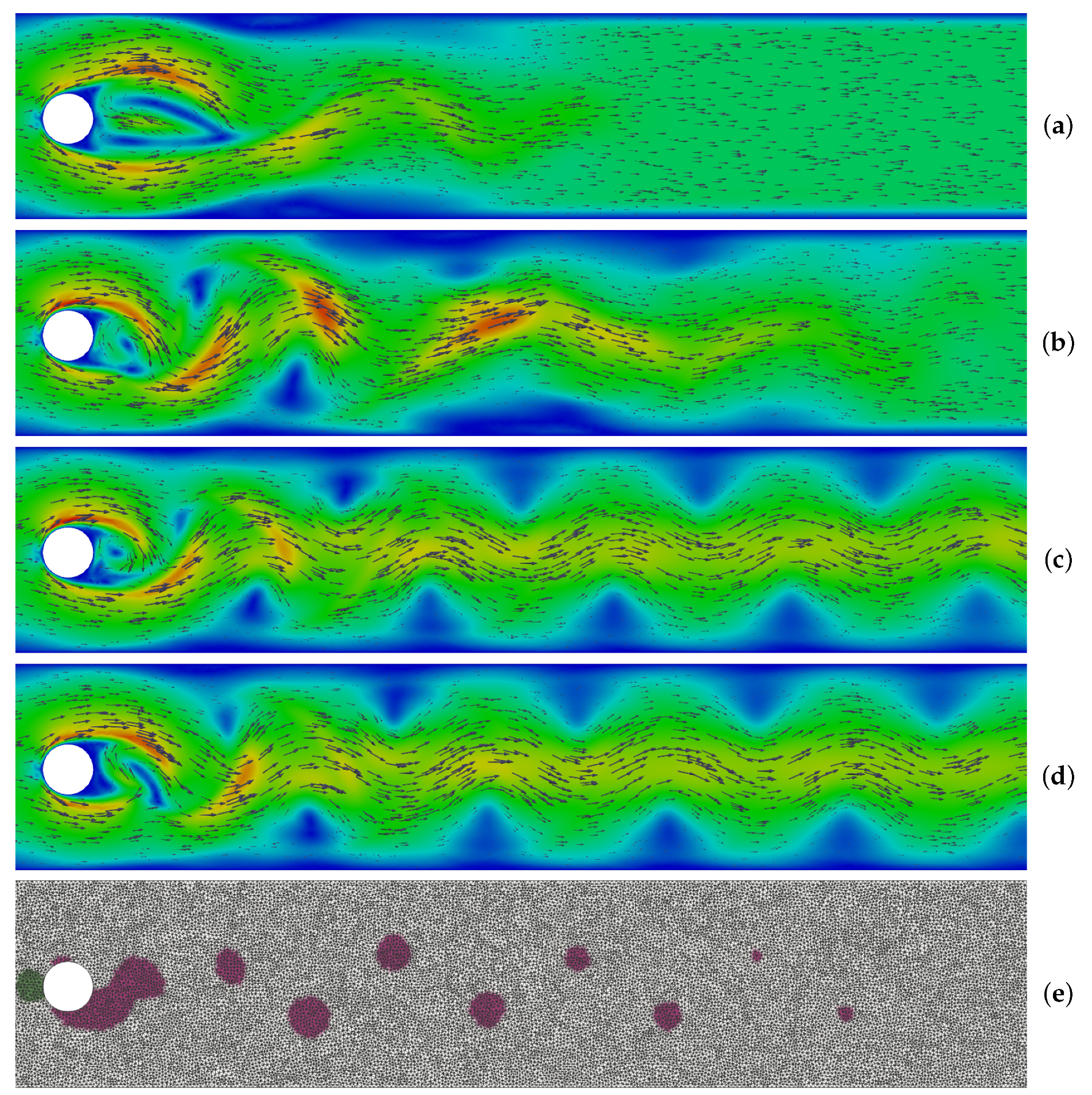
5.4. Karman Vortex Street
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Darrigol, O. Between hydrodynamics and elasticity theory: The first five births of the Navier-Stokes equation. Arch. Hist. Exact Sci. 2002, 56, 95–150. [Google Scholar]
- Babuska, I.; Rheinboldt, W. Error estimates for adaptive finite element computations. SIAM J. Numer. Anal. 1978, 15, 736–754. [Google Scholar]
- Taylor, C.; Hood, P. A numerical solution of the Navier-Stokes equations using the finite element technique. Comput. Fluids 1973, 1, 73–100. [Google Scholar]
- Arnold, D.N.; Brezzi, F.; Fortin, M. A stable finite element for the Stokes equations. Calcolo 1984, 21, 337–344. [Google Scholar]
- Abali, B.E.; Reich, F.A. Thermodynamically consistent derivation and computation of electro-thermo-mechanical systems for solid bodies. Comput. Methods Appl. Mech. Eng. 2017, 319, 567–595. [Google Scholar]
- Book, D.L.; Boris, J.P.; Hain, K. Flux-corrected transport II: Generalizations of the method. J. Comput. Phys. 1975, 18, 248–283. [Google Scholar]
- Hughes, T.J.R.; Brooks, A. A theoretical framework for Petrov-Galerkin methods with discontinuous weighting functions: Application to the streamline-upwind procedure. Finite Elem. Fluids 1982, 4, 47–65. [Google Scholar]
- Hughes, T.J.R.; Franca, L.P.; Balestra, M. A new finite element formulation for computational fluid dynamics: circumventing the Babuska-Brezzi condition: A stable Petrov- Galerkin formulation of the Stokes problem accommodating equal-order Interpolation. Comput. Methods Appl. Mech. Eng. 1986, 59, 85–99. [Google Scholar]
- Tezduyar, T.E.; Mittal, S.; Ray, S.; Shih, R. Incompressible flow computations with stabilized bilinear and linear equal order interpolation velocity pressure elements. Comput. Methods Appl. Mech. Eng. 1992, 95, 221–242. [Google Scholar]
- Silvester, D.J.; Kechkar, N. Stabilised bilinear-constant velocity-pressure finite elements for the conjugate gradient solution of the Stokes problem. Comput. Methods Appl. Mech. Eng. 1990, 79, 71–86. [Google Scholar]
- Franca, L.P.; Farhat, C. Bubble functions prompt unusual stabilized finite element methods. Comput. Methods Appl. Mech. Eng. 1995, 123, 299–308. [Google Scholar]
- Blank, H.; Rudgyard, M.; Wathen, A. Stabilised finite element methods for steady incompressible flow. Comput. Methods Appl. Mech. Eng. 1999, 174, 91–105. [Google Scholar]
- Brezzi, F.; Fortin, M. A minimal stabilisation procedure for mixed finite element methods. Numerische Mathematik 2001, 89, 457–491. [Google Scholar]
- Gravemeier, V. The variational multiscale method for laminar and turbulent flow. Arch. Comput. Methods Eng. 2006, 13, 249. [Google Scholar]
- Morton, K.W. Finite element methods for non-self-adjoint problems. In Topics in Numerical Analysis; Turner, P., Ed.; Springer: Berlin/Heidelberg, Germany, 1982; Volume 965, pp. 113–148. [Google Scholar]
- Kuzmin, D.; Turek, S. Flux correction tools for finite elements. J. Comput. Phys. 2002, 175, 525–558. [Google Scholar]
- Rannacher, R. Chapter 6. Incompressible viscous flows. In Encyclopedia of Computational Mechanics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2004; Volume 3, pp. 155–181. [Google Scholar]
- Hughes, T.J.R.; Scovazzi, G.; Franca, L.P. Chapter 2. Multiscale and stabilized methods. In Encyclopedia of Computational Mechanics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2004; Volume 3, pp. 5–59. [Google Scholar]
- Donea, J.; Huerta, A. Finite Element Methods for Flow Problems; John Wiley & Sons, Ltd.: Chichester, UK, 2005. [Google Scholar]
- Hoffman, J.; Johnson, C. Computational Turbulent Incompressible Flow, Applied Mathematics: Body and Soul 4; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Löhner, R. Applied Computational Fluid Dynamics Techniques: An Introduction Based on Finite Element Methods; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Förster, C.; Wall, W.; Ramm, E. Stabilized finite element formulation for incompressible flow on distorted meshes. Int. J. Numer. Methods Fluids 2009, 60, 1103–1126. [Google Scholar]
- Arzani, A.; Shadden, S.C. Characterizations and correlations of wall shear stress in aneurysmal flow. J. Biomech. Eng. 2016, 138, 014503. [Google Scholar]
- Barth, T.; Bochev, P.; Gunzburger, M.; Shadid, J. A taxonomy of consistently stabilized finite element methods for the Stokes problem. SIAM J. Sci. Comput. 2004, 25, 1585–1607. [Google Scholar]
- Bowers, A.L.; Cousins, B.R.; Linke, A.; Rebholz, L.G. New connections between finite element formulations of the Navier–Stokes equations. J. Comput. Phys. 2010, 229, 9020–9025. [Google Scholar]
- Eggels, J.; Unger, F.; Weiss, M.; Westerweel, J.; Adrian, R.; Friedrich, R.; Nieuwstadt, F. Fully developed turbulent pipe flow: A comparison between direct numerical simulation and experiment. J. Fluid Mech. 1994, 268, 175–210. [Google Scholar]
- Hirsch, C. Numerical Computation of Internal and External Flows: The Fundamentals of Computational Fluid Dynamics; Elsevier: New York, NY, USA, 2007. [Google Scholar]
- Varghese, S.S.; Frankel, S.H.; Fischer, P.F. Direct numerical simulation of stenotic flows. Part 1. Steady flow. J. Fluid Mech. 2007, 582, 253–280. [Google Scholar]
- Lee, M.; Moser, R.D. Direct numerical simulation of turbulent channel flow up to Re = 5200. J. Fluid Mech. 2015, 774, 395–415. [Google Scholar]
- Tryggvason, G. 2.2 Direct Numerical Simulations of Gas–Liquid Flows. In Multiphase Flow Handbook; CRC Press: Boca Raton, FL, USA, 2016; p. 95. [Google Scholar]
- Hoffman, J.; Jansson, J.; Jansson, N. FEniCS-HPC: Automated predictive high-performance finite element computing with applications in aerodynamics. In Proceedings of the International Conference on Parallel Processing and Applied Mathematics, Krakow, Poland, 6–9 September 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 356–365. [Google Scholar]
- Nguyen, V.D. High-Performance Finite Element Methods: With Application to Simulation of Diffusion MRI and Vertical Axis Wind Turbine. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2018. [Google Scholar]
- Chorin, A.J. On the convergence of discrete approximations to the Navier-Stokes equations. Math. Comput. 1969, 23, 341–353. [Google Scholar]
- Temam, R. Sur l’approximation de la solution des équations de Navier-Stokes par la méthode des pas fractionnaires (I). Arch. Ration. Mech. Anal. 1969, 32, 135–153. [Google Scholar]
- Temam, R. Sur l’approximation de la solution des équations de Navier-Stokes par la méthode des pas fractionnaires (II). Arch. Ration. Mech. Anal. 1969, 33, 377–385. [Google Scholar]
- Goda, K. A multistep technique with implicit difference schemes for calculating two-or three-dimensional cavity flows. J. Comput. Phys. 1979, 30, 76–95. [Google Scholar]
- Bell, J.B.; Colella, P.; Glaz, H.M. A second-order projection method for the incompressible Navier-Stokes equations. J. Comput. Phys. 1989, 85, 257–283. [Google Scholar]
- Zienkiewicz, O.C.; Codina, R. A general algorithm for compressible and incompressible flow—Part I. The split, characteristic-based scheme. Int. J. Numer. Methods Fluids 1995, 20, 869–885. [Google Scholar]
- Brown, D.L.; Cortez, R.; Minion, M.L. Accurate projection methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 2001, 168, 464–499. [Google Scholar]
- Anderson, J.D.; Wendt, J. Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1995; Volume 206. [Google Scholar]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. PhD Thesis, University of London and Imperial College, London, UK, 1996. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: London, UK, 2007. [Google Scholar]
- Wang, Z.J.; Fidkowski, K.; Abgrall, R.; Bassi, F.; Caraeni, D.; Cary, A.; Deconinck, H.; Hartmann, R.; Hillewaert, K.; Huynh, H.T.; et al. High-order CFD methods: Current status and perspective. Int. J. Numer. Methods Fluids 2013, 72, 811–845. [Google Scholar]
- Dohrmann, C.R.; Bochev, P.B. A stabilized finite element method for the Stokes problem based on polynomial pressure projections. Int. J. Numer. Methods Fluids 2004, 46, 183–201. [Google Scholar]
- He, Y.; Li, J. A stabilized finite element method based on local polynomial pressure projection for the stationary Navier–Stokes equations. Appl. Numer. Math. 2008, 58, 1503–1514. [Google Scholar]
- Li, J.; He, Y. A stabilized finite element method based on two local Gauss integrations for the Stokes equations. J. Comput. Appl. Math. 2008, 214, 58–65. [Google Scholar]
- Burman, E. Pressure projection stabilizations for Galerkin approximations of Stokes’ and Darcy’s problem. Numer. Methods Partial Differ. Equ. 2008, 24, 127–143. [Google Scholar]
- Olshanskii, M.A.; Rebholz, L.G. Velocity–vorticity–helicity formulation and a solver for the Navier–Stokes equations. J. Comput. Phys. 2010, 229, 4291–4303. [Google Scholar]
- Abali, B.E.; Müller, W.H.; Georgievskii, D.V. A discrete-mechanical approach for computation of three-dimensional flows. ZAMM J. Appl. Math. Mech. 2013, 93, 868–881. [Google Scholar] [CrossRef]
- Palha, A.; Gerritsma, M. A mass, energy, enstrophy and vorticity conserving (MEEVC) mimetic spectral element discretization for the 2D incompressible Navier–Stokes equations. J. Comput. Phys. 2017, 328, 200–220. [Google Scholar]
- Charnyi, S.; Heister, T.; Olshanskii, M.A.; Rebholz, L.G. On conservation laws of Navier–Stokes Galerkin discretizations. J. Comput. Phys. 2017, 337, 289–308. [Google Scholar]
- Fu, G.; Jin, Y.; Qiu, W. Parameter-free superconvergent H(div)-conforming HDG methods for the Brinkman equations. IMA J. Numer. Anal. 2018. [Google Scholar] [CrossRef]
- Abali, B.E. Technical University of Berlin, Institute of Mechanics, Chair of Continuum Mechanics and Material Theory, Computational Reality. 2017. Available online: http://www.lkm.tu-berlin.de/ComputationalReality/ (accessed on 7 January 2019).
- GNU Public. Gnu General Public License. 2007. Available online: http://www.gnu.org/copyleft/gpl.html (accessed on 7 January 2019).
- Müller, W.H.; Muschik, W. Bilanzgleichungen offener mehrkomponentiger Systeme I. Massen- und Impulsbilanzen. J. Non-Equilib. Thermodyn. 1983, 8, 29–46. [Google Scholar]
- Muschik, W.; Müller, W.H. Bilanzgleichungen offener mehrkomponentiger Systeme II. Energie-und Entropiebilanz. J. Non-Equilib. Thermodyn. 1983, 8, 47–66. [Google Scholar]
- Hilbert, D. The Foundations of Geometry; Townsend, E.J., Translator; The Open Court Publishing Co.: Chicago, IL, USA, 1902. [Google Scholar]
- Logg, A.; Mardal, K.A.; Wells, G. Automated Solution of Differential Equations by the Finite Element Method: The FEniCS Book; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 84. [Google Scholar]
- Alnaes, M.S.; Mardal, K.A. On the Efficiency of Symbolic Computations Combined with Code Generation for Finite Element Methods. ACM Trans. Math. Softw. 2010, 37, 6. [Google Scholar] [CrossRef]
- Alnaes, M.S.; Mardal, K.A. SyFi and SFC: Symbolic Finite Elements and Form Compilation. In Automated Solution of Differential Equations by the Finite Element Method, Volume 84 of Lecture Notes in Computational Science and Engineering; Logg, A., Mardal, K.A., Wells, G.N., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Chapter 15. [Google Scholar]
- Elman, H.; Silvester, D.; Wathen, A. Finite Element and Fast Iterative Solvers. Numerical Mathematics and Scientific Computation; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Abali, B.E. Computational Reality, Solving Nonlinear and Coupled Problems in Continuum Mechanics; Advanced Structured Materials; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Savaş, Ö. Advanced Fluid Mechanics, ME-260 A/B Lecture Notes; University of California at Berkeley: Berkeley, CA, USA, 2017. [Google Scholar]
- Ghia, U.; Ghia, K.N.; Shin, C. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar]
- Erturk, E.; Corke, T.C.; Gökçöl, C. Numerical solutions of 2-D steady incompressible driven cavity flow at high Reynolds numbers. Int. J. Numer. Methods Fluids 2005, 48, 747–774. [Google Scholar]
- Williamson, C.H. Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 1996, 28, 477–539. [Google Scholar]
- Karman, T.V. Über den Mechanismus des Wiederstandes, den ein bewegter Körper in einer Flüssigkeit erfährt. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse 1912, 1912, 547–556. [Google Scholar]
- Langtangen, H.P.; Logg, A. Solving PDEs in Python: The FEniCS Tutorial I; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Schäfer, M.; Turek, S.; Durst, F.; Krause, E.; Rannacher, R. Benchmark computations of laminar flow around a cylinder. In Flow Simulation with High-Performance Computers II; Springer: Berlin/Heidelberg, Germany, 1996; pp. 547–566. [Google Scholar]
- John, V. Reference values for drag and lift of a two-dimensional time-dependent flow around a cylinder. Int. J. Numer. Methods Fluids 2004, 44, 777–788. [Google Scholar]
| z | f | ||
|---|---|---|---|
| 0 | 0 | ||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abali, B.E. An Accurate Finite Element Method for the Numerical Solution of Isothermal and Incompressible Flow of Viscous Fluid. Fluids 2019, 4, 5. https://doi.org/10.3390/fluids4010005
Abali BE. An Accurate Finite Element Method for the Numerical Solution of Isothermal and Incompressible Flow of Viscous Fluid. Fluids. 2019; 4(1):5. https://doi.org/10.3390/fluids4010005
Chicago/Turabian StyleAbali, Bilen Emek. 2019. "An Accurate Finite Element Method for the Numerical Solution of Isothermal and Incompressible Flow of Viscous Fluid" Fluids 4, no. 1: 5. https://doi.org/10.3390/fluids4010005
APA StyleAbali, B. E. (2019). An Accurate Finite Element Method for the Numerical Solution of Isothermal and Incompressible Flow of Viscous Fluid. Fluids, 4(1), 5. https://doi.org/10.3390/fluids4010005





