Flow-Induced Stresses and Displacements in Jointed Concrete Pipes Installed by Pipe Jacking Method
Abstract
:1. Introduction
Literature Review and Motivation
2. Materials and Methods
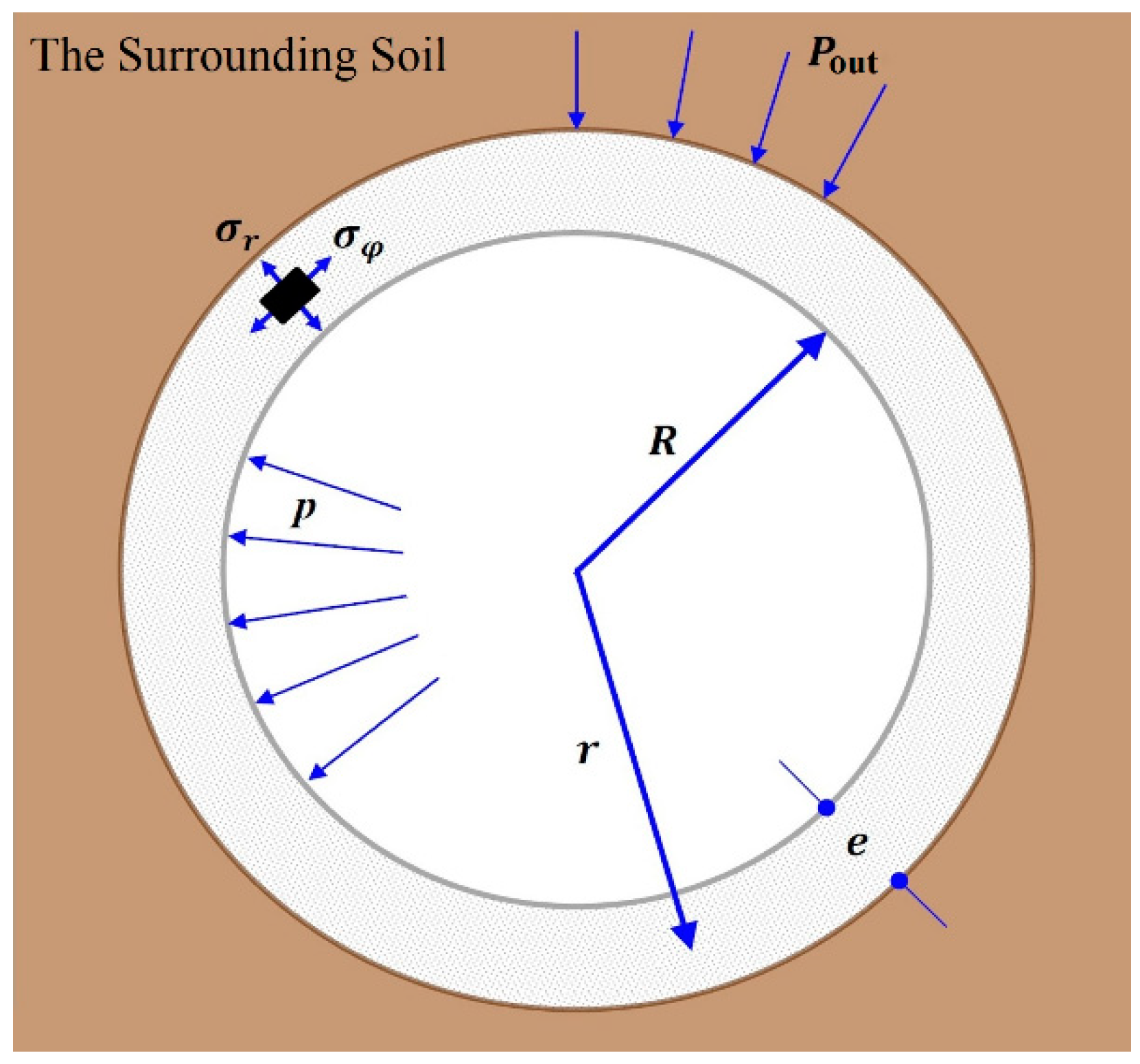
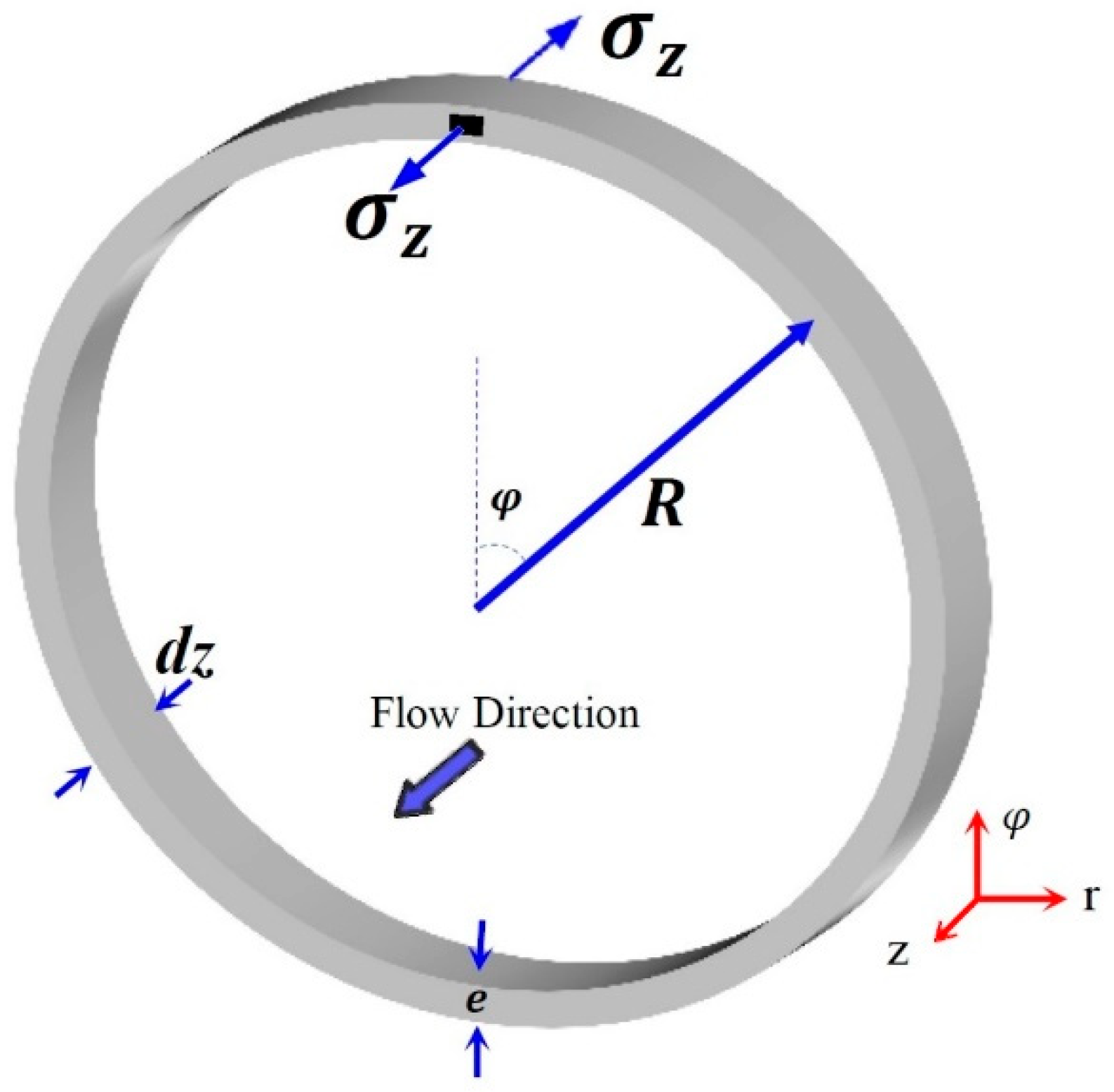
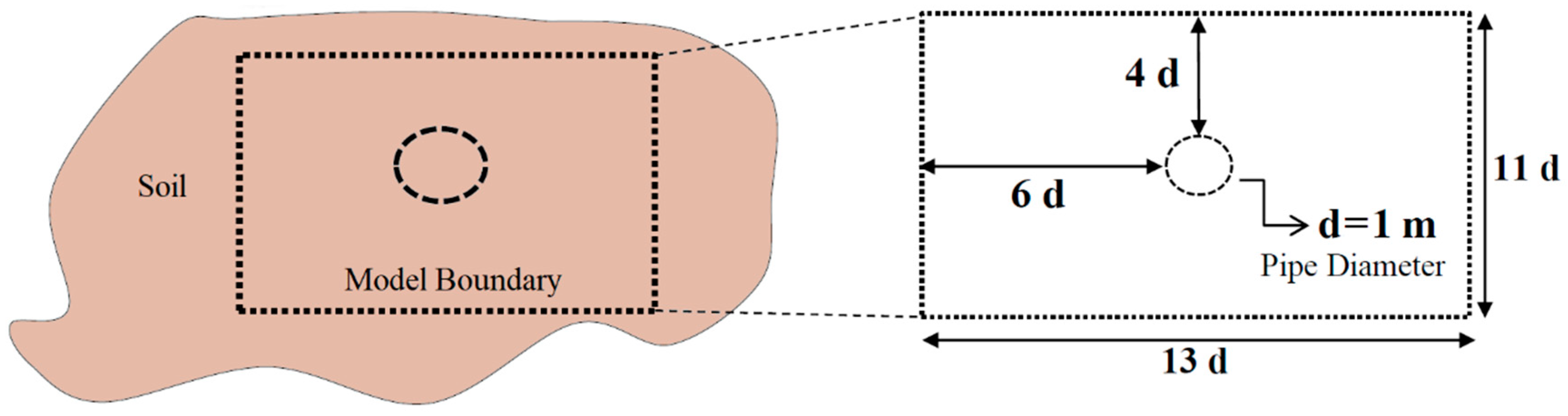
2.1. Model Geometry
2.2. Soil and Material Properties
2.3. Flow Characteristics
2.4. Modeling Procedure
- The surrounding soil is monolith.
- The concrete lining behavior is considered as non-linear.
- A damage plasticity behavior is considered in the concrete lining.
- The CPE8R (eight-node plane strain quadrilateral, biquadratic displacement, reduced integration) elements are used for the simulation of the concrete pipe.
- Based on the Cam-Clay criterion, the soil is considered as a plastic material.
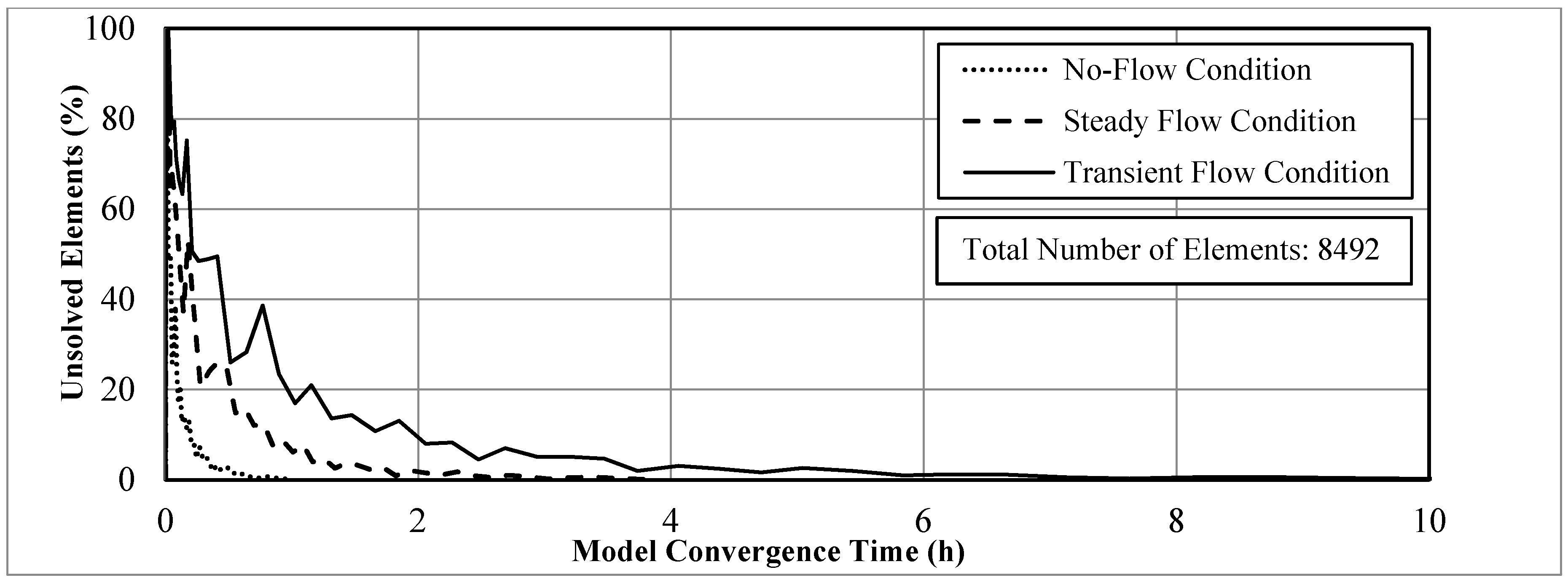
- Dynamic explicit method is applied to solve the finite element equations in the Abaqus FEA.
2.4.1. Acoustic Environment
2.4.2. Interactions between Model Components and Meshing
2.4.3. Transient Flow in the Pipe
3. Results
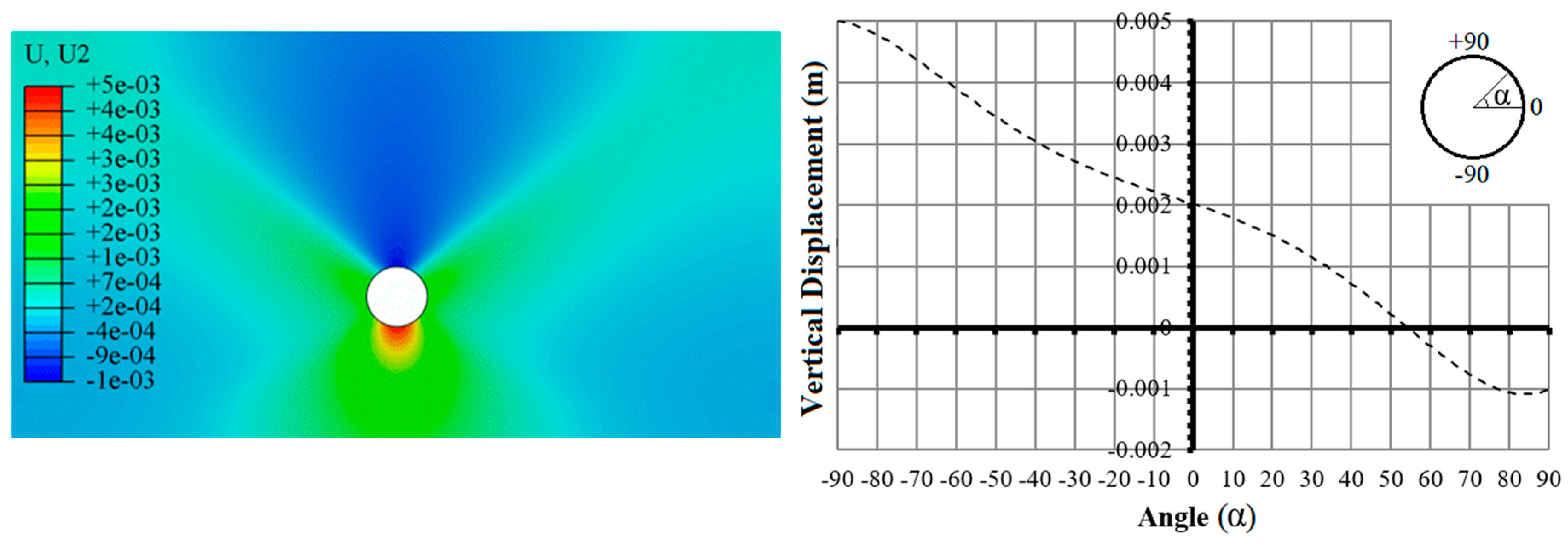
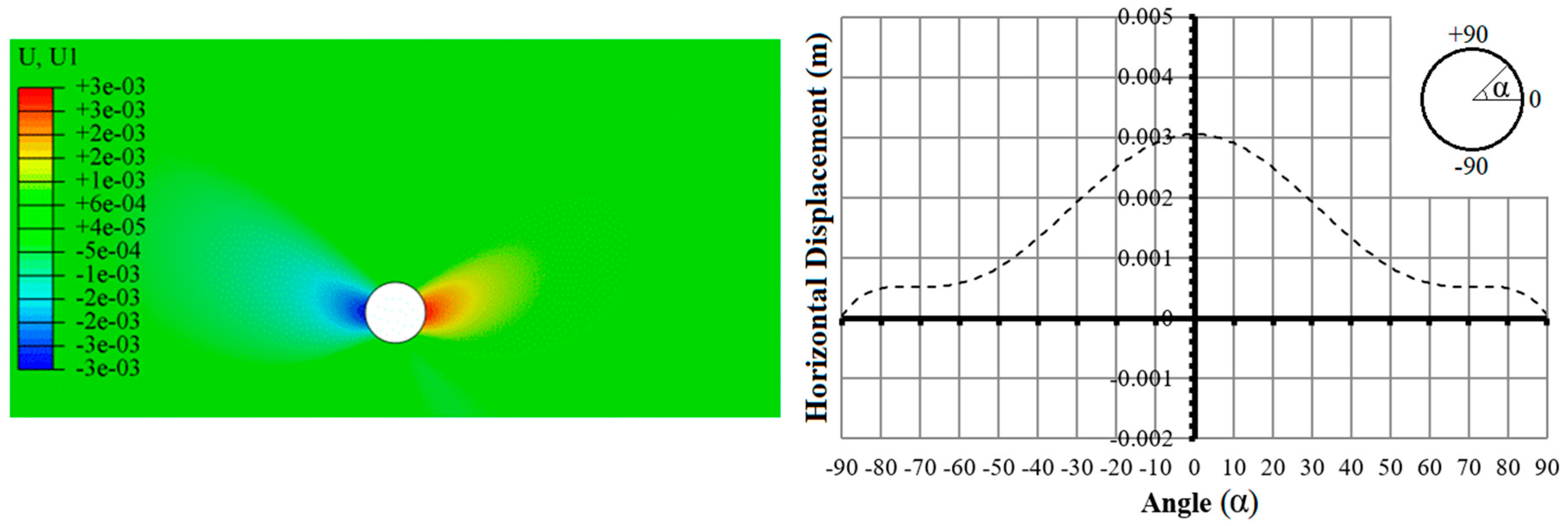
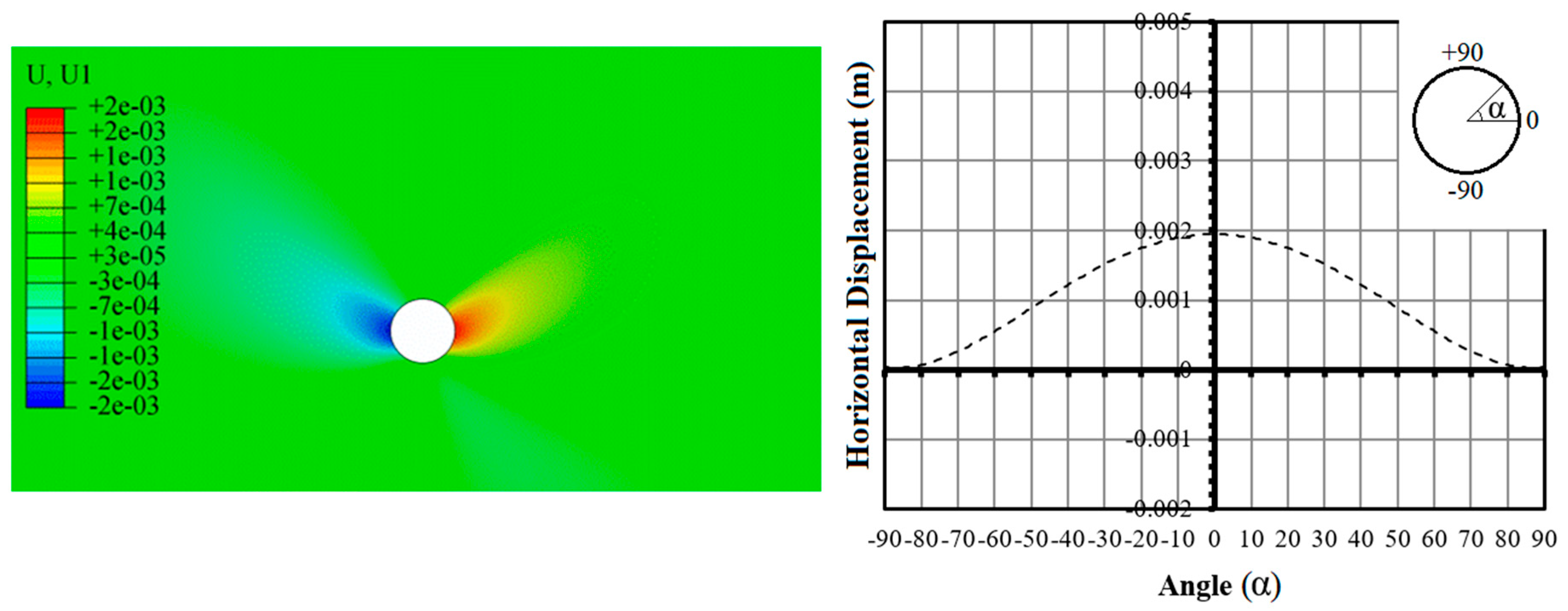
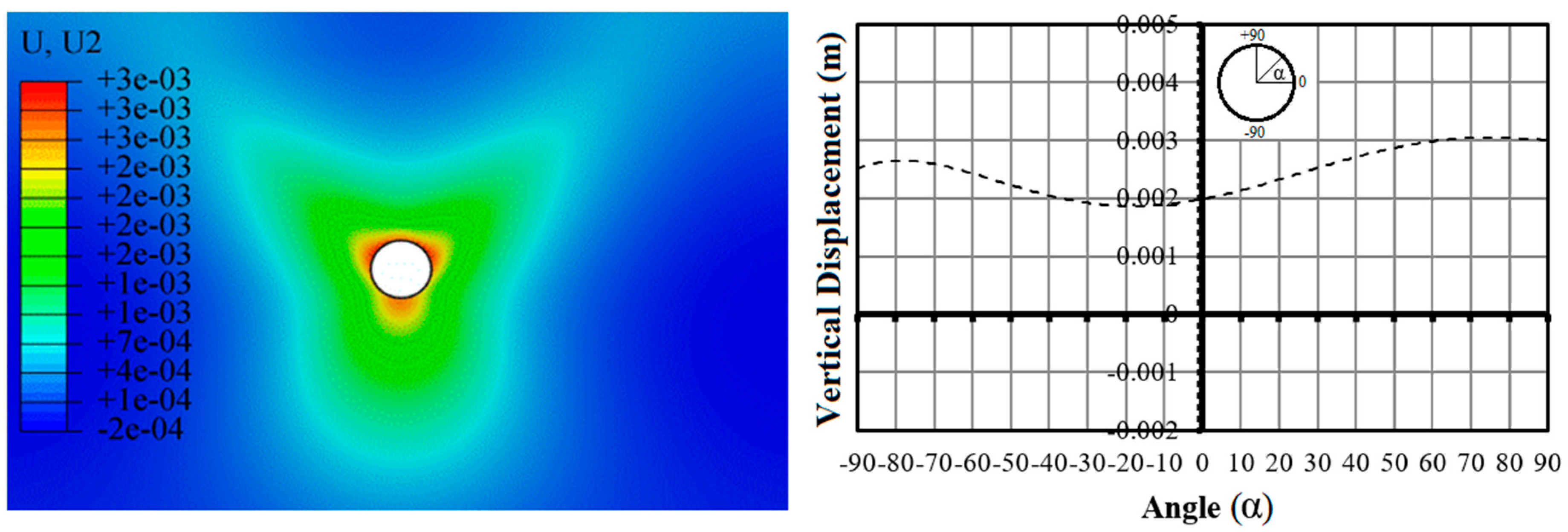
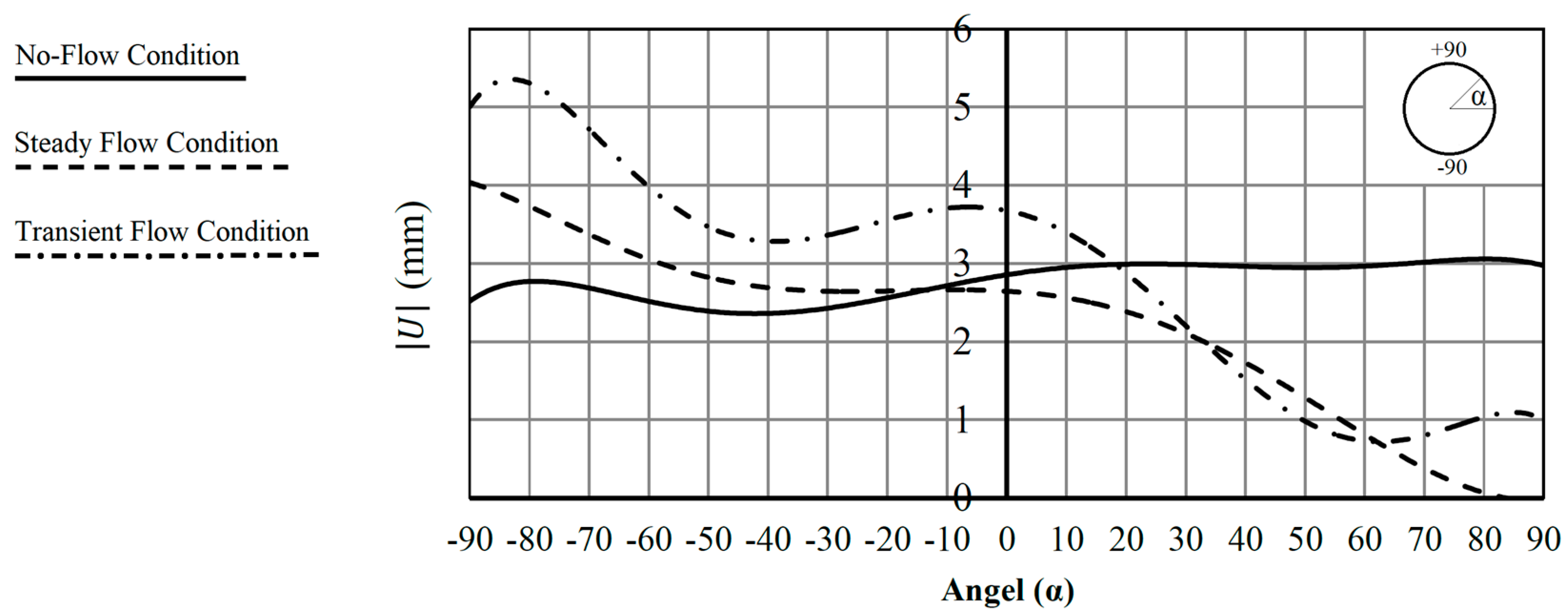
3.1. No-Flow Condition
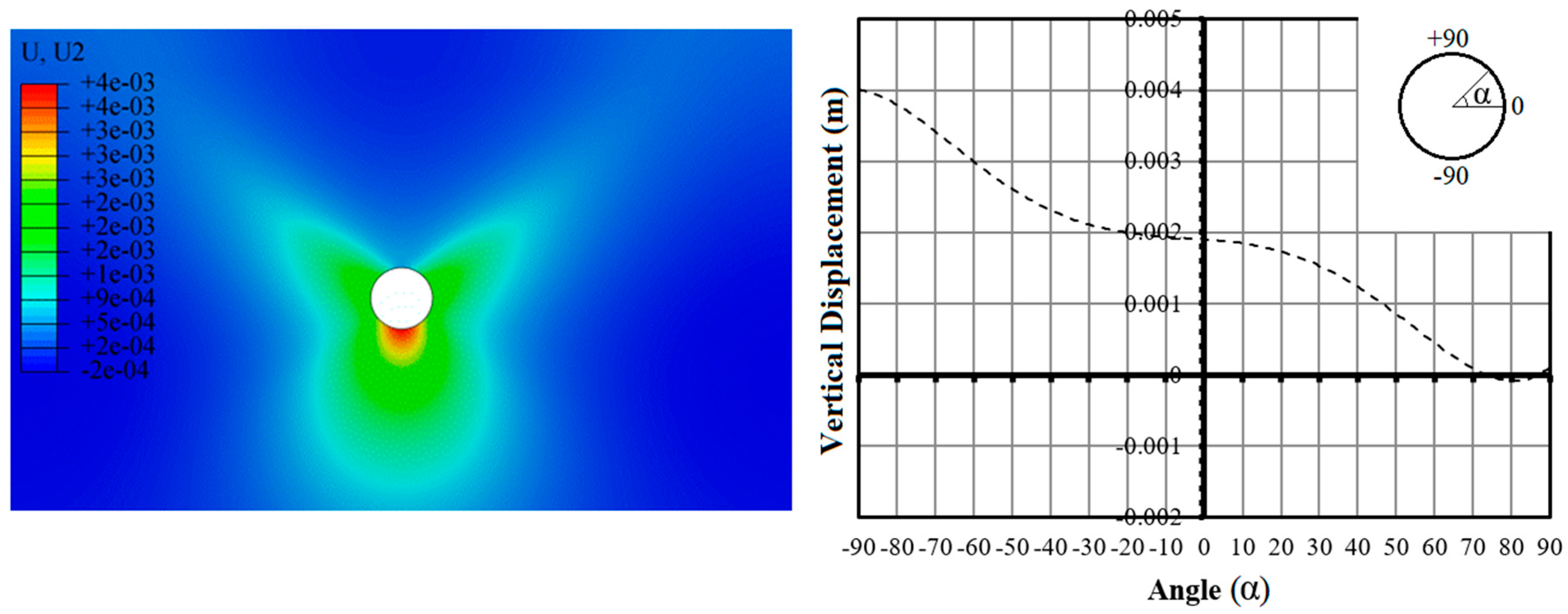
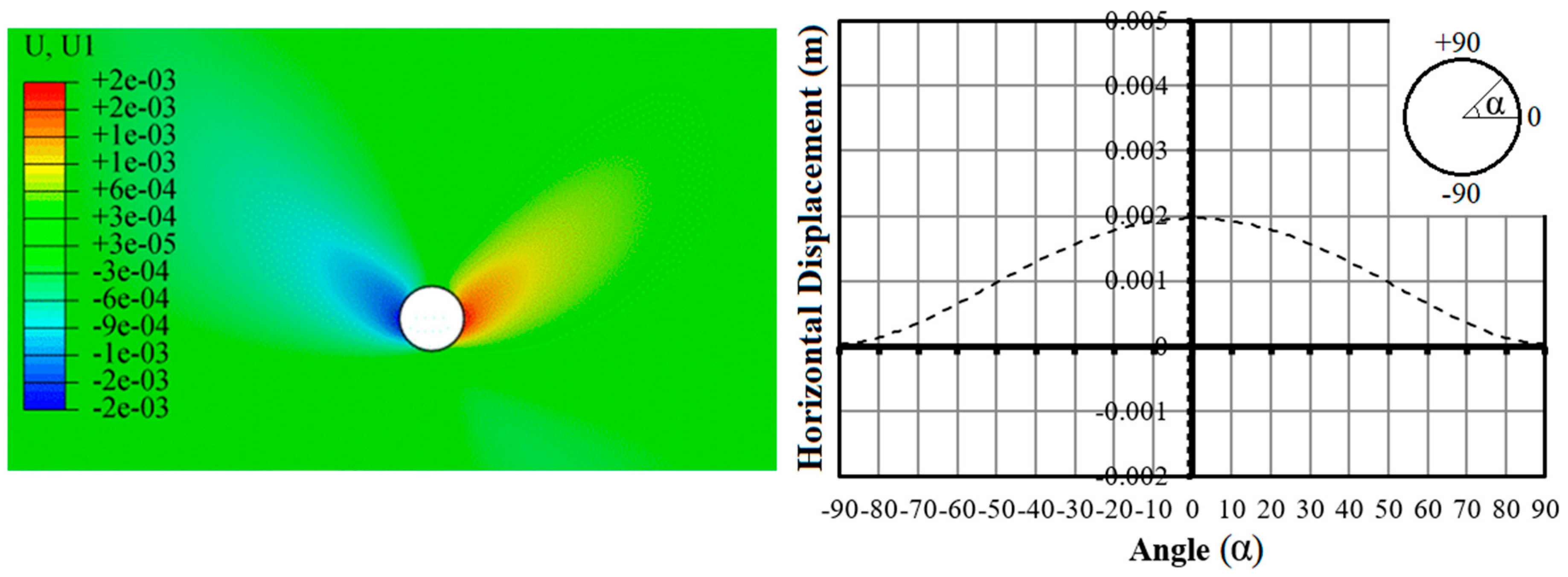
3.2. Steady Flow Condition
3.3. Transient Flow Condition
4. Discussion
5. Conclusions
- Under the no-flow condition, the most significant displacements occurred at the bottom of the section. This can be attributed to the soil inflation phenomenon, as a result of drilling and alteration of stress distribution in the soil environment.
- Under steady flow condition, the soil environment showed small displacements, due to the internal pressure and fluid weight in the pipe.
- By the occurrence of transient pressure due to the event of transient flow in the pipe, the displaced region was enlarged, and the pipe and surrounding soil showed an upward movement.
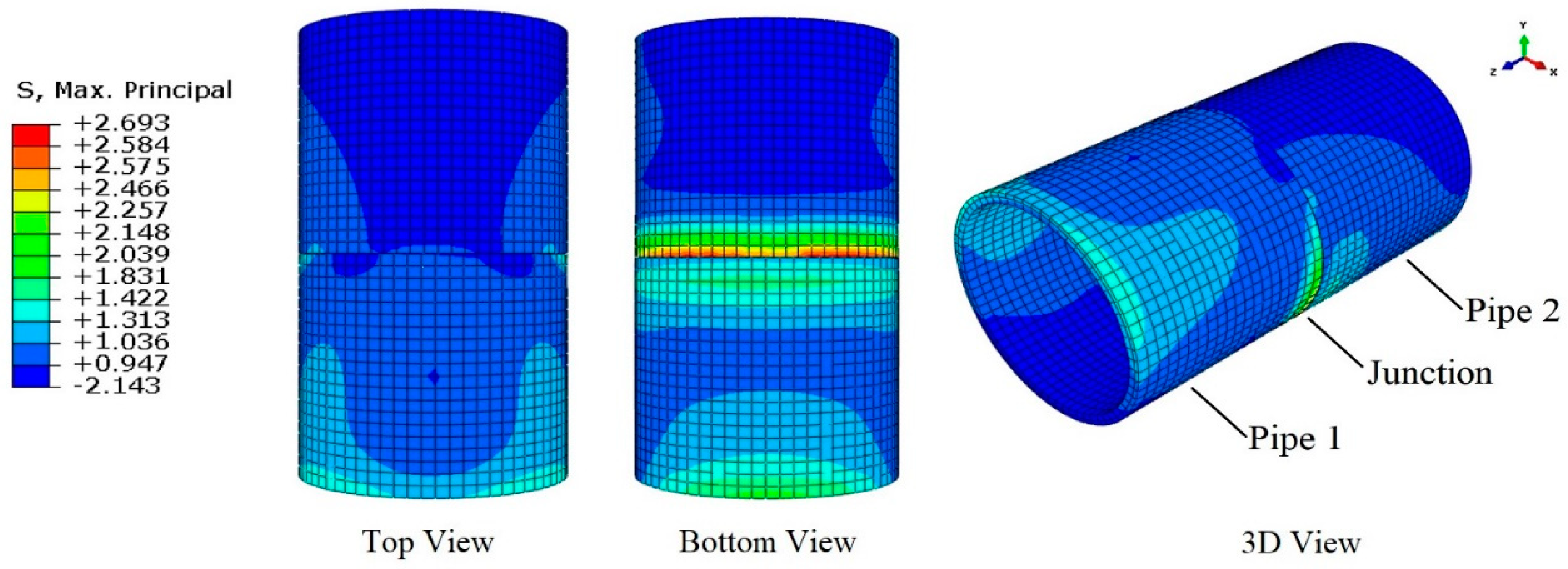
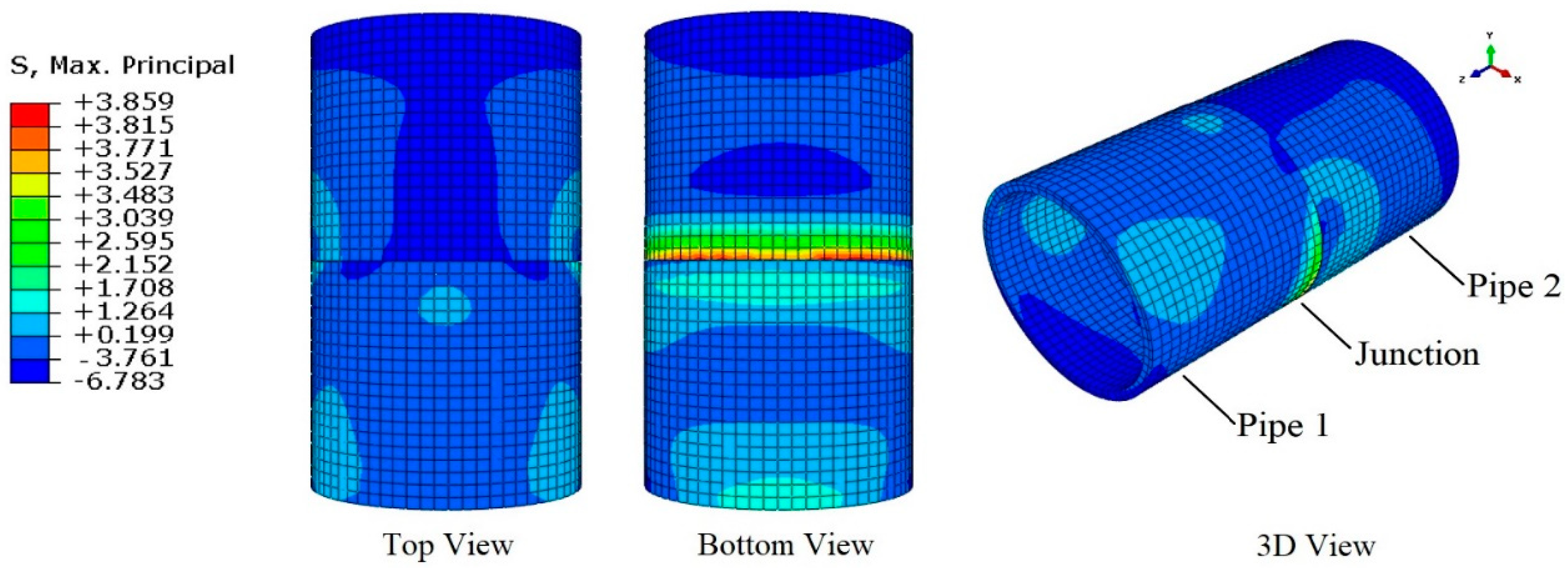
- Under all scenarios, maximum compressive and tensile stresses were formed at the junction. The maximum value was observed under the transient flow condition, where the tensile stress exceeded the allowable tensile capacity of the concrete. This situation will cause cracks in the pipe wall and consequently lead to water leakage and reduced operational capacity of the pipeline.
Author Contributions
Funding
Conflicts of Interest
References
- Rezaei, H.; Ryan, B.; Stoianov, I. Pipe failure analysis and impact of dynamic hydraulic conditions in water supply networks. Procedia Eng. 2015, 119, 253–262. [Google Scholar] [CrossRef]
- Kodikara, J.; Rathnayaka, S.; Zhang, J.; Crawly, C.; Zhang, D.; Blaha, F. Lessons Learned from Large-Diameter Pipe Failure Case Studies. Pipelines 2017, 561–571. [Google Scholar] [CrossRef]
- Zarghamee, M.S.; Ojdrovic, R.P. Some Lessons Learned from Failure of a Pipeline. Pipelines 2006. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Frisinghelli, M.; Mazzetti, E.; Larentis, M.; Costisella, C. Safe transients for pipe survey in a real transmission main by means of a portable device: The case study of the Trento (I) supply system. Procedia Eng. 2017, 186, 228–235. [Google Scholar] [CrossRef]
- Tijsseling, A.S. Water hammer with fluid–structure interaction in thick-walled pipes. Comput. Struct. 2007, 11, 844–851. [Google Scholar] [CrossRef]
- Ma, B.; Najafi, M. Development and applications of trenchless technology in China. Tunn. Undergr. Space Technol. 2008, 23, 476–480. [Google Scholar] [CrossRef]
- Yen, J.; Shou, K. Numerical simulation for the estimation the jacking force of pipe jacking. Tunn. Undergr. Space Technol. 2015, 49, 218–229. [Google Scholar] [CrossRef]
- Kyriakides, S.; Babcock, C.D. Experimental determination of the propagation pressure of circular pipes. J. Press. Vessel Technol. 1981, 103, 328–336. [Google Scholar] [CrossRef]
- Milligan, G.W.E.; Norris, P. Pipe–soil interaction during pipe jacking. Proc. Inst. Civ. Eng. Geotech. Eng. 1999, 137, 27–44. [Google Scholar] [CrossRef]
- Valiente, A. Stress corrosion failure of large diameter pressure pipelines of prestressed concrete. Eng. Fail. Anal. 2001, 8, 245–261. [Google Scholar] [CrossRef]
- Gysling, D.L. Displacement Based Pressure Sensor Measuring Unsteady Pressure in a Pipe. U.S. Patent No. 6,463,813, 15 October 2002. [Google Scholar]
- Wasmer, K.; Nikbin, K.M.; Webster, G.A. Creep crack initiation and growth in thick section steel pipes under internal pressure. Intl. J. Press. Vessels Pip. 2003, 80, 489–498. [Google Scholar] [CrossRef] [Green Version]
- Meis, R.D.; Maragakis, E.M.; Siddharthan, R. Behavior of Underground Piping Joints Due to Static and Dynamic Loading; MCEER: Buffalo, NY, USA, 2003. [Google Scholar]
- Guo, P. Numerical modeling of pipe–soil interaction under oblique loading. J. Geotech. Geoenviron. Eng. 2005, 131, 260–268. [Google Scholar] [CrossRef]
- Schmitt, C.; Pluvinage, G.; Hadj-Taieb, E.; Akid, R. Water pipeline failure due to water hammer effects. Fatigue Fract. Eng. Mater. Struct. 2006, 29, 1075–1082. [Google Scholar] [CrossRef]
- Lydell, B.; Riznic, J. OPDE—The international pipe failure data exchange project. Nuclear Eng. Des. 2008, 238, 2115–2123. [Google Scholar] [CrossRef]
- Vazouras, P.; Karamanos, S.A.; Dakoulas, P. Finite element analysis of buried steel pipelines under strike-slip fault displacements. Soil Dyn. Earthq. Eng. 2010, 30, 1361–1376. [Google Scholar] [CrossRef]
- Wu, G.Y.; Smith, D.J.; Pavier, M.J. Effects of load and displacement controlled bending on plastic collapse of pressurized pipes. Procedia Mater. Sci. 2014, 3, 1204–1209. [Google Scholar] [CrossRef]
- Wang, S. Evaluation of underground pipe-structure interface for surface impact load. Nuclear Eng. Des. 2017, 317, 59–68. [Google Scholar] [CrossRef]
- Xu, M.; Shen, D.; Rakitin, B. The longitudinal response of buried large-diameter reinforced concrete pipeline with gasketed bell-and-spigot joints subjected to traffic loading. Tunn. Undergr. Space Technol. 2017, 64, 117–132. [Google Scholar] [CrossRef]
- Ortiz, M.; Pandolfi, A. A variational Cam-clay theory of plasticity. Comput. Methods Appl. Mech. Eng. 2004, 193, 2645–2666. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, Z.G.; Zhu, H.H.; Ju, J.W. Experimental study on the structural behaviors of jacking prestressed concrete cylinder pipe. Tunn. Undergr. Space Technol. 2018, 73, 60–70. [Google Scholar] [CrossRef]
- ABAQUS. Theory Guide, Release 6.14; ABAQUS, Inc.: Palo Alto, CA, USA, 2014. [Google Scholar]
- Hachem, F.E.; Schleiss, A.J. A review of wave celerity in frictionless and axisymmetrical steel-lined pressure tunnels. J. Fluids Struct. 2011, 27, 311–328. [Google Scholar] [CrossRef] [Green Version]
- Wylie, E.B.; Streeter, V.L.; Suo, L. Fluid Transients in Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1993; Volume 1, p. 464. [Google Scholar]
- Joukowsky, N. On the Hydraulic Hammer in Water Supply Pipes; Division of Physical Sciences of O.L.E., University of California: Berkeley, CA, USA, 1897. [Google Scholar]
- Halliwell, A.R. Velocity of a water-hammer wave in an elastic pipe. J. Hydraul. Div. 1963, 89, 1–21. [Google Scholar]




| Material | Parameter | Value |
|---|---|---|
| Soil | Log. of Bulk Modulus | 0.026 |
| Poisson’s Ratio | 0.4 | |
| Tensile Limit | 0 | |
| The Angle of Internal Friction | 23 | |
| Log. of Plastic Bulk Modulus | 0.174 | |
| Density (Kg/m3) | 1800 | |
| Stress Ratio | 0.94 | |
| Initial Yield Surface Size (Pa) | 4884 | |
| Wet Yield Surface Size | 1 | |
| Flow Stress Ratio | 0.778 | |
| Concrete | Young’s Modulus (GPa) | 20 |
| Compressive Strength (MPa) | 28.3 | |
| Tensile Strength (MPa) | 3 | |
| Poisson’s Ratio | 0.25 | |
| Density (Kg/m3) | 2500 | |
| Water | Density (kg/m3) | 1000 |
| Bulk Modulus (GPa) | 2.7 |
| Parameter | Value |
|---|---|
| a (m/s) | 854 |
| Max. Pressure (MPa) | 2.61 (378.55 psi) |
| Scenario | Max. Displacements (mm) | Max. Stresses (MPa) | ||
|---|---|---|---|---|
| Vertical | Horizontal | Tensile | Compressive | |
| No-flow Condition | 5 | 3 | 2.69 (390.15 psi) | 2.14 (310.38 psi) |
| Steady Flow | 1 | 1 | 3.86 (559.85 psi) | 6.78 (983.36 psi) |
| Transient Flow | 4 | 1 | 8.11 (1174.81 psi) | 1.73 (250.92 psi) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karakouzian, M.; Karami, M.; Nazari-Sharabian, M.; Ahmad, S. Flow-Induced Stresses and Displacements in Jointed Concrete Pipes Installed by Pipe Jacking Method. Fluids 2019, 4, 34. https://doi.org/10.3390/fluids4010034
Karakouzian M, Karami M, Nazari-Sharabian M, Ahmad S. Flow-Induced Stresses and Displacements in Jointed Concrete Pipes Installed by Pipe Jacking Method. Fluids. 2019; 4(1):34. https://doi.org/10.3390/fluids4010034
Chicago/Turabian StyleKarakouzian, Moses, Mehrdad Karami, Mohammad Nazari-Sharabian, and Sajjad Ahmad. 2019. "Flow-Induced Stresses and Displacements in Jointed Concrete Pipes Installed by Pipe Jacking Method" Fluids 4, no. 1: 34. https://doi.org/10.3390/fluids4010034
APA StyleKarakouzian, M., Karami, M., Nazari-Sharabian, M., & Ahmad, S. (2019). Flow-Induced Stresses and Displacements in Jointed Concrete Pipes Installed by Pipe Jacking Method. Fluids, 4(1), 34. https://doi.org/10.3390/fluids4010034








