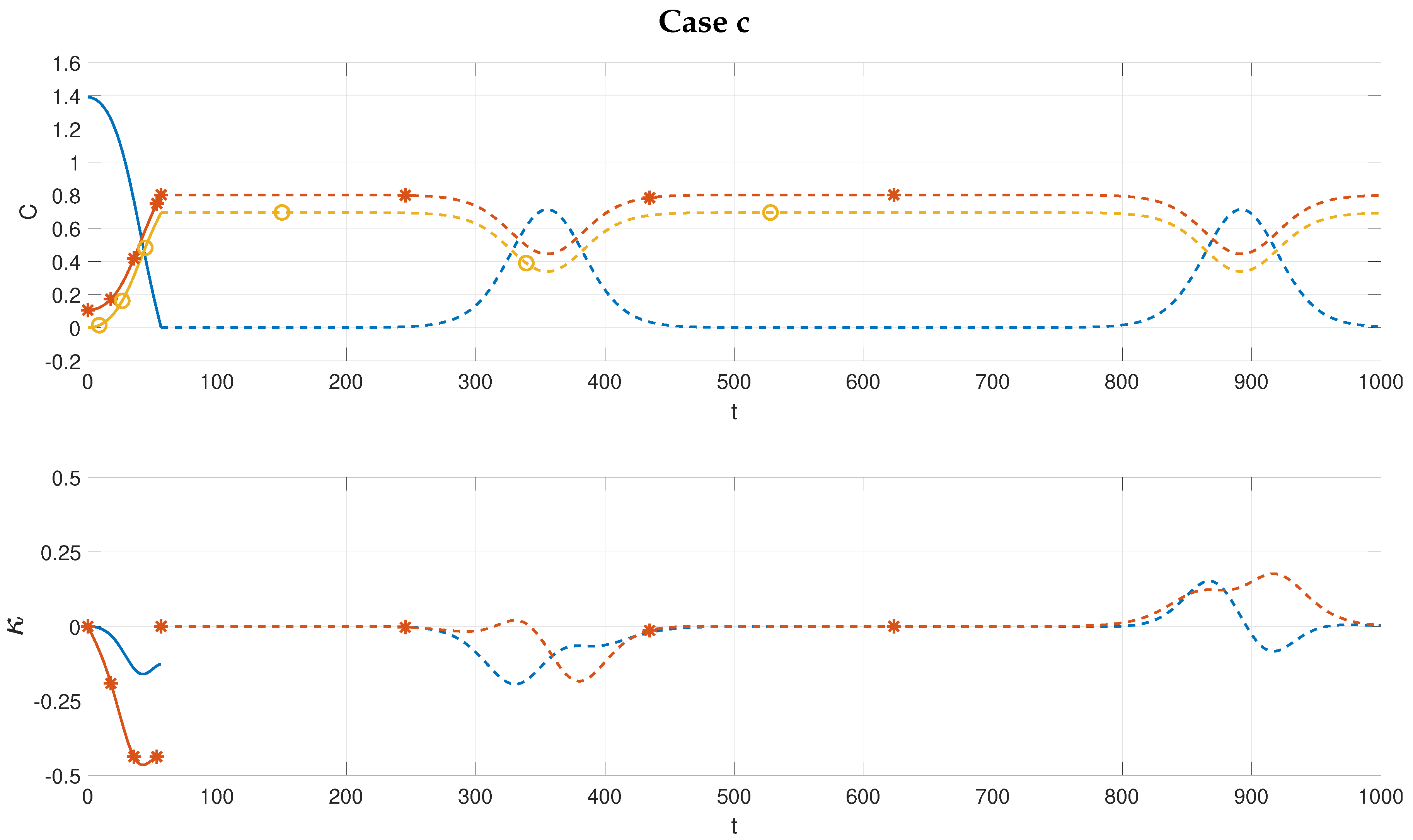1. Introduction
The dominant non-linear effect on the propagation of surface gravity waves in deep water is due to the resonant and almost resonant four-wave interactions discovered by Phillips [
1]. This process of four-wave interaction is succinctly described by the Zakharov equation [
2] which is a deterministic model accurate to third order in the wave steepness.
In the continuous case the Zakharov equation is written in terms of complex amplitudes
as
Here, and elsewhere, subscripts denote a wavenumber component, so
. The wavenumber resonance condition for quartets of waves is evident in the delta function
while the frequency detuning
marks the departure from exact resonance. The asterisk denotes complex conjugation, while the kernel
is given in Krasitskii [
3], and throughout this article the dispersion relation for deep water
, is used.
To describe averaged properties of a wave field, a statistical theory of wave evolution was developed in the 1950s. This culminated in Hasselmann’s [
4] derivation of what is often called the kinetic equation for water waves, or the Hasselmann equation. This equation describes the time evolution of the wave spectral density due to four-wave interactions in exact resonance.
The Hasselmann equation is derived under three basic premises that, in principle, pose limitations on its applicability. These assumptions are (i) spatial homogeneity and weak non-Gaussianity of the wave field, (ii) slow temporal evolution of the spectral density on a time-scale , for a typical wave steepness, and (iii) an assumption of quasi-stationarity for the fourth order cumulants.
One of the consequences of assumption (iii) is that near resonant interactions are ruled out in Hasselmann’s equation. In the deterministic description, near resonant interactions are responsible for the side-band instability of a uniform wave train. Stiassnie and Shemer [
5] have further highlighted the equal importance of nearly resonant and exactly resonant interactions for the Zakharov equation. It is therefore desirable to include them in any statistical model.
The limitation imposed by quasi-stationarity was first studied in detail by Janssen [
6], who derived a more general form of Hasselmann’s equation. Janssen’s equation essentially modifies (iii) by assuming the wave field to be strictly Gaussian at an arbitrary (but finite) initial time
. This has the immediate consequence that a Dirac delta function appearing in Hasselmann’s equation is smeared out into a time dependent term involving the frequency detuning
, thereby including near resonant interactions. Although Janssen’s equation includes near-resonant interactions, which leads to a time evolution on the time scale
, it still uses a simplification that is justified under assumption (ii).
A simple physical example serves to demonstrate why it is advantageous to dispense with assumption (ii). Assuming a wave of period s and steepness leads to an evolution time–scale hours. To justify wave evolution under this paradigm, a sea-state must remain spatially homogeneous on such a time-scale, which is clearly an idealization. On the other hand, evolution on a faster time scale , or min in the physical example above, would be a more suitable alternative.
A generalization of Janssen’s approach was presented by Annenkov and Shrira [
7]. Their result, called the generalized kinetic equation (GKE) is obtained as an intermediate step in the derivation of the kinetic equation, before assumptions (ii) and (iii) are imposed. This results in an equation valid on a fast time scale of order
. The equation was further generalized by Gramstad and Stiassnie [
8], who also included higher order terms corresponding to the non-linear Stokes correction in their so-called phase averaged equation (PAE). Recently Gramstad and Babanin implemented the GKE, without Stokes’ correction, in the third generation wave model WAVEWATCH-III [
9].
The two equations dealt with in what follows will be Janssen’s kinetic equation (henceforth JKE), and the generalized kinetic equation (GKE) of Annenkov and Shrira. While some recent efforts have been focused on the influence of inhomogeneities on the evolution of wave spectra, see Stuhlmeier and Stiassnie [
10], thereby dispensing with assumption (i) along lines first suggested by Crawford et al. [
11], it is important to put the homogeneous theory on sound footing. Thus, while JKE and GKE both essentially use the spatial homogeneity and weak non-Gaussianity of the wave field, they are differentiated by assumption (ii) on the slow evolution of the wave field. It will be shown that this seemingly small difference has a significant effect on the qualitative behavior of the solutions.
Our main result is that some solutions of the generalized kinetic equation exhibit blow-up. This means that the components of the spectrum tend to infinity in finite time. This raises a red flag on the GKE, as the blow-up is possible for initial conditions that are physically legitimate. Moreover, based only on the initial conditions we characterize when the blow-up occurs. One possible method to circumvent blow-up, by means of phase-mixing, is also explored in the appendix. On the other hand we show that solutions of the JKE always remain bounded, even in cases when there is blow-up in the GKE. Surprisingly, away from blow-up, periodic and bounded solutions of the GKE are qualitatively similar to those of the JKE.
2. Theoretical Background
Our starting point is the discrete version of Zakharov’s equation, which assumes that the complex amplitudes can be written as
Substituting (
2) into (
1) yields the following system of ordinary differential equations for the discrete complex amplitudes
where
denotes the Kronecker delta
Randomness is introduced by regarding the complex amplitudes as stochastic processes, where
is used to denote an ensemble average. Assuming that
the next quantities of interest are the second-order moments, the pair correlators. Homogeneity, from assumption (i) above, imposes the following constraint on the correlators
The set of functions
form the wave-action spectrum and
is the Kronecker delta.
The evolution equation for the wave action is found by multiplying (
3) by
and adding its complex conjugate. The resulting equation is
Higher order averages, such as the one appearing on the right hand side of (
6), can be decomposed into products of lower order averages as follows
where
is called the fourth-order cumulant. It is well known that all higher-order cumulants vanish for a Gaussian distribution, thus
indicates a deviation from Gaussianity.
Substituting (
7) into (
6), the evolution equation for the wave action becomes
In order to find an equation for
we differentiate the fourth order average as follows
and use (
3) in the right hand side of (
9) to yield
To close what would otherwise be an infinite hierarchy of equations we invoke the weak non-Gaussianity assumption. Akin to (
7), one may decompose the sixth order averages in (
10) into products of lower order averages and cumulants, as detailed in Lvov et al [
12]. The terms are then ordered with respect to the small parameter
;
and
, as in Gramstad and Stiassnie [
8]. Therefore, up to order
the decomposition of the averages is
Differentiating (
7) with respect to
t and using Equation (
10) together with (
11) for the sixth-order terms we reach the following equation for
, valid up to order
Equations (
8) and (
12) form the discrete version of the generalized kinetic equation first derived by Annenkov and Shrira [
7] for a continuous wavenumber spectrum. Later, Gramstad and Stiassnie [
8] derived their phase-averaged equation, by extending (
11) to include terms up to
Our focus shall remain on the GKE, rather than the higher order extension.
The GKE contains both Janssen’s and Hasselmann’s kinetic equations. To derive Janssen’s result we set
and integrate Equation (
12) from 0 to
yielding
Now we use assumption (ii). We assume that
varies slowly in time and we extract it out of the integral to obtain
Substituting (
14) into (
8) yields a single equation for
C:
Equation (
15) is the discrete version of Janssen’s kinetic equation (denoted JKE), originally derived in continuous form by Janssen [
6].
To elucidate the difference between the JKE (
15) and the GKE (
8) and (
12), it is instructive to consider simple cases with few waves. The fundamental interaction in deep water is between quartets of waves, and the simplest such case consists of three distinct wavenumbers forming a degenerate quartet.
4. Analytic Solution for the GKE
In this section we study the initial value problem associated with the system of equations (
18)–(
21). We begin by defining an auxiliary real function
as the solution to the initial value problem
with
. All subsequent calculations are based on the degenerate quartet, so we will omit subscripts and denote
,
and
where there is no risk of confusion.
In terms of
Equation (
18)–(
20) simplify to
Denoting the initial values by
,
and
and integrating in time we find an expression for
in terms of
Z:
Our goal is to find an equation that determines
. To this end we define a further auxiliary real function
Differentiating in time and using (
21) yields
which becomes, after integration,
where
. Taking the time derivative of (
25) yields
Now we use Equations (
27)–(
29) to express the right hand side of (
33) in terms of
Z. The resulting equation has the form
where the coefficients of
are:
We multiply both sides of (
34) by
and integrate
obtaining a non-linear first order differential equation for
Z
The coefficients of
are:
4.1. Analytical Solution for Z
We assume that
is real, so that 0 is always a root of
(see (
41)) and we are able to factor
as
where
is a cubic polynomial of the form
with coefficients given by (
42)–(
45) (note that the JKE is derived assuming
(see (
13)), and for a consistent comparison this initial condition is used in all subsequent examples).
It is known that the nature of the roots of a third order polynomial is determined by the sign of the following discriminant
If
then all non-zero roots of
are real and distinct. If
then
has a multiple non-zero real root. If
then
has two real roots and two complex conjugate roots. We refer to [
13] for a detailed exposition about the discriminant of a cubic polynomial, and formula (
48). Knowing the roots of
allows us to find exact formulas for the solution of (
40).
4.1.1. Case
In all cases of interest, when
, the roots of
can be written from largest to smallest as
. Therefore the solution of (
40) can be found by inverting the integral
by applying formulas
of Byrd and Friedman [
14]. Let
be the modulus of the Jacobian elliptic functions sn, cn and dn. Also let
Then
where
is the inverse of sn. In term of
u the inverse of (
49) is
We point out that the denominator of (
54) never vanishes because
whereas
. Finally we compute the value of
by means of addition formulas for elliptic functions. The resulting expression is
The solution of (
40), given by (
54), is a bounded and periodic function of time with period
where
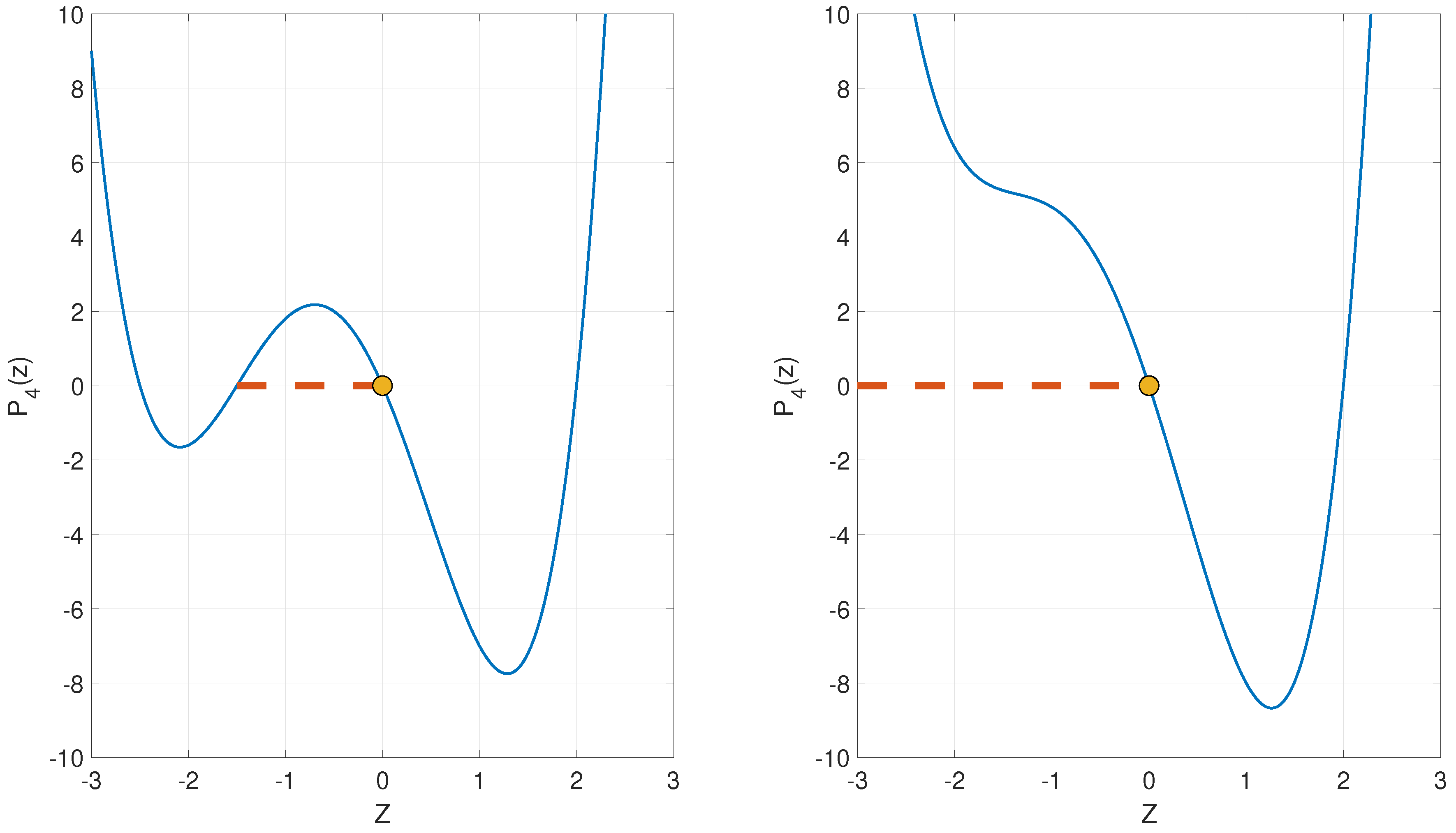
is the complete elliptic integral of the first kind. The qualitative behavior of the solution is shown in the left panel of
Figure 1. The function
oscillates back and forth between the roots
and
of the polynomial, starting from the initial value
.
4.1.2. Case
In this case let
,
,
be the roots of
. Notice that
if and only if
and
if and only if
. In either case the solution of (
40) is found by inverting the integral
The value of (
57) is found by applying formulas
of Byrd and Friedman [
14]. Let
be the elliptic modulus and define the parameters
We invert this relation to find
Z as a function of
tIn this case we expect the solution to blow up when the denominator of (
62) vanishes. The critical time
when this happens is
In the right panel of
Figure 1 we show a schematic representation of the blow-up in terms of the roots of the quartic polynomial. The function
initially at the root
tends towards
as
t goes from 0 to
.
5. Analytic Solution of JKE
Our analysis for the JKE follows the steps of the previous section. First we reduce the three coupled Equations (
22)–(
24) to a single equation for a new auxiliary function. To this end, let
be the solution of the initial value problem
with
. The relationship between
z and
C is given by (
27)–(
29), as in
Section 4. This is substituted into the right-hand side of (
64) to obtain the following equation for
z
where
is a third order polynomial
with coefficients
Let
be the roots of
. Notice that
, for
, satisfies Equation (
65). Moreover if
, then for all time
t,
. The subsequent analysis will be restricted to those cases encountered for physically relevant initial conditions—namely where
has two negative roots and one positive root.
We integrate Equation (
65) to obtain
with exponents
Equation (
71) defines
implicitly. Nevertheless it shows that
has period
. In case of exact resonance we take the limit as
obtaining
This shows that in exact resonance conditions the solution is no longer periodic, but instead converges to the root .
In the examples presented below, rather than solving Equation (
71) for
we integrate the system of Equations (
22)–(
24) directly using MATLAB’s ode15s solver with absolute and relative tolerances set to
.
6. List of Examples
In the following examples we consider three waves of the form
,
and
and, following Stuhlmeier and Stiassnie [
10], we assume that the initial complex amplitudes are independent, Gaussian random variables, written as
where the real amplitudes
are Rayleigh distributed and the phases
are uniformly distributed over the interval
.
Under these assumptions we have
and we relate the average value of
to the wave amplitude by
where
are the wave slopes. Finally we set
in order to have consistent initial conditions with which to compare GKE and JKE. In all calculations we take
m
,
m s
and the period of the wave
is
s.
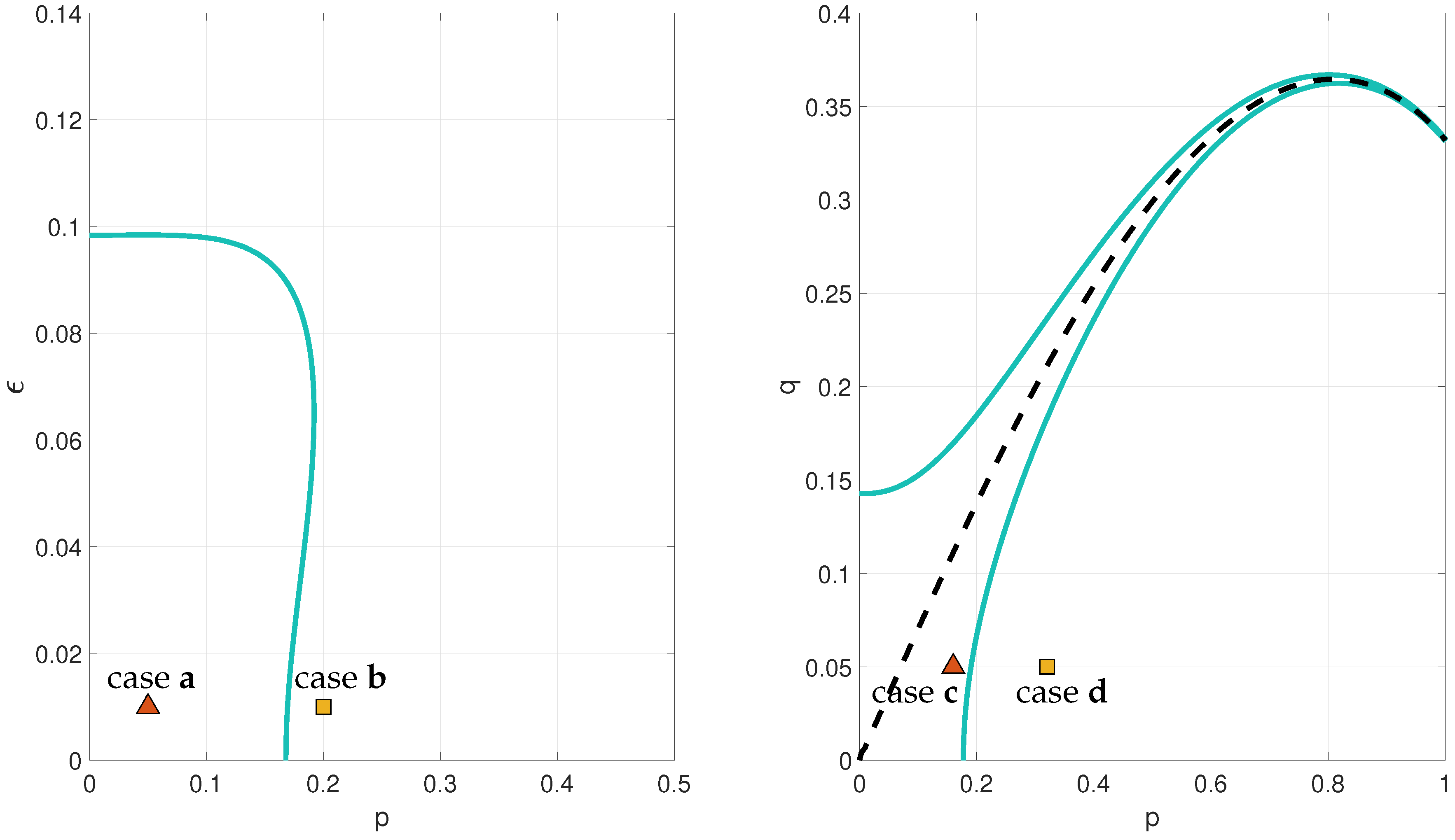
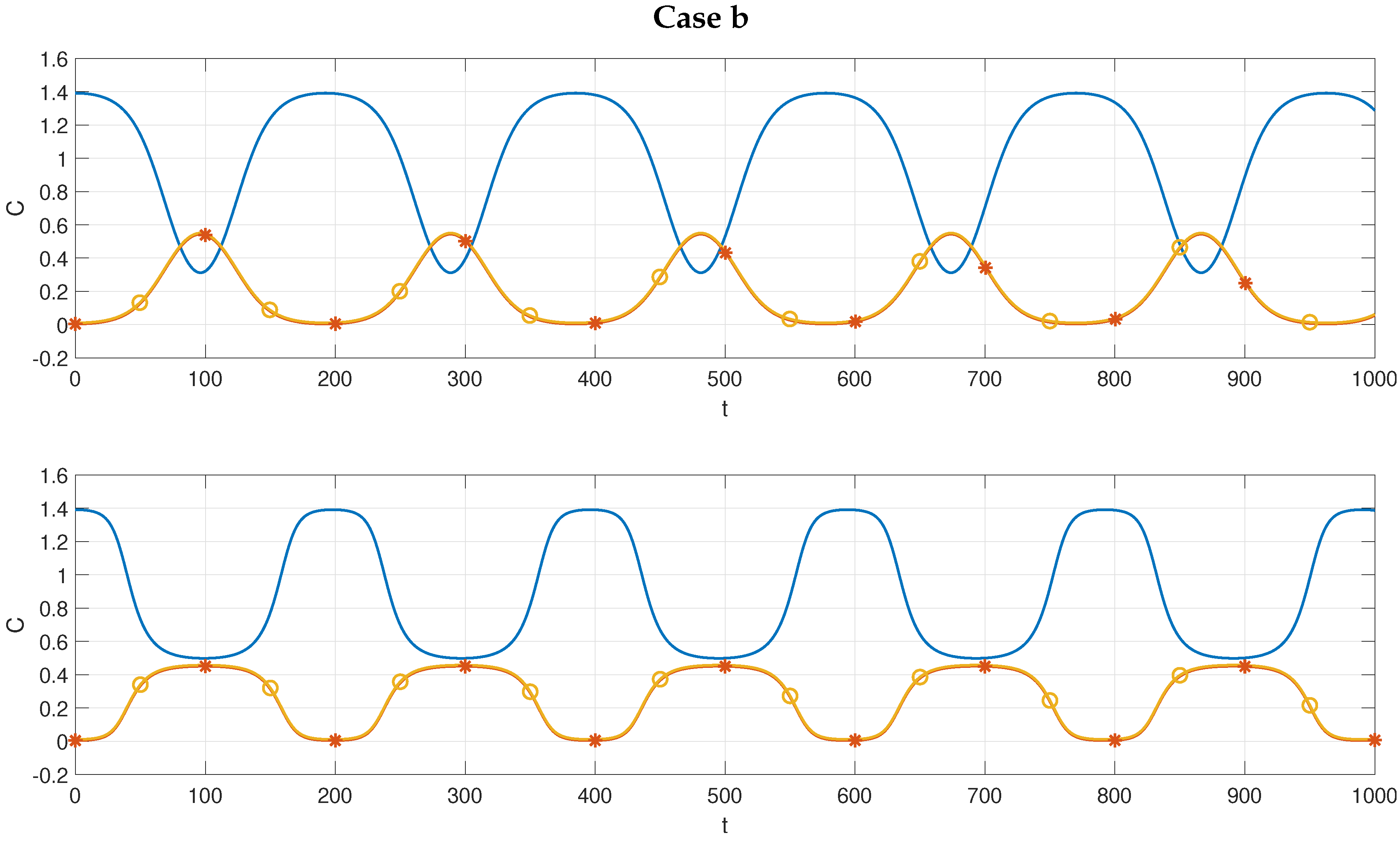
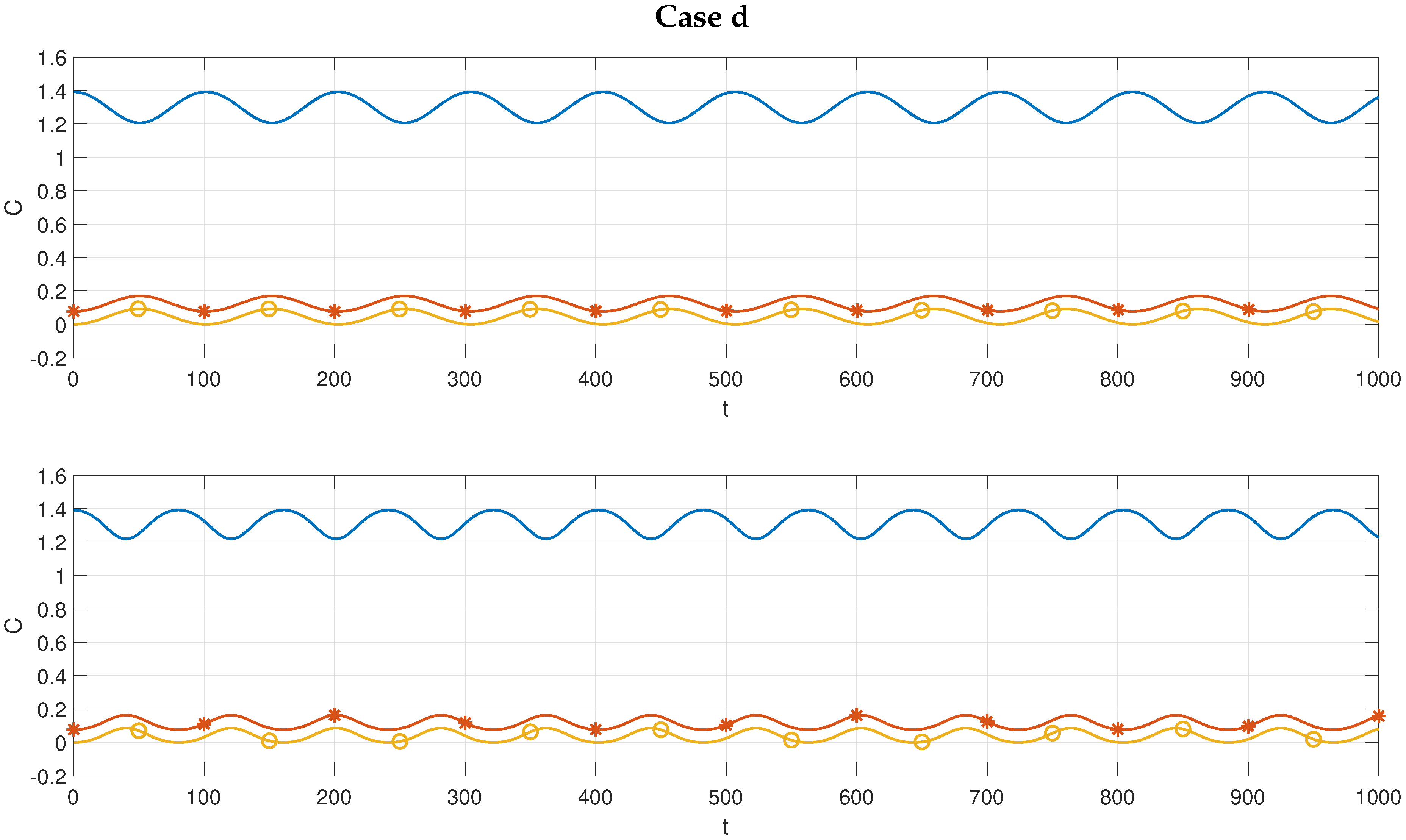
We shall consider four particular initial conditions below. In cases
a and
b we initially assume that the waves are collinear (
) and fix the steepness
of the wave
. Then we take
to be the steepness of the waves
and
. In cases
c and
d the wave slopes are fixed
,
and
and we explore the nature of the solutions in the
-plane. Notice that
implies a two-dimensional disturbance. We recall that while solutions to the JKE are periodic, the behavior of the GKE is determined by the initial conditions via the discriminant
D given in (
48). To visualize how wave slope and wavenumber impact the solutions of the GKE, the sign of
D is plotted in
Figure 2. It establishes when the solutions remain bounded
or tend to infinity in finite time
.
The four cases
a–
d marked in
Figure 2 are studied numerically, and the relevant parameters for these cases are summarized in
Table 1.
7. Comparison between GKE and JKE—Blow Up
We compare the solutions of the GKE with those of the JKE for cases
a and
c (see
Table 1), shown as triangles in
Figure 2.
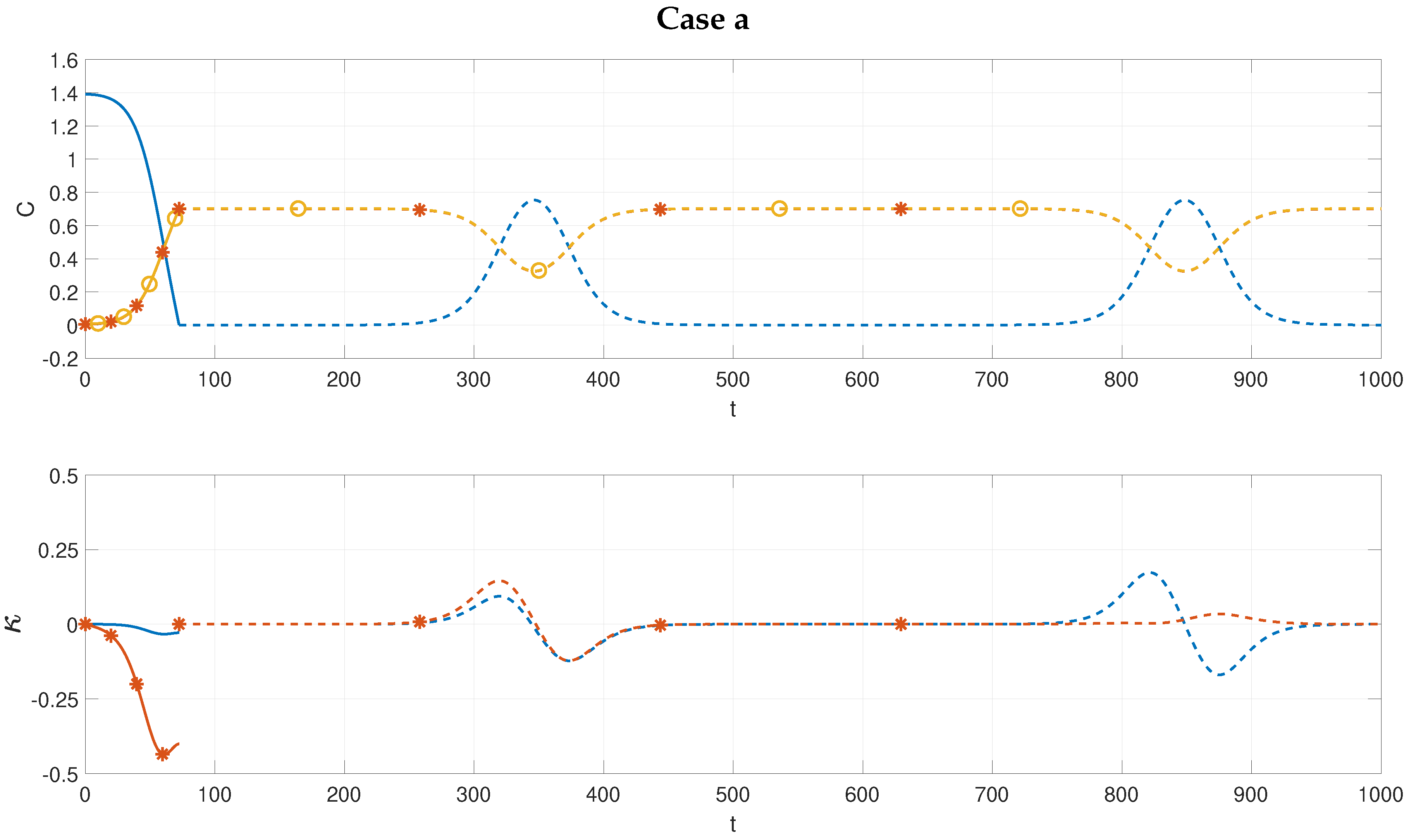
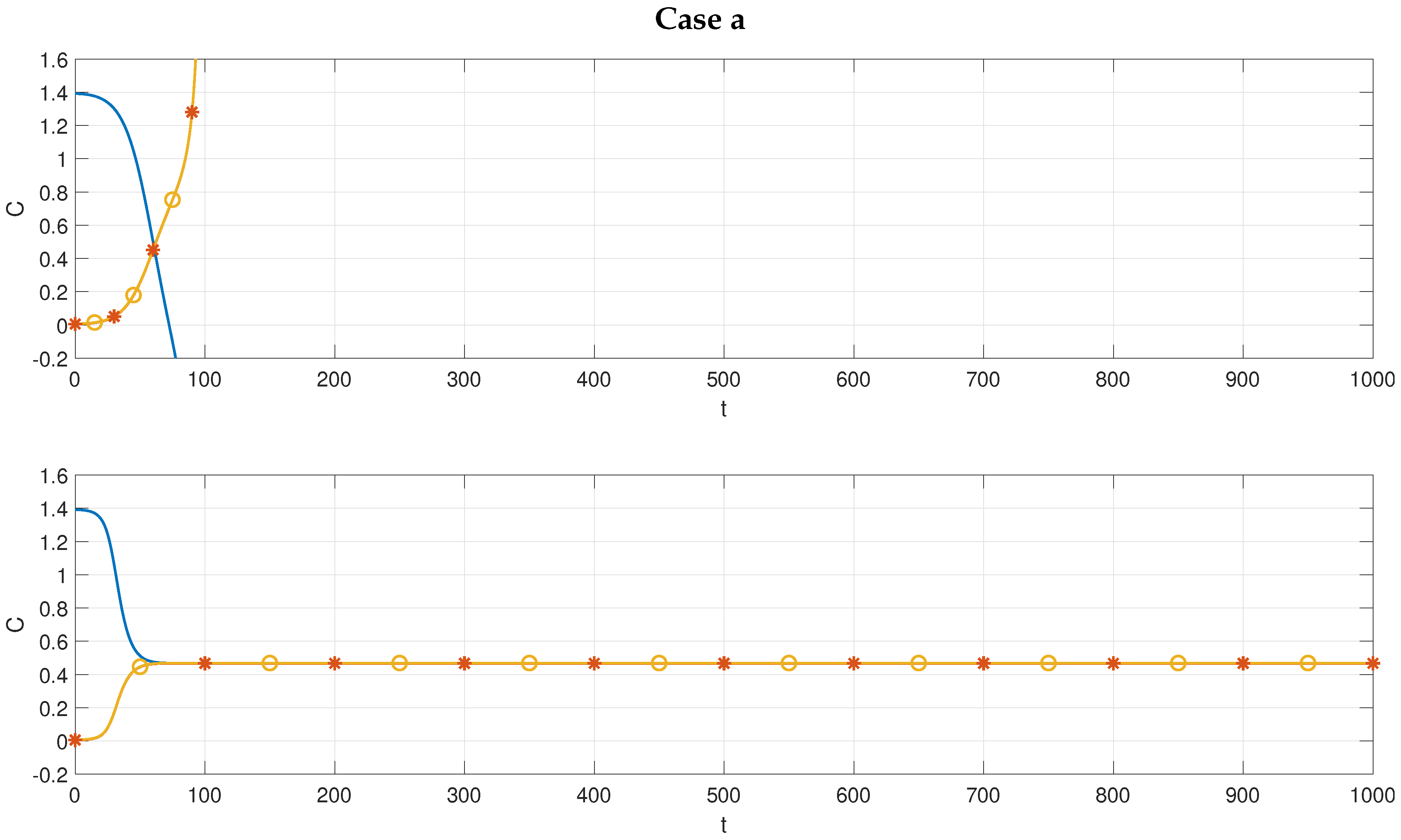
Figure 3 shows the time evolution of case
a. In the upper panel we see the solution of the GKE that tends to infinity as time approaches
s, see (
63). The solution becomes physically meaningless as
and
become negative, prior to the critical time. On the other hand the solution of the JKE, on the lower panel of
Figure 3 remains bounded, and is periodic with period
s. Adopting the notation
for the time scales we see that the blow-up occurs at
. The corresponding evolution for the JKE looks initially similar, but settles down to near equipartition of wave action, before eventually exhibiting periodicity on a time scale
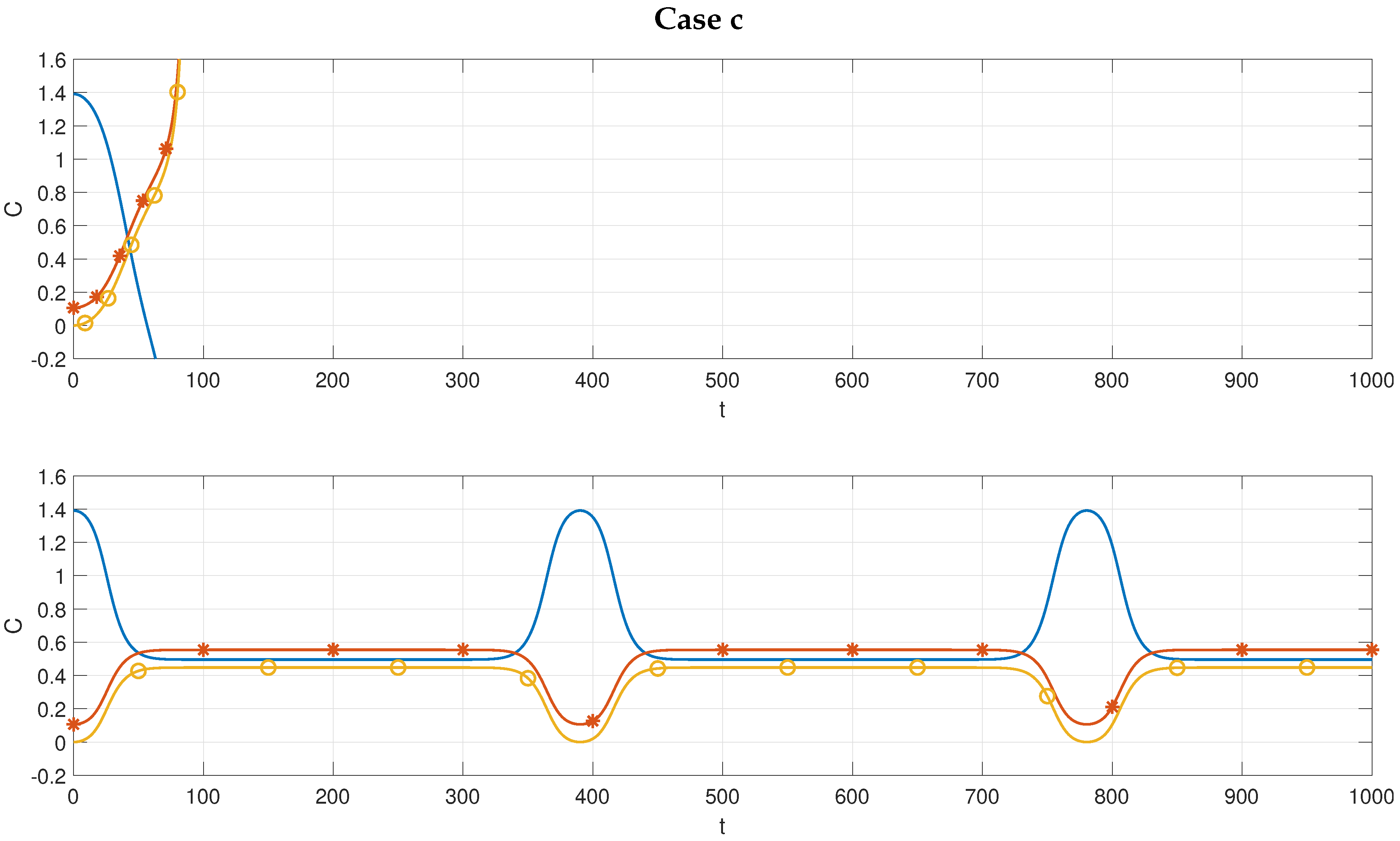
The time evolution for case
c is shown in
Figure 4. The upper panel shows blow-up for the solution of the GKE. The critical time is
s. This non-physical behavior is similar to case
a (above) and occurs on the same time scale
.
On the lower panel we have the solution of the JKE. The system also reaches a state where the energy among the three wavenumbers is similar, at a time of , and is periodic and bounded with a period s which is of order .
According to Hasselmann’s kinetic equation the time evolution of the wave action depends only on exact resonant waves. With the settings of cases
c and
d it is possible to have triads that are in exact resonance. The dashed line on the right panel of
Figure 2 shows such triads. According to the GKE the time evolution of exact resonant triads blows up.