Acoustic Streaming and Its Applications
Abstract
1. Introduction
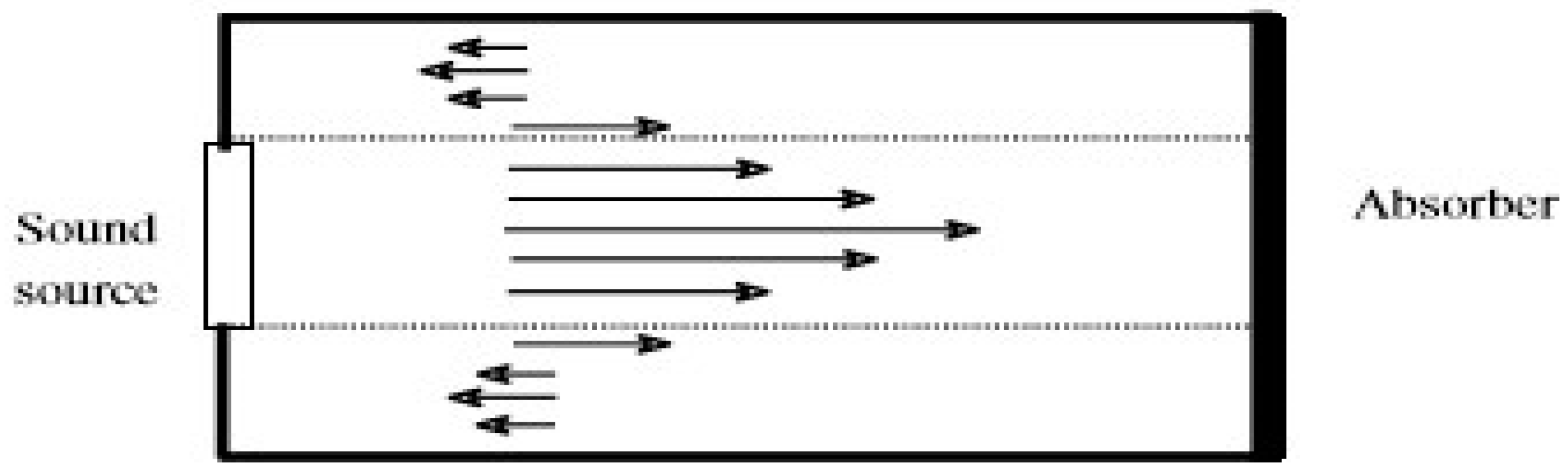
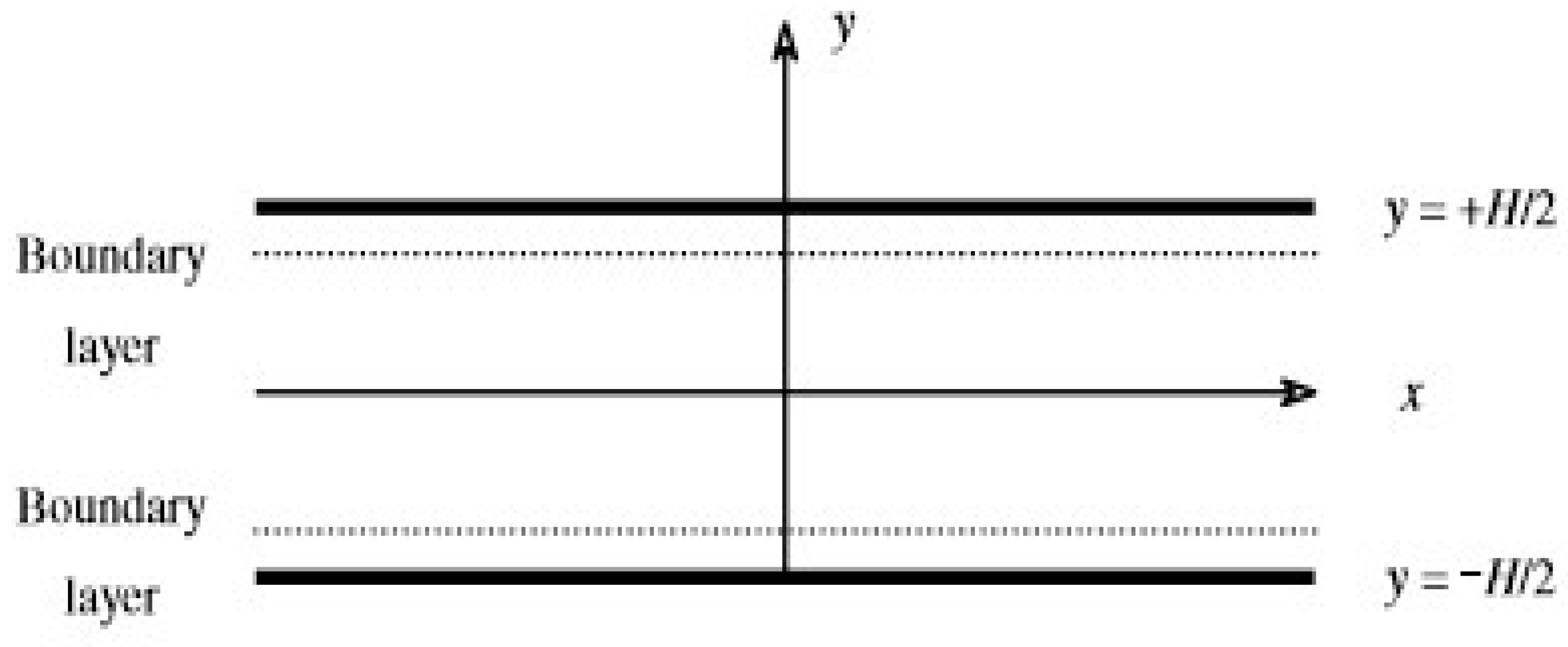
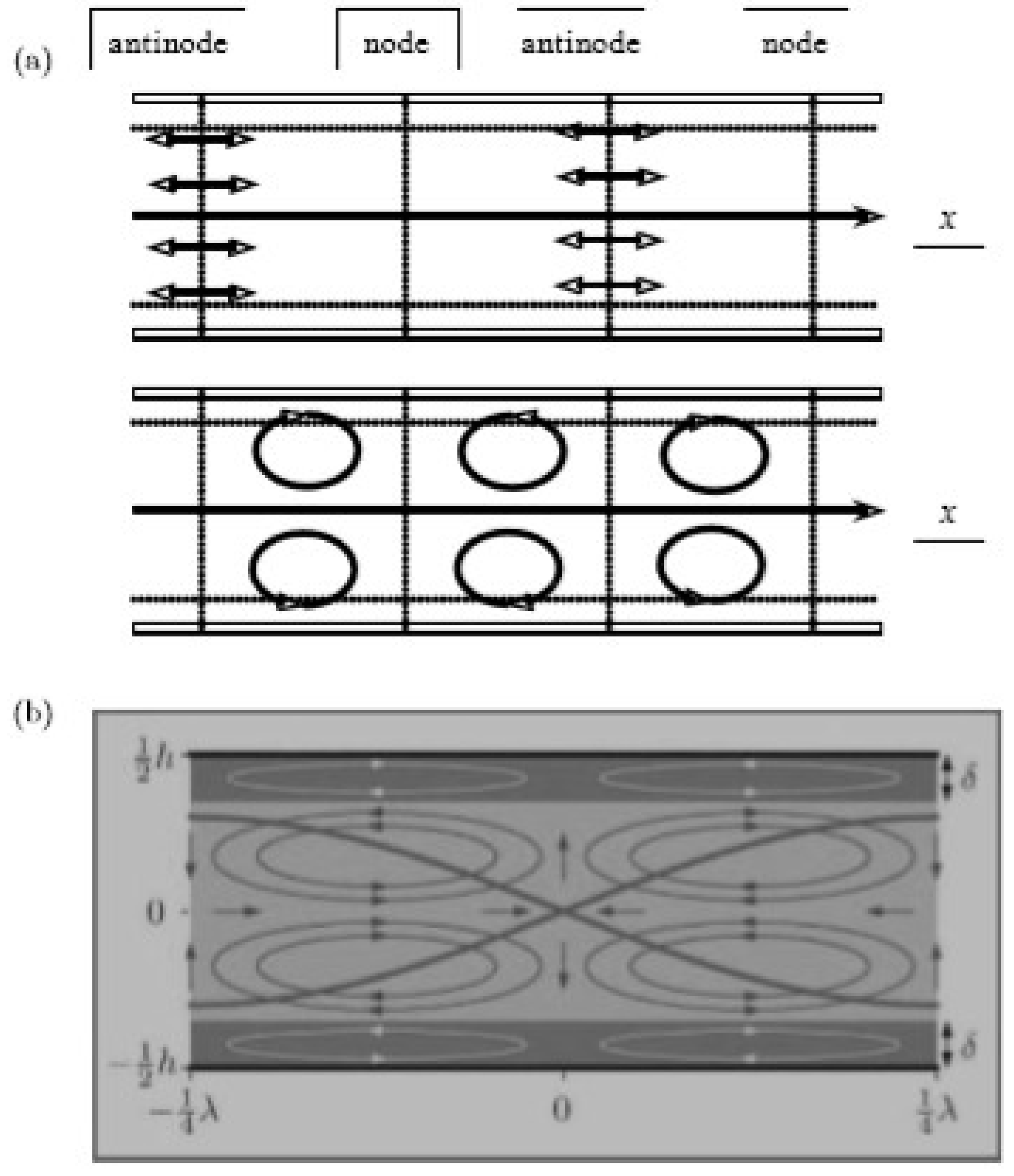
2. The Fundamental Theory of the Acoustic Streaming
3. Applications of Acoustic Microstreaming
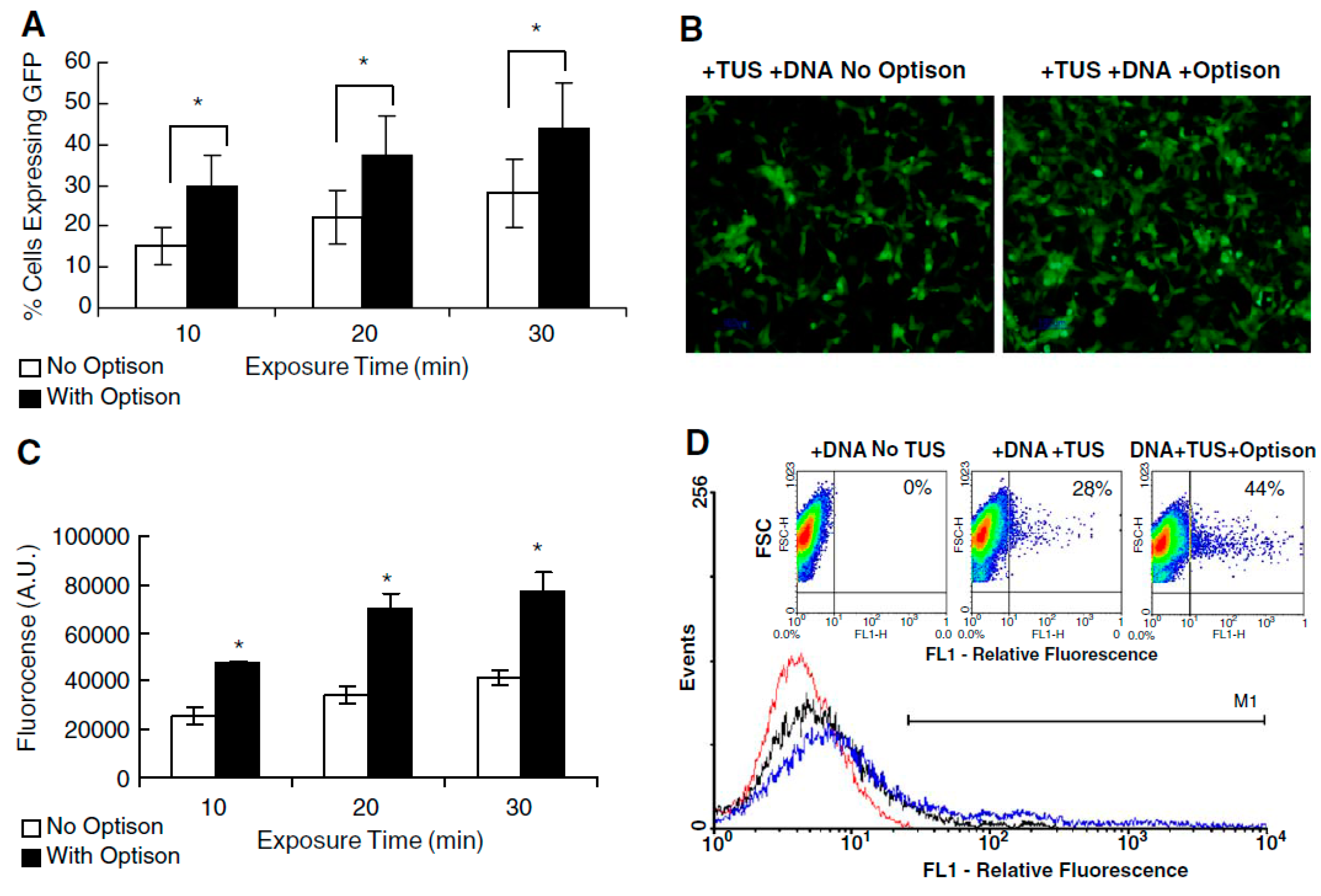
3.1. Preclinical Applications of Sonoporation with EMBs
3.2. Thrombolysis and Stroke Treatment
3.3. Cancer Treatment
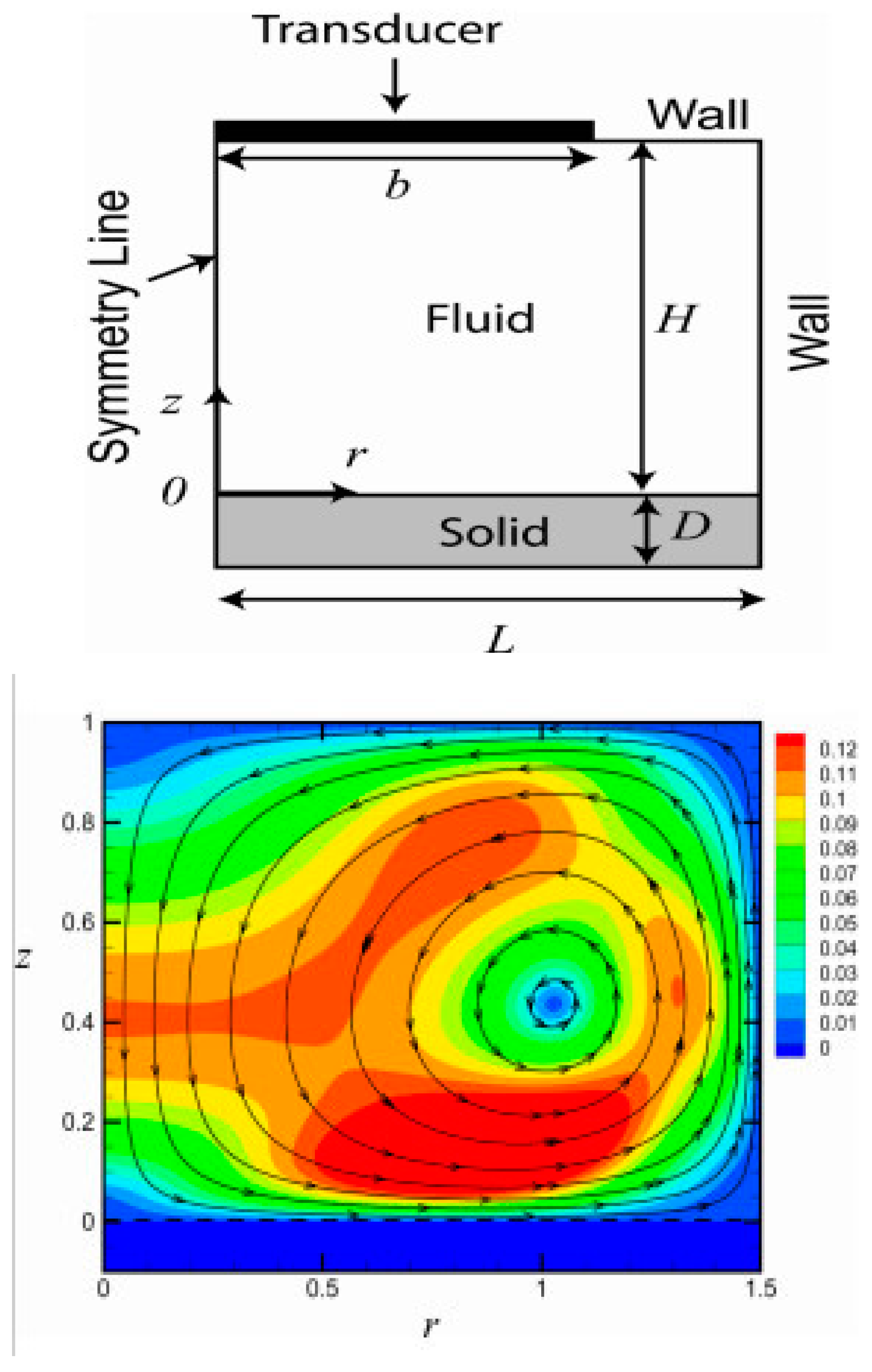
4. Ultrasound Promotes Fluids’ Mixing within Microfluidic Devices
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Eckart, C. Vortices and streamings caused by sound waves. Phys. Rev. 1948, 73, 68–73. [Google Scholar] [CrossRef]
- Rayleigh, L. On the circulation of air observed in Kundt’s tube, and on some allied acoustic problem. Philos. Trans. 1883, 175, 1–21. [Google Scholar] [CrossRef]
- Lighthill, J. Acoustic streaming. J. Sound Vib. 1978, 61, 391–418. [Google Scholar] [CrossRef]
- Nyborg, W.L. Acoustic streaming near a boundary. J. Acoust. Soc. Am. 1958, 30, 329–339. [Google Scholar] [CrossRef]
- Kuznetsova, L.A.; Coakley, W.T. Applications of ultrasound streaming and radiation force in biosensors. Biosens. Bioelectron. 2007, 22, 1567–1577. [Google Scholar] [CrossRef] [PubMed]
- Marshall, J.; Wu, J. Acoustic streaming, fluid mixing, and particle transport by a Gaussian ultrasound beam in a cylindrical container. Phys. Fluids 2015, 27, 103601–1036021. [Google Scholar] [CrossRef]
- Pepe, J.; Ricon, M.; Wu, J. Experimental comparison of sonoporation and electroporation in cell transfection applications. Acoust. Res. Lett. Online 2004. [Google Scholar] [CrossRef]
- Wu, J.; Nyborg, W.L. Ultrasound, cavitation bubbles and their interaction with cells. Adv. Drug Deliv. Rev. 2008, 60, 1103–1116. [Google Scholar] [CrossRef] [PubMed]
- Crum, L.A. Measurements of the growth of air bubbles by rectified diffusion. J. Acoust. Soc. Am. 1980, 68, 203–211. [Google Scholar] [CrossRef]
- Gormley, G.; Wu, J. Observation of acoustic streaming near albunex spheres. J. Acoust. Soc. Am. 1998, 104, 3115–3118. [Google Scholar] [CrossRef]
- Rooney, J.A. Hemolysis near an ultrasonically pulsating gas bubble. Science 1970, 169, 869–871. [Google Scholar] [CrossRef] [PubMed]
- Rooney, J.A. Shear as a mechanism for sonically induced biological effects. J. Acoust. Soc. Am. 1972, 6, 1718–1724. [Google Scholar] [CrossRef]
- Elder, A.E. Cavitation microstreaming. J. Acoust. Soc. Am. 1959, 31, 54–64. [Google Scholar] [CrossRef]
- Inoue, H.; Arai, Y.; Kishida, T.; Shin-Ya, M.; Terauchi, R.; Nakagawa, S.; Saito, M.; Tsuchida, S.; Inoue, A.; Shirai, T.; et al. Sonoporation-mediated transduction of siRNA ameliorated experimental arthritis using 3 MHz pulsed ultrasound. Ultrasonics 2014, 54, 874–881. [Google Scholar] [CrossRef] [PubMed]
- van Wamel, A.; Bouakaz, A.; Versluis, M.; de Jong, N. Micromanipulation of endothelial cells: Ultrasound-microbubble-cell interaction. Ultrasound Med. Biol. 2004, 30, 1255–1258. [Google Scholar] [CrossRef] [PubMed]
- Meijering, B.D.M.; Juffermans, L.J.M.; van Wamel, A.; Henning, R.H.; Zuhorn, I.S.; Emmer, M.; Versteilen, A.M.G.; Paulus, W.J.; van Gilst, W.H.; Kooiman, K.; et al. Ultrasound and microbubble-targeted delivery of macromolecules is regulated by induction of endocytosis and pore formation. Circ. Res. 2009, 104, 679–687. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, V. Ultrasound mediated delivery of drugs and genes to solid tumors. Adv. Drug Deliv. Rev. 2008, 60, 1193–1208. [Google Scholar] [CrossRef] [PubMed]
- Guzmán, H.; Nguyen, D.; Khan, S.; Prausnitz, M. Ultrasound-mediated disruption of cell membranes. II. Heterogeneous effects on cells. J. Acoust. Soc. Am. 2001, 110, 597–606. [Google Scholar] [CrossRef] [PubMed]
- Karshafian, R.; Samac, S.; Bevan, P.; Burns, P. Microbubble mediated sonoporation of cells in suspension: Clonogenic viability and influence of molecular size on uptake. Ultrasonics 2010, 50, 691–697. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Ross, J.P.; Chiu, J.-F. Reparable Sonoporation Generated by Microstreaming. J. Acoust. Soc. Am. 2001, 111, 1460–1464. [Google Scholar] [CrossRef]
- Wu, J. Theoretical study on shear stress generated by microstreaming surrounding contrast agents attached to living cells. Ultrasound Med. Biol. 2002, 28, 125–129. [Google Scholar] [CrossRef]
- Peruzzi, G.; Massimo, C. Perspectives on cavitation enhanced endotherlia layer permeability. Colloids Surf. B Biointerfaces 2018. [Google Scholar] [CrossRef] [PubMed]
- Ma, D.; Wu, J. Biofilm mitigation by drug (gentamicin) loaded liposomes promoted by pulsed ultrasound. J. Acoust. Soc. Am. 2016. [Google Scholar] [CrossRef] [PubMed]
- Ma, D.; Adam Green, A.M.; Willsey, G.G.; Marshall, J.S.; Wargo, M.J.; Wu, J. Effects of acoustic streaming of moderate pulsed ultrasound promoting bacteria eradication of biofilms using drug loading liposomes. J. Acoust. Soc. Am. 2015, 138, 1043–1051. [Google Scholar] [CrossRef] [PubMed]
- Wiklund, M.; Green, R.; Ohlin, M. Acoustofluidics 14: Applications of acoustic streaming in microfluidic devices. Lab Chip 2012, 12, 2438–2451. [Google Scholar] [CrossRef] [PubMed]
- Leslie, Y.; Yeo, L.Y.; Friend, J.R. Surface acoustic wave microfluidics. Annu. Rev. Fluid Mech. 2014, 46, 379–406. [Google Scholar]
- Ding, X.; Li, P.; Lin, S.C.; Stratton, Z.S.; Nama, N.; Guo, F.; Slotcavage, D.; Mao, X.; Shi, J.; Costanzo, F.; et al. Surface acoustic wave microfluidics. Lab Chip 2013, 13, 3626–3649. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Friend, J.R.; Yeo, L.Y. Surface acoustic wave concentration of particle and bioparticle suspensions. Biomed. Microdevices 2007, 9, 647–656. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Lin, S.-C.S.; Kiraly, B.; Yue, H.; Li, S.; Chiang, I.-K.; Stephen, S.J.; Benkovic, J.; Huang, T.J. On-chip manipulation of single microparticles, cells, and organisms using surface acoustic waves. PNAS 2012, 109, 11105–11109. [Google Scholar] [CrossRef] [PubMed]
- Meng, L.; Cai, F.; Jin, Q.; Niu, L.; Jiang, C.; Wang, Z.; Wu, J.; Zheng, H. Acoustic aligning and trapping of microbubbles in an enclosed PDMS microfluidic device. Sens. Actuators B Chem. 2011, 160, 1599–1605. [Google Scholar] [CrossRef]
- Meng, L.; Cai, F.; Wu, J.; Zheng, H. Precise and programmable manipulation of microbubbles by two-dimensional standing surface acoustic waves. Appl. Phys. Lett. 2012, 100, 173701. [Google Scholar] [CrossRef]
- Meng, L.; Deng, Z.; Niu, L.; Li, F.; Yan, F.; Wu, J.; Cai, F.; Zheng, H. A disposable microfluidic device for controlled drug release from thermal-sensitive liposomes by high intensity focused ultrasound. Theranostics 2015, 5, 1203–1213. [Google Scholar] [CrossRef] [PubMed]
- Green, A.; Marshall, J.S.; Ma, D.; Wu, J. Acoustic streaming and thermal instability of flow generated by ultrasound in a cylindrical container. Phys. Fluids 2016, 28, 104105. [Google Scholar] [CrossRef]
- Wu, J. Handbook of Contemporary Acoustics and Its Application; World Scientific Co.: Hackensack, NJ, USA, 2016; p. 327. [Google Scholar]
- Riley, K.F.; Hobson, M.P. Solution methods for PDEs. In Essential Mathematical Methods; Cambridge University Press: New York, NY, USA, 2011; pp. 421–479. [Google Scholar]
- Lei, J.; Glynne-Jones, P.; Hill, M. Acoustic streaming in the transducer plane in ultrasonic particle manipulation devices. Lab Chip 2013, 13, 2133. [Google Scholar] [CrossRef] [PubMed]
- Duvshani-Eshet, M.; Adam, D.; Machluf, M. The effects of albumin-coated microbubbles in DNA delivery mediated by therapeutic ultrasound. J. Control. Release 2006, 112, 156–166. [Google Scholar] [CrossRef] [PubMed]
- Farokhzad, O.C.; Cheng, J.; Teply, B.A.; Sherifi, I.; Jon, S.; Kantoff, P.W. Targeted nanoparticle-aptamer bioconjugates for cancer chemotherapy in vivo. Proc. Natl. Acad. Sci. USA 2006, 103, 6315–6320. [Google Scholar] [CrossRef] [PubMed]
- Alter, J.; Sennoga, C.A.; Lopes, D.M.; Eckersley, R.J.; Wells, D. Microbubble stability is a major determinant of the efficiency of ultrasound and microbubble mediated in vivo gene transfer. Ultrasound Med. Biol. 2009, 35, 976–984. [Google Scholar] [CrossRef] [PubMed]
- Fujii, H.; Sun, Z.; Li, S.H.; Wu, J.; Fazel, S.; Weisel, R.D.; Rakowski, H.; Lindner, J.; Li, R.K. Ultrasound-targeted gene delivery induces angiogenesis after a myocardial infarction in mice. J. Am. Coll. Cardiol. 2009, 2, 869–879. [Google Scholar] [CrossRef] [PubMed]
- Czarnota, G.J.; Karshafian, R.; Burns, P.N.; Wong, S.; Mahrouki, A.A.; Lee, J.W.; Caissie, A.; Tran, W.; Kim, C.; Furukawa, M.; et al. Tumor radiation response enhancement by acoustical stimulation of the vasculature. PNAS 2012, 9, E2033–E2041. [Google Scholar] [CrossRef] [PubMed]
- Alexandrov, A.V.; Mikulik, R.; Ribo, M.; Sharma, V.K.; Lao, A.Y.; Tsivgoulis, G.; Sugg, R.M.; Barreto, A.; Sierzenski, P.; Malkoff, M.D.; et al. A Pilot randomized clinical safety study of sonothrombolysis augmentation with ultrasound-activated perflutren-lipid microspheres for acute ischemic stroke. Stroke 2008, 39, 1464–1469. [Google Scholar] [CrossRef] [PubMed]
- Heath, C.H.; Sorace, A.; Knowles, J.; Rosenthal, E.; Hoyt, K. Microbubble therapy enhances anti-tumor properties of cisplatin and cetuximab in vitro and in vivo. Otolaryngol. Head Neck Surg. 2012, 146, 938–945. [Google Scholar] [CrossRef] [PubMed]
- Sorace, A.G.; Warram, J.M.; Umphrey, H.; Hoyt, K. Microbubble-mediated ultrasonic techniques for improved chemotherapeutic delivery in cancer. J. Drug Target. 2012, 20, 43–54. [Google Scholar] [CrossRef] [PubMed]
- Tachibana, K.; Tachibana, S. Emerging technologies using ultrasound for drug delivery. In Emerging Therapeutic Ultrasound; Wu, J., Nyborg, W.L., Eds.; World Scientific Co.: Hackensack, NJ, USA, 2007. [Google Scholar]
- Culp, W.C.; Porter, T.R.; Lowery, J.; Xie, F.; Roberson, P.K.; Marky, L. Intracranial clot lysis with intravenous microbubbles and transcranial ultrasound in swine. Stroke 2004, 35, 2407–2411. [Google Scholar] [CrossRef] [PubMed]
- Samiotaki, G.; Konofagou, E.E. Dependence of the reversibility of focused-ultrasound-induced blood–brain barrier opening on pressure and pulse length in vivo. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 2257–2265. [Google Scholar] [CrossRef] [PubMed]
- Leinenga, G.; Gotz, J. Scanning ultrasound removes Amylaid-β and restores memory in an Alzheimer’s disease mouse model. Sci. Transl. Med. 2015, 7, 278ra33. [Google Scholar] [CrossRef]
- Nowicki, A.; Kowaleski, T.; Worjeik, J. Estimation of acoustic streaming: Theoretical model, Doppler measurements and optical visualization. Eur. J. Ultrasound 1998, 7, 73–81. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J. Acoustic Streaming and Its Applications. Fluids 2018, 3, 108. https://doi.org/10.3390/fluids3040108
Wu J. Acoustic Streaming and Its Applications. Fluids. 2018; 3(4):108. https://doi.org/10.3390/fluids3040108
Chicago/Turabian StyleWu, Junru. 2018. "Acoustic Streaming and Its Applications" Fluids 3, no. 4: 108. https://doi.org/10.3390/fluids3040108
APA StyleWu, J. (2018). Acoustic Streaming and Its Applications. Fluids, 3(4), 108. https://doi.org/10.3390/fluids3040108