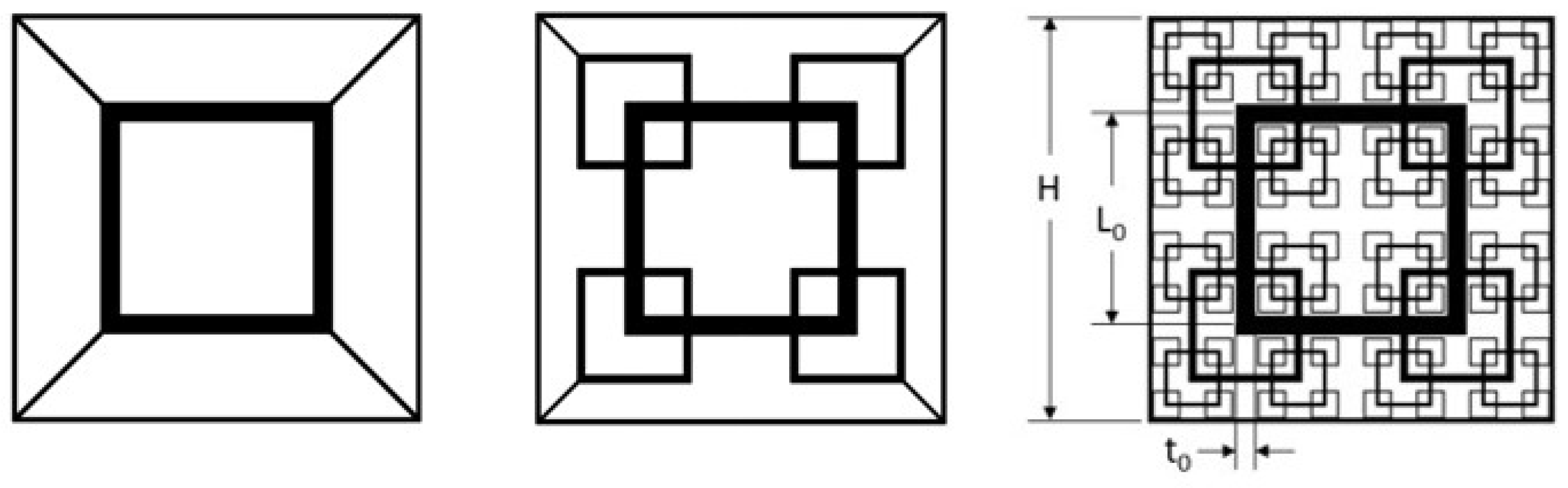
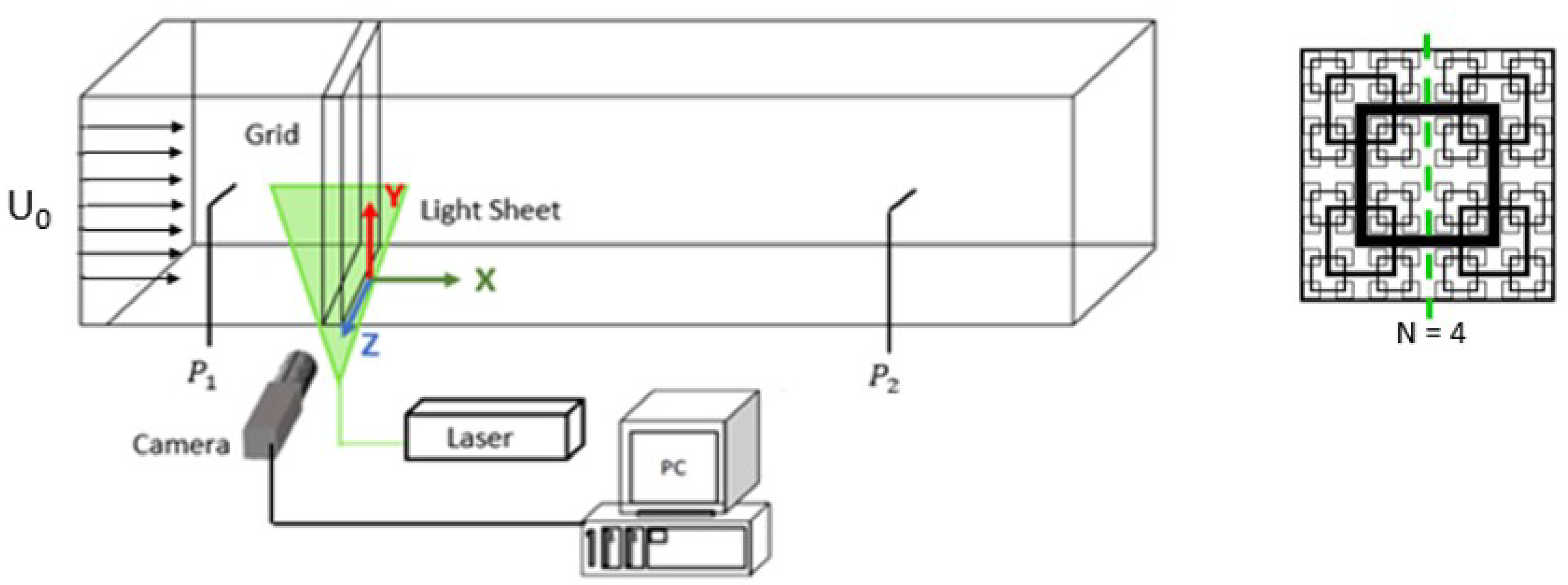
3.1. Characteristic Flow Field: Jets and Wakes of Various Scales
A fundamental characteristic of these turbulence-generating grids is that they produce wakes immediately behind the bars and jets immediately behind the openings. More importantly, the multiple wakes are the strong signature of the different length scales of bars. This is distinctly different from the nearly uniform distribution of wakes and jets generated by a uniform grid, reported in previous studies, e.g., [
13]. While the multi-scale jet-wake flow behavior was observed for complete fractal grids [
10,
16,
24], the current results highlight the evolution of the jets and wakes with gradually including smaller scales by increasing
N.
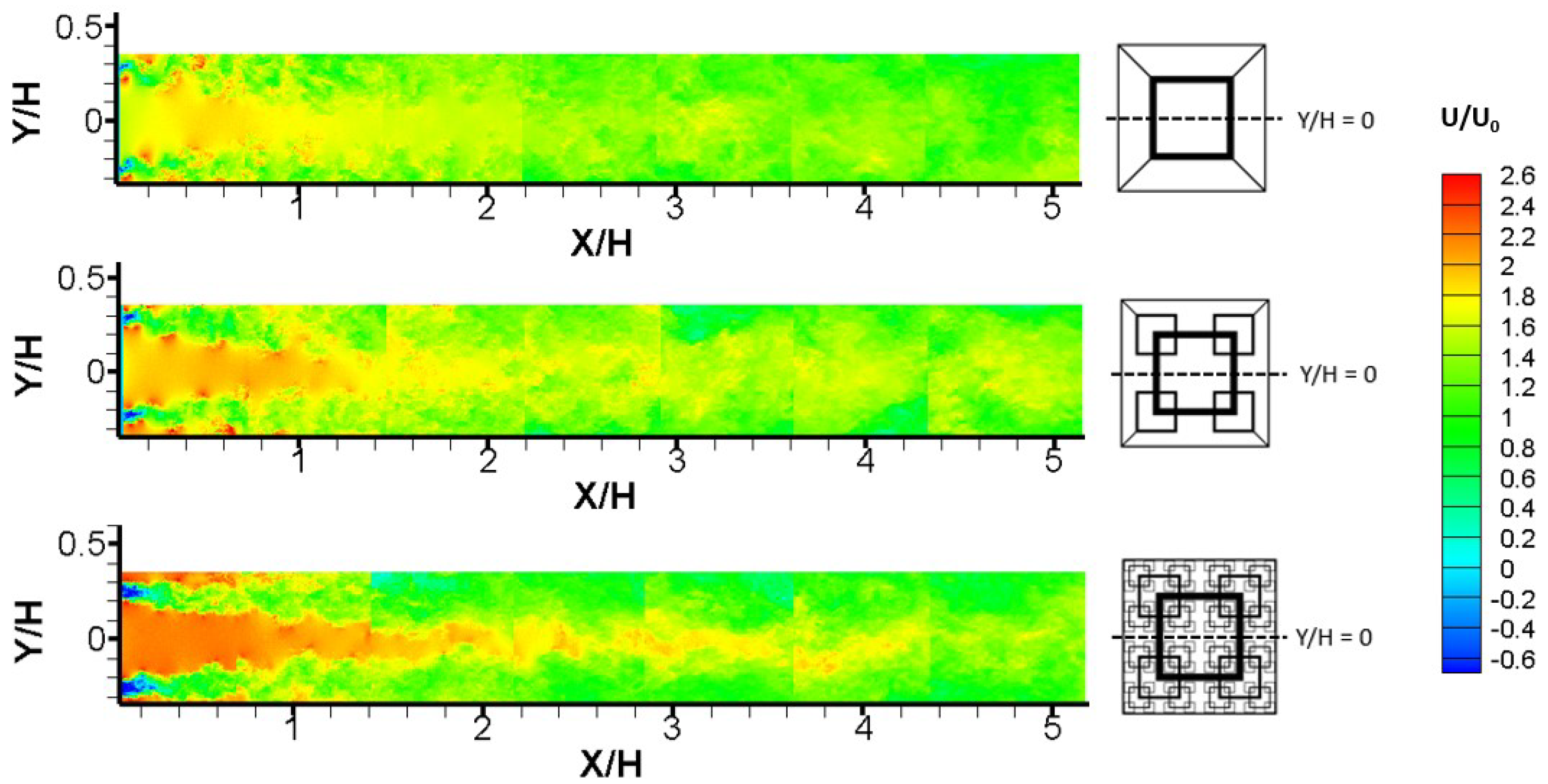
The instantaneous velocity fields in
Figure 3 show that the division between the major jet and two adjacent wakes becomes more visible as additional fractal scales are added to the fractal grid (from FG1 to FG4). The near-wake is characterized by a reversed flow region. Immediately behind FG1, the reversed flow region is within
= 0.1. It keeps increasing to
= 0.17 for FG2 and reaches
= 0.2 for FG4, owing to the cumulative reversed flow from each bar of different scales. In addition, as
N increases the central jet becomes more intensive, evidenced by the highest
(along the centerline) for FG4 and the lowest for FG1. The enhancement of jet velocity is about 25% comparing FG4 and FG1. The accelerated jet flow formed by the largest square is expected due to the gradual increase in blockage ratio with increasing
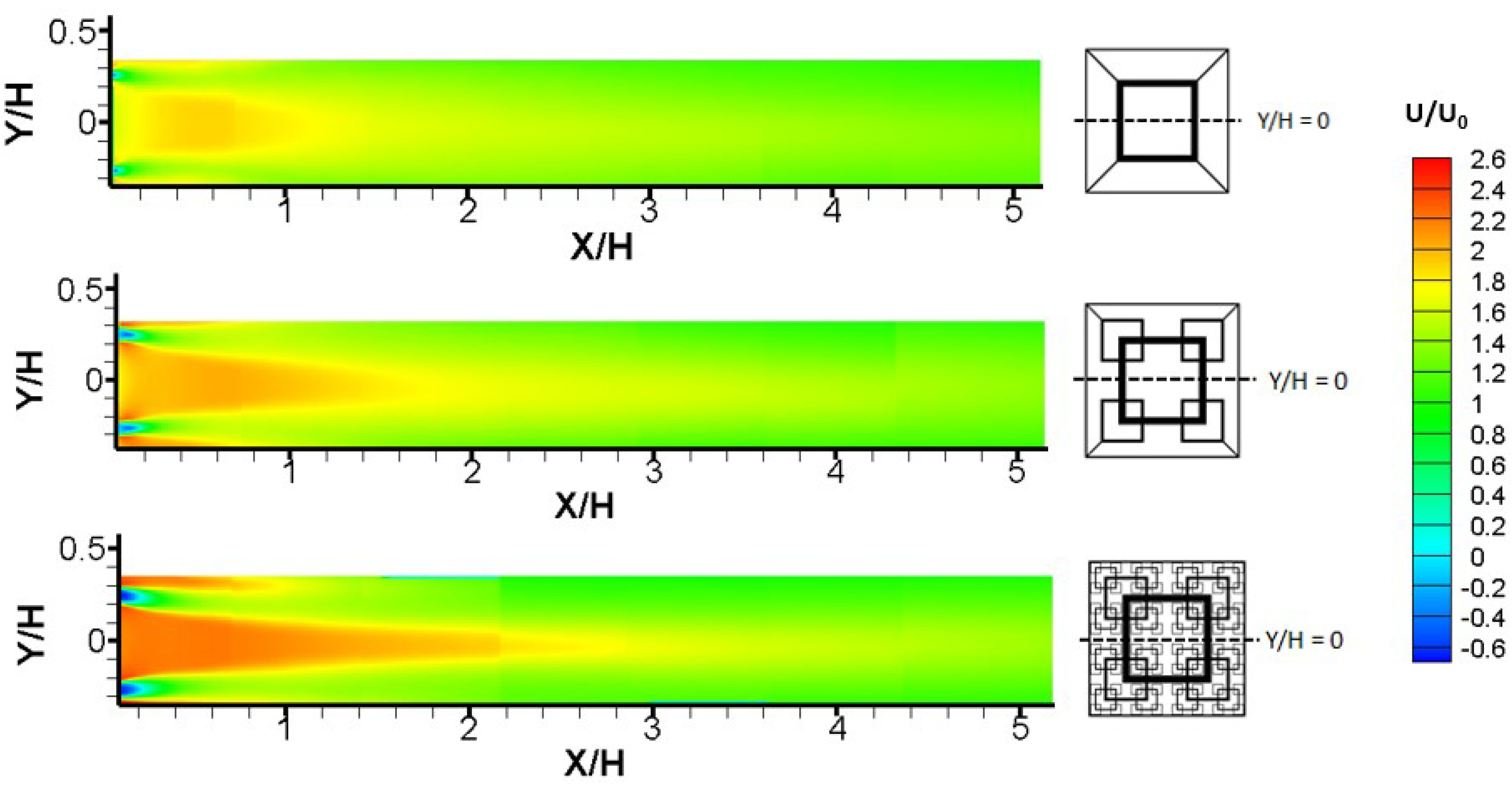
N. Meanwhile, the jet becomes narrower and intensifies with two major wakes occupying larger areas before merging together. The ensemble-averaged velocity fields in
Figure 4 confirm this flow characteristics with smoothing division of the central jet and two symmetric wake regions.
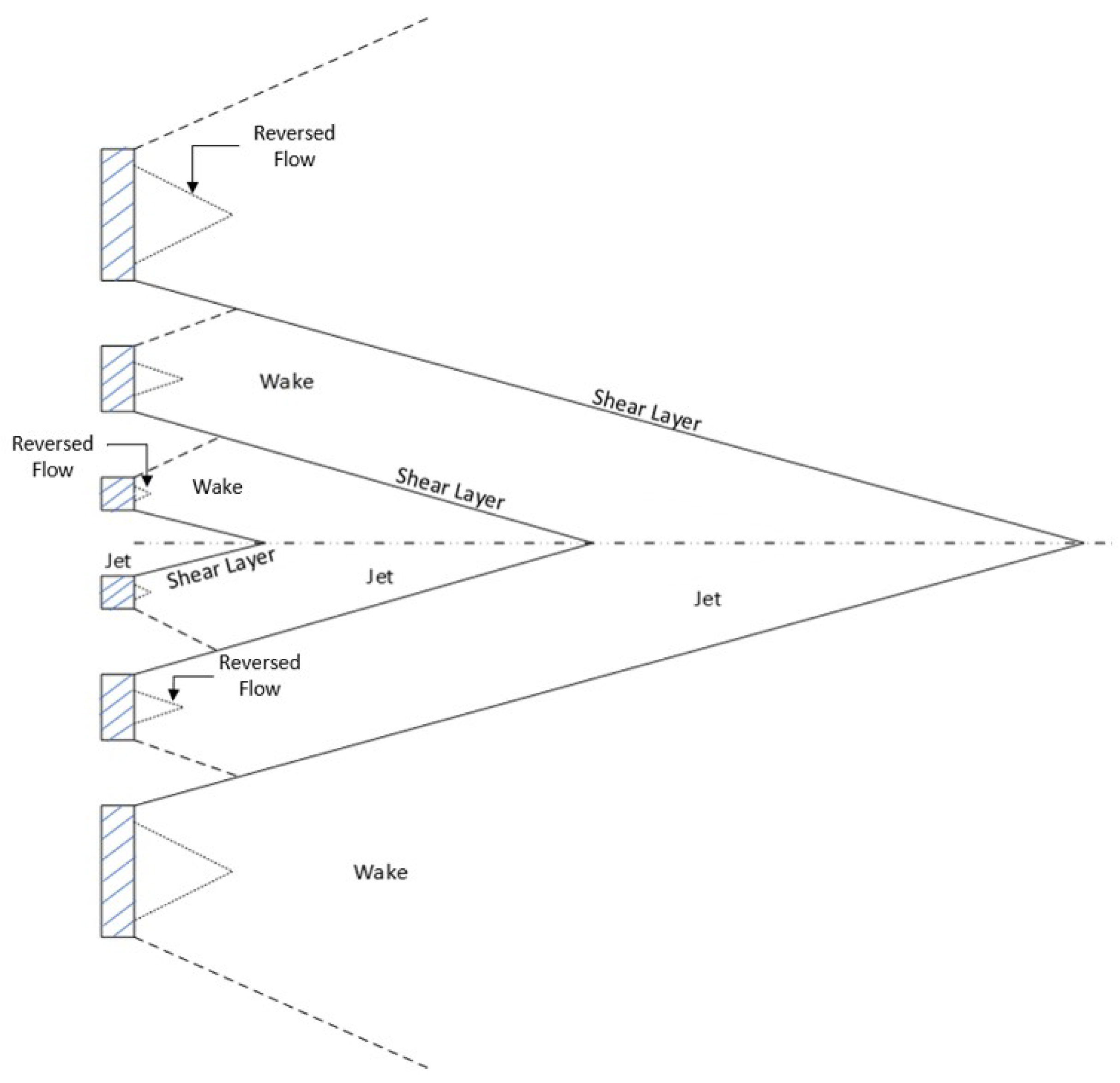
A conceptual diagram of the different flow regions induced by a fractal square grid is illustrated in
Figure 5. Several typical flow regions are marked—jet, wake (reversed flow), and shear layers. The distribution of each flow feature is directly related to the number of length scales of the grid, with a bar causing a wake and an opening (space between the bars) causing a jet. A shear layer of steep velocity gradient occurs between the jet and wake region, which drives a significant increase in the momentum transport between these regions. A detailed view of the instantaneous streamlines of these different flow regions can be seen in
Figure 6.
3.2. Effect of Multiple Scales on Turbulence Statistics
The change in the flow structure by the addition of multiple scales highlights the significance of interaction of the multiple scales, which is expected to affect the turbulence statistics, responsible for enhanced turbulent mixing and heat transfer rate. The streamwise, , vertical, , turbulence intensities and the Reynolds shear stress or RSS, , of the turbulent flow downstream of each fractal grid are examined in this section. They are critical quantities in the design of effective mixers, heat exchangers, and other flow control devices.
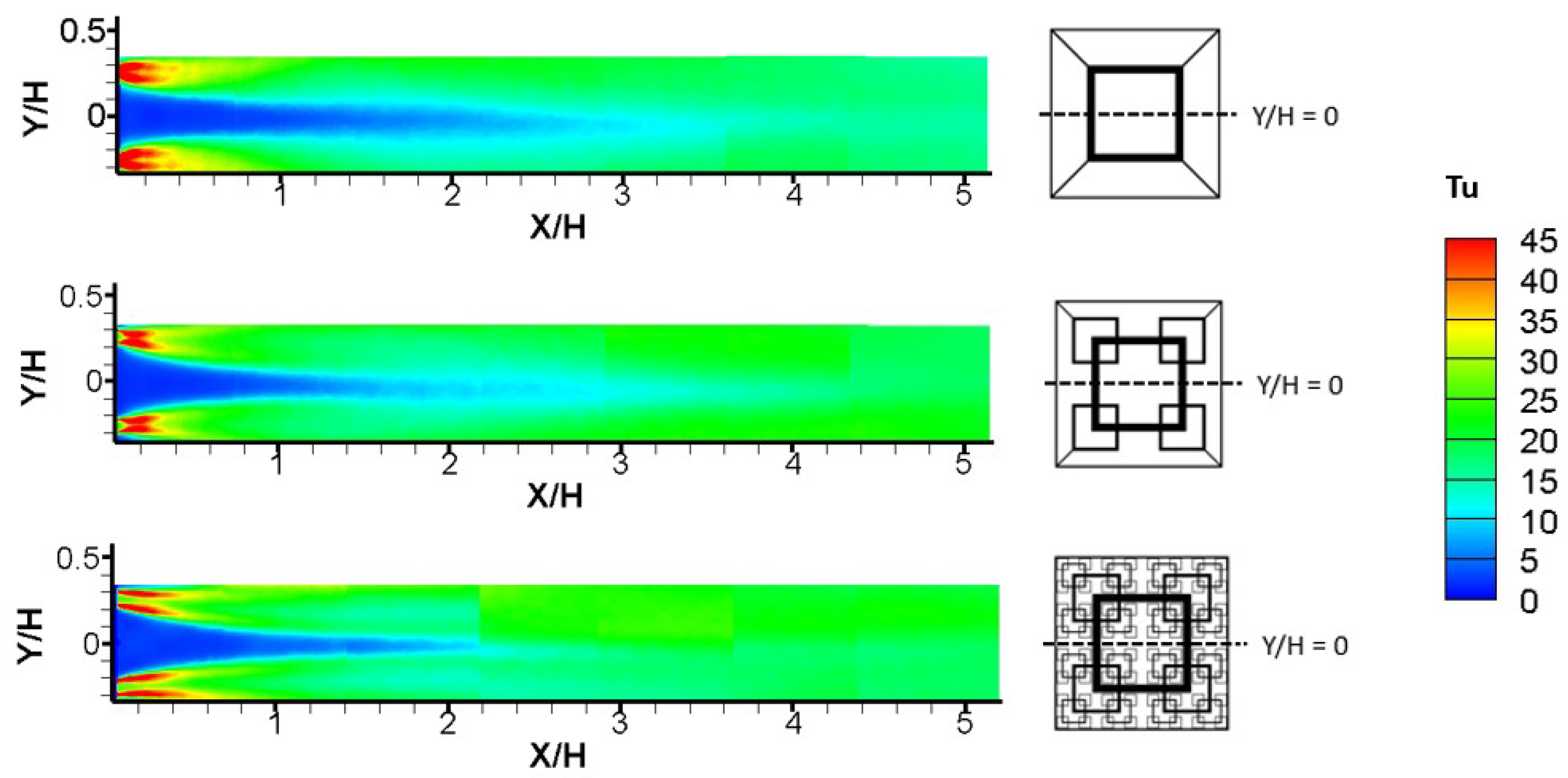
The contour plots of streamwise turbulence intensity
, shown in
Figure 7, exhibit common characteristics for the set of fractal grids. The turbulence intensity level varies remarkably for the different flow features identified in
Section 3.1. Immediately behind the largest bars the highest
is generated by the shear layers, reaching 45% for all fractal grids, where turbulence is reduced by half in the wake region. The central major jet, of the lowest
less than 5%, is observed just behind the grid. The center line (
y = 0)
is subject to an increase from the lowest 0–5% to the moderate level of 20–25%. The spatial distribution of the
behind the fractal square grids is consistent with that of previous DNS results in [
16].
Clear differences are observed in the turbulence intensities in the induced flow; however, when including smaller scales gradually by systematically changing the iteration
N, which have not been previously reported. The high
immediately behind the grid displays an elongated trend as smaller scales present and interaction of multiple scales occur. Most distinctly, the centerline
increases downstream of the grid at a different rate: at
= 1, sharing a very similar
level of 5% but at
= 3 the
reaches different level of 12.5% (FG1), 13.5% (FG2) and 20% (FG4). The flow behind the grids of
N = 3 reported by [
16], is similar to the current FG2 that falls in between the two extreme cases. The vertical turbulence intensity
, in
Figure 8, generally follows the same trend with respect to increasing
N as that of
, but with a lower magnitude. The level of
with respect to
, expressed in terms of the global isotropy parameter
/
, was found to match well with the results presented from previous PIV experiments [
17].
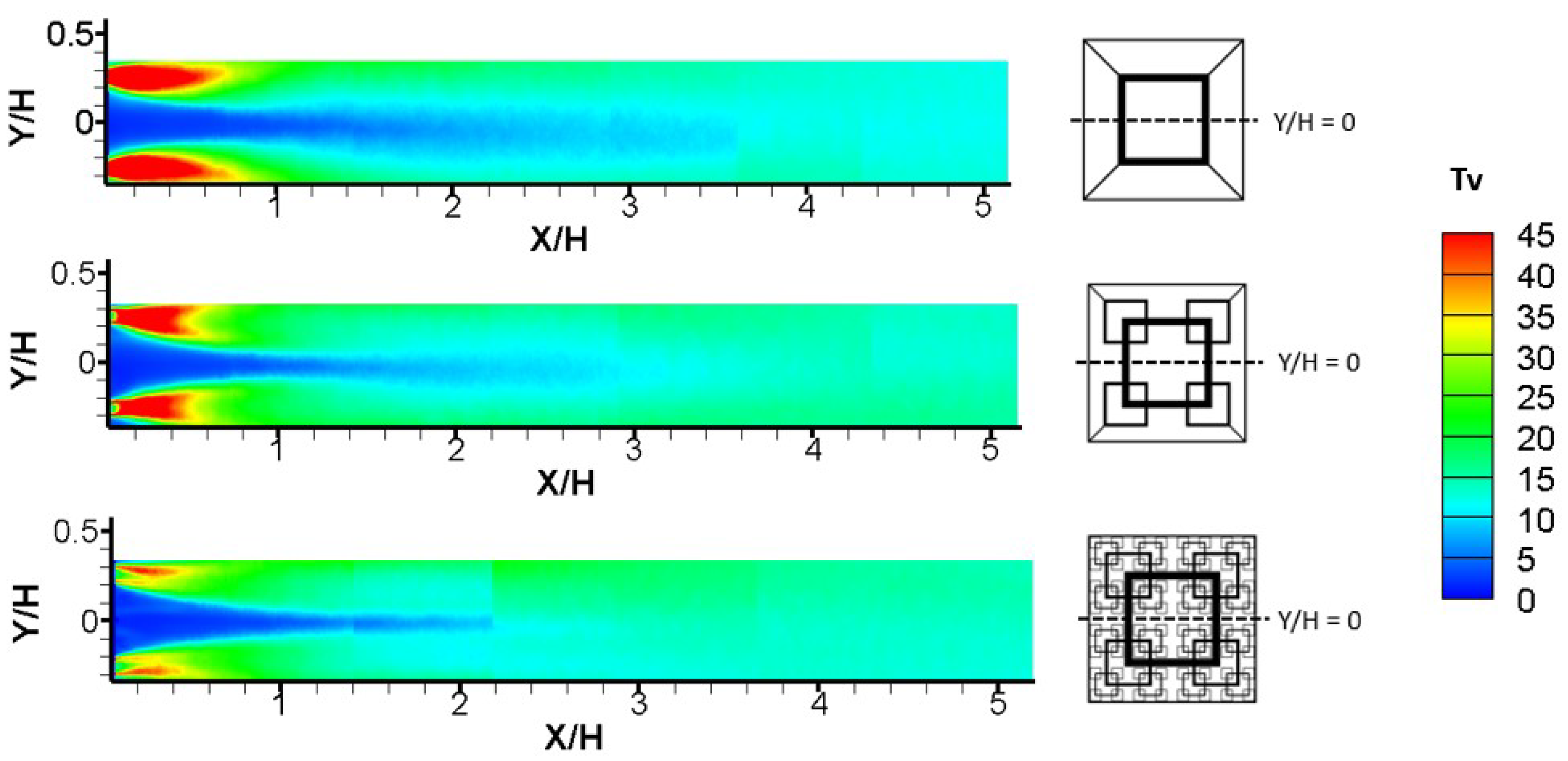
The distribution of the Reynolds shear stress (RSS)
of turbulent flow induced by each fractal square grid is shown in
Figure 9. The high magnitude of RSS immediately behind each grid, is associated with the strong shear between the jet and wake areas. The most intense region is more protracted as
N increases, from
= 0.6 for FG1 to
= 1.0 for FG4. The RSS contours behind the FG4 show a notable increase along the shear layer between the large jet region and the outer adjacent wakes of the flow. This is attributed to the effect of the shear layers enhanced from the interaction between the multiple jet and wake regions surrounding the largest wakes. This effect can also be seen in the RSS distribution of the FG2, but not nearly as intense, which is evidenced that each additional scale (even the smallest ones) has a significant impact on the momentum transport in the flow. The increase in the momentum transport between the multiple jet and wake regions leads to enhanced turbulent mixing among different length scales.
3.3. Revisit the Wake Interaction Length Scale Model
The wake interaction length scale model, introduced by Mazellier and Vassilicos (2010) [
10], has been extensively used to predict how far downstream the centerline turbulence intensity reaches its peak value. This model relates the location of the peak streamwise turbulence intensity
along the fractal grid’s centerline to the scales of the largest bars
and
:
where
and
is the wake interaction length scale coefficient. The coefficient
was originally determined to be a constant (0.45) based on data for fractal square grids having a similar blockage ratio [
10]. However, it has been later realized to vary dramatically depending on grid geometry, inflow conditions and experimental facility, etc. [
16,
17,
18,
24,
25]. The flow structure and turbulence statistics, in
Section 3.1 and
Section 3.2, evidenced the importance of the smaller scales in addition to the largest scale. Therefore, it is reasonable to account for the effects of smaller scales into the model to better predict
.
Using the framework of the wake interaction length scale model, we examined both the streamwise turbulence intensity and the vertcial turbulence intensity , at the center line, which are readily available via PIV tests. All fractal square grids have the same = 131.8 mm and = 11.7 mm, therefore = 1487.3 mm is kept constant in this study. By maintaining the same parameters of , , , and across the set of fractal square grids, the effect of additional fractal iterations can be determined.
The peak location
and the peak turbulence intensities are summarized in
Table 2. It can be seen that
varies with fractal grids of the same dimensions of the largest bar or
. Therefore, the wake interaction length scale model proposed by Mazellier et al. (2010) [
10] does not seem to capture the trend of the turbulence intensity of the fractal square grids tested here, which are of identical
and
but different blockage ratio
, varying with the number of fractal iterations,
N.
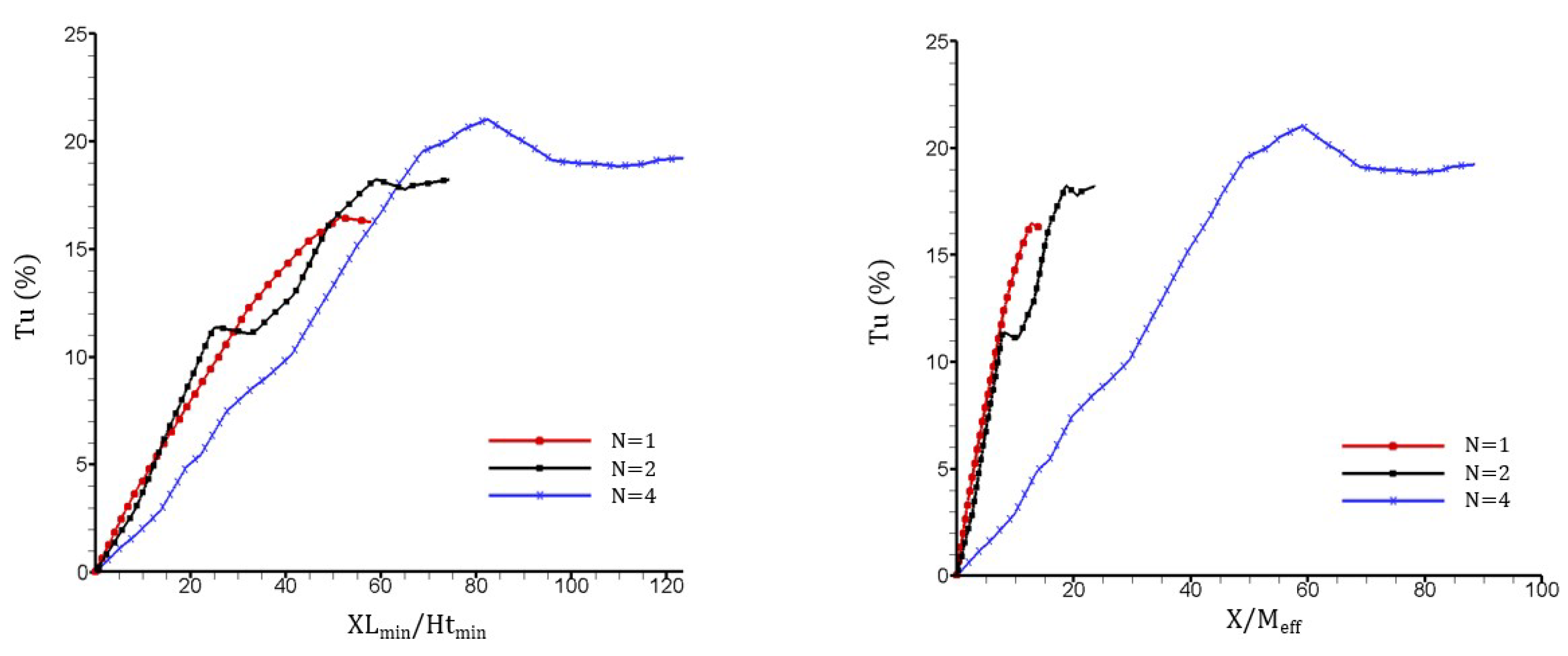
Figure 10a and
Figure 11a compare the centerline streamwise and vertical turbulence intensities,
and
, normalized by the smallest scale
, for the set of fractal square grids.
Figure 10a indicates that the normalized peak location shifts downstream gradually with additional scales being introduced (by varying the iteration,
N). It is further reasoned that the location of the peak turbulence intensity is associated to not only the largest and smallest scales, but the complex interaction among them. To incorporate the effects of multiple scales and thereof interaction, the effective mesh size
is considered. This scaling parameter accounts for every scale with the fractal perimeter
P and the blockage ratio
, instead of only the largest ([
10]) or the smallest scales ([
14]). When normalized by
,
shifts downstream with
N varied from 1 to 4, following an exponential trend (
Figure 10b). Therefore, we propose to include the effective mesh size
explicitly into the model, to predict the change in location of
with each additional scale relative to the single scale grid. The modified wake interaction length model is expressed as follows:
and
where
is the location of peak turbulence intensity for grid of
N iteration,
and
are the effective mesh size of the grids of the fractal iteration
N and 1, and
is the iteration scaling coefficient derived from the experimental data.
grows exponentially with
N for both the streamwise and vertical turbulence intensities, which is approximated in Equation (
11). The modified model was tested using data presented by Nagata et al. (2017) [
22]. To set the comparable base parameters of FG1,
takes into account different blockage ratio
and
for fractal grids in this study and in [
22]. It is interesting that values of
are nearly the same for the current data and [
22] summarized in
Table 2, even though the two sets of grids are of different
and
. It is noted that the values of
were obtained from the set of fractal square grids in our experiments and may not apply under other experimental conditions.
The exponential trend of the location
with increasing
N can be understood by the various dimensions of wakes generated by the different sized bars. First, the addition of smaller scales to the grid create multiple shear layers surrounding the wakes from the largest bars, leading to an elevated and elongated region of turbulence production. Furthermore, the additional scales enlarge the reversed flow areas immediately behind the grid, and the consequential increase in blockage ratio causes an acceleration of the flow through the center of the grid. The instantaneous streamlines of the flow behind the reversed flow areas, in
Figure 6, diverge away from the grid centerline, and this trend is more intense as
N increases. Such a trend has also been noted in the DNS simulations comparing grids with increasing thickness ratios and increasing blockage ratios [
16]. Overall, this flow pattern leads to the tendency for the largest wakes to meet further downstream as
N increases.
The magnitude of the peak centerline turbulence intensities was compared in order to determine the effect of the additional scales. Previously, the magnitude of the peak turbulence intensity was proposed to be proportional to
/
for fractal square grids, where
is the drag coefficient of the largest bars of the grid [
17]. Subsequent research focused on the largest scale being the dominant factor to determine the peak turbulence intensity magnitude, i.e.,
/
[
18,
25]. This relation has shown to be true for both multi-scale and single-scale grids having different ratios of
/
. For example, single square grids with a higher ratio of
/
and lower blockage ratio are found to produce higher centerline turbulence intensities than fractal square grids [
18]. While the drag of the bars is not directly measured here, it is assumed to be the same and will not change the results because the dimensions of the largest bars are identical for each grid.
Regarding the magnitude of the centerline turbulence intensities, our results show that each fractal grid generates a different level of turbulence along the centerline, for both the streamwise and vertical turbulence intensities, as summarized in
Table 2. The peak centerline turbulence intensity follows approximately linear relationship, if normalized with the effective mesh size
. We find that not only do the additional fractal scales influence the location of peak turbulence intensities, but their magnitude as well.
3.4. Pressure Drop across Fractal Square Grids
While the effect of multiple scales on the turbulence intensity and Reynolds shear stress is key to understand the dynamics of fractal grid-generated turbulence, the static pressure drop across the grid is essential to effectively implement such a flow control device in practical engineering applications. Therefore, the non-dimensional pressure drop at
is chosen to compare the set of fractal grids. The level of pressure drop is primarily linked to the increasing blockage ratio,
, with the increased fractal iteration
N [
23]. This is not different from what we understand regarding conventional or uniform grids. It would be difficult to quantitatively compare the magnitude of pressure drop in the current results with the previous wind-tunnel experiments, due to the difference in the inflow conditions and grid mounting mechanism. Nevertheless, the current results follow a similar trend to the previous experiments of a fractal square grid, single square grid, and conventional grid [
18].
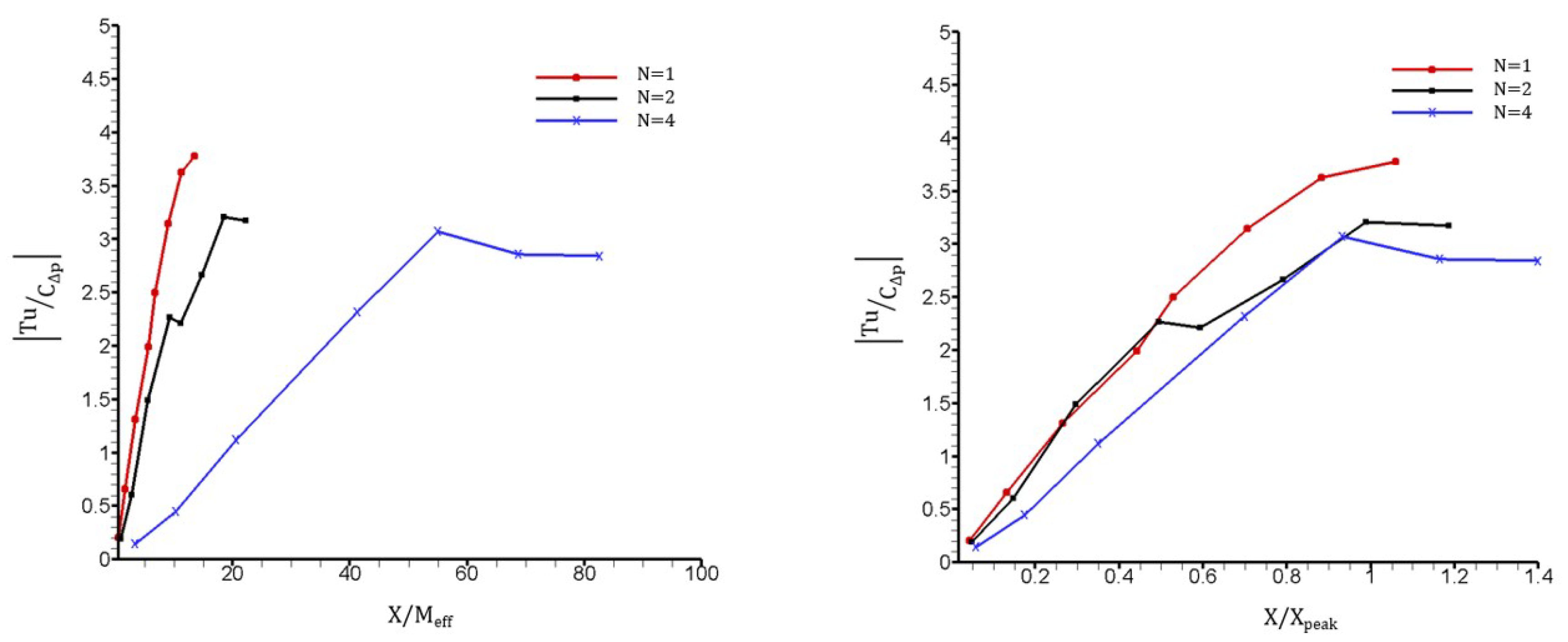
The ratio of the centerline turbulence intensity to the static pressure drop (
) of the set of fractal grids is in
Figure 12. Immediately behind the grid, the ratio of the turbulence enhancement to the pressure loss of each fractal grid is comparable. However, further downstream the expense of pressure caused by the increase in blockage ratio
(with increasing
N) becomes more significant than the enhancement in the turbulence intensity. As the downstream location increases, there is a clear difference in the performance of each grid: the FG1 being most effective past
= 0.5, with a 24% increase over that of FG4 at
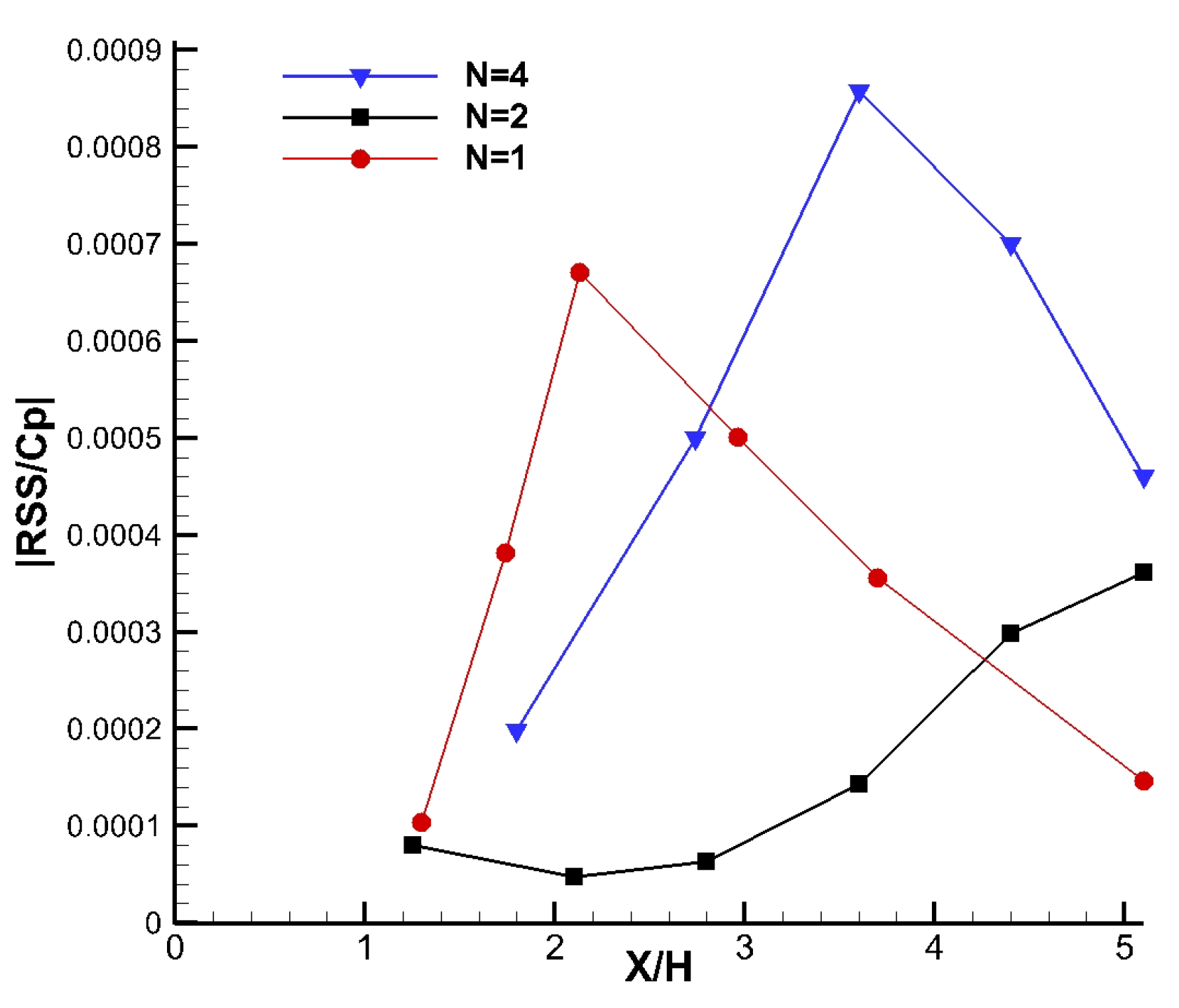
. Additionally, the ratio of Reynolds shear stress (RSS) to the pressure drop of the set of fractal grids is shown in
Figure 13. RSS is another measure of momentum transport and turbulent mixing. Here RSS is averaged vertically using the PIV data in the measurement plane (
Figure 9). Because the high values of RSS are not at the centerline, it has rarely been discussed in previous studies. The RSS downstream of FG4 is remarkably higher than FG1 further downstream. In particular, the maximum of RSS induced by FG4 is doubled that of the FG1.
The ratio of RSS to the pressure drop suggests that the addition of the multiple scales creates a dramatic increase in the momentum transport, attributed to the interaction between the multiple jet and wake regions. When adopting fractal square grids to design flow mixers and heat exchangers, although the level of turbulent mixing or enhanced heat transfer is often the primary design parameter, it is desirable to the maintain the amount of energy to compensate pressure loss at a reasonable level, depending on specific objectives in engineering applications. It should be noted that, the trend of
or
varies downstream for each of the grids. In case that a particular distance to install a grid is specified,
Figure 12 and
Figure 13 are helpful to determine which grid best fits the requirement. Fractal grids with more scales would be advantageous if a longer distance is required for turbulence enhancement.