Abstract
In the present paper, direct numerical simulation (DNS) and particle image velocimetry (PIV) have been applied complementarily in order to generate a database of near-wall turbulence properties of a highly turbulent jet impinging on a solid surface under different inclination angles. Thereby, the main focus is placed on an impingement angle of , since it represents a good generic benchmark test case for a wide range of technical fluid flow applications. This specific configuration features very complex flow properties including the presence of a stagnation point, development of the shear boundary layer and strong streamline curvature. In particular, this database includes near-wall turbulence statistics along with mean and rms velocities, budget terms in the turbulent kinetic energy equation, anisotropy invariant maps, turbulent length/time scales and near-wall shear stresses. These properties are useful for the validation of near-wall modeling approaches in the context of Reynolds-averaged Navier–Stokes (RANS) and large-eddy simulations (LES). From this study, in which further impingement angles (, ) have been considered in the experiments only, it turns out that (1) the production of turbulent kinetic energy appears negative at the stagnation point for an impingement angle other than and is balanced predominantly by pressure-related diffusion, (2) quasi-coherent thin streaks with large characteristic time scales appear at the stagnation region, while the organization of the flow is predominantly toroidal further downstream, and (3) near-wall shear stresses are low at the stagnation region and intense in regions where the direction of the flow changes suddenly.
1. Introduction
Impinging jets are used in a variety of engineering applications as they enable localized heat and mass transfer, e.g., cooling of electronic components, quenching of metals and glass, cooling of turbine-blades or drying of paper and other materials. Given their practical relevance, several jet geometries and flow conditions were examined, like nozzle shapes, Reynolds number effects, the influence of jet-to-plate spacing, pulsed jets, flame impingement, ribbed walls, jet impingement angle and many more. From the gained insights, various empirical correlations for the practical use of impinging flows were derived. Reviews of experimental studies, numerical modeling, general uses and performance of impinging jets can be found in [1,2,3,4].
Characterized by a strong wall/flow interaction process, impinging jets feature very complex flow properties including the presence of a stagnation point, shear boundary layer development in the free jet region and strong streamline curvature. In this respect, several experimental and direct numerical simulations (DNS) studies have been carried out in the past (e.g., [5,6,7,8,9,10,11,12,13,14,15,16,17]) in order to provide a deeper understanding about the underlying physical effects in such flows. The majority of these studies were focused on a single jet impinging normally on a heated solid surface using well-defined, fully-developed turbulent inlet conditions. Today, this specific jet configuration serves as a model geometry for a wide range of engineering application and is often used to validate turbulence models in the context of Reynolds-averaged Navier–Stokes (RANS) [18,19,20] and large-eddy simulations (LES) [21,22,23].
Regarding experimental studies focusing on the general flow characteristics of fully-developed turbulent jets impinging normally on a solid surface, Copper et al. [7] used hot-wire anemometry (HWA) and laser doppler velocimetry (LDV) techniques to determine mean velocities and Reynolds stresses at different wall-normal traverses. Fairweather and Hargrave [10] applied particle image velocimetry (PIV) to analyze the recirculation zone within the flow that carries material from the periphery of the wall-jet back to its initial regions. Regarding turbulent flow dynamics at the stagnation region, Tummers et al. [5] reported on detailed near-wall measurements of mean velocities and Reynolds stresses using two-component LDV and PIV. Furthermore, features of the budget of turbulent kinetic energy and turbulent stress anisotropy in the stagnation region were examined by Nishino et al. [8] by means of particle tracking velocimetry (PTV). This study revealed that the turbulence is almost in an axisymmetric state at the stagnation point and that negative production of turbulent kinetic energy takes place in the vicinity of the wall, which is compensated by the pressure diffusion. Besides this, the dynamics of coherent structures in a single impinging jet were examined by Hall and Ewing [24], among others, using pressure transducer and microphone measurements of the instantaneous pressure field at the wall. The measurements indicate that large-scale ring structures are present at the stagnation and wall-jet regions, which act to promote the heat transfer. Other aspects like Reynolds number effects, heat transport phenomena or the influence of jet-to-plate spacing have been also addressed in various experimental studies, e.g., [6,25,26].
With respect to numerical investigations, existing DNS studies of fully-developed turbulent jets impinging perpendicularly on a solid surface are mostly limited to moderate Reynolds numbers. Satake and Kunugi [13] analyzed the flow mechanism by which eddies are generated at the edge of the round nozzle and transported into the impingement region for a Reynolds number of . Flow characteristics and heat transport phenomena in a plane turbulent impinging jet () were addressed by Hattori and Nagano [15]. The authors provided turbulence statistics of the velocity and temperature, turbulent heat fluxes, local Nusselt numbers, budget terms of turbulent kinetic energy among other turbulent quantities. Recently, DNS of impinging jet flows at 10,000 and were performed with high spatial resolution and high order numerical methods by Dairay et al. [27] and by Wilke and Sesterhenn [28], respectively. The first study focused on the role of unsteady processes to explain the spatial distribution of the heat transfer coefficient at the wall, while the latter analyzed the influence of Mach number, Reynolds number and ambient temperature on the mean velocity and temperature fields. Several Reynolds analogies were also assessed. Besides a better understanding about the underlying physical effects in fully-developed turbulent impinging jets, comprehensive datasets for validation purposes were made available by means of DNS studies, which are difficult to obtain experimentally, especially budget terms of turbulent kinetic energy and other quantities.
While fully-developed jets impinging perpendicularly on a solid surface have drawn the interest of many researchers, little attention has been paid to impinging flows that are not fully developed and impinge at a particular angle, even though such flow conditions can be found in several technical applications. This is for example the case of hollow jets impinging on the cylinder wall in internal combustion (IC) engines [29] or fluid flow inside valves [30].
The present paper therefore intends to examine impinging flows more closely related to such technical applications at moderate Reynolds number. For this purpose, DNS and PIV techniques are applied complementarily with two objectives: first to examine and deepen the understanding of the turbulent flow features in oblique jets impinging on a solid surface; secondly to generate and provide a comprehensive database for model development and validation. Thereby, the jets’ inflow is highly turbulent (turbulent intensity of ∼10%) and not fully developed. Three different impingement angles of and are experimentally investigated, while DNS is only focused on the -inclination configuration, which includes the most flow features of both extremal cases of and inclination. In this context, a comprehensive database including fluid flow statistics, budget terms of the turbulent kinetic energy, wall shear stresses and turbulence scales are made available.
This paper is organized as follows. In Section 2, the applied measurement techniques and numerical approach are introduced. Next, the PIV and DNS setups of the oblique impinging jets are described (Section 3). Then, experimental results are reported and discussed (Section 4), for the three impingement angles of and . Subsequently, DNS results of the -inclination configuration are presented and compared with the experiment in Section 5. Finally, some concluding remarks are provided in the last section. For the sake of completeness, a detailed code verification study is provided in the Appendix A.
2. Methods
In this work, an isothermal fluid flow jet impinging on a solid flat wall is investigated using both experiment and DNS. In this section, the applied methods are introduced.
2.1. Direct Numerical Simulation
For a viscous Newtonian fluid flow with constant physical properties, the applied governing equations in the present DNS study are the continuity:
and momentum equations:
where is the velocity field, p the kinematic pressure and the kinematic viscosity.
The governing Equations (1) and (2) are solved numerically using a low-dissipative projection method proposed by [31], which was added to the open source C++ library OpenFOAM v1612+ (OpenCFD Ltd., Reading, UK). In contrast to other pressure correction methods, (e.g., pressure implicit with splitting of operator (PISO) [32] or semi-implicit method for pressure-linked equations (SIMPLE) [33]), no corrector loop is required, which significantly speed up the calculation. Moreover, it was shown by [34] that it is further less dissipative than the standard methods in OpenFOAM and well suited for time-resolved numerical simulations. The method is applied with a three-stage explicit Runge–Kutta scheme of second order accuracy for time integration [35].
The velocity-pressure coupling method can be summarized in three steps. First an intermediate velocity is computed explicitly for each Runge–Kutta step k using the momentum equation (Equation (2)), whereby the pressure term is omitted:
Here, is the time increment, the velocity at the n-th time step, the step size of the Runge–Kutta stages and the right-hand term of the momentum equation excluding the pressure gradient. Subsequently, the pressure is calculated in such a way that the velocity field satisfies the divergence free condition. It follows for the pressure Poisson equation that:
In the last step, the intermediate velocity field is corrected to obtain the final value of the velocity as:
In the present three-stage Runge–Kutta method, , and are chosen, leading to second order accuracy in time. It stands that and .
A second order central differencing scheme is applied for the convection term of the momentum equation, and a second order, conservative scheme is used for the Laplacian and gradient terms. Since the numerical resolution of the pressure Poisson equation is the crucial step in the present approach [36], convergence optimization and acceleration techniques are incorporated. In particular, the geometric agglomerated algebraic multigrid solver is applied for the resolution of the pressure equation including a diagonal-based incomplete Cholesky preconditioner. To reduce the mesh dependency, a smoother based on the Gauss–Seidel method is utilized.
2.2. Experimental Methods
Measurements of the flow field using planar two-component particle image velocimetry have been carried out. For this purpose, a frequency doubled-pulsed neodymium yttrium vanadate laser (, nm, 4.0 mJ/pulse, pulse separation s, Edgewave IS 4II-DE (EdgeWave GmbH, Würselen, Germany)) is applied to illuminate the aluminum oxide () seeding particles (m). Mie-scattering from the particles is recorded with a digital complementary metal-oxide-semiconductor (CMOS) camera (Phantom v711, Vision Research, Wayne, NJ, USA) and a 180-mm f/3.5 macro camera lens. A repetition rate of 20 Hz is used to ensure statistically independent samples. Three thousand PIV images were recorded for each region of interest to obtain reliable statistical results. All PIV images are processed with LaVision DaVis 8.2.1 software (LaVision GmbH, Göttingen, Germany). Interrogation windows of 24 pixels × 24 pixels and overlap are used, resulting to a vector spacing of ∼200 m.
3. Test Case
The experimental and numerical setups of the inclined impinging jet configurations are outlined in this section. Regarding the experiment, three different impingement angles of , and are investigated, while only the -configuration is computed in the DNS.
3.1. Experimental Setup
A representation of the measurement setup of the inclined impinging jet configuration is sketched in Figure 1. In the test section, dry air ( K, atm) seeded with particles (m) enters a settling chamber and streams through honeycombs followed by two screens in order to homogenize the flow. Then, the air stream is accelerated by means of a contraction nozzle and, before exiting, encounters a turbulence generating grid. Finally, the generated turbulent air stream leaves the square nozzle and flows along or impinges on a solid surface, respectively, according to the angle of inclination of the plate.
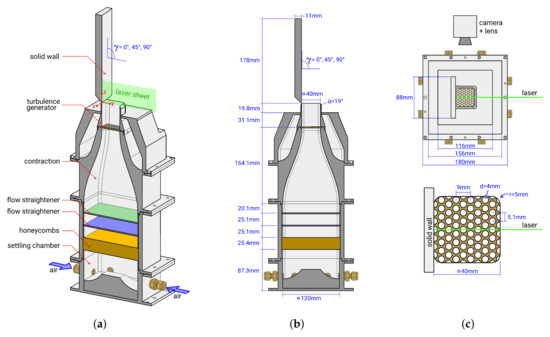
Figure 1.
Experimental setup of the inclined impinging jet configuration. (a) Trimetric view, (b) side view and (c) top view of the -configuration and turbulence generating grid.
The contraction nozzle has a length of 150 mm, an entrance area of 120 mm × 120 mm and an exit area of 40 mm × 40 mm. It results in a contraction ratio, , between the entrance and exit section areas of . At the contraction inlet section, the flow is inherently laminar with , while it reaches a Reynolds number of at the exit section of the nozzle. Thereby, due to the shape of the nozzle geometry, the flow field resembles a plug flow at the contraction exit with a very low turbulence level. A detailed design description of the nozzle geometry and estimations of the pressure drop and flow turbulence can be found in [37].
The turbulence generating grid is installed directly after the contraction. A 2.5 mm-thick perforated plate with hole diameters of mm is utilized. Note that the turbulence generating grid is not symmetric. The orientation of the grid with respect to the impingement wall, laser sheet and digital CMOS camera is shown in Figure 1c.
As indicated in Figure 1a,b, the inclination of the solid wall can be adjusted according to the desired impingement angle. Three different angles of , and are investigated as depicted in Figure 2. Thereby, the jet-to-plate spacing at the centerline of the jet ( and inclination) equals one hydraulic diameter of the nozzle exit. Figure 2 shows the regions of interest (highlighted in red) where PIV measurements are performed.
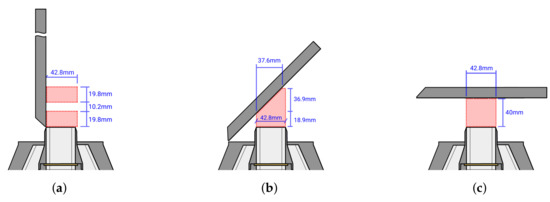
Figure 2.
Regions of interest for measurements. Red shaded areas: particle image velocimetry (PIV) measurements at (a) -, (b) - and (c) -inclination, respectively.
3.2. Numerical Setup
As pointed out above, only the -inclination angle case is numerically investigated. Figure 3 shows: (a) the portion of the experimental section that is numerically investigated, (b) the corresponding computational domain and (c) a map of the ratio between the local mesh size and the Kolmogorov length scale . Thereby, is computed for each location using the predicted local turbulent kinetic energy dissipation rate and the kinematic viscosity .
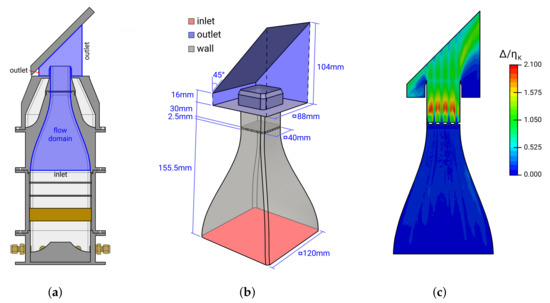
Figure 3.
Numerical setup of the -inclined impinging jet configuration. (a) Portion of the experimental section that is numerically investigated, (b) computational domain and boundary conditions and (c) map of the ratio between the local mesh size and the Kolmogorov length scale .
In line with the experimental setup, the computational domain (Figure 3a,b) consists of a contraction section, turbulence generating grid and impinging region after the nozzle. The settling chamber, honeycombs and flow straighteners are excluded in the numerical simulation. At the contraction inlet, a uniform velocity field is imposed, and no-slip conditions are utilized at the walls. Regarding the outflows, a velocity inlet/outlet boundary condition is used to allow entrainment of air from the surroundings. Thereby, the incoming fluid velocity is obtained by the internal cell value, while Neumann conditions are applied in the case of outflow. In contrast to the experimental setup, the small enclosed corner at the lower-left-hand side of the plate (see Figure 3a) is omitted in the numerical study. Here, an outflow condition is applied in order to allow an unrestricted fluid flow directed outward along the impinged wall in all directions. As will be shown later, this boundary condition has no influence on the region of interest around the stagnation point.
A block-structured, three-dimensional grid is employed in the present study. It consists of approximately 109 million control volumes and is refined around the perforated plate and towards the walls. Considering the commonly-used DNS spatial resolution criterion [38], the ratio of local mesh size and Kolmogorov length scale is below in almost the entire domain, as shown in Figure 3c, which ensures sufficient spatial resolution.
To avoid uncertainties caused by the initial solution, a fully-developed turbulent velocity field is generated by means of a separate large-eddy simulation (LES), which is interpolated on the numerical grid of the DNS. Afterwards, two flows through the domain (after the turbulence generating grid) are solved before sampling is started. In the case of LES, the same computational domain and boundary conditions are used as in the DNS study, while a numerical grid of approximately six million cells is utilized. Closure is obtained by means of the (wall-adapting local eddy-viscosity) subgrid scale model (WALE) by [39]. Furthermore, an universal equilibrium stress model based on the wall function of [40] is applied at the walls for the turbulent viscosity terms in order to bridge with a single cell the thin viscous sublayer, which is not fully resolved in the LES.
All the essential features of the investigated cases are summarized in the next subsection.
3.3. Summary of the Case Studies
Important features of the experimental and numerical investigations of the inclined impinging jets are listed in Table 1. It should be noted here that in the case of PIV measurements, all three inclination angles are investigated, while in the DNS, only the -configuration is examined.

Table 1.
Summary of the experimental and numerical studies with respect to the inclination angle.
4. Experimental Results
In this section, general flow features of the inclined impinging jets are analyzed by means of two-component PIV measurements. Thereby, mean flow properties and features of the turbulence dynamics as apparent in the impinging flows are examined and compared for different impingement angles. Mean and rms velocity profiles close to the nozzle exit, which may be used as realistic turbulent inflow conditions for numerical simulations, are provided in Appendix B.
4.1. Mean Flow Properties
Figure 4 presents contour plots of the time-averaged magnitude velocity at the mid-plane section of the jet. Results of the low-speed PIV measurements are shown for the -, - and -inclination configurations, respectively. Notice that an additional coordinate system is introduced with representing the wall-normal direction, and is the direction along the wall.
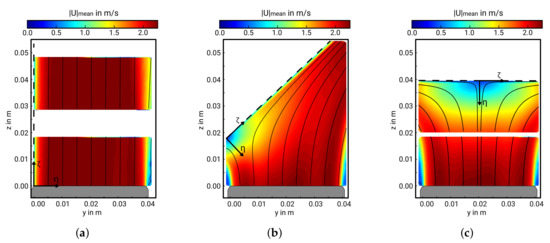
Figure 4.
Contour plots of the time-averaged magnitude velocity at the mid-plane section of the jet obtained by low-speed PIV measurements. (—) streamlines of the flow field; (- -) position of the wall. (a) -, (b) - and (c) -configuration.
Regarding the -inclination angle as shown in Figure 4a, the stream of dry air leaves the nozzle and flows along the solid surface. Streamlines are parallel to the wall, and a characteristic turbulent boundary layer is formed in the vicinity of the solid surface, where the effects of viscosity become significant. In contrast, mean flow features and streamline patterns are inherently different in the - and -configurations (Figure 4b,c). Here, the jet can be seen to decay and spread in the y-direction, then impinges on the plate, next deflecting and splitting into two main streams along the plate. Thereby, streamlines are highly curved, especially around the stagnation region.
Next, profiles of the time-averaged wall-parallel and wall-normal velocity components are examined. Results are shown for wall-normal traverses at , , for the - and -configurations and at , , 1 for the -configuration. Profiles are normalized by the bulk velocity of the jet and the hydraulic diameter of the nozzle D.
As can be clearly observed in Figure 5, general flow features of the -, - and -configurations are fundamentally different. In the case of -inclination, the flow field resembles a boundary layer flow where the mean flow is predominantly parallel to the wall, with the mean velocity varying mainly in the -direction. Thereby, the velocity component in the wall-normal direction is almost zero. In contrast, regarding the -configuration, is initially zero at the stagnation point (). Further downstream, a wall-jet is formed as the flow deflects in -direction, and the fluid is subject to a strong acceleration. Thereby, the velocity component in wall-normal direction decreases with decreasing wall distance. Flow features of both the - and -configurations can be retrieved in the -inclination case. Initially, as the flow deflects in -direction, a wall-jet begins to form in the -direction (Figure 5a) with a steep velocity gradient of in the -direction (Figure 5b), similar to that found in the -configuration. Further downstream, the mean flow is predominantly in the -direction, and the velocity component in wall-normal direction vanishes. At this stage, the flow field resembles that of a -configuration.
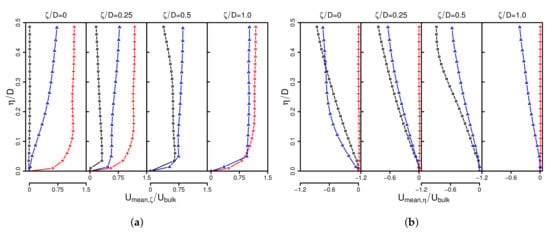
Figure 5.
Time-averaged velocity components in wall-parallel (a) and wall-normal (b) directions for different wall-normal traverses. (+) -configuration; (Δ) -configuration; (○) -configuration.
It turned out that the mean flow features and streamline patterns are inherently different in the -, - and -configurations. The -configuration resembles a boundary layer flow, while the stagnation region and wall-jets are predominant in the -configuration. Flow features of both configurations ( and ), particularly boundary layer flow properties, stagnation point and wall jet interactions, prevail in the -inclination case.
4.2. Turbulence Dynamics
The effects of the inclination angle on turbulence dynamics are analyzed in Figure 6 in terms of magnitude root-mean-square (rms) velocity and production of turbulent kinetic energy for several wall-normal traverses. Notice that in order to simplify the calculations of , the symmetric condition in the span-wise direction x is used.
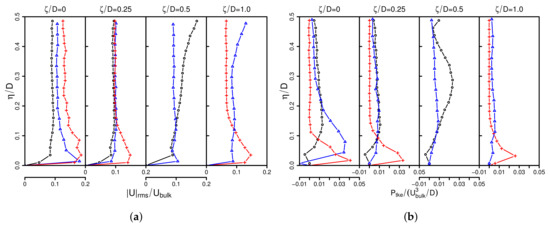
Figure 6.
Magnitude rms velocity (a) and production of turbulent kinetic energy (b) for different wall-normal traverses. (+) -configuration; (Δ) -configuration; (○) -configuration.
As is visible in Figure 6a, there is approximately self-similarity far away from the wall. Thereby, normalized rms velocities are all in the same order of magnitude and essentially uniform. In contrast, close to the wall, the effects of the inclination angle are more dominant. It appears that the -configuration contains the most vigorous turbulent activity, while rms velocities are small for the other inclination angles especially in the case of . Regarding the production of turbulent kinetic energy in Figure 6b, it is interesting to observe that appears negative at the stagnation point in the - and -inclination configurations, while it is always positive in the case of . Far away from the wall, values of are essentially smaller and more uniform. Therefore, it can be concluded that the flow dynamics are especially affected by the impinging region rather than by the far field. These findings are in good agreement with observations in fully-developed jets impinging normally on a solid surface (see, e.g., [8,21]) and hold obviously also for impinging flows that are not fully developed and impinge at a particular angle other than .
To summarize: The turbulence flow dynamics differ considerably for the different inclination angles under consideration. Root-mean-square velocities decrease with increasing inclination angle in the vicinity of the wall and are fairly small at the stagnation region. Furthermore, the production of turbulent kinetic energy appears negative at the stagnation point in the - and -inclination configurations, while it is always positive in the case of .
5. Numerical Results
After examining the general flow features of the inclined impinging jets with respect to the inclination angles using PIV measurement technique, DNS is utilized now to complement the experimental results of the -configuration. Relying on the experimental findings discussed above, this inclination angle is selected since it includes all the flow features predominant in turbulent impinging flows, namely boundary layer flow properties, stagnation point and wall jet interaction. First, numerical results are compared with the experiment in order to validate the DNS and vice versa. Then, budget terms of the turbulent kinetic energy, turbulence structures and wall shear stresses are analyzed.
5.1. Comparison with Experimental Results
Figure 7 shows predicted time-averaged wall-parallel (a) and wall-normal (b) velocity components in comparison to the PIV measurements at several wall-normal traverses (, , , ). In order to supplement the measurements, profiles at are additionally provided.
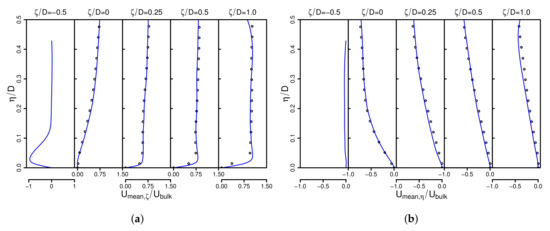
Figure 7.
Time-averaged velocity components in wall-parallel (a) and wall-normal (b) directions for different wall-normal traverses. Comparison of experimental results (○) with predictions of DNS (—).
Figure 7 reveals clearly that the jet is separated into a primary stream in the flow direction and a smaller secondary one in the opposite direction, leading to two distinctive wall-jets. Both experiment and DNS are able to reproduce this characteristic flow pattern. Furthermore, measurements and numerical results are very close to each other, which confirms the validity of DNS and experimental results in terms of mean flow.
A comparison of rms velocity components is depicted in Figure 8. Again, DNS results at , where experimental data are not available, are provided.
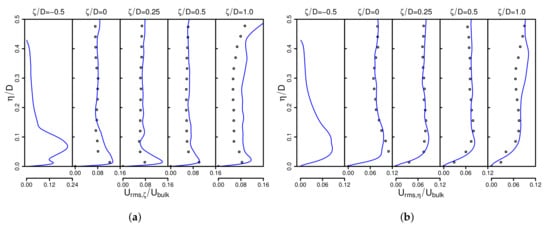
Figure 8.
Comparison of predicted wall-parallel (a) and wall-normal (b) rms velocity components with experimental results. PIV measurement (○); DNS results (—).
As it is apparent in Figure 8, the most vigorous turbulent activity appears in the vicinity of the wall, associated with high rms velocities that decline with increasing wall distance and remain approximately constant for . Thereby, it can be seen that rms velocities of the experiment and DNS differ slightly near the wall and close to the boundary of the PIV window (). These discrepancies may be caused by reflections of the laser light from the solid wall and low particle seeding density at the boundary of the PIV window, respectively. Note that measurements of the fluid flow close to a solid wall are very challenging and associated with uncertainties. Nevertheless, deviations of numerical and experimental results are fairly small for such circumstances, which leads to the conclusion that the present DNS is appropriate to describe the turbulent flow field in the -inclined impinging jet configuration.
5.2. Budget of Turbulent Kinetic Energy Transport
It was observed in the experiment (Section 4.2) that the production of turbulent kinetic energy appears negative at the stagnation point for inclination angles other than . This observation warrants a closer examination of budget terms of the turbulent kinetic energy equation at the stagnation point. Regarding isothermal turbulent flows, the balance equation of turbulent kinetic energy reads [41]:
where denotes the turbulent kinetic energy, is production, viscous dissipation, pressure-related diffusion, viscous diffusion and turbulent velocity-related diffusion due to third order moments. is the symmetric part of the velocity gradient tensor. Figure 9 shows a contour plot of the turbulent kinetic energy (a) and the corresponding normalized budget terms (b) along the wall-normal direction at the stagnation point (). Budget terms are normalized by .
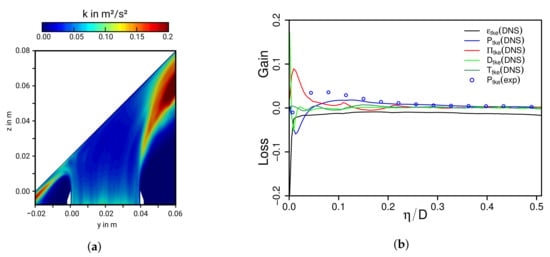
Figure 9.
Contour plot of the the turbulent kinetic energy k (a) and the normalized budget terms of k along the wall-normal direction at the stagnation point () (b). Budget terms are normalized using the bulk velocity and the nozzle exit diameter D.
As might be expected, values of k are high at the shear layers and increase as the jet develops. Apart from the jet-edges, the turbulent kinetic energy remains relatively small, especially at the jet core. Surprisingly, values of k are also fairly small at the stagnation region, roughly in the range of the inflow turbulence. The reasons for such a behavior around the stagnation point becomes clearer by examining the budget terms of k in Figure 9b, that substantially differ from those of other turbulent wall-bounded flows. Far away from the wall, where k is relatively small, viscous dissipation is the dominant term, while other contribution terms in Equation (6) are small. This holds more or less up to . Then, in the vicinity of the wall, steep gradients prevail in the wall-parallel and wall-normal direction, leading to negative production of turbulent kinetic energy. Thereby, dissipation and viscous diffusion decrease, while pressure-related diffusion, which is usually negligibly small in wall-bounded flows, becomes notably large. Indeed, it is the pressure-related diffusion term that balances the negative production of turbulent kinetic energy in the case of impinging flows. Finally, very close to the wall, dissipation is balanced by viscous transport, while the other terms in Equation (6) are zero, just as is the case for turbulent kinetic energy. A similar behavior of turbulent kinetic energy budget terms was reported in experimental studies of fully-developed jets impinging normally on a solid surface (see, e.g., [8]), which holds also in impinging flows that are not fully developed and impinge at a particular angle of . Note that PIV measurements of from the present experimental study are also displayed in Figure 9b. Thereby, DNS and experimental results agree very well far away from the wall, while they differ in the near-wall region. As mentioned before, discrepancies may be caused by reflections of the laser light from the solid wall or limited resolution in the PIV measurements. Nevertheless, the principle physical behavior with negative production close to the wall and small values elsewhere are clearly retrieved by both experiment and DNS.
To sum up, the blockage of the impermeable wall has a considerable effect on the generation and destruction mechanisms of turbulent kinetic energy k. In particular, it turns out that values of k are relatively small at the stagnation region. Thereby, production of turbulent kinetic energy appears negative close to the wall, which is balanced predominantly by the pressure-related diffusion term.
5.3. Turbulence Structures
As figured out in the previous sections, turbulent impinging jets feature very complex flow properties including the presence of a stagnation point, shear layers and strong streamline curvature. Their impact on vortical and turbulence structures is addressed in this subsection, with the main focus on the near-wall region. First, in order to obtain a global perception of the flow structures, coherent vortices are identified by means of the Q-criterion [42]. It is defined as , where is the velocity gradient tensor and Q its second invariant. represents the spatial region of a vortex and implies that irrotational straining is small compared with the vorticity [42]. Instantaneous isocontours of positive Q around the mid-plane section of the jet and in the vicinity of the impinging wall colored by the magnitude velocity are shown in Figure 10a,b, respectively. In order to illustrate the strength of flow circulation associated with the coherent structures, Figure 10c depicts the corresponding magnitude vorticity close to the wall.
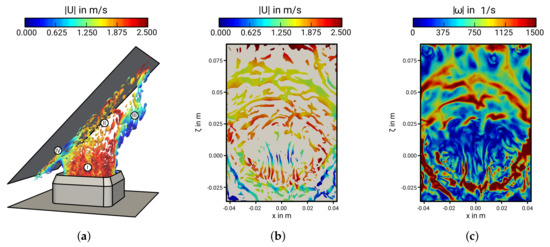
Figure 10.
Instantaneous isocontour of positive Q around the mid-plane section (a) and in the vicinity of the wall (b) and snapshot of the vorticity magnitude close to the wall (c).
Considering Figure 10a, four main regions associated with the general flow pattern of the inclined impinging jet and the resulting nature of turbulent structures can be distinguished. First, the jet core region close to the nozzle exit (I) is dominated by relatively small turbulent scales of uniform shape that are generated by the turbulence grid inside the nozzle. These flow structures are carried along with the main flow and seem to dissolve further downstream. Secondly, the wall jet directed outward along the wall (II), where the flow interacts with the solid surface and outer shear layer. Here, flow structures are considerably larger and toroidally organized, especially in the vicinity of the wall. Thirdly, the shear layer on the side away from the impinging wall (III), which is triggered by the interaction of the jet with the ambient fluid. Thereby, large coherent roll-up vortices are created by the induced shearing that increase downstream. Finally the stagnation region (IV), where the fluid is subject to a strong acceleration and stretching, leading to thin streaks orientated in the flow direction. The resulting instances of the large-scale structures on the impinging wall are shown Figure 10b. Here, it can be seen as well that coherent fluid flow structures are extremely elongated and axisymmetric at the stagnation region. Thereby, the magnitude velocity is small, which suggests that these flow structures persist for a significant period of time until they slowly migrate away. Further downstream, turbulent structures are predominantly toroidally organized among many other random structures within the background. These structures have a considerably higher magnitude velocity and convect outward along the wall. A similar conclusion of the organization of vortical structures close to the wall can be drawn by examining the vorticity magnitude displayed in Figure 10c. Vorticity appears small at the stagnation region with isolated stretched nests of concentrated vorticity that are orientated in the flow direction. Further downstream, vorticity becomes circumferentially interconnected resulting in ring structures of strong flow circulation that serve as precursors of large coherent turbulent eddies in the near-wall region.
Next, anisotropy invariant maps are utilized in order to analyze the underlying physics of the turbulence associated with the fluid flow structures in the inclined impinging jet configuration. For this purpose, Figure 11 shows plots of the second and third invariants, II and III, of the Reynolds stress anisotropy tensor defined as (see, e.g., [41]). Results are shown for wall-normal traverses at (a) and (b).
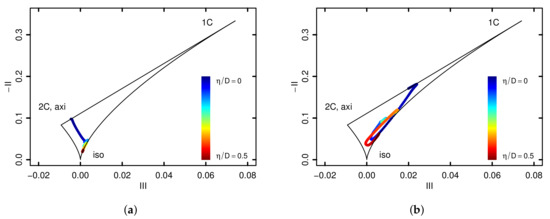
Figure 11.
Non-linear anisotropy invariant maps at (a) and (b).
In line with the visual appearance of the turbulent structures in Figure 10a, it can be clearly observed in Figure 11a that the turbulence is in fact axisymmetric at the stagnation point with a negative third invariant and one small eigenvalue of the Reynolds stress anisotropy tensor. Away from the wall, anisotropic turbulence decays on a more or less straight trajectory directed towards the origin. After reaching the plane-strain limit (III) at , which is located close to the jet shear layer facing the impinging wall, the turbulence tends towards the one-component direction. Subsequently, far away from the wall and close to the nozzle exit, the turbulence returns to the isotropic state. Here, turbulent structures have to a large extent a uniform shape. A rather different behavior of the turbulence appears farther downstream at the wall-jet region as depicted in Figure 11b. Very close to the wall, the turbulence is essentially two-component. Then, anisotropic turbulence reaches a peak at and is close to being axisymmetric far away from the wall with III. This behavior of the Reynolds stresses is very similar to that found in turbulent boundary layer flows, which confirms again the visual perception in Figure 10a.
Finally, characteristic turbulence length and time scales along the wall-normal traverse at the stagnation point () are provided in Figure 12. These data may be useful to evaluate turbulence models, especially in the context of RANS. Thereby, is the turbulence length scale, the Kolmogorov length scale and the Eulerian integral time scale of the velocity component i calculated using the temporal autocorrelation function of the recorded time series (see, e.g., [41]).
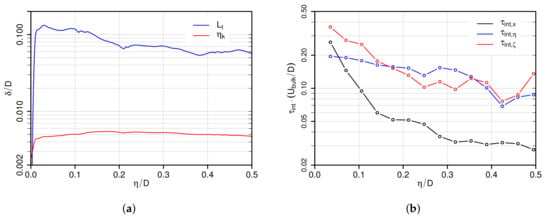
Figure 12.
Turbulent length (a) and time (b) scales as a function of wall distance. Turbulent length scale: ; Kolmogorov length scale: ; integral time scales: .
As it is expected, is small very close to the stagnation point, increases immediately and then declines gradually with increasing wall distance. Similar, is small close to the stagnation point, increases away from the wall and remains approximately constant for . Thereby, the energy containing turbulent length scales are approximately ten to twenty times larger than smallest scales . Regarding the integral time scales as shown in Figure 12b, they are indeed large at the stagnation point and decrease with increasing wall distance. This confirms that characteristic time scales of turbulent processes are relatively large around the stagnation point and that turbulent flow structures persist for a significant period of time at this region while they are convected slowly away.
By examining turbulent flow structures, it turns out that quasi-coherent thin streaks appear around the stagnation point. Thereby, the turbulence is essentially axisymmetric with large characteristic turbulence time scales. Further downstream, at the wall-jet region, the organization of the flow is predominantly toroidal, and the turbulence behavior is similar to that found in turbulent boundary layer flows.
5.4. Near-Wall Shear Stress
From the observations above, it is evident that the inclined impinging jet flow is characterized by a strong wall/flow interaction process. Close to the wall, Reynolds stresses vanish, and viscous shearing, exerted by the fluid on the impermeable wall, along with steep pressure gradients around the stagnation region dominate the fluid flow. Thereby, a thin but very important sub-layer is formed immediately adjacent to the solid surface. Usually, due to limited computing power, classical wall-function approaches are used in the context of LES and RANS to bridge with a single cell this very thin sub-layer where viscosity modifies the turbulence structure. However, it is well known that wall-functions based on the semi-logarithmic variation of the near-wall velocity do not apply under non-equilibrium flow conditions including impingement and steep pressure gradients, as is apparent in the inclined impinging jet (see, e.g., [43,44]). In such cases, advanced wall treatments are typically used, e.g., generalized wall functions [45], analytical wall-functions [46,47] or numerical integration of boundary layer equations [48], that produce the required value of the wall shear stress over the near-wall cell. Such values are difficult to obtain experimentally. It is therefore of particular interest to provide reliable reference data of wall shear stresses for validation purpose in order to appraise the assumptions made in the near-wall modeling approaches. For this reason and in order to explain the strong wall/flow interaction process in the inclined impinging jet flow, Figure 13 shows instances of the instantaneous (a) and time-averaged (b) absolute wall shear stress induced by the inclined jet on the wall.
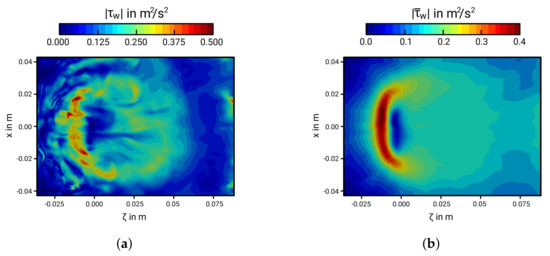
Figure 13.
Instantaneous (a) and time-averaged (b) instances of the absolute wall shear stress on the impinging wall.
Similar to fully-developed turbulent jets impinging perpendicularly on a solid surface, wall shear stresses are very low at the stagnation region and peak in its immediate vicinity (for a comparison, see, e.g., [5,49,50]). It is interesting to observe that, in the case of a inclination angle, the wall shear stress is predominantly concentrated at the secondary opposed wall jet region (), where the direction of the flow changes suddenly and the fluid is subject to a high acceleration in the wall-parallel direction. At the wall jet region in the main flow direction (), values of are considerably lower (approximately half the peak value of the opposed wall jet region), and the peak is significantly smoother and tends to smear out in the main flow direction. Furthermore, it can be clearly observed that the fluctuations in the near-wall shear stress are more pronounced at the opposed wall jet region, indicating strong transient fluid flow processes at this region. These observations suggest that the wall/flow interaction process depends inherently on the impingement angle and is obviously more intensive in regions where the direction of the flow changes suddenly and the fluid is subject to high acceleration in the wall-parallel direction.
Finally, profiles of the wall shear stress in span-wise direction x and in wall-parallel direction are provided in Figure 14a,b, respectively, which may be used for validation purposes in the context of LES and RANS.
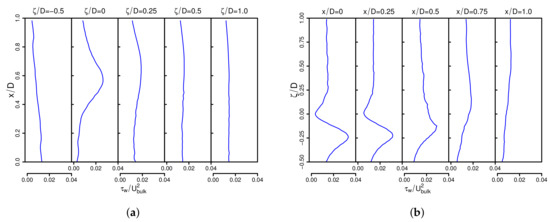
Figure 14.
Profiles of the wall shear stress in span-wise direction x (a) and in wall-parallel direction (b).
6. Concluding Remarks
Direct numerical simulation and particle image velocimetry have been applied complementarily in order to generate a database that allows characterizing the general flow features and turbulent flow properties of a highly turbulent, non-fully-developed jet impinging on a solid surface under different inclination angles (, , ), with the main focus on the -inclination. This comprehensive dataset includes near-wall turbulence statistics, budget terms in turbulent kinetic energy equation, anisotropy invariant maps, turbulent length/time scales and near-wall shear stresses that may be useful for the validation of near-wall modeling approaches of LES and RANS.
Some important observations found in the present study can be outlined as follows:
- I
- Mean flow patterns are inherently different in the , and jet configurations. In particular, the -configuration resembles a boundary layer flow, while the stagnation region and wall-jets are predominant in the -configuration. Flow features of both configurations, namely boundary layer flow properties, stagnation point and strong wall/jet interactions, prevail in the -inclination case, which represents therefore a good generic benchmark test case for a wide range of technical applications.
- II
- It turns out that the production of turbulent kinetic energy appears negative at the stagnation region in the - and -configurations, which is balanced predominantly by pressure-related diffusion. In the case of the -inclination angle, the production term is always positive.
- III
- By examining turbulent flow structures in the -configuration, it turns out that quasi-coherent thin streaks appear around the stagnation point. Thereby, the turbulence is essentially axisymmetric with large characteristic turbulence time scales. Further downstream, at the wall-jet region, the organization of the flow is predominantly toroidal, and the turbulence behaves similarly to that found in turbulent boundary layer flows.
- IV
- In the case of the -inclination angle, near-wall shear stresses are very low at the stagnation point and primarily concentrated at the secondary opposed wall jet region. This suggests that the wall/flow interaction process depends inherently on the impinging angle and is obviously more intense in regions where the direction of the flow changes suddenly and the fluid is subject to high acceleration in the wall-parallel direction.
Acknowledgments
The authors gratefully acknowledge the financial support by the DFG (German Research Council) Sonderforschungsbereich/Transregio SFB/TRR 150 and the support of the numerical simulations on the Lichtenberg High Performance Computer at the University of Darmstadt. Andreas Dreizler was financially supported by Gottfried Wilhelm Leibniz-Preis (DFG).
Author Contributions
Florian Ries and Martin Rißmann performed the experiments, which were conceived of and designed by Andreas Dreizler, Benjamin Böhm and Martin Rißmann. Martin Rißmann, Yongxiang Li and Florian Ries evaluated and analyzed the experimental data. Florian Ries implemented the numerical approach and performed the DNS, while Yongxiang Li and Dario Klingenberg verified and validated the source code. Dario Klingenberg generated the numerical grid and provided analysis tools. Florian Ries and Yongxiang Li treated and exploited the numerical data and analyzed together with Amsini Sadiki and Kaushal Nishad the numerical results. Florian Ries wrote the paper, while Amsini Sadiki and Andreas Dreizler further supported improving the manuscript. Amsini Sadiki, Andreas Dreizler and Johannes Janicka contributed by providing materials and computing resources.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Code Verification
The method of manufactured solution (MMS) is applied to verify that the discretized governing equations, as implemented in the source code, are solved consistently. A manufactured solution is an exact solution to a set of PDE’s that has been constructed by solving the problem backwards [51]. In this context, the analyst first selects a sufficiently differentiable function to describe the desired evolution of the variables in space and time. This solution does not necessarily satisfy the original set of PDE’s, therefore a corresponding set of source terms are manufactured by applying the set of PDE’s to and added to the source code in order to balance the system [52]. The resulting set of PDE’s including the source terms is then solved for different spatial and/or temporal resolutions. Finally, the order-of-accuracy in space and time is quantified and verified for the numerical approach, leading to a rigorous code verification in full generality. Further information about the concept and procedure of MMS can be found in [51,52,53,54].
Appendix A.1. Spatial Accuracy
A three-dimensional manufactured solution is chosen in the present study to quantify the spatial accuracy of the applied numerical approach. Thereby, the velocity field resembles a Taylor-Green vortex [55], which leads to the following smoothly varying solution for the velocity and pressure fields
where x, y, z are the coordinates in space. The solution is applied to the governing equations as introduced in Section 2.1 leading to non-zero source terms in the momentum equation (not shown here, due to its length), which are implemented in the source code. No source term appears in the continuity equation since the manufactured solution satisfies the divergence free condition. The kinematic viscosity is set to one to balance the order of magnitude of convection and diffusion terms equally in the momentum equation. A computational domain with for x, y and z is selected. Four equidistant computational grids consisting of 512, 4096, 32,768 and 262,144 control volumes are used for the verification study. Figure A1 shows a graph of the mean absolute errors (MAE) as a function of the mesh size for the magnitude velocity and kinematic pressure.
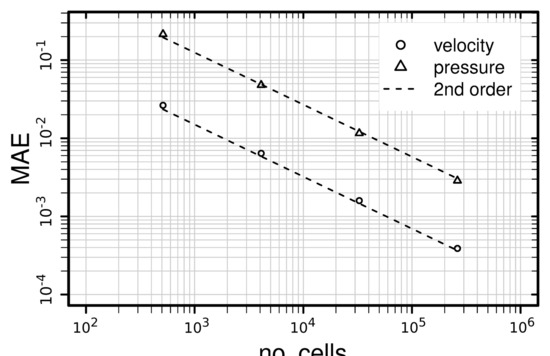
Figure A1.
Mean absolute error (MAE) as a function of mesh size for the magnitude velocity and kinematic pressure.
As it is apparent in Figure A1, the mean absolute error (MAE) of the magnitude velocity and kinematic pressure both drop by a factor of four with each mesh refinement, thus matching the second-order slope and verifying that the numerical approach is of second-order accuracy in space.
Appendix A.2. Temporal Accuracy
Next, the temporal accuracy of the three-stages explicit Runge-Kutta scheme for time integration is addressed. For this purpose, the following manufactured solution is selected
where t is the time. Note that a temporal analysis of the pressure is omitted, since no time derivative occurs in the Navier-Stokes equations. In accordance with the verification of the spatial accuracy, the solution is applied to the governing equations leading to non-zero source terms in the momentum equation and no source term in the continuity equation. For the analysis, the time step is gradually increased from up to by a factor of two and a time interval is chosen as . The resulting graph of the mean absolute error norm with respect to the time step size is depicted in Figure A2.
As it can be clearly observed in Figure A2, the global errors decrease by a factor of four with each time step size refinement, verifying that the numerical approach is of second-order accuracy in time.
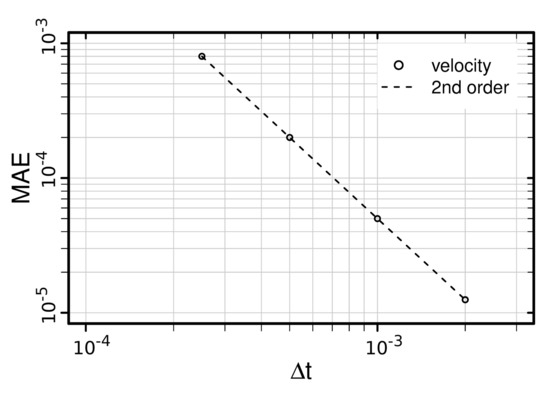
Figure A2.
Mean absolute error (MAE) as a function of time step size for the magnitude velocity and kinematic pressure.
Appendix B. Inflow Conditions for Numerical Simulations
Profiles of mean and rms velocities measured at mm downstream the nozzle exit are provided in Figure A3, which may be used as realistic turbulent inflow conditions for numerical simulations.
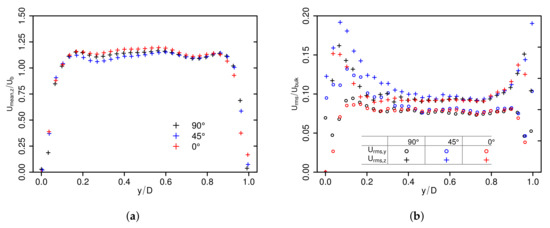
Figure A3.
Profiles of axial mean (a) and rms (b) velocities measured at 0.6 mm downstream the nozzle exit for the -, - and -inclination configurations, respectively.
Thereby, the velocity profiles are not fully developed at the nozzle exit and the turbulent intensities are of ∼10–20%, which is approximately two times the intensity found in fully developed turbulent flows in a square duct at a similar Reynolds number (see e.g., [56,57]). Furthermore, it is apparent, that measured inflow mean and rms velocity profiles differ slightly for different inclination angles, especially at the side facing the solid wall.
References
- Martin, H. Heat and mass transfer between impinging gas jets and solid surfaces. Adv. Heat Transf. 1997, 13, 1–60. [Google Scholar] [CrossRef]
- Jambunathan, K.; Lai, E.; Moss, M.A.; Button, B.L. A review of heat transfer data for single circular jet impingement. Int. J. Heat Fluid Flow 1992, 13, 106–115. [Google Scholar] [CrossRef]
- Viskanta, R. Heat transfer to impinging isothermal gas and flame jets. Exp. Therm. Fluid Sci. 1993, 6, 106–115. [Google Scholar] [CrossRef]
- Zuckerman, N.; Lior, N. Jet impingement heat transfer: Physics, correlations, and numerical modeling. Adv. Heat Transf. 2006, 39, 565–631. [Google Scholar] [CrossRef]
- Tummers, M.J.; Jacobse, J.; Voorbrood, S.G.J. Turbulent flow in the near field of a round impinging jet. Int. J. Heat Mass Transf. 2011, 54, 4939–4948. [Google Scholar] [CrossRef]
- Boughn, J.W.; Shimizu, S. Heat transfer measurements from a surface with uniform heat flux and an impinging jet. J. Heat Transf. 1989, 111, 1096–1098. [Google Scholar] [CrossRef]
- Cooper, D.; Jackson, D.C.; Launder, B.E.; Liao, G.X. Impinging jet studies for turbulence model assessment-I. Flow-field experiments. Int. J. Heat Mass Transf. 1993, 36, 2675–2684. [Google Scholar] [CrossRef]
- Nishino, K.; Samada, M.; Kasuya, K.; Torii, K. Turbulence statistics in the stagnation region of an axisymmetric impinging jet flow. Int. J. Heat Fluid Flow 1996, 17, 193–201. [Google Scholar] [CrossRef]
- Behrouzi, P.; McGuirk, J.J. Laser Doppler velocimetry measurements of twin-jet impingement flow for validation of computational models. Opt. Laser Eng. 1998, 30, 265–277. [Google Scholar] [CrossRef]
- Fairweather, M.; Hargrave, G. Experimental investigation of an axisymmetric, impinging turbulent jet. 1. Velocity field. Exp. Fluids 2002, 33, 464–471. [Google Scholar] [CrossRef]
- Geers, L.F.G.; Tummers, M.J.; Hanjalić, K. Experimental investigation of impinging jet arrays. Exp. Fluids 2004, 36, 946–958. [Google Scholar] [CrossRef]
- Katti, V.; Prabhu, S.V. Experimental study and theoretical analysis of local heat transfer distribution between smooth flat surface and impinging air jet from a circular straight pipe nozzle. Int. J. Heat Mass Transf. 2008, 51, 4480–4495. [Google Scholar] [CrossRef]
- Satake, S.; Kunugi, T. Direct numerical simulation of an impinging jet into parallel disks. Int. J. Numer. Methods Heat Fluid Flow 1998, 8, 768–780. [Google Scholar] [CrossRef]
- Chung, Y.M.; Luo, K.H. Unsteady Heat Transfer Analysis of an Impinging Jet. J. Heat Transf. 2002, 124, 1039–1048. [Google Scholar] [CrossRef]
- Hattori, H.; Nagano, Y. Direct numerical simulation of turbulent heat transfer in plane impinging jet. Int. J. Heat Fluid Flow 2004, 25, 749–758. [Google Scholar] [CrossRef]
- Wilke, R.; Sesterhenn, J. Numerical Simulation of Impinging Jets. In High Performance Computing in Science and Engineering ’14; Springer: Cham, Switzerland, 2015; pp. 275–287. [Google Scholar]
- Jainski, C.; Lu, L.; Sick, V.; Dreizler, A. Laser imaging investigation of transient heat transfer processes in turbulent nitrogen jets impinging on a heated wall. Int. J. Heat Mass Transf. 2014, 74, 101–112. [Google Scholar] [CrossRef]
- Behnia, M.; Parneix, S.; Durbin, P.A. Prediction of heat transfer in an axisymmetric turbulent jet impinging on a flat plate. Int. J. Heat Mass Transf. 1998, 41, 1845–1855. [Google Scholar] [CrossRef]
- Hanjalić, K.; Popovac, M.; Hadžiabdić, M. A robust near-wall elliptic-relaxation eddy-viscosity turbulence model for CFD. Int. J. Heat Fluid Flow 2004, 25, 1047–1051. [Google Scholar] [CrossRef]
- Jaramillo, J.E.; Pérez-Segarra, C.D.; Rodriguez, I.; Oliva, A. Numerical study of plane and round impinging jets using RANS models. Numer. Heat Transf. B Fundam. 2008, 54, 213–237. [Google Scholar] [CrossRef]
- Hadžiabdić, M.; Hanjalić, K. Vortical structures and heat transfer in a round impinging jet. J. Fluid Mech. 2008, 596, 221–260. [Google Scholar] [CrossRef]
- Uddin, N.; Neumann, A.O.; Weigand, B. LES simulations of an impinging jet: On the origin of the second peak in the Nusselt number distribution. Int. J. Heat Mass Transf. 2013, 57, 356–368. [Google Scholar] [CrossRef]
- Krumbein, B.; Jakirlić, S.; Tropea, C. VLES study of a jet impinging onto a heated wall. Int. J. Heat Fluid Flow 2017, in press. [Google Scholar] [CrossRef]
- Hall, J.W.; Ewing, D. On the dynamics of the large-scale structures in round impinging jets. J. Fluid Mech. 2005, 555, 439–458. [Google Scholar] [CrossRef]
- Hall, J.W.; Ewing, D. The development of the large-scale structures in round impinging jets exiting long pipes at two Reynolds numbers. Exp. Fluids 2005, 38, 50–58. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S.-J. Stagnation region heat transfer of a turbulent axisymmetric jet impingement. Exp. Heat Transf. 1999, 12, 137–156. [Google Scholar] [CrossRef]
- Dairay, T.; Fortuné, V.; Lamballais, E.; Brizzi, L.-E. Direct numerical simulation of a turbulent jet impinging on a heated wall. J. Fluid Mech. 2015, 764, 362–394. [Google Scholar] [CrossRef]
- Wilke, R.; Sesterhenn, J. Statistics of fully turbulent impinging jets. J. Fluid Mech. 2017, 825, 795–824. [Google Scholar] [CrossRef]
- Schmitt, M.; Frouzakis, C.E.; Tomboulides, A. Direct numerical simulation of multiple cycles in a valve/piston assembly. Phys. Fluids 2014, 26, 035105. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, Z.; Liu, M.; Hu, J.A. Numerical Simulation of Fluid Flow inside the Valve. Procedia Eng. 2011, 23, 543–550. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical Solution of the Navier-Stokes Equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Vuorinen, V.; Keskinen, J.-P.; Duwig, C.; Boersma, B.J. On the implementation of low-dissipative Runge–Kutta projection methods for time dependent flows using OpenFOAM. Comput. Fluids 2014, 93, 153–163. [Google Scholar] [CrossRef]
- Van der Houwen, P.J. Explicit Runge-Kutta formulas with increased stability boundaries. Numer. Math. 1972, 20, 149–164. [Google Scholar] [CrossRef]
- Hirsch, C. Numerical Computation of Internal and External Flows: The Fundamentals of Computational Fluid Dynamics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2007; ISBN 9780080550022. [Google Scholar]
- González Hernandéz, M.A.; Moreno López, A.I.; Jarzabek, A.A.; Perales Perales, J.M.; Wu, Y.; Xiaoxiao, S. Design Methodology for a Quick and Low-Cost Wind Tunnel, Wind Tunnel Designs and Their Diverse Engineering Applications; InTechOpen: London, UK, 2013. [Google Scholar] [CrossRef]
- Grötzbach, G. Spatial resolution requirements for direct numerical simulation of the Rayleigh-Bérnard convection. J. Comput. Phys. 1983, 49, 241–264. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Spalding, D.B. A Single formula for the “Law of the Wall”. J. Appl. Mech. 1961, 28, 455–458. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; 11th Printing; Cambridge University Press: Cambridge, UK, 2011; ISBN 9780521598866. [Google Scholar]
- Hunt, J.C.R.; Wray, A.A.; Moin, P. Eddies, stream, and convergence zones in turbulent flows. In Proceedings of the 1988 Summer Program, Stanford University, CA, USA, June 1988; pp. 193–208. [Google Scholar]
- Launder, B.E. Numerical computation of convective heat transfer in complex turbulent flows: Time to abandon wall functions? Int. J. Heat Mass Transf. 1984, 27, 1485–1491. [Google Scholar] [CrossRef]
- Launder, B.E. On the computation of convective heat transfer in complex turbulent flows. J. Heat Transf. 1988, 110, 1112–1128. [Google Scholar] [CrossRef]
- Shih, T.-H.; Povinelli, L.A.; Liu, N.-S. Application of generalized wall function for complex turbulent flows. J. Turbul. 2003, 4, N15. [Google Scholar] [CrossRef]
- Craft, T.J.; Gerasimov, A.V.; Iacovides, H.; Launder, B.E. Progress in the generalization of wall-function treatments. Int. J. Heat Fluid Flow 2002, 23, 148–160. [Google Scholar] [CrossRef]
- Suga, K.; Craft, T.J.; Iacovides, H. An analytical wall-function for turbulent flows and heat transfer over rough walls. Int. J. Heat Fluid Flow 2006, 27, 852–866. [Google Scholar] [CrossRef]
- Craft, T.J.; Gant, S.E.; Iacovides, H.; Launder, B.E. A new wall function strategy for complex turbulent flows. Numer. Heat Transf. B Fundam. 2004, 45, 301–318. [Google Scholar] [CrossRef]
- El Hassan, M.; Assoum, H.H.; Sobolik, V.; Vétel, J.; Abed-Meraim, K.; Garon, A.; Sakout, A. Experimental investigation of the wall shear stress and the vortex dynamics in a circular impinging jet. Exp. Fluids 2012, 52, 1475–1489. [Google Scholar] [CrossRef]
- Tu, C.V.; Wood, D.H. Wall pressure and shear stress measurements beneath an impinging jet. Exp. Therm. Fluid Sci. 1996, 13, 364–373. [Google Scholar] [CrossRef]
- Salari, K.; Knupp, P. Code Verification by the Method of Manufactured Solutions; SAND2000-1444; SciTech Connect: Washington, DC, USA, 2000. [Google Scholar]
- Shunn, L.; Ham, F. Method of Manufactured Solutions Applied to Variable-Density Flow Solvers. In Annual Research Briefs; Center for Turbulence Research: Stanford, CA, USA, 2007; pp. 155–168. [Google Scholar]
- Roache, P.J. Verification and Validation in Computational Science and Engineering, 1nd ed.; Hermosa Publishers: Socorro, NM, USA, 1998; ISBN 9780913478080. [Google Scholar]
- Oberkampf, W.L.; Roy, C.J. Verification and Validation in Scientific Computing; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-0-521-11360-1. [Google Scholar]
- Taylor, G.I.; Green, A.E. Mechanism of the production of small eddies from large ones. Proc. R. Soc. A Math. Phys. 1937, 151, 499–521. [Google Scholar] [CrossRef]
- Joung, Y.; Choi, S.-U.; Choi, J.I. Direct numerical simulation of turbulent flow in a square duct: Analysis of secondary flows. J. Eng. Mech. ASCE 2007, 133, 213–221. [Google Scholar] [CrossRef]
- Gavrilakis, S. Numerical simulation of low-Reynolds-number turbulent flow through a straight square duct. J. Fluid Mech. 1992, 244, 101–129. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).