Numerical Study on Mixed Convection in Ventilated Cavities with Different Aspect Ratios

Abstract

An unsteady numerical investigation on mixed convection in a two dimensional open ended cavity with different aspect ratios is carried out. In this investigation, uniform temperature is set to the left and the right sides of the cavity while the other surfaces are adiabatic. The simulation is performed for a wide range of Reynolds numbers (Re = 100–1000) and Richardson numbers (Ri = 0.132–6.5 × 10²), and various cavity aspect ratios (L/D = 0.5–4.0) and H/D = 0.1. Governing equations are solved using a cell centered finite volume code, a SIMPLE numerical projection scheme and a 2nd order accuracy. Results are presented in the form of streamlines, isothermal lines, and velocity profiles in the channel. The conclusion is that the enhancement of heat transfer rate is generated principally by the increasing Re and the assisting configuration is thermally more efficient when compared to the opposing one.

1. Introduction

Combined natural convection and forced convection gets great attention for its importance in practical applications in various modern systems such as electronic cooling, nuclear reactors and solar energy systems. Many of these cases involve a heat source on a vertical wall of a cavity. Sometimes the only natural convection is insufficient for thermal management and control of such systems, so forced convection is required. A number of papers dealt with a heat source on the surface under the forced flow. The case of a source on a different surface has been studied little. The phenomenological understanding of interaction between buoyancy-induced flow from the heated surfaces of open cavity and pressure-driven external flow becomes important in thermal design of systems. The configuration of a cavity located below a channel is of interest in several applications. In this geometry, air flows into a channel and a vertical wall of the cavity has a uniform heat source, the other walls are adiabatic. An interaction between a buoyancy-induced flow and a forced flow, whose direction is perpendicular to the gravity vector, is present. Two different cases are possible: (a) the forced flow in the channel assists the motion due to the natural convection in the cavity; (b) the forced flow in the channel opposes the motion due to the natural convection in the cavity. Convection in the cavity is of great interest among researchers in the field of Heat Transfer. As for concerns that natural one, some important applications are furnaces, ovens and combustion chambers, as far as incinerators. The mixed convection, however, finds warning increasing especially on the part of electronic systems manufacturers. In fact, by virtue of achieving more and superior hardware potential, and needed a cooling system boards and components more and more effective.

Studies in this field provide valuable support to address problems such as the ventilation in the presence of heat sources, as was underlined by Papanicolaou and Jaluria [1]. These studies have been applied to the chemical vapor deposition (CVP) technology and in the control of the propagation of fire and smoke. According to Raji and Hasnaoui [2], the use of these studies would lead to profitable results in the design of buildings, associated with their exercise costs, and in heat accumulation systems and solar energy. Many researchers have performed efforts in the analysis of these problems although, for the moment, they are grappled more in numerical that in that experimental ones. Lage et al. [3] appear to place more importance on the design of the cavity in which combustion occurs in a modern plant of low-emission cogeneration. Convection is natural, but the article is also good for the mixed convection. The study analyzes numerically the heat transfer by natural convection and radiation in a two-dimensional cavity with a heated side, the other and the basic blocks, the summit opened. The first part of the study was focused on the natural convection and has brought the development of correlations for every wall. In the second part, solutions are presented accounting for radiation. The objective in this case is to obtain steam and electric energy from compressed coal, used as fuel, mixed with limestone to reduce SO₂ emissions in the atmosphere. A big problem is to eliminate the whole ash and evaluate the heat exchanges that take place between the walls of the cavity and the environment. Through the numerical analysis they found a correlation of the following type:

Nu = C₁ + C₂ Ra^a

(1)

where a, C₁ and C₂ are constant.

In [4], more arguments have been analyzed and compared with experimental data. They have been useful to study the variation of the heat transmission with the geometry. It was observed that the effects of the flow of the main current and the presence of vortices in the cavity are important in heat exchange. Furthermore, it was found that the heat exchange does not always worsen with increasing L/D, where L is the depth of the cavity, that is, the vertical length, while D is the axial length. The experimental data were obtained with: L/D equal to 0, 0.04, 0.08, 0.12, 0.2, 0.3, 0.5 and 1.0. From this experiment the following correlations have been derived. For L/D = 0:

Nu = 0.0772 Re_L^2/3, for Re ≤ 1.7 × 10⁴

(2)

Nu = 0.0363 Re_L^0.8, for Re ≥ 3.0 × 10⁴

(3)

In this case, the cavity effect seems absent, indeed the lower wall is smooth. Different correlations are derived:

Nu = 0.427 Re^1/3, for Re ≥ 2.8 × 10⁴ and L/D ≤ 0.08

(4)

The other one is:

Nu = 0.390 Re^1/2 (L/D)^−0.27, for Re ≥ 2.5 × 10⁴ and L/D ≥ 0.12

(5)

The article [5] is on mixed convection in a rectangular cavity in which a heat source is present. The numerical analysis has the aim of simulating a practical system, such as that of the cooling of an electronic component. The motion is considered laminar and, while the cooling air inlet position is fixed, the output is made to vary. In this case, the numerical analysis with the related diagrams and streamlines, have allowed qualitative considerations. If the output section is moved down the vortex, it is pushed by the flow towards the bottom of the cavity. The conduct numerical analysis was carried out for Re = 50 ÷ 2000 and for Gr/Re² = 0 to 10. For values of Ri greater it was observed that the numerical solution oscillates. In addition, it was observed that, the higher you place the heating plate, the better the cooling. The same authors, in a later article [6], have studied the geometry with inlet and outlet along the top, with the Reynolds number Re of 1000 and 2000. This time Ri ranged from 12.5 to 200 and the oscillatory pattern of solution was confirmed. For the medium on the surface Nu is a correlation was found: Nu = 0.134 Gr^0.26 Re^0.06, expressed as follows:

Nu = 0.134 Re^0.58Ri^0.26

(6)

The analysis carried out in the article [7] was twofold: a cavity with air inlet from the bottom and exit at top (bottom-top); a cavity with entrance and exit down (bottom-bottom). In this case the flow of solar energy was in the area overlying the inlet opening. This study has produced correlations of Nusselt in function of Rayleigh and the thermal power as a function of the Reynolds number. An interesting proposal is [8], which considers an auxiliary wall in a central position and different positions for the heating plates. This arrangement of the elements may bring useful practical implications. It has come to the conclusion that, if the heat source is located on the right of the auxiliary wall, the number of Nusselt is independent of the position of the heated plate and of the auxiliary wall. If it is located on the left side Nu strongly depends on the position of these two elements. Other considerations on the influence of the conductivity of the auxiliary wall and on the simultaneous presence of two heated plates on it were made and can be suitably studied. In article [9], the laminar flow in mixed convection on a vertical step has been studied experimentally. The step and the side wall arranged downstream of the same are heated and maintained at a uniform temperature greater than the air one, while the upstream wall is adiabatic. The experimental results show that the strength of buoyancy in opposing significantly influences the distributions of speed and temperature, the position and the length of the region of recirculation upstream of the step and the number of local Nusselt. This region of recirculation moves towards the ridge and its length decreases with the increase of the temperature of the wall downstream. Downstream of the step in the region of laminar flow without recirculation occurs a reduction in the number of local Nusselt to the increase of the force of buoyancy in opposing and an opposite trend occurs within the region of recirculation. In article [10], three-dimensional simulations for laminar flow incompressible in forced convection near one step in a rectangular duct are reported and are investigated the effects of the height of the ridge on the flow and on the characteristics of the heat transfer. The Reynolds number, the width and the height of the duct downstream of the step are kept constant while the height of the ridge varies. A flow of constant and uniform heat is supplied from the wall in the lower valley of the ridge, while all the other walls are treated as adiabatic. Downstream of the step a complex three-dimensional motion develops with a vortex counterclockwise close to the step. By increasing the height of the ridge will increase the number of Nusselt, the size of the region of recirculation and the general appearance of the three-dimensional flow. To increase the height of the ridge develops, adjacent to the bottom corner of the same, a second region of recirculation. The combined action of heat transfer by natural convection, conduction and radiation in a cavity that is open at the top is dealt with in article [9]. It is possible to note the presence of a heat source placed at the center of the vertical wall left, and outside all the walls are adiabatic. From experimental observations you note that the exchange of heat radiation has a significant influence on the motion field and in the field of heat. It is possible to note the presence of a cell in the vicinity of the vertical surface right, whose size increases with the increase of the emissivity of the surface. The heat flux is for the most part dissipated by convection and radiation in the vicinity of the source and the contribution of the radiation on the thermal power transferred, increases with the emissivity of the surface and with the number of Rayleigh. The numerical study on mixed convection in a cavity with an isotherm vertical wall is addressed in article [11]. The study shows the interaction between the buoyancy and the forced flow in the square cavity with inlet and outlet located in the vicinity of the edge of the vertical surface isotherm, where the other three walls are adiabatic. The buoyancy is generated by the difference in temperature between the wall and the flow at constant speed. At low values of the number of Grashof, the heat transfer increases with the increase of the forced flow in both directions of buoyancy. The highest values of number of Grashof interaction becomes complex and it is observed an abnormal behavior of the heat transfer with the variation of the ratio Gr/Re². In article [12], for three different angles of attack, the mixed convection in a limited and open cavity is studied numerically. The horizontal walls are at a constant temperature T_w and the fluid is located at ambient temperature T_∞ lower, the walls in the vicinity of the opening assume adiabatic, the fluid is a Newtonian behavior, laminar flow and incompressible. The study is carried out by varying numbers of Grashof and Reynolds in a wide range. Various results are reported and discussed in function of the number of average Nusselt. The thermal insulation of the cavity can be achieved by using a high speed stream and horizontal, so as to minimize the heat exchange between the cavity and what surrounds it. Article [13] is a numerical study on the heat exchange in the mixed convection inside a rectangular ventilated cavity, subjected to a thermal flow uniform coming laterally. Fields of speed, temperature and the percentage amount of heat exchanged are examined for different values of the Rayleigh and Reynolds (10³ < Ra < 10⁶ and 5 < Re < 5 × 10³). Useful correlations are derived whereas as working fluid air (Pr = 0.72) and a height of constant openings. From the results it can be deduced that the effect of natural convection persists for the whole range of Reynolds numbers and Rayleigh considered. The number of Nusselt presents a maximum for a critical Reynolds Re_c which decreases linearly with Rayleigh. The values of Re_c were related by the expressions

Re_c = 461.12 Ra^−0.1095 and Re_c = 768.22 Ra^−0.151

(7)

The phenomenon of stratification of temperature, which has been shown for the cases of injection in countercurrent, is lacking in the case of examined configurations, where the injection is in co-current. In article [14], the mixed convection in an open cavity with a heated wall joined to a not heated horizontal plate is studied experimentally. The motion of the fluid and the heat exchange inside the cavity are governed by the parameter of buoyancy, number of Richardson and Reynolds number. The results are reported in terms of temperature profiles on the heated wall and display of motion for Re = 100 ÷ 1000, with Ri = 30 ÷ 110 (for Re = 1000) and 2800–8700 (for Re = 100), the ratio between the length and height of the recess (L/D) is in the range 0.5 to 1.5 and the ratio of the height of the Canal and cavity (H/D) equal to 0.5 and 1. The results show that the maximum value of the temperature decreases with decreasing Reynolds and Richardson. The visualization of the motion shows that there are two distinct motions present for Re = 1000 and very close, a parallel flow that is forced into the channel, and a recirculating one within the cavity. For Re = 100, the effects of a stronger buoyancy determines a penetration of thermal plumes from the heated area inside the channel. Maximum dimensional wall temperatures in terms of L/D have values ±5% compared to an average function. The Nusselt number Nu increases when L/D increases in the studied values of the number of Richardson Ri.

Bahlaoui et al. [15,16,17,18] report numerical results of mixed convection and surface radiation within a horizontal ventilated cavity heated from below and provided with an adiabatic thin partition on the heated surface. Air, a radiatively transparent medium, is considered to be the cooling fluid. The maximum and mean temperatures, the ratio, QE/QL, of the heat quantities leaving the cavity through the exit, QE, and through the vertical cold left side, QL, are also presented versus the above controlling parameters. Air, a radiatively transparent medium, is considered to be the cooling fluid. The effect of the governing parameters, which are the Reynolds number, 200 < Re < 5000, the relative height of the baffle, 0 < H < 0.75, and the emissivity of the walls, 0 < ε < 1, on the fluid flow and heat transfer characteristics is studied in detail. Some meaningful studies [19,20,21,22,23,24,25,26] have been performed on open ventilated cavities subject to mixed convection are listed, with a list of the main studied parameters and the eventual correlations found. To the author’s knowledge, it seems that there is a lack of investigation on mixed convection in a channel with open cavity below with a fixed temperature on side walls and in transient regime.

A numerical study on transition from a steady laminar regime to a period regime in a similar problem analyzed in Papanicolaou and Jaluria [2], which was investigated also in (Papanicolaou and Jaluria [4].

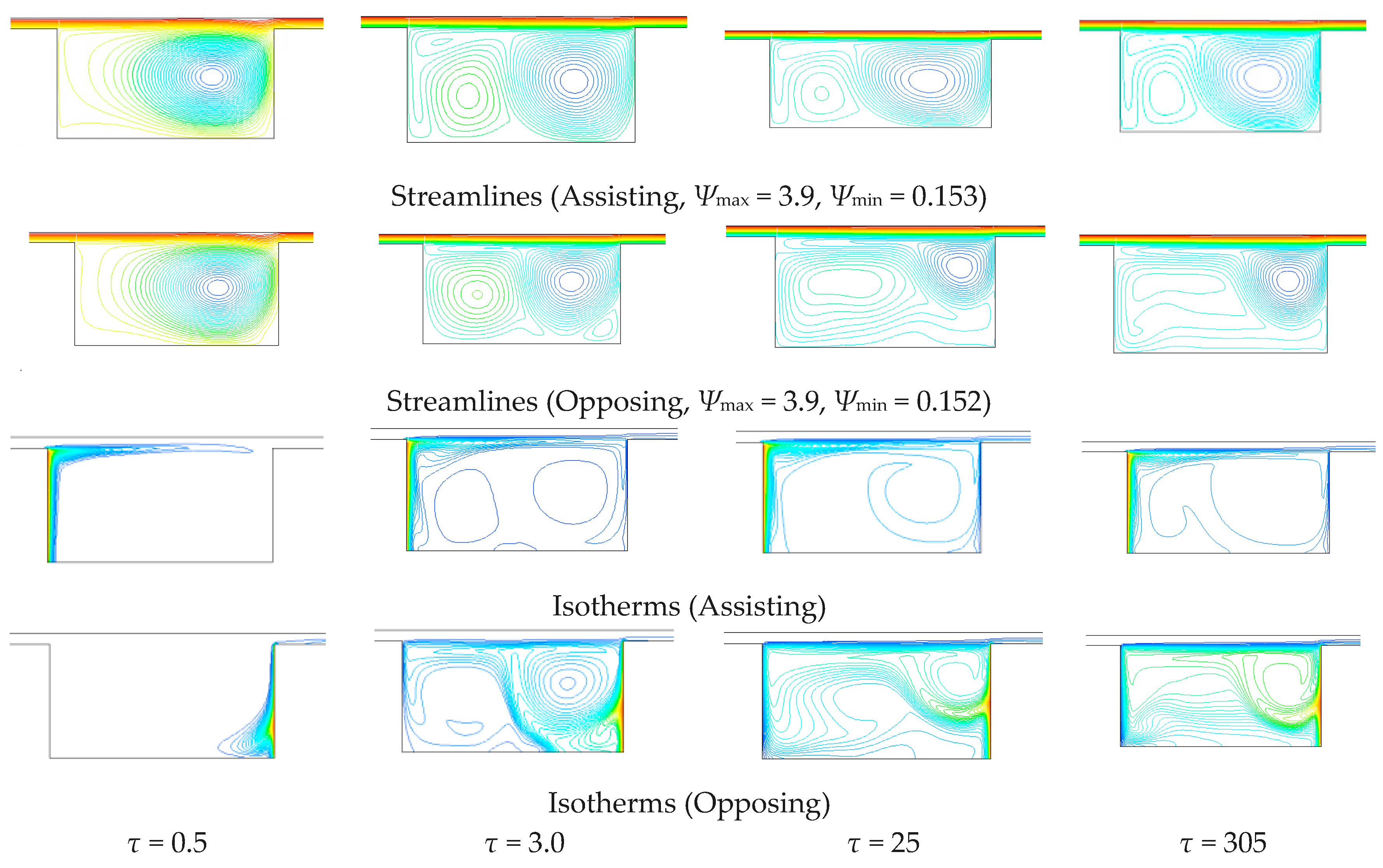
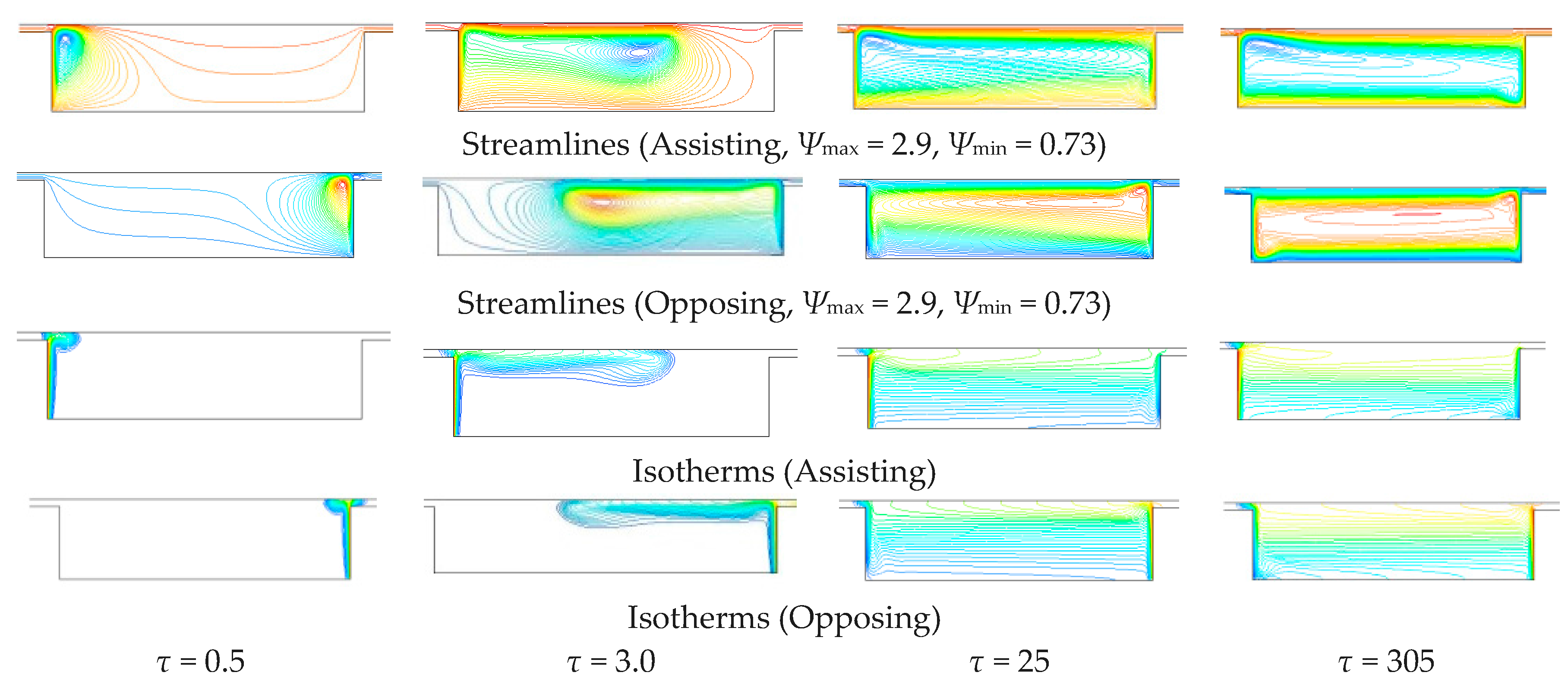
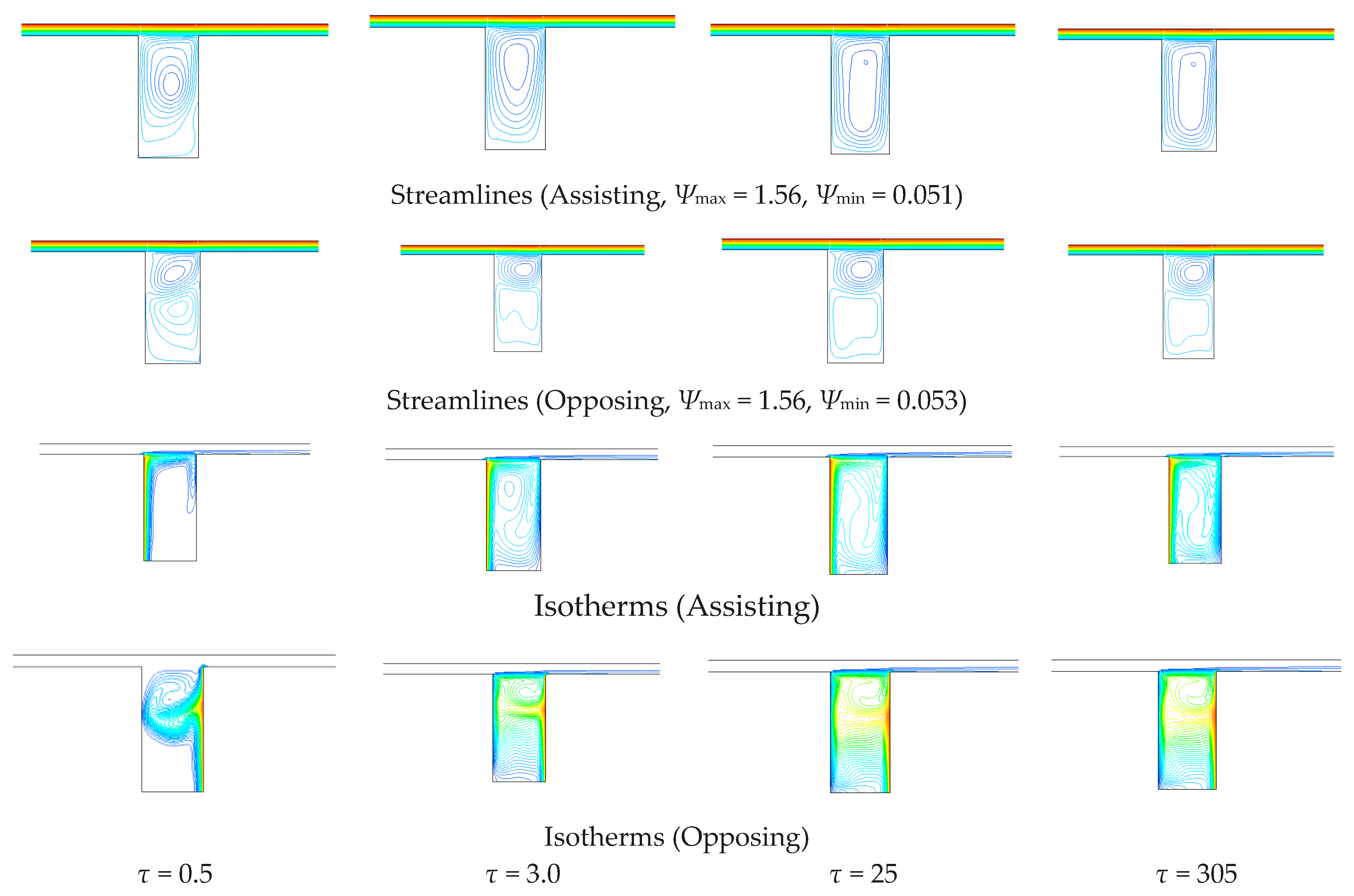
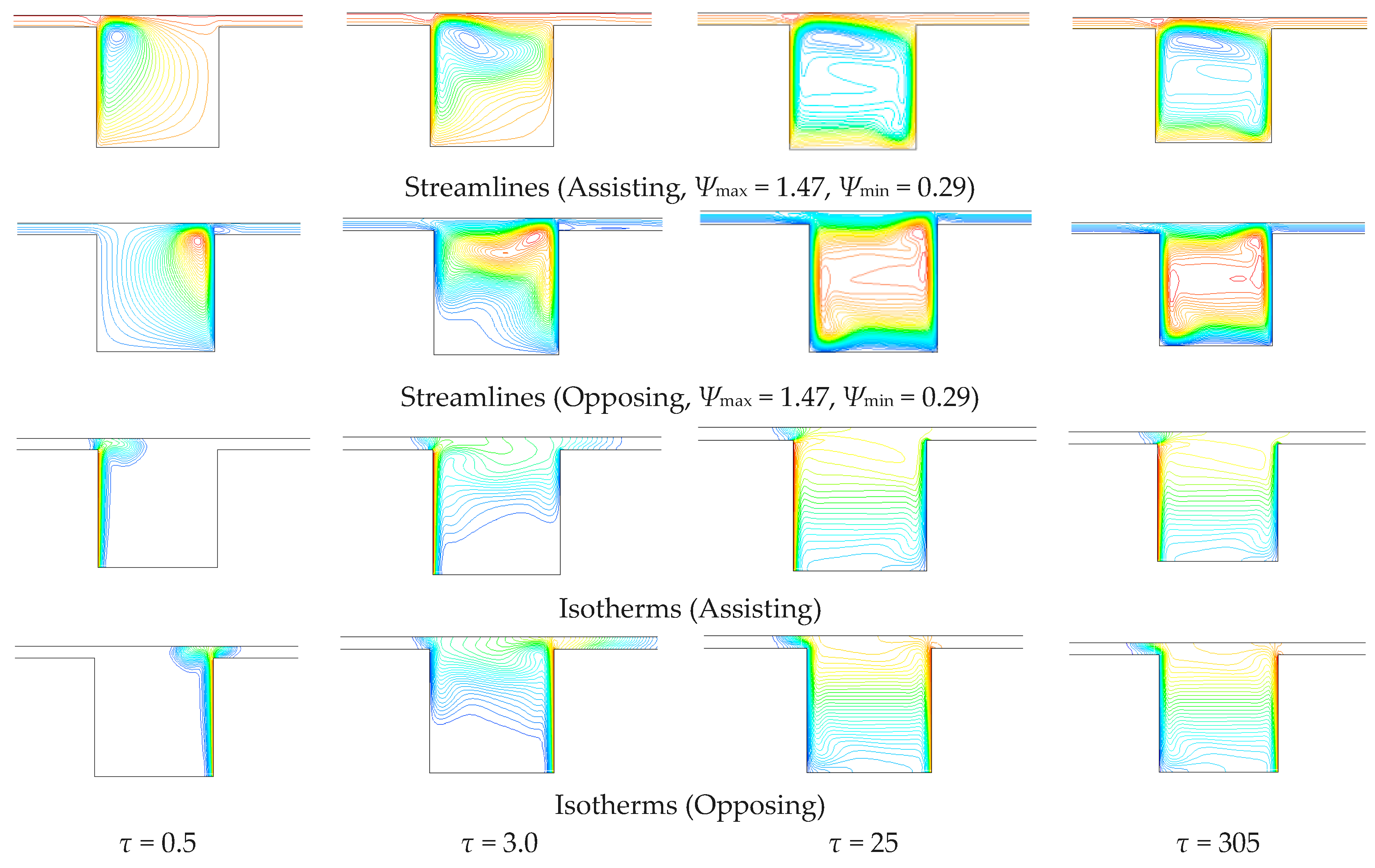
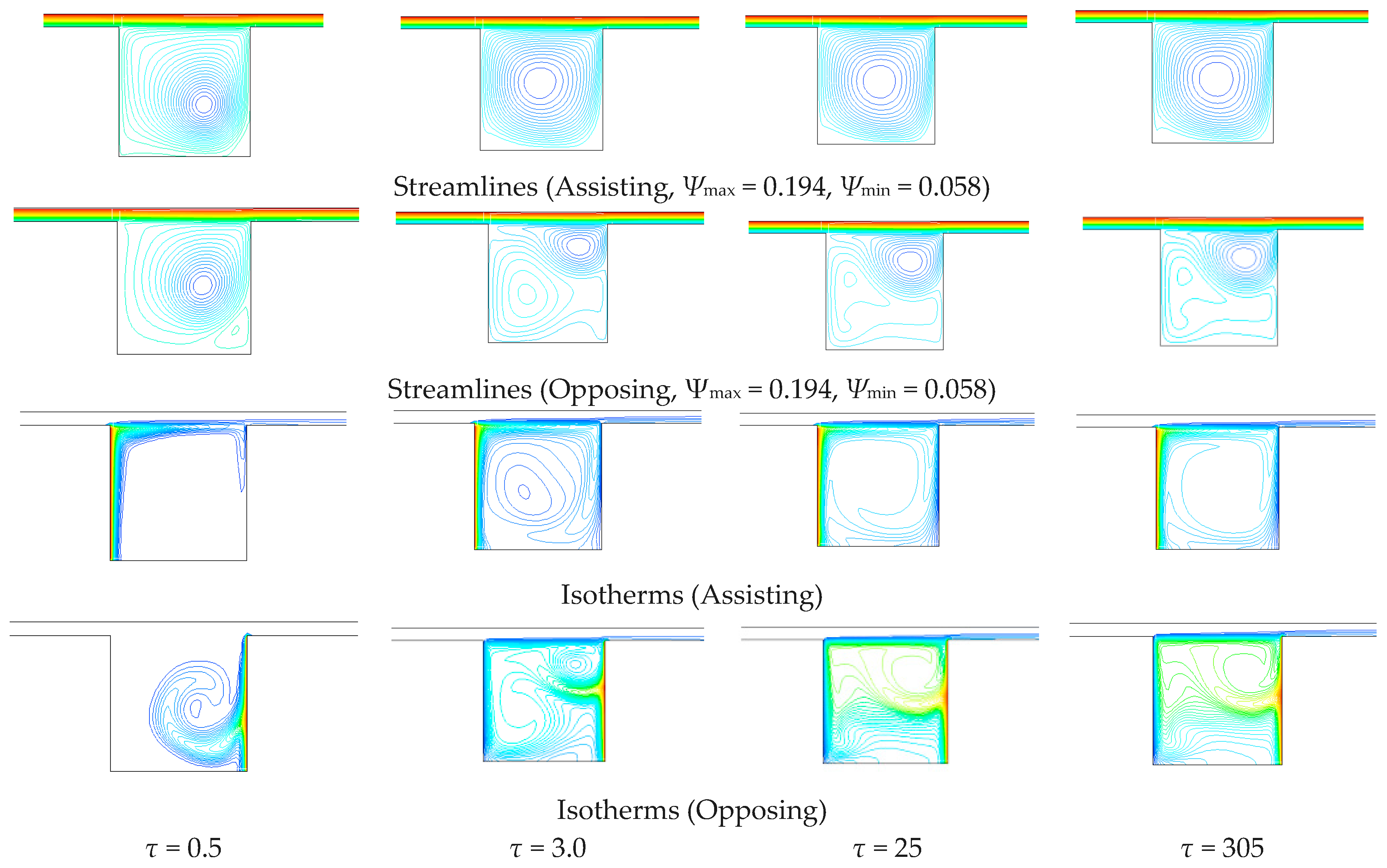
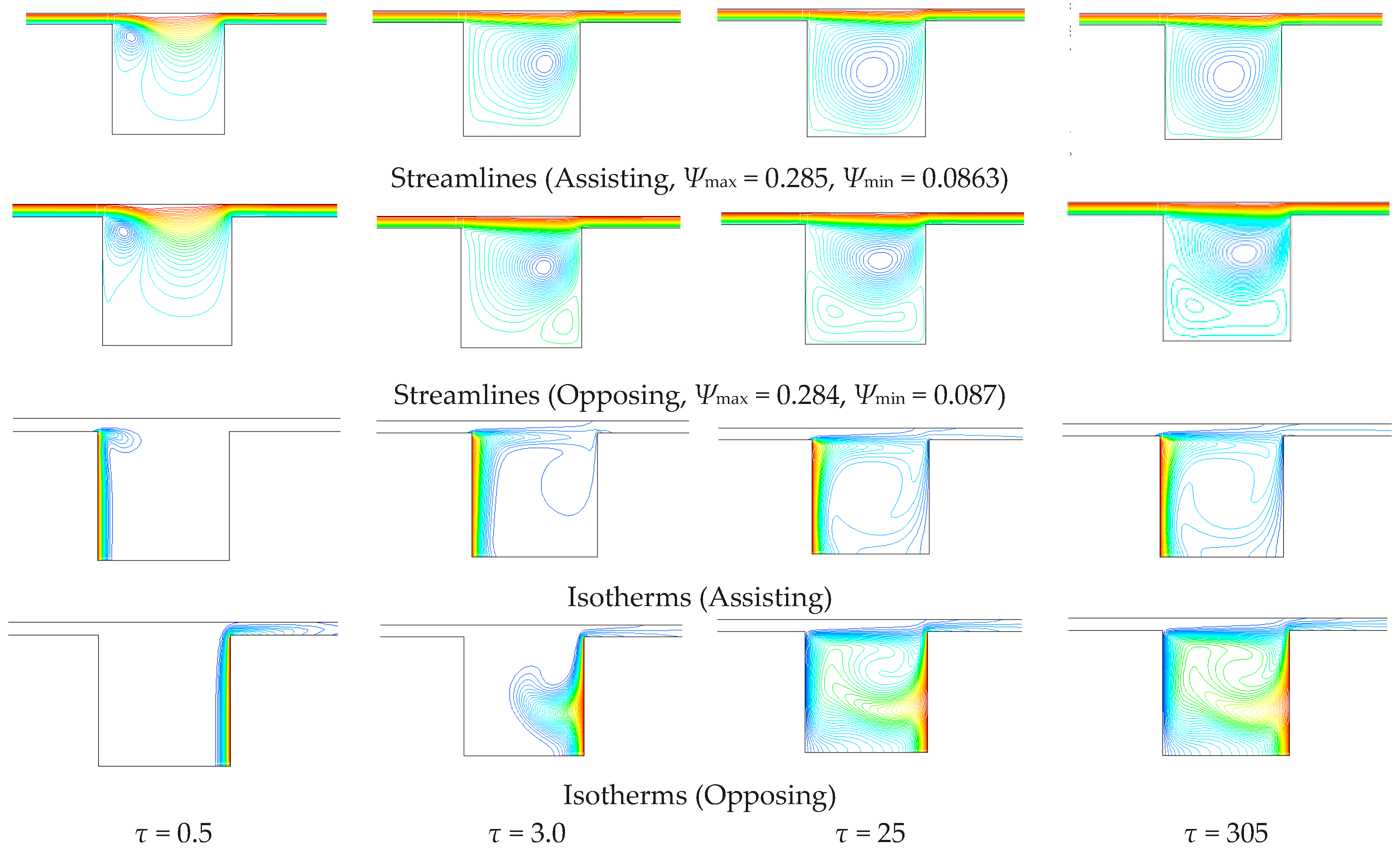
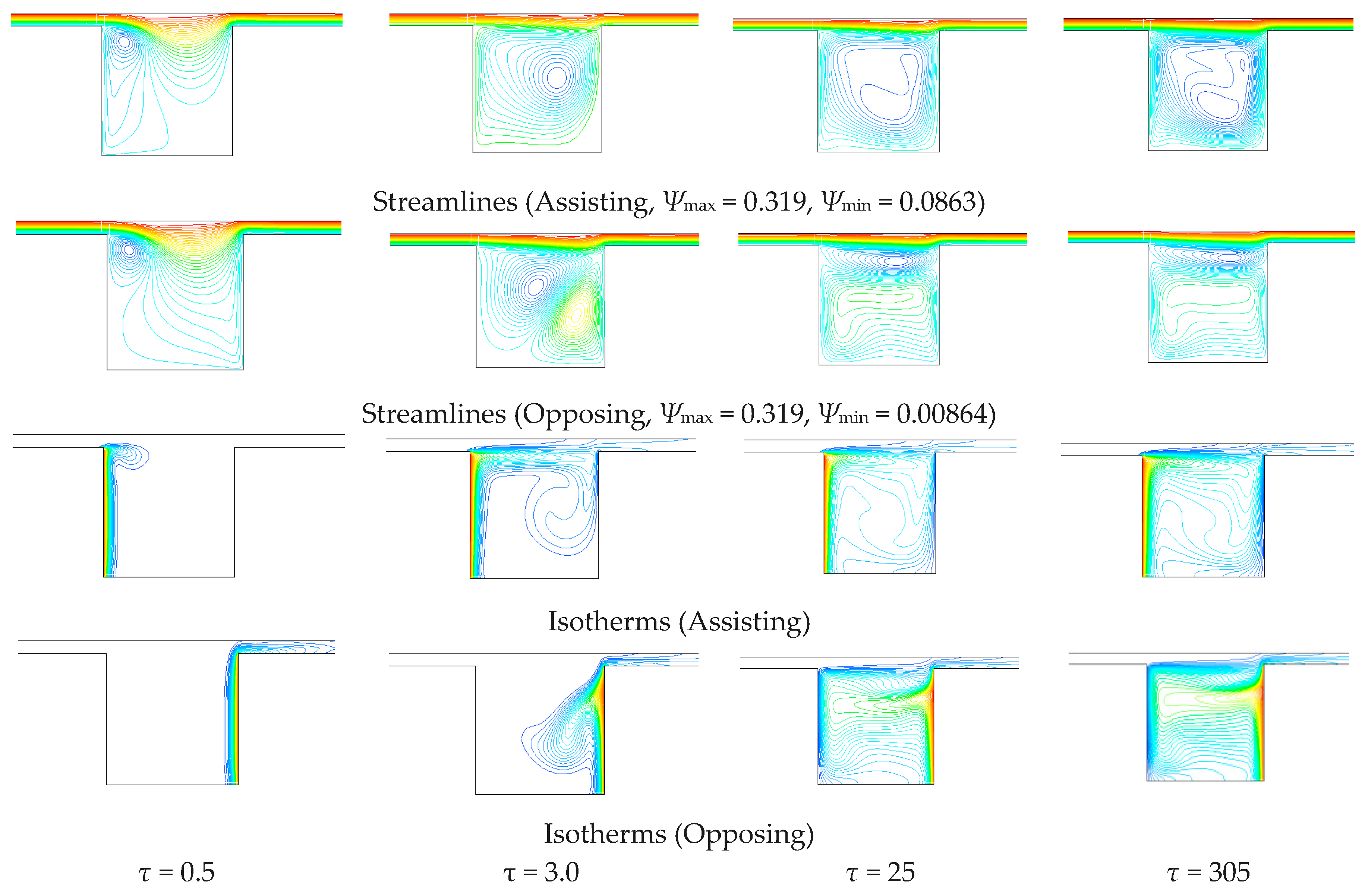
The analysis was carried out in transient regime to evaluate the transition from the laminar flow to a periodic flow. In this work, the configuration of a cavity located below a channel is considered, as reported in Figure 1. Air flows into the channel. A vertical wall of the cavity is at uniform temperature, the other walls are adiabatic, so an interaction between a buoyancy-induced flow and a forced flow, whose direction is perpendicular to the gravity vector, is present. The case of forced flow in the channel assisting the motion due to the natural convection within the cavity is investigated. A two-dimensional thermal transient is considered in the analysis. The channel length upstream the cavity is such that the forced flow is fully developed. Furthermore, the Reynolds number values guarantee a laminar flow in the region upstream the cavity.

The investigation is carried out for several values of the Richardson number Ri, the Reynolds number Re and the cavity aspect ratio (AR). The results are obtained by means of the commercially available code FLUENT, based on the finite volume method. The fields of the stream function and isotherms are reported at different times.

2. Geometries and Governing Equations

A two-dimensional vented cavity model has been used as a standard practice, see Figure 1. The geometrical configurations were generated taking as a reference the height (mm) of the inlet section. The configurations are indicated like H10L50, H10L150, H10L200, H10L300, H10L400, respectively.

In Figure 1 the dimensions are indicated with letters. They are reported in the

Table 1. Size of the configuration.

Test Case N°	H (mm)	A (mm)	B (mm)	D (mm)	L (mm)
H10	10	600	500	100	100
H10L50	10	600	500	100	50
H10L150	10	600	500	100	150
H10L200	10	600	500	100	200
H10L300	10	600	500	100	300
H10L400	10	600	500	100	400

for all the test cases.

The equations describing the physical phenomenon in two dimensions are as follows:

$$\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}=0$$

(8)

$$\frac{\partial U}{\partial \tau }+U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}=-\frac{\partial P}{\partial X}+\frac{1}{Re}\left(\frac{{\partial }^{2}U}{\partial X^2}+\frac{{\partial }^{2}U}{\partial Y^2}\right)$$

(9)

$$\frac{\partial V}{\partial \tau }+U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}=-\frac{\partial P}{\partial X}+\frac{1}{Re}\left(\frac{{\partial }^{2}V}{\partial X^2}+\frac{{\partial }^{2}V}{\partial Y^2}\right)+\frac{Gr}{R{e}^2}$$

(10)

$$\frac{\partial \theta }{\partial \tau }+U\frac{\partial \theta }{\partial X}+V\frac{\partial \theta }{\partial Y}=\frac{1}{PrRe}\left(\frac{{\partial }^2\theta }{\partial X^2}+\frac{{\partial }^2\theta }{\partial Y^2}\right)$$

(11)

where, naturally $Re=U_{0}D/\upsilon$ is the Reynolds number, $Gr=g{\beta }_T\left(T_h-T_c\right)D^3/{\upsilon }^2$ is Grashof number, and $Pr=\upsilon /\alpha$ is the Prandtl number. The aforementioned equations have been non dimentionalized using the following variables:

$$\tau =\frac{t{U}_0}{D}X=\frac{x}{D}Y=\frac{y}{D}\theta =\frac{T-T_C}{T_H-T_C}$$

(12)

$$u=\frac{U}{U_0}v=\frac{V}{U_0}P=\frac{pD}{\mu U_0}$$

(13)

In the precedent equations, ${\beta }_T$, D is the height of the hotted wall, p the fluid pressure, u and v are the components of the velocity, respectively in the x and y directions, T is the fluid temperature, T₀ is inlet air temperature. At the end, the average Nusselt is computed by the following relation:

$$Nu=\frac{1}{L_H}{{\displaystyle \int }}_0^{L_H}Nu\left(y\right)dy=\frac{1}{L_H}{{\displaystyle \int }}_0^{L_H}\frac{h\left(y\right)y}{k}dy$$

(14)

with

$$h\left(y\right)=\frac{q}{T\left(y\right)-T_0}$$

(15)

where L_H is the length of the wall. D is the height of the cavity and y is the coordinate variable depending on the chosen reference system. An interesting matter is the thermal balance within the examined geometric configuration that has the following formulation:

Q₀ = k (T_h − T_c)D/L

(16)

That represents the reference conductive thermal power and

$$Q_h-Q_c=Q_{out}$$

(17)

where $Q_h$ is the heat generated on the hot wall, $Q_c$ is the heat ejected by the cold wall and $Q_{out}$ is the thermal power exiting from the outflow channel.

The cavity has two walls on which uniform temperature is imposed, one hot and another one cold. Forced flow enters through the left inlet of the channel at a uniform velocity U₀ and at ambient temperature. At the exit, zero diffusion flux for all variables (outflow boundary conditions) is considered. All the thermo-physical properties of the fluid are assumed constant except for the variation in density with temperature (Boussinesq approximation) giving rise to the buoyancy forces. The thermo-physical properties of the fluid are evaluated at the ambient temperature, T₀, which is equal to 300 K in all cases, see

Table 2. Thermo-physical properties used in the simulations.

ρ [kg/m3]	Cp [J/kgK]	k [W/mK]	βT [K−1]	µ [Pa·s]	Th [K]	Tc [K]
1.158	1007	0.02650	3.280 × 10−3	18.77 × 10−6	310	300
1.0090	1009	0.02970	2.857 × 10−3	20.81 × 10−6	400	300

. In order to assess the order of accuracy of the present method, a factor of safety F_s of 1.25 is used (Roache [27,28]). Furthermore, the theoretical order (p = 2) is maintained for this procedure. The r value is 2 since the grid size is doubled. In Table 2 the results of the grid convergence indexes (GCI) calculations are presented and compared with the experimental values. Furthermore, the GCI limits differ from the numerical solution by less than 0.2%. This leads to the conclusion that the asymptotic range is reached. Therefore, a finer mesh will not represent a significant improvement to the solution in terms of the discretization error, while the cost of increasing the mesh resolution can grow considerably.

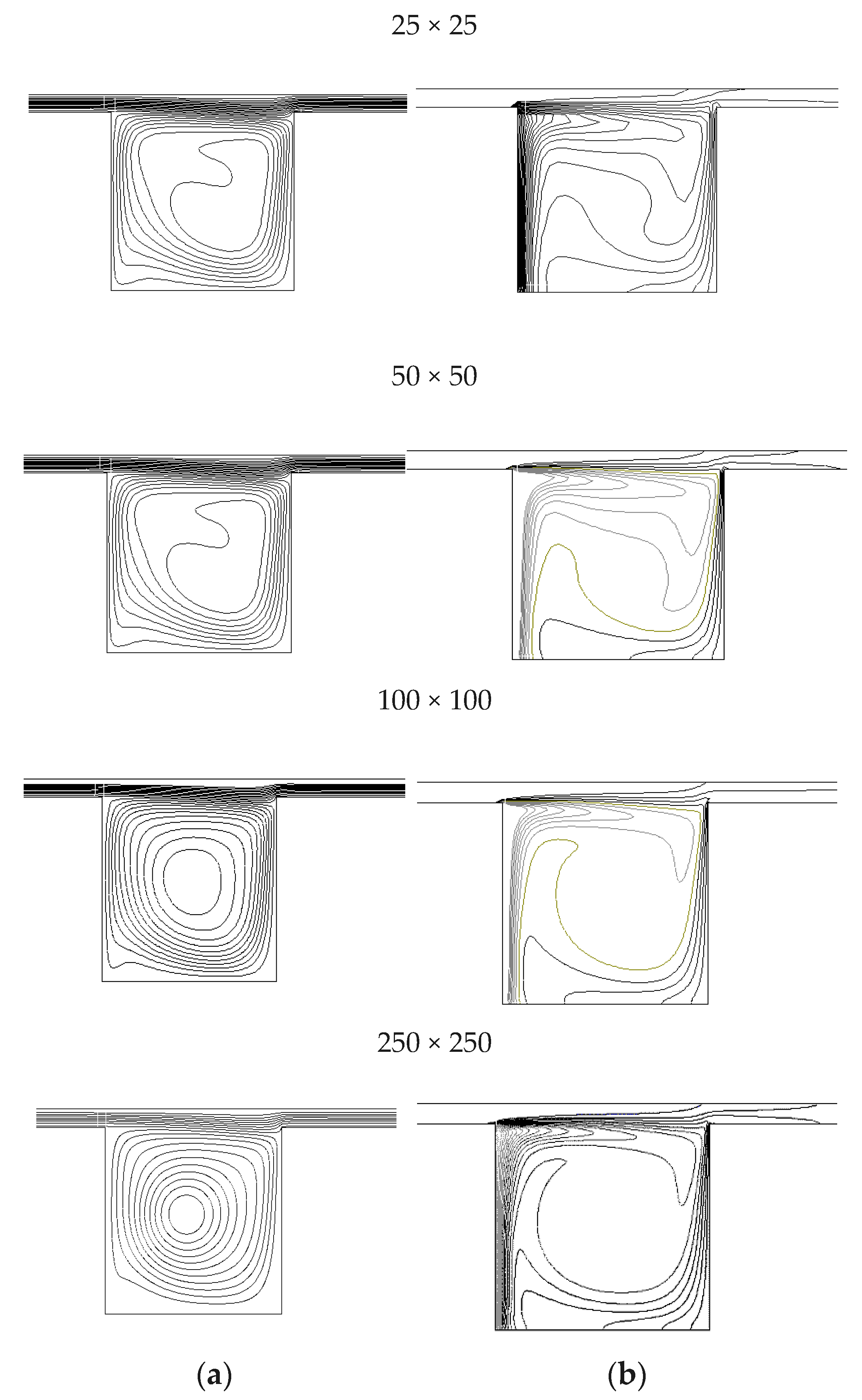
As it can be noticed in the Figure 2 and in

Table 3. Nusselt number Nu for the vertical walls with the grid convergence indexes (GCI).

Number of Nodes	Nuh	Error (%)	GCI	Nuc	Error (%)	GCI
25 × 25	27.24	12.66	–	10.68	11.60	–
50 × 50	25.51	5.50	0.02646	9.98	4.28	0.02731
100 × 100	24.70	2.15	0.01323	9.68	1.15	0.01253
250 × 250	24.31	0.54	0.00658	9.60	0.31	0.00344

, the comparison has been done among meshes 25 × 25, 50 × 50 and 100 × 100, 250 × 250. It can be observed that good results can be achieved using a mesh of 50 × 50, because passing to a finer mesh appreciable variation cannot be seen while, on the other hand, there is a noticeable increase of the times necessary to complete each single simulation (see also Figure 2).

3. Model Solver

A segregated, implicit, unsteady, second order, finite volume solver has been chosen for our investigations. The finite volume method (FVM) is a method of discretizing partial differential equations to algebraic equations [29,30]. For the finite volume method, the usual approach is to divide the physical space into many small sub-domains which are called control volumes or “cells”. The shape of cells can be arbitrary while triangular cell and rectangular cell are the most popular two types. The partial differential equations are recast on these cells and approximated by the nodal values or central values of the control volumes. The advantage of performing finite volume method is straight as is in FVM’s definition. In Fluent, in particular, each transport equation has the following integral form:

$${{\displaystyle \int }}_S\left(\rho \varphi \overrightarrow{u}\right)·\overrightarrow{n}dS={{\displaystyle \int }}_S\mathsf{\Gamma }\nabla \varphi ·\overrightarrow{n}dS+{{\displaystyle \int }}_{CV}{q}_{\varphi }dV$$

(18)

by a proper discretization it assumes the following shape at each control volume

$$A_P{\varphi }_P+{\displaystyle \sum }_l{A}_l{\varphi }_l=Q_P$$

(19)

or in matrix form

$$\left[A\right]·\left[\varphi \right]=\left[Q\right]$$

(20)

Two types of solvers:

-

Direct methods

-

Indirect or iterative methods

In the case of incompressible flow, velocity and pressure are to be considered linked and a proper relation is established by a so called projection method with be required, in this case SIMPLE [30].

The working fluid is air (Pr = 0.72) with the properties computed at a mean temperature between the hot wall temperature and the cold one. The operating conditions are: atmospheric pressure, gravitational force field, ambient temperature T₀ of 300 K. The boundary conditions regard few walls, see

Table 4. Hot wall Temperatures T_h and Richardson and Reynolds numbers, Ri and Re, respectively.

Th [K]	Re	Ri
301	10	1.32 × 103
301	100	13.2
301	1000	0.132
310	10	1.23 × 104
310	100	1.23 × 102
310	1000	1.23
400	10	6.58 × 104
400	100	6.59 × 102
400	1000	6.59

and

Table 5. Values assumed by velocity at the inlet section.

H/D	U0 − Re = 10	U0 − Re = 100	U0 − Re = 1000
0.10	0.0157	0.157	1.57

.

The aforementioned walls have a fixed temperature illustrated in Table 4, in function of Re and Ri.

The inlet reference velocity U₀ assumes the following values.

The iterations are performed with a variable time step, that for the first 5 s of the time history, it was fixed to 0.01 s. Then the time step has been increased to 0.1 s, and such value remain constant up to a time of 50 s, when the time step is increased up to 1 s for 50 s and up to10 s for other 200 s to achieve the regime. What has been said before is true except that in some particular cases when there are still periodical oscillations after 300 s in the heat transfer, likely due to a temporary transition to a natural convection or a forced convection. However, the values vary by 5% of the mean value so the Nusselt number Nu taken into consideration can be considered correct. The convergence to steady state was determined by monitoring the average temperature on the heated wall.

$$\frac{{\left|{\Phi }^{n+1}-{\Phi }^n\right|}_{\infty }}{{\Phi }_{\infty }^{n+1}}\le {10}^{-5}$$

(21)

where Ф is the dependent variable and n is the iteration index.

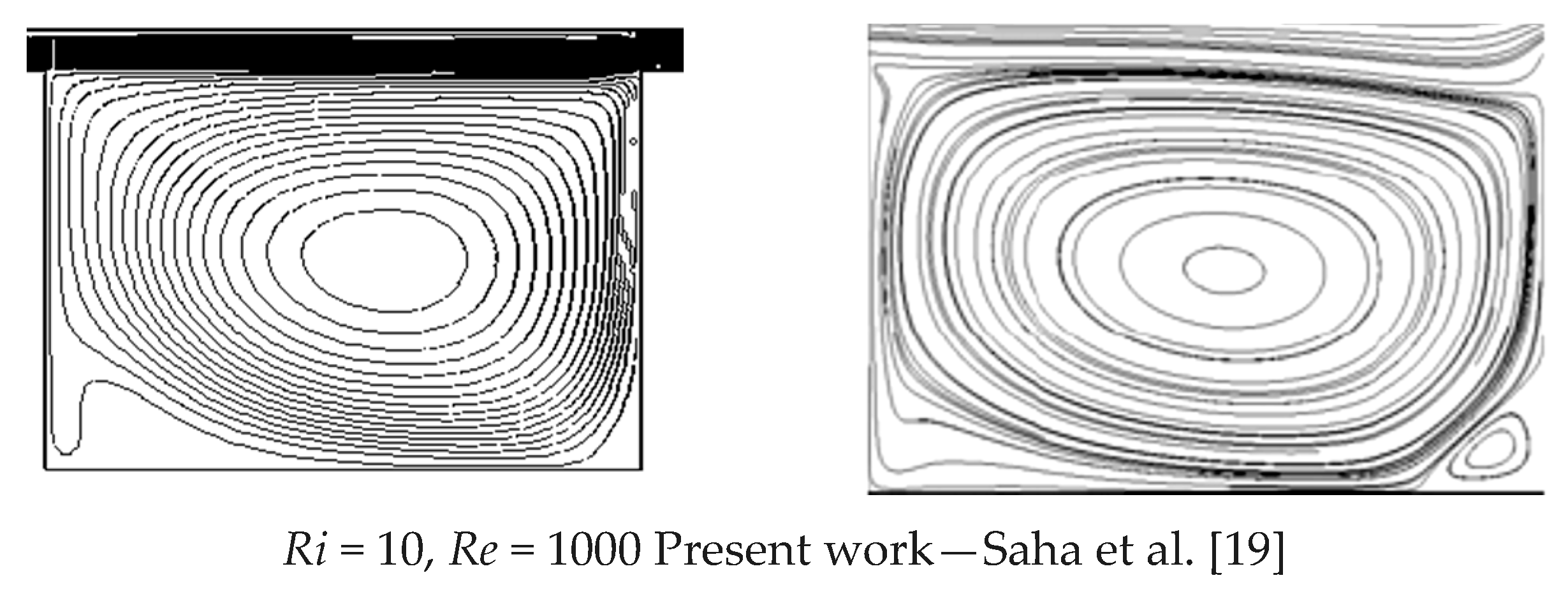
This numerical model was validated both numerically and experimentally by solving the configuration investigated in [17] and making more comparisons. The comparisons are presented in

Table 6. Validation cases for the presented numerical model (L/D = 1.0).

Flow Regime	Nu	Nu (Present Work)	Error (%)
Re = 1000 − Ri = 17.0	11.06	10.86	−1.81
Manca et al. [17] (Opposing)
Re = 100 − Ri = 2800	20.12	20.05	−0.35
Manca et al. [16] (Assisting)

in terms of the Nusselt number Nu, and by stream function fields in Figure 3.

4. Results and Discussion

Studies are being carried out for the vented cavity considering air as the working fluid (Pr = 0.71) when the forced flow aids or opposes to the convection in the cavity. The cavity aspect ratio was in the range [0.5–4.0] and the channel—cavity ratio H/L has been set equal to 0.1. The values of the Reynolds number have been taken in the range [10²–10³], the values of the Grashof number Gr in the range [1.32 × 10⁵–1.32 × 10⁶] and the values of the Richardson number Ri have been taken in the range [0.1–6.5 × 10²]. In this way, no oscillations in time for average Nusselt number and maximum stream function are expected, according with the results on transition given in the study performed by Papanicolaou and Jaluria [3]. In the following, the numerical results are presented for Reynolds numbers and Richardson numbers pairs by using streamlines, isotherms, non-dimensional temperatures and velocity components.

4.1. Effect of the Richardson Number Ri

The influence of the variation of the Richardson number Ri on the streamlines and the isotherms is shown in Figure 4, Figure 5 and Figure 6. For small values of Richardson number (Ri = 13.20), a small recirculating cell is present in the open cavity and the heat transfer between the heat source and the externally induced airflow is provided mainly by heat conduction. This is because the buoyancy effect is overwhelmed by the mechanical effect of the externally induced flow. As the Richardson number increases, as shown in Figure 3, the intensity of the main circulation increases and fills the entire enclosure. As seen in the Figure 3, the region affected by the heat source is quite small for small Ri since the induced flow does not mix with the fluid inside the enclosure. Moreover, the isotherms show that the temperature distribution is nearly uniform with respect to the y coordinate except close to the induced flow, indicating that most of the heat transfer is carried out by conduction. In addition, the formation of a plume becomes more pronounced at higher Richardson numbers Ri. Figure 5 shows two different regions within the enclosure.

The upper part of the enclosure is characterized by almost stratified isotherms, indicating that the heat is transferred from the recirculating flow to the externally induced flow by diffusion. The isotherms within the remaining region are clustered close to the heated wall, which points to the existence of a steep temperature gradient. In the assisting configuration, as Ri increases the number of cells present within the cavity increases. The isotherms are more concentrated near the walls because of the fluid motion is mainly due to the buoyancy force and the effect of forced convection is lower.

The heat flux is higher near the walls just because the recirculating cells fill almost the whole cavity. The conductive component of the heat flux is predominant when compared to lower Reynolds and higher Grashof numbers (Ri and Gr) cases.

Temperature and stream function fields related to the opposing configuration are also shown in Figure 4, Figure 5 and Figure 6. The streamlines and isotherms, as Ri increases, present forced convection as the main transport mechanism and several small not uniform recirculating cells are detected inside the cavity. They are located near the upper and lower part of the cavity and near the end of the inlet channel. The heat transfer seems to work better because the isotherms at higher temperatures are more clustered near the walls. This is true since the beginning of the heat exchange.

Due to the buoyancy effect, for Ri = 13.20, the number of recirculating cells increases as shown in Figure 4. With the increase in Richardson number Ri, the cells are nearer to the cold wall and the hot wall as it is observed in Figure 5. It is due to the increase in buoyancy forces determining a greater suction in hot wall. Thermal field is governed more or less by interaction between incoming cold fluid stream and the circulating vortex.

It also depends on where the vortex is created inside the cavity. For Ri = 13.20, the zone with high temperature becomes thinner near the hot wall and the temperature distribution is more uniform in the remaining parts of the cavity. On the other hand, the temperature decreases near the hot wall as the value of Ri increases, as shown in Figure 6. It can be seen that isothermal lines are vertically parallel to each other and clustered around the heated wall, which is similar to a distribution of lines in a conduction heat transfer case.

Saha et al. [19] have performed a numerical study for laminar double-diffusive mixed convection in a two-dimensional vented square cavity with discrete heat and contaminant sources applied on the bottom wall. They show that at Re = 100 that the location of inlet and outlets alters significantly the temperature distribution in the flow fields and the heat transfer across the heated wall of the cavities. At higher Reynolds values, instead, the induced flow cannot penetrate in the enclosure and natural convection dominates the heat transfer in it. The isotherms reflect this behavior. Indeed, for lower Reynolds values, they are clustered near the vertical walls where the conduction is more important while in the center of the enclosure the isothermal lines are horizontal and parallel because the vertical temperature gradient related to the buoyancy force is predominant.

The local heat flux distribution has higher values on the higher part of the cavity both in assisting configuration and in opposing configuration for both Reynolds numbers (Re = 100, 1000), see Figure 7 and Figure 8. The stream function field shows that at lower Reynolds number the flow motion inside the cavity is very slow and there are small cells inside the cavity in each configuration. For the opposing forced flow and Ri = 123.0, as shown in Figure 5, a weak recirculating cell is present in the enclosure. In addition, the forced flow does not penetrate much in the cavity and exits by the upper corner of the heat source.

4.2. Effect of the Aspect Ratio (AR)

The values of the cavity aspect ratios considered were L/D = 0.5, 1.0, 1.5, 2.0 and 4.0. Only the region near the open cavity is showed in the Figure 7, Figure 8 and Figure 9 where the effects of the cavity aspect ratios in the stream function and temperature distribution for minimum and maximum values of Ri are shown.

Observing the Figure 10, one can notice how, as L/D ratio increases at lower Richardson number Ri, the number of recirculating cells inside the enclosure increases at greater L/D while at greater Ri most of cells evanish. The isotherms are clustered close to the side walls overall at greater Ri showing a strong conduction predominance in the heat transfer.

When the induced flow opposes to the natural convection, as shown in Figure 7, Figure 8 and Figure 9, inside the cavity two small counter rotating cells can be noticed in the enclosure, in the upper and lower corner, respectively. This behavior is still present at L/D = 2 but evanishes at L/D approaching a value of 4.0. Also in this configuration the conduction is the main mechanism of heat transfer because the isotherms still appear parallel to each other while at greater Gr the buoyancy forces are evident as we observe the recirculating cells inside the enclosure.

Some further observations can be made taking into account Figure 10. The thermal efficiency of the combination of the induced forced flow and the natural convection achieves the maximum value at lower values of aspect ratios in assisting flow due to the capability of the upper channel to carry out a part of the rotating flow of the cavity. When the induced flow aids the natural buoyancy motion the recirculating cell present in the cavity aids the flow entering in the channel on outlet carrying out as much flow as greater is the cavity aspect ratio.

Other researchers have studied the effect of position of the heated wall with respect to the inflow.

Benachour et al. in [20] studied mixed convection numerically in a ventilated room with the presence of a constant heat. A flow of air enters the enclosure through an opening in a vertical wall and exits from another opening in the wall and even in the face. The calculation results show that the location of entrances and exits significantly alters the temperature distribution in the flow fields and heat transfer through the heated wall cavities. Aminossadati and Ghazemi [21] have numerically investigated mixed convection heat transfer in a two-dimensional horizontal channel with an open cavity. A discrete heat source is considered to be located on one of the walls of the cavity. Three different heating modes are considered which relate to the location of the heat source on three different walls (left, right and bottom) of the cavity. When the heat source is located on the bottom wall, the flow field in the cavity with an aspect ratio of two experiences a fluctuating behavior for Richardson number Ri of 10. The results also show that at a fixed value of Richardson number, all three different heating modes show noticeable improvements in the heat transfer mechanism as the cavity aspect ratio increases.

4.3. Effect of the Reynolds Number Re

The influence of the variation of the Reynolds number on the streamlines and the isotherms for high Grashof is also shown. First considering the assisting configuration, at small Reynolds values, Figure 11, Re = 10, more cells can be noticed in the cavity, while for a further increase in the Reynolds number (Re = 100), Figure 5, the streamlines seem to have a symmetrical behavior about the vertical centerline of the cavity. At higher Reynolds values, a single well-defined recirculating eddy can be noticed in the cavity, see also Figure 12. In the opposing configuration, instead, at lower Reynolds number, the force flow enters in the enclosure while more eddies originate in the remaining part of the cavity. The force flow cools the enclosure, and this can be attributed to the effect of the external airflow penetration into the cavity, which lowers the temperature. At Re = 100, higher temperatures are more diffused in the cavity when compared with the assisting flow, see Figure 5.

4.4. Nusselt Number

If you look at the values for the Nusselt number and Reynolds number reported in Figure 11, the opposing configuration is considerably more effective in heat exchange as Reynolds increases if the values of average Nusselt number increase as Re increases, which is expected. At the end of our considerations, wall averaged thermal fluxes can be compared on hot wall and cold wall, respectively, and their weight with respect to the thermal power in outlet. The heat transfer efficiency of the opposing and the assisting configurations can be stated observing Figure 11. The heat fluxes have a greater weight at higher Ri showing that the forced flow, at higher Re, can pull out part of the heat flux from the cavity while for higher Ri the buoyancy weight is predominant.

4.5. Correlations

Two correlations have been built, one in aiding configuration and another one in the opposing configuration. The proposed correlations are in the following form:

Nu = c Ri^a A^b

(22)

Using the logarithms, it reads:

ln Nu = z₀ + b ln Ri +b ln A

(23)

Data in the previous formula are inserted:

z = z₀ + a x + b y

(24)

In place of z we pose values of ln Nu, as x values the ln Ri ones and in the place of y the Aspect Ratio A values. C = exp(z₀) are the constant value, while a and b are the coefficients of the Equation (24).

In the following

Table 7. Coefficients for the correlations for Ri in the range (1.23–6.5).

Assisting		Opposing
z0	3.746	z0	2.953
a	−0.174	a	1.894
b	0.0265	b	13.94
c	42.35	c	19.16
R2	0.838	R2	0.96

values of a, b and c regression values are presented.

Where R² is the correlation error. From the found correlations, the Nusselt number Nu is function of the Grashof number Gr, because the coefficient b is small, so the Reynolds number Re has the greater influence on the mean value of the Nusselt number Nu.

5. Conclusions

Numerical data collection efforts have been carried out to show symmetrical qualitative and quantitative ratings about the characteristics of heat transfer in a vented cavity with side walls at a fixed temperature, as well as to appropriate correlations. Authors have analyzed configurations for H/D equal to 0.1, L/D between 0.5 and 4, Re equal to 10, 100, 1000 and a hot surface temperature of 301 K, 310 K, 400 K, respectively. It was noted that to achieve a greater heat dissipation, it is better to have a heated surface aiding type configuration, which is in the same direction of air inlet into the channel. This conclusion becomes important in relation to the electronic components cool computers. It was noted also that for lower Re it is better to use a configuration in assisting and a minor cavity length, while the opposing one is preferred for higher Re along with an increased cavity length. The results have appeared homogeneous, because they made it possible to obtain, as a function of L/D, good correlations, which can definitely be improved with an additional wealth of data. A further consequence that extrapolates from the views and the temperature profiles is, surely, that for which further decreases the L/D ratio, that is, more it tightens the cavity, the greater the temperature along the wall and inside the cavity. The proposals for H/D = 1, 100 < Re < 1000, 1.32 × 10⁵ < Gr < 6.5 × 10⁶, 1.32 < Ri < 6.5 × 10² and for L/D between 0.50 and 4.00 show that the most important parameter is the Reynolds number Re.