Abstract
We present a numerical study of axisymmetric flow in a rotating annulus in which local thermal forcing, via a heated annular ring on the outside of the base and a cooled circular disk in the centre of the top surface, drives convection. This new configuration is a variant of the classical thermally-driven annulus, where uniform heating and cooling are applied through the outer and inner sidewalls respectively. The annulus provides an analogue to a planetary circulation and the new configuration, with its more relaxed vertical thermal boundary conditions, is expected to better emulate vigorous convection in the tropics and polar regions as well as baroclinic instability in the mid-latitude baroclinic zone. Using the Met Office/Oxford Rotating Annulus Laboratory (MORALS) code, we have investigated a series of equilibrated, two dimensional axisymmetric flows across a large region of parameter space. These are characterized in terms of their velocity and temperature fields. When rotation is applied several distinct flow regimes may be identified for different rotation rates and strengths of differential heating. These regimes are defined as a function of the ratio of the horizontal Ekman layer thickness to the non-rotating thermal boundary layer thickness and are found to be similar to those identified in previous annulus experiments. Convection without rotation is also considered and the scaling of the heat transport with Rayleigh number is calculated. This is then compared with existing work on the classical annulus as well as horizontal and Rayleigh-Bénard convection. As with previous studies on both rotating and non-rotating convection the system’s behaviour is found to be aspect ratio dependent. This dependence is seen in the scaling of the non-rotating Nusselt number and in transitions between regimes in the rotating case although further investigation is required to fully explain these observations.
1. Introduction
The differential solar heating of the Earth’s atmosphere leads to a temperature gradient between the warm equator and cooler poles. This results in large scale convective transport; warm air flows poleward at altitude and cooler air flows toward the equator near the surface. However, due to the constraint of angular momentum conservation the global flow is not as simple as a single large convective cell, large scale eddies must also play a key role in the global transport of heat and angular momentum. Between the convective Hadley cells in the tropics and the polar cells northwards of about 60° there exists a baroclinic zone within which these large scale eddies may be generated. The tropics are primarily heated from below due to the absorption and re-emission of radiation by the Earth’s surface while atmospheric cooling is strongest at high altitude at high latitudes [1]. Despite this heating configuration the mid-latitude baroclinic zone is statically stable.
The formation of this statically stable region is not quantitatively well understood despite the apparent ability of numerical models to predict it in simulations. This is partly because, due to the inability of numerical models to accurately represent small-scale convection, such processes must be parameterised. Parameterisation methods often involve empirical calibration which reproduces the observed structures by construction. In particular, there is no well established theory which accounts for the vertical thermal structure of the atmosphere in mid-latitudes. However, there is ongoing debate about the possible role of baroclinic instabilities acting to stabilise their own thermal environment (e.g., [2,3]). There are many uncertainties as to how nonlinear feedbacks may arise and how they may be maintained in the presence of continuous radiative forcing amongst other factors.
Along with theoretical and computational models, laboratory experiments have been used for many years to provide a valuable insight into atmospheric (and also oceanic) heat transport. Advantages of this approach include the absence of parameterisation schemes which are necessary in numerical models and a much wider accessible parameter space than when using observations of the real atmosphere. The archetypal laboratory experiment used in studies of baroclinic instability is the rotating annulus which involves a fluid held between two vertical, coaxial cylinders, the outer of which is heated whilst the inner is cooled and the entire system is uniformly rotated. This setup has been studied extensively through both experiment [4,5,6,7,8,9,10] and numerical models [5,11,12,13,14]. The success of annulus experiments as laboratory analogues to planetary atmospheres has been confirmed as many flow structures, including the mid latitude baroclinic zone, familiar from the atmosphere may be observed [14,15]. Other annulus configurations, such as with internal heating [16] or a horizontal temperature gradient across the base [17] have also been investigated and applied to problems such as the large scale ocean circulation.
However, the classical annulus is not well suited to studying the interaction between baroclinic instabilities and their environment as the isothermal vertical walls which span the depth of the tank promote an intense overturning circulation in the horizontal Ekman and vertical thermal boundary layers. Therefore, internal baroclinic waves have only a minor influence on the internal stratification. Due to the heating of the atmosphere by re-emission from the surface and cooling at high altitudes a more realistic analogue to a planetary atmosphere is to heat the annulus through the bottom surface and cool it at the top. A new annulus experiment is currently undergoing construction in the Atmospheric, Oceanic and Planetary Physics laboratory in Oxford within which top cooling and bottom heating will be used [18]. The cooling takes place in a narrow ring around the central cylinder whilst the fluid is heated through a ring covering the outermost radii. This arrangement of thermal forcing is expected to result in freely convecting regions at the sides of the tank with a baroclinic zone sandwiched between them. Such a configuration is comparable to the structure of Earth’s atmosphere in one hemisphere, as shown in Figure 1.
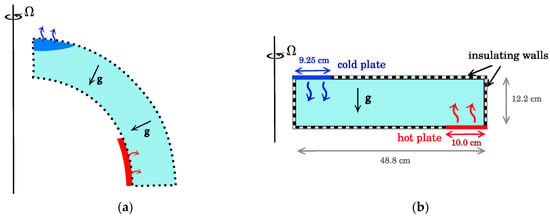
Figure 1.
(a) Schematic of a whole hemispheric atmosphere. (b) Vertical cross-section through the new rotating annulus laboratory experiment with thermal forcing at top and bottom. is the rotation vector and g the gravity vector. The dark blue regions represent the heat sink and the red regions represent the heat source.
The aim of this work is to take the first steps in investigating the flow dynamics of the new annulus experiment using numerical simulations. With a view to making comparisons with future data from the laboratory experiment, the simulations will be run using the same dimensions and system properties as the laboratory experiment, for example the same Prandtl number and density for the working fluid. Preliminary experimental results are presented by Scolan and Read [18]. The numerical simulations are carried out for axisymmetric circulations over a wide range of control parameters. An axisymmetric flow regime is actually observed in experiments at low rotation rates, at least in the baroclinic zone between the heated and cooled plates, although non-axisymmetric features are also present in practice, especially at higher rotation rates. These non-axisymmetric features include 3D convective structures in regions where the static stability is unstable as well as fully developed, azimuthally travelling baroclinic waves. Quantifying the features of axisymmetric flows that are consistent with the applied boundary conditions is important as it provides a state which may be compared with three-dimensional calculations e.g., to identify the impact of non-axisymmetric processes on the circulation and heat transport. If the ultimate goal of the experiment and associated numerical studies is to investigate how baroclinic turbulence exerts an influence on the background flow it is necessary to initially define this background state in the absence of baroclinic instability.
Two dimensional simulations also provide a computationally cheaper way of investigating aspects of the system dynamics, some of which may translate directly to the three dimensional system. It is conceivable that important features of a fully three dimensional flow may not be captured in 2D. This issue has been addressed in previous studies of both horizontal and Rayleigh-Bénard convection. Schmalzl et al. [19] found that at moderate Rayleigh numbers, with Prandtl number greater than unity and rigid boundary conditions the behaviour of Rayleigh-Bénard convection was similar in two and three dimensional systems. van der Poel et al. [20] extended this result to higher Rayleigh numbers and found that the global properties of the flow, including the heat transfer characterised by the Nusselt number, were again similar for 2D and 3D simulations for Rayleigh numbers less than . In the case of horizontal convection many numerical studies have been carried out in the two dimensional limit and, despite some disagreements with experiment over the form of the flow, the scaling of the Rayleigh number with heat transfer is found to be the same as in three dimensions [21,22].
Previous theoretical and experimental studies of thermally driven flows in an annular domain have identified a number of different axisymmetric flow regimes which exist for different combinations of thermal forcing and background rotation [12,14,16,17]. The regime in which a certain experiment lies may be characterised by the squared ratio, P, of the non-rotating thermal boundary layer thickness to that of the Ekman layer [17,23]. The boundary layers play a significant role in the system, especially the competition between viscous effects occurring in the Ekman layer (where viscous forces and the Coriolis force are comparable) and diffusive thermal effects in the thermal boundary layer [24]. P is defined as
where is the characteristic thickness of the Ekman layer defined as where is the Ekman number and d is the depth of the fluid layer. is the thickness of the non-rotating thermal boundary layer given by where is the Nusselt number of the non-rotating system and L is the horizontal length of the domain. The horizontal scale is used to be consistent with the definition of the Rayleigh number and to aid comparison with horizontal convection. P is proportional to the rotation rate. The numerical experiments carried out herein will be used to study whether similar regimes exist for the new annulus experiment and how they compare to those for the classical annulus.
In this paper, emphasis will be placed on considering the heat transfer within the annulus and how it depends on properties of the system such as the strength of thermal forcing and the aspect ratio. The goal in many heat transfer studies has been to find a scaling relationship between the Nusselt number, , and the Rayleigh number, , of the form . The new configuration may be considered in comparison to Rayleigh-Bénard convection, where the entire top surface is cooled and the entire bottom surface is heated, and horizontal convection, where there is differential heating along a single horizontal level, as well as previous annulus experiments. There is an extensive literature on the mechanisms of heat transfer and associated scaling laws for both Rayleigh-Bénard and horizontal convection in rotating and non-rotating systems (see e.g., [21,25,26] for reviews). Hignett et al. [17] developed a theoretical framework for deriving this scaling law for the heat transfer in an annulus with a differentially heated base and found . An exponent of 1/5 is also given by the Rossby scaling for non-rotating horizontal convection [27], although the universality of this law has been questioned [28]. Hignett et al.’s [17] analysis has since been applied to an internally heated annulus [16] and the classical configuration [14] to give , which is in agreement with experiment.
The value of for Rayleigh-Bénard convection is still disputed; classical results predict [29] or 2/7 [30,31] but values ranging from 1/4 to 1/3 have been observed and predicted by experiment and theory [32,33]. Over a large Rayleigh number range, the heat transport was found overall to be well described by a phenomenological model proposed by Grossmann and Lohse (the GL model) [33,34,35,36,37,38] based on an assumption of low Reynolds number and laminar boundary layers. More recently the approach has also been applied to horizontal convection [28,39]. The model proposes that there is no universal scaling law for the Nusselt number but that is dependent on the region of Rayleigh/Prandtl number space in which the experiment takes place (see [28] Figure 2). In the new annulus the heat source and sink are displaced both vertically and horizontally from each other. Therefore, unlike in horizontal convection, the net vertical flux through the source boundary is not equal to zero. Unlike in Rayleigh-Bénard convection there is a horizontal displacement between the heat source and sink and so perhaps coupling between the two will happen less strongly. It is possible that similarities with both Rayleigh-Bénard and horizontal convection will be observed.
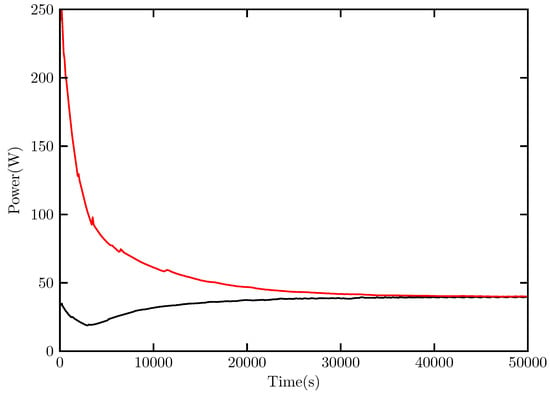
Figure 2.
The time series of total power (W) for °C, rads and cm. The red line shows the power dissipated by the heat sink and the black line the power input by the heat source, these converge after a stabilisation time of about 45,000 s.
The model, dimensionless parameters and equations used in our simulations are discussed in Section 2. The results of the simulations with both the presence and absence of rotation are given in Section 3. Section 4 discusses the results and summarises the conclusions of this work as well as giving some ideas for the direction of future work.
2. The Numerical Model
2.1. Dimensionless Parameters
The laboratory experiment under investigation is shown in Figure 1 . This analysis focuses on the meridional plane with aspect ratio, , where a and b are the radii of the inner and outer cylinders respectively, so is the width of the annulus gap. d is the height of the fluid.
For the rotating annulus, much of the dynamical behaviour is governed by the Ekman layers characterised by the Ekman number,
where is the rotation rate and is the kinematic viscosity. The Prandtl number is defined as , where is the thermal diffusivity, and the Rayleigh number, , is defined by
where is the thermal expansion coefficient, g is the gravitational acceleration and is the applied temperature difference between the heat source and sink. Due to expected similarities with horizontal convection the Rayleigh number is defined with respect to the horizontal length of the domain. In horizontal convection the dynamically important lengthscale is the thermal boundary layer thickness [27].
The efficiency of the heat transfer in the annulus is quantified by the Nusselt number, which is the ratio of total heat transfer, q, to heat transfer by conduction alone, ,
2.2. The Numerical Model
Experiments were undertaken using the Met. Office/Oxford Rotating Annulus Laboratory Simulation (MORALS) [5,40,41]. This is a direct numerical simulation code which employs a finite difference scheme using a leapfrog method with Robert-Asselin filter for the integration. The model was run in two dimensions - variation in the azimuthal direction was suppressed to give an axisymmetric flow. The code solves the Navier-Stokes (Equation (5)), continuity (Equation (6)) and heat equations (Equation (7)) for an incompressible, non-hydrostatic, Boussinesq fluid in cylindrical co-ordinates:
where is the velocity in the r, , z directions respectively. p is the pressure and is a reference density. is a viscous diffusive term which is more complex than the familiar term as it allows for spatial variations of the diffusion coefficient caused by the temperature field [40] (see Appendix). The equation of state for the density of the fluid, , is given by
where , and are constants and is a reference temperature. The viscosity and thermal diffusivity vary similarly with temperature with coefficients given in Table 1. The fluid used is the same 17% glycerol water/83% water mixture (by volume) used by Young and Read [42].

Table 1.
Parameters used in the experiments described herein.
The heat transfer is characterised by the Nusselt number (Equation (4)) and is calculated from the flux, , through the heat source and sink, which can be computed from the temperature field at any time as
where is the heat capacity. This flux is integrated over the area of the source or sink under consideration to give the power plotted in Figure 2. The conductive heat transfer (which excludes any heat transfer due to fluid motion) was calculated using a separate code with a forward Euler solver and a significantly faster runtime than the full fluid model. This solved the steady state thermal conduction equation for T in cylindrical co-ordinates
after which the corresponding heat flux, , was computed and integrated over the area of the heat source or sink. The Nusselt number is given by the ratio of the heat transfer from the full simulation to the heat transfer in the thermal conduction solution. The power from the heat source should equal that dissipated by the heat sink once the model has equilibrated and thus the Nusselt numbers for the heat source and sink should also be equal. To reduce any effect of fluctuations in the Nusselt number across the domain, the Nusselt number used here is taken to be the mean of the Nusselt number over the heat sink and that over the heat source.
The numerical simulations carried out were configured to emulate the setup of the laboratory experiment [18]. The fluid is contained between two upright, rigid, coaxial cylinders and a flat horizontal base. On the base, the region with cm is heated to a constant temperature and the innermost 9.25 cm of the upper surface is cooled to a temperature of , hence . Elsewhere, the boundaries are insulating which requires a temperature gradient of zero in the direction normal to the boundary. The velocity boundary conditions are non-slip everywhere, i.e. at the boundaries. This differs from the lab experiment where the top of the cylinder is a free surface. The pressure gradient across all surfaces is zero.
To ensure adequate resolution of the boundary layers in the numerical simulation, an Arakawa C grid [43], which is stretched in r and z, is used. 3 grid points lie within the thinner of the thermal and kinetic boundary layers. Tests with up to 9 boundary layer points were carried out and higher resolution was found to produce a change of no more than 1% in . All simulations contain 384 grid points in the radial direction but the number in the vertical direction scales with the height of the fluid. For simulations with fluid height d = 12.2 cm there are 96 grid points in the z direction and 192 and 288 respectively for simulations of height 24.4 cm and 36.6 cm.
The fluid used in the laboratory experiments is a mixture of 17% glycerol by volume in water and the properties of the simulated fluid are set to reflect this. The parameters used are listed in Table 1. Simulations were computed over a range of rotation rates, temperature differences and aspect ratios. Runtime for the simulations with the most gridpoints was approximately two weeks on a Dell Optiplex 9020 desktop. Data for the lowest aspect ratios at the highest rotation rates is not included as its runtime would have been even longer with the current code. The model was initialised with an isothermal (T = °C, midway between the temperatures of the heat source and sink), immobile fluid in the rotating frame. When the thermal and rotational forcing are applied the fluid enters a transient regime until the stabilisation time where the model reaches equilibrium. As the convection is taking place convective plumes are resolved, as illustrated in Figure 3 and in Supplementary Movie Material S1. The asymmetry between the intensity of the plumes over the heat source and sink is most likely due to the smaller area of the heat sink. A timestep of 0.01 s was used and most simulations were run for a total time of 50,000 s. Those runs which reached equilibrium more quickly were stopped after 30,000 s. In equilibrium the total power integrated over the entire volume which enters the fluid from the heat source should equal that leaving through the heat sink as all other boundaries are insulating. This fact was used as a diagnostic to check whether the runs had equilibrated. Figure 2 shows that the run with °C , rads and d = 24.4 cm equilibrated within about 45,000 s. Supplementary Material movie S2 is a short animation in the beginning of a simulation for rads and d = 12.2 cm and reveals the expected occurrence of Taylor column features due to the major influence of rotation on plumes at that rotation rate.
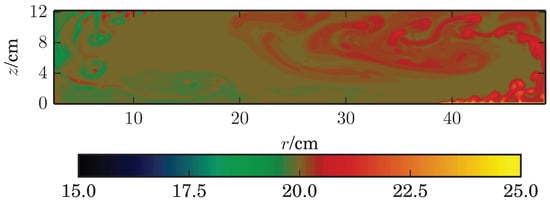
Figure 3.
The instantaneous temperature field after 100 s of simulation time for a run with °C, cm and rads. Plumes above the heat source and below the heat sink are resolved. Supplementary Material movie S1 animates the first 250 s of this simulation.
3. Results
3.1. Non-Rotating Flow
Initially it is helpful to consider the behaviour of the convection without the influence of rotation. The non-rotating Nusselt number, is used to estimate the thickness of the thermal boundary layer which is in turn used to calculate the boundary layer parameter, P. It can also be used to normalise the Nusselt number for the rotating system. The non-rotating Nusselt number is often characterised by a scaling law of the form where the value of is determined theoretically or empirically from experimental data [26].
Overall, the scaling exponent appears to be close to 2/7 but has an aspect ratio dependence - the Nusselt numbers of the lower aspect ratio runs increase more slowly with Rayleigh number than those at the highest aspect ratio.The maximum difference in for a given Ra for runs at different aspect ratio is about 10% at the highest Rayleigh number. Table 2 gives the values for for each of the different aspect ratios as well as the overall value calculated from a least squares fit. As illustrated in Figure 4, data were found to present a reasonable agreement with a scaling exponent of 2/7, as predicted both by Shraiman and Siggia [30] and Castaing et al. [31] for Rayleigh-Bénard convection and observed experimentally [32,44], except for one aspect ratio 3.8 where the scaling law is less clear but where 1/3 exponent seems to be more consistent with the data. This exponent has been predicted by Malkus [29] for Rayleigh-Bénard convection and observed experimentally (see [29,33,45]).

Table 2.
Least squares fit parameters for the non-rotating Nusselt number vs. the Rayleigh number. is the exponent in the power law .
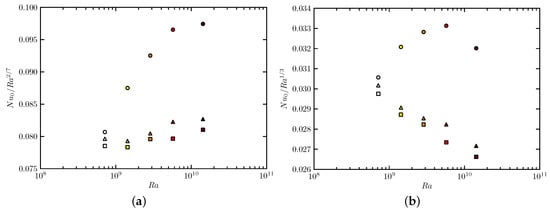
Figure 4.
The dependence of the Nusselt number for the non-rotating system, , on the Rayleigh number, with (a) compensation by a scaling law, (b) compensation by a scaling law. Darker colours represent higher applied temperature differences, ∘ for °C, • for °C, • for °C, • for ° C and • for °C. Shapes represent different aspect ratios, circles for whilst and are represented by squares and triangles respectively.
The 2/7 exponent could be expected to be valid in the range of Rayleigh numbers for the present experiments () [32] and suggests the existence of turbulent boundary layers as assumed in Shraiman and Siggia’s model. The 1/3 scaling law in the case of suggests a more turbulent regime and a configuration with more independent behaviour of each plate and with heat transport which is independent of height (see [26,29]). This confirms the complex role of aspect ratio in such convective flow regimes. The relevant lengthscale for defining the Rayleigh number is found to be the horizontal length of the domain as in horizontal convection, which renders the analysis independent of height. As discussed, the measured exponent appears to be close to those previously found for Rayleigh-Bénard convection which suggests this system does behave as some hybrid of the two archetypal convection configurations.
As only three different aspect ratio values were tested it is not possible to rigorously determine a functional form for the dependence of the exponent on the aspect ratio. Both Funfschilling et al. [46] and Sun et al. [47] found the Nusselt number to be a weakly decreasing function of aspect ratio for Rayleigh-Bénard convection while Bailon-Cuba et al. [48] found the Nusselt number to be a non-monotonic function for aspect ratios of order one and increasing for aspect ratios greater than one. From the current data it is not clear that the relationship between the Nusselt number and the aspect ratio is necessarily monotonic. Observations of the temperature and velocity fields do not reveal very different flow patterns for the different aspect ratios. In previous studies differences in flow patterns have been cited as an explanation of aspect ratio dependence [48,49,50].
3.2. Rotating Flow Regimes
We now investigate dynamical regimes and evolution of heat transfer for simulations with rotation. Using the definition of P from Section 1, six axisymmetric flow regimes have been identified in previous annulus experiments [12,14,16,17]. Figure 5 shows the temperature and azimuthal velocity fields for P ranging from 0 to approximately 90 for runs with °C and . The existence of a number of different regimes, approximately equivalent to those found in previous studies, is evident:
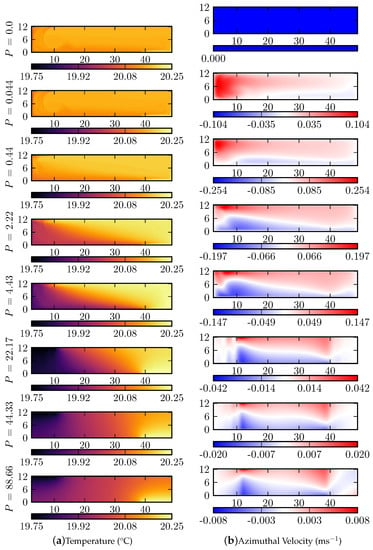
Figure 5.
(a) r,z cross-sections of the equilibrated, time averaged temperature field for °C, cm and the full range of rotation rates. The value of P for each run is shown on the left hand side. These correspond to rotation rates of 0, 0.001, 0.01, 0.05, 0.1, 0.5, 1 and 2 rads; (b) r,z cross-sections of the equilibrated, time averaged azimuthal velocity fields for the same runs.
- No rotation (): A density current flows beneath the heat sink, down the side of the inner cylinder and along the base towards the heat source. A corresponding density current is not seen above the heat source, presumably because of the larger area of the hot plate. At high z and for 10 cm the fluid interior is approximately isothermal at a temperature close to that of the hot plate. Since all fields are time averaged the plumes observed in Figure 3 are not seen here. The azimuthal velocity is zero everywhere.
- Weak rotation (): The density current is reduced and replaced by a more uniform thermal gradient. Close to the inner and outer cylinders the isotherms are approximately vertical and confined to Stewartson layers which are a few centimetres thick and on the vertical boundaries. The azimuthal velocity is now non-zero and takes a maximum value near the top of the tank, but outside the boundary layers, close to the inner cylinder. As the rotation increases this region of maximal velocity becomes more confined towards the top of the tank. Close to the bottom of the tank at small radii retrograde motion begins to develop. Using streaklines to visualise the flow, Scolan and Read [18] showed that for weak rotation the flow in the experiment remains approximately axisymmetric.
- Moderate rotation (): For moderate rotation P is of order unity and thus the thicknesses of the thermal boundary layer and the Ekman layer are comparable. Free convection results in well mixed, approximately isothermal regions above and below the heat source and sink respectively. Sandwiched between these two convective zones is a baroclinic region with approximately uniformly sloping isotherms. This thermal structure has also been observed in experiment as shown by Scolan and Read [18] (Figure 6 of that paper). As before, prograde azimuthal velocity is seen close to the top of the tank and retrograde motion near the bottom with the most intense movement occuring at small radii. The azimuthal velocity begins to transition towards geostrophic balance as the rotation rate increases.
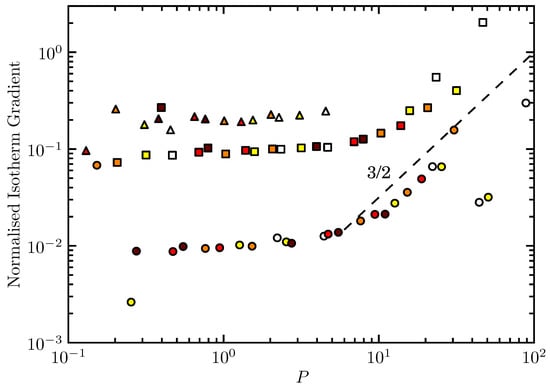 Figure 6. The isotherm gradient, normalised by the gradient of the conductive isotherms, as a function of P. Lower P data is not included as the interior of the annulus is approximately isothermal for low rotation and so the isotherm slope is not well defined. The dashed line shows the predicted dependence of the isotherm gradient on P and has a gradient of 3/2. Symbols have the same meaning as in Figure 4.
Figure 6. The isotherm gradient, normalised by the gradient of the conductive isotherms, as a function of P. Lower P data is not included as the interior of the annulus is approximately isothermal for low rotation and so the isotherm slope is not well defined. The dashed line shows the predicted dependence of the isotherm gradient on P and has a gradient of 3/2. Symbols have the same meaning as in Figure 4. - Strong Rotation (): The Ekman layer thickness is less than that of the thermal boundary layer and thus the radial transport becomes inhibited. The suppression of vertical convection results in the replacement of the well mixed regions by statically unstable temperature gradients. The isotherms in the central baroclinic region steepen and, for the highest value of P, are seen to surpass the vertical and slope in the opposite direction. The flow fields approach those expected for a purely conducting sample as the rotation organises the flow via the Taylor Proudman effect and so mixing is suppressed [51]. The azimuthal velocity is now approximately zero in the regions directly over/under the heat source/sink but in the central zone an azimuthal flow which follows the applied rotation at the top of the tank and goes against it at the bottom is observed. This induces a thermal wind shear.
Read et al. [14] identified changes in the slope of the isotherms as a function of P associated with transitions between different flow regimes. The isotherm slope, , is characterised by
where and are the widths of the heat sink and source respectively. Figure 6 shows the normalised isotherm gradient as a function of P. This is the ratio of the isotherm slope in the full flow to that in a purely conducting sample. The gradient is computed excluding the regions directly above/below the heat source/sink where the slope is non-linear. Figure 5 shows that for low rotation rates the interior of the fluid is approximately isothermal and so the isotherm slope is not meaningfully defined and so these data are not included in the plot. Initially the isotherm gradient is approximately constant and at higher P it begins to increase with a slope of about 3/2 which is in good agreement with the prediction for the classical annulus [14]. However, for the classical annulus, this transition is expected to occur at [14]. Here the transition appears to have some aspect ratio dependence and occur at higher values of . At high enough rotation rates the fluid begins to behave as a purely conducting sample and so the isotherm gradient normalised by the gradient of the isotherms in a conducting sample is expected to tend to 1. However, this is not clearly evident within the parameter space tested herein. An aspect ratio dependence of the isotherm slope is observed with lower aspect ratios giving steeper isotherms for the same value of P. Smaller aspect ratios in this case have a larger vertical separation between the heat source and sink.
3.3. Heat Transfer
Figure 7 shows the variation in the reduced Nusselt number, , with P. This may also be described as a Péclet number, , which is the ratio of advective to conductive heat transfer and may be written . The major trend is that the Nusselt number remains close to that of the non-rotating system, until , when it begins to decrease rapidly with P. This transition occurs in the moderately rotating regime where the Ekman layer has a thickness comparable to that of the thermal boundary layer and thus begins to suppress radial transport. This behaviour has been observed in previous annulus experiments [16,17,52]. A least squares fit for vs. at high P gives a slope of and for respectively. These gradients are consistent with the -3/2 scaling found by Read [16], Hignett [52]. The Ekman mass transport is proportional to [51]. At high rotation the azimuthal flow is governed by the thermal wind which results in . Thus the mass transport, and hence the Péclet number, is proportional to . For the highest aspect ratio (indicated by circular markers on Figure 7) there appears to be another transition to a constant or slightly increasing Nusselt number at . Although more data at higher P would be necessary to confirm this trend, it is notable that these data points correspond to the temperature fields where the isotherms were observed to surpass the vertical.
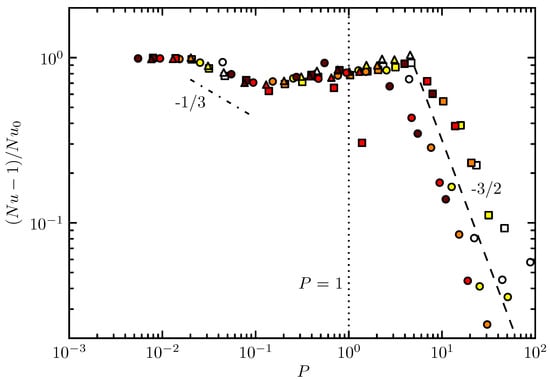
Figure 7.
The reduced Nusselt number plotted against P. The dashed line has a slope of −3/2 which can be compared with the slope of the datapoints. The Nusselt number is expected to decrease at this rate for high P. The dashed-dotted line has a gradient of −1/3, this rate of decrease in the Nusselt number may be expected if Stewartson layers were throttling the flow. The vertical dotted line marks the point where the Ekman layer and thermal boundary layer have approximately equal thickness at . The symbols are the same as in Figure 4.
Additionally, more subtle variation in the Nusselt number is observed at low P. At the Nusselt number begins to decrease with P to a minimum of about 70% of the non-rotating value. The Nusselt number then increases again to close to the non-rotating value before the rapid decrease with P begins. This increase was also observed in experiment by Scolan and Read [18] despite the experiments being fully three dimensional compared to the axisymmetric simulations. A possible physical explanation may be offered by considering the temperature fields in Figure 5. For the Stewartson layer thickness on the vertical sidewall is about 6 cm, within the same order of magnitude as the width of the hot and cold plates at approximately 10cm. When P increases to 0.44 the thickness of the Stewartson layer halves to about 3 cm, less than half the width of the source/sink, and so the vertical motion is throttled, potentially reducing the heat transport. At higher values of P the heat transport is increased again as the regions above and below the heat source and sink become fully convective. The Stewartson layer thickness is proportional to and so the reduction in heat transport may be expected to go as . This value is possibly in agreement with the slope of the reduction observed in Figure 7, as shown by the dashed-dotted line, but further investigation would be needed to fully support this argument.
For each of the three aspect ratios the general behaviour follows a similar trend. However, the value of P at which the transition to the regime where is proportional to occurs is a function of aspect ratio. Read [16] predicted an aspect ratio dependence of the regime transitions for an annulus with internal heating and observed transitions occurring at lower P for higher aspect ratio in numerical simulations. Aspect ratio dependence of transitions between different behaviours has also been seen in Rayleigh-Bénard convection [53]. As the analysis stands P is independent of the height of the fluid. The aspect ratio dependence suggests that at higher values of P the depth of the fluid influences the heat transfer through the flow, perhaps because of the inhibition of radial flow via the Taylor-Proudman effect. A full explanation for the aspect ratio dependence remains currently unknown.
3.4. The Azimuthal Velocity Scale
Following Read [16] the azimuthal velocity scale, V, of the flow may be estimated by considering the volume averaged azimuthal kinetic energy defined as
The reduced azimuthal velocity scale plotted in Figure 8 is derived via a scaling analysis of Equations (5) and (7) in the weakly rotating regime to find the theoretical maximum of V. This is akin to Read [16] but with heating on the horizontal surface as for our experiment. As with the Nusselt number, the scaling of V is expected to change with increasing rotation (and hence increasing P) and such behaviour is observed in Figure 8.
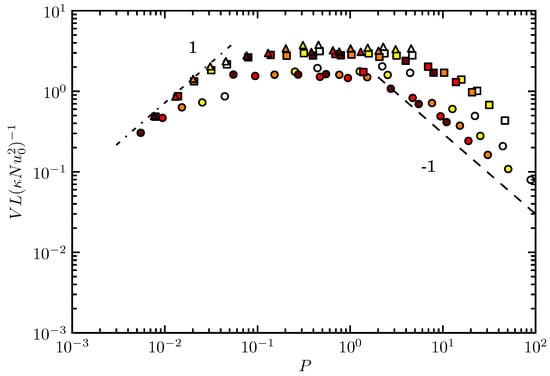
Figure 8.
The azimuthal velocity scale, scaled following Read [16], as a function of P. The dashed-dotted line has a gradient of 1 and thus it is clear that the azimuthal velocity scale increases approximately linearly with P at low P. The dashed line has a gradient of −1 showing that for the velocity scale tends to the thermal wind scale. Symbols have the same meaning as in Figure 4.
For very weak rotation, there is a balance of inertial and Coriolis forces and so, from the azimuthal momentum equation, it may be shown that . Therefore it is expected that V should increase linearly with P as both P and f are proportional to the rotation rate. For slightly stronger, but still weak, rotation the Coriolis force balances viscous effects in the Ekman layer and thus the expected scaling of V can be found by equating these two terms in the azimuthal momentum equation. This gives , the transition to the shallower slope of 1/2 can be observed in Figure 8 for for . For the azimuthal velocity scale reaches a maximum of before beginning to decrease. For the azimuthal velocity is proportional to , which follows from thermal wind balance. These results are concurrent with those found from previous annulus experiments [16,17].
As in the case of the Nusselt number there is clearly an aspect ratio dependence of the azimuthal velocity which has not been included in the analysis. The two lower aspect ratios collapse well onto a single line but the data for gives a lower value for the scaled velocity for a given value of P. The dependence of the transitions between regimes on the aspect ratio is less marked here than in the case of the Nusselt number.
4. Conclusion
This study has explored and identified a number of distinct axisymmetric circulation regimes in a novel experimental configuration which combines statically unstable convection with large-scale overturning. The resulting flows include cases, at moderate rotation rates, where a stably stratified baroclinic zone, with sloping isopycnals and isotherms, is obtained between two convectively unstable regions adjacent to the laterally displaced heat source and sink. This flow structure was verified by the initial experimental results of Scolan and Read [18]. This flow may be thought of as an analogue to the Earth’s atmosphere where vigorous convection takes place in the tropics and to some extent in the polar regions and the mid-latitude atmosphere is baroclinic. The regimes identified herein are comparable to regimes (iii)—(v) of Read [16], Hignett et al. [17] and Read et al. [14]. The similarity between the regimes of the new annulus and the classical annulus suggests that vigorous baroclinic instability is likely to occur for . Therefore, future experimental and numerical work will focus on such conditions to explore the equilibration of baroclinic instability and possible effects of ‘baroclinic adjustment’ and the role of non-linear eddy-eddy interactions [2,3]. This axisymmetric study has provided a means of defining the background flow in the absence of baroclinic instability and thus provides a base state for comparison with future three dimensional experiments which will aim to quantify how the baroclinic turbulence interacts with the background state.
From investigations of the heat transfer in the non-rotating system it is clear that more work is needed to elucidate, in detail, the behaviour of the convection in this system. Although comparisons may be drawn with the classical annulus, Rayleigh-Bénard and horizontal convection, the new system does not seem to behave exactly as any of these three. In particular the aspect ratio dependence of both the non-rotating and rotating systems remains unexplained and requires further attention in future studies. In the rotating case, the observed aspect ratio dependency of the transitions between regimes suggests that aspect ratio dependency may exist in the threshold of the development of baroclinic instability. This would be interesting to test in future experiments and 3D numerical simulations.
Supplementary Materials
The following are available online at http://www.mdpi.com/2311-5521/2/3/41/s1, Video S1: Simulation of the baroclinic sandwich experiment in 2D at low rotation rate, Video S2: Simulation of the baroclinic sandwich experiment in 2D at high rotation rate. Movies S1 and S2 show short animations of the temperature field at the beginning of two simulations. Both simulations have cm and . S1 has rotation rate · s−1 (same as Figure 2) and S2 has · s−1.
Acknowledgments
We would like to thank two anonymous reviewers for their comments and suggestions. The authors are grateful to the Oxford-Met. Office Academic Partnership (Ox-MOAP) for supporting Sylvie Su’s summer project. This work has also been partially supported by EPSRC grant EP/K029428/1 (HS), STFC grant ST/K00106X/1 (RMBY), and NERC grant NE/M009440/1 (SW).
Author Contributions
Sylvie Su adapted the MORALS numerical model to produce the new annulus configuration, ran initial simulations, and performed initial analysis of the results, supervised by Hélène Scolan, Roland M. B. Young, and Peter L. Read. Susie Wright ran further simulations, performed the bulk of the analysis, and produced the majority of the figures, supervised by Peter L. Read. Susie Wright wrote the majority of the manuscript, with sections contributed by Hélène Scolan, Roland M. B. Young, and Peter L. Read. Roland M. B. Young wrote the code to solve the thermal conduction equation, and produced the animations. Peter L. Read conceived the design of the new annulus configuration, assisted by Hélène Scolan. All authors contributed to discussion of the results.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The diffusive term, , used in the momentum equation (Equation (5)) consists of a radial component,
an azimuthal component,
and a vertical component,
The diffusion operators, and , are given by
where A is a component of the velocity vector.
References
- Chan, S.C.; Nigam, S. Residual diagnosis of diabatic heating from ERA-40 and NCEP reanalyses, intercomparisons with TRMM. J. Clim. 2009, 22, 414–428. [Google Scholar] [CrossRef]
- Schneider, T. The General Circulation of the Atmosphere. Annu. Rev. Earth Planet. Sci. 2006, 34, 655–688. [Google Scholar] [CrossRef]
- Zurita-Gotor, P.; Lindzen, R. Theories of baroclinic adjustment and eddy equilibration. In The Global Circulation of the Atmosphere; Princeton University Press: Princeton, NJ, USA, 2007; pp. 22–46. [Google Scholar]
- Hide, R.; Mason, P. Sloping convection in a rotating fluid. Adv. Phys. 1975, 24, 47–100. [Google Scholar] [CrossRef]
- Hignett, P.; White, A.; Carter, R.; Jackson, W.; Small, R. A comparison of laboratory measurements and numerical simulations of baroclinic wave flows in a rotating cylindrical annulus. Q. J. Roy. Meteor. Soc. 1985, 111, 131–154. [Google Scholar] [CrossRef]
- Read, P.; Bell, M.; Johnson, D.; Small, R. Quasi-periodic and chaotic flow regimes in a thermally driven, rotating fluid annulus. J. Fluid Mech. 1992, 238, 599–632. [Google Scholar] [CrossRef]
- Früh, W.G.; Read, P. Wave interactions and the transition to chaos of baroclinic waves in a thermally driven rotating annulus. Philos. T. R. Soc. A 1997, 355, 101–153. [Google Scholar] [CrossRef]
- Von Larcher, T.; Egbers, C. Experiments on transitions of baroclinic waves in a differentially heated rotating annulus. Nonlinear Process. Geophys. 2005, 12, 1033–1041. [Google Scholar] [CrossRef]
- Harlander, U.; von Larcher, T.; Wang, Y.; Egbers, C. PIV-and LDV-measurements of baroclinic wave interactions in a thermally driven rotating annulus. Exp. Fluids 2011, 51, 37–49. [Google Scholar] [CrossRef]
- Vincze, M.; Harlander, U.; von Larcher, T.; Egbers, C. An experimental study of regime transitions in a differentially heated baroclinic annulus with flat and sloping bottom topographies. Nonlinear Process. Geophys. 2014, 21, 237–250. [Google Scholar] [CrossRef]
- Williams, G.P. Numerical integration of the three-dimensional Navier-Stokes equations for incompressible flow. J. Fluid Mech. 1969, 37, 727–750. [Google Scholar] [CrossRef]
- Read, P. A combined laboratory and numerical study of heat transport by baroclinic eddies and axisymmetric flows. J. Fluid Mech. 2003, 489, 301–323. [Google Scholar] [CrossRef]
- Young, R.M.B.; Read, P.L. Flow transitions resembling bifurcations of the logistic map in simulations of the baroclinic rotating annulus. Physics D 2008, 237, 2251–2262. [Google Scholar] [CrossRef]
- Read, P.L.; Pérez, E.P.; Moroz, I.M.; Young, R.M.B. General Circulation of Planetary Atmospheres: Insights from Rotating Annulus and Related Experiments. In Modeling Atmospheric and Oceanic Flows: Insights from Laboratory Experiments and Numerical Simulations; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 7–44. [Google Scholar]
- Read, P. Dynamics and circulation regimes of terrestrial planets. Planet. Space Sci. 2011, 59, 900–914. [Google Scholar] [CrossRef]
- Read, P.L. Regimes of axisymmetric flow in an internally heated rotating fluid. J. Fluid Mech. 1986, 168, 255–289. [Google Scholar] [CrossRef]
- Hignett, P.; Ibbetson, A.; Killworth, P.D. On rotating thermal convection driven by non-uniform heating from below. J. Fluid Mech. 1981, 109, 161. [Google Scholar] [CrossRef]
- Scolan, H.; Read, P.L. A rotating annulus driven by localized convective forcing: A new atmosphere-like experiment. Exp. Fluids 2017, 58, 75. [Google Scholar] [CrossRef]
- Schmalzl, J.; Breuer, M.; Hansen, U. On the validity of two-dimensional numerical approaches to time-dependent thermal convection. EPL (Europhys. Lett.) 2004, 67, 390. [Google Scholar] [CrossRef]
- van der Poel, E.P.; Stevens, R.J.A.M.; Lohse, D. Comparison between two- and three-dimensional Rayleigh–Bénard convection. J. Fluid Mech. 2013, 736, 177–194. [Google Scholar] [CrossRef]
- Hughes, G.O.; Griffiths, R.W. Horizontal Convection. Annu. Rev. Fluid Mech. 2008, 40, 185–208. [Google Scholar] [CrossRef]
- Ilicak, M.; Vallis, G.K. Simulations and scaling of horizontal convection. Tellus A 2012, 64, 18377. [Google Scholar] [CrossRef]
- King, E.M.; Stellmach, S.; Aurnou, J.M. Heat transfer by rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 2012, 691, 568–582. [Google Scholar] [CrossRef]
- King, E.M.; Stellmach, S.; Noir, J.; Hansen, U.; Aurnou, J.M. Boundary layer control of rotating convection systems. Nature 2009, 457, 301–304. [Google Scholar] [CrossRef] [PubMed]
- Ahlers, G.; Grossmann, S.; Lohse, D. Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection. Rev. Mod. Phys. 2009, 81, 503–537. [Google Scholar] [CrossRef]
- Chillà, F.; Schumacher, J. New perspectives in turbulent Rayleigh-Bénard convection. Eur. Phys. J. E 2012, 35. [Google Scholar] [CrossRef] [PubMed]
- Rossby, H. On thermal convection driven by non-uniform heating from below: An experimental study. Deep-Sea Res. 1965, 12, 9–16. [Google Scholar] [CrossRef]
- Shishkina, O.; Grossmann, S.; Lohse, D. Heat and momentum transport scalings in horizontal convection. Geophys. Res. Lett. 2016, 43, 1219–1225. [Google Scholar] [CrossRef]
- Malkus, W.V.R. The Heat Transport and Spectrum of Thermal Turbulence. Proc. R. Soc. Lond. Math. 1954, 225, 196–212. [Google Scholar] [CrossRef]
- Shraiman, B.I.; Siggia, E.D. Heat transport in high-Rayleigh-number convection. Phys. Rev. A 1990, 42, 3650–3653. [Google Scholar] [CrossRef] [PubMed]
- Castaing, B.; Gunaratne, G.; Heslot, F.; Kadanoff, L.; Libchaber, A.; Thomae, S.; Wu, X.Z.; Zaleski, S.; Zanetti, G. Scaling of hard thermal turbulence in Rayleigh-Bénard convection. J. Fluid Mech. 1989, 204, 1–30. [Google Scholar] [CrossRef]
- Chavanne, A.X.; Chilla, F.; Castaing, B.; Hebral, B.; Chabaud, B.; Chaussy, J. Observation of the ultimate regime in Rayleigh-Bénard convection. Phys. Rev. Lett. 1997, 79, 3648. [Google Scholar] [CrossRef]
- Grossmann, S.; Lohse, D. Scaling in thermal convection: A unifying theory. J. Fluid Mech. 2000, 407, 30. [Google Scholar] [CrossRef]
- Grossmann, S.; Lohse, D. Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 2001, 86, 3316–3319. [Google Scholar] [CrossRef] [PubMed]
- Grossmann, S.; Lohse, D. Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 2002, 66, 016305. [Google Scholar] [CrossRef] [PubMed]
- Grossmann, S.; Lohse, D. Fluctuations in turbulent Rayleigh–Benard convection: The role of plumes. Phys. Fluids 2004, 16, 4462. [Google Scholar] [CrossRef]
- Grossmann, S.; Lohse, D. Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 2011, 23, 045108. [Google Scholar] [CrossRef]
- Stevens, R.J.A.M.; van der Poel, E.P.; Grossmann, S.; Lohse, D. The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 2013, 730, 295–308. [Google Scholar] [CrossRef]
- Shishkina, O.; Wagner, S. Prandtl-number dependence of heat hransport in laminar horizontal convection. Phys. Rev. Lett. 2016, 116, 024302. [Google Scholar] [CrossRef] [PubMed]
- Farnell, L.; Plumb, R. Numerical Integration of Flow in a Rotating Annulus I: Axisymmetric Model; Geophysical Fluid Dynamics Laboratory, UK, Meteorological Office: Exeter, UK, 1975; pp. 1–39.
- Read, P.; Thomas, N.; Risch, S. An evaluation of Eulerian and semi-Lagrangian advection schemes in simulations of rotating, stratified flows in the laboratory. Part I: Axisymmetric flow. Mon. Weather Rev. 2000, 128, 2835–2852. [Google Scholar] [CrossRef]
- Young, R.M.B.; Read, P.L. Data assimilation in the laboratory using a rotating annulus experiment. Q. J. R. Meteor. Soc. 2013, 139, 1488–1504. [Google Scholar] [CrossRef]
- Arakawa, A.; Lamb, V.R. Computational Design of the Basic Dynamical Processes of the UCLA General Circulation Model. In Methods in Computational Physics: Advances in Research and Applications; Elsevier: Amsterdam, The Netherlands, 1977; Volume 17. [Google Scholar]
- Xu, X.; Bajaj, K.M.; Ahlers, G. Heat transport in turbulent Rayleigh-Bénard convection. Phys. Rev. Lett. 2000, 84, 4357. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, R.; Tokuda, S. Heat transfer by thermal convection at high Rayleigh numbers. Int. J. Heat Mass Transfer 1980, 23, 738–740. [Google Scholar]
- Funfschilling, D.; Brown, E.; Nikolaenko, A.; Ahlers, G. Heat transport by turbulent Rayleigh–Bénard convection in cylindrical samples with aspect ratio one and larger. J. Fluid Mech. 2005, 536, 145–154. [Google Scholar] [CrossRef]
- Sun, C.; Ren, L.Y.; Song, H.; Xia, K.Q. Heat transport by turbulent Rayleigh–Bénard convection in 1 m diameter cylindrical cells of widely varying aspect ratio. J. Fluid Mech. 2005, 542, 165. [Google Scholar] [CrossRef]
- Bailon-Cuba, J.; Emran, M.S.; Schumacher, J. Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 2010, 655, 152–173. [Google Scholar] [CrossRef]
- van der Poel, E.P.; Stevens, R.J.A.M.; Lohse, D. Connecting flow structures and heat flux in turbulent Rayleigh-Bénard convection. Phys. Rev. E 2011, 84, 045303. [Google Scholar] [CrossRef] [PubMed]
- du Puits, R.; Resagk, C.; Thess, A. Thermal boundary layers in turbulent Rayleigh–Bénard convection at aspect ratios between 1 and 9. New J. Phys. 2013, 15, 013040. [Google Scholar] [CrossRef]
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Hignett, P. A note on the heat transfer by the axisymmetric thermal convection in a rotating fluid annulus. Geophys. Astrophys. Fluid Dyn. 1982, 19, 293–299. [Google Scholar] [CrossRef]
- Weiss, S.; Ahlers, G. Heat transport by turbulent rotating Rayleigh–Bénard convection and its dependence on the aspect ratio. J. Fluid Mech. 2011, 684, 407–426. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).