Regimes of Axisymmetric Flow and Scaling Laws in a Rotating Annulus with Local Convective Forcing
Abstract
:1. Introduction
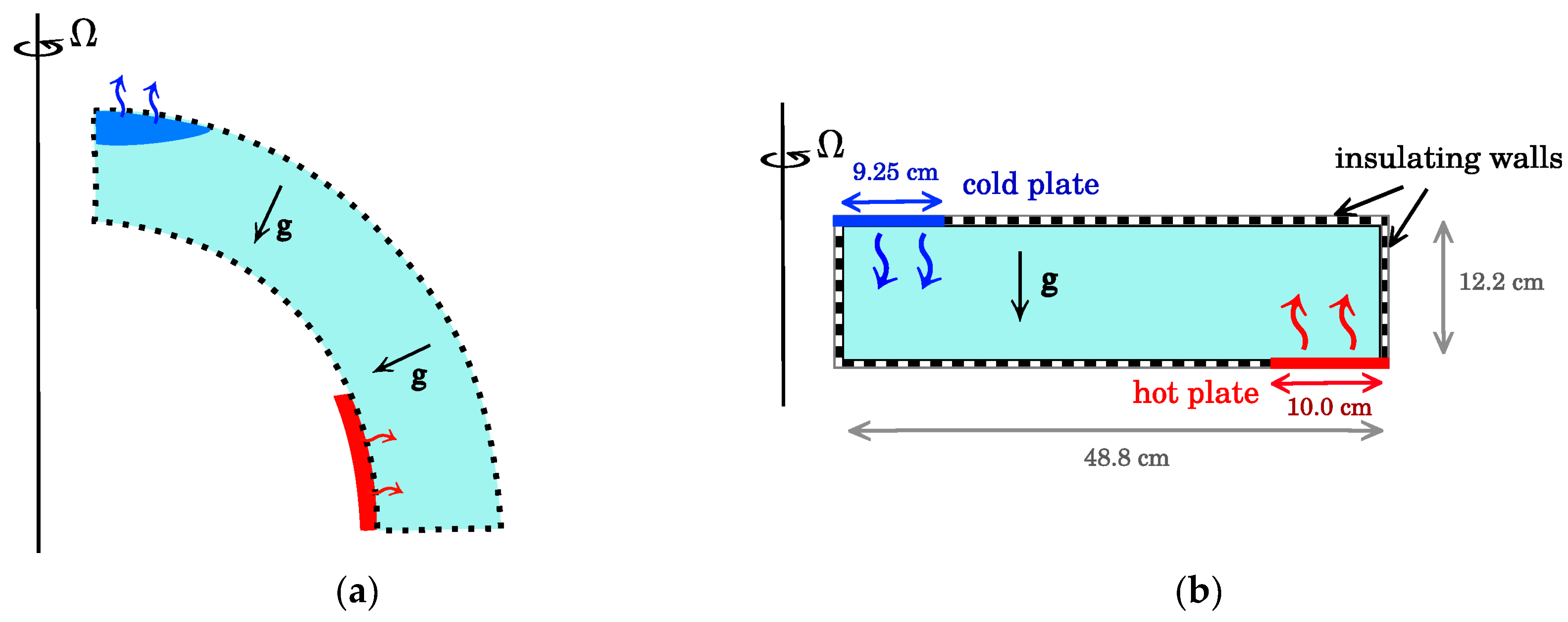
2. The Numerical Model
2.1. Dimensionless Parameters
2.2. The Numerical Model
3. Results
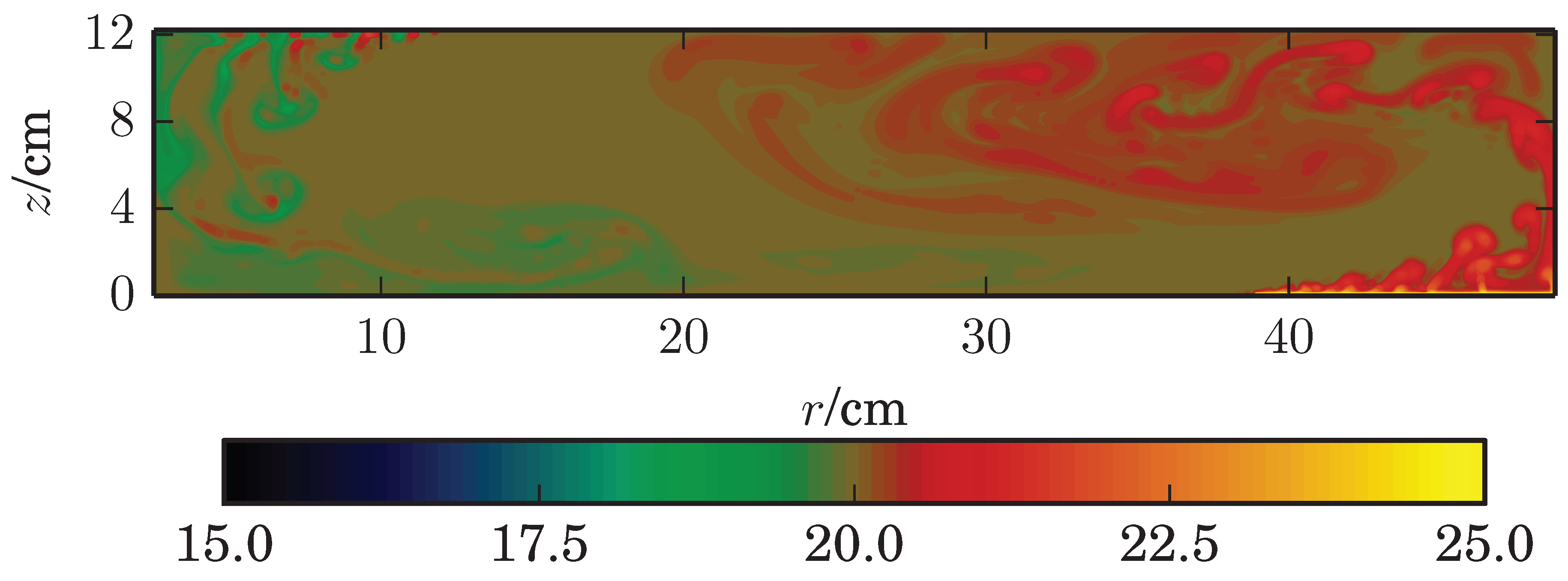
3.1. Non-Rotating Flow
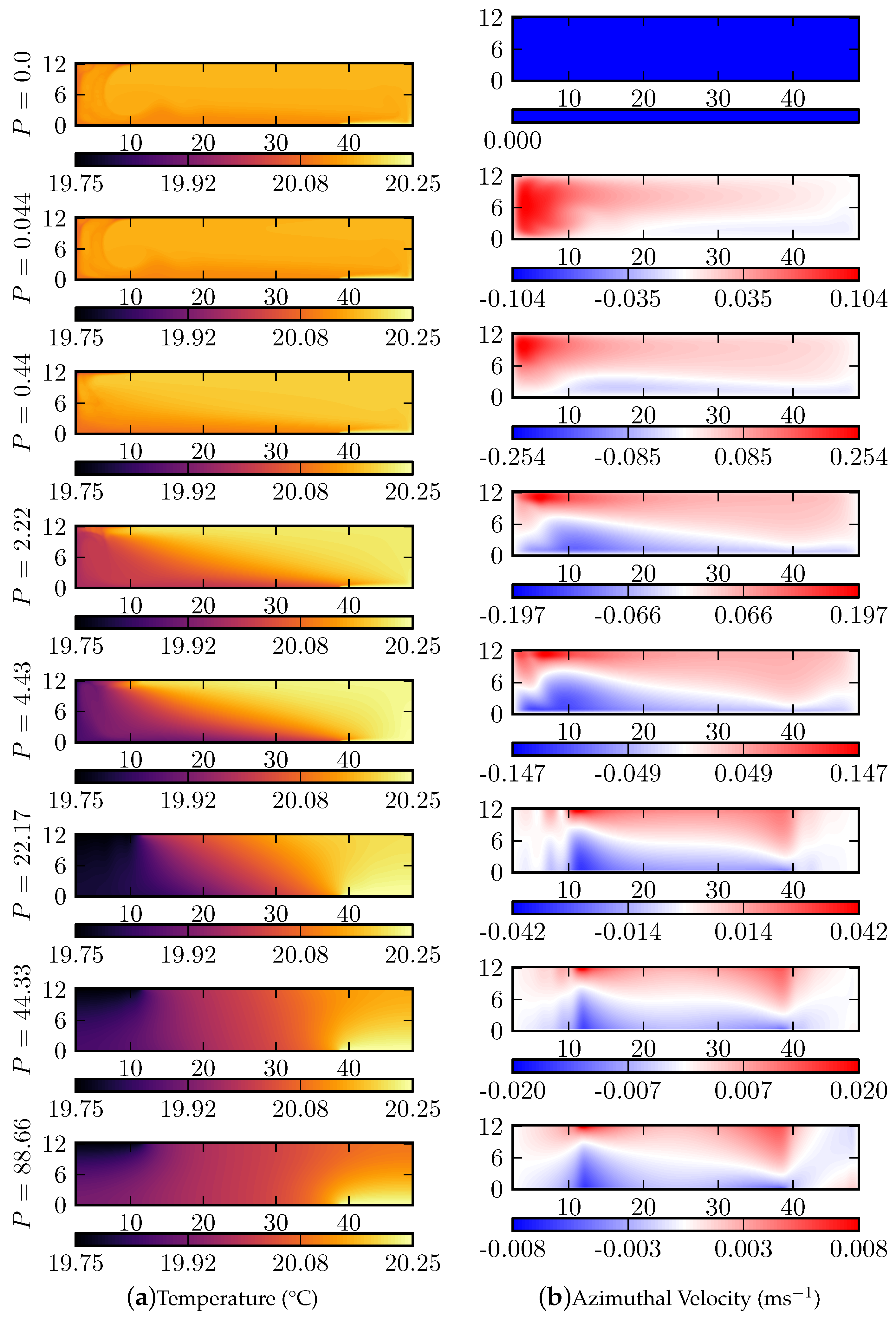
3.2. Rotating Flow Regimes
- No rotation (): A density current flows beneath the heat sink, down the side of the inner cylinder and along the base towards the heat source. A corresponding density current is not seen above the heat source, presumably because of the larger area of the hot plate. At high z and for 10 cm the fluid interior is approximately isothermal at a temperature close to that of the hot plate. Since all fields are time averaged the plumes observed in Figure 3 are not seen here. The azimuthal velocity is zero everywhere.
- Weak rotation (): The density current is reduced and replaced by a more uniform thermal gradient. Close to the inner and outer cylinders the isotherms are approximately vertical and confined to Stewartson layers which are a few centimetres thick and on the vertical boundaries. The azimuthal velocity is now non-zero and takes a maximum value near the top of the tank, but outside the boundary layers, close to the inner cylinder. As the rotation increases this region of maximal velocity becomes more confined towards the top of the tank. Close to the bottom of the tank at small radii retrograde motion begins to develop. Using streaklines to visualise the flow, Scolan and Read [18] showed that for weak rotation the flow in the experiment remains approximately axisymmetric.
- Moderate rotation (): For moderate rotation P is of order unity and thus the thicknesses of the thermal boundary layer and the Ekman layer are comparable. Free convection results in well mixed, approximately isothermal regions above and below the heat source and sink respectively. Sandwiched between these two convective zones is a baroclinic region with approximately uniformly sloping isotherms. This thermal structure has also been observed in experiment as shown by Scolan and Read [18] (Figure 6 of that paper). As before, prograde azimuthal velocity is seen close to the top of the tank and retrograde motion near the bottom with the most intense movement occuring at small radii. The azimuthal velocity begins to transition towards geostrophic balance as the rotation rate increases.
- Strong Rotation (): The Ekman layer thickness is less than that of the thermal boundary layer and thus the radial transport becomes inhibited. The suppression of vertical convection results in the replacement of the well mixed regions by statically unstable temperature gradients. The isotherms in the central baroclinic region steepen and, for the highest value of P, are seen to surpass the vertical and slope in the opposite direction. The flow fields approach those expected for a purely conducting sample as the rotation organises the flow via the Taylor Proudman effect and so mixing is suppressed [51]. The azimuthal velocity is now approximately zero in the regions directly over/under the heat source/sink but in the central zone an azimuthal flow which follows the applied rotation at the top of the tank and goes against it at the bottom is observed. This induces a thermal wind shear.
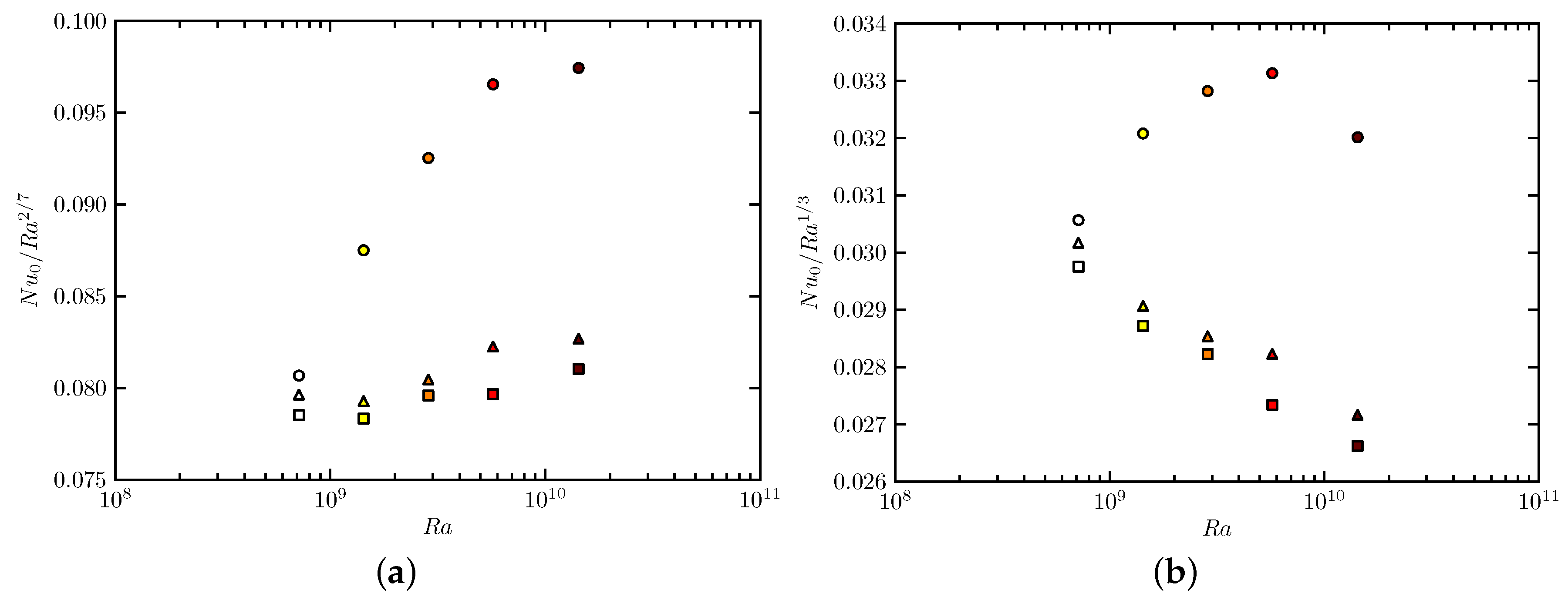
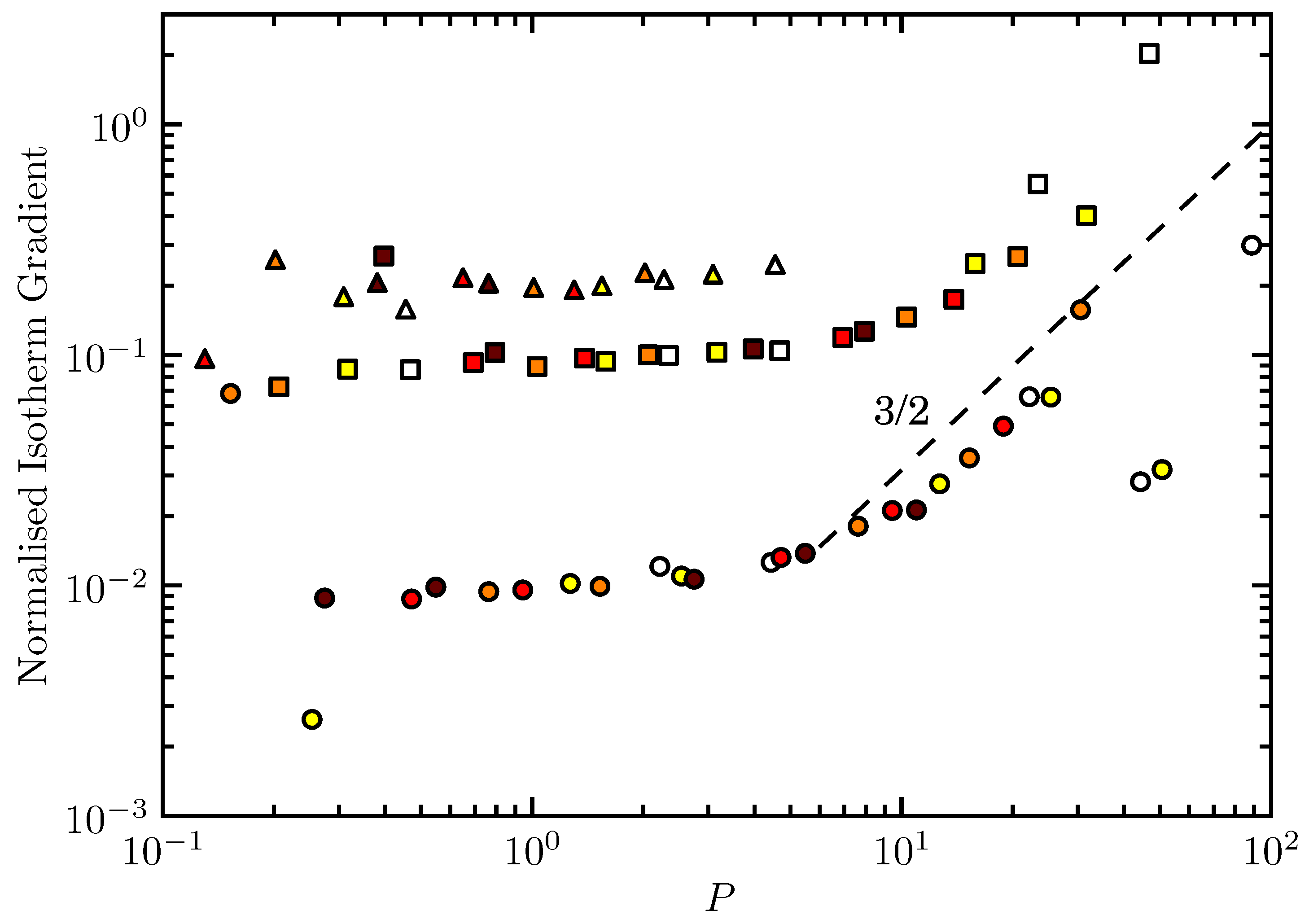
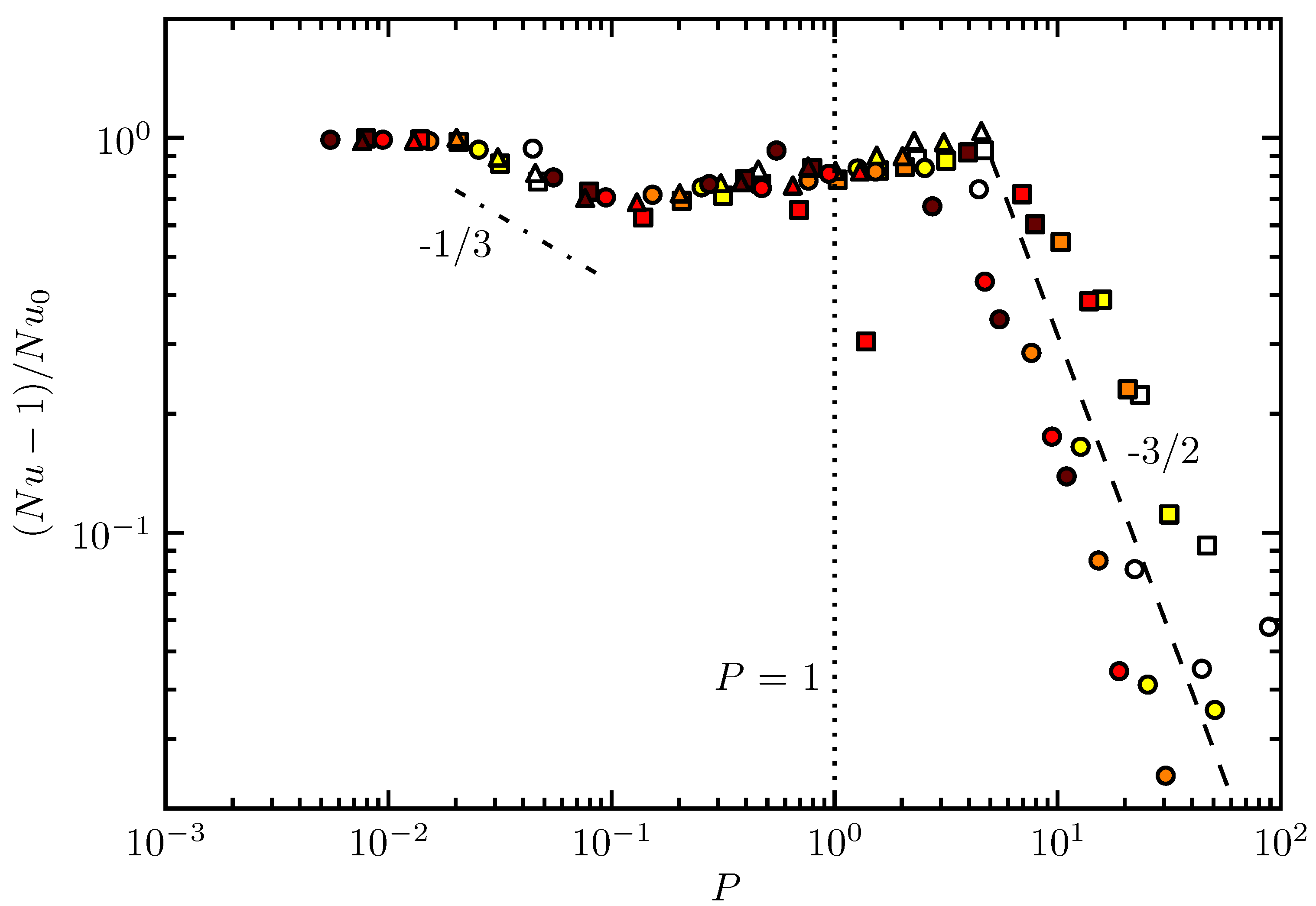
3.3. Heat Transfer
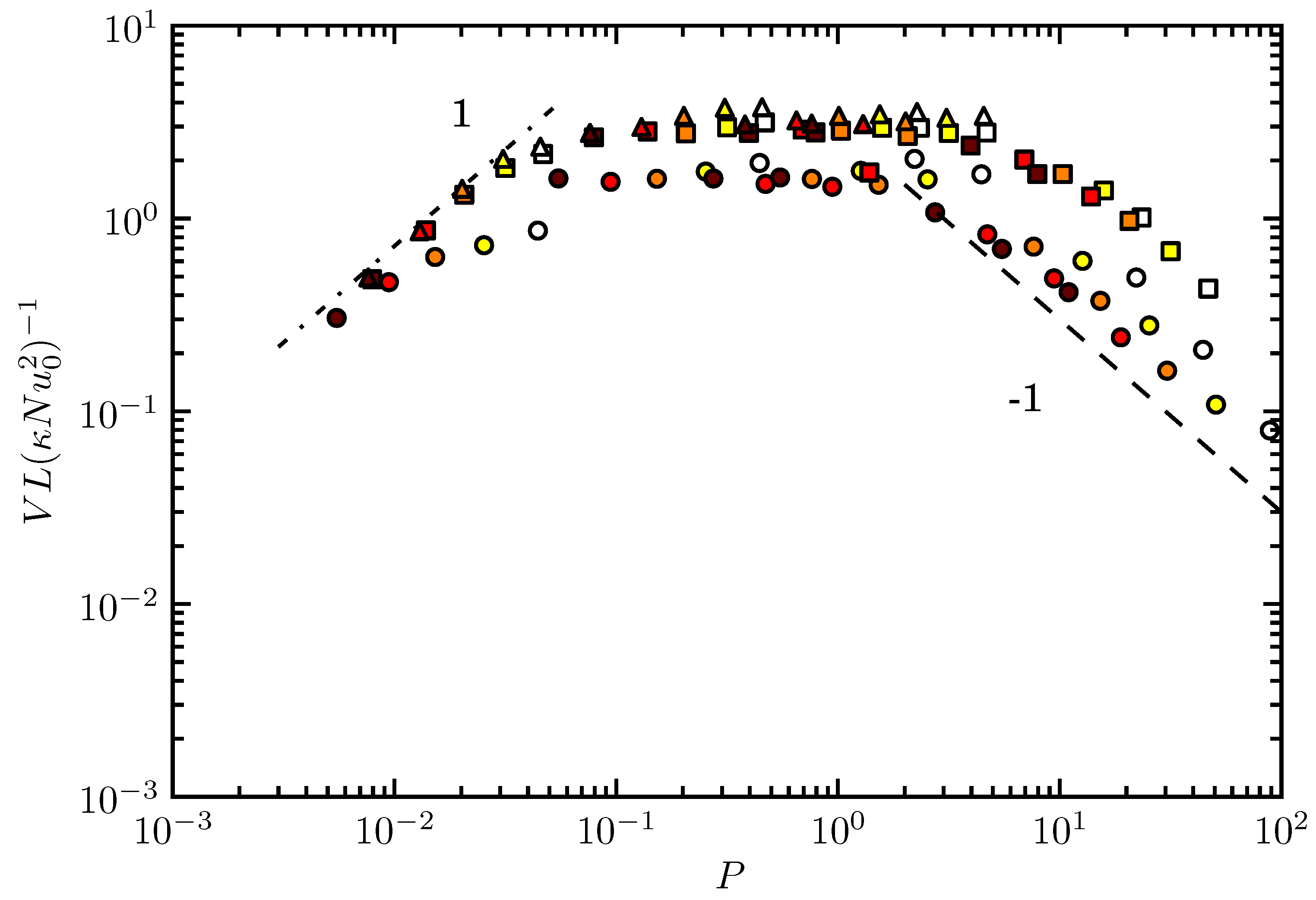
3.4. The Azimuthal Velocity Scale
4. Conclusion
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Chan, S.C.; Nigam, S. Residual diagnosis of diabatic heating from ERA-40 and NCEP reanalyses, intercomparisons with TRMM. J. Clim. 2009, 22, 414–428. [Google Scholar] [CrossRef]
- Schneider, T. The General Circulation of the Atmosphere. Annu. Rev. Earth Planet. Sci. 2006, 34, 655–688. [Google Scholar] [CrossRef]
- Zurita-Gotor, P.; Lindzen, R. Theories of baroclinic adjustment and eddy equilibration. In The Global Circulation of the Atmosphere; Princeton University Press: Princeton, NJ, USA, 2007; pp. 22–46. [Google Scholar]
- Hide, R.; Mason, P. Sloping convection in a rotating fluid. Adv. Phys. 1975, 24, 47–100. [Google Scholar] [CrossRef]
- Hignett, P.; White, A.; Carter, R.; Jackson, W.; Small, R. A comparison of laboratory measurements and numerical simulations of baroclinic wave flows in a rotating cylindrical annulus. Q. J. Roy. Meteor. Soc. 1985, 111, 131–154. [Google Scholar] [CrossRef]
- Read, P.; Bell, M.; Johnson, D.; Small, R. Quasi-periodic and chaotic flow regimes in a thermally driven, rotating fluid annulus. J. Fluid Mech. 1992, 238, 599–632. [Google Scholar] [CrossRef]
- Früh, W.G.; Read, P. Wave interactions and the transition to chaos of baroclinic waves in a thermally driven rotating annulus. Philos. T. R. Soc. A 1997, 355, 101–153. [Google Scholar] [CrossRef]
- Von Larcher, T.; Egbers, C. Experiments on transitions of baroclinic waves in a differentially heated rotating annulus. Nonlinear Process. Geophys. 2005, 12, 1033–1041. [Google Scholar] [CrossRef]
- Harlander, U.; von Larcher, T.; Wang, Y.; Egbers, C. PIV-and LDV-measurements of baroclinic wave interactions in a thermally driven rotating annulus. Exp. Fluids 2011, 51, 37–49. [Google Scholar] [CrossRef]
- Vincze, M.; Harlander, U.; von Larcher, T.; Egbers, C. An experimental study of regime transitions in a differentially heated baroclinic annulus with flat and sloping bottom topographies. Nonlinear Process. Geophys. 2014, 21, 237–250. [Google Scholar] [CrossRef]
- Williams, G.P. Numerical integration of the three-dimensional Navier-Stokes equations for incompressible flow. J. Fluid Mech. 1969, 37, 727–750. [Google Scholar] [CrossRef]
- Read, P. A combined laboratory and numerical study of heat transport by baroclinic eddies and axisymmetric flows. J. Fluid Mech. 2003, 489, 301–323. [Google Scholar] [CrossRef]
- Young, R.M.B.; Read, P.L. Flow transitions resembling bifurcations of the logistic map in simulations of the baroclinic rotating annulus. Physics D 2008, 237, 2251–2262. [Google Scholar] [CrossRef]
- Read, P.L.; Pérez, E.P.; Moroz, I.M.; Young, R.M.B. General Circulation of Planetary Atmospheres: Insights from Rotating Annulus and Related Experiments. In Modeling Atmospheric and Oceanic Flows: Insights from Laboratory Experiments and Numerical Simulations; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 7–44. [Google Scholar]
- Read, P. Dynamics and circulation regimes of terrestrial planets. Planet. Space Sci. 2011, 59, 900–914. [Google Scholar] [CrossRef]
- Read, P.L. Regimes of axisymmetric flow in an internally heated rotating fluid. J. Fluid Mech. 1986, 168, 255–289. [Google Scholar] [CrossRef]
- Hignett, P.; Ibbetson, A.; Killworth, P.D. On rotating thermal convection driven by non-uniform heating from below. J. Fluid Mech. 1981, 109, 161. [Google Scholar] [CrossRef]
- Scolan, H.; Read, P.L. A rotating annulus driven by localized convective forcing: A new atmosphere-like experiment. Exp. Fluids 2017, 58, 75. [Google Scholar] [CrossRef]
- Schmalzl, J.; Breuer, M.; Hansen, U. On the validity of two-dimensional numerical approaches to time-dependent thermal convection. EPL (Europhys. Lett.) 2004, 67, 390. [Google Scholar] [CrossRef]
- van der Poel, E.P.; Stevens, R.J.A.M.; Lohse, D. Comparison between two- and three-dimensional Rayleigh–Bénard convection. J. Fluid Mech. 2013, 736, 177–194. [Google Scholar] [CrossRef]
- Hughes, G.O.; Griffiths, R.W. Horizontal Convection. Annu. Rev. Fluid Mech. 2008, 40, 185–208. [Google Scholar] [CrossRef]
- Ilicak, M.; Vallis, G.K. Simulations and scaling of horizontal convection. Tellus A 2012, 64, 18377. [Google Scholar] [CrossRef]
- King, E.M.; Stellmach, S.; Aurnou, J.M. Heat transfer by rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 2012, 691, 568–582. [Google Scholar] [CrossRef]
- King, E.M.; Stellmach, S.; Noir, J.; Hansen, U.; Aurnou, J.M. Boundary layer control of rotating convection systems. Nature 2009, 457, 301–304. [Google Scholar] [CrossRef] [PubMed]
- Ahlers, G.; Grossmann, S.; Lohse, D. Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection. Rev. Mod. Phys. 2009, 81, 503–537. [Google Scholar] [CrossRef]
- Chillà, F.; Schumacher, J. New perspectives in turbulent Rayleigh-Bénard convection. Eur. Phys. J. E 2012, 35. [Google Scholar] [CrossRef] [PubMed]
- Rossby, H. On thermal convection driven by non-uniform heating from below: An experimental study. Deep-Sea Res. 1965, 12, 9–16. [Google Scholar] [CrossRef]
- Shishkina, O.; Grossmann, S.; Lohse, D. Heat and momentum transport scalings in horizontal convection. Geophys. Res. Lett. 2016, 43, 1219–1225. [Google Scholar] [CrossRef]
- Malkus, W.V.R. The Heat Transport and Spectrum of Thermal Turbulence. Proc. R. Soc. Lond. Math. 1954, 225, 196–212. [Google Scholar] [CrossRef]
- Shraiman, B.I.; Siggia, E.D. Heat transport in high-Rayleigh-number convection. Phys. Rev. A 1990, 42, 3650–3653. [Google Scholar] [CrossRef] [PubMed]
- Castaing, B.; Gunaratne, G.; Heslot, F.; Kadanoff, L.; Libchaber, A.; Thomae, S.; Wu, X.Z.; Zaleski, S.; Zanetti, G. Scaling of hard thermal turbulence in Rayleigh-Bénard convection. J. Fluid Mech. 1989, 204, 1–30. [Google Scholar] [CrossRef]
- Chavanne, A.X.; Chilla, F.; Castaing, B.; Hebral, B.; Chabaud, B.; Chaussy, J. Observation of the ultimate regime in Rayleigh-Bénard convection. Phys. Rev. Lett. 1997, 79, 3648. [Google Scholar] [CrossRef]
- Grossmann, S.; Lohse, D. Scaling in thermal convection: A unifying theory. J. Fluid Mech. 2000, 407, 30. [Google Scholar] [CrossRef]
- Grossmann, S.; Lohse, D. Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 2001, 86, 3316–3319. [Google Scholar] [CrossRef] [PubMed]
- Grossmann, S.; Lohse, D. Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 2002, 66, 016305. [Google Scholar] [CrossRef] [PubMed]
- Grossmann, S.; Lohse, D. Fluctuations in turbulent Rayleigh–Benard convection: The role of plumes. Phys. Fluids 2004, 16, 4462. [Google Scholar] [CrossRef]
- Grossmann, S.; Lohse, D. Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 2011, 23, 045108. [Google Scholar] [CrossRef]
- Stevens, R.J.A.M.; van der Poel, E.P.; Grossmann, S.; Lohse, D. The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 2013, 730, 295–308. [Google Scholar] [CrossRef]
- Shishkina, O.; Wagner, S. Prandtl-number dependence of heat hransport in laminar horizontal convection. Phys. Rev. Lett. 2016, 116, 024302. [Google Scholar] [CrossRef] [PubMed]
- Farnell, L.; Plumb, R. Numerical Integration of Flow in a Rotating Annulus I: Axisymmetric Model; Geophysical Fluid Dynamics Laboratory, UK, Meteorological Office: Exeter, UK, 1975; pp. 1–39.
- Read, P.; Thomas, N.; Risch, S. An evaluation of Eulerian and semi-Lagrangian advection schemes in simulations of rotating, stratified flows in the laboratory. Part I: Axisymmetric flow. Mon. Weather Rev. 2000, 128, 2835–2852. [Google Scholar] [CrossRef]
- Young, R.M.B.; Read, P.L. Data assimilation in the laboratory using a rotating annulus experiment. Q. J. R. Meteor. Soc. 2013, 139, 1488–1504. [Google Scholar] [CrossRef]
- Arakawa, A.; Lamb, V.R. Computational Design of the Basic Dynamical Processes of the UCLA General Circulation Model. In Methods in Computational Physics: Advances in Research and Applications; Elsevier: Amsterdam, The Netherlands, 1977; Volume 17. [Google Scholar]
- Xu, X.; Bajaj, K.M.; Ahlers, G. Heat transport in turbulent Rayleigh-Bénard convection. Phys. Rev. Lett. 2000, 84, 4357. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, R.; Tokuda, S. Heat transfer by thermal convection at high Rayleigh numbers. Int. J. Heat Mass Transfer 1980, 23, 738–740. [Google Scholar]
- Funfschilling, D.; Brown, E.; Nikolaenko, A.; Ahlers, G. Heat transport by turbulent Rayleigh–Bénard convection in cylindrical samples with aspect ratio one and larger. J. Fluid Mech. 2005, 536, 145–154. [Google Scholar] [CrossRef]
- Sun, C.; Ren, L.Y.; Song, H.; Xia, K.Q. Heat transport by turbulent Rayleigh–Bénard convection in 1 m diameter cylindrical cells of widely varying aspect ratio. J. Fluid Mech. 2005, 542, 165. [Google Scholar] [CrossRef]
- Bailon-Cuba, J.; Emran, M.S.; Schumacher, J. Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 2010, 655, 152–173. [Google Scholar] [CrossRef]
- van der Poel, E.P.; Stevens, R.J.A.M.; Lohse, D. Connecting flow structures and heat flux in turbulent Rayleigh-Bénard convection. Phys. Rev. E 2011, 84, 045303. [Google Scholar] [CrossRef] [PubMed]
- du Puits, R.; Resagk, C.; Thess, A. Thermal boundary layers in turbulent Rayleigh–Bénard convection at aspect ratios between 1 and 9. New J. Phys. 2013, 15, 013040. [Google Scholar] [CrossRef]
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Hignett, P. A note on the heat transfer by the axisymmetric thermal convection in a rotating fluid annulus. Geophys. Astrophys. Fluid Dyn. 1982, 19, 293–299. [Google Scholar] [CrossRef]
- Weiss, S.; Ahlers, G. Heat transport by turbulent rotating Rayleigh–Bénard convection and its dependence on the aspect ratio. J. Fluid Mech. 2011, 684, 407–426. [Google Scholar] [CrossRef]
| Parameter | Symbol | Present range | Units |
|---|---|---|---|
| Rotation rate | 0–2 | rads | |
| Temperature difference | 0.5–10 | K | |
| Fluid properties are listed at 20 : | |||
| Density | 1044 | kgm | |
| Thermal expansion coefficient | K | ||
| Kinematic viscosity | 1.71 | ms | |
| Thermal diffusivity | 1.28 | ms | |
| Channel geometry: | |||
| Inner radius | a | 0.025 | m |
| Outer radius | b | 0.488 | m |
| Mean fluid depth | d | 0.122, 0.244, 0.366 | m |
| Non-dimensional: | |||
| Ekman number (Equation (2)) | |||
| Prandtl number | 12.6 | ||
| Rayleigh number (Equation (3)) | – | ||
| Aspect ratio | 3.8, 1.89, 1.27 |
| Aspect Ratio, | |
|---|---|
| 1.3 | |
| 1.9 | |
| 3.8 | |
| All |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wright, S.; Su, S.; Scolan, H.; Young, R.M.B.; Read, P.L. Regimes of Axisymmetric Flow and Scaling Laws in a Rotating Annulus with Local Convective Forcing. Fluids 2017, 2, 41. https://doi.org/10.3390/fluids2030041
Wright S, Su S, Scolan H, Young RMB, Read PL. Regimes of Axisymmetric Flow and Scaling Laws in a Rotating Annulus with Local Convective Forcing. Fluids. 2017; 2(3):41. https://doi.org/10.3390/fluids2030041
Chicago/Turabian StyleWright, Susie, Sylvie Su, Hélène Scolan, Roland M. B. Young, and Peter L. Read. 2017. "Regimes of Axisymmetric Flow and Scaling Laws in a Rotating Annulus with Local Convective Forcing" Fluids 2, no. 3: 41. https://doi.org/10.3390/fluids2030041
APA StyleWright, S., Su, S., Scolan, H., Young, R. M. B., & Read, P. L. (2017). Regimes of Axisymmetric Flow and Scaling Laws in a Rotating Annulus with Local Convective Forcing. Fluids, 2(3), 41. https://doi.org/10.3390/fluids2030041





