Surface Quasi-Geostrophy
Abstract
:1. Introduction
2. General Formulation of Surface Quasi-Geostrophy (SQG)
2.1. General Quasi-Geostrophic (QG) Theory
2.2. Inversion of Potential Vorticity () Equation
2.3. Surface Quasi-Geostrophy (SQG) Formulation
2.4. Invariants
2.5. Relation between the Active Tracer and Streamfunction
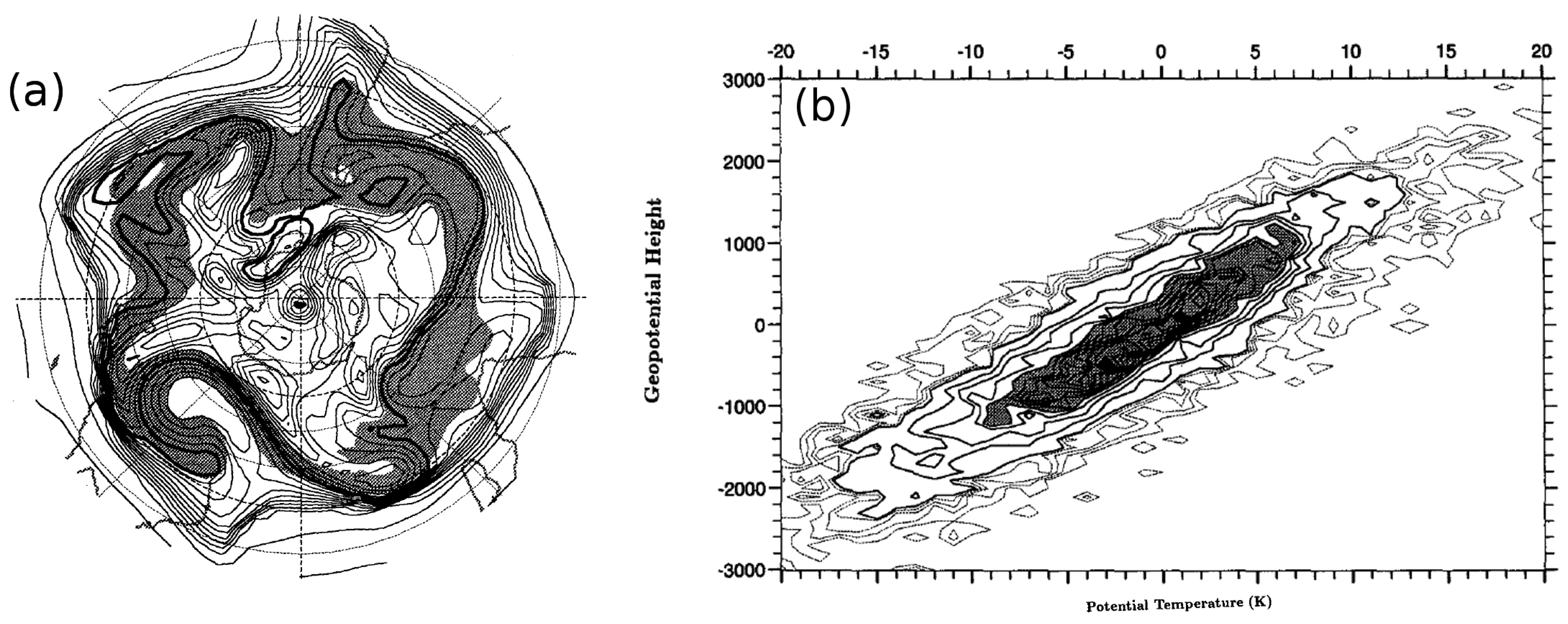
3. Coherent Structure Dynamics
3.1. Exact Surface Quasi-Geostrophy (SQG) Solutions
3.2. Contour Dynamics
3.3. Instabilities
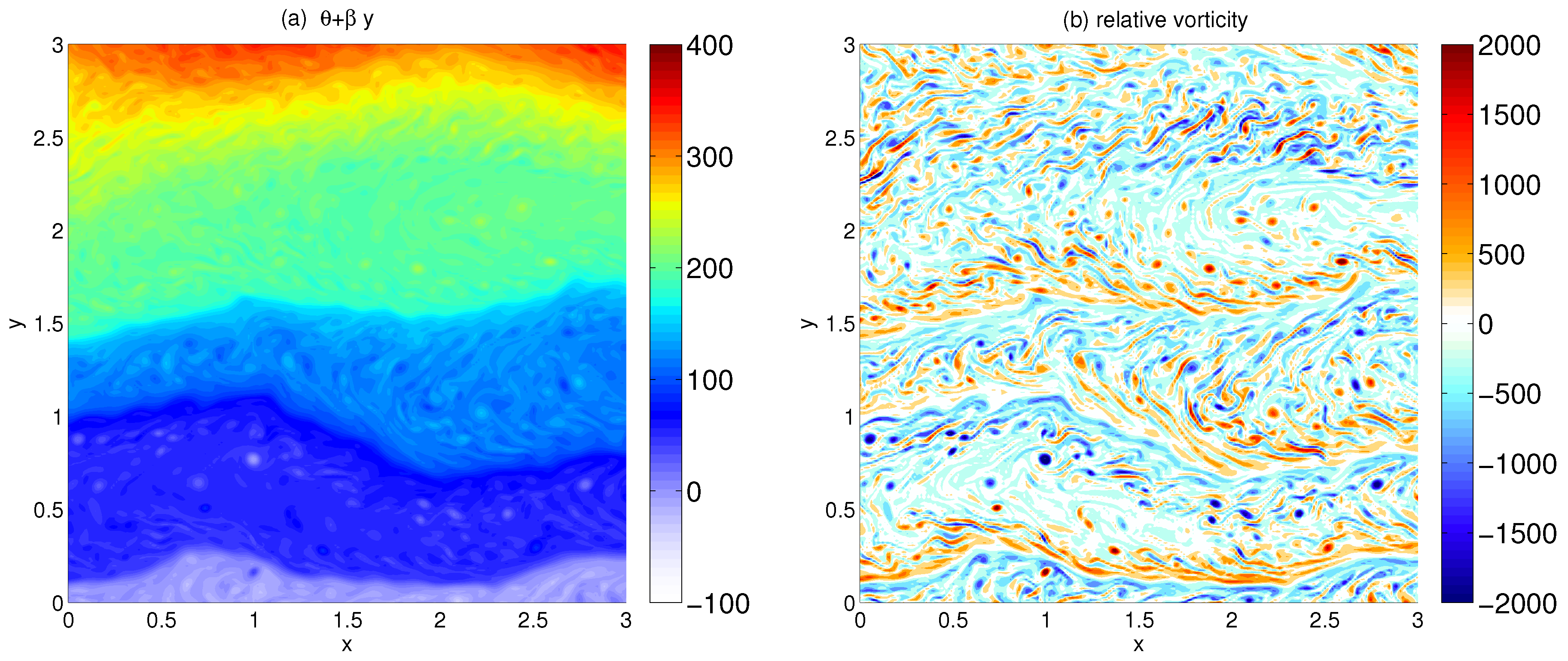
4. Turbulent Cascades
4.1. Buoyancy Variance Spectra
4.2. Physical Properties of the Cascade
4.3. Role of Meridional Gradients and Linear Damping
4.4. Energy Transfers
5. Surface Quasi-Geostrophy (SQG) from a Mathematical Point of View
5.1. Analogy with 3D Euler Equations
5.2. Regularity of Surface Quasi-Geostrophy (SQG) Solutions
6. Passive Tracers
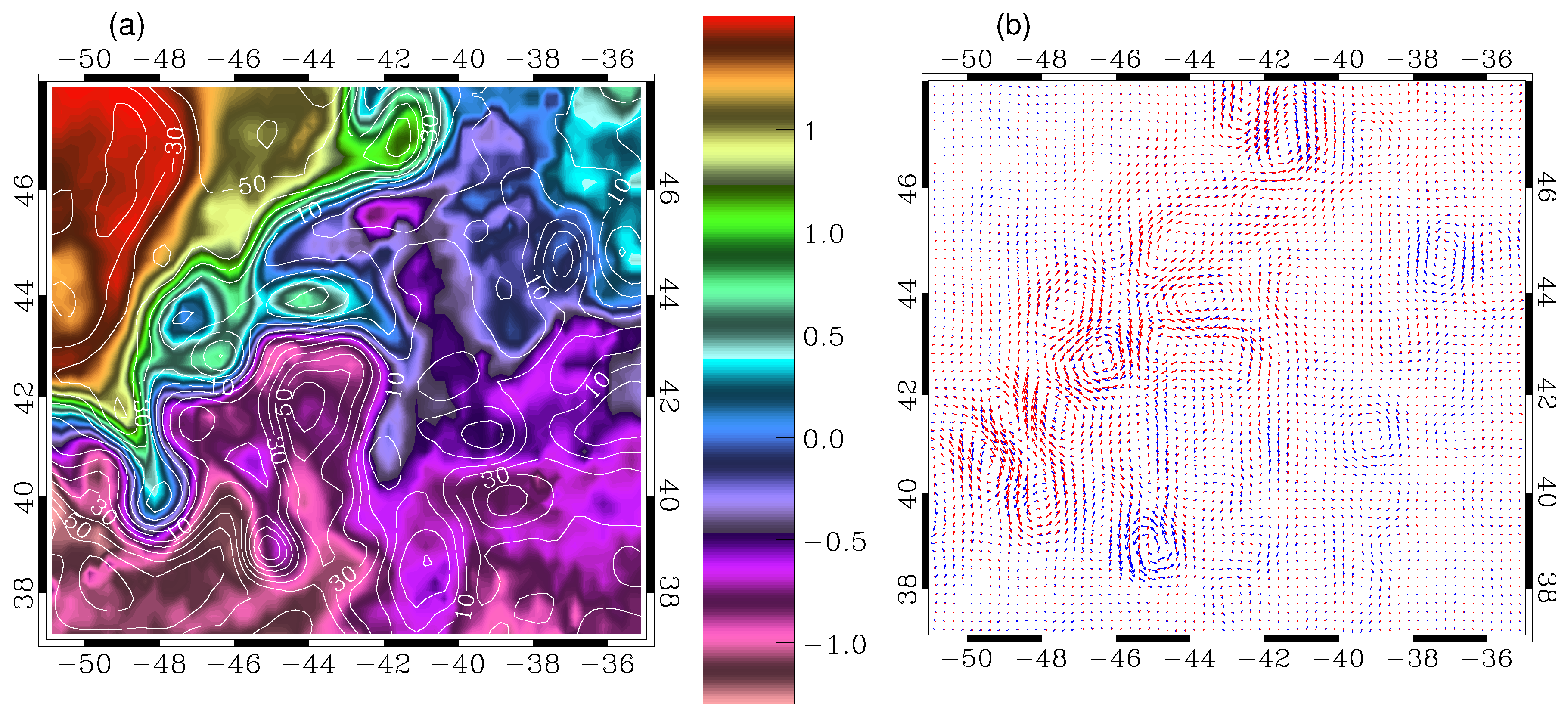
7. Surface Quasi-Geostrophy (SQG) and the Ocean Dynamics
7.1. Horizontal Motions from Surface Quasi-Geostrophy (SQG) Equilibrium
7.2. Relation between Surface and Interior Dynamics
7.3. Vertical Motions from Surface Quasi-Geostrophy (SQG) Equilibrium
7.4. Frontogenesis
7.5. Impact on Tracers
8. Surface Quasi-Geostrophy (SQG) and the Atmosphere Dynamics
9. Conclusions
Acknowledgments
Conflicts of Interest
References
- Charney, J.G. Geostrophic turbulence. J. Atmos. Sci. 1971, 28, 1087–1095. [Google Scholar] [CrossRef]
- Pedlosky, J. Geophysical Fluid Dynamics; Springer: Berlin, Germany, 1987. [Google Scholar]
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Eady, E.T. Long waves and cyclone waves. Tellus 1949, 1, 33–52. [Google Scholar] [CrossRef]
- Hakim, G.J. Developing wave packets in the north Pacific storm track. Mon. Weather Rev. 2003, 131, 2837. [Google Scholar] [CrossRef]
- LaCasce, J.H.; Mahadevan, A. Estimating sub-surface horizontal and vertical velocities from sea surface temperature. J. Mar. Res. 2006, 64, 695–721. [Google Scholar] [CrossRef]
- Lapeyre, G.; Klein, P. Dynamics of the upper oceanic layers in terms of surface quasigeostrophy theory. J. Phys. Oceanogr. 2006, 36, 165–176. [Google Scholar] [CrossRef]
- Blumen, W. Uniform potential vorticity flow: Part I. Theory of wave interactions and two-dimensional turbulence. J. Atmos. Sci. 1978, 35, 774–783. [Google Scholar] [CrossRef]
- Held, I.M.; Pierrehumbert, R.T.; Garner, S.T.; Swanson, K.L. Surface quasi-geostrophic dynamics. J. Fluid Mech. 1995, 282, 1–20. [Google Scholar] [CrossRef]
- Constantin, P.; Majda, A.J.; Tabak, E. Formation of strong fronts in the 2-D quasigeostrophic thermal active scalar. Nonlinearity 1994, 7, 1495–1533. [Google Scholar] [CrossRef]
- Hoskins, B.J.; McIntyre, M.E.; Robertson, A.W. On the use and significance of isentropic potential vorticity maps. Q. J. R. Meteorol. Soc. 1985, 111, 877–946. [Google Scholar] [CrossRef]
- Bretherton, F.P. Critical layer instability in baroclinic flows. Q. J. R. Meteorol. Soc. 1966, 92, 325–334. [Google Scholar] [CrossRef]
- Schneider, T.; Held, I.M.; Garner, S.T. Boundary effects in potential vorticity dynamics. J. Atmos. Sci. 2003, 60, 1024–1040. [Google Scholar] [CrossRef]
- Charney, J.G.; Stern, M.E. On the stability of internal baroclinic jets in a rotating atmosphere. J. Atmos. Sci. 1962, 19, 159–172. [Google Scholar] [CrossRef]
- Hua, B.L.; Haidvogel, D.B. Numerical simulations of the vertical structure of quasi-geostrophic turbulence. J. Atmos. Sci. 1986, 43, 2923–2936. [Google Scholar] [CrossRef]
- Smith, K.S.; Vallis, G.K. The scales and equilibration of midocean eddies: Freely evolving flow. J. Phys. Oceanogr. 2001, 31, 554–571. [Google Scholar] [CrossRef]
- Smith, K.S.; Boccaletti, G.; Henning, C.C.; Marinov, I.N.; Tam, C.Y.; Held, I.M.; Vallis, G.K. Turbulent diffusion in the geostrophic inverse cascade. J. Fluid Mech. 2002, 469, 14–47. [Google Scholar] [CrossRef]
- Juckes, M. Instability of surface and upper-tropospheric shear lines. J. Atmos. Sci. 1995, 52, 3247–3262. [Google Scholar] [CrossRef]
- Dritschel, D.G. An exact steadily-rotating surface quasi-geostrophic elliptical vortex. Geophys. Astrophys. Fluid Dyn. 2011, 105, 368–376. [Google Scholar] [CrossRef]
- Castro, A.; Cordoba, D.; Gomez-Serrano, J.; Zamora, A.M. Remarks on geometric properties of SQG sharp fronts and alpha-patches. Discret. Contin. Dyn Syst. 2014, 34, 5045–5059. [Google Scholar] [CrossRef]
- Castro, A.; Córdoba, D.; Gómez-Serrano, J. Existence and regularity of rotating global solutions for the generalized surface quasi-geostrophic equations. Duke Math. J. 2016, 165, 935–984. [Google Scholar] [CrossRef]
- Lim, C.C.; Majda, A.J. Point vortex dynamics for coupled surface/interior QG and propagating heton clusters in models for ocean convection. Geophys. Astrophys. Fluid Dyn. 2001, 94, 177–220. [Google Scholar] [CrossRef]
- Muraki, D.J.; Snyder, C. Vortex dipoles for surface quasigeostrophic models. J. Atmos. Sci. 2004, 61, 2961–2967. [Google Scholar] [CrossRef]
- Carton, X.; Ciani, D.; Verron, J.; Reinaud, J.; Sokolovskyi, M. Vortex merger in surface quasi-geostrophy. Geophys. Astrophys. Fluid Dyn. 2015, 110, 1–22. [Google Scholar] [CrossRef]
- Zabusky, N.J.; Hugues, M.H.; Roberts, K.V. Contour dynamics for the Euler equations in two dimensions. J. Comput. Phys. 1979, 30, 96–106. [Google Scholar] [CrossRef]
- Cordoba, D.; Fefferman, C.; Rodrigo, J.L. Almost sharp fronts for the surface quasi-geostrophic equation. Proc. Natl. Acad. Sci. USA 2004, 101, 2687–2691. [Google Scholar] [CrossRef] [PubMed]
- Fefferman, C.L.; Rodrigo, J.L. Construction of almost-sharp fronts for the surface quasi-geostrophic equation. Arch. Rational Mech. Anal. 2015, 218, 123–162. [Google Scholar] [CrossRef]
- Rodrigo, J.L. The vortex patch problem for the surface quasi-geostrophic equation. Proc. Natl. Acad. Sci. USA 2004, 101, 2684–2686. [Google Scholar] [CrossRef] [PubMed]
- Gancedo, F. Existence for the α-patch model and the QG sharp front in Sobolev spaces. Adv. Math. 2008, 217, 2579–2598. [Google Scholar] [CrossRef]
- Cordoba, D.; Fontelos, M.A.; Mancho, A.M.; Rodrigo, J.L. Evidence of singularities for a family of contour dynamics equations. Proc. Natl. Acad. Sci. USA 2005, 102, 5249–5252. [Google Scholar] [CrossRef] [PubMed]
- Scott, R.K.; Dritschel, D.G. Numerical simulation of a self-similar cascade of filament instabilities in the Surface quasigeostrophic System. Phys. Rev. Lett. 2014, 112, 144505. [Google Scholar] [CrossRef] [PubMed]
- Gancedo, F.; Strain, R.M. Absence of splash singularities for surface quasi-geostrophic sharp fronts and the Muskat problem. Proc. Natl. Acad. Sci. USA 2014, 111, 635–639. [Google Scholar] [CrossRef]
- Dritschel, D.G.; Haynes, P.H.; Juckes, M.N.; Shepherd, T.G. The stability of a two-dimensional vorticity filament under uniform strain. J. Fluid Mech. 1991, 230, 647–665. [Google Scholar] [CrossRef]
- Harvey, B.J.; Ambaum, M.H.P. Instability of surface temperature filaments in strain and shear. Q. J. R. Meteorol. Soc. 2010, 136, 1506–1513. [Google Scholar] [CrossRef]
- Scott, R.K. A scenario for finite-time singularity in the quasigeostrophic model. J. Fluid Mech. 2011, 687, 492–502. [Google Scholar] [CrossRef]
- Carton, X. Instability of surface quasi-geostrophic vortices. J. Atmos. Sci. 2009, 66, 1051–1062. [Google Scholar] [CrossRef]
- Harvey, B.J.; Ambaum, M.H.P. Perturbed Rankine vortices in surface quasi-geostrophic dynamics. Geophys. Astrophys. Fluid Dyn. 2010, 105, 377–391. [Google Scholar] [CrossRef]
- Harvey, B.J.; Ambaum, M.H.P.; Carton, X. Instability of shielded surface temperature vortices. J. Atmos. Sci. 2011, 68, 964–971. [Google Scholar] [CrossRef]
- Friedlander, S.; Shvydkoy, R. The unstable spectrum of the surface quasi-geostrophic equation. J. Math. Fluid Mech. 2005, 7, S81–S93. [Google Scholar] [CrossRef]
- Friedlander, S.; Pavlovic, N.; Vicol, V. Nonlinear instability for the critically dissipative quasi-geostrophic equation. Commun. Math. Phys. 2009, 292, 797–810. [Google Scholar] [CrossRef]
- Rotunno, R.; Snyder, C. A generalization of Lorenz’s model for the predictability of flows with many scales of motion. J. Atmos. Sci. 2008, 65, 1063–1076. [Google Scholar] [CrossRef]
- Tran, C.V.; Blackbourn, L.A.K.; Scott, R.K. Number of degrees of freedom and energy spectrum of surface quasi-geostrophic turbulence. J. Fluid Mech. 2011, 684, 427–440. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Inertial ranges in two-dimensional turbulence. Phys. Fluids 1967, 10, 1417–1423. [Google Scholar] [CrossRef]
- Hoyer, J.M.; Sadourny, R. Closure modeling of fully developed baroclinic turbulence. J. Atmos. Sci. 1982, 39, 707–721. [Google Scholar] [CrossRef]
- Tran, C.V.; Bowman, J.C. Large-scale energy spectra in surface quasi-geostrophic turbulence. J. Fluid Mech. 2005, 526, 349–359. [Google Scholar] [CrossRef]
- Tran, C.V. Diminishing inverse transfer and non-cascading dynamics in surface quasi-geostrophic turbulence. Physica D 2006, 213, 76–84. [Google Scholar] [CrossRef]
- Pierrehumbert, R.T.; Held, I.M.; Swanson, K.L. Spectra of local and nonlocal two-dimensional turbulence. Chaos Solitons Fractals 1994, 4, 1111–1116. [Google Scholar] [CrossRef]
- Celani, A.; Cencini, M.; Mazzino, A.; Vergassola, M. Active and passive fields face to face. New J. Phys. 2004, 6, 72. [Google Scholar] [CrossRef]
- Sukhatme, J.; Pierrehumbert, R.T. Surface Quasi-Geostrophic turbulence: The study of an active scalar. Chaos 2002, 12, 439–450. [Google Scholar] [CrossRef] [PubMed]
- Capet, X.; Klein, P.; Hua, B.L.; Lapeyre, G.; McWilliams, J.C. Surface kinetic and potential energy transfer in SQG dynamics. J. Fluid Mech. 2008, 604, 165–174. [Google Scholar] [CrossRef]
- Watanabe, T.; Iwayama, T. Unified scaling theory for local and non-local transfers in generalized two-dimensional turbulence. J. Phys. Soc. Jpn. 2004, 73, 3319–3330. [Google Scholar] [CrossRef]
- Constantin, P. Energy spectrum of quasigeostrophic turbulence. Phys. Rev. Lett. 2002, 89, 184501. [Google Scholar] [CrossRef] [PubMed]
- Burgess, B.H.; Scott, R.K.; Shepherd, T.G. Kraichnan-Leith-Batchelor similarity theory and two-dimensional inverse cascades. J. Fluid Mech. 2015, 767, 467–496. [Google Scholar] [CrossRef]
- Tobias, S.M.; Cattaneo, F. Dynamo action in complex flows: The quick and the fast. J. Fluid Mech. 2008, 601, 101–122. [Google Scholar] [CrossRef]
- Bernard, D.; Boffetta, G.; Celani, A.; Falkovich, G. Inverse turbulent cascades and conformally invariant curves. Phys. Rev. Lett. 2007, 98, 024501. [Google Scholar] [CrossRef] [PubMed]
- Venaille, A.; Dauxois, T.; Ruffo, S. Violent relaxation in two-dimensional flows with varying interaction range. Phys. Rev. E 2015, 92, 011001. [Google Scholar] [CrossRef] [PubMed]
- Teitelbaum, T.; Mininni, P.D. Thermalization and free decay in surface quasigeostrophic flows. Phys. Rev. E 2012, 86, 016323. [Google Scholar] [CrossRef] [PubMed]
- Rhines, P.B. Waves and turbulence on a β-plane. J. Fluid Mech. 1975, 69, 417–443. [Google Scholar] [CrossRef]
- Sukhatme, J.; Smith, L.M. Local and nonlocal dispersive turbulence. Phys. Fluids 2009, 21, 056603. [Google Scholar] [CrossRef]
- Watanabe, T.; Iwayama, T. Interacting scales and triad enstrophy transfers in generalized two-dimensional turbulence. Phys. Rev. E 2007, 76, 046303. [Google Scholar] [CrossRef] [PubMed]
- Scott, R.B.; Wang, F. Direct evidence of an oceanic inverse kinetic energy cascade from satellite altimetry. J. Phys. Oceanogr. 2005, 35, 1650–1666. [Google Scholar] [CrossRef]
- Constantin, P.; Majda, A.J.; Tabak, E. Singular front formation in a model for quasi-geostrophic flow. Phys. Fluids 1994, 9, 6–11. [Google Scholar]
- Yudovich, V.I. On the loss of smoothness of the solutions of the Euler equations. Dyn. Contin. Media 1974, 16, 71–78. (In Russian) [Google Scholar]
- Marchioro, C.; Pulvirenti, M. Mathematical theory of incompressible nonviscous fluids. In Applied Mathematical Sciences; Springer: New York, NY, USA, 1994; Volume 96. [Google Scholar]
- Yudovich, V.I. Loss of smoothness and inherent instability of 2D inviscid fluid flows. Commun. Partial Diff. Equal. 2000, 33, 943–968. [Google Scholar]
- Dutton, J.A. The nonlinear quasi-geostrophic equation: Existence and uniqueness of solutions on a bounded domain. J. Atmos. Sci. 1974, 31, 422–433. [Google Scholar] [CrossRef]
- Bennett, A.F.; Kloeden, P.E. The periodic quasigeostrophic equations: Existence and uniqueness of strong solutions. Proc. R. Soc. Edinb. 1982, 91A, 185–203. [Google Scholar] [CrossRef]
- Chae, D. The global regularity for the 3D continuously stratified inviscid quasi-geostrophic equations. J. Nonlinear Sci. 2015, 25, 959–966. [Google Scholar] [CrossRef]
- Beale, J.T.; Kato, T.; Majda, A. Remarks on the breakdown of smooth solutions for the 3-D Euler equations. Commun. Math. Phys. 1984, 94, 61–66. [Google Scholar] [CrossRef]
- Ohkitani, K.; Yamada, M. Invicid and invicid-limit behavior of a surface quasigeostrophic flow. Phys. Fluids 1997, 9, 876–882. [Google Scholar] [CrossRef]
- Denisov, S.A. Double exponential growth of the vorticity gradient for the two-dimensional Euler equation. Proc. Natl. Acad. Sci. USA 2015, 143, 1199–1210. [Google Scholar] [CrossRef]
- Cordoba, D. On the geometry of solutions of the quasi-geostrophic and Euler equations. Proc. Natl. Acad. Sci. USA 1997, 94, 12769–12770. [Google Scholar] [CrossRef] [PubMed]
- Cordoba, D. Nonexistence of simple hyperbolic blow-up for the quasi-geostrophic equation. Ann. Math. 1998, 148, 1135–1152. [Google Scholar] [CrossRef]
- Constantin, P.; Nie, Q.; Schörghofer, N. Front formation in an active scalar. Phys. Rev. E 1999, 60, 2858–2863. [Google Scholar] [CrossRef]
- Wu, J. Quasi-geostrophic-type equations with initial data in Morrey spaces quasi-geostrophic. Nonlinearity 1997, 10, 1409–1420. [Google Scholar] [CrossRef]
- Ju, N. Global solutions for the two dimensional quasi-geostrophic equation with critical or super-critical dissipation. Math. Ann. 2006, 334, 627–642. [Google Scholar] [CrossRef]
- Resnick, S.G. Dynamical Problems in Non-Linear Advective Partial Differential Equations. Ph.D. Thesis, University of Chicago, Chicago, IL, USA, January 1995. [Google Scholar]
- Constantin, P.; Wu, J. Behavior of solutions of 2D quasi-geostrophic equations. SIAM J. Math. Anal. 1999, 30, 937–948. [Google Scholar] [CrossRef]
- Ju, N. Dissipative 2D quasi-geostrophic equation: Local well-posedness, global regularity and similarity solutions. Indiana Univ. Math. J. 2007, 56, 187–206. [Google Scholar] [CrossRef]
- Wu, J. Existence and uniqueness results for the 2-D dissipative quasi-geostrophic equation. Nonlinear Anal. 2007, 67, 3013–3036. [Google Scholar] [CrossRef]
- Chae, D.; Lee, J. Global well-posedness in the super-critical dissipative quasi-geostrophic equations. Commun. Math. Phys. 2003, 233, 297–311. [Google Scholar] [CrossRef]
- Cordoba, A.; Cordoba, D. A maximum principle applied to quasi-geostrophic equations. Commun. Math. Phys. 2004, 249, 511–528. [Google Scholar] [CrossRef]
- Constantin, P.; Cordoba, D.; Wu, J. On the critical dissipative quasi-geostrophic equation. Indiana Univ. Math. J. 2001, 50, 97–107. [Google Scholar] [CrossRef]
- Kiselev, A.; Nazarov, F.; Volberg, A. Global well-posedness for the critical 2D dissipative quasi-geostrophic equation. Invent. Math. 2007, 167, 445–463. [Google Scholar] [CrossRef]
- Caffarelli, L.A.; Vasseur, A. Drift diffusion equations with fractional diffusion and the quasi-geostrophic equation. Ann. Math. 2010, 171, 1903–1930. [Google Scholar] [CrossRef]
- Constantin, P.; Tarfulea, A.; Vicol, V. Long time dynamics of forced critical SQG. Commun. Math. Phys. 2015, 335, 93–141. [Google Scholar] [CrossRef]
- Lesieur, M.; Sadourny, R. Satellite-sensed turbulent ocean structure. Nature 1981, 294, 673. [Google Scholar] [CrossRef]
- Scott, R.K. Local and nonlocal advection of a passive scalar. Phys. Fluids 2006, 56, 122–125. [Google Scholar] [CrossRef]
- Batchelor, G.K. The effect of homogeneous turbulence on material lines and surfaces. Proc. R. Soc. Lond. Ser. A 1952, 213, 349–366. [Google Scholar] [CrossRef]
- Wirth, V.; Borth, H.; López, J.F.; Panhans, W.G.; Riemer, M.; Szabo, T. Dynamics in the extratropical tropopause region: A case of transition between dynamically active and passive tracer advection? Q. J. R. Meteorol. Soc. 2005, 131, 247–257. [Google Scholar] [CrossRef]
- Klein, P.; Hua, B.L.; Lapeyre, G.; Capet, X.; Gentil, S.L.; Sasaki, H. Upper ocean turbulence from high 3-D resolution simulations. J. Phys. Oceanogr. 2008, 38, 1748–1763. [Google Scholar] [CrossRef]
- Capet, X.; McWilliams, J.C.; Molemaker, M.; Shchepetkin, A. Mesoscale to submesoscale transition in the California current system. Part III: Energy balance and flux. J. Phys. Oceanogr. 2008, 38, 2256–2269. [Google Scholar] [CrossRef]
- Shcherbina, B.A.Y.; Sundermeyer, M.A.; Kunze, E.; D’Asaro, E.; Badin, G. The LATMIX summer campaign. Bull. Am. Meteor. Soc. 2015, 96, 1257–1279. [Google Scholar] [CrossRef]
- Johnson, E.R. Topographically bound vortices. Geophys. Astrophys. Fluid Dyn. 1978, 11, 61–71. [Google Scholar] [CrossRef]
- Isern-Fontanet, J.; Lapeyre, G.; Klein, P.; Chapron, B.; Hecht, M.W. Three-dimensional reconstruction of oceanic mesoscale currents from surface information. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S.; Klein, P.; Ubelmann, C.; Fu, L.L.; Sasaki, H. Reconstructability of three-dimensional upper-ocean circulation from SWOT sea surface height measurements. J. Phys. Oceanogr. 2016, 46, 947–963. [Google Scholar] [CrossRef]
- Klein, P.; Lapeyre, G.; Roullet, G.; Le Gentil, S.; Sasaki, H. Ocean turbulence at meso and submesoscales: Connection between surface and interior dynamics. Geophys. Astrophys. Fluid Dyn. 2011, 105, 421–437. [Google Scholar] [CrossRef]
- Lapeyre, G. What vertical mode does the altimeter reflect? On the decomposition in baroclinic modes and on a surface-trapped mode. J. Phys. Oceanogr. 2009, 39, 2857–2874. [Google Scholar] [CrossRef]
- Isern-Fontanet, J.; Chapron, B.; Lapeyre, G.; Klein, P. Potential use of microwave Sea surface temperatures for the estimation of ocean currents. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Gonzalez-Haro, C.; Isern-Fontanet, J. Global ocean current reconstruction from altimetric and microwave SST measurements. J. Geophys. Res. 2014, 119, 3378–3391. [Google Scholar] [CrossRef]
- Wunsch, C. The vertical partition of oceanic horizontal kinetic energy. J. Phys. Oceanogr. 1997, 27, 1770–1794. [Google Scholar] [CrossRef]
- Stammer, D. Global characteristics of ocean variability estimated from regional TOPEX/POSEIDON altimeter measurements. J. Phys. Oceanogr. 1997, 27, 1743–1769. [Google Scholar] [CrossRef]
- Smith, K.S.; Vanneste, J. A surface-aware projection basis for quasigeostrophic flow. J. Phys. Oceanogr. 2013, 43, 548–562. [Google Scholar] [CrossRef]
- Roullet, G.; McWilliams, J.C.; Capet, X.; Molemaker, M.J. Properties of steady geostrophic turbulence with isopycnal outcropping. J. Phys. Oceanogr. 2012, 42, 18–38. [Google Scholar] [CrossRef]
- Ponte, A.; Klein, P. Reconstruction of the upper ocean 3D dynamics from high-resolution sea surface height. Ocean Dyn. 2013, 63, 777–791. [Google Scholar] [CrossRef]
- Tulloch, R.; Smith, K.S. A note on the numerical representation of surface dynamics in quasigeostrophic turbulence: Application to the nonlinear Eady model. J. Atmos. Sci. 2009, 66, 1063–1068. [Google Scholar] [CrossRef]
- Tulloch, R.; Smith, K.S. Quasigeostrophic turbulence with explicit surface dynamics: Application to the atmospheric energy spectrum. J. Atmos. Sci. 2009, 66, 450–467. [Google Scholar] [CrossRef]
- Wang, J.; Flierl, G.R.; LaCasce, J.H.; McClean, J.L.; Mahadevan, A. Reconstructing the ocean’s interior from surface data. J. Phys. Oceanogr. 2013, 43, 1611–1626. [Google Scholar] [CrossRef]
- Lacasce, J.H.; Wang, J. Estimating subsurface velocities from surface fields with idealized stratification. J. Phys. Oceanogr. 2015, 9, 2424–2435. [Google Scholar] [CrossRef]
- Chavanne, C.P.; Klein, P. Quasigeostrophic diagnosis of mixed layer dynamics embedded in a mesoscale turbulent field. J. Phys. Oceanogr. 2016, 46, 275–287. [Google Scholar] [CrossRef]
- Callies, J.; Flierl, G.; Ferrari, R.; Fox-Kemper, B. The role of mixed-layer instabilities in submesoscale turbulence. J. Fluid Mech. 2016, 788, 5–41. [Google Scholar] [CrossRef]
- Boccaletti, G.; Ferrari, R.; Fox-Kemper, B. Mixed layer instabilities and restratification. J. Phys. Oceanogr. 2007, 37, 2228–2250. [Google Scholar] [CrossRef]
- Hoskins, B.J.; Draghici, I.; Davies, H.C. A new look at the ω-equation. Q. J. R. Meteorol. Soc. 1978, 104, 31–38. [Google Scholar] [CrossRef]
- Klein, P.; Isern-Fontanet, J.; Lapeyre, G.; Roullet, G.; Danioux, E.; Chapron, B.; Le Gentil, S.; Sasaki, H. Diagnosis of vertical velocities in the upper ocean from high resolution Sea Surface Height. Geophys. Res. Lett. 2009, 36, L12603. [Google Scholar] [CrossRef]
- Ponte, A.; Klein, P.; Capet, X.; Le Traon, P.Y.; Chapron, B.; Lherminier, P. Diagnosing surface mixed layer dynamics from high-resolution satellite observations: Numerical insights. J. Phys. Oceanogr. 2013, 43, 1345–1355. [Google Scholar] [CrossRef]
- Garrett, C.; Loder, J. Dynamical aspects of shallow sea fronts. Philos. Trans. R. Soc. Lond. 1981, A94, 563–581. [Google Scholar] [CrossRef]
- Hakim, G.J.; Snyder, C.; Muraki, D.J. A new surface model for cyclone-anticyclone asymmetry. J. Atmos. Sci. 2002, 59, 2405–2420. [Google Scholar] [CrossRef]
- Petterssen, S. Contribution to the theory of frontogenesis. Geofys. Pub. 1936, 11, 5–27. [Google Scholar]
- Williams, R.T.; Plotkin, J. Quasi-geostrophic frontogenesis. J. Atmos. Sci. 1968, 25, 201–206. [Google Scholar] [CrossRef]
- Sawyer, J.S. The vertical circulation at meteorological fronts and its relation to frontogenesis. Proc. R. Soc. Lond. Ser. A 1956, A234, 346–362. [Google Scholar] [CrossRef]
- Eliassen, A. On the vertical circulation in frontal zones. Geofys. Publik. 1962, 24, 147–160. [Google Scholar]
- Hoskins, B.J.; Bretherton, F.P. Atmospheric frontogenesis models: Mathematical formulation and solution. J. Atmos. Sci. 1972, 29, 11–37. [Google Scholar] [CrossRef]
- Lapeyre, G.; Klein, P.; Hua, B.L. Does the tracer gradient vector align with the strain eigenvectors in 2-D turbulence? Phys. Fluids A. 1999, 11, 3729–3737. [Google Scholar] [CrossRef]
- Gower, J.F.R.; Denman, K.L.; Holyer, R.J. Phytoplankton patchiness indicates the fluctuation spectrum of mesoscale oceanic structure. Nature 1980, 288, 157–159. [Google Scholar] [CrossRef]
- Lapeyre, G.; Klein, P. Impact of the small-scale elongated filaments on the oceanic vertical pump. J. Mar. Res. 2006, 64, 935–951. [Google Scholar] [CrossRef]
- Perruche, C.; Rivière, P.; Lapeyre, G.; Carton, X.; Pondaven, P. Effects of Surface Quasi-Geostrophic turbulence on phytoplankton competition and coexistence. J. Mar. Res. 2011, 69, 105–135. [Google Scholar] [CrossRef]
- Juckes, M. Quasigeostrophic dynamics of the tropopause. J. Atmos. Sci. 1994, 51, 2756–2768. [Google Scholar] [CrossRef]
- Smith, K.S.; Bernard, E. Geostrophic turbulence near rapid changes in stratification. Phys. Fluids 2013, 25, 046601. [Google Scholar] [CrossRef]
- Plougonven, R.; Vanneste, J. Quasi-geostrophic dynamics of a finite-thickness tropopause. J. Atmos. Sci. 2010, 67, 3149–3163. [Google Scholar] [CrossRef]
- Rivest, C.; Davis, C.A.; Farrell, B.F. Upper-tropospheric synoptic-scale waves. Part I: Maintenance as Eady normal modes. J. Atmos. Sci. 1992, 49, 2108–2119. [Google Scholar] [CrossRef]
- Tomikawa, Y.; Sato, K.; Shepherd, T.G. A diagnostic study of waves on the tropopause. J. Atmos. Sci. 2006, 63, 3315–3332. [Google Scholar] [CrossRef]
- Wirth, V.; Appenzeller, C.; Juckes, M. Signatures of induced vertical air motion accompanying quasi-horizontal roll-up of stratospheric intrusions. Mon. Weather Rev. 1997, 125, 2504–2519. [Google Scholar] [CrossRef]
- Nastrom, G.D.; Gage, K.S. A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft. J. Atmos. Sci. 1985, 42, 950–960. [Google Scholar] [CrossRef]
- Lindborg, E. The effect of rotation on the mesoscale energy cascade in the free atmosphere. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Hamilton, K.; Takahashi, Y.O.; Ohfuchi, W. Mesoscale spectrum of atmospheric motions investigated in a very fine resolution global general circulation model. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Tulloch, R.; Smith, K.S. A new theory for the atmospheric energy spectrum: Depth-limited temperature anomalies at the tropopause. Proc. Natl. Acad. Sci. USA 2006, 103, 14690–14694. [Google Scholar] [CrossRef] [PubMed]
- Asselin, O.; Bartello, P.; Straub, D.N. On quasi-geostrophic dynamics near the tropopause. Phys. Fluids 2016, 28, 026601. [Google Scholar] [CrossRef]
- Morss, R.; Snyder, C.; Rotunno, R. Spectra, spatial scales, and predictability in a quasigeostrophic model. J. Atmos. Sci. 2009, 66, 3115–3130. [Google Scholar] [CrossRef]
- Greenslade, M.D.; Haynes, P.H. Vertical transition in transport and mixing in baroclinic flows. J. Atmos. Sci. 2008, 65, 1137–1157. [Google Scholar] [CrossRef]
- Bracco, A. Boundary layer separation in the surface quasigeostrophic equations. Il Nuovo Cimento 2000, 23, 487–505. [Google Scholar]
- Charney, J.G. The dynamics of long waves in a baroclinic westerly current. J. Meteor. 1947, 4, 135–162. [Google Scholar] [CrossRef]
- Green, J.S.A. A problem in baroclinic instability. Q. J. R. Meteorol. Soc. 1960, 86, 237–251. [Google Scholar] [CrossRef]
- Heifetz, E.; Methven, J.; Hoskins, B.J.; Bishop, C.H. The counter-propagating Rossby-wave perspective on baroclinic instability. II: Application to the Charney model. Q. J. R. Meteorol. Soc. 2004, 130, 233–258. [Google Scholar] [CrossRef]
- Held, I.M. The vertical scale of an unstable baroclinic wave and its importance for eddy heat flux parameterizations. J. Atmos. Sci. 1978, 35, 572–576. [Google Scholar] [CrossRef]
- Venaille, A.; Vallis, G.K.; Griffies, S.M. The catalytic role of the beta effect in barotropization processes. J. Fluid Mech. 2012, 709, 490–515. [Google Scholar] [CrossRef]
- Perrot, X.; Reinaud, J.N.; Carton, X.; Dritschel, D.G. Homostrophic vortex interaction under external strain, in a coupled QG-SQG model. Reg. Chaot. Dyn. 2010, 15, 66–83. [Google Scholar] [CrossRef]
- Reinaud, J.N.; Dritschel, D.G.; Carton, X. Interaction between a surface quasi-geostrophic buoyancy filament and an internal vortex. Geophys. Astrophys. Fluid Dyn. 2016, 110, 461–490. [Google Scholar] [CrossRef]
- Williams, R.T. Atmospheric frontogenesis: A numerical experiment. J. Atmos. Sci. 1967, 24, 627–641. [Google Scholar] [CrossRef]
- Hoskins, B.J. The geostrophic momentum approximation and the semi-geostrophic equations. J. Atmos. Sci. 1975, 32, 233–242. [Google Scholar] [CrossRef]
- Badin, G. Surface semi-geostrophic dynamics in the ocean. Geophys. Astrophys. Fluid Dyn. 2013, 107, 526–540. [Google Scholar] [CrossRef]
- Ragone, F.; Badin, G. A study of surface semi-geostrophic turbulence: Freely decaying dynamics. J. Fluid Mech. 2016, 792, 740–774. [Google Scholar] [CrossRef]
- Lapeyre, G.; Klein, P.; Hua, B.L. Oceanic restratification forced by surface frontogenesis. J. Phys. Oceanogr. 2006, 36, 1577–1590. [Google Scholar] [CrossRef]
- Juckes, M. The structure of idealized upper-tropospheric shear lines. J. Atmos. Sci. 1999, 56, 2830–2845. [Google Scholar] [CrossRef]
- Bembenek, E.; Poulin, F.J.; Waite, M.L. Realizing surface-driven flows in the primitive equations. J. Phys. Oceanogr. 2015, 45, 1376–1392. [Google Scholar] [CrossRef]
- Snyder, C.; Muraki, D.J.; Plougonven, R.; Zhang, F. Inertia-gravity waves generated within a dipole Vortex. J. Atmos. Sci. 2007, 64, 4417–4431. [Google Scholar] [CrossRef]

© 2017 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lapeyre, G. Surface Quasi-Geostrophy. Fluids 2017, 2, 7. https://doi.org/10.3390/fluids2010007
Lapeyre G. Surface Quasi-Geostrophy. Fluids. 2017; 2(1):7. https://doi.org/10.3390/fluids2010007
Chicago/Turabian StyleLapeyre, Guillaume. 2017. "Surface Quasi-Geostrophy" Fluids 2, no. 1: 7. https://doi.org/10.3390/fluids2010007
APA StyleLapeyre, G. (2017). Surface Quasi-Geostrophy. Fluids, 2(1), 7. https://doi.org/10.3390/fluids2010007





