Evolutionary Optimization of Colebrook’s Turbulent Flow Friction Approximations
Abstract
:1. Introduction
2. Genetic Algorithm Optimization Technique
3. Explicit Approximations of Colebrook’s Equation
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Colebrook, C.F.; White, C.M. Experiments with fluid friction in roughened pipes. Proc. R. Soc. Ser. A Math. Phys. Sci. 1937, 161, 367–381. [Google Scholar] [CrossRef]
- Colebrook, C.F. Turbulent flow in pipes with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civ. Eng. (Lond.) 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Moody, L.F. Friction factors for pipe flow. Trans. ASME 1944, 66, 671–684. [Google Scholar]
- LaViolette, M. On the history, science, and technology included in the Moody diagram. J. Fluids Eng. ASME 2017, 139, 030801. [Google Scholar] [CrossRef]
- Mikata, Y.; Walczak, W.S. Exact analytical solutions of the Colebrook-White equation. J. Hydraul. Eng. ASCE 2016, 142. [Google Scholar] [CrossRef]
- Brkić, D. W solutions of the CW equation for flow friction. Appl. Math. Lett. 2011, 24, 1379–1383. [Google Scholar] [CrossRef]
- Biberg, D. Fast and accurate approximations for the Colebrook equation. J. Fluids Eng. ASME 2017, 139, 031401. [Google Scholar] [CrossRef]
- Keady, G. Colebrook-White formula for pipe flow. J. Hydraul. Eng. ASCE 1998, 124, 96–97. [Google Scholar] [CrossRef]
- Clamond, D. Efficient resolution of the Colebrook equation. Ind. Eng. Chem. Res. 2009, 48, 3665–3671. [Google Scholar] [CrossRef]
- Brkić, D. Review of explicit approximations to the Colebrook relation for flow friction. J. Petrol. Sci. Eng. 2011, 77, 34–48. [Google Scholar] [CrossRef]
- Brkić, D. Determining friction factors in turbulent pipe flow. Chem. Eng. (N. Y.) 2012, 119, 34–39. [Google Scholar]
- Gregory, G.A.; Fogarasi, M. Alternate to standard friction factor equation. Oil Gas J. 1985, 83, 125–127. [Google Scholar]
- Zigrang, D.J.; Sylvester, N.D. A review of explicit friction factor equations. J. Energy Resour. Technol. ASME 1985, 107, 280–283. [Google Scholar] [CrossRef]
- Yıldırım, G. Computer-based analysis of explicit approximations to the implicit Colebrook-White equation in turbulent flow friction factor calculation. Adv. Eng. Softw. 2009, 40, 1183–1190. [Google Scholar] [CrossRef]
- Genić, S.; Aranđelović, I.; Kolendić, P.; Jarić, M.; Budimir, N.; Genić, V. A review of explicit approximations of Colebrook’s equation. FME Trans. 2011, 39, 67–71. [Google Scholar]
- Winning, H.K.; Coole, T. Explicit friction factor accuracy and computational efficiency for turbulent flow in pipes. Flow Turbul. Combust. 2013, 90, 1–27. [Google Scholar] [CrossRef]
- Lira, I. On the uncertainties stemming from use of the Colebrook-White equation. Ind. Eng. Chem. Res. 2013, 52, 7550–7555. [Google Scholar] [CrossRef]
- Giustolisi, O.; Berardi, L.; Walski, T.M. Some explicit formulations of Colebrook–White friction factor considering accuracy vs. computational speed. J. Hydroinformatics 2011, 13, 401–418. [Google Scholar] [CrossRef]
- Brkić, D. An explicit approximation of the Colebrook equation for fluid flow friction factor. Petrol. Sci. Technol. 2011, 29, 1596–1602. [Google Scholar] [CrossRef]
- Brkić, D. New explicit correlations for turbulent flow friction factor. Nucl. Eng. Des. 2011, 241, 4055–4059. [Google Scholar] [CrossRef]
- Fang, X.; Xu, Y.; Zhou, Z. New correlations of single-phase friction factor for turbulent pipe flow and evaluation of existing single-phase friction factor correlations. Nucl. Eng. Des. 2011, 241, 897–902. [Google Scholar] [CrossRef]
- Ghanbari, A.; Farshad, F.F.; Rieke, H.H. Newly developed friction factor correlation for pipe flow and flow assurance. J. Chem. Eng. Mater. Sci. 2011, 2, 83–86. [Google Scholar]
- Papaevangelou, G.; Evangelides, C.; Tzimopoulos, C. A new explicit relation for the friction factor coefficient in the Darcy–Weisbach equation. In Proceedings of the Protection and Restoration of the Environment, Corfu, Greece, 5–9 July 2010; pp. 166–172. [Google Scholar]
- Avci, A.; Karagoz, I. A novel explicit equation for friction factor in smooth and rough pipes. J. Fluids Eng. ASME 2009, 131, 061203. [Google Scholar] [CrossRef]
- Buzzelli, D. Calculating friction in one step. Mach. Des. 2008, 80, 54–55. [Google Scholar]
- Sonnad, J.R.; Goudar, C.T. Turbulent flow friction factor calculation using a mathematically exact alternative to the Colebrook–White equation. J. Hydraul. Eng. ASCE 2006, 132, 863–867. [Google Scholar] [CrossRef]
- Romeo, E.; Royo, C.; Monzón, A. Improved explicit equations for estimation of the friction factor in rough and smooth pipes. Chem. Eng. J. 2002, 86, 369–374. [Google Scholar] [CrossRef]
- Manadilli, G. Replace implicit equations with signomial functions. Chem. Eng. (N. Y.) 1997, 104, 129–130. [Google Scholar]
- Chen, J.J.J. A simple explicit formula for the estimation of pipe friction factor. Proc. Inst. Civ. Eng. 1984, 77, 49–55. [Google Scholar] [CrossRef]
- Serghides, T.K. Estimate friction factor accurately. Chem. Eng. (N. Y.) 1984, 91, 63–64. [Google Scholar]
- Haaland, S.E. Simple and explicit formulas for the friction factor in turbulent pipe flow. J. Fluids Eng. ASME 1983, 105, 89–90. [Google Scholar] [CrossRef]
- Zigrang, D.J.; Sylvester, N.D. Explicit approximations to the solution of Colebrook’s friction factor equation. AIChE J. 1982, 28, 514–515. [Google Scholar] [CrossRef]
- Barr, D.I.H. Solutions of the Colebrook-White function for resistance to uniform turbulent flow. Proc. Inst. Civ. Eng. 1981, 71, 529–535. [Google Scholar]
- Round, G.F. An explicit approximation for the friction factor-Reynolds number relation for rough and smooth pipes. Can. J. Chem. Eng. 1980, 58, 122–123. [Google Scholar] [CrossRef]
- Schorle, B.J.; Churchill, S.W.; Shacham, M. Comments on: “An explicit equation for friction factor in pipe”. Ind. Eng. Chem. Fundam. 1980, 19, 228–230. [Google Scholar] [CrossRef]
- Chen, N.H. An explicit equation for friction factor in pipes. Ind. Eng. Chem. Fundam. 1979, 18, 296–297. [Google Scholar] [CrossRef]
- Swamee, D.K.; Jain, A.K. Explicit equations for pipe flow problems. J. Hydraul. Div. ASCE 1976, 102, 657–664. [Google Scholar]
- Eck, B. Technische Stromungslehre; Springer: New York, NY, USA, 1973. [Google Scholar]
- Wood, D.J. An explicit friction factor relationship. Civ. Eng. 1966, 36, 60–61. [Google Scholar]
- Moody, L.F. An approximate formula for pipe friction factors. Trans. ASME 1947, 69, 1005–1006. [Google Scholar]
- Brkić, D. A note on explicit approximations to Colebrook’s friction factor in rough pipes under highly turbulent cases. Int. J. Heat Mass Tran. 2016, 93, 513–515. [Google Scholar] [CrossRef]
- Ćojbašić, Ž.; Brkić, D. Very accurate explicit approximations for calculation of the Colebrook friction factor. Int. J. Mech. Sci. 2013, 67, 10–13. [Google Scholar] [CrossRef]
- Vatankhah, A.R.; Kouchakzadeh, S. Discussion of Turbulent flow friction factor calculation using a mathematically exact alternative to the Colebrook-White equation. J. Hydraul. Eng. ASCE 2008, 134, 1187. [Google Scholar] [CrossRef]
- Vatankhah, A.R.; Kouchakzadeh, S. Discussion: Exact equations for pipe-flow problems. J. Hydraul. Res. IAHR 2009, 47, 537–538. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Inc.: Reston, VA, USA, 1989. [Google Scholar]
- Fleming, P.J.; Purshouse, R.C. Evolutionary algorithms in control systems engineering: A survey. Control Eng. Pract. 2002, 10, 1223–1241. [Google Scholar] [CrossRef]
- Samadianfard, S. Gene expression programming analysis of implicit Colebrook-White equation in turbulent flow friction factor calculation. J. Petrol. Sci. Eng. 2012, 92–93, 48–55. [Google Scholar] [CrossRef]
- Brkić, D. Discussion of “Gene expression programming analysis of implicit Colebrook–White equation in turbulent flow friction factor calculation”. J. Petrol. Sci. Eng. 2014, 124, 399–401. [Google Scholar] [CrossRef]
- Vatankhah, A.R. Comment on “Gene expression programming analysis of implicit Colebrook–White equation in turbulent flow friction factor calculation”. J. Petrol. Sci. Eng. 2014, 124, 402–405. [Google Scholar] [CrossRef]
- Brkić, D.; Ćojbašić, Ž. Intelligent flow friction estimation. Comput. Intell. Neurosci. 2016, 2016, 5242596. [Google Scholar] [CrossRef] [PubMed]
- Ćojbašić, Ž.; Nikolić, V.; Petrović, E.; Pavlović, V.; Tomić, M.; Pavlović, I.; Ćirić, I. A real time neural network based finite element analysis of shell structure. Facta Univ. Mech. Eng. 2014, 12, 149–155. [Google Scholar]
- Dučić, N.; Ćojbašić, Ž.; Radiša, R.; Slavković, R.; Milićević, M. CAD/CAM design and genetic optimization of feeders for sand casting process. Facta Univ. Mech. Eng. 2016, 14, 147–158. [Google Scholar]
- Brkić, D. Efficiency of Distribution and Use of Natural Gas in Households (Ефикасност дистрибуције и коришћења природног гаса у домаћинствима, In Serbian). Ph.D. Thesis, University of Belgrade, Belgrade, Serbia, 2010. [Google Scholar]
- Allen, J.J.; Shockling, M.A.; Kunkel, G.J.; Smits, A.J. Turbulent flow in smooth and rough pipes. Proc. R. Soc. Ser. A Math. Phys. Sci. 2007, 365, 699–714. [Google Scholar] [CrossRef] [PubMed]
- Brkić, D. A gas distribution network hydraulic problem from practice. Petrol. Sci. Technol. 2011, 29, 366–377. [Google Scholar] [CrossRef]
- Brkić, D. Can pipes be actually really that smooth? Int. J. Refrig. 2012, 35, 209–215. [Google Scholar] [CrossRef]
- Brkić, D. Discussion of “Jacobian matrix for solving water distribution system equations with the Darcy-Weisbach head-loss model”. J. Hydraul. Eng. ASCE 2012, 138, 1000–1002. [Google Scholar] [CrossRef]
- Brkić, D. Discussion of “Water distribution system analysis: Newton-Raphson method revisited”. J. Hydraul. Eng. ASCE 2012, 138, 822–824. [Google Scholar] [CrossRef]
- Brkić, D. Discussion of “Method to cope with zero flows in newton solvers for water distribution systems”. J. Hydraul. Eng. ASCE 2014, 140, 07014003. [Google Scholar] [CrossRef]
- Sonnad, J.R.; Goudar, C.T. Constraints for using Lambert W function-based explicit Colebrook–White equation. J. Hydraul. Eng. ASCE 2004, 130, 929–931. [Google Scholar] [CrossRef]
- Brkić, D. Comparison of the Lambert W-function based solutions to the Colebrook equation. Eng. Comput. 2012, 29, 617–630. [Google Scholar] [CrossRef]
- Rollmann, P.; Spindler, K. Explicit representation of the implicit Colebrook–White equation. Case Stud. Therm. Eng. 2015, 5, 41–47. [Google Scholar] [CrossRef]
- Brkić, D. Spreadsheet-based pipe networks analysis for teaching and learning purpose. Spreadsheets Educ. (eJSiE) 2016, 9. Available online: http://epublications.bond.edu.au/ejsie/vol9/iss2/4/ (accessed on 03 April 2017).
- Brkić, D. Iterative methods for looped network pipeline calculation. Water Resour. Manag. 2011, 25, 2951–2987. [Google Scholar] [CrossRef]
- Simpson, A.; Elhay, S. Jacobian matrix for solving water distribution system equations with the Darcy-Weisbach head-loss model. J. Hydraul. Eng. ASCE 2011, 137, 696–700. [Google Scholar] [CrossRef]
- Spiliotis, M.; Tsakiris, G. Water distribution system analysis: Newton-Raphson method revisited. J. Hydraul. Eng. ASCE 2011, 137, 852–855. [Google Scholar] [CrossRef]
- Brkić, D. An improvement of Hardy Cross method applied on looped spatial natural gas distribution networks. Appl. Energy 2009, 86, 1290–1300. [Google Scholar] [CrossRef]
- Brkić, D.; Tanasković, T. Systematic approach to natural gas usage for domestic heating in urban areas. Energy 2008, 33, 1738–1753. [Google Scholar] [CrossRef]
- Ćojbašić, Ž.; Petković, D.; Shamshirband, S.; Tong, C.W.; Ch, S.; Janković, P.; Dučić, N.; Baralić, J. Surface roughness prediction by extreme learning machine constructed with abrasive water jet. Precis Eng. 2016, 43, 86–92. [Google Scholar] [CrossRef]
- Shamshirband, S.; Petković, D.; Saboohi, H.; Anuar, N.B.; Inayat, I.; Akib, S.; Ćojbašić, Ž.; Nikolić, V.; Kiah, M.L.M.; Gani, A. Wind turbine power coefficient estimation by soft computing methodologies: Comparative study. Energy Convers. Manag. 2014, 81, 520–526. [Google Scholar] [CrossRef]
- Ćojbašić, Ž.; Nikolić, V.D.; Ćirić, I.; Grigorescu, S. Advanced evolutionary optimization for intelligent modeling and control of FBC process. Facta Univ. Ser. Mech. Eng. 2010, 8, 47–56. [Google Scholar]
- Cross, H. Analysis of Flow in Networks of Conduits or Conductors; University of Illinois at Urbana Champaign: Champaign, IL, USA, 1936; Volume 34, pp. 3–29. [Google Scholar]
- Praks, P.; Kopustinskas, V.; Masera, M. Probabilistic modelling of security of supply in gas networks and evaluation of new infrastructure. Reliab. Eng. Sys. Saf. 2015, 144, 254–264. [Google Scholar] [CrossRef]
- Pambour, K.A.; Bolado, L.R.; Dijkema, G.P.J. An integrated transient model for simulating the operation of natural gas transport systems. J. Nat. Gas. Sci. Eng. 2016, 28, 672–690. [Google Scholar] [CrossRef]
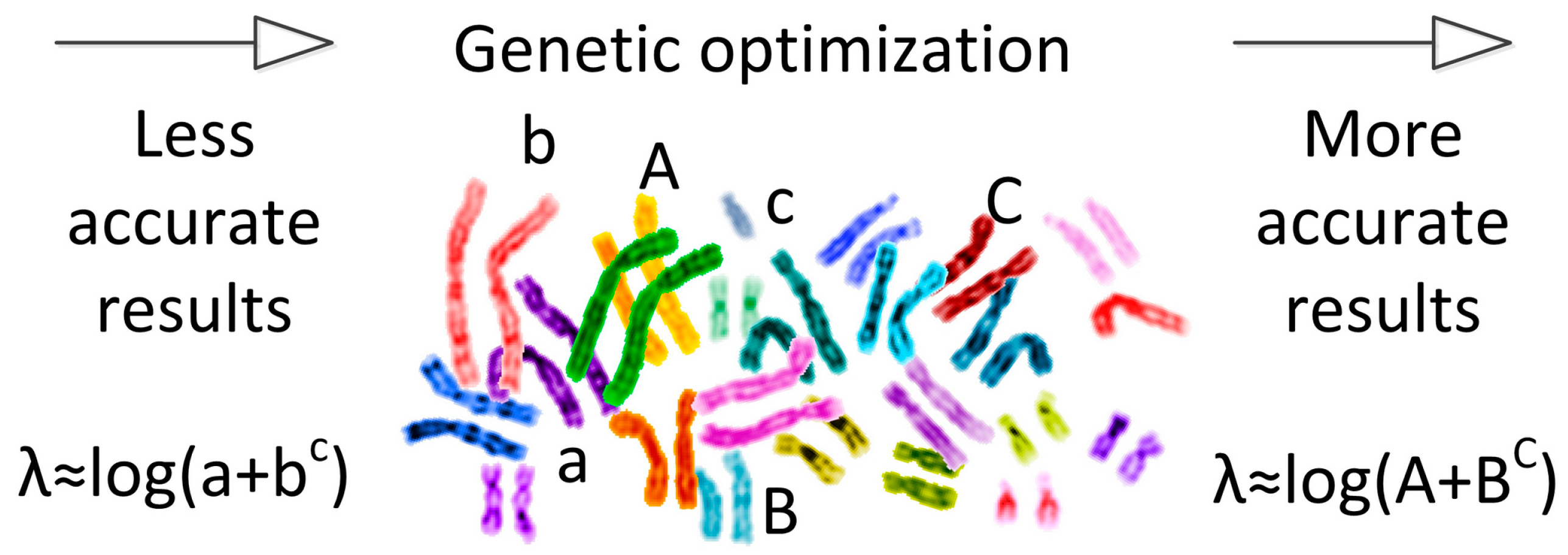
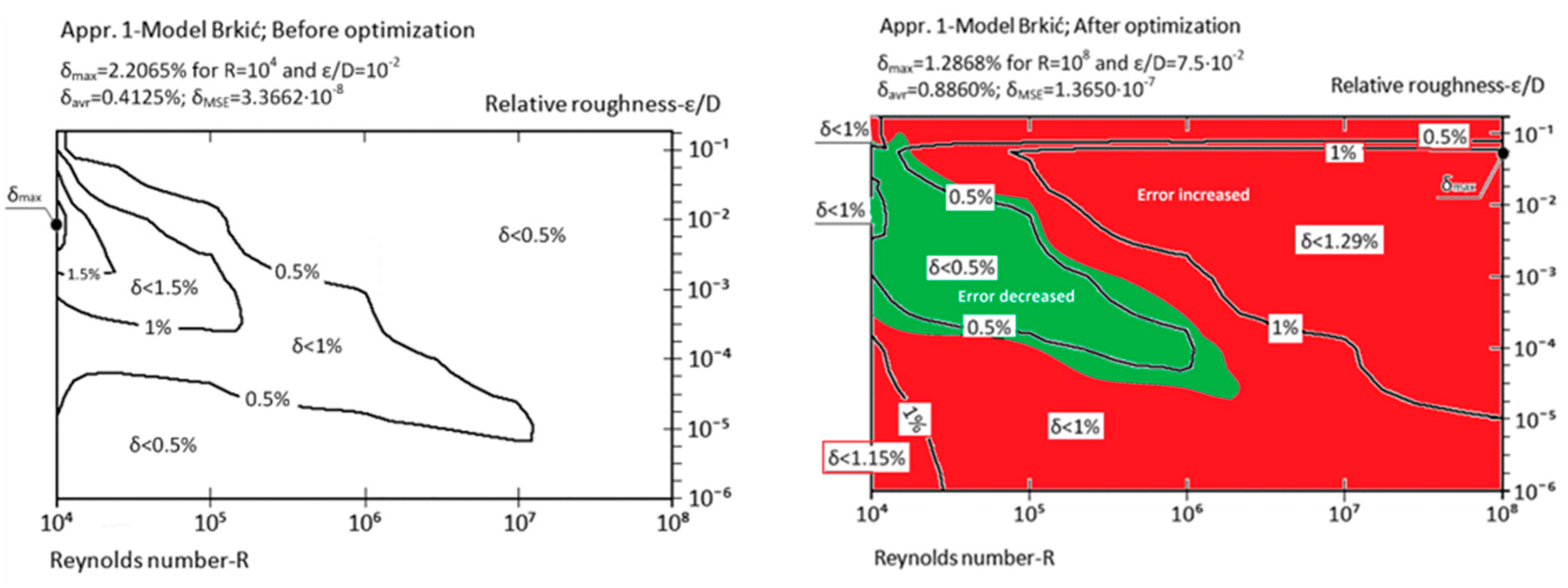

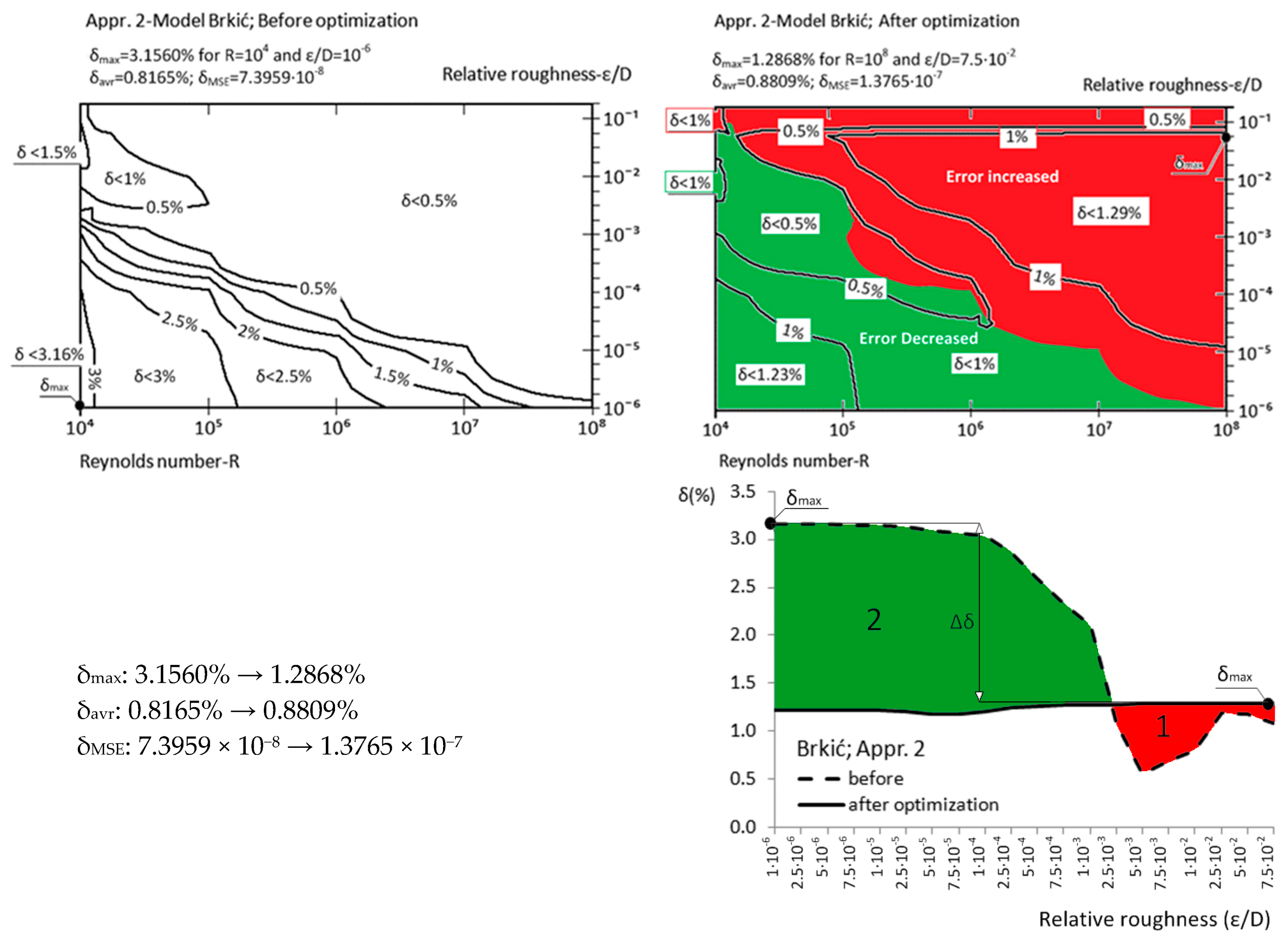
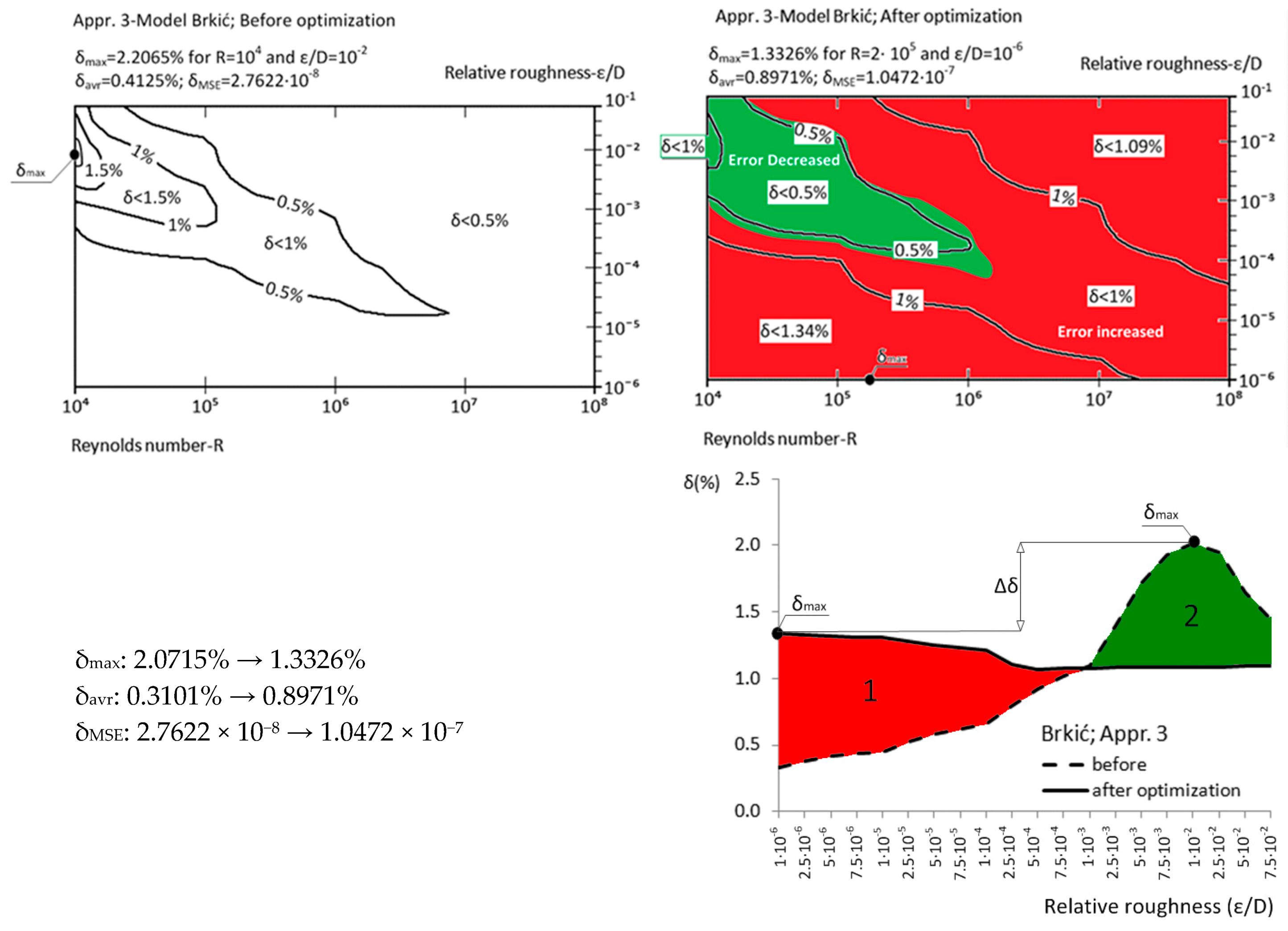


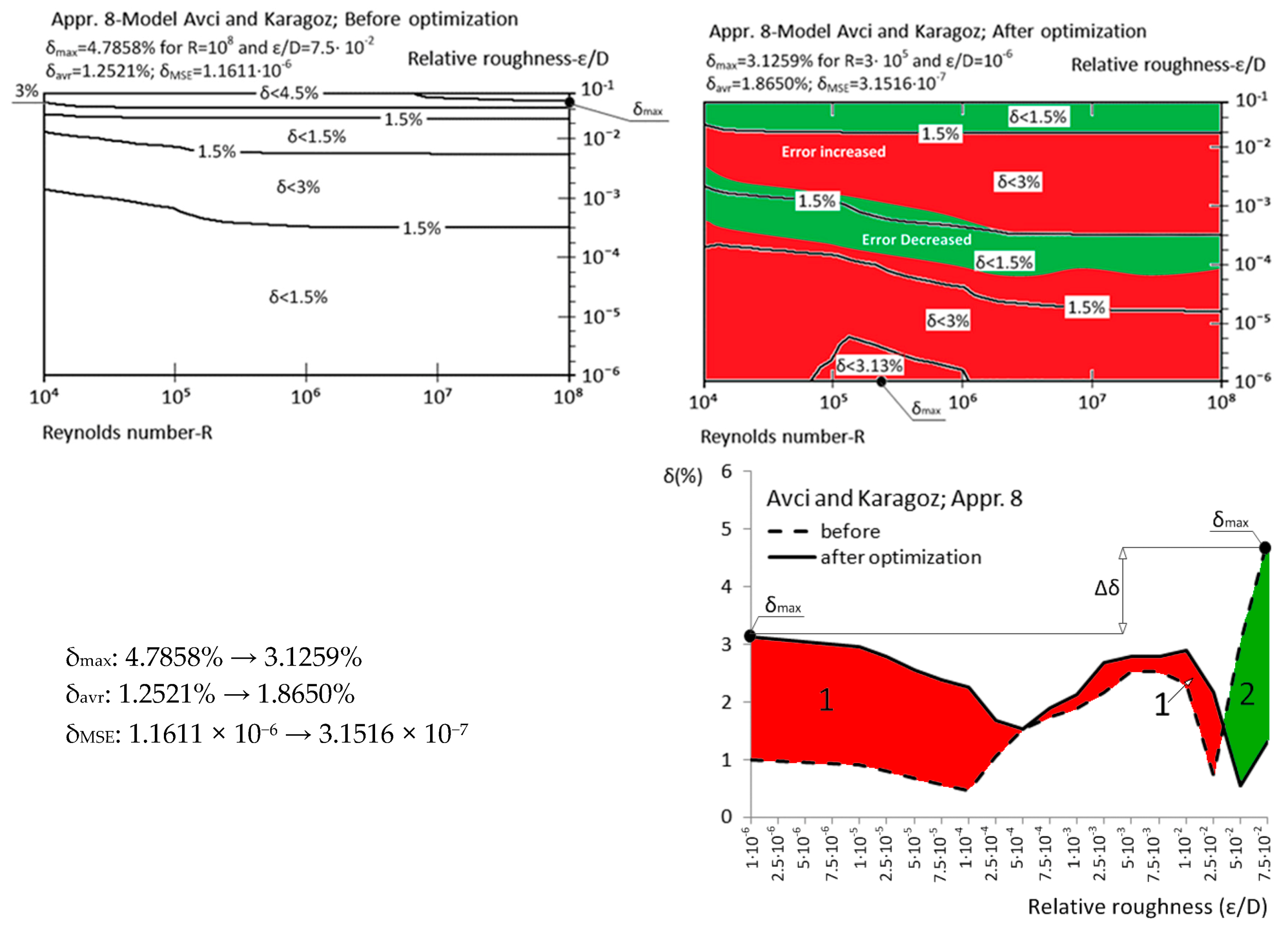
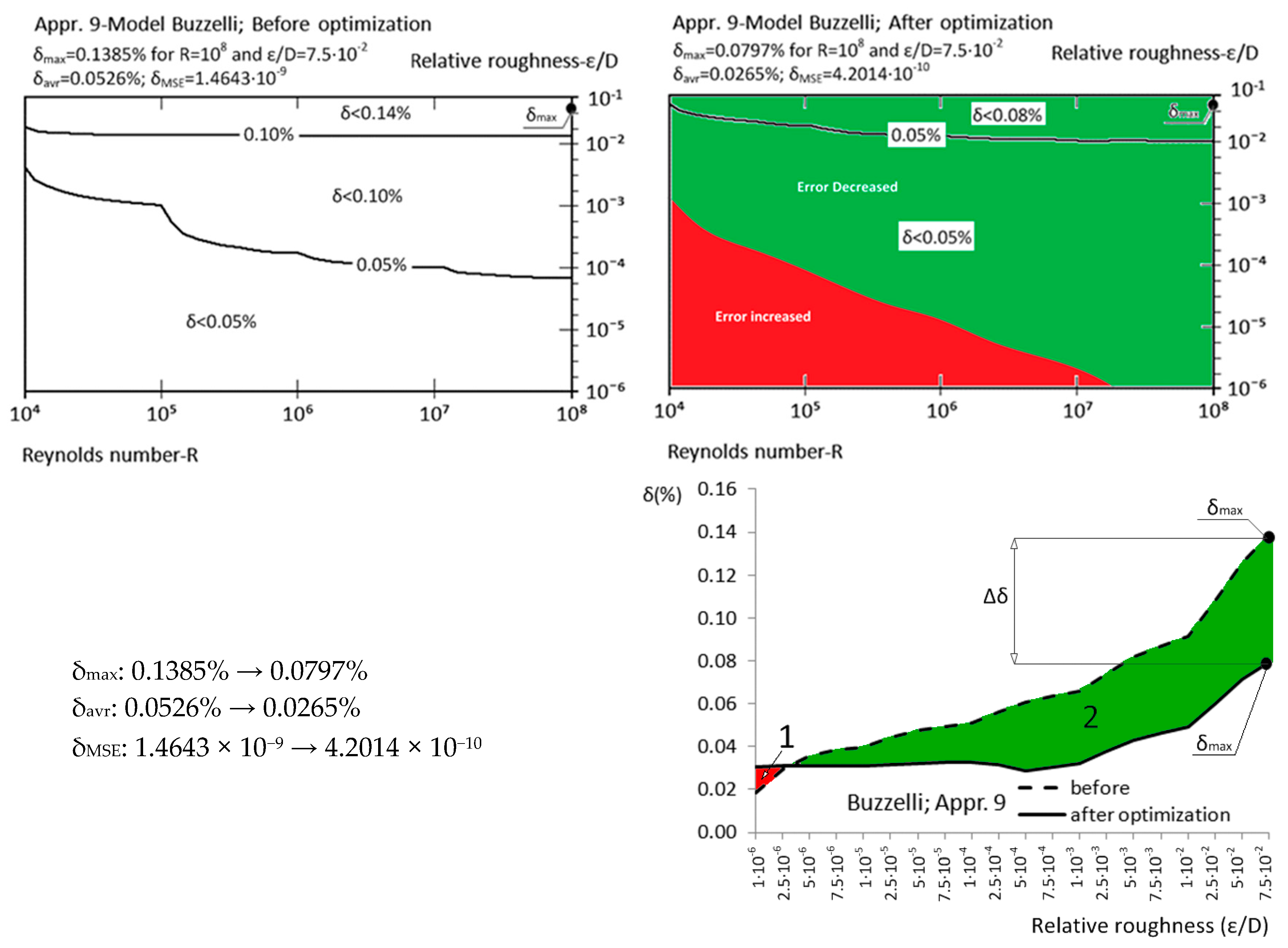
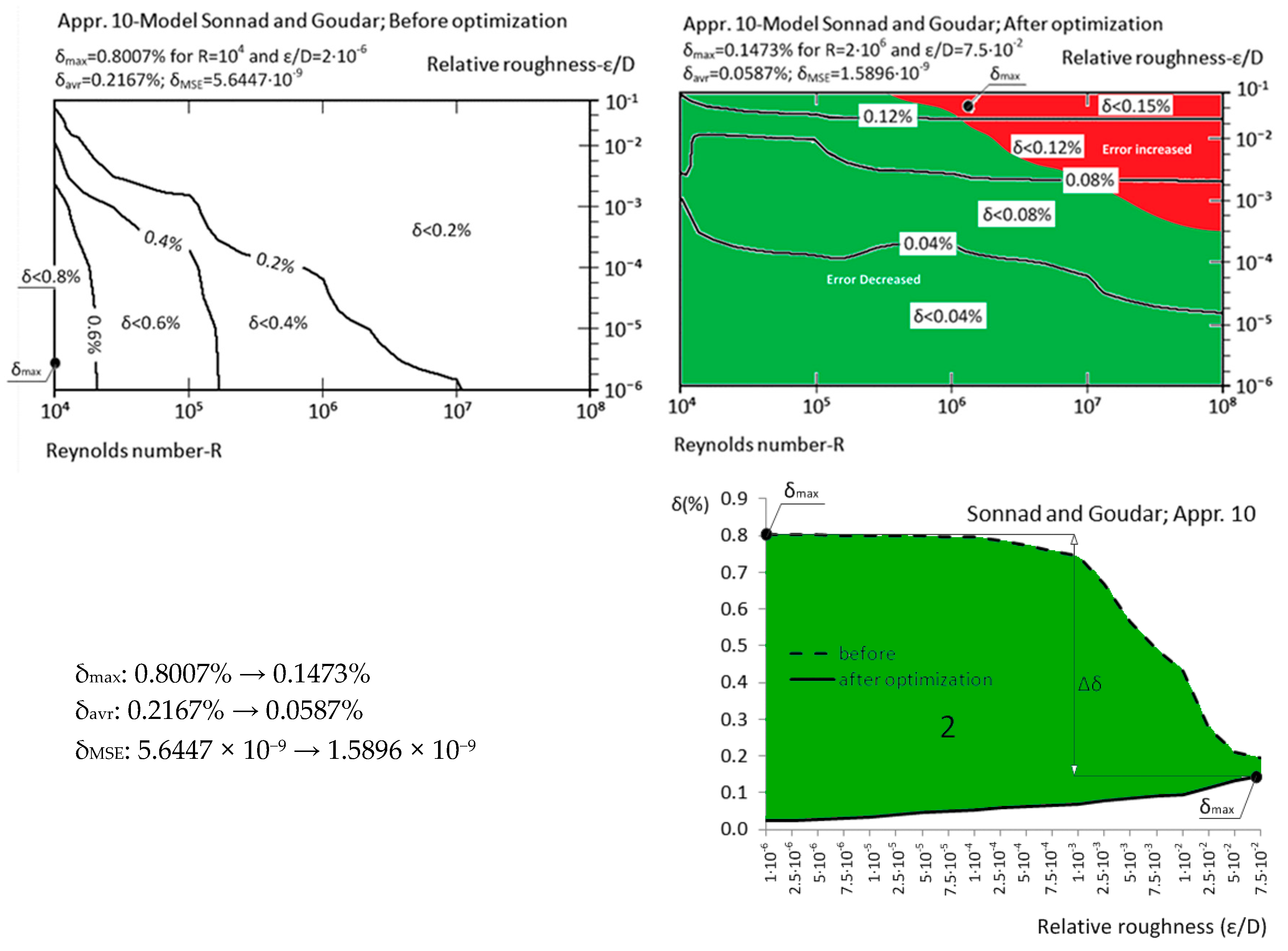
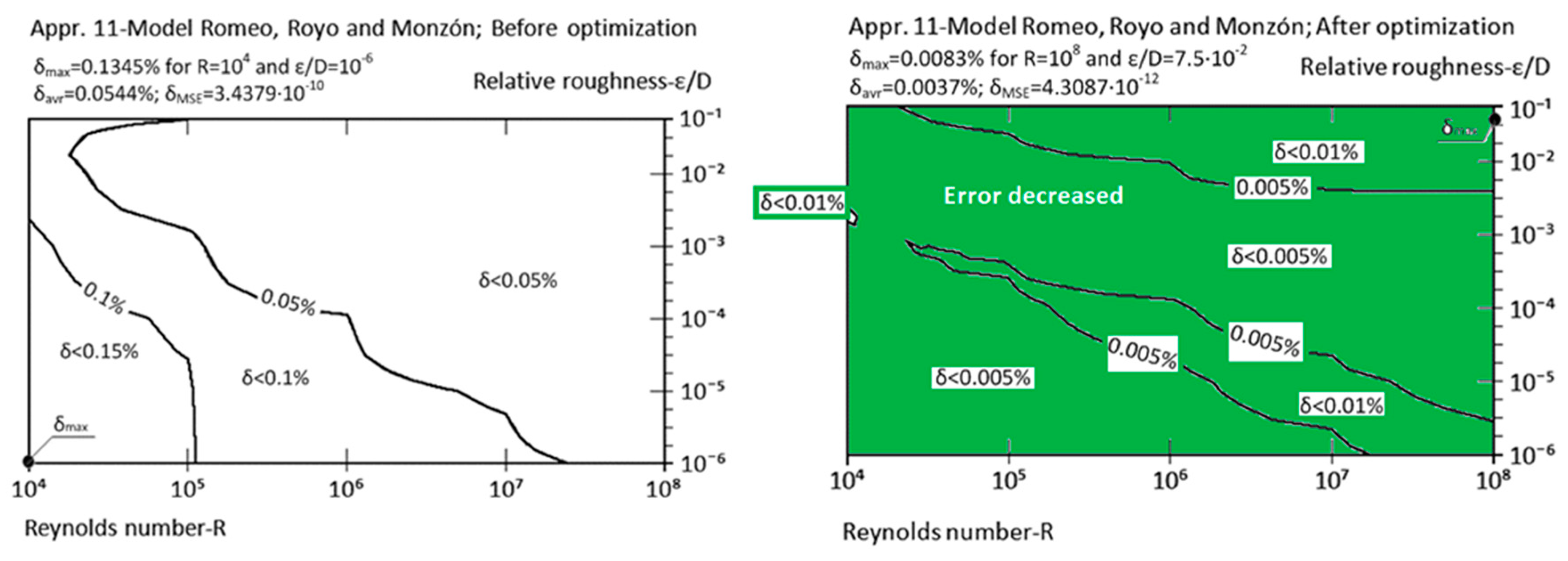



| Approximation No. | With Original Parameters | After Genetic Optimization | Estimation of Improvement | Source |
|---|---|---|---|---|
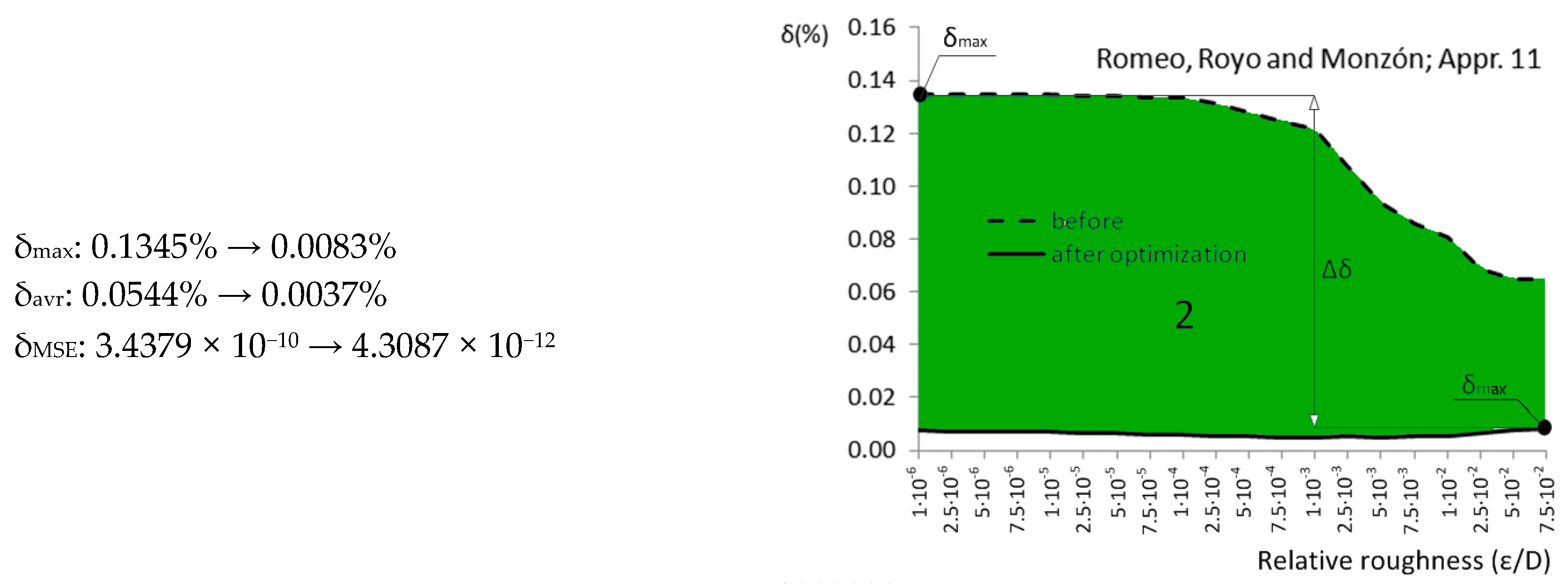
| Appr. 11; Equation (16) | 0.1345% | 0.0083% | extremely successful | Romeo et al. [27,42] |
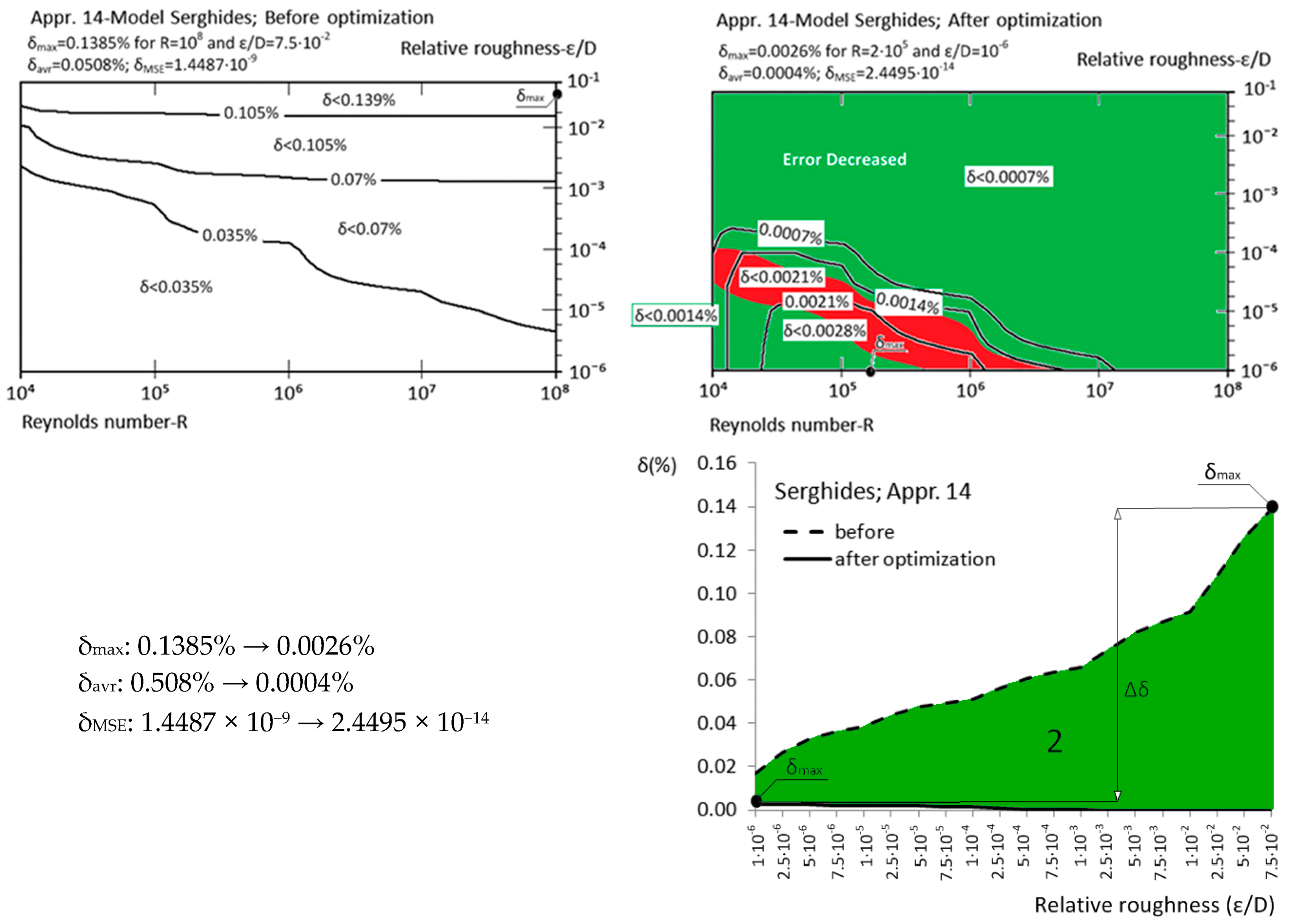
| Appr. 14; Equation (19) | 0.1385% | 0.0026% | extremely successful | Serghides [30,42] |
| Appr. 10; Equation (15) | 0.8007% | 0.1473% | successful | Sonnad and Goudar [26,43] |
| Appr. 2; Equation (7) | 3.1560% | 1.2871% | successful | Brkić [19] |
| Appr. 9; Equation (14) | 0.1385% | 0.0797% | successful | Buzzelli [25] |
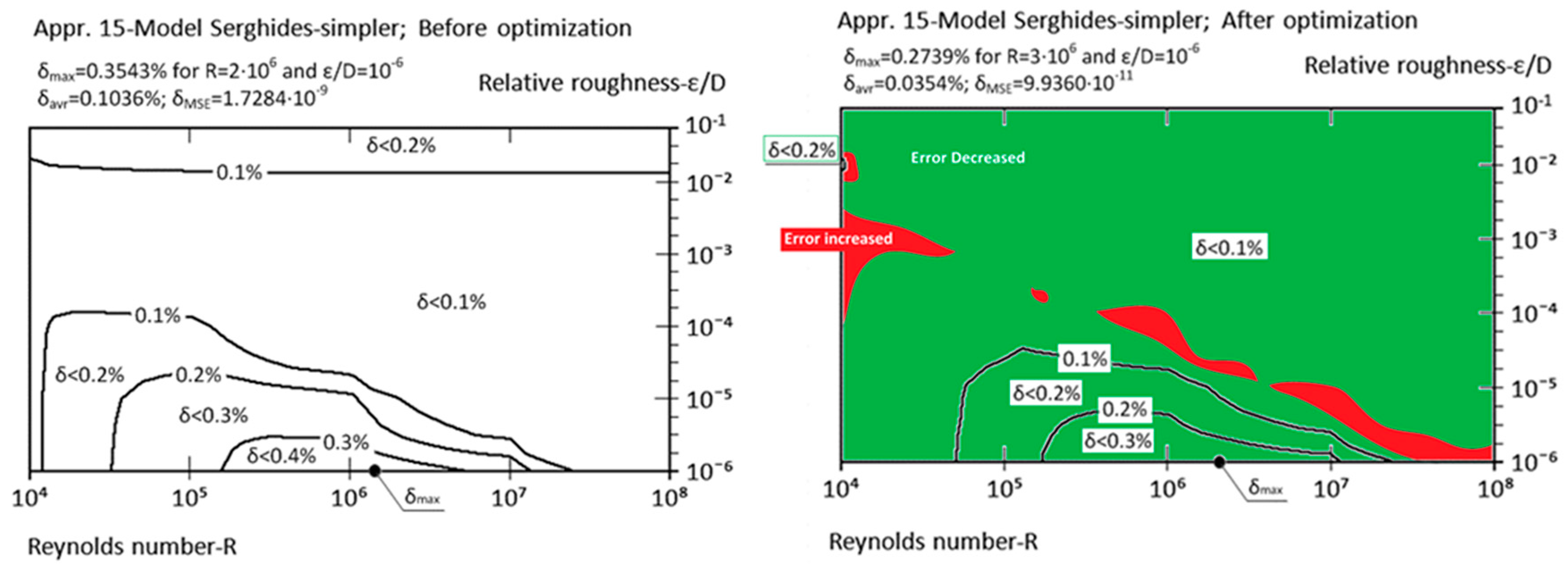
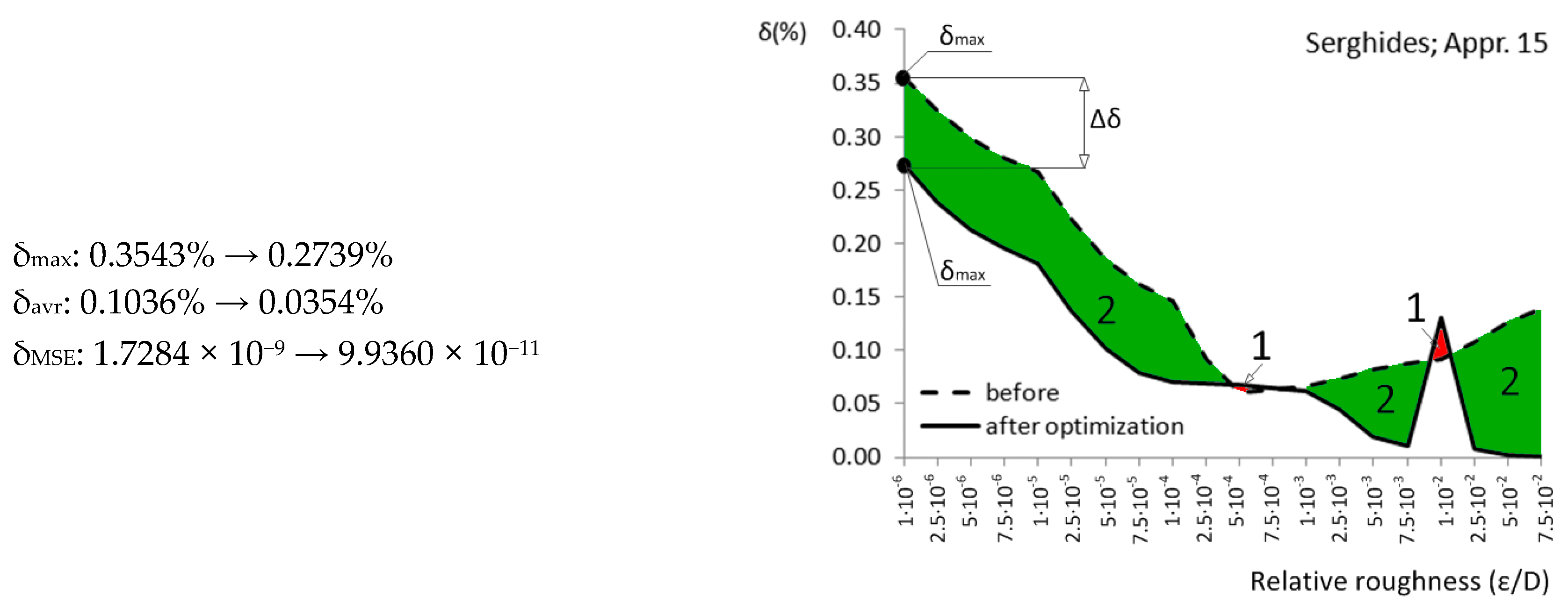
| Appr. 15; Equation (20) | 0.3543% | 0.2739% | successful | Serghides [30] |
| Appr. 17; Equation (22) | 0.1385% | 0.0831% | successful | Zigrang and Sylvester [32] |
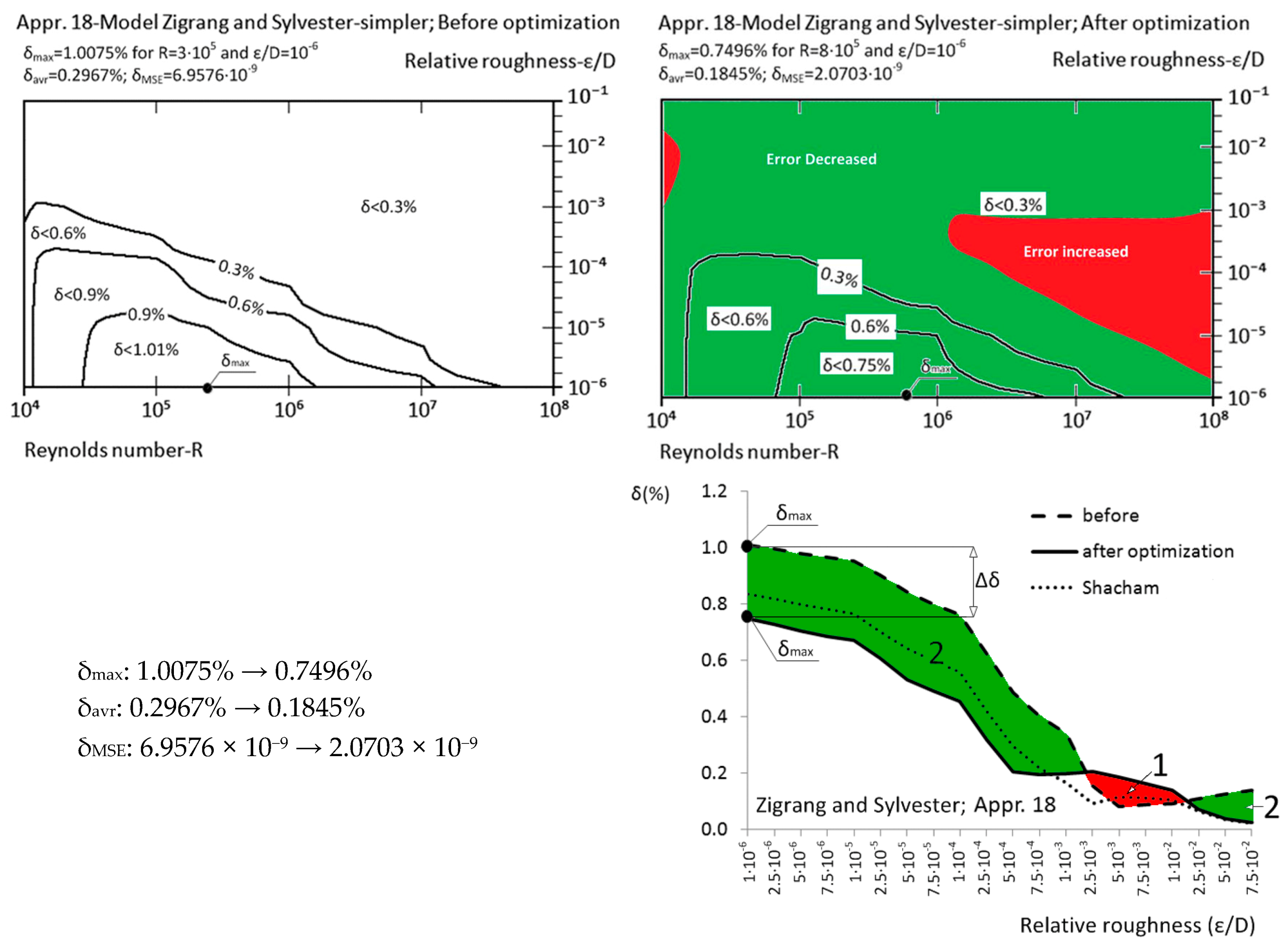
| Appr. 18; Equation (23) | 1.0075% | 0.7496% | successful | Zigrang and Sylvester [32] |
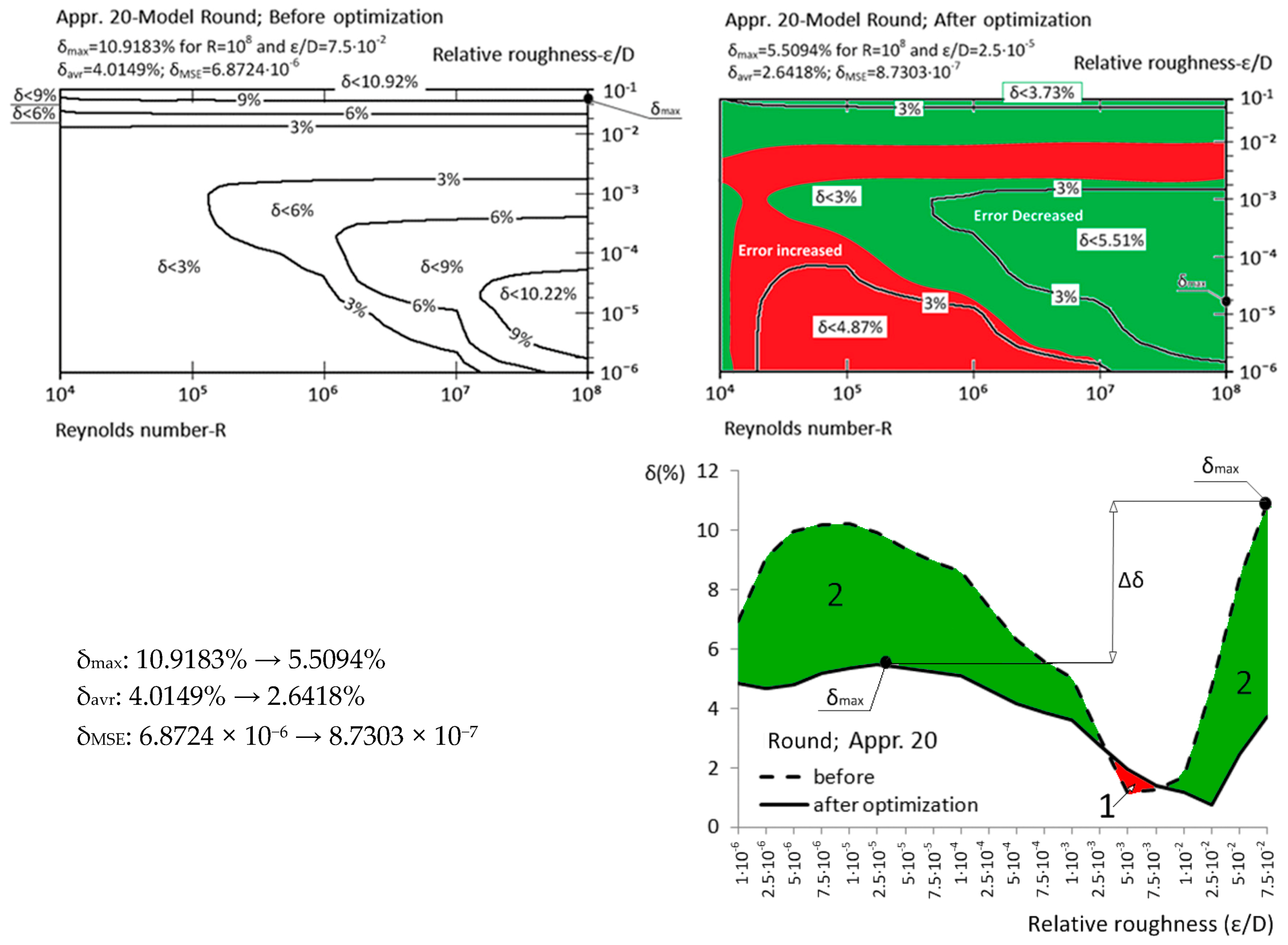
| Appr. 20; Equation (25) | 10.9183% | 5.5094% | successful | Round [34] |
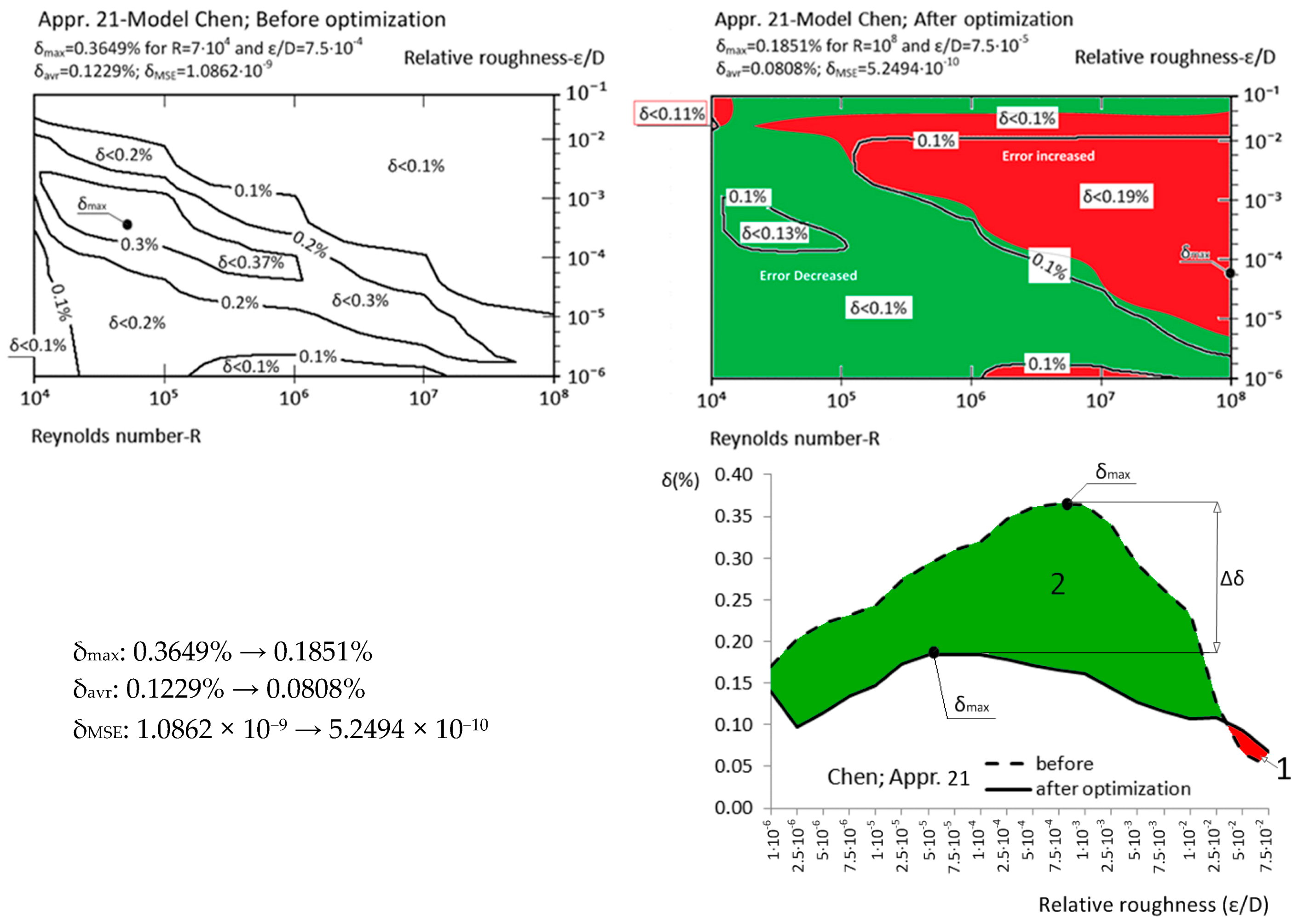
| Appr. 21; Equation (26) | 0.3649% | 0.1851% | successful | Chen [36] |
| Appr. 1; Equation (6) | 2.2065% | 1.2868% | moderately successful | Brkić [19] |
| Appr. 3; Equation (8) | 2.0715% | 1.3326% | moderately successful | Brkić [20] |
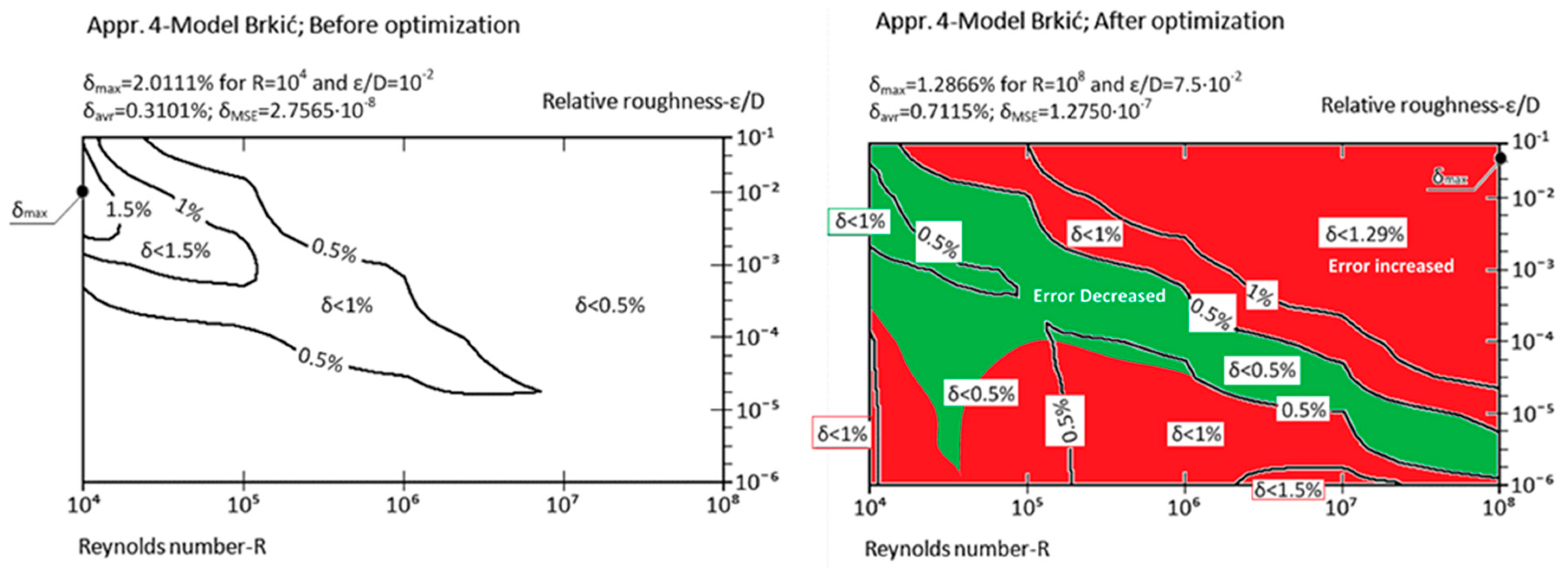
| Appr. 4; Equation (9) | 2.0111% | 1.2866% | moderately successful | Brkić [20] |
| Appr. 5; Equation (10) | 0.6167% | 0.5669% | moderately successful | Fang et al. [38] |
| Appr. 12; Equation (17) | 2.0651% | 1.5018% | moderately successful | Manadilli [28] |
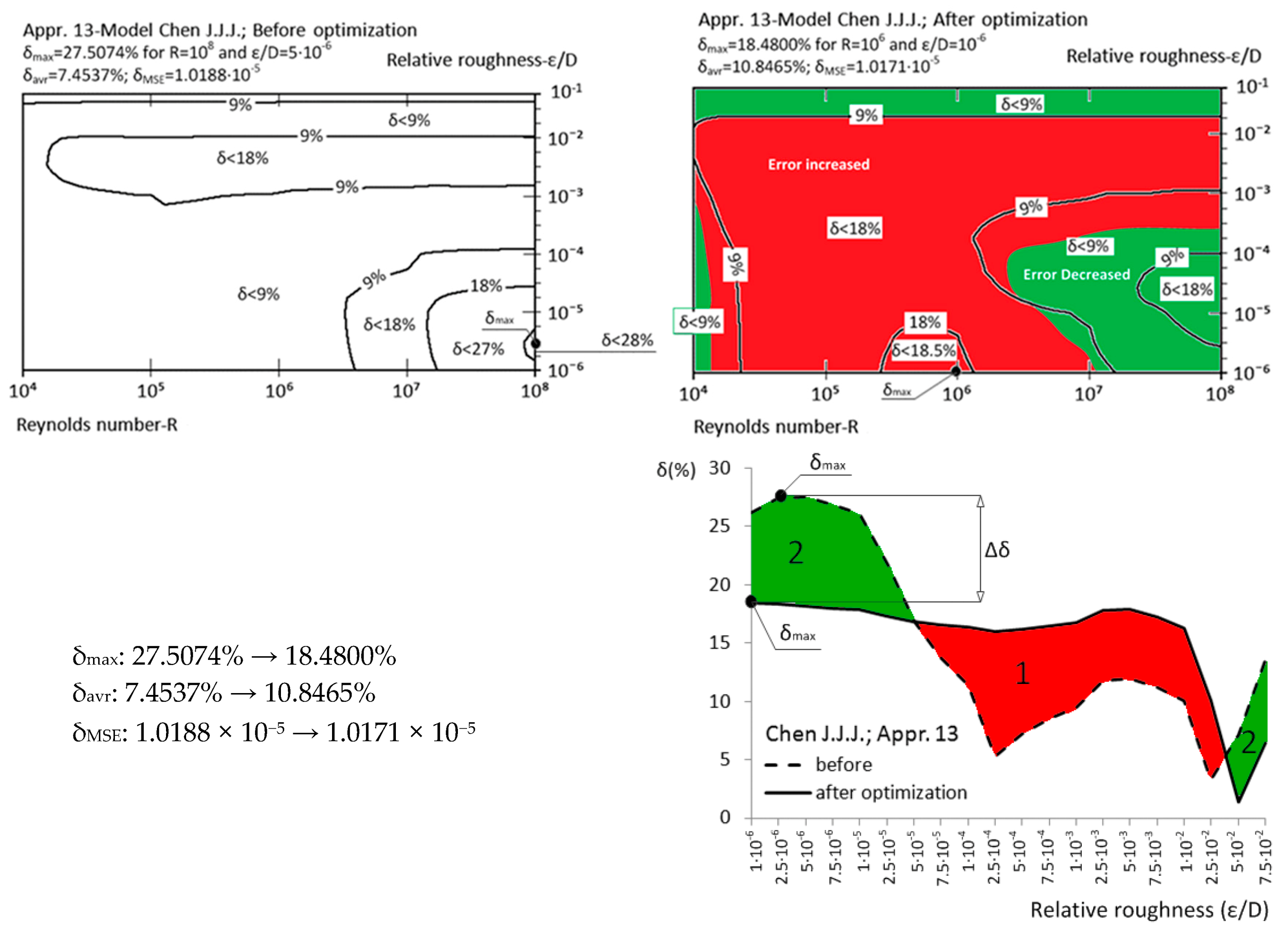
| Appr. 13; Equation (18) | 27.5074% | 18.4800% | moderately successful | Chen [29] |
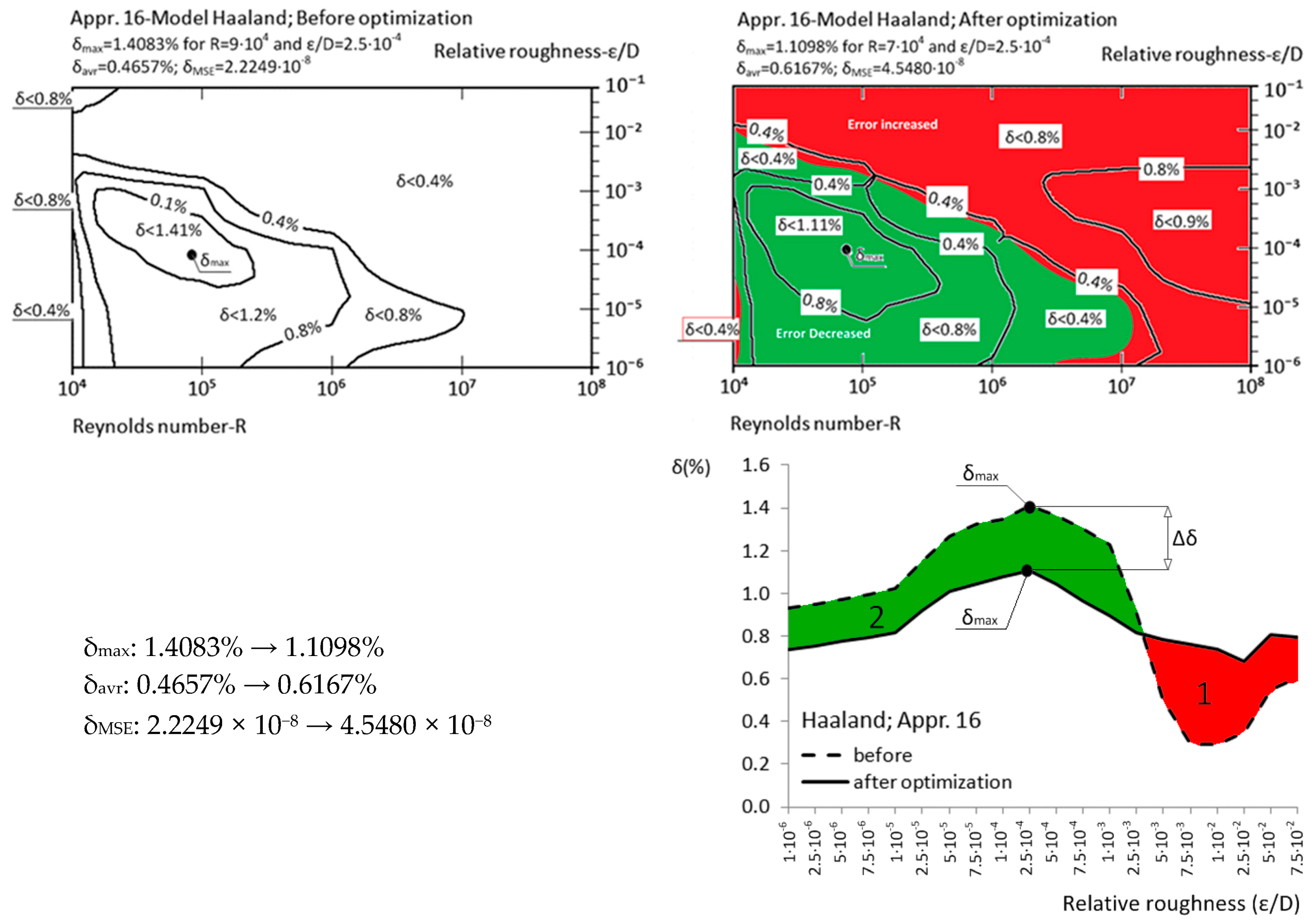
| Appr. 16; Equation (21) | 1.4083% | 1.1098% | moderately successful | Haaland [31] |
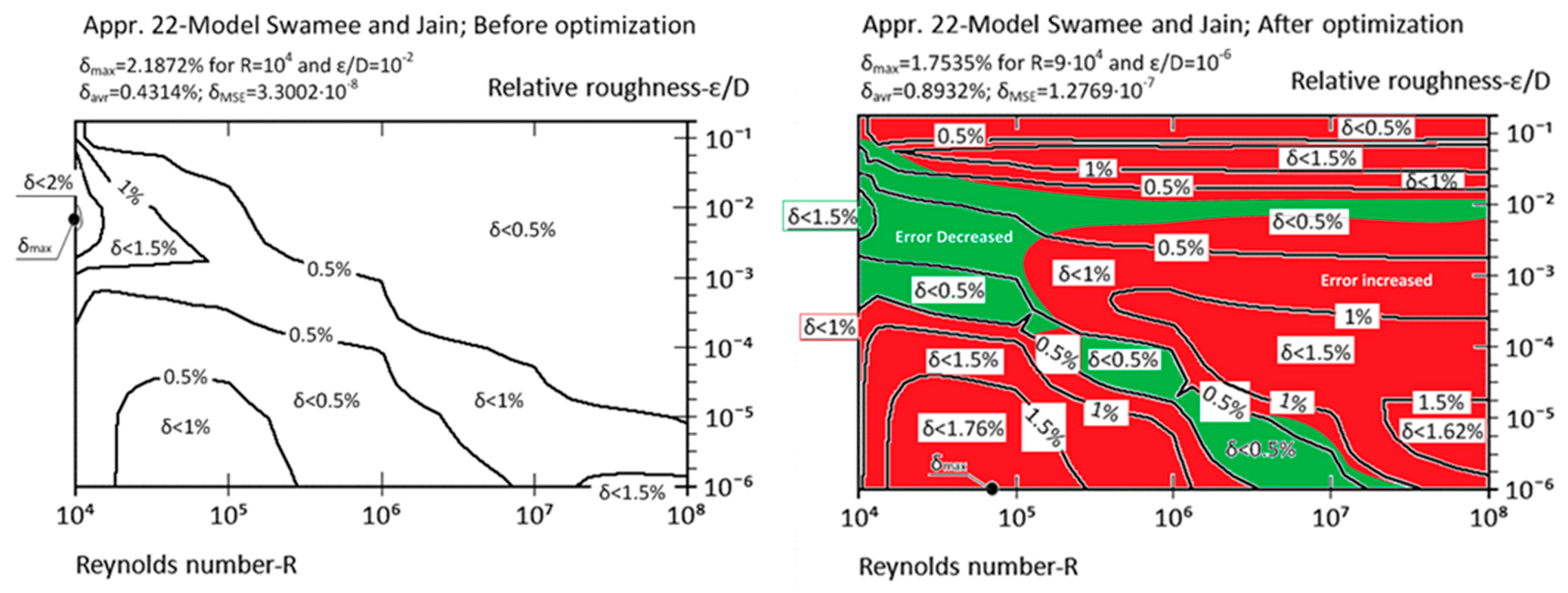
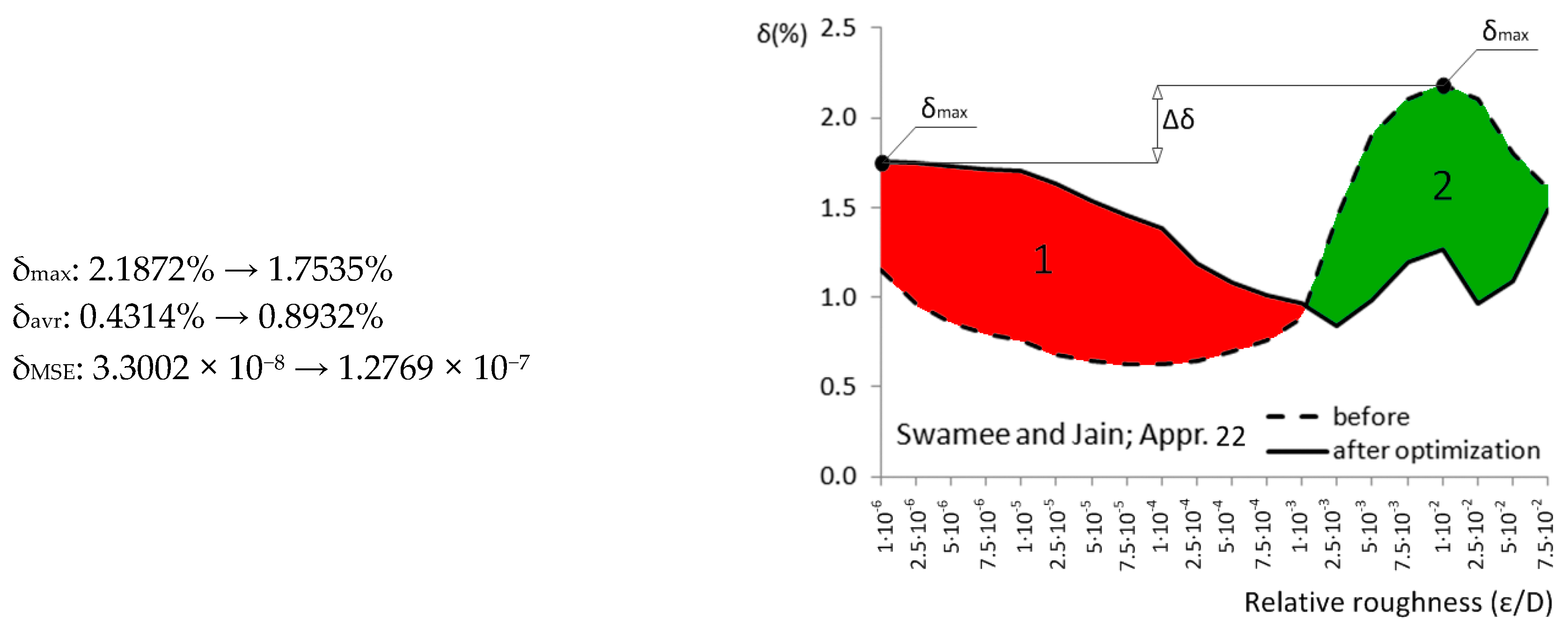
| Appr. 22; Equation (27) | 2.1872% | 1.7535% | moderately successful | Swamee and Jain [37] |
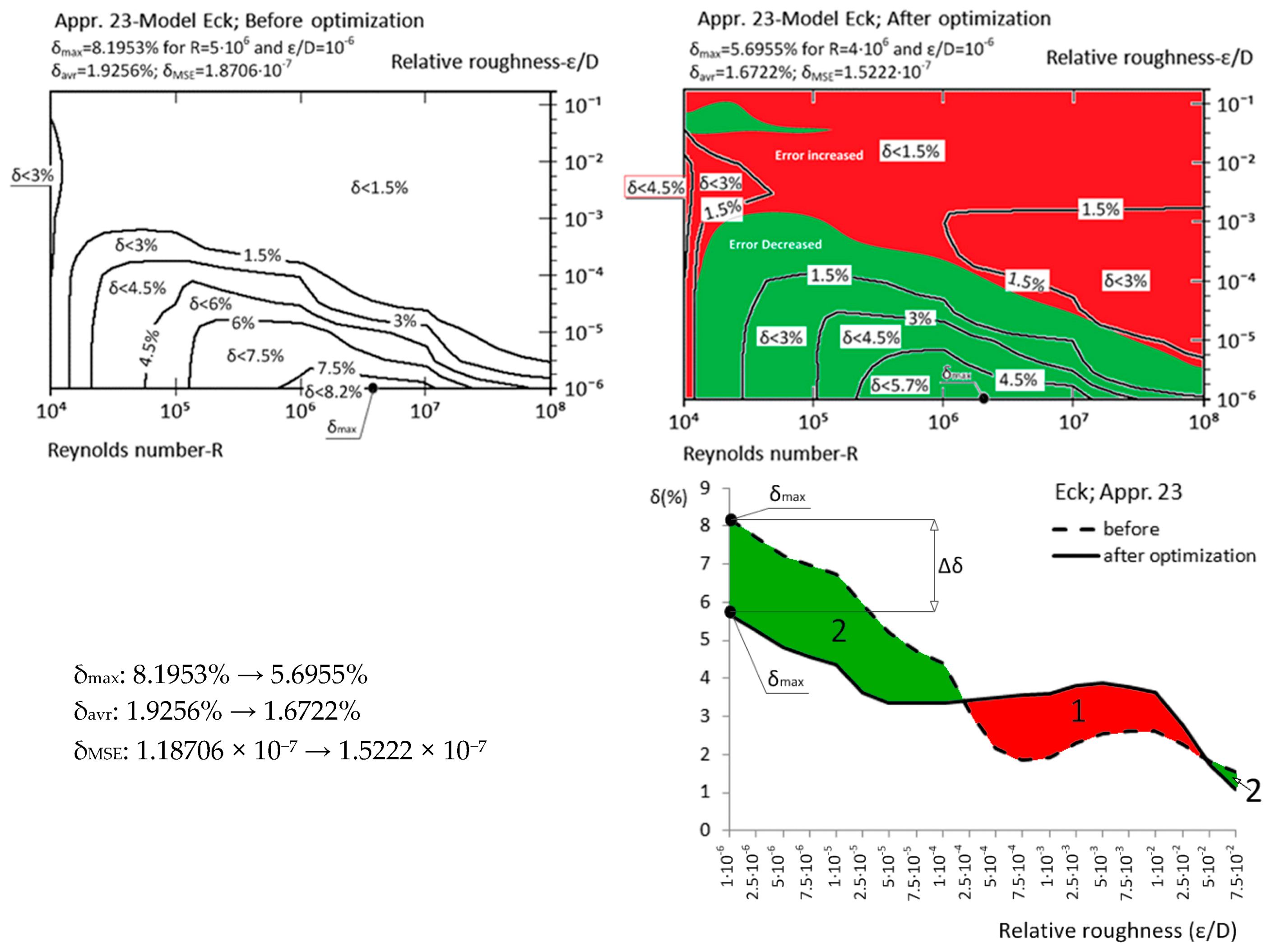
| Appr. 23; Equation (28) | 8.1953% | 5.6955% | moderately successful | Eck [21] |
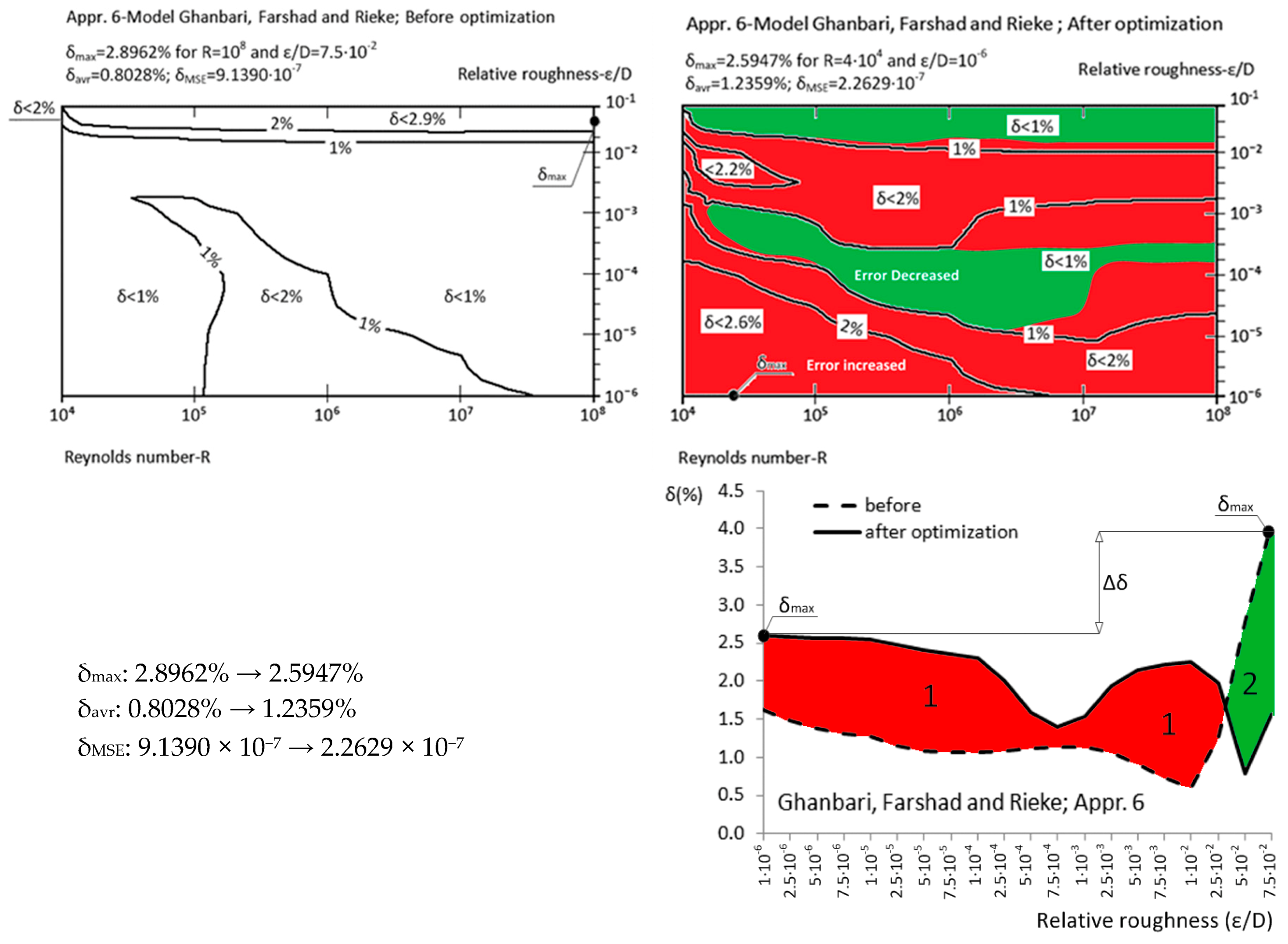
| Appr. 6; Equation (11) | 2.8962% | 2.5947% | not very successful | Ghanbari et al. [22] |
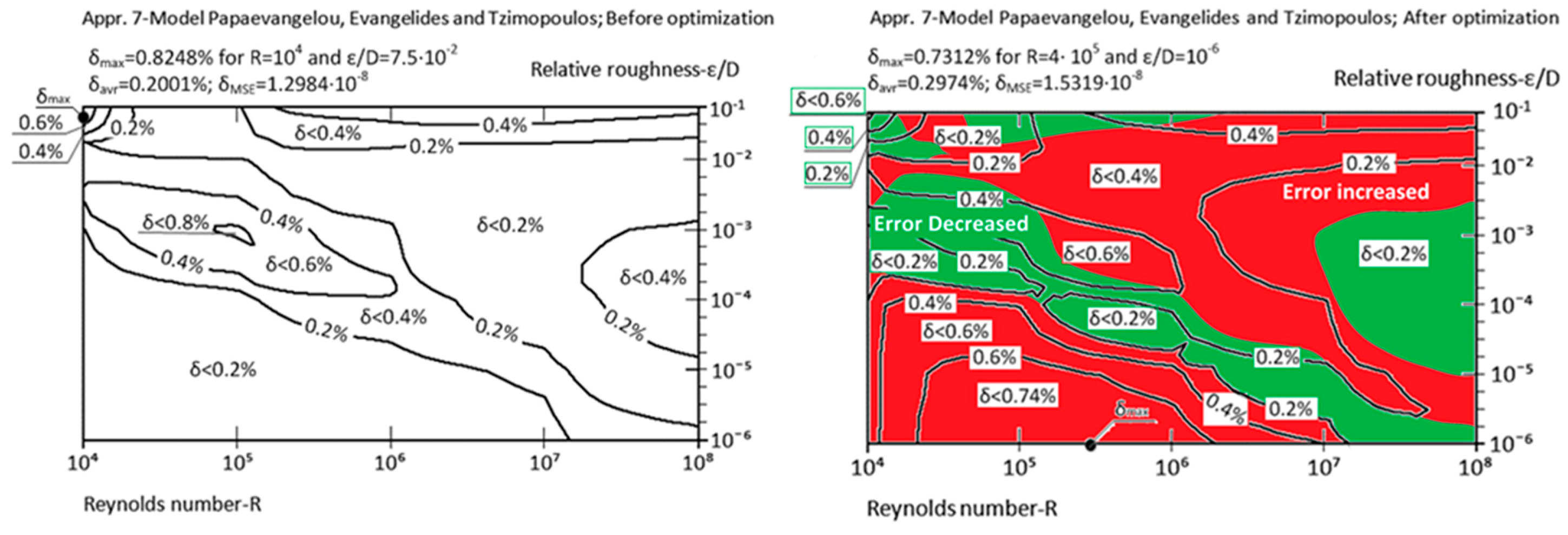
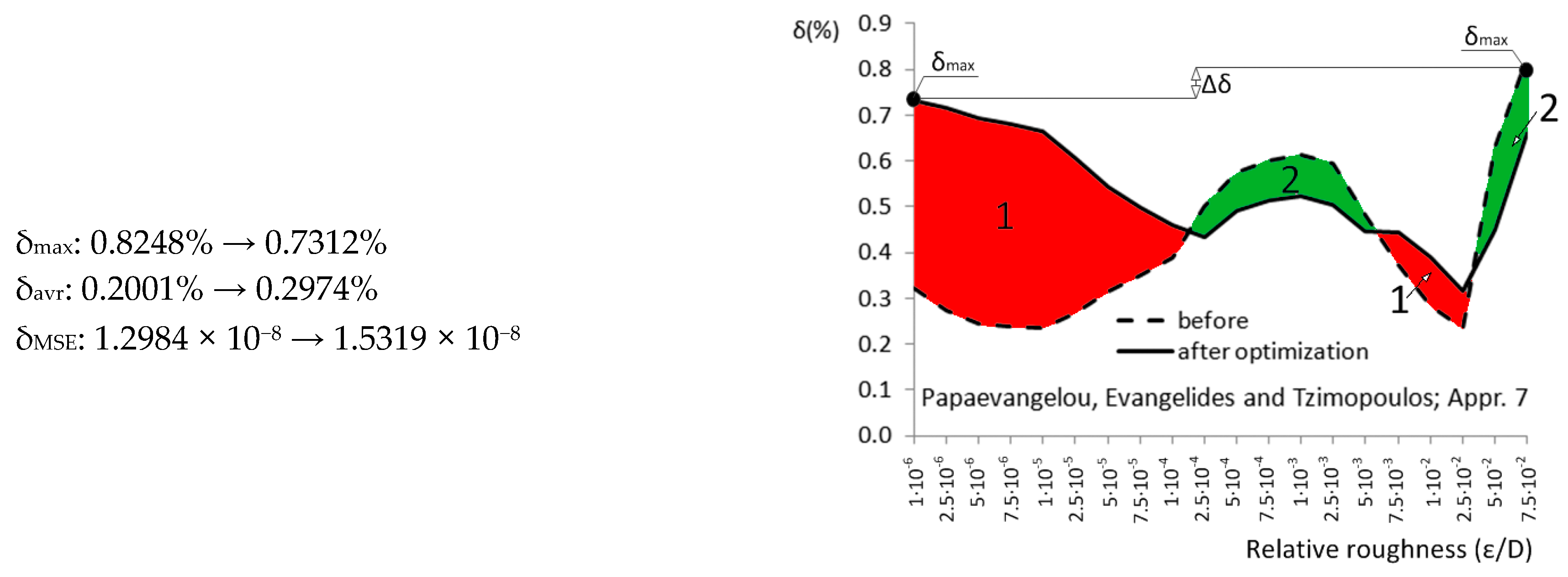
| Appr. 7; Equation (12) | 0.8248% | 0.7312% | not very successful | Papaevangelou et al. [23] |
| Appr. 8; Equation (13) | 4.7858% | 3.1259% | not very successful | Avci and Karagoz [24] |
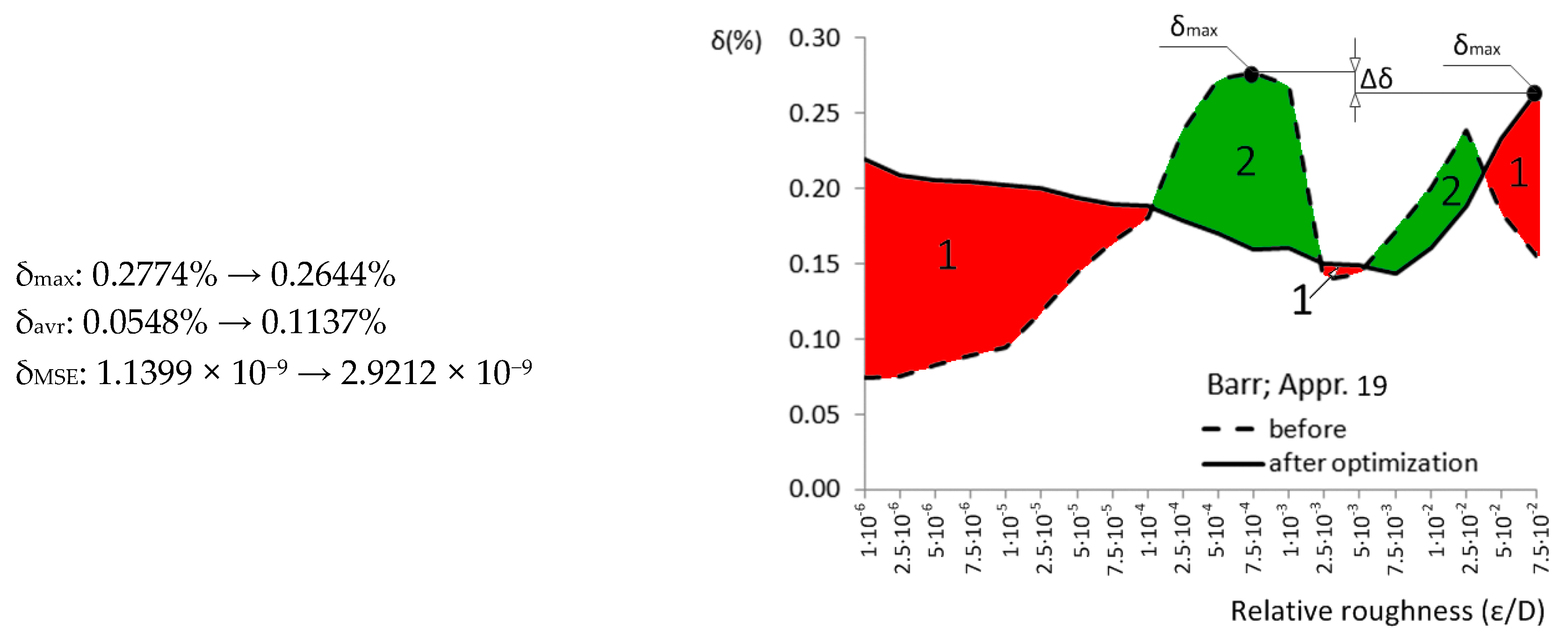
| Appr. 19; Equation (24) | 0.2774% | 0.2644% | not very successful | Barr [33] |
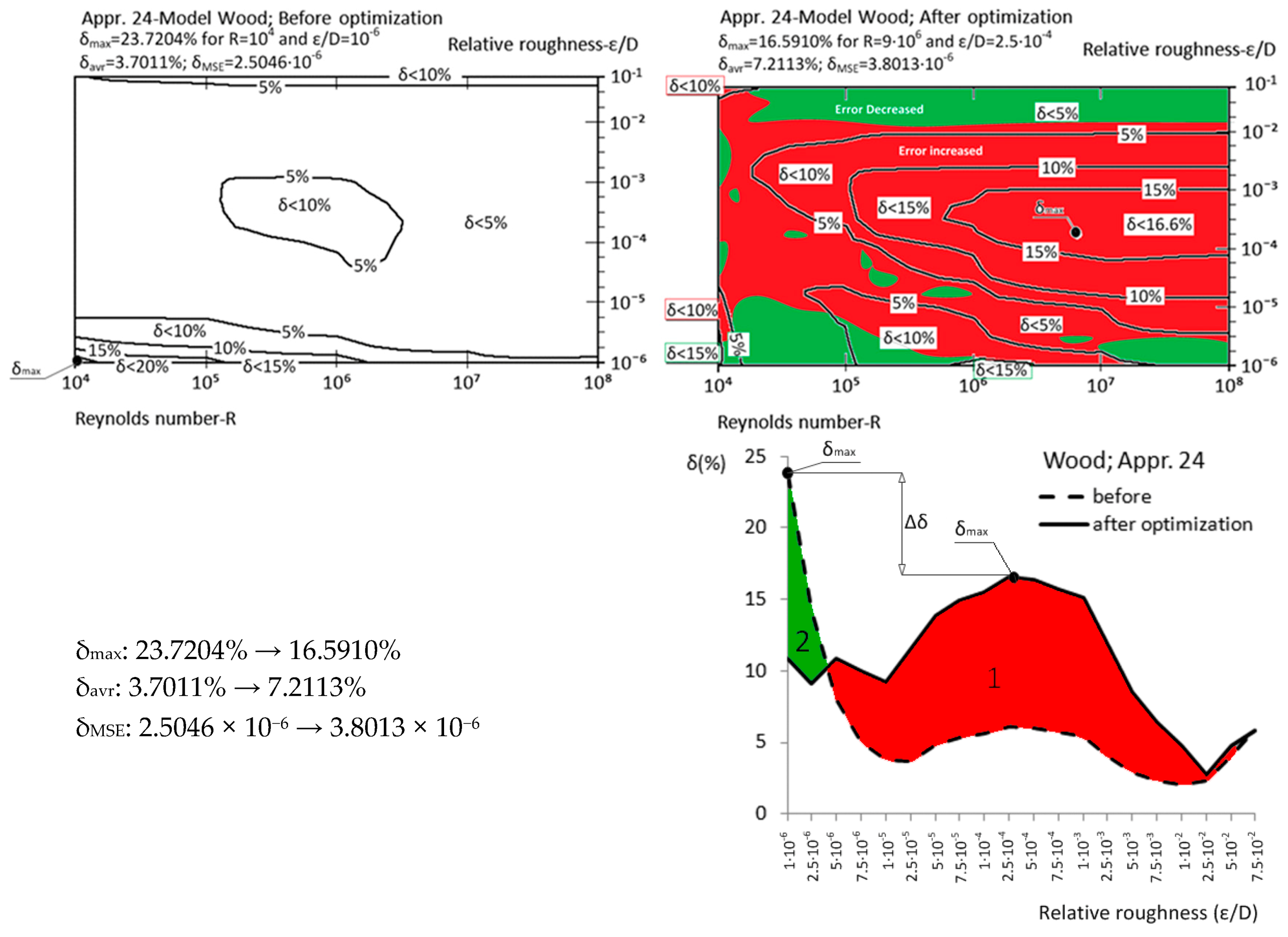
| Appr. 24; Equation (29) | 23.7204% | 16.5910% | not very successful | Wood [39] |
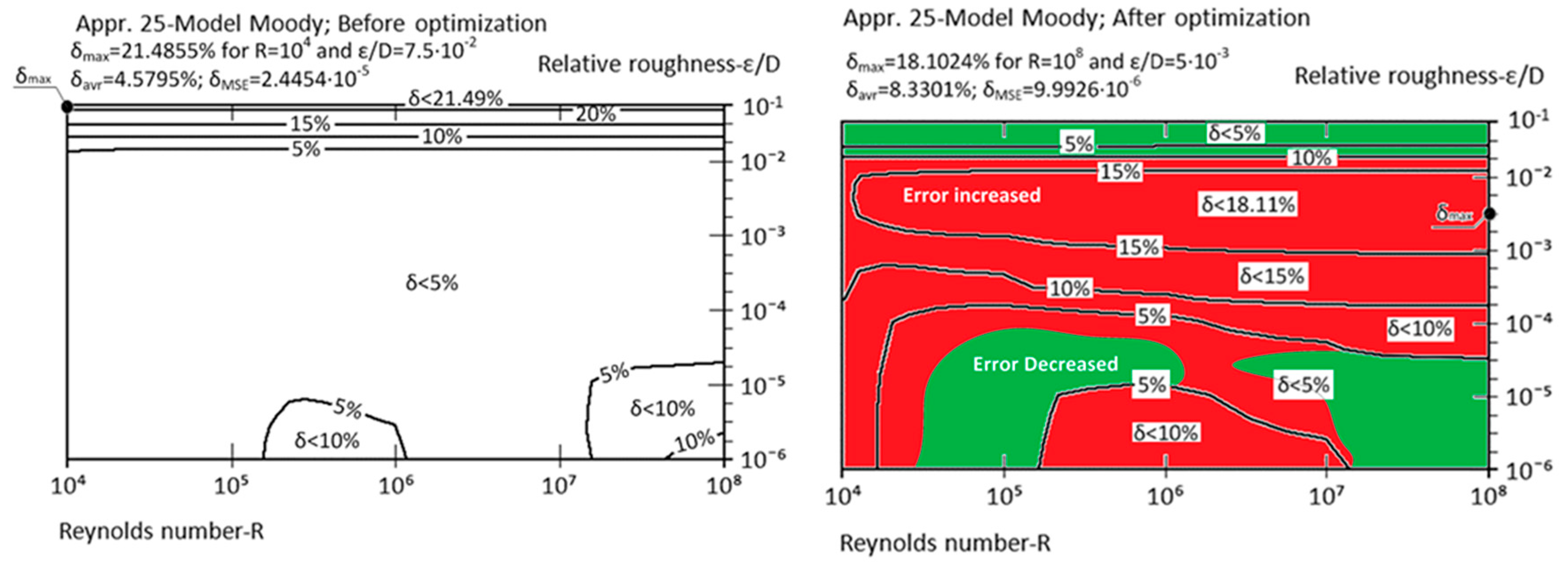
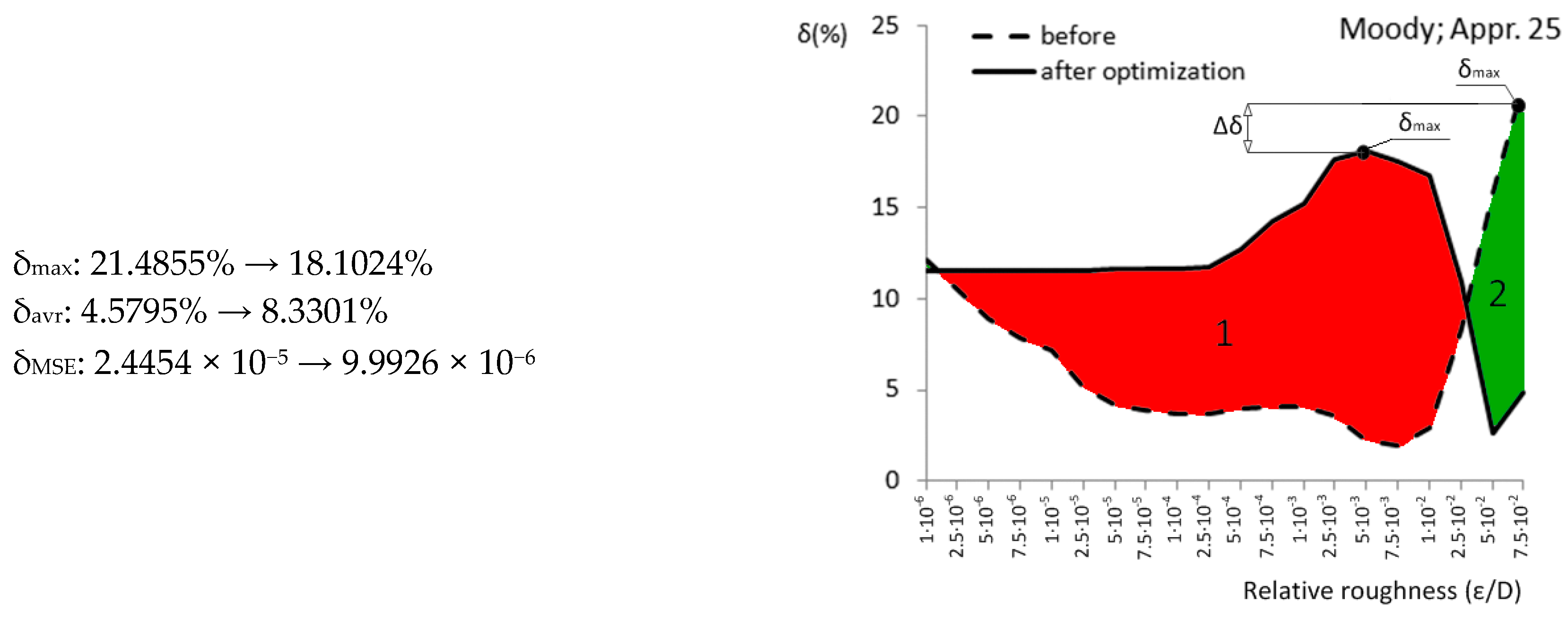
| Appr. 25; Equation (30) | 21.4855% | 18.1024% | not very successful | Moody [40] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brkić, D.; Ćojbašić, Ž. Evolutionary Optimization of Colebrook’s Turbulent Flow Friction Approximations. Fluids 2017, 2, 15. https://doi.org/10.3390/fluids2020015
Brkić D, Ćojbašić Ž. Evolutionary Optimization of Colebrook’s Turbulent Flow Friction Approximations. Fluids. 2017; 2(2):15. https://doi.org/10.3390/fluids2020015
Chicago/Turabian StyleBrkić, Dejan, and Žarko Ćojbašić. 2017. "Evolutionary Optimization of Colebrook’s Turbulent Flow Friction Approximations" Fluids 2, no. 2: 15. https://doi.org/10.3390/fluids2020015
APA StyleBrkić, D., & Ćojbašić, Ž. (2017). Evolutionary Optimization of Colebrook’s Turbulent Flow Friction Approximations. Fluids, 2(2), 15. https://doi.org/10.3390/fluids2020015







