The Influence of the Installation Angle of a Blade’s Low-Pressure Edge on the Cavitation Performance of Francis Pump-Turbines
Abstract
1. Introduction
2. Methodology
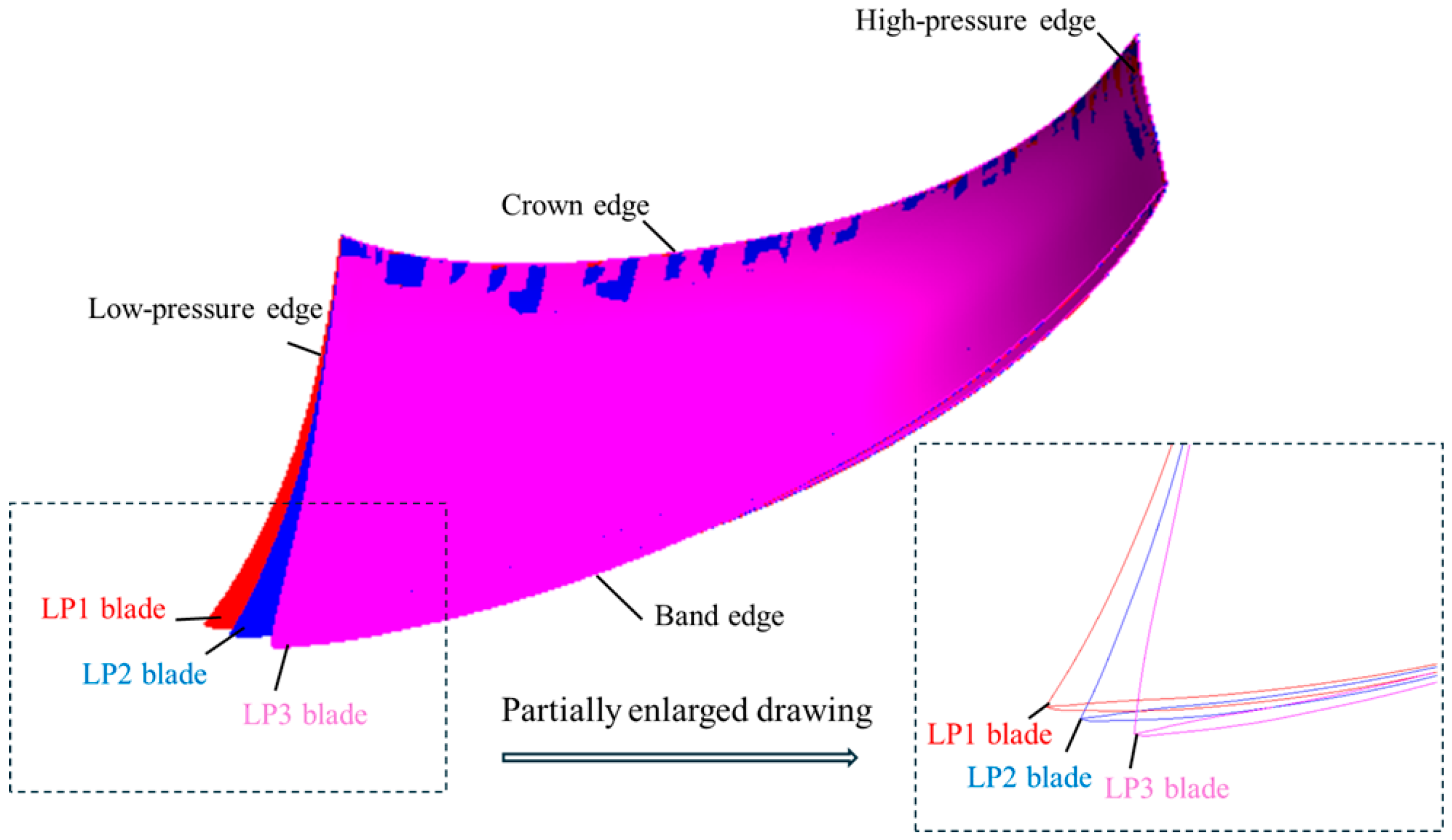
2.1. Blade Design
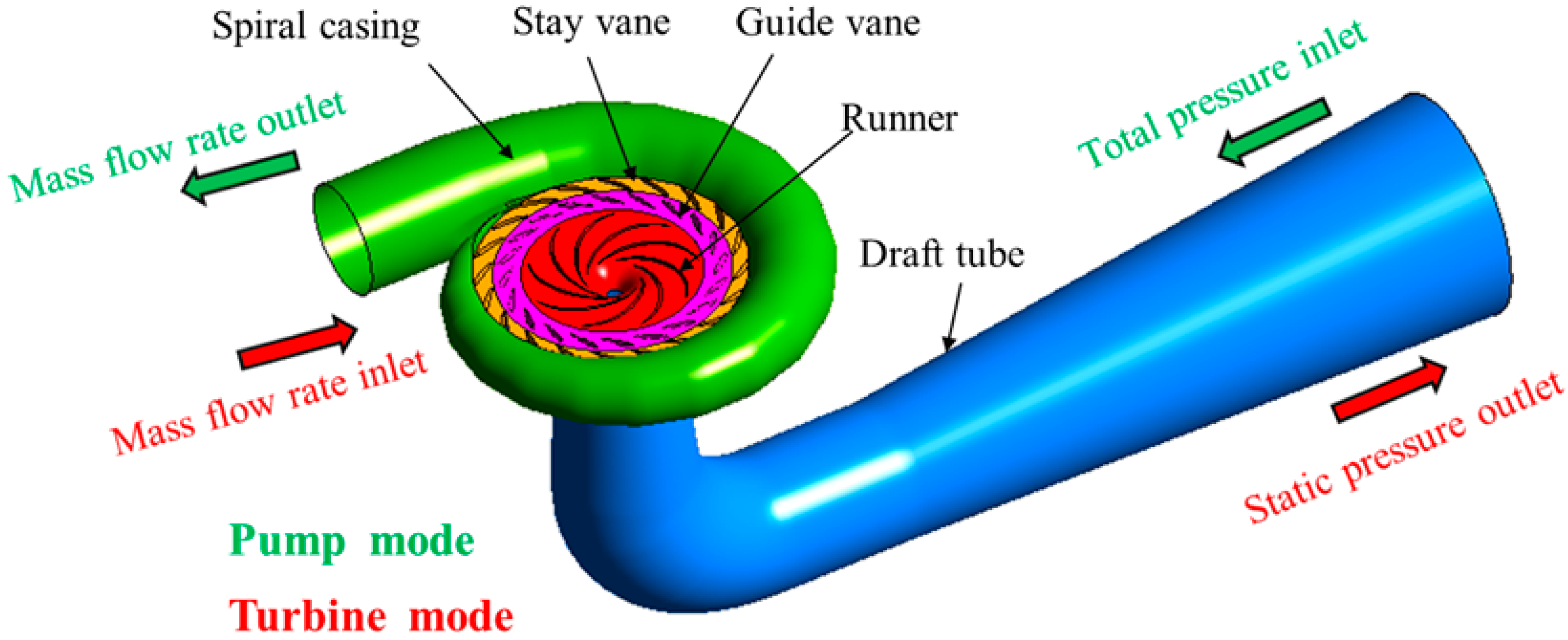
2.2. Numerical Schemes and Boundary Conditions
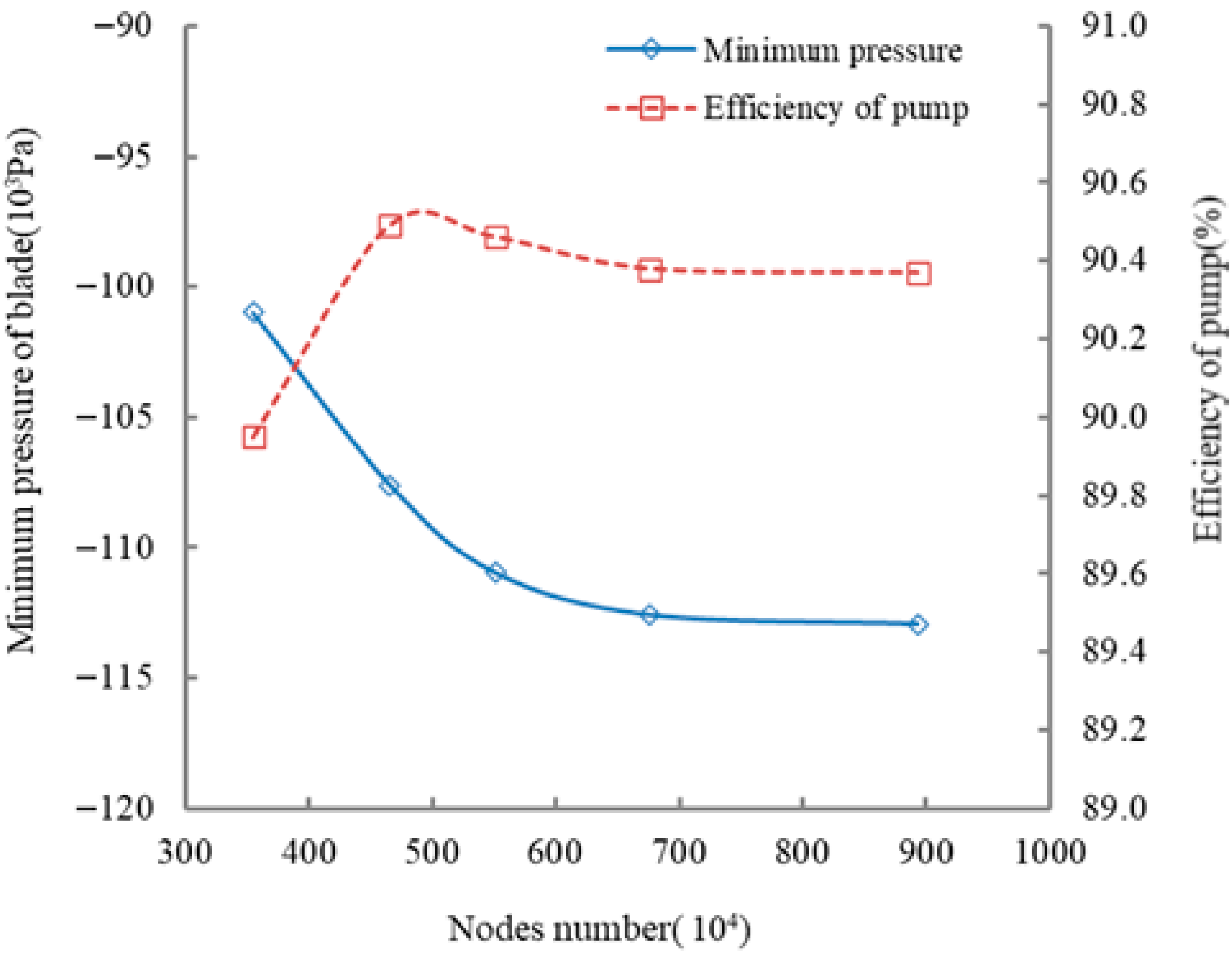
2.3. Grid Generation and Independence Validation
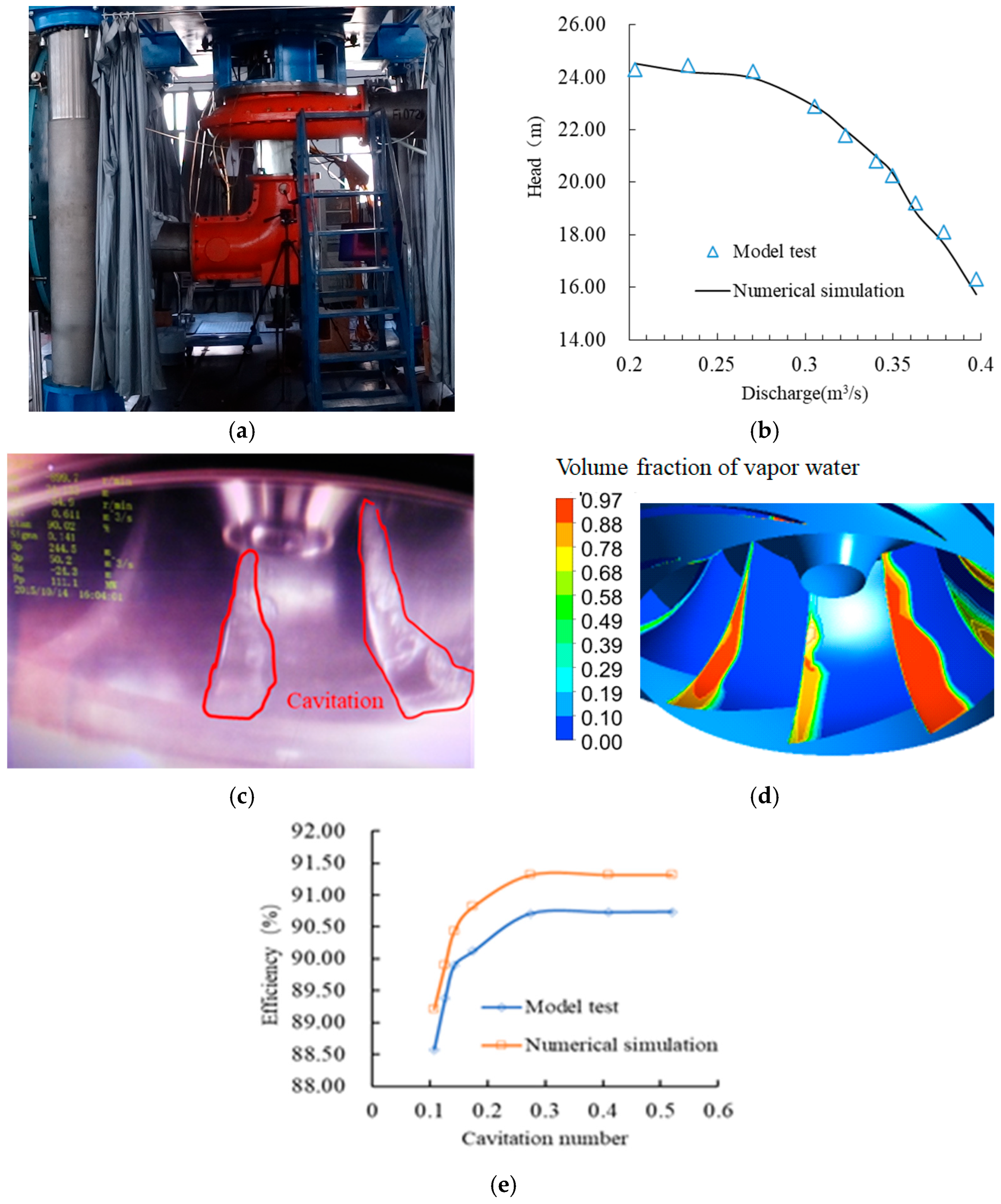
2.4. Experimental Validation
3. Result Analysis and Discussion
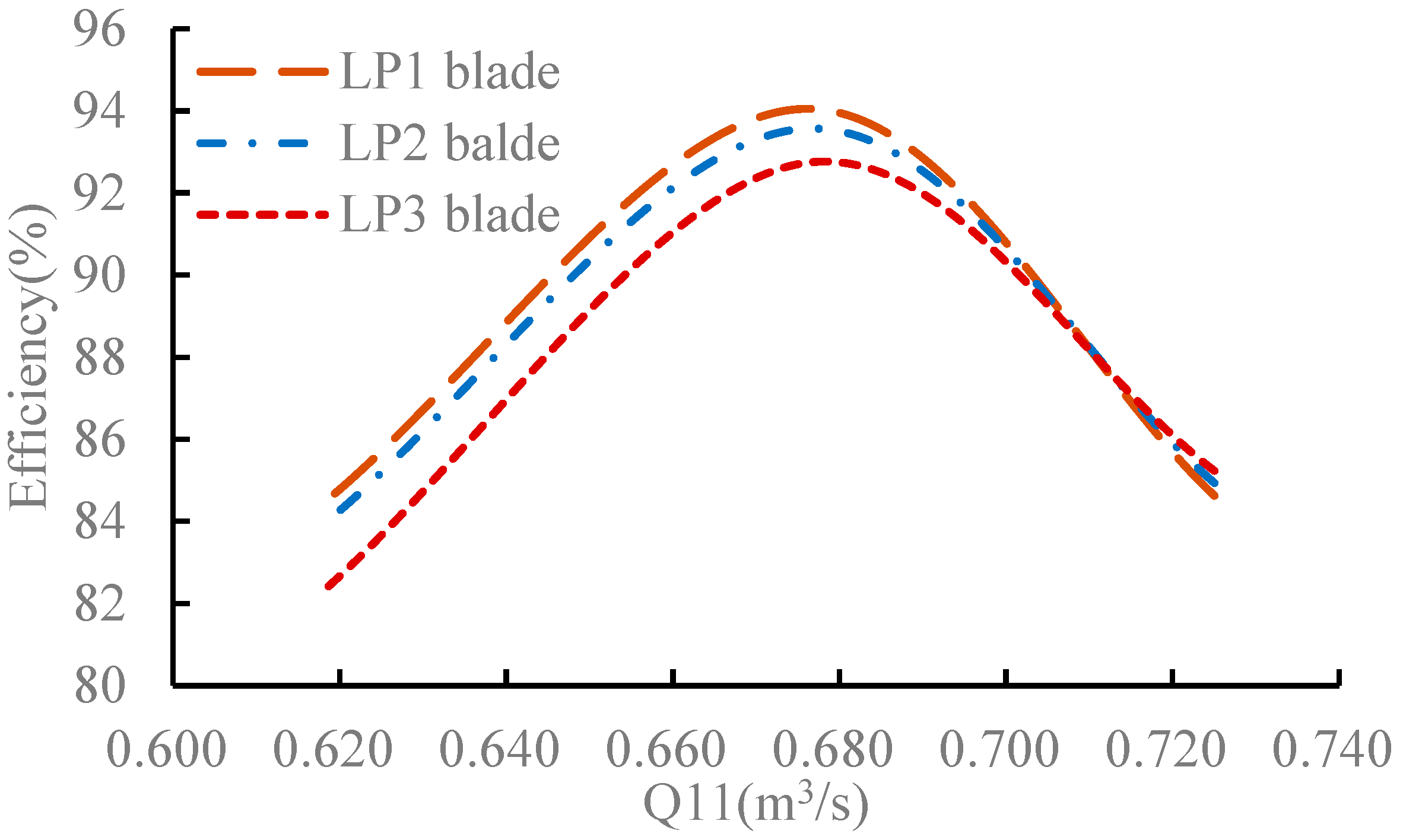
3.1. Comparative Analysis of Energy Performance Under the Turbine Operating Conditions
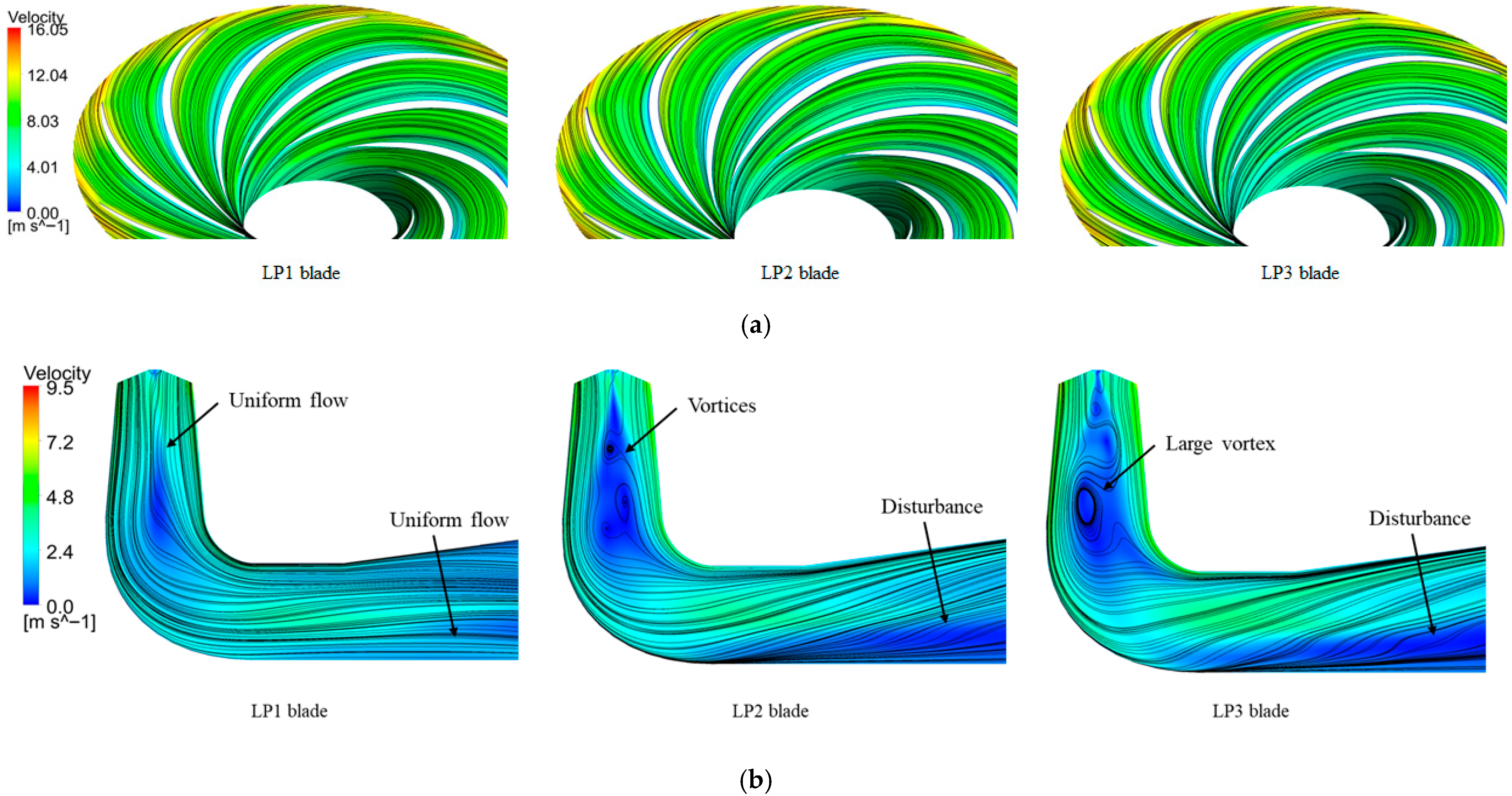
3.2. Comparative Analysis of Flow Characteristics Under the Turbine Operating Conditions
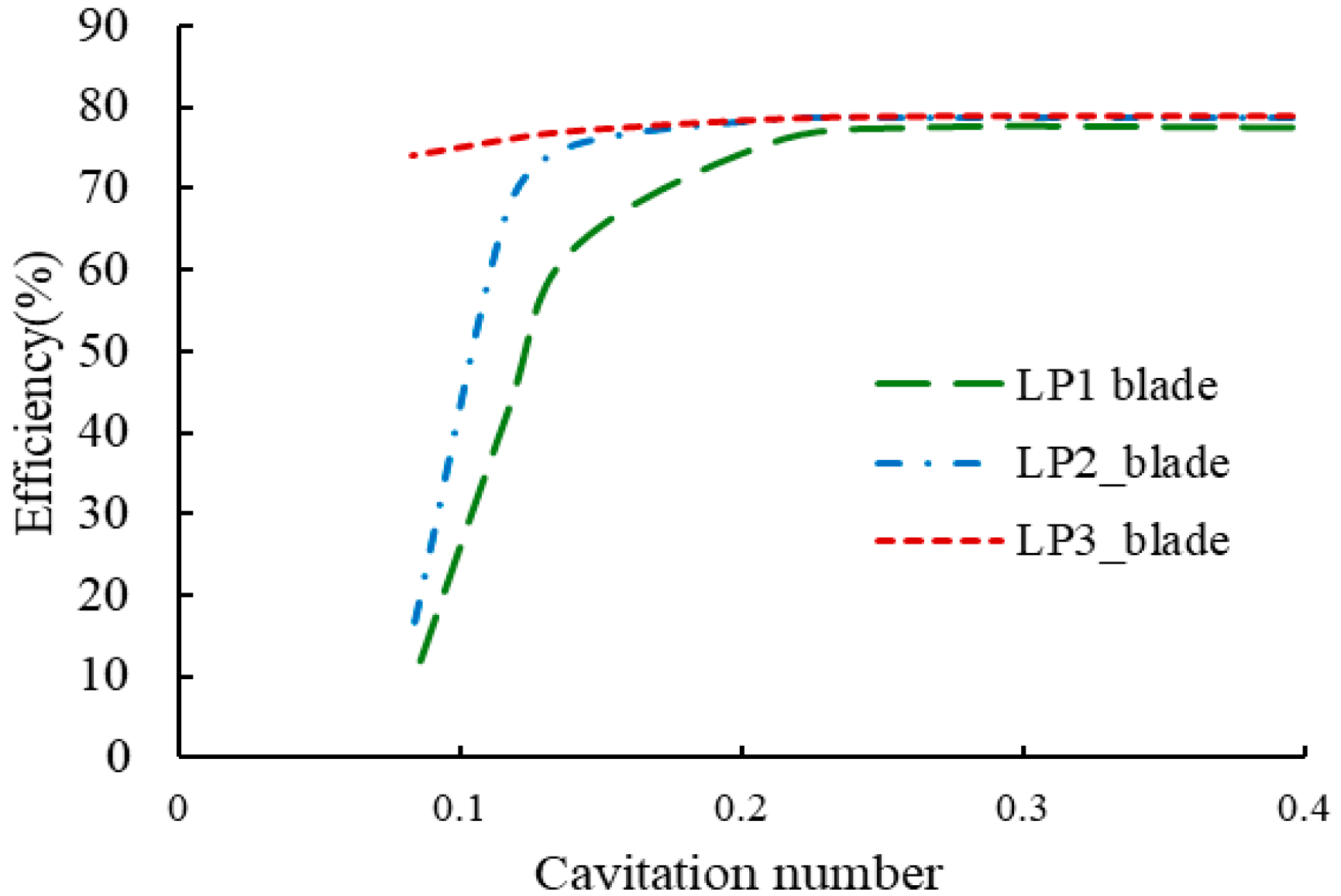
3.3. Comparative Analysis of Cavitation Characteristics Under the Pump Operating Conditions
4. Conclusions
- (1)
- The low-pressure edge blade installation angles have a significant influence on the efficiencies of turbine operations and the internal flow field of the draft tube. The blade design with the LP1 blade installation angle calculated based on the normal outflow design principle can ensure the normal outflow of the runner under the rated turbine operation condition, with uniform internal flow lines in the draft tube and high energy recovery efficiency. It achieves a hydraulic efficiency of 94.05%, indicating that the low-pressure edge installation angle calculated based on the normal outflow principle in this paper is accurate. The installation angles of the LP2 and LP3 blades are slightly increased based on that of the LP1 blade, but this leads to disturbances and vortices in the draft tube; the greater the increase in the low-pressure edge installation angle, the more severe the disturbances and vortices in the draft tube.
- (2)
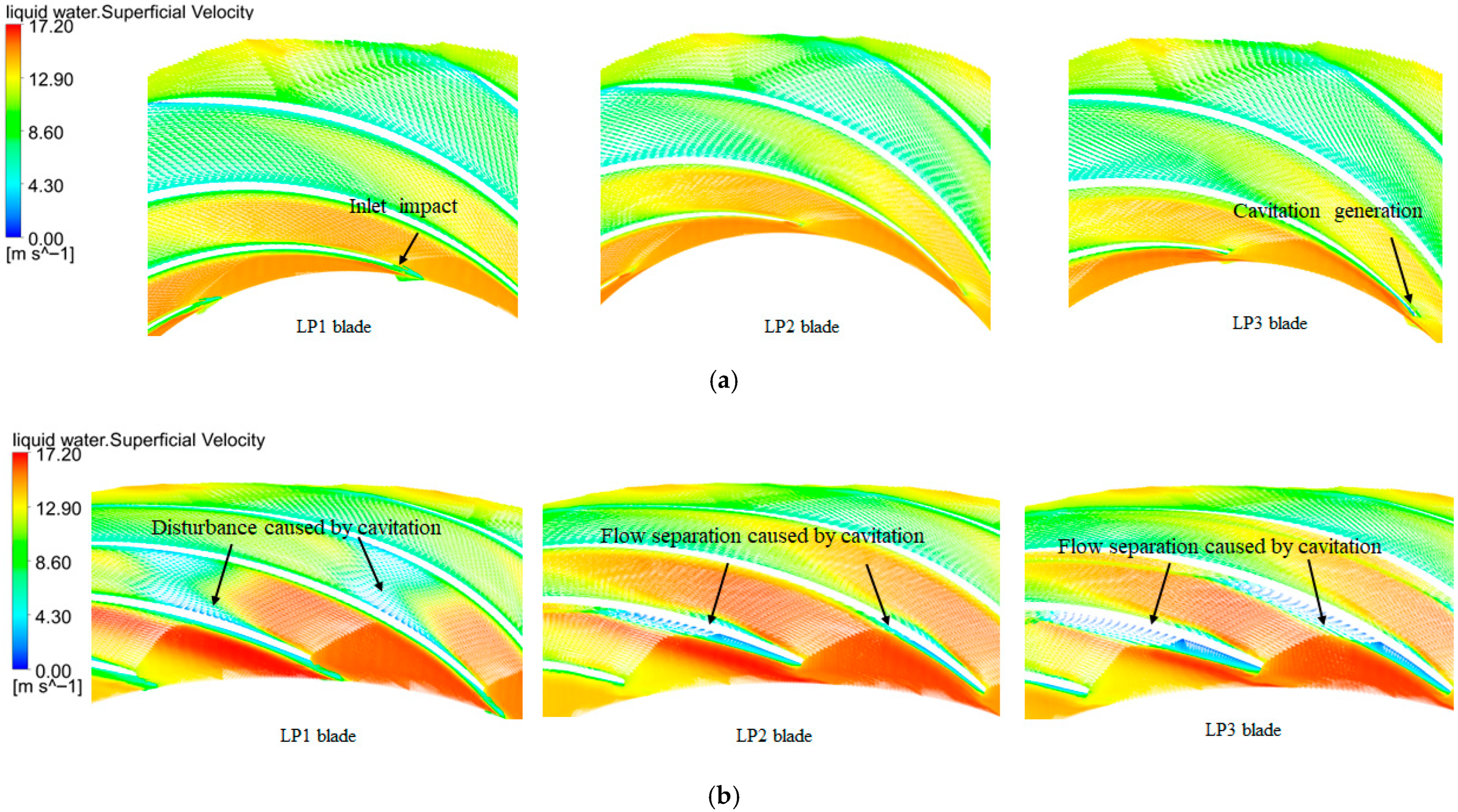
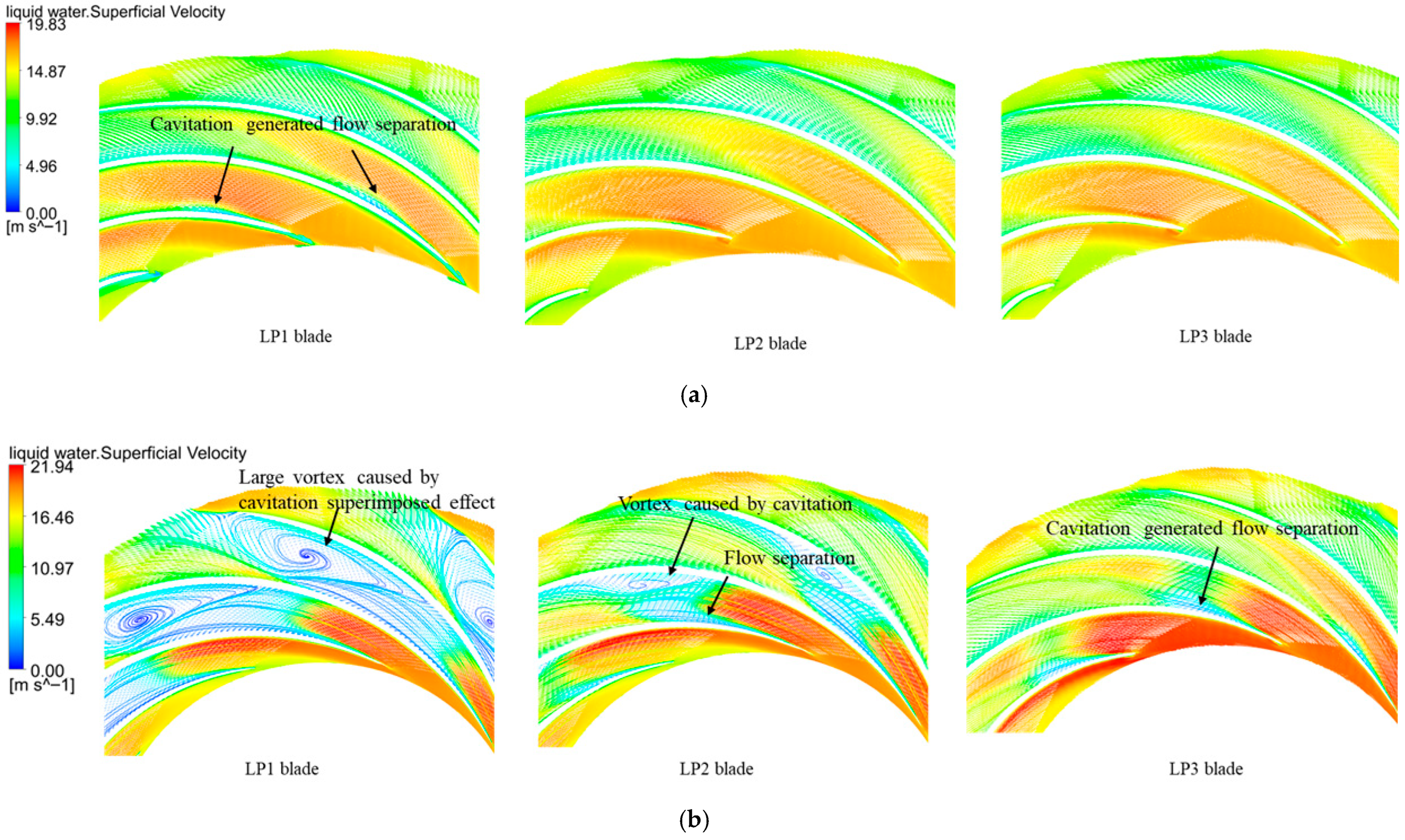
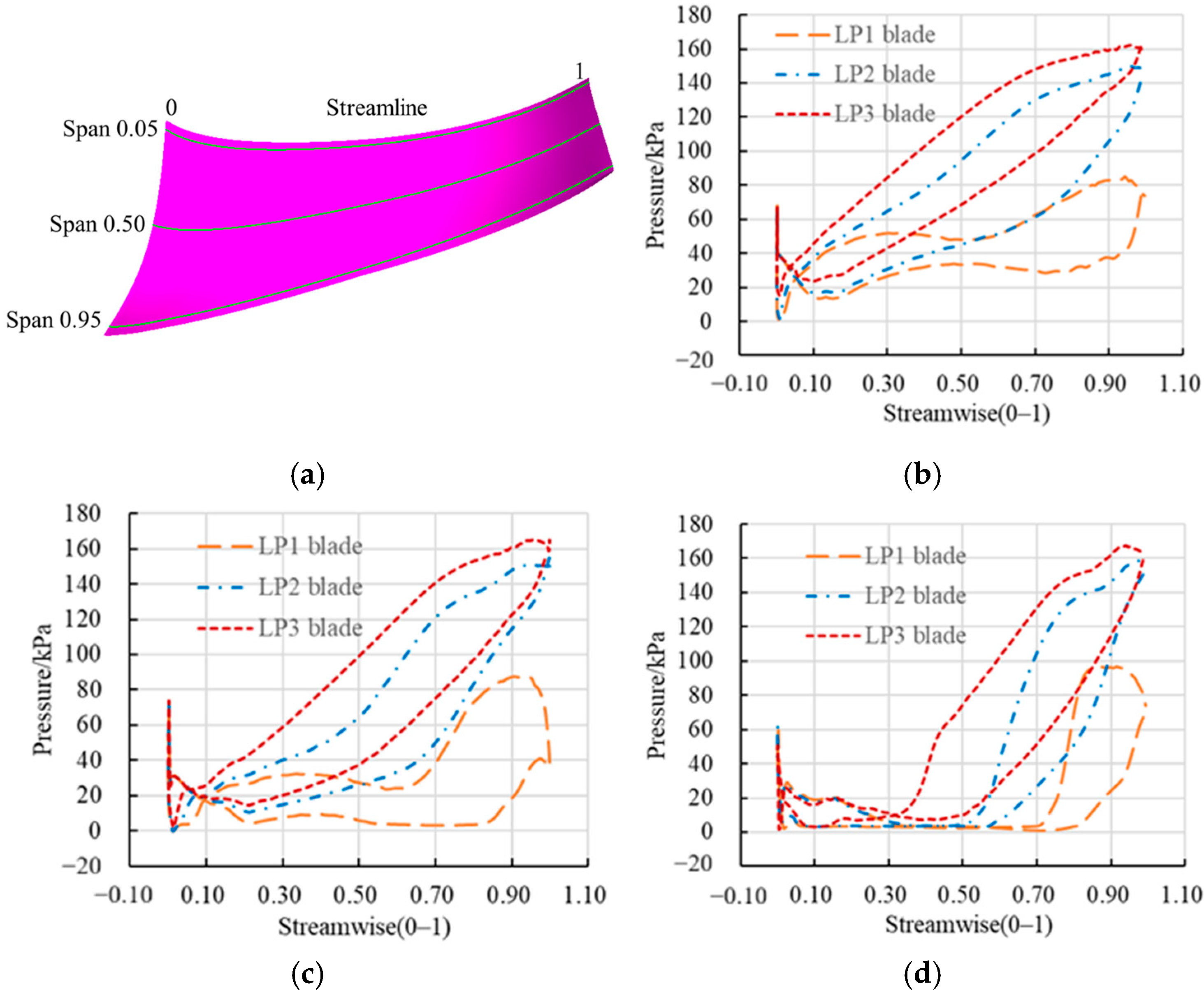
- Although the LP1 blade has high efficiency and a good flow pattern under the rated turbine operating condition, its cavitation performance under the pump operating condition is very poor. This is because the discharge at the pump’s optimal operating condition is generally greater than that at the turbine’s rated operating condition, resulting in the installation angle of LP1 being smaller than the inlet angles of water under the pump’s optimal operating condition. This causes impact and flow separation. Moreover, as the discharge increases, the attack angle of the inflow becomes larger, the impact becomes more intense, and the flow separation becomes more severe, causing a low-pressure area on the blade. Especially under the condition of a low cavitation number, the large areas of low pressure on the blade’s suction surface accelerate water vaporization, and the flow separation on the pressure surface of the adjacent blade produces an additive effect, forming a large vortex, which causes the pump performance to decline rapidly. The LP2 and LP3 blades improve the pump’s inlet conditions by increasing the low-pressure edge blade installation angles and reducing the attack angles under the optimal pump operating condition and large-discharge condition, thereby enhancing the performance under pump operating conditions.
- (3)
- By comparing the cavitation performance of the LP2 and LP3 blades under pump operating conditions, it is found that the improvement effect of LP2’s blade installation angle on cavitation performance under large-discharge conditions is less than that of LP3’s. Through an analysis of the internal flow field, it is discovered that although the installation angle of the LP2 blade has reduced the attack angle of incoming flow and improved the flow separation problem on the blade pressure surface caused by inlet impact, the flow separation problem caused by the pressure decrease on the blade suction surface is not effectively solved. As the cavitation number decreases, the flow separation on the blade pressure surface and that on the suction surface of the adjacent blade form a superimposed effect, resulting in a large-area vortex and hindering water flow. However, the installation angle of the LP3 blade at the band is 1.8° larger than that of the LP2 blade at the band, and the blade wrap angle of the LP3 blade is reduced by 4.65°. This design further reduces the attack angle of incoming flow, reduces flow separation on the blade pressure surface, and mitigates the formation of the low-pressure area in the middle position of the blade suction surface. It effectively avoids the superimposed effect between the flow separation on the blade pressure surface caused by inlet impact and that on the adjacent blade suction surface caused by cavitation-induced low-pressure areas, thereby significantly improving cavitation performance under large-discharge and low cavitation number conditions.
- (4)
- Taking into account the turbine operation efficiency, pump operation efficiency, and pump cavitation performance, the LP3 blade exhibits the best comprehensive performance for the pump-turbine researched in this paper. With the LP1 blade as the reference, although the LP3 blade shows a 1.31% decrease under rated turbine operation, its efficiency in pump design operation increases by 0.48%, and its efficiency in the pump’s large-discharge and high cavitation number operation condition increases by 1.29%. Under this condition, the LP3 blade still maintains an efficiency of 73.96% with a good internal flow state. However, under this condition, the LP1 and LP2 blades could no longer operate due to internal flow field blockage caused by severe internal cavitation. In actual power station operation, the LP3 blade has good cavitation performance, which can reduce unit maintenance downtime and extend the runner’s service life.
- (5)
- The research has found that when designing the blades of a pump-turbine runner, using the traditional method of specifying velocity moment is very complicated. The distribution of velocity moment makes it difficult to simultaneously meet the comprehensive performance requirements of both pump and turbine operating conditions, and it is not easy to determine, with a large trial calculation workload. However, this paper adopts the method of specifying blade installation angle distribution, which is simple and effective. Firstly, the blade installation angle of the low-pressure side is calculated according to the normal outflow principle of the turbine’s rated operating condition; then, the installation angle at the band position (where cavitation is prone to occur) is increased, with a gradual change implemented in the middle section, to obtain the corrected low-pressure edge blade installation angle; finally, the blade design is carried out based on the corrected low-pressure edge blade installation angle. The determination of the increment value requires calculation according to the flow parameters and changes in the blade wrap angle. The research object of this paper is the pump-turbine in the 200 m head section. Within the range of 5° control for blade wrap angle changes, the low-pressure edge blade installation angle is increased by approximately 1 to 2°, and after two trials, a relatively optimal LP3 blade installation angle is obtained. This method can be applied to the research, modification, and optimization of Francis pump-turbine runners.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luo, X.; Zhu, G.; Feng, J. Progress and development trends in hydraulic turbine technology. J. Hydroelectr. Eng. 2020, 39, 1–18. [Google Scholar]
- Wang, L.; Tang, F.P.; Liu, H.Y.; Zhang, X.; Sun, Z.; Wang, F. Investigation of cavitation and flow characteristics of tip clearance of bi directional axial flow pump with different clearances. Ocean. Eng. 2023, 288, 115960. [Google Scholar] [CrossRef]
- Liu, H.Y.; Tang, F.P.; Shi, L.J.; Dai, L.; Shen, J.; Liu, J. The analysis of cavitation flow and pressure pulsation of bi-directional pump. J. Mar. Sci. Eng. 2023, 11, 268. [Google Scholar] [CrossRef]
- Liu, T.; Feng, C.; Yang, M.; Tao, J.; Zhu, H. Experimental investigation on cavitation induced noise and vibration characteristics of mixed-flow pump model. Fluid Mach. 2023, 51, 7–12. [Google Scholar]
- Tao, Y.; Qian, Y.; Xiang, X. Reaserch and Repair Applcation on Cavitation Erosion of Runner Blades in Shitang Power Statio. Large Mot. Technol. 2023, 5, 77–89. [Google Scholar]
- Kang, W.; Zhou, L.; Wang, Z. Analysis of flow characteristics and cavitation in the vanes of a reversible pump-turbine in pump mode. J. Energy Storage 2023, 68, 690–699. [Google Scholar] [CrossRef]
- Yang, W. Cavitation Characteristics of Pump Turbine in High Head Pumped Storage Power Station; Xi’an University of Thechnology: Xi’an, China, 2017. [Google Scholar]
- Zhang, J. Study on Cavitation Characteristics of the Pump-Turbine Under Partial Load Condition; Lanzhou University of Technology: Lanzhou, China, 2017. [Google Scholar]
- Qian, X. Research on the Effect Mechanism of Pump’s Pulsation Characteristics and Cavitation Characteristics on Blades Stress; Shanghai Jiao Tong University: Shaihai, China, 2020. [Google Scholar]
- Ruan, H.; Guo, P.; Yu, L.; Zhou, C.; Chao, W.; Li, X. Cavitation induced flow instability mechanism of pump-turbine under pump conditions. J. Drain. Irrig. Mach. Eng. 2023, 41, 779–786. [Google Scholar]
- Tao, R.; Zhou, X.; Xu, B. Numerical investigation of the flow regime and cavitation in the vanes of reversible pump-turbine during pump mode’s starting up. Renew. Energy 2019, 141, 9–19. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhang, Y.; Zhang, J.; Zhu, J. Experimental studies of unsteady cavitation at the tongue of a pump-turbine in pump mode. Renew. Energy 2021, 177, 1265–1281. [Google Scholar] [CrossRef]
- Wu, Y.; Zhu, D.; Tao, R.; Xiao, R.; Liu, W. Analysis of two-phase flow in cavitation condition of pump-turbine based on dynamic mode decomposition method in turbine mode. J. Energy Storage 2022, 56, 107–113. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Yuan, Z.; Ji, K. Development and application of the entropy production diagnostic model to the cavitation flow of a pump-turbine in pump mode. Renew. Energy 2020, 154, 774–785. [Google Scholar] [CrossRef]
- Cao, J.; Luo, Y.; Presas, A. Numerical analysis on the modal characteristics of a pumped storage unitrunner in cavitating flow. J. Energy Storage 2022, 56, 105998–106010. [Google Scholar] [CrossRef]
- Li, Q.; Chen, X.; Meng, Q.; Cai, T.; Zhou, F.; Wei, X. Analysis of Correlation Characteristics of Pump-turbine under Different Cavitation Numbers. Trans. Chin. Soc. Agric. Mach. 2020, 51, 130–138. [Google Scholar]
- Li, Q.; Zhang, J.; Liu, M.; Liu, Q. Analysis of the Internal Cavitation Characteristics of a Reversible Turbine under the Pump Condition. Therm. Energy Power Eng. 2017, 32, 84–89. [Google Scholar]
- Li, D.; Zhu, Y.; Lin, S.; Gong, R.; Wang, H.; Luo, X. Cavitation effects on pressure fluctuation in pump-turbine hump region. J. Energy Storage 2022, 47, 936–945. [Google Scholar] [CrossRef]
- Lu, G.; Zuo, Z.; Sun, Y. Experimental evidence of cavitation influences on the positive slope on the pump performance curve of a low specific speed model pump-turbine. Renew. Energy 2017, 113, 1539–1550. [Google Scholar] [CrossRef]
- Fu, X.; Li, D.; Wang, H. Cavitation mechanism and effect on pump power-trip transient process of apumped-storage unit. J. Energy Storage 2023, 66, 405–457. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, D.; Shao, Y. Simulation of Load Rejection Transition Process of Pump Turbine Based on Cavitation. J. Eng. Thermophys. 2023, 44, 2106–2111. [Google Scholar]
- Shang, C. Cavitation Effect on the S-Shaped Characteristics of Pump-Turbine; Harbin Institute of Technology: Harbin, China, 2020. [Google Scholar]
- Song, L. Study on the Influence of Cavitation on The Hump Characteristics of Pump-Turbine; Harbin Institute of Technology: Harbin, China, 2019. [Google Scholar]
- Liang, Y.; Ma, Y.; Zhou, L.; Liu, Y. New Developments in the Research of Wear-Resistant Coatings for Hydraulic Machinery. J. Beijing Univ. Civ. Eng. Archit. 2025, 41, 123–127. [Google Scholar]
- Li, Y.; Yang, W.; Zheng, Z.; Zhang, T.; Li, J. Cavitation Characteristics of Optimized Runner in ShaHe Pumped Storage Power Station. J. Northeast. Electr. Power Univ. 2021, 41, 82–89. [Google Scholar]
- Hu, Z.; Cheng, Y.; Liu, D.; Chen, H.; Ji, B.; Ding, J. Broadening the operating range of pump-turbine to deep-part load by runner optimization. Renew. Energy 2023, 207, 73–88. [Google Scholar] [CrossRef]
- Ni, N.; Lai, X.; Li, P. Effects of low-pressure edges of short blades on cavitation performance of pump-turbine. J. Hydroelectr. Eng. 2019, 38, 97–105. [Google Scholar]
- Tao, R.; Xiao, R.; Wang, F.; Liu, W. Improving the cavitation inception performance of a reversible pump-turbine in pump mode by blade profile redesign, design concept, method and applications. Renew. Energy 2019, 133, 325–342. [Google Scholar] [CrossRef]
- Zhu, D.; Xiao, R.; Liu, W. Influence of leading-edge cavitation on impeller blade axial force in the pump mode of reversible pump-turbine. Renew. Energy 2021, 163, 939–949. [Google Scholar] [CrossRef]
- Ruan, H.; Liao, W.; Luo, X.; Zhao, Y.; Qin, H.; Yang, Z. Effects of low-pressure meridional position on cavitation performance for high-head pump-turbine. Trans. Chin. Soc. Agric. Eng. 2016, 32, 73–81. [Google Scholar]
- Ruan, H.; Luo, X.; Liao, W.; Zhao, Y. Effects of low-pressure edge thickness on cavitation performance and strength for pump-turbine. Trans. Chin. Soc. Agric. Eng. 2015, 31, 32–39. [Google Scholar]
- International Electrotechnical Comission. Hydraulic Turbines, Storage Pumps and Pump-Turbines Model Acceptance Tests; International standard IEC: Geneva, Switzerland, 1999. [Google Scholar]
- Ruan, H. Performance Analysis and Optimization for High-Head Pump-Turbine Considering the Compressibility of Water; Xi’an University of Technology: Xi’an, China, 2018. [Google Scholar]
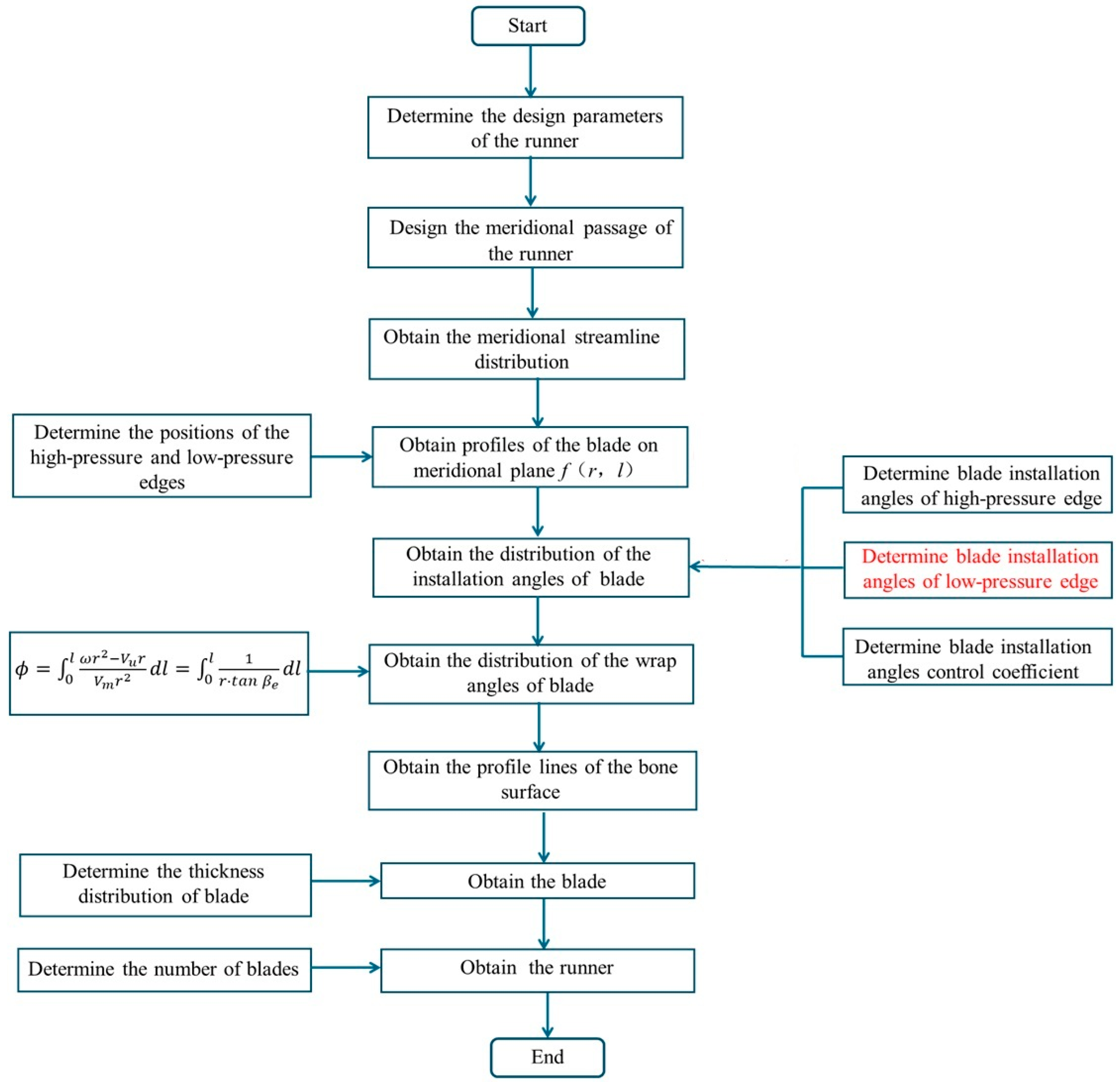
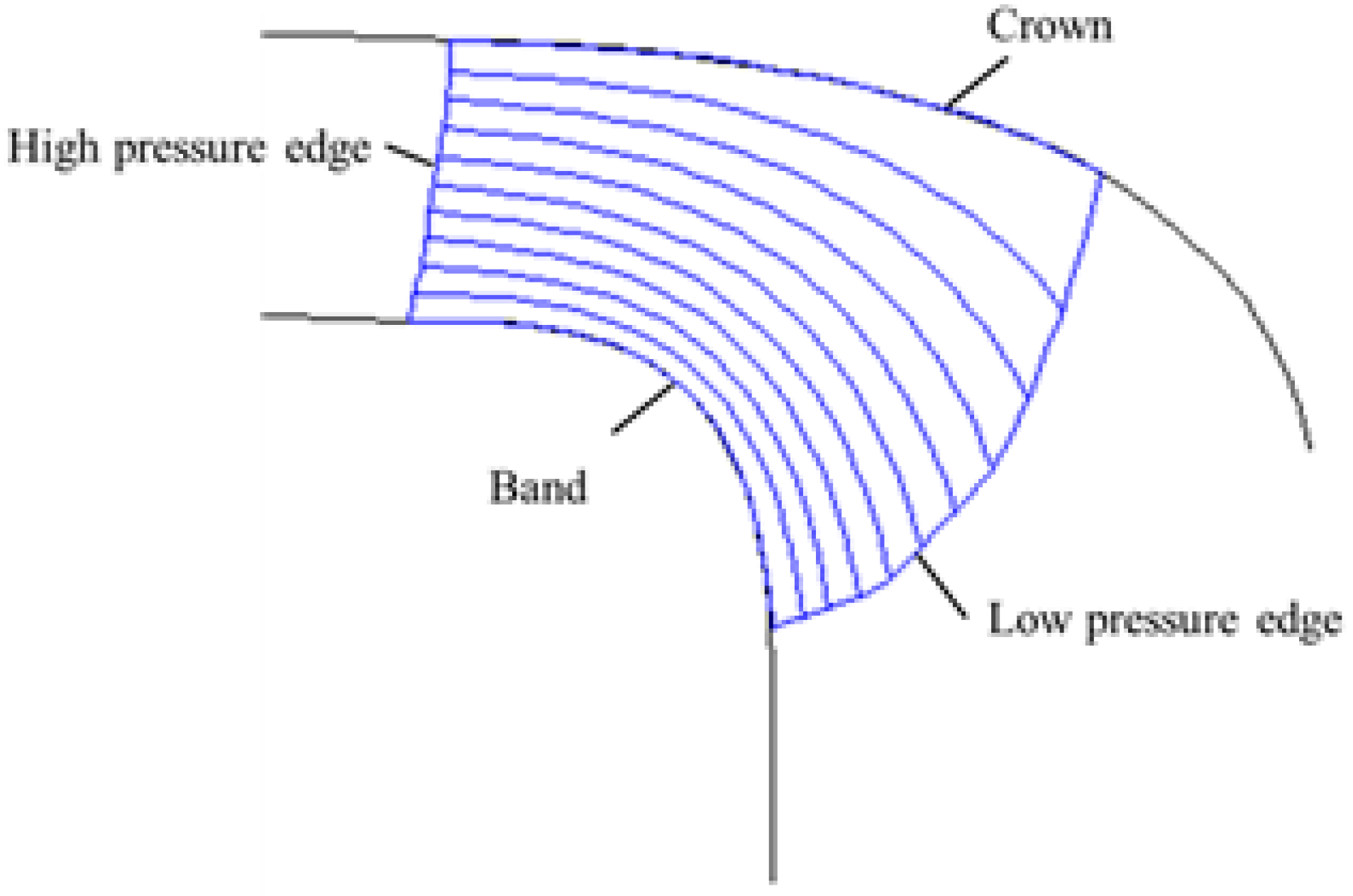
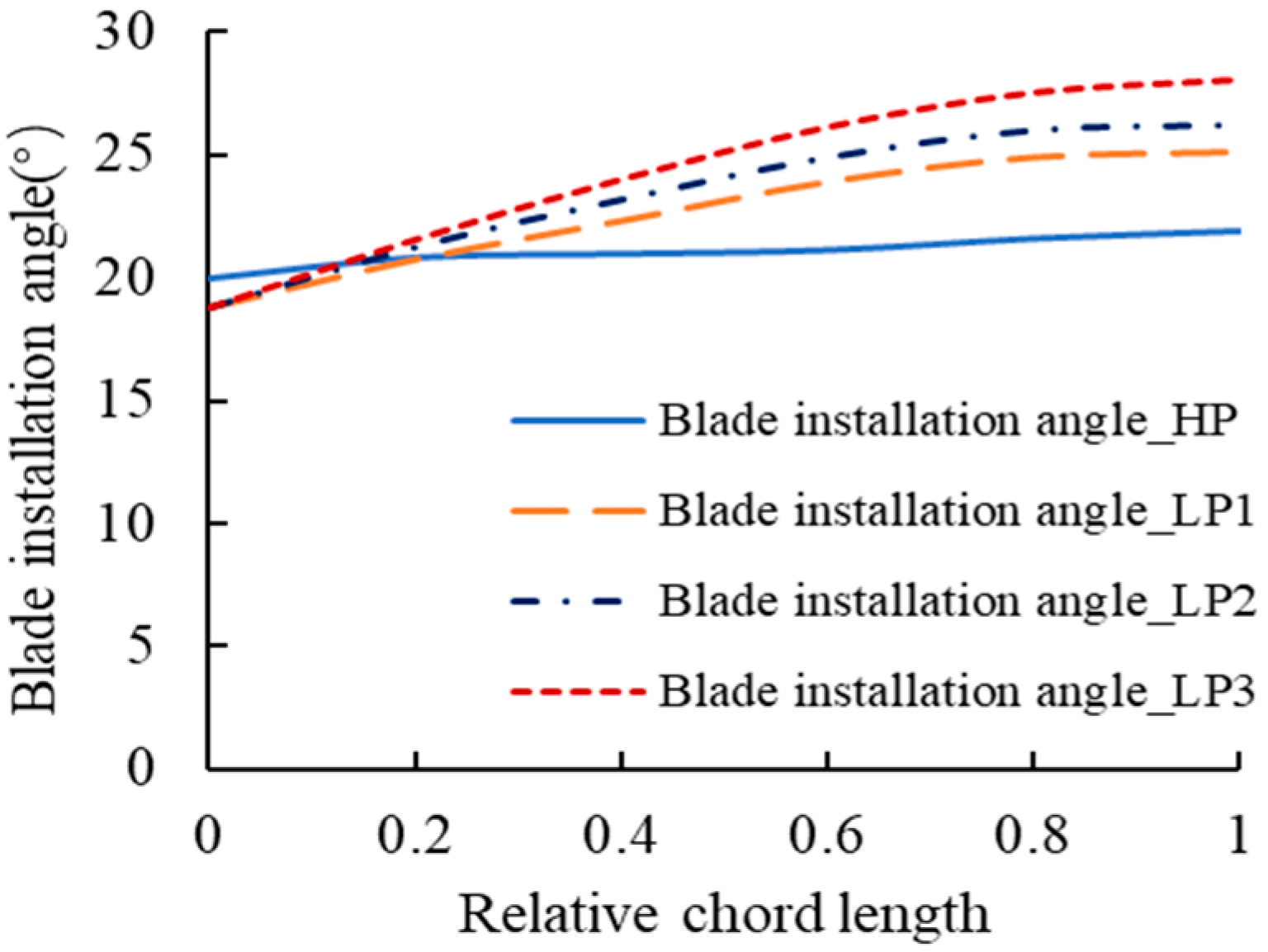
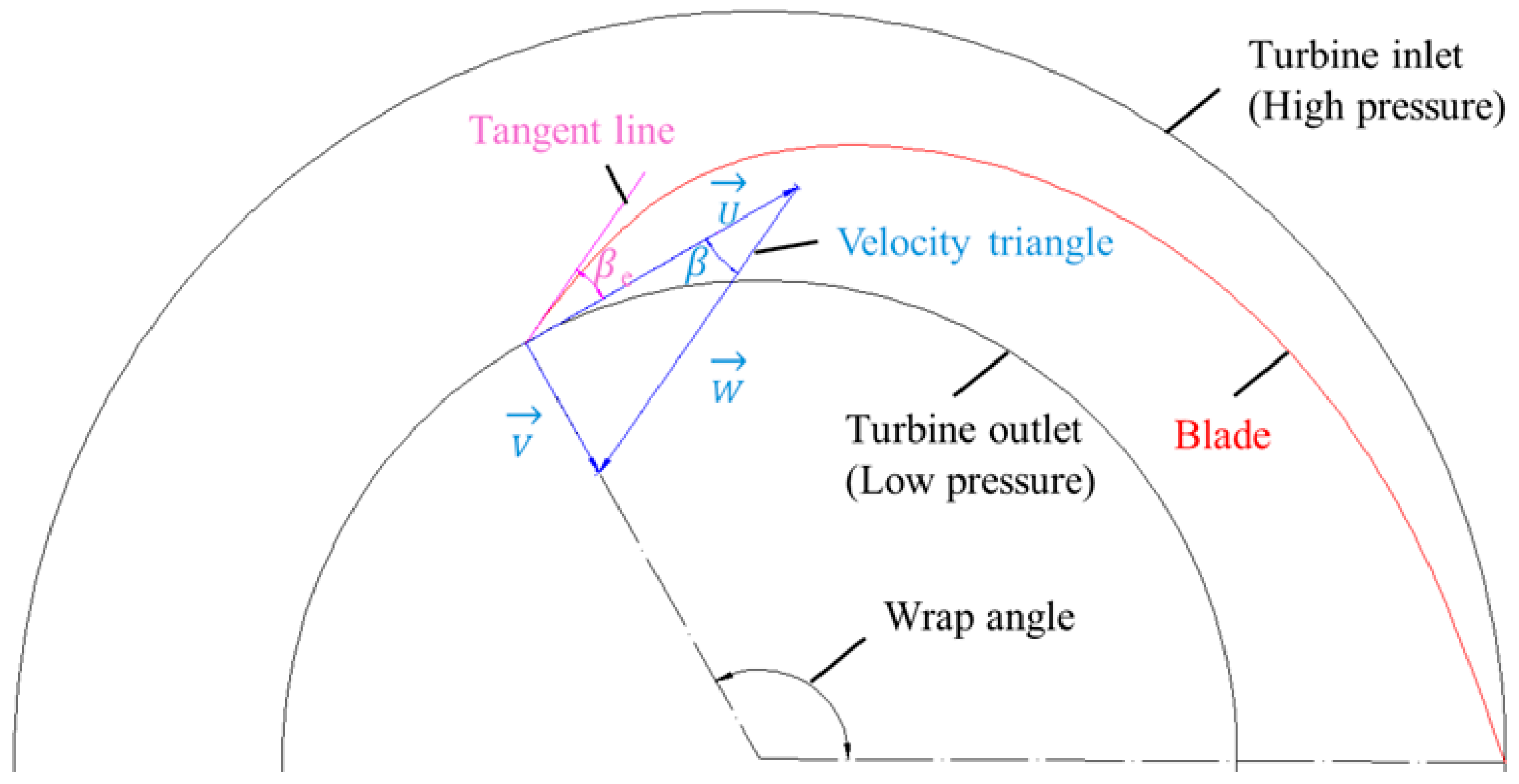





| Parameter | Value |
|---|---|
| Maximum head of the turbine | 214.7 m |
| Rated head of the turbine | 190.0 m |
| Minimum head of the turbine | 160.0 m |
| Maximum head of the pump | 216.7 m |
| Minimum head of the pump | 163.7 m |
| Operating Condition | Speed | Guide Vane Opening | Discharge | Cavitation Number of Device |
|---|---|---|---|---|
| nm (r/min) | αm (°) | Qm (m3/s) | σp | |
| OP4 | −900 | 22 | 0.32279 | 0.288 |
| OP5 | −900 | 22 | 0.37889 | 0.319 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, H.; Chao, W.; Li, X.; Zhang, Q.; Qing, L.; Wei, C. The Influence of the Installation Angle of a Blade’s Low-Pressure Edge on the Cavitation Performance of Francis Pump-Turbines. Fluids 2025, 10, 248. https://doi.org/10.3390/fluids10090248
Ruan H, Chao W, Li X, Zhang Q, Qing L, Wei C. The Influence of the Installation Angle of a Blade’s Low-Pressure Edge on the Cavitation Performance of Francis Pump-Turbines. Fluids. 2025; 10(9):248. https://doi.org/10.3390/fluids10090248
Chicago/Turabian StyleRuan, Hui, Wenxiong Chao, Xiangyang Li, Qingyang Zhang, Lvjun Qing, and Chunmei Wei. 2025. "The Influence of the Installation Angle of a Blade’s Low-Pressure Edge on the Cavitation Performance of Francis Pump-Turbines" Fluids 10, no. 9: 248. https://doi.org/10.3390/fluids10090248
APA StyleRuan, H., Chao, W., Li, X., Zhang, Q., Qing, L., & Wei, C. (2025). The Influence of the Installation Angle of a Blade’s Low-Pressure Edge on the Cavitation Performance of Francis Pump-Turbines. Fluids, 10(9), 248. https://doi.org/10.3390/fluids10090248






