CFD Analysis of Non-Isothermal Viscoelastic Flow of HDPE Melt Through an Extruder Die
Abstract
1. Introduction
2. Mathematical Modelling
2.1. Assumptions
2.1.1. Fluid Properties and Behavior
- The polymer melt (HDPE) is treated as an incompressible, viscoelastic fluid;
- The flow follows the Oldroyd-B constitutive model to capture viscoelastic effects;
- The effect of thermal radiation is neglected, assuming it has a negligible contribution compared to conduction and convection, under the present operating conditions.
2.1.2. Simulation and Geometry
- The study is conducted in 2D for computational efficiency, while preserving flow characteristics;
- The extruder die is simplified as a steady-state flow problem;
- The mesh resolution is optimized based on a grid independence study.
2.1.3. Boundary Conditions and Temperature Effects
- Constant inlet velocity is assumed at the extruder entrance;
- The inner and outer die walls are maintained at constant temperatures with no-slip boundary conditions.
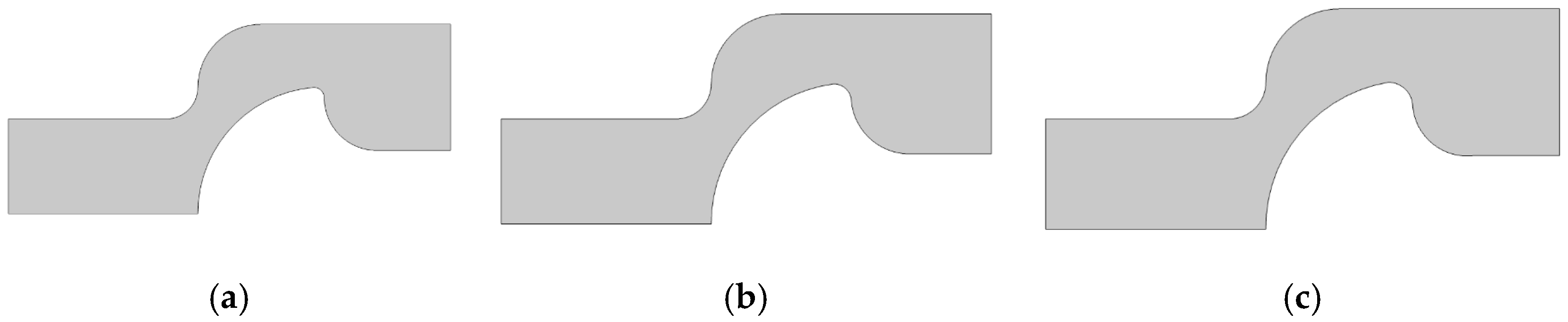
2.2. Die Geometry
2.2.1. Oldroyd-B Model
2.2.2. Weissenberg Numbers
2.3. Dimensionless Parameters
2.4. Numerical Methodology
2.5. Boundary Conditions
2.5.1. Viscoelastic Flow
2.5.2. Heat Transfer
2.6. Numerical Model Validation
3. Result and Discussion
3.1. Simulated Multi-Field Analysis
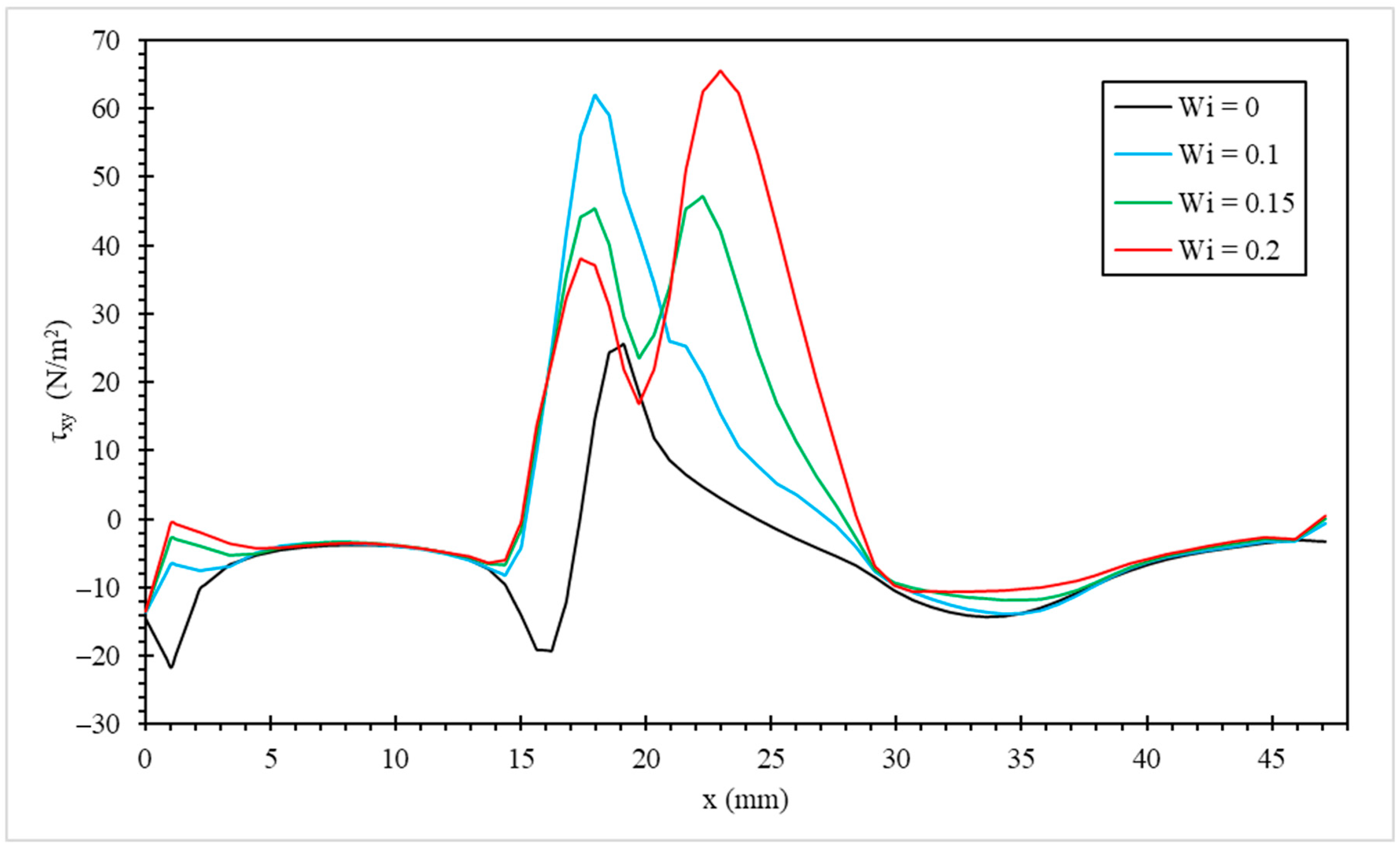
3.2. Effect of Weissenberg Number
3.3. Parametric Study
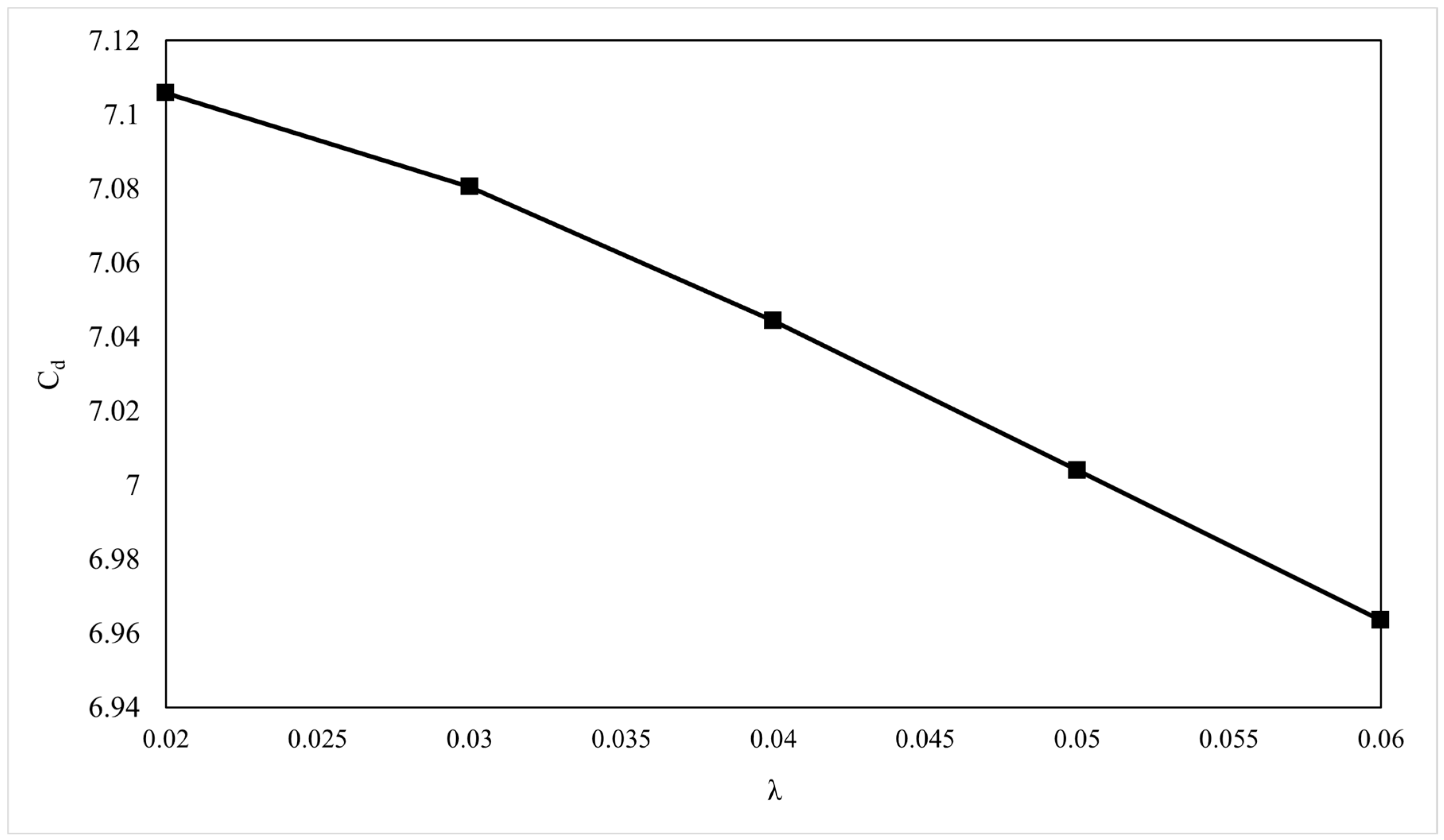
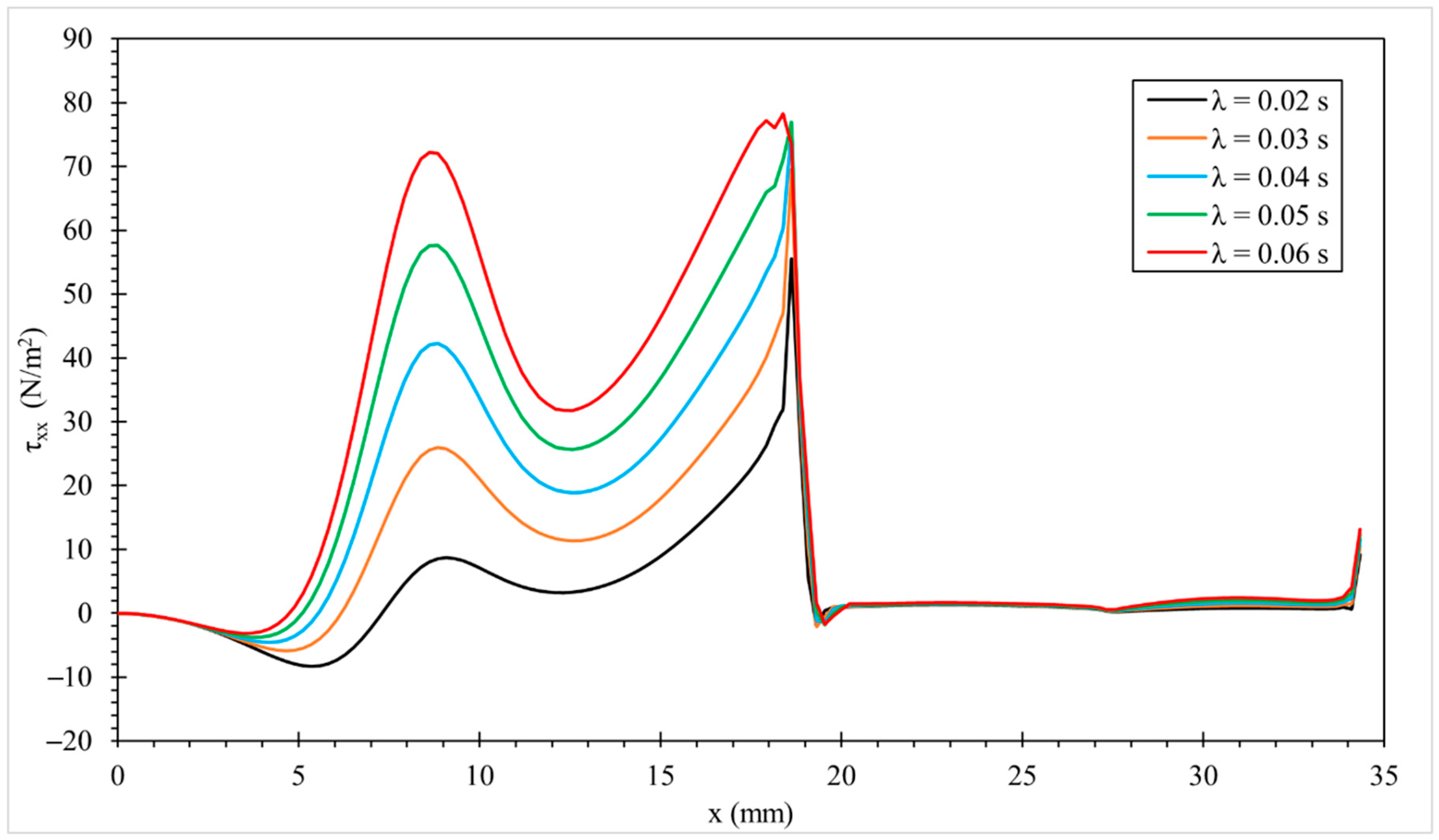
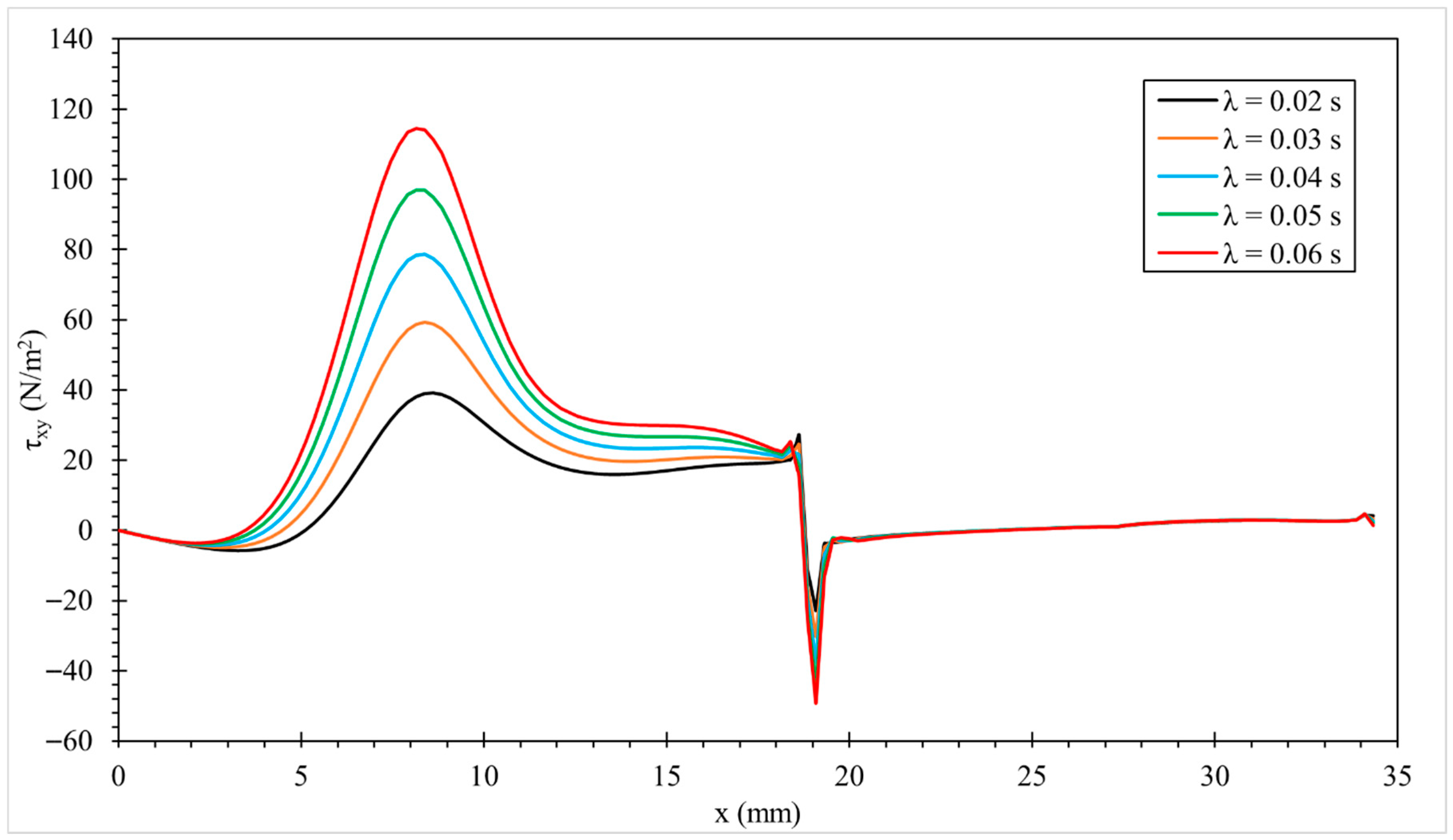
3.3.1. Effect of the Characteristic Relaxation Time (λ)
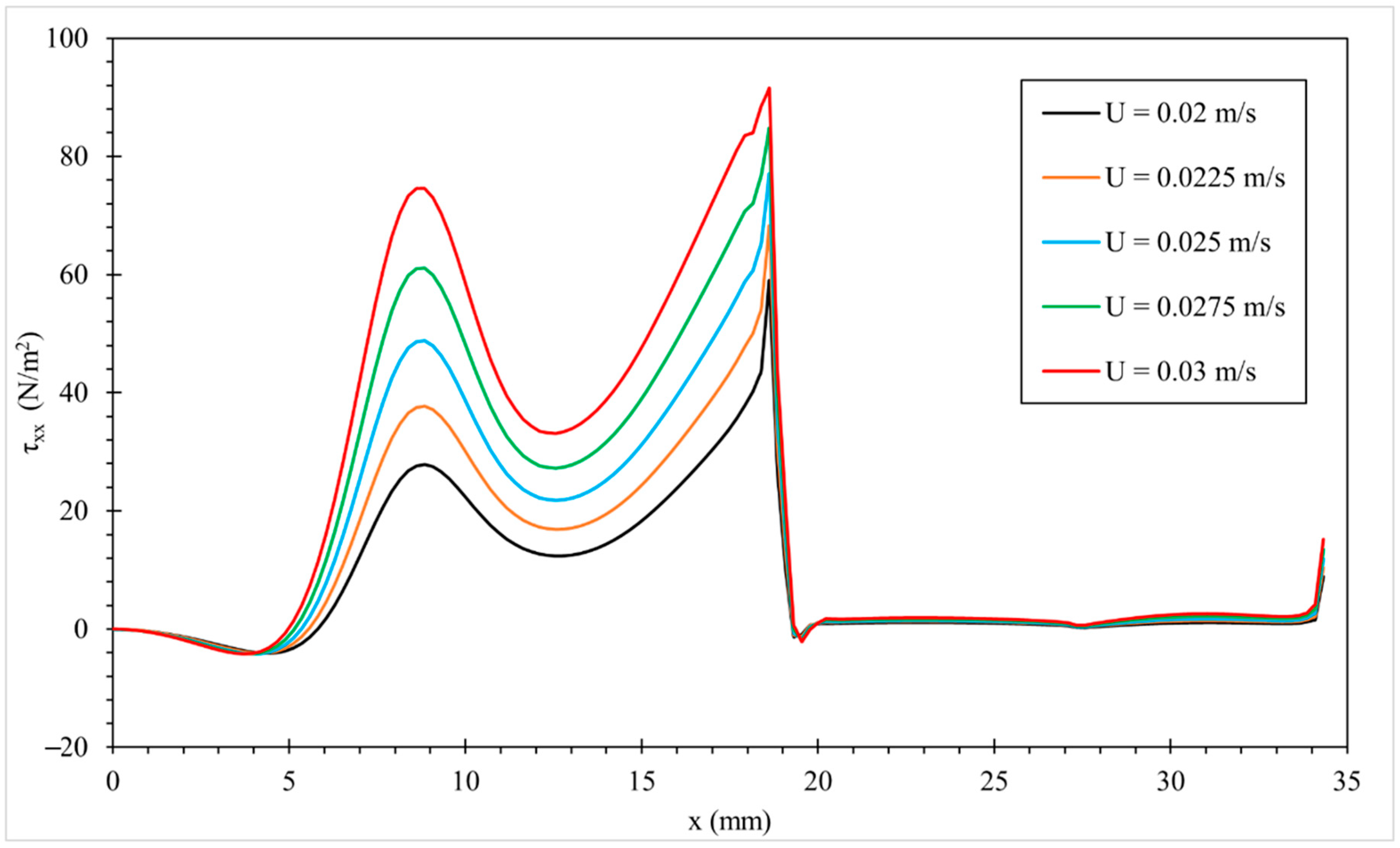
3.3.2. Effect of Inlet Velocity
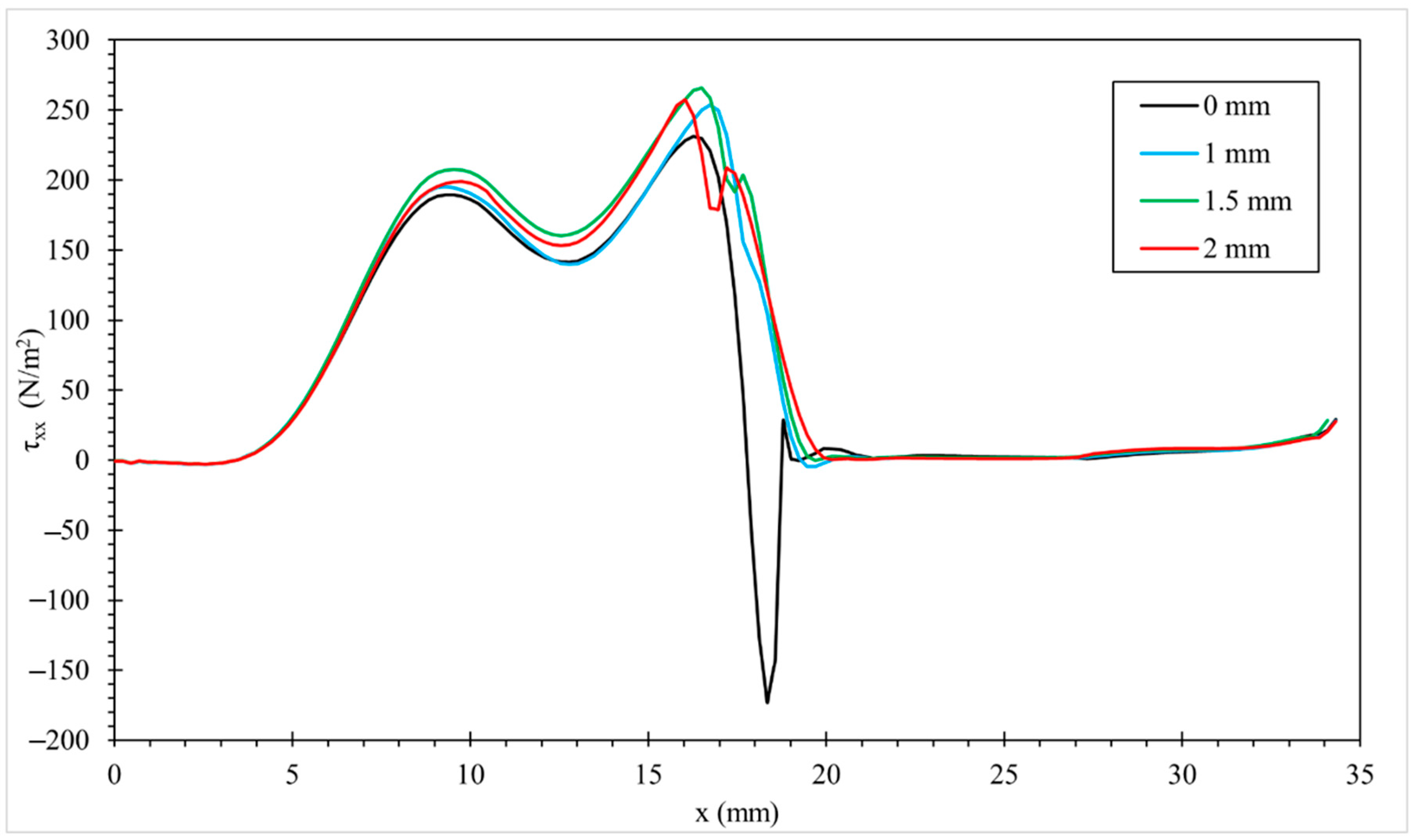
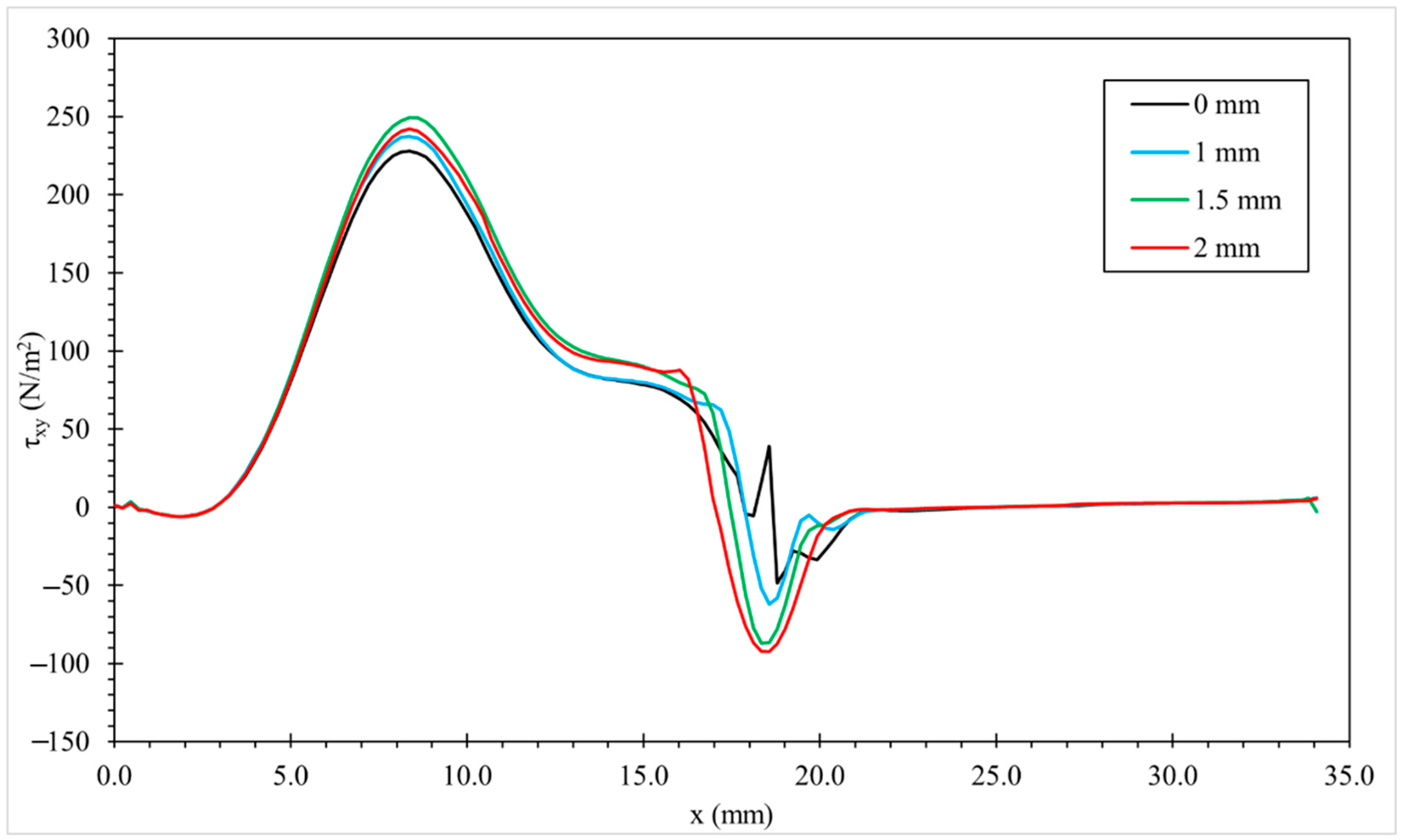
3.3.3. Effect of Geometry
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Cd | dimensionless drag coefficient |
| Cp | specific heat capacity, J/(Kg·K) |
| Dij | components of the rate of the deformation tensor, 1/s |
| radius length scale at the die inlet of flow geometry, m | |
| P | pressure, Pa |
| Qvd | viscous dissipation heat, W/m3 |
| velocity component, m/s | |
| average velocity, m/s | |
| T | temperature, K |
| Wi | Weissenberg number |
| β | relative solvent viscosity with respect to total viscosity |
| strain rate, 1/s | |
| η | viscosity, N·s/m2 |
| ηs | solvent viscosity, N·s/m2 |
| ηp | polymer viscosity, N·s/m2 |
| λ | relaxation time, s |
| ρ | density, Kg/m3 |
| τxx | normal stress, N/m2 |
| τxy | shear stress, N/m2 |
| polymeric part of the extra stress tensor, N/m2 |
References
- Ishtiaq, F.; Ellahi, R.; Bhatti, M.M.; Anwar, M. Convective heat transfer with Hall current using magnetized non-Newtonian Carreau fluid model on the cilia-attenuated flow. Int. J. Numer. Methods Heat Fluid Flow 2024, 34, 3328–3354. [Google Scholar] [CrossRef]
- Schreiber, H.P.; Rudin, A.; Bagley, E.B. Separation of elastic and viscous effects in polymer melt extrusion. J. Appl. Polym. Sci. 1965, 9, 887–892. [Google Scholar] [CrossRef]
- Carella, J.M.; Graessley, W.W.; Fetters, L.J. Effects of chain microstructure on the viscoelastic properties of linear polymer melts: Polybutadienes and hydrogenated polybutadienes. Macromolecules 1984, 17, 2775–2786. [Google Scholar] [CrossRef]
- Graessley, W.W. Effect of long branches on the temperature dependence of viscoelastic properties in polymer melts. Macromolecules 1982, 15, 1164–1167. [Google Scholar] [CrossRef]
- Abeykoon, C.; Pérez, P.; Kelly, A.L. The effect of materials’ rheology on process energy consumption and melt thermal quality in polymer extrusion. Polym. Eng. Sci. 2020, 60, 1244–1265. [Google Scholar] [CrossRef]
- Cha, J.; Song, H.Y.; Hyun, K.; Kim, S.; Lee, Y. Rheological measurement of the nonlinear viscoelasticity of the ABS polymer and numerical simulation of thermoforming process. Int. J. Adv. Manuf. Technol. 2020, 107, 2449–2464. [Google Scholar] [CrossRef]
- Liao, Z.; Hossain, M.; Yao, X.; Li, H.; Zhou, D. On thermo-viscoelastic experimental characterization and numerical modelling of VHB polymer. Int. J. Non-Linear Mech. 2020, 118, 103263. [Google Scholar] [CrossRef]
- Janardhana Reddy, G.; Kumar, M.; Anwar Beg, O. Effect of temperature dependent viscosity on entropy generation in transient viscoelastic polymeric fluid flow from an iso-thermal vertical plate. Physica A 2018, 510, 426–445. [Google Scholar] [CrossRef]
- Ansari, M.; Hatzikiriakos, S.G.; Mitsoulis, E. Slip effects in HDPE flows. J. Non-Newton. Fluid Mech. 2012, 167–168, 18–29. [Google Scholar] [CrossRef]
- Debbaut, B. Non-isothermal and viscoelastic effects in the squeeze flow between infinite plates. J. Non-Newton. Fluid Mech. 2001, 98, 15–31. [Google Scholar] [CrossRef]
- Mu, Y.; Zhao, G.; Qin, S.; Li, X.; Wang, J. Numerical simulation of three-dimensional polymer extrusion flow with differential viscoelastic model. Polym. Adv. Technol. 2007, 18, 1004–1014. [Google Scholar] [CrossRef]
- Mu, Y.; Zhao, G.; Wu, X.; Li, H. Modeling and simulation of three-dimensional planar contraction flow of viscoelastic fluids with PTT, Giesekus and FENE-P constitutive models. Appl. Math. Comput. 2012, 218, 8429–8443. [Google Scholar] [CrossRef]
- Cao, W.; Shen, Y.; Wang, P.; Liu, Q. Viscoelastic modeling and simulation for polymer melt flow in injection/compression molding. J. Non-Newton. Fluid Mech. 2019, 274, 104186. [Google Scholar] [CrossRef]
- Wan, R.; Zhang, H.; Liu, Q. Some new global results to the incompressible Oldroyd-B model. Z. Angew. Math. Phys. 2019, 70, 28. [Google Scholar] [CrossRef]
- Barrett, J.W.; Boyaval, S. Existence and approximation of a (regularized) Oldroyd-B model. Math. Models Methods Appl. Sci. 2011, 21, 1783–1837. [Google Scholar] [CrossRef]
- Bush, M.B. A numerical study of extrudate swell in very dilute polymer solutions represented by the Oldroyd-B model. J. Non-Newton. Fluid Mech. 1990, 34, 15–24. [Google Scholar] [CrossRef]
- Fan, Y.; Tanner, R.I.; Phan-Thien, N. Galerkin/least-square finite-element methods for steady viscoelastic flows. J. Non-Newton. Fluid Mech. 1999, 84, 233–256. [Google Scholar] [CrossRef]
- Alves, M.A.; Pinho, F.T.; Oliveira, P.J. The flow of viscoelastic fluids past a cylinder: Finite-volume high-resolution methods. J. Non-Newton. Fluid Mech. 2001, 97, 207–232. [Google Scholar] [CrossRef]
- Xiong, Y.L.; Bruneau, C.H.; Yang, D. Numerical study on viscoelastic fluid flow past a rigid body. Appl. Math. Model. 2017, 42, 188–208. [Google Scholar] [CrossRef]
- Dou, H.-S.; Phan-Thien, N. Viscoelastic flow past a confined cylinder: Instability and velocity inflection. Chem. Eng. Sci. 2007, 62, 3909–3929. [Google Scholar] [CrossRef]
- Mamalis, A.; Kouzilos, G.; Vortselas, A. Design feature sensitivity analysis in a numerical model of an extrusion spider die. J. Appl. Polym. Sci. 2011, 122, 3537–3543. [Google Scholar] [CrossRef]
- Rabhi, F.; Barriere, T.; Sahli, M. Multiphysics modeling and simulation of monolayer flow and die swelling in industrial tube extrusion process. Polym. Eng. Sci. 2024, 64, 5315–5328. [Google Scholar] [CrossRef]
- Mamalis, A.; Spentzas, K.; Kouzilos, G. On the high-density polyethylene extrusion: Numerical, analytical and experimental modeling. Adv. Polym. Technol. 2010, 29, 173–184. [Google Scholar] [CrossRef]
- Kihara, S.; Gouda, T.; Matsunaga, K. Numerical simulation of three-dimensional viscoelastic flow within dies. Polym. Eng. Sci. 1999, 39, 152–163. [Google Scholar] [CrossRef]
- Norouzi, M.; Davoodi, M.; Anwar Bég, O. Theoretical study of Oldroyd-B visco-elastic fluid flow through curved pipes with slip effects in polymer flow processing. Int. J. Appl. Comput. Math. 2018, 4, 108. [Google Scholar] [CrossRef]
- Turkoz, E.; Lopez-Herrera, J.M.; Eggers, J. Axisymmetric simulation of viscoelastic filament thinning with the Oldroyd-B model. J. Fluid Mech. 2018, 851, R2. [Google Scholar] [CrossRef]
- Castillo Sánchez, H.A.; Jovanović, M.R.; Kumar, S. Understanding viscoelastic flow instabilities: Oldroyd-B and beyond. J. Non-Newton. Fluid Mech. 2022, 302, 104742. [Google Scholar] [CrossRef]
- Bird, R.B.; Drugan, W.J. An exploration and further study of an enhanced Oldroyd model. Phys. Fluids 2017, 29, 5. [Google Scholar] [CrossRef]
- Silbermann, M.; Schenkel, M.; Hoffmann, T. Die for a Hollow Profile Extruder. U.S. Patent US20190299514A1, 26 March 2019. [Google Scholar]
- Mu, Y.; Zhao, G.; Wang, Y. Numerical study of nonisothermal polymer extrusion flow with a differential viscoelastic model. Polym. Eng. Sci. 2008, 48, 316–328. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Franca, L.P.; Hulbert, G.M. A new finite element formulation for computational fluid dynamics: VIII. The Galerkin/least-squares method for advective-diffusive equations. Comput. Methods Appl. Mech. Eng. 1989, 73, 173–189. [Google Scholar] [CrossRef]
- Behr, M.A.; Franca, L.P.; Tezduyar, T.E. Stabilized finite element methods for the velocity-pressure-stress formulation of incompressible flows. Comput. Methods Appl. Mech. Eng. 1993, 104, 31–48. [Google Scholar] [CrossRef]
- Xia, K.; Yao, H.; Li, Z. A Galerkin/least-square finite element formulation for nearly incompressible elasticity/Stokes flow. Appl. Math. Model. 2007, 31, 513–529. [Google Scholar] [CrossRef]
- Wang, X.; Ye, X.; Zhang, S. A weak Galerkin least squares finite element method of Cauchy problem for Poisson equation. J. Comput. Appl. Math. 2022, 401, 113767. [Google Scholar] [CrossRef]
- Behr, M.; Arora, D.; Pasquali, M. Stabilized finite element methods of GLS type for Oldroyd-B viscoelastic fluid. In Proceedings of the European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS), Jyväskylä, Finland, 24–28 July 2004. [Google Scholar]
- Craven, T.; Rees, J.; Zimmerman, W.B. Stabilised finite element modelling of Oldroyd-B viscoelastic flows. In Proceedings of the COMSOL Conference, Boston, MA, USA, 8–10 November 2006. [Google Scholar]
- Yu, T.-H.; Wilkes, G.L. Influence of molecular weight distribution on the melt extrusion of high density polyethylene (HDPE): Effects of melt relaxation behavior on morphology and orientation in HDPE extruded tubular films. J. Rheol. 1996, 40, 1079–1093. [Google Scholar] [CrossRef]
- Kraft, M.; Meissner, J.; Stutz, J. Linear viscoelastic characterization of polymer melts with long relaxation times. Macromolecules 1999, 32, 751–757. [Google Scholar] [CrossRef]
- Chaturvedi, E.; Rajput, N.S.; Upadhyaya, S.; Pandey, P. Experimental study and mathematical modeling for extrusion using high-density polyethylene. Mater. Today Proc. 2017, 4, 1670–1676. [Google Scholar] [CrossRef]
- Kouzilos, G.N.; Seretis, G.V.; Provatidis, C.G. Design of polymer extrusion dies using finite element analysis. In Extrusion of Metals, Polymers, and Food Products; IntechOpen: Rijeka, Croatia, 2017; Chapter 10. [Google Scholar]
- Marschik, C.; Roland, W.; Dörner, M. Application of network analysis to flow systems with alternating wave channels: Part B (superimposed drag-pressure flows in extrusion). Polymers 2020, 12, 1900. [Google Scholar] [CrossRef]
- Hopmann, C.; Bastian, M.; Windeck, C. A method for the validation of simulated mixing characteristics of single-screw extrusion. Polymers 2020, 12, 2234. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, P.J. Method for time-dependent simulations of viscoelastic flows: Vortex shedding behind cylinder. J. Non-Newton. Fluid Mech. 2001, 101, 113–137. [Google Scholar] [CrossRef]
- Kato, H.; Mizuno, Y. Method for time-dependent simulations of viscoelastic flows: Vortex shedding behind cylinder. Bull. JSME 1983, 26, 529–536. [Google Scholar] [CrossRef]
- Reddy, B.; Kumar, K.A.; Bujula, R. Impact of Soret and Dufour on MHD mixed convective flow of non-Newtonian fluid over a coagulated surface. Heat Transfer 2021, 50, 567–580. [Google Scholar]
- Renardy, M. High Weissenberg number boundary layers for the upper convected Maxwell fluid. J. Non-Newton. Fluid Mech. 1997, 68, 125–132. [Google Scholar] [CrossRef]
- McLeish, T.C.B. Tube theory of entangled polymer dynamics. Adv. Phys. 2010, 51, 1379–1527. [Google Scholar] [CrossRef]
- Somani, R.H.; Yang, L.; Zhu, L.; Hsiao, B.S. Flow-induced shish–kebab precursor structures in entangled polymer melts. Polymer 2005, 46, 8587–8623. [Google Scholar] [CrossRef]
- Cao, Y.; Yang, W.-J.; Guo, X.-W. Role of nonmonotonic constitutive curves in extrusion instabilities. Int. J. Polym. Sci. 2015, 2015, 312839. [Google Scholar] [CrossRef]
- Kwon, Y.; Park, J.; Lee, S. Melt fracture modeled as 2D elastic flow instability. Rheol. Acta 2015, 54, 445–453. [Google Scholar] [CrossRef]
- Agrawal, P.; Silva, M.H.A.; Cavalcanti, S.N. Rheological properties of high-density polyethylene/linear low-density polyethylene and high-density polyethylene/low-density polyethylene blends. Polym. Bull. 2022, 79, 2321–2343. [Google Scholar] [CrossRef]
- Erbetta, C.; Manoel, G.; Oliveira, A. Rheological and thermal behavior of high-density polyethylene (HDPE) at different temperatures. Mater. Sci. Appl. 2014, 5, 923–931. [Google Scholar] [CrossRef]
- Tanner, R.I. Engineering Rheology, 2nd ed.; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
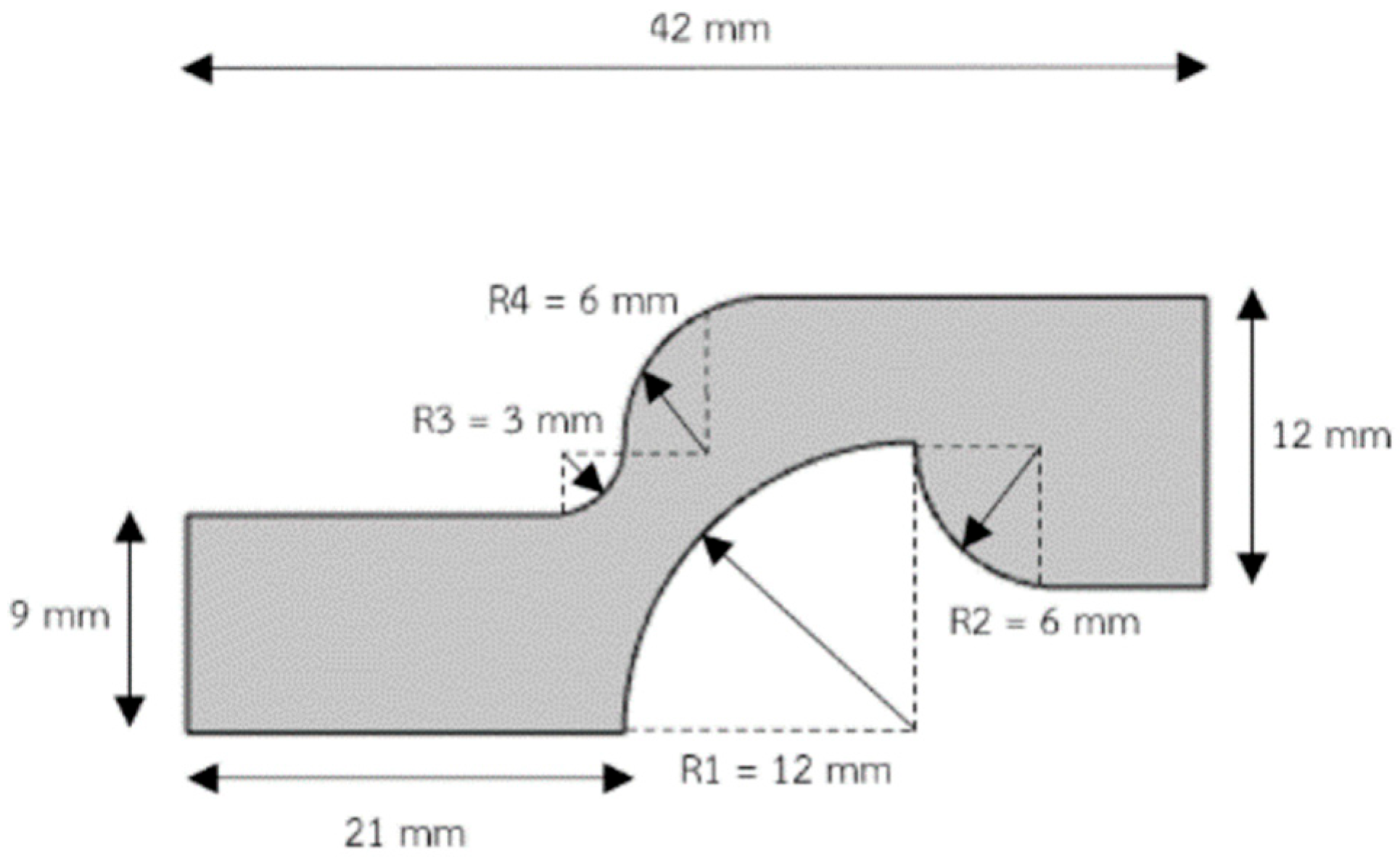
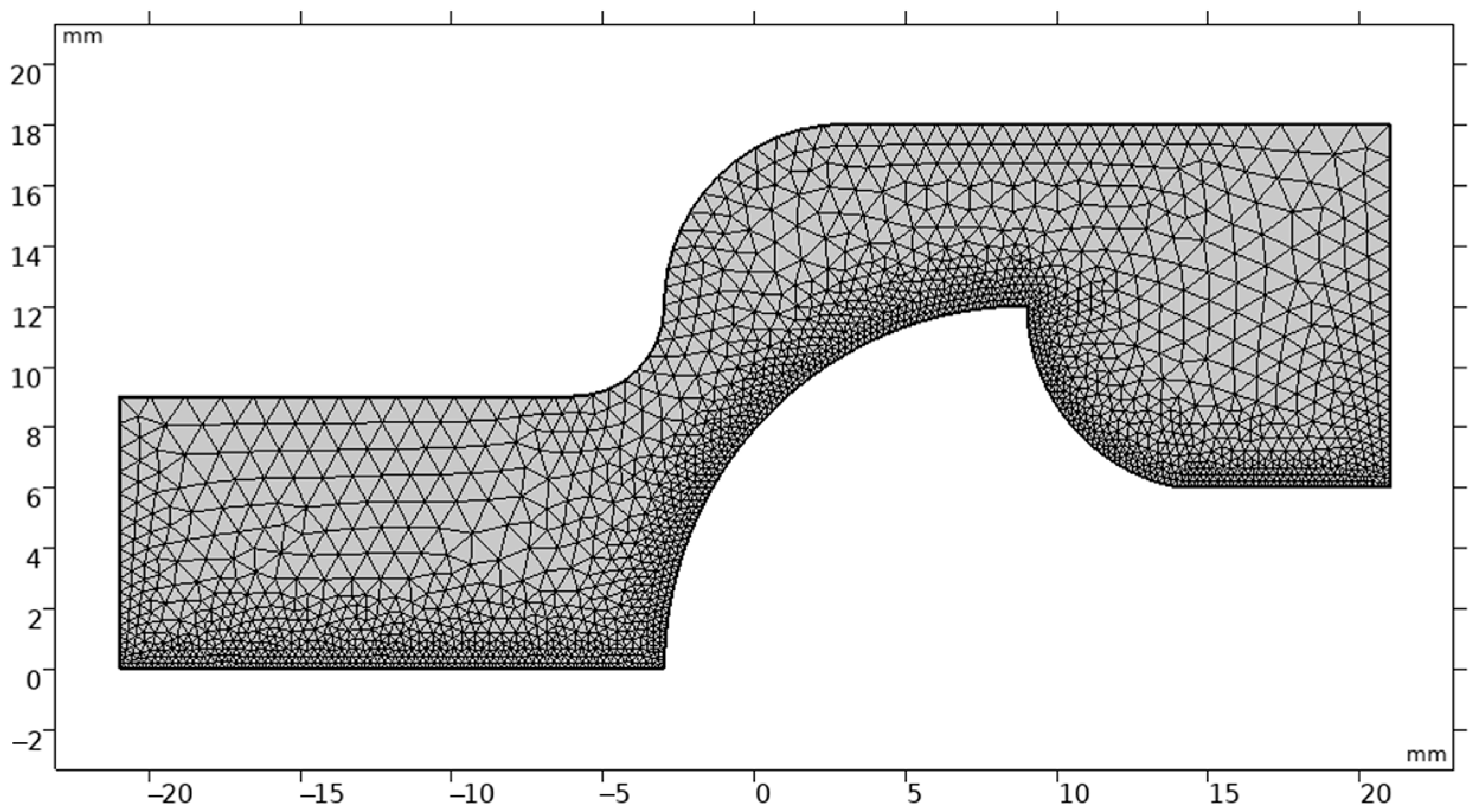
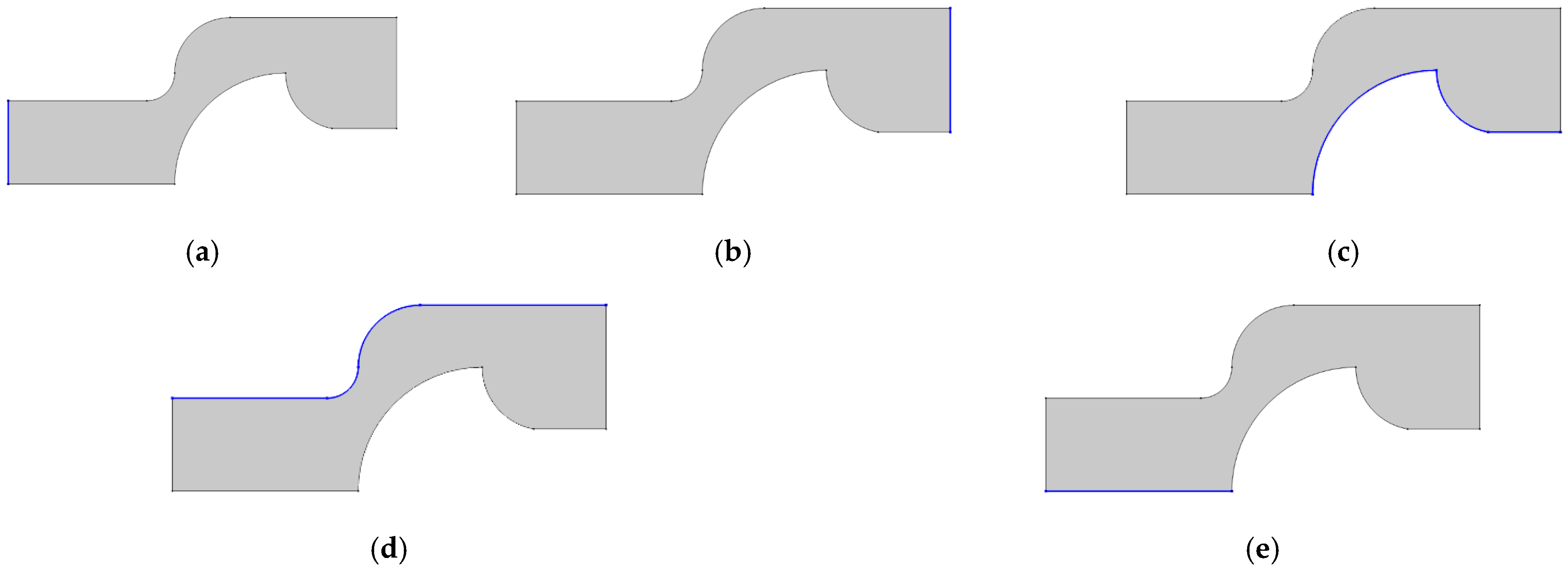
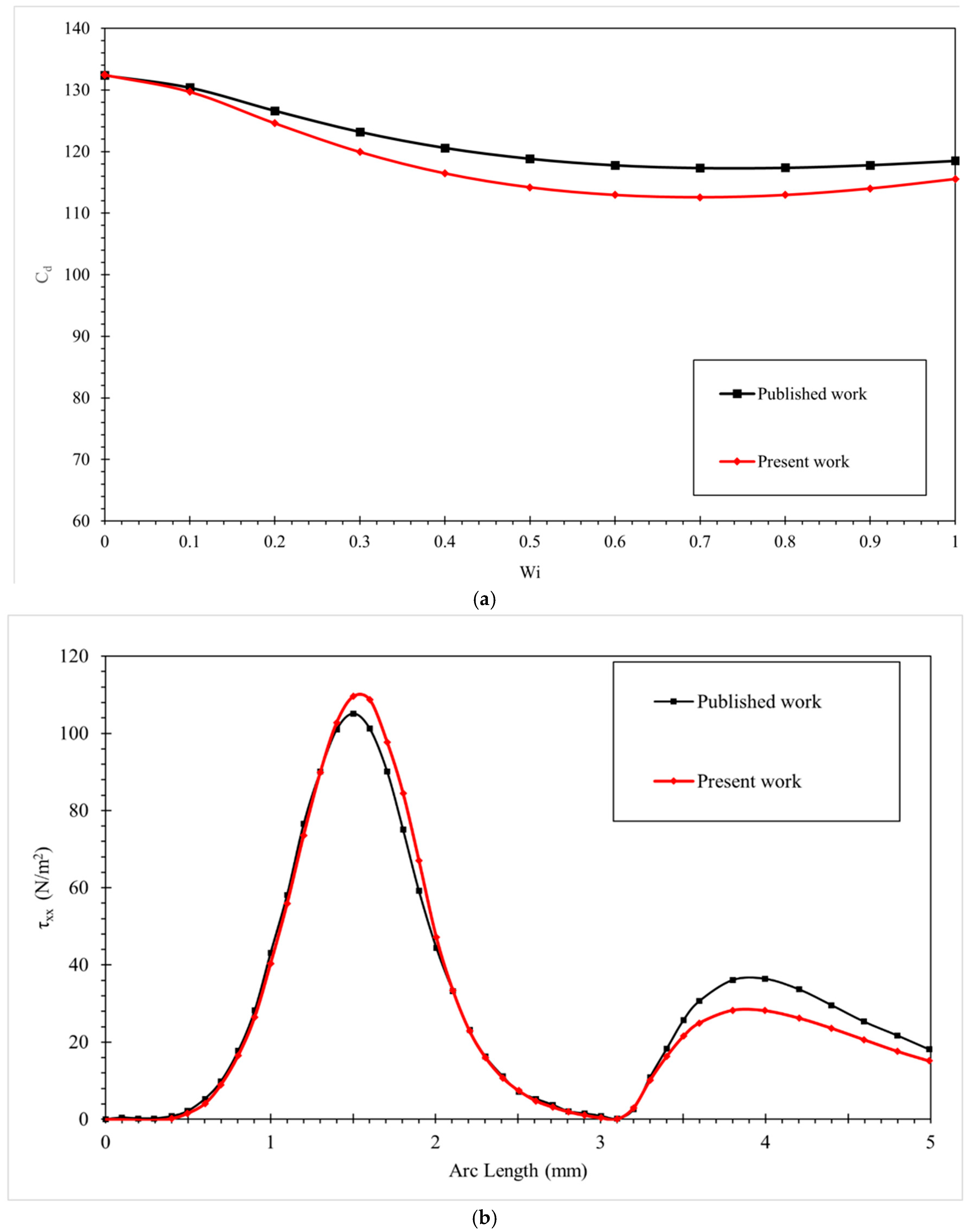
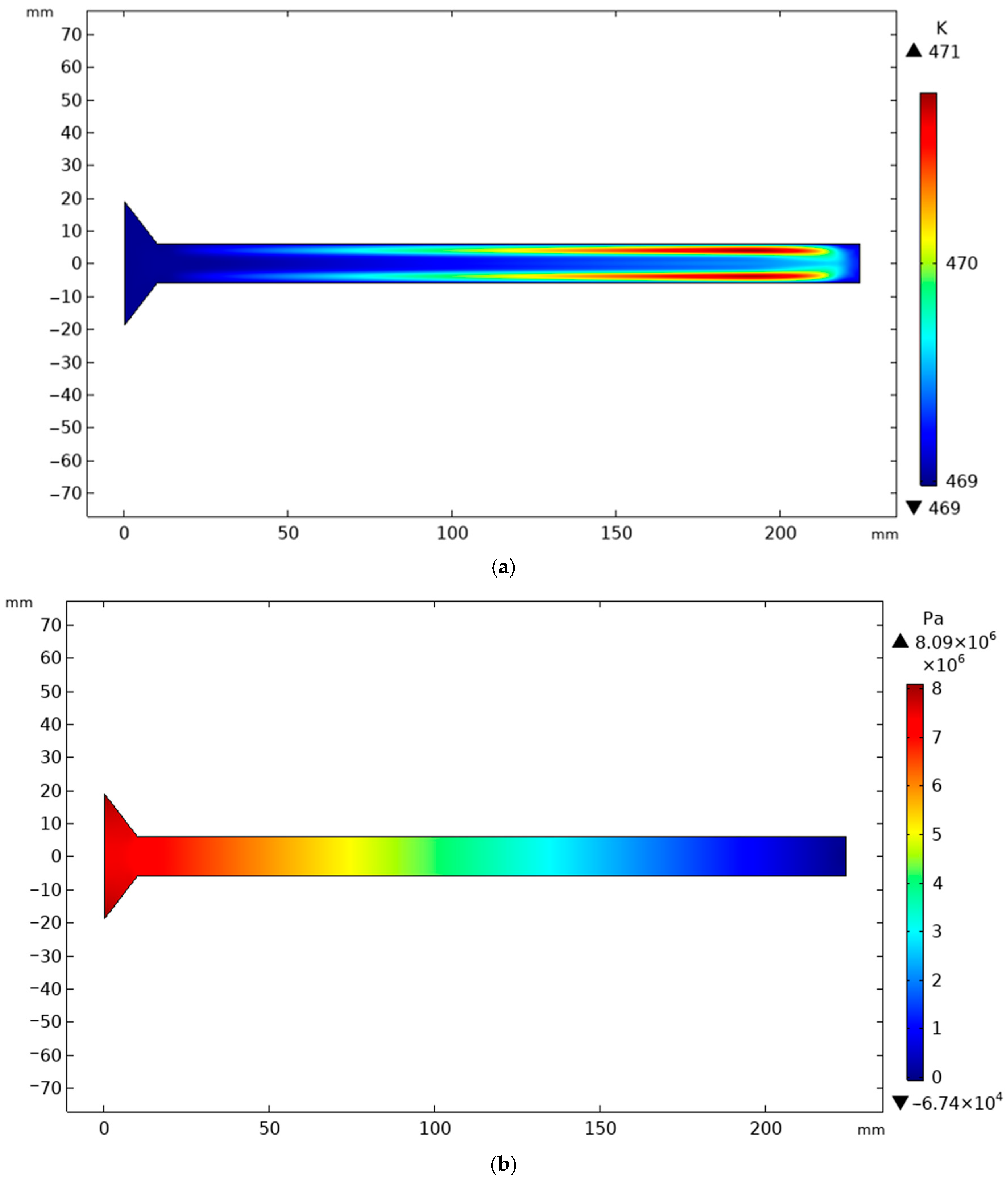

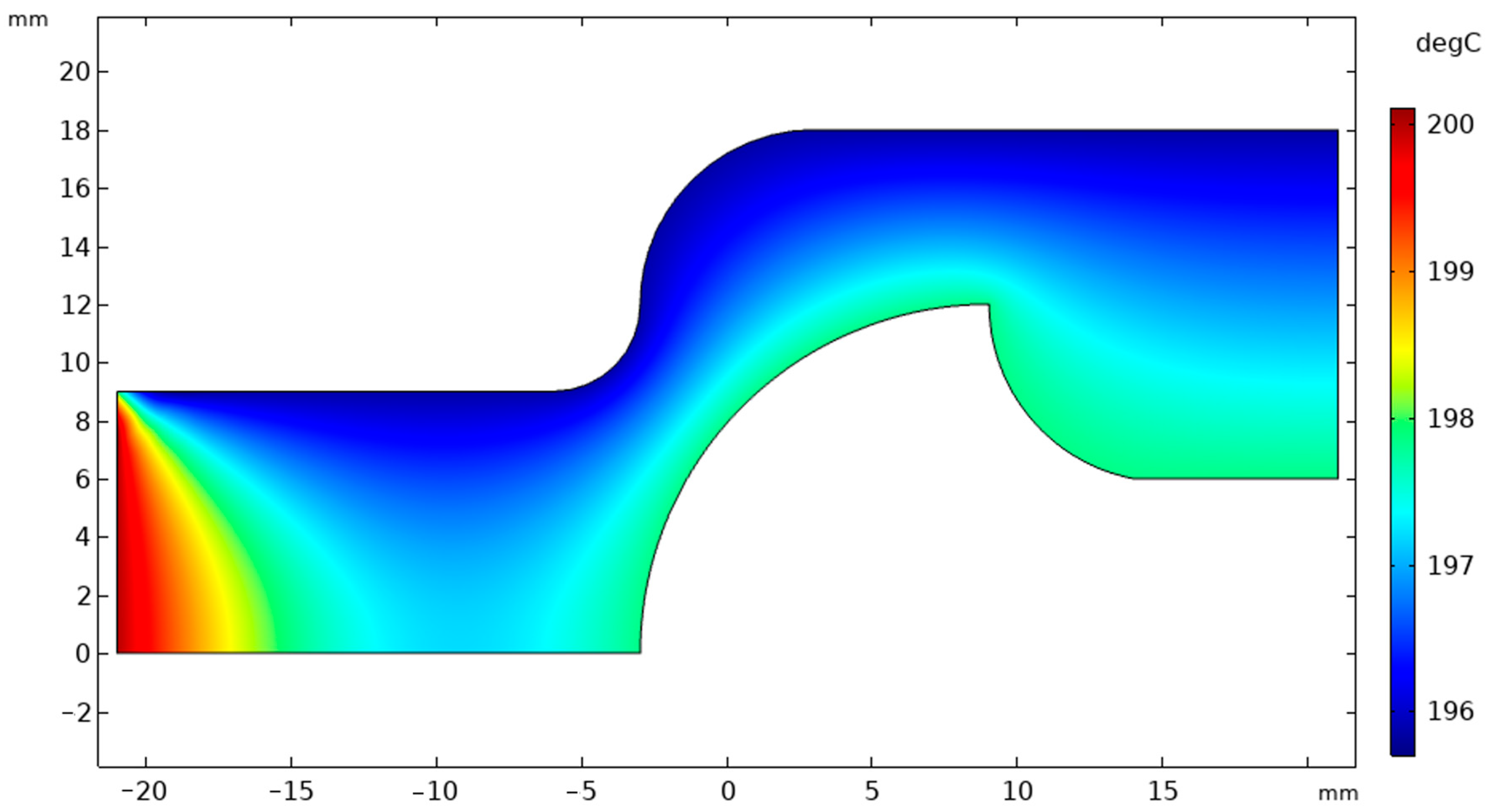
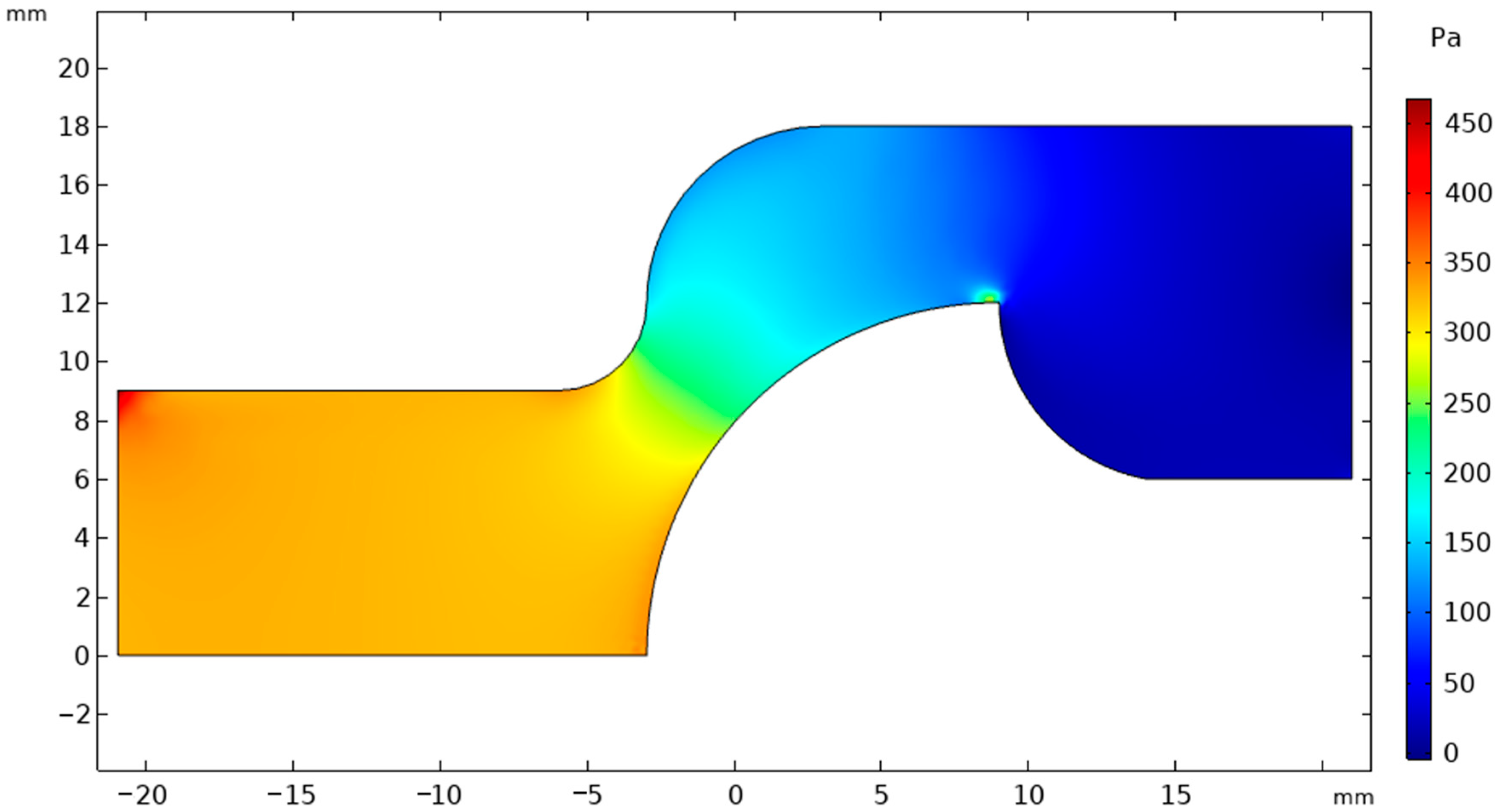

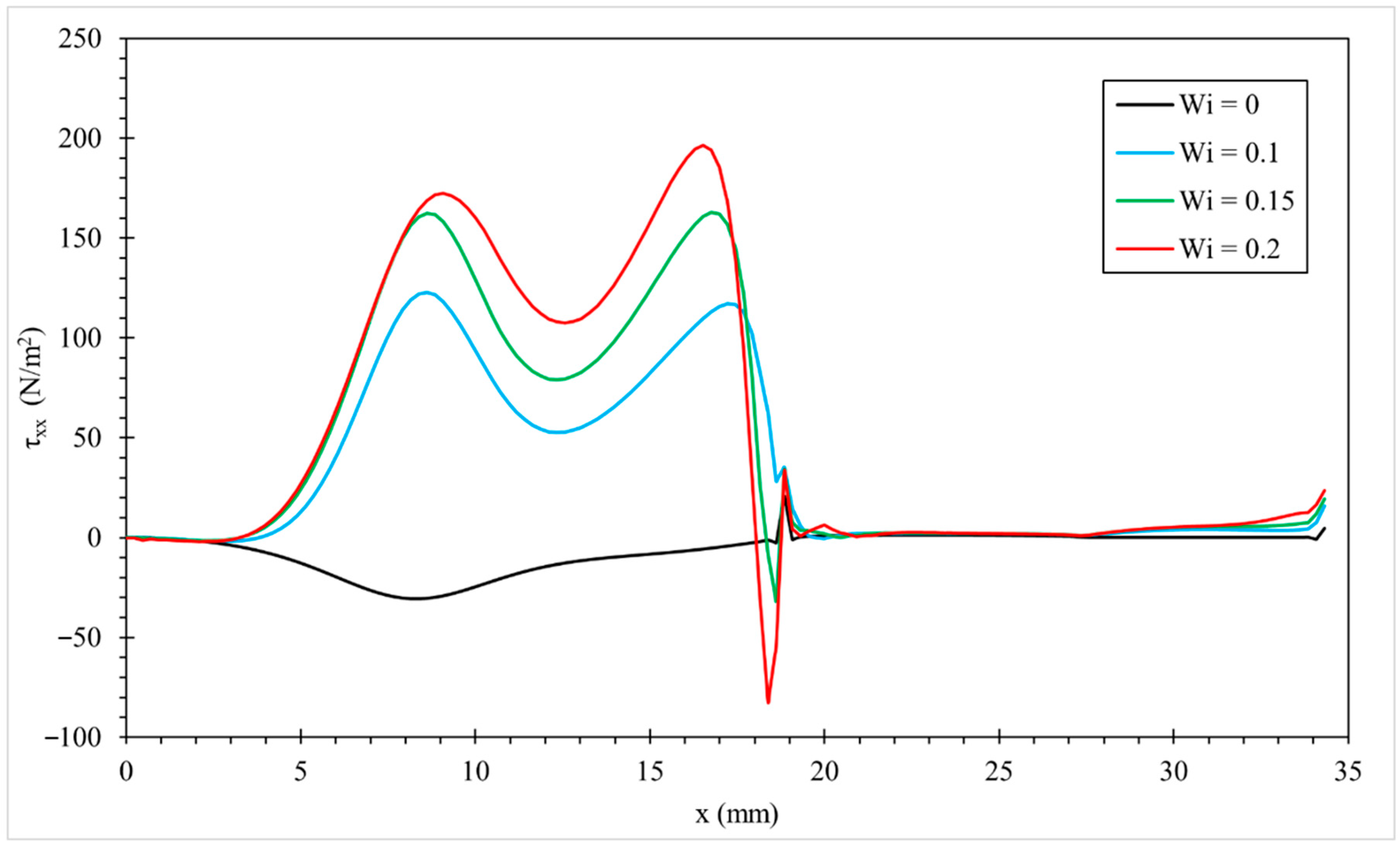



| Mesh Level | Elements | Cd | (Pa) | CPU Time (Relative) |
|---|---|---|---|---|
| Coarse | 1200 | 7.03 | 201.2 | 1.0× |
| Medium | 2500 | 7.10 | 199.0 | 2.15× |
| Fine | 3867 | 7.11 | 198.5 | 3.57× |
| (s) | Wi | Cd |
|---|---|---|
| 0.02 | 0.056 | 7.1059 |
| 0.03 | 0.083 | 7.0806 |
| 0.04 | 0.111 | 7.0444 |
| 0.05 | 0.139 | 7.0040 |
| 0.06 | 0.167 | 6.9635 |
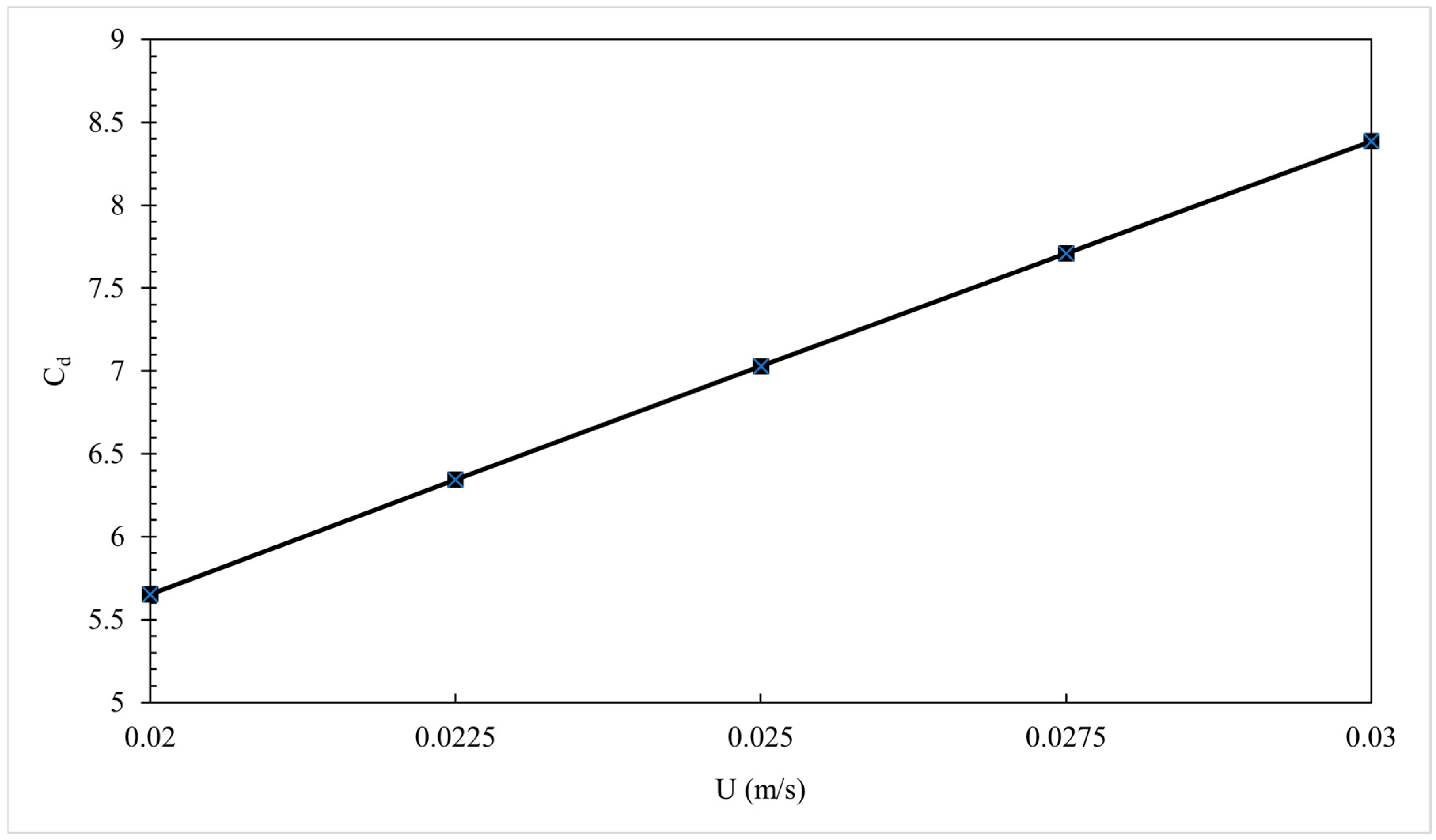
| U (m/s) | Wi | Cd |
|---|---|---|
| 0.02 | 0.098 | 5.6521 |
| 0.0225 | 0.111 | 6.3421 |
| 0.025 | 0.123 | 7.0276 |
| 0.0275 | 0.135 | 7.709 |
| 0.03 | 0.147 | 8.3863 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Myint, A.K.K.; Taithong, N.; Pakdee, W. CFD Analysis of Non-Isothermal Viscoelastic Flow of HDPE Melt Through an Extruder Die. Fluids 2025, 10, 238. https://doi.org/10.3390/fluids10090238
Myint AKK, Taithong N, Pakdee W. CFD Analysis of Non-Isothermal Viscoelastic Flow of HDPE Melt Through an Extruder Die. Fluids. 2025; 10(9):238. https://doi.org/10.3390/fluids10090238
Chicago/Turabian StyleMyint, Aung Ko Ko, Nontapat Taithong, and Watit Pakdee. 2025. "CFD Analysis of Non-Isothermal Viscoelastic Flow of HDPE Melt Through an Extruder Die" Fluids 10, no. 9: 238. https://doi.org/10.3390/fluids10090238
APA StyleMyint, A. K. K., Taithong, N., & Pakdee, W. (2025). CFD Analysis of Non-Isothermal Viscoelastic Flow of HDPE Melt Through an Extruder Die. Fluids, 10(9), 238. https://doi.org/10.3390/fluids10090238








