A Physics-Informed Neural Network Solution for Rheological Modeling of Cement Slurries
Abstract
1. Introduction
2. Problem Statement
2.1. Governing Equations
- Conservation of Mass:
- Conservation of Linear Momentum:
- Conservation of Angular Momentum:
- Convection–Diffusion Equation:
2.2. Constitutive Relations
- Stress Tensor:
- Particle Flux:
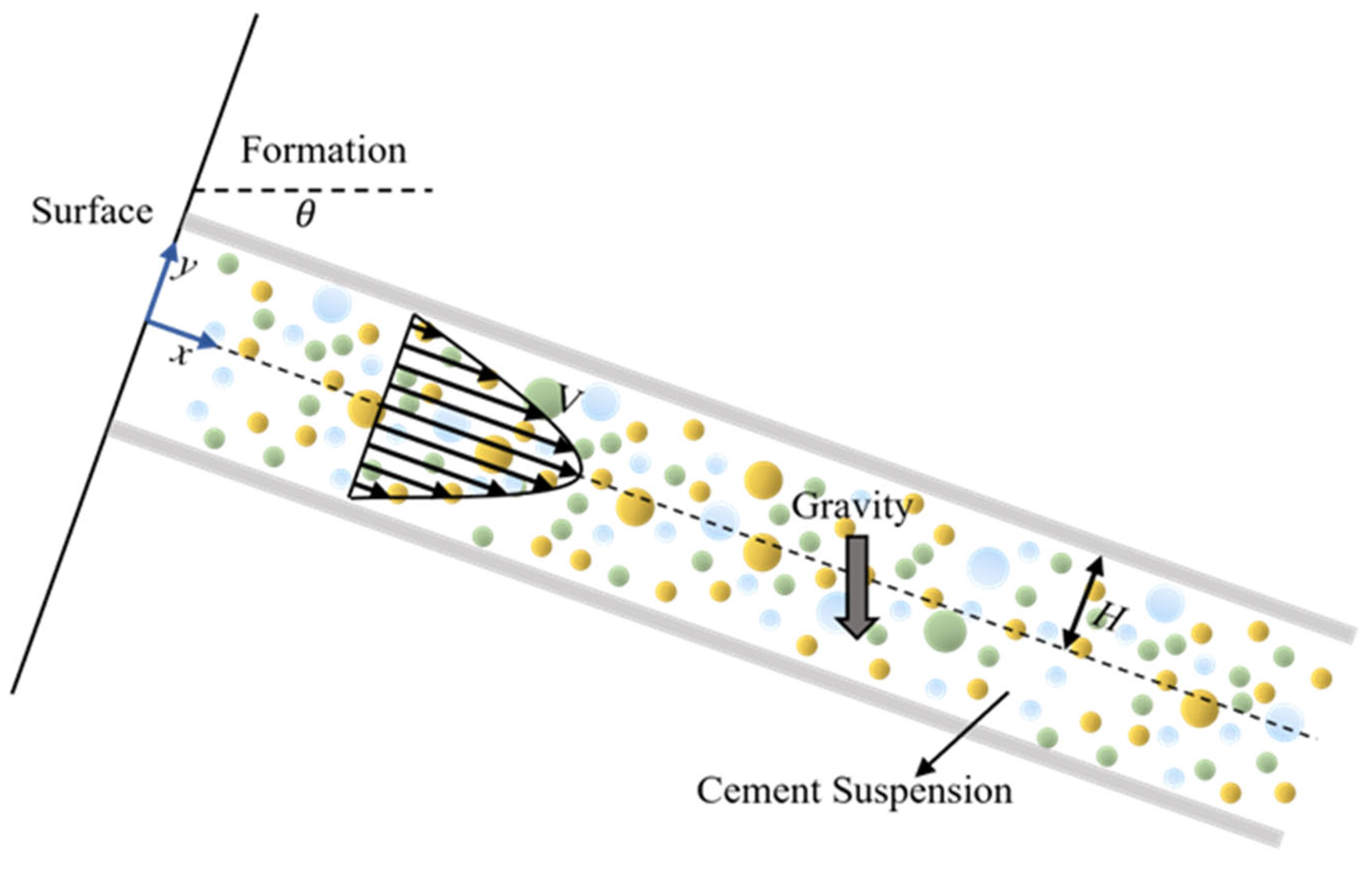
2.3. Flow Between Two Plates
3. Methodology
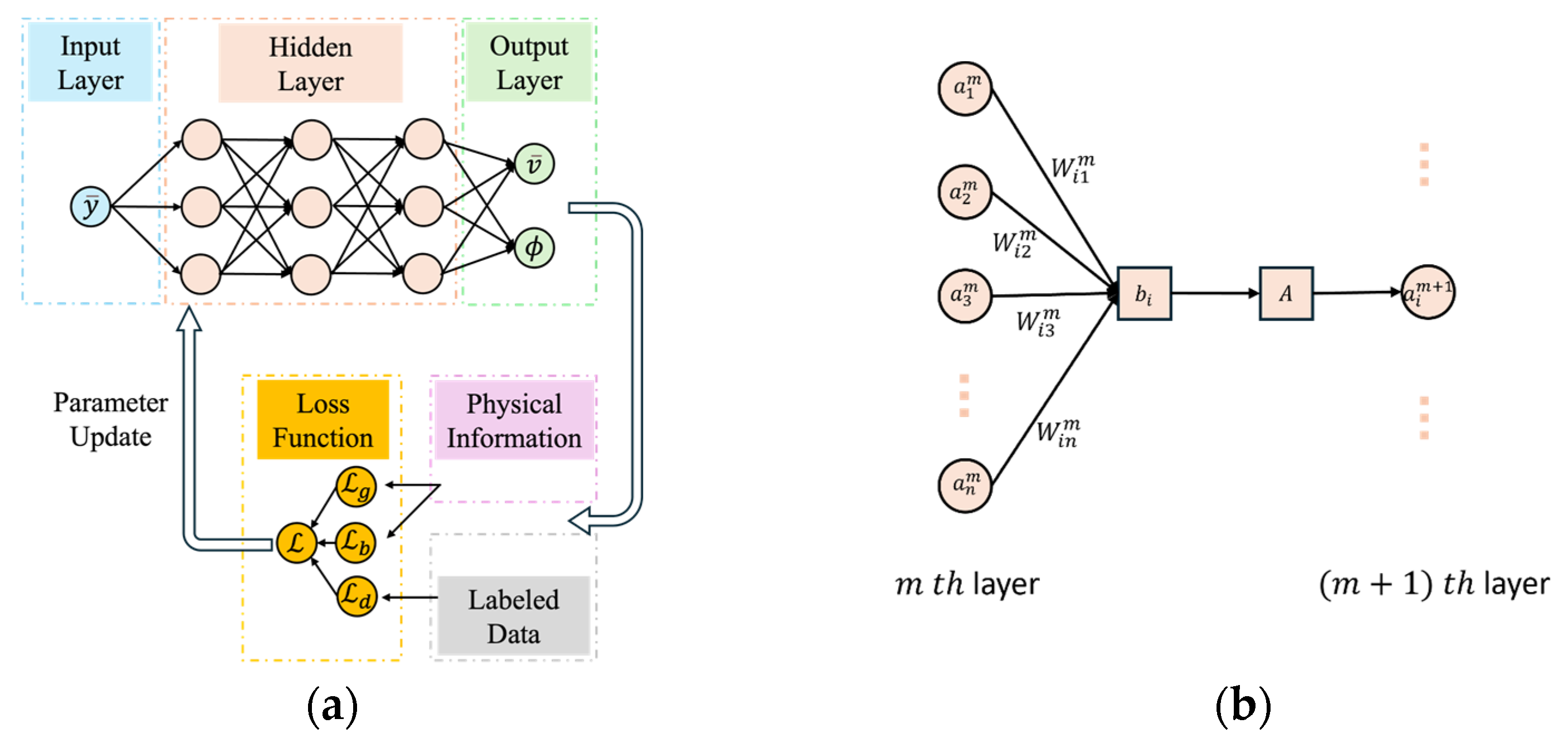
3.1. PINN Settings
- Loss of governing equations (): the residuals of the governing Equations (11) and (12), evaluated across collocation points on the equation solution domain ;
- Loss of boundary conditions (): penalties for violations of the boundary conditions specified in Equations (14) and (15);
- Loss of labeled data (): optional supervised loss using labeled data when available, such as from simulations or experiments, evaluated across known labeled data points for velocity and volume faction
3.2. Performance Metrics
4. Results and Discussion
4.1. Network Architecture Tuning
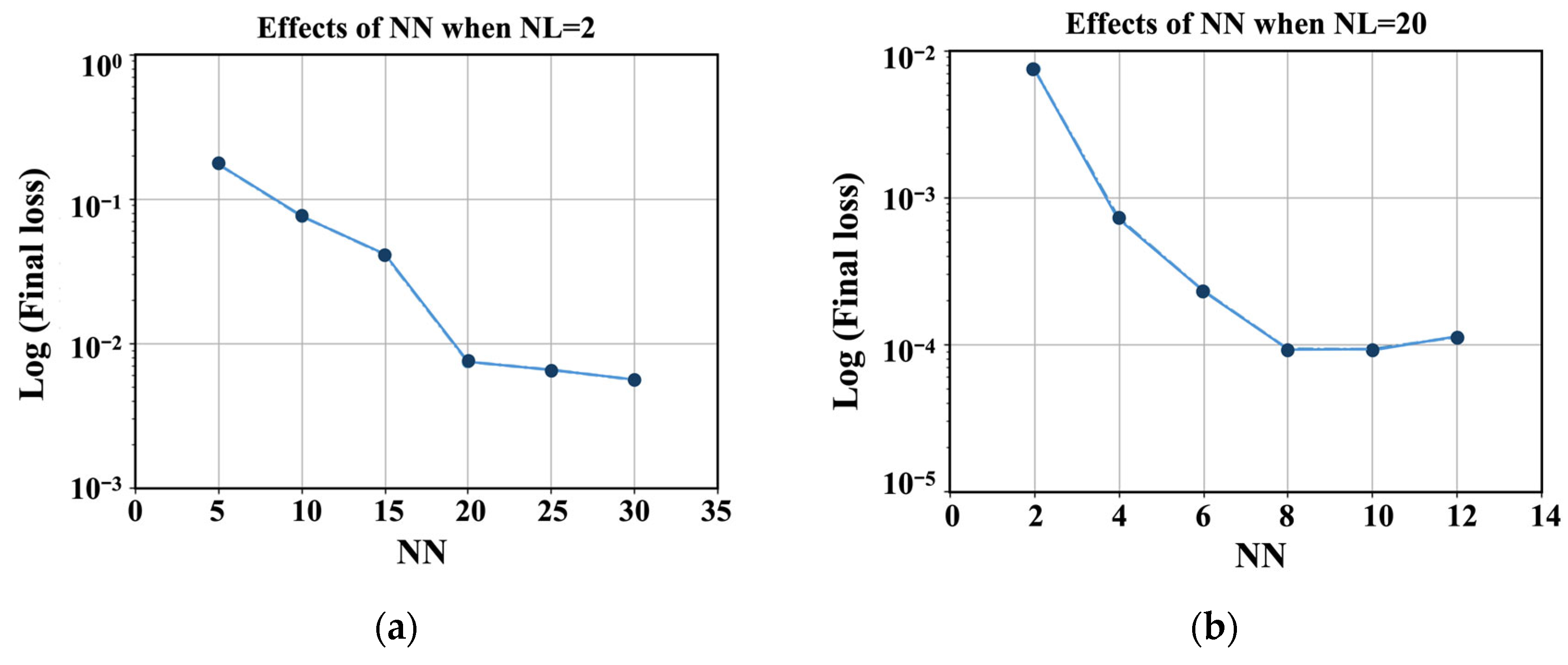
4.1.1. Neural Network Structure
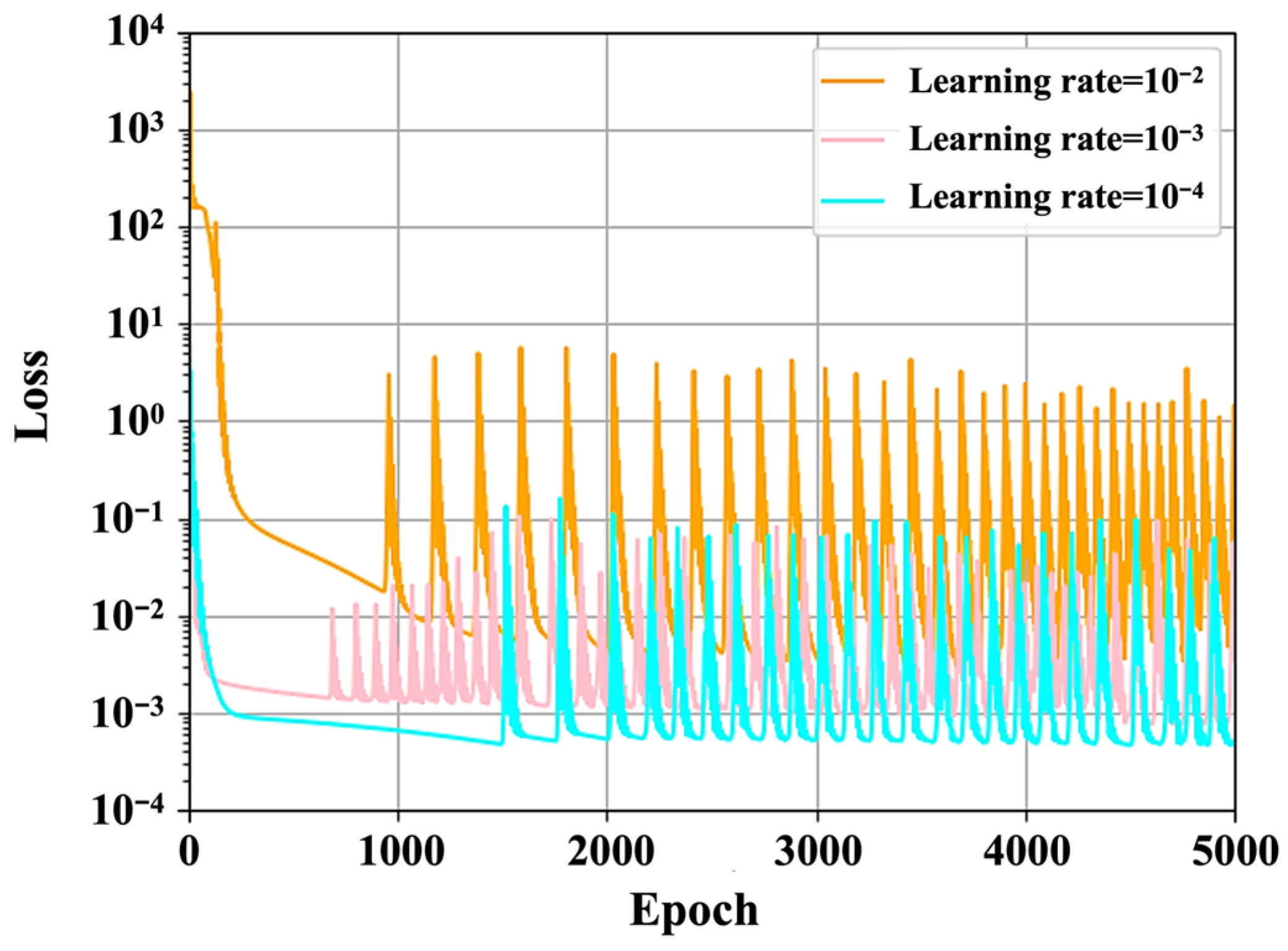
4.1.2. Training Epochs and Learning Rate
4.2. Parametric Studies on Cement Rheology with PINN
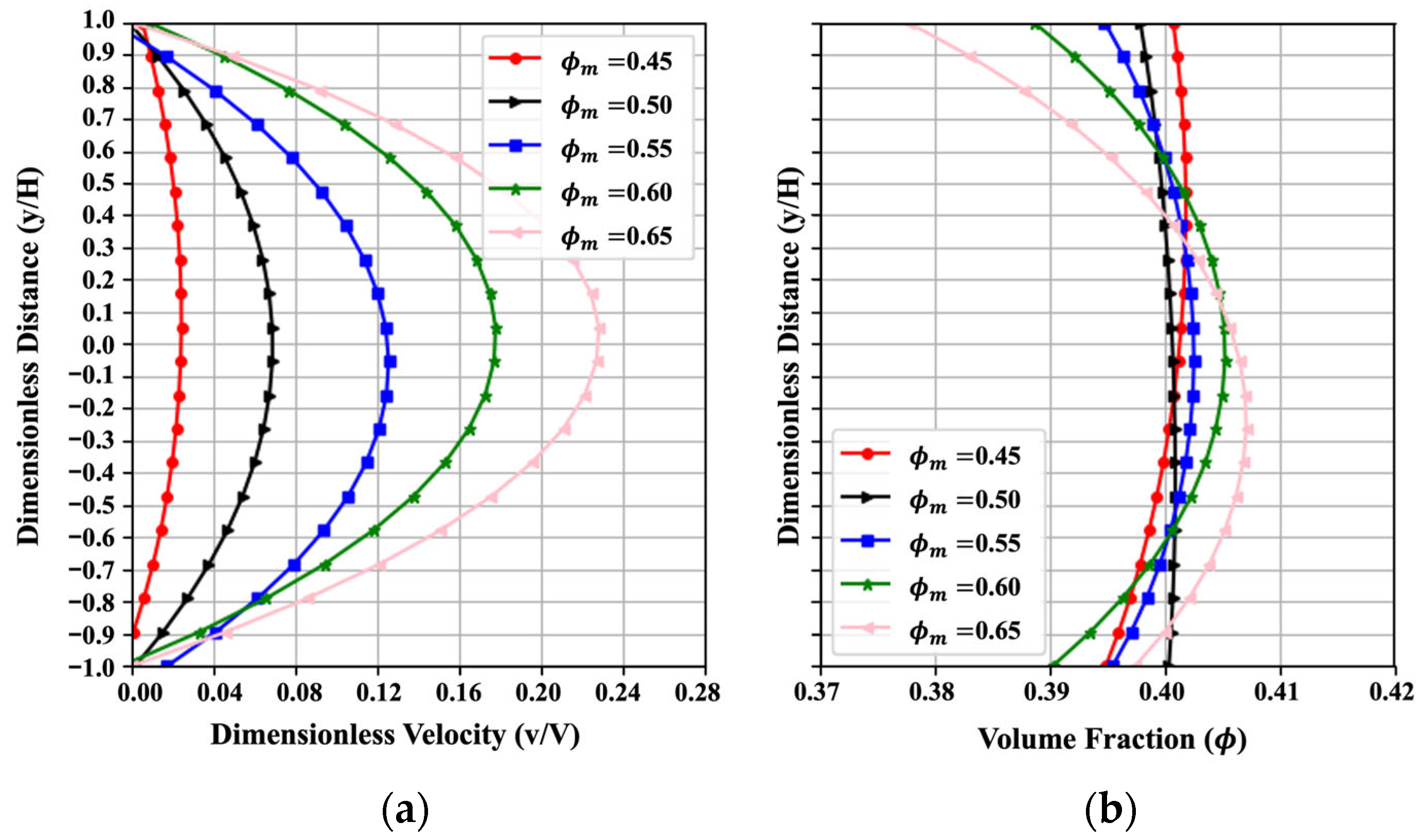
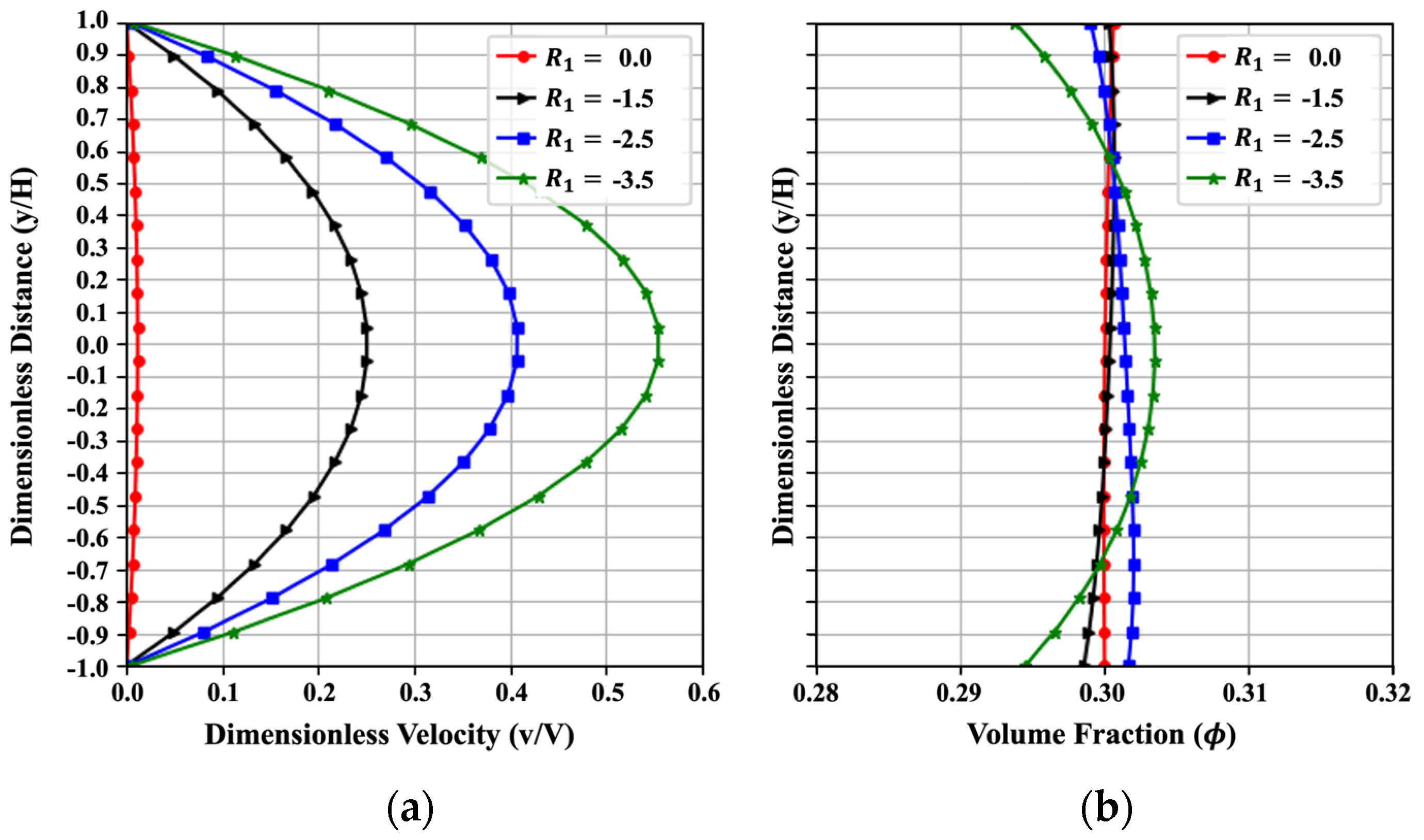
4.2.1. Effect of
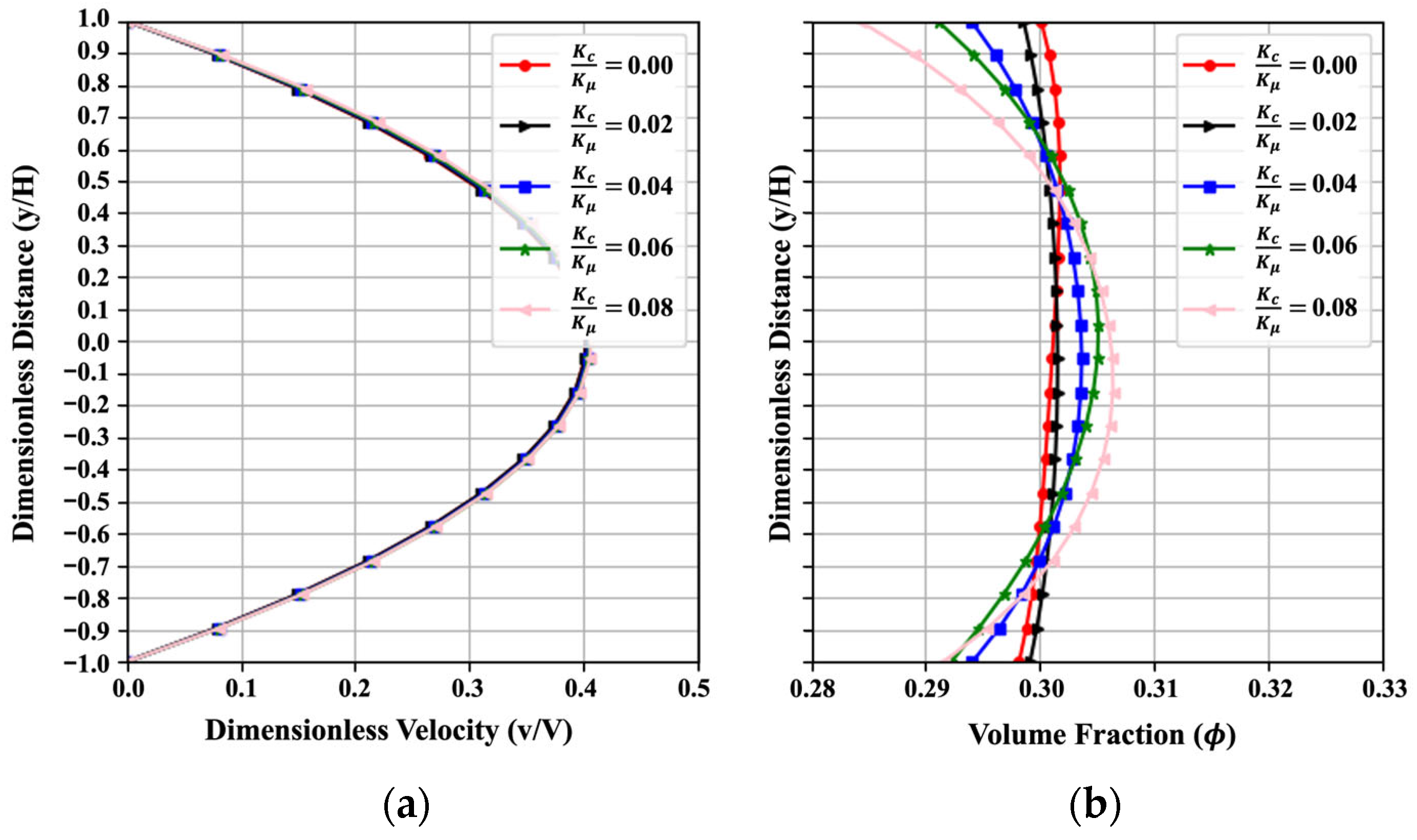
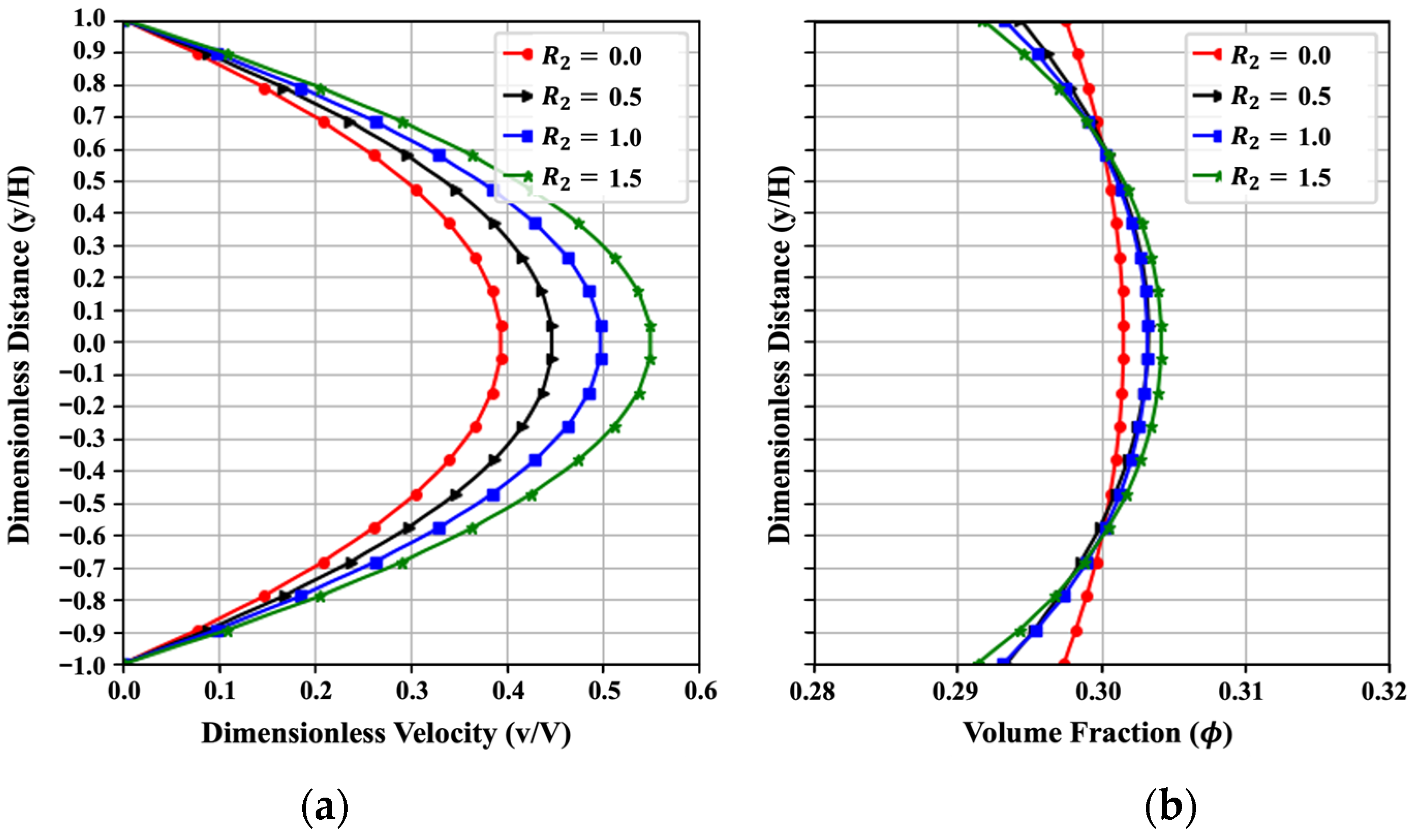
4.2.2. Effect of
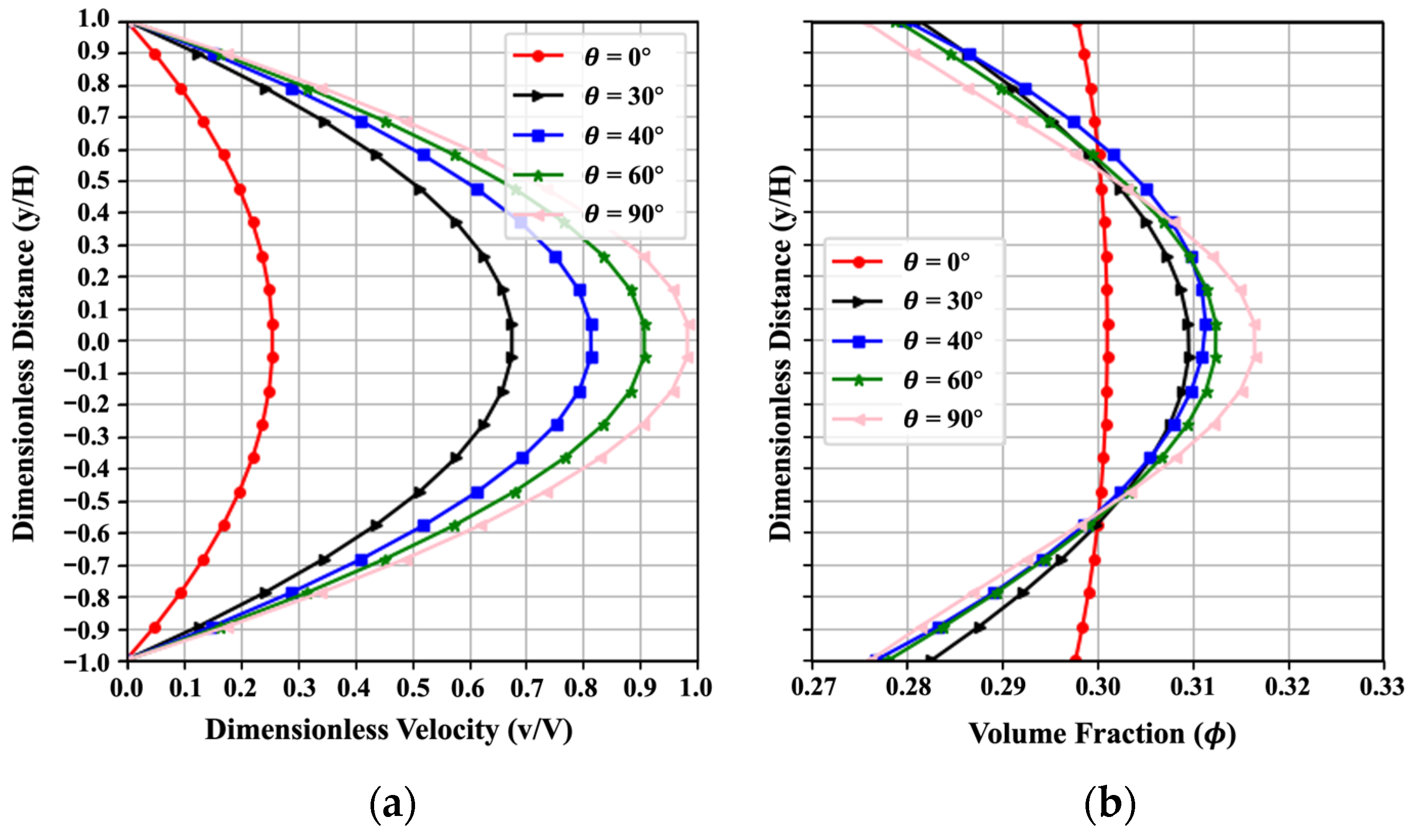
4.2.3. Effect of
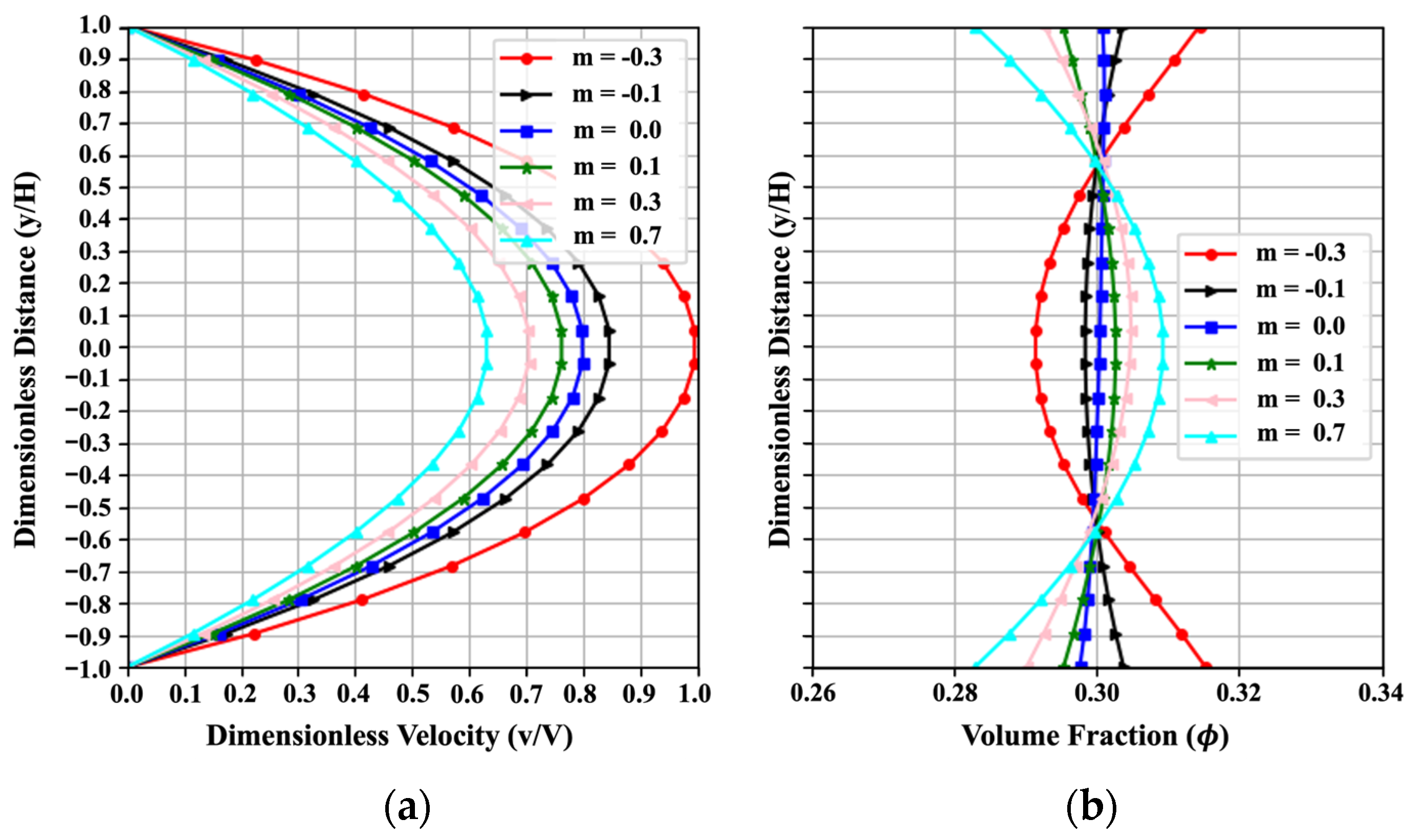
4.2.4. Effect of
4.2.5. Effect of
4.2.6. Effect of
4.2.7. Effect of
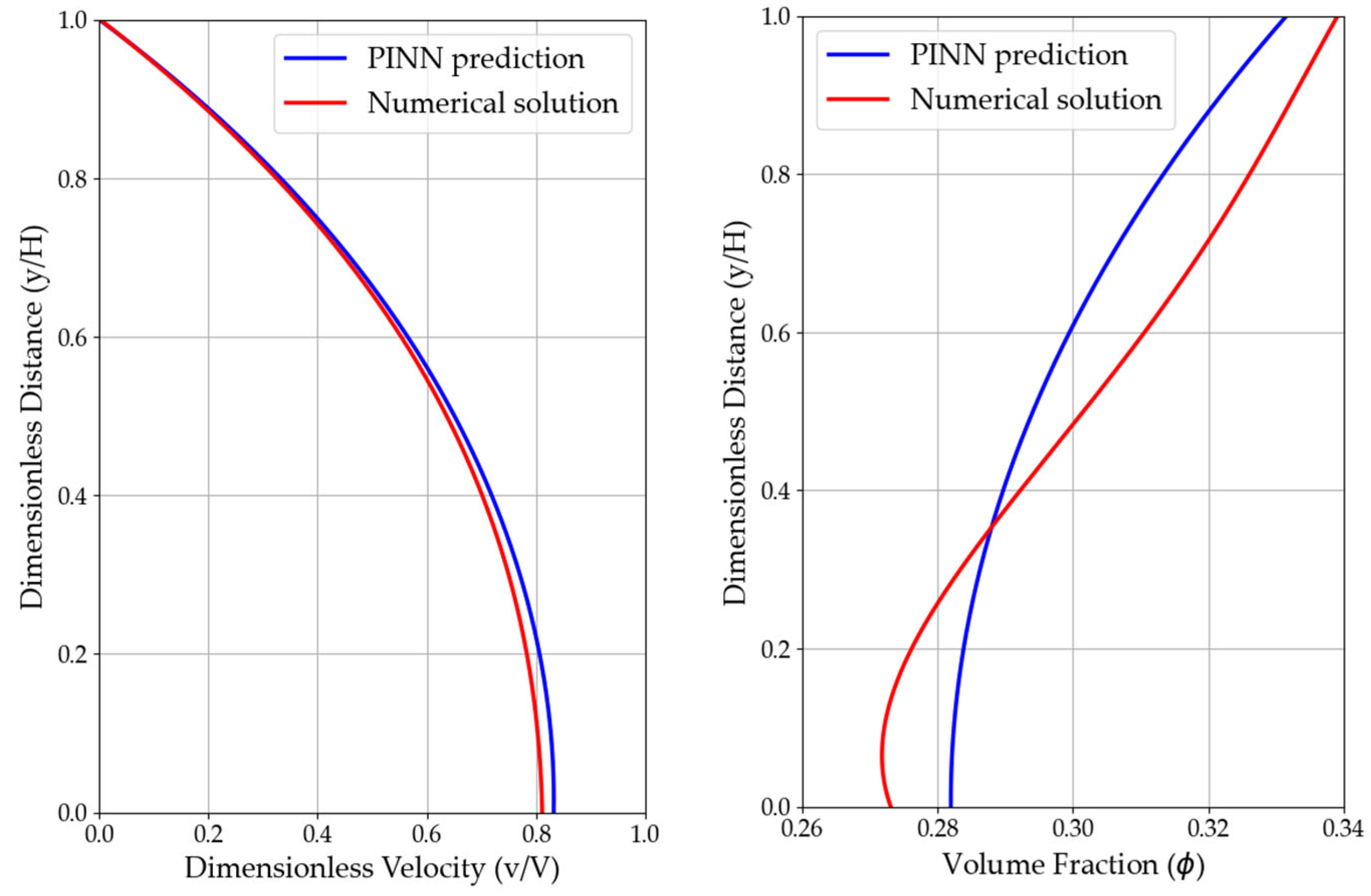
4.3. Further Improvements of PINN
5. Conclusions and Future Work
- Mesh-free modeling: Unlike conventional CFD approaches that rely on meshing and discretization, the PINN approach inherently avoids mesh generation, reducing preprocessing complexity and enabling efficient solutions in geometrically flexible domains.
- Robust trend prediction: Across a variety of parametric conditions, including maximum volume fraction, inclination angle, material coefficients, and dimensionless rheological numbers, the PINN consistently reproduces expected flow and particle concentration profiles with low mean absolute error.
- Data efficiency: The model demonstrates strong generalization without requiring labeled data, yet it allows for precision enhancement by incorporating sparse experimental labels. This balance makes it suitable for data-limited industrial scenarios.
- Modularity and extensibility: The dual-network architecture and hybrid loss function formulation provide a customizable and scalable solution framework for modeling other complex non-Newtonian slurry systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tao, C.; Rosenbaum, E.; Kutchko, B.G.; Massoudi, M. A Brief Review of Gas Migration in Oilwell Cement Slurries. Energies 2021, 14, 2369. [Google Scholar] [CrossRef]
- Tao, C.; Kutchko, B.G.; Rosenbaum, E.; Massoudi, M. A Review of Rheological Modeling of Cement Slurry in Oil Well Applications. Energies 2020, 13, 570. [Google Scholar] [CrossRef]
- Tao, C.; Kutchko, B.G.; Rosenbaum, E.; Wu, W.-T.; Massoudi, M. Steady flow of a cement slurry. Energies 2019, 12, 2604. [Google Scholar] [CrossRef]
- Tao, C.; Rosenbaum, E.; Kutchko, B.; Massoudi, M. Pulsating Poiseuille flow of a cement slurry. Int. J. Non-Linear Mech. 2021, 133, 103717. [Google Scholar] [CrossRef]
- Tao, C.; Watts, B.; Ferraro, C.C.; Masters, F.J. A Multivariate Computational Framework to Characterize and Rate Virtual Portland Cements. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 266–278. [Google Scholar] [CrossRef]
- Tao, C.; Massoudi, M. On the Flow of a Cement Suspension: The Effects of Nano-Silica and Fly Ash Particles. Materials 2024, 17, 1504. [Google Scholar] [CrossRef]
- Tao, C.; Wang, Q.; Ahmadi, G.; Massoudi, M. Numerical Analysis of Cement Placement into Drilling Fluid in Oilwell Applications. Materials 2025, 18, 3098. [Google Scholar] [CrossRef]
- Dvoynikov, M.V.; Nikitin, V.I.; Kopteva, A.I. Analysis of Methodology for Selecting Rheological Model of Cement Slurry for Determining Technological Parameters of Well Casing. Int. J. Eng. 2024, 37, 2042–2050. [Google Scholar] [CrossRef]
- Guillot, D. 4 Rheology of Well Cement Slurries. In Developments in Petroleum Science; in Well Cementing; Nelson, E.B., Ed.; Elsevier: Amsterdam, The Netherlands, 1990; Volume 28. [Google Scholar] [CrossRef]
- Casson, N. Flow Equation for Pigment-oil Suspensions of the Printing Ink-type. In Rheology of Disperse Systems; Pergamon Press: Oxford, UK, 1959; pp. 84–104. [Google Scholar]
- Parzonka, W.; Vočadlo, J. Méthode de la caractéristique du comportement rhéologique des substances viscoplastiques d’après les mesures au viscosimètre de Couette (modèle nouveau à trois paramètres). Rheol. Acta 1968, 7, 260–265. [Google Scholar] [CrossRef]
- Herschel, W.H.; Bulkley, R. Konsistenzmessungen von Gummi-Benzollösungen. Kolloid-Z. 1926, 39, 291–300. [Google Scholar] [CrossRef]
- Memon, K.R.; Mahesar, A.A.; Baladi, S.A.; Sukar, M.T. Analyzing Cement Rheological Properties Using Different Additive Schemes at High Pressure and High Temperature Conditions. Mehran Univ. Res. J. Eng. Technol. 2020, 39, 466–474. [Google Scholar] [CrossRef]
- Memon, K.R.; Shuker, M.T. Investigating Rheological Properties of High Performance Cement System for Oil Wells. Res. J. Appl. Sci. Eng. Technol. 2013, 6, 3865–3870. [Google Scholar] [CrossRef]
- Tariq, Z.; Murtaza, M.; Mahmoud, M. Development of New Rheological Models for Class G Cement with Nanoclay as an Additive Using Machine Learning Techniques. ACS Omega 2020, 5, 17646–17657. [Google Scholar] [CrossRef] [PubMed]
- Dissanayake, M.W.M.G.; Phan-Thien, N. Neural-network-based approximations for solving partial differential equations. Commun. Numer. Methods Eng. 1994, 10, 195–201. [Google Scholar] [CrossRef]
- Lagaris, I.E.; Likas, A.C.; Papageorgiou, D.G. Neural-network methods for boundary value problems with irregular boundaries. IEEE Trans. Neural Netw. 2000, 11, 1041–1049. [Google Scholar] [CrossRef]
- Aarts, L.; van der Veer, P. Solving nonlinear differential equations by a neural network method. In Proceedings of the Computational Science International Conference, San Fransisco, CA, USA, 28–30 May 2001; pp. 181–189. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Eivazi, H.; Wang, Y.; Vinuesa, R. Physics-informed deep-learning applications to experimental fluid mechanics. Meas. Sci. Technol. 2024, 35, 075303. [Google Scholar] [CrossRef]
- Lee, J.; Shin, S.; Kim, T.; Park, B.; Choi, H.; Lee, A.; Choi, M.; Lee, S. Physics informed neural networks for fluid flow analysis with repetitive parameter initialization. Sci. Rep. 2025, 15, 16740. [Google Scholar] [CrossRef]
- Bandai, T.; Ghezzehei, T.A. Physics-Informed Neural Networks with Monotonicity Constraints for Richardson-Richards Equation: Estimation of Constitutive Relationships and Soil Water Flux Density From Volumetric Water Content Measurements. Water Resour. Res. 2021, 57, e2020WR027642. [Google Scholar] [CrossRef]
- Han, J.; Nica, M.; Stinchcombe, A.R. A derivative-free method for solving elliptic partial differential equations with deep neural networks. J. Comput. Phys. 2020, 419, 109672. [Google Scholar] [CrossRef]
- Almajid, M.M.; Abu-Al-Saud, M.O. Prediction of porous media fluid flow using physics informed neural networks. J. Pet. Sci. Eng. 2022, 208, 109205. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific Machine Learning Through Physics–Informed Neural Networks: Where we are and What’s Next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Meng, Z.; Qian, Q.; Xu, M.; Yu, B.; Yıldız, A.R.; Mirjalili, S. PINN-FORM: A new physics-informed neural network for reliability analysis with partial differential equation. Comput. Methods Appl. Mech. Eng. 2023, 414, 116172. [Google Scholar] [CrossRef]
- Krishnapriyan, A.S.; Gholami, A.; Zhe, S.; Kirby, R.M.; Mahoney, M.W. Characterizing possible failure modes in physics-informed neural networks. arXiv 2021, arXiv:2109.01050. [Google Scholar] [CrossRef]
- Wang, S.; Sankaran, S.; Perdikaris, P. Respecting causality for training physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2024, 421, 116813. [Google Scholar] [CrossRef]
- Lawal, Z.K.; Yassin, H.; Lai, D.T.C.; Che Idris, A. Physics-Informed Neural Network (PINN) Evolution and Beyond: A Systematic Literature Review and Bibliometric Analysis. Big Data Cogn. Comput. 2022, 6, 140. [Google Scholar] [CrossRef]
- Reyes, B.; Howard, A.A.; Perdikaris, P.; Tartakovsky, A.M. Learning unknown physics of non-Newtonian fluids. Phys. Rev. Fluids 2021, 6, 073301. [Google Scholar] [CrossRef]
- Liu, K.; Luo, K.; Cheng, Y.; Liu, A.; Li, H.; Fan, J.; Balachandar, S. Parameterized physics-informed neural networks (P-PINNs) solution of uniform flow over an arbitrarily spinning spherical particle. Int. J. Multiph. Flow 2024, 180, 104937. [Google Scholar] [CrossRef]
- Lu, D.; Christov, I.C. Physics-informed neural networks for understanding shear migration of particles in viscous flow. Int. J. Multiph. Flow 2023, 165, 104476. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, D.; Lu, Y. RheologyNet: A physics-informed neural network solution to evaluate the thixotropic properties of cementitious materials. Cem. Concr. Res. 2023, 168, 107157. [Google Scholar] [CrossRef]
- Banfill, P.F.G.; Kitching, D.R. 14 Use of a controlled stress rheometer to study the yield stress of oilwell cement. In Rheology of Fresh Cement and Concrete: Proceedings of an International Conference, Liverpool, 1990; CRC Press: London, UK, 1990; p. 125. [Google Scholar]
- Struble, L.; Sun, G.-K. Viscosity of Portland cement paste as a function of concentration. Adv. Cem. Based Mater. 1995, 2, 62–69. [Google Scholar] [CrossRef]
- Foroushan, H.K.; Ozbayoglu, E.M.; Miska, S.Z.; Yu, M.; Gomes, P.J. On the instability of the cement/fluid interface and fluid mixing. SPE Drill. Complet. 2018, 33, 63–76. [Google Scholar] [CrossRef]
- Skadsem, H.J.; Kragset, S.; Lund, B.; Ytrehus, J.D.; Taghipour, A. Annular displacement in a highly inclined irregular wellbore: Experimental and three-dimensional numerical simulations. J. Pet. Sci. Eng. 2019, 172, 998–1013. [Google Scholar] [CrossRef]
- Liu, L.; Fang, Z.; Qi, C.; Zhang, B.; Guo, L.; Song, K.-I. Numerical study on the pipe flow characteristics of the cemented paste backfill slurry considering hydration effects. Powder Technol. 2019, 343, 454–464. [Google Scholar] [CrossRef]
- Slattery, J.C. Advanced Transport Phenomena; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Probstein, R.F. Physicochemical Hydrodynamics: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Rivlin, R.S. Further Remarks on the Stress-Deformation Relations for Isotropic Materials. In Collected Papers of R.S. Rivlin; Barenblatt, G.I., Joseph, D.D., Eds.; Springer: New York, NY, USA, 1997; pp. 1014–1035. [Google Scholar] [CrossRef]
- Truesdell, C.; Noll, W. The Non-Linear Field Theories of Mechanics. In The Non-Linear Field Theories of Mechanics; Antman, S.S., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 1–579. [Google Scholar] [CrossRef]
- Massoudi, M.; Vaidya, A. On some generalizations of the second grade fluid model. Nonlinear Anal. Real World Appl. 2008, 9, 1169–1183. [Google Scholar] [CrossRef]
- Li, Y.; Wu, W.-T.; Liu, X.; Massoudi, M. The effects of particle concentration and various fluxes on the flow of a fluid-solid suspension. Appl. Math. Comput. 2019, 358, 151–160. [Google Scholar] [CrossRef]
- Phillips, R.J.; Armstrong, R.C.; Brown, R.A.; Graham, A.L.; Abbott, J.R. A constitutive equation for concentrated suspensions that accounts for shear-induced particle migration. Phys. Fluids Fluid Dyn. 1992, 4, 30–40. [Google Scholar] [CrossRef]
- Massoudi, M. Boundary conditions in mixture theory and in CFD applications of higher order models. Comput. Math. Appl. 2007, 53, 156–167. [Google Scholar] [CrossRef]
- Wu, W.-T.; Massoudi, M. Heat transfer and dissipation effects in the flow of a drilling fluid. Fluids 2016, 1, 4. [Google Scholar] [CrossRef]
- Miao, L.; Massoudi, M. Heat transfer analysis and flow of a slag-type fluid: Effects of variable thermal conductivity and viscosity. Int. J. Non-Linear Mech. 2015, 76, 8–19. [Google Scholar] [CrossRef]
- Gudhe, R.; Yalamanchili, R.C.; Massoudi, M. The flow of granular materials in a pipe: Numerical solutions. ASME Appl. Mech. Div.-Publ.-AMD 1993, 160, 41. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, H.; Ding, J.; Tao, C. A Physics-Informed Neural Network Solution for Rheological Modeling of Cement Slurries. Fluids 2025, 10, 184. https://doi.org/10.3390/fluids10070184
Yan H, Ding J, Tao C. A Physics-Informed Neural Network Solution for Rheological Modeling of Cement Slurries. Fluids. 2025; 10(7):184. https://doi.org/10.3390/fluids10070184
Chicago/Turabian StyleYan, Huaixiao, Jiannan Ding, and Chengcheng Tao. 2025. "A Physics-Informed Neural Network Solution for Rheological Modeling of Cement Slurries" Fluids 10, no. 7: 184. https://doi.org/10.3390/fluids10070184
APA StyleYan, H., Ding, J., & Tao, C. (2025). A Physics-Informed Neural Network Solution for Rheological Modeling of Cement Slurries. Fluids, 10(7), 184. https://doi.org/10.3390/fluids10070184







